Балка размеры: Слишком много запросов
Содержание
Балки стальные горячекатаные | Виды | Варианты исполнения
Двутавр стальной горячекатаный чаще именуемый Балка изготавливается на крупных сортовых станах методом горячей прокатки стальной горячекатаной заготовки. Балки предназначены преимущественно для сооружения перекрытий различной площади производственных и торговых помещений, многоэтажных гаражей и прочих крупных сооружений и строительных конструкций. Специальная форма Балки обеспечивает максимально высокую прочность при низком весе, что является определяющим параметром снижения стоимости строительной конструкции.
Балки с параллельными гранями полок, произведенные в соответствии с СТО АСЧМ 20-93 (ГОСТ 26020-83) в настоящее время являются наиболее востребованными по причине большей экономичности этих профилей в сравнении с двутаврами с уклоном внутренних граней, произведенных в соответствии с ГОСТ 8239-89.
|
H — высота профиля | ||
|
С уклоном внутренних граней |
С параллельными гранями | |
Доступные размеры балок (двутавров)
| № балки | ГОСТ 8639-89 | ГОСТ 19425-74 | ГОСТ 26020-83 | СТО АСЧМ 20-93 | |||||
| С | М | Б | Ш | К | Б | Ш | К | ||
| 10 | + | 1 | 1 | ||||||
| 12 | + | 1,2 | 1,2 | ||||||
| 14 | + | + | 1,2 | 1,2 | |||||
| 16 | + | 1,2 | 1,2 | ||||||
| 18 | + | + | 1,2 | 1,2 | |||||
| 20 | + | + | 1 | 1 | 1,2 | 1 | 1 | 1,2 | |
| 22 | + | + | |||||||
| 23 | 1 | 1 | 1,2 | ||||||
| 24 | + | + | |||||||
| 25 | 1,2 | 1 | 1,2,3 | ||||||
| 26 | 1,2 | 1,2 | 1,2,3 | ||||||
| 27 | + | + | |||||||
| 30 | + | + | 1,2 | 1,2,3 | 1,2,3 | 1,2 | 1,2 | 1,2,3,4 | |
| 33 | + | ||||||||
| 35 | 1,2 | 1,2,3 | 1,2,3 | 1,2 | 1,2 | 1,2 | |||
| 36 | + | + | + | ||||||
| 40 | + | 1,2 | 1,2,3 | 1,2,3,4 | 1,2 | 1,2 | 1,2,3,4 | ||
| 45 | + | + | 1,2 | 1,2 | 1 | ||||
| 50 | + | 1,2 | 1,2,3,4 | 1,2,3 | 1,2,3,4 | ||||
| 55 | + | 1,2 | 1,2 | ||||||
| 60 | + | 1,2 | 1,2,3,4 | 1,2 | 1,2,3,4 | ||||
| 70 | 1,2 | 1,2,3,4 | 1,2 | 1,2,3,4 | |||||
| 80 | 1,2 | 1,2 | |||||||
| 90 | 1,2 | 1,2 | |||||||
| 100 | 1,2,3,4 | 1,2,3,4 | |||||||
Требования по точности изготовления балок, произведенных по различным ГОСТ, отличаются незначительно.
Скорее всего, это объясняется тем фактом, что все стандарты разработаны и введены в течение 10 лет.
Основные отличия двутавров заключаются в уклоне внутренних граней полок и различных размерах. Кроме того, в ГОСТ 26020 и СТО АЧСМ 20 предусмотрено несколько вариантов исполнения одного профиля, что значительно расширяет возможности проектировщиков при расчете несущих конструкций. Так же к отличиям можно отнести разные взгляды на ширину полки некоторых профилей и толщину стойки (перемычки между полками).
Применение
Балки с уклоном внутренних граней полок — преимущественно используются малых и средних размеров, в случаях, когда требуется высокая прочность при малых габаритах.
Балки с параллельными гранями полок (обычные) — такие балки считаются «облегченными» в зависимости от типа их исполнения и применяются во всех остальных случаях.
Широкополочные балки — применяют при многоэтажном строительстве для перекрытий, в колонных и мостовых конструкциях (для сооружения пролетов между опорами).
Колонные балки — преимущественно применяются для сооружения колонн и опор в гражданском и промышленном строительстве, но могут быть использованы и в других конструкциях.
Специальные балки 14С, 20С, 22С, 27С, 36С — предназначены для армирования шахтных стволов.
Монорельсовые балки 24М, 36М, 45М — предназначены для сооружения подвесных путей.
Марки стали
В строительстве используются Балки из следующих видов стали:
Углеродистые — Ст3сп/пс
Низколегированные — 09Г2С
Двутавры из углеродистых марок преимущественно используют для организаций внутренних перекрытий (защищенных от погодных явлений). Двутавры из низколегированных марок, в частности 09Г2С, чаще используются для сооружения наружных конструкций, а так же конструкций с повышенными требованиями к прочности, например для сооружения сильно нагружаемых конструкций.
Упаковка, маркировка, транспортировка, хранение
Большинство балок не упаковывают в связки (пачки) по причине большого веса каждого изделия.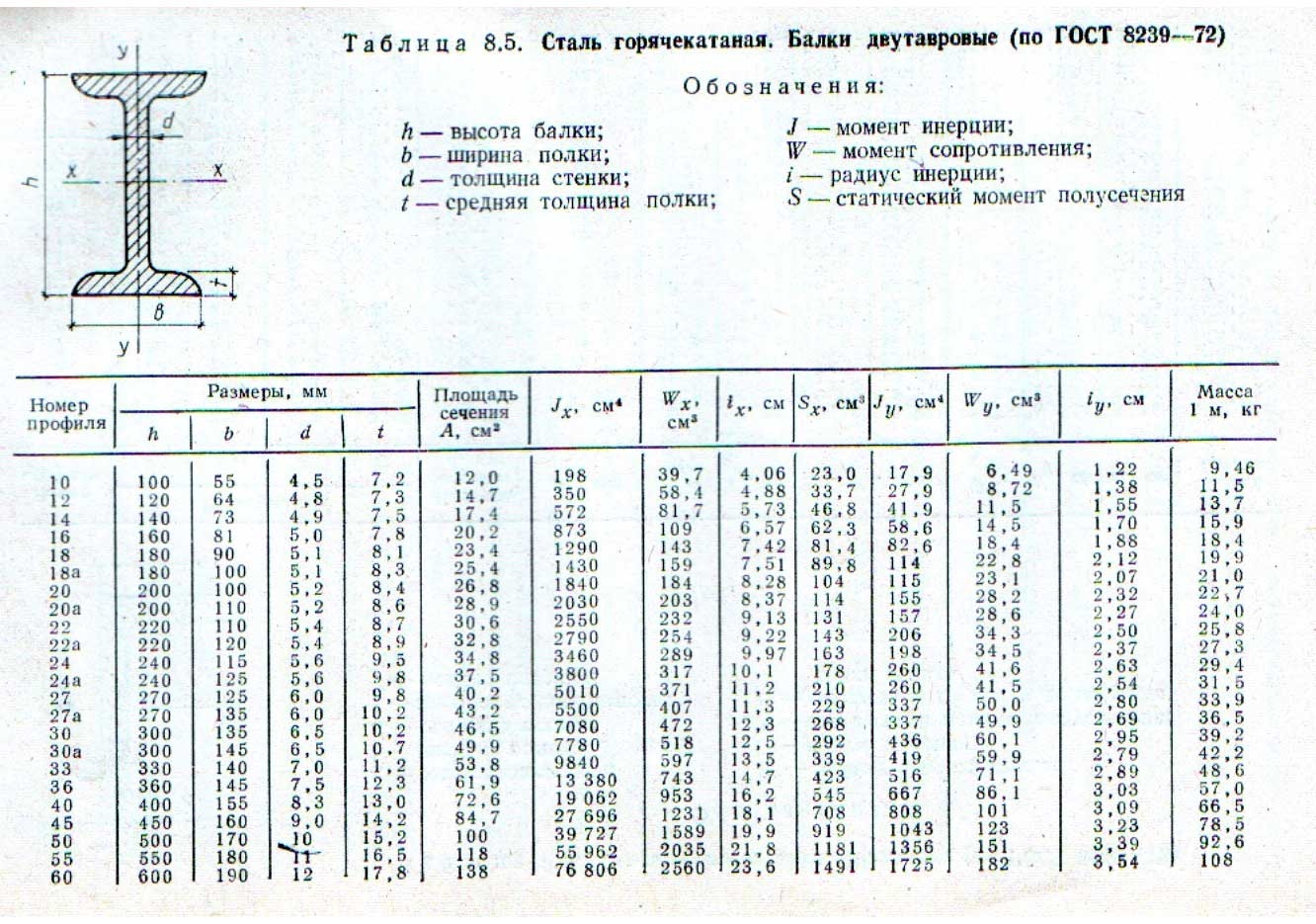
Маркировка балок производится краской на торцах изделий различными цветами или комбинацией из двух цветов, что позволяет визуально отличать балки из различных марок стали.
Транспортировка двутавров производится в открытых транспортных средствах, «навалом», обычно без применения дополнительных средств упаковки и крепления груза.
Балку хранят на открытых площадках, с твердой поверхностью, приспособленных для хранения металлопроката.
Размеры двутавровой балки из стали — Knoll Steel Inc. 19
900 06 8 1/8
9 0006 11 1/8
90 006 14
90 006 10
9001 2
9000 6 11 1/4
9 0790
Как рассчитать размеры деревянных балок
Последнее обновление: 8 ноября 2022 г.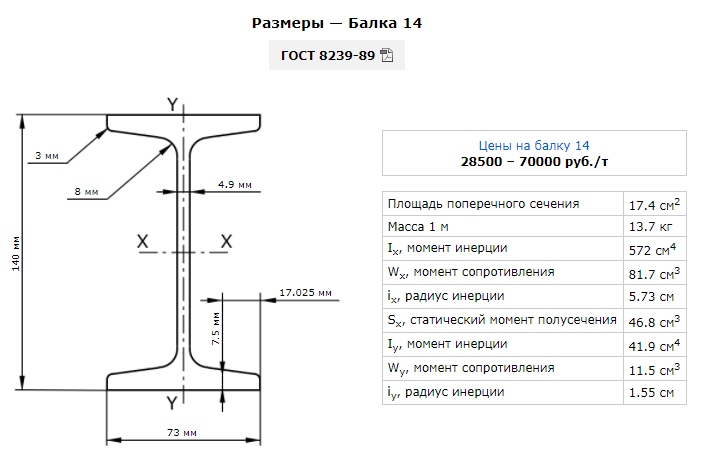
После того, как мы рассмотрели все необходимые основы, мы наконец можем определить размеры деревянной балки. Если вы не читали посты о Статических системах деревянных крыш, Нагрузках и Комбинациях нагрузок, я рекомендую вам взглянуть, прежде чем начать читать этот пост в блоге.
Во-первых: что мы имеем в виду, когда измеряем или измеряем балку ?
Для расчета размеров/размеров деревянных балок необходимо выполнить расчеты как ULS (предельное состояние), так и SLS (предельное состояние эксплуатационной пригодности). В конструкции ULS размеры деревянной балки определяются по предельным напряжениям изгиба и сдвига деревянного материала. В конструкции SLS деревянная балка проверяется на предмет непревышения предела прогиба.
Я знаю, что все это звучит довольно сложно🤔 но не волнуйтесь, мы объясним это на практических примерах и картинках. Позвольте мне объяснить вам шаги, которые мы должны сделать, чтобы измерить балку.
Давайте рассмотрим шаги, которые нам нужно выполнить. Вы можете увидеть их визуально на следующем рисунке.
- Выберите статическую систему, например, свободно опертую балку
- Рассчитайте все типичные нагрузки (постоянные, снеговые, ветровые, динамические нагрузки и т. д.)
- Рассчитайте все комбинации нагрузок
- Выберите древесный материал и найдите свойства материала ($k_{mod}$, $f_{c.0.k}$, $f_{m.k}$, $\gamma_{M}$)
- Примем ширину w и высоту h поперечного сечения
- Проверьте балку на изгиб. Если не проверено, увеличьте ширину или высоту балки и повторите расчет
- Проверьте балку на сдвиг. Если не проверено, увеличьте ширину или высоту балки и повторите расчет
- Проверьте балку на соответствие критерию мгновенного отклонения. Если не проверено, увеличьте ширину или высоту балки и повторите расчет
- Проверьте балку на окончательные критерии прогиба. Если не проверено, увеличьте ширину или высоту балки и повторите расчет
- Если все эти проверки выполнены, значит, вы определили правильные размеры балки.
Рецепт для определения размеров деревянной балки
Мы рассмотрим свободно опертую балку, которая используется в плоской крыше.
Статическая система свободно опертой балки может быть визуализирована, как на следующем рисунке. Он состоит из одного ролика (воспринимает вертикальную силу V2) и одной шарнирной опоры (воспринимает вертикальную V1 и горизонтальную силу h2).
Статическая система | Просто поддерживаемая балка.
Чтобы сохранить контекст, эта свободно опертая балка может быть второстепенной балкой в плоской крыше.
Плоская крыша 3D
Теперь, когда мы визуализируем второстепенные балки (пунктирные на рисунке) в 2D разрезе, мы можем легко сравнить их со статической системой.
Статическая система второстепенных балок
В этом посте вы можете узнать больше о различных типах деревянных крыш и о том, как работают их статические системы.
Нагрузки
Мы будем использовать нагрузки, которые мы предполагали в нашем блоге о сочетаниях нагрузок.
Если вы хотите узнать больше о различных типах нагрузок, что они собой представляют и как их применять, вы можете прочитать это в этом посте.
| $g_{k}$ | 1,08 кН/ м2 | Нормативное значение статической нагрузки |
| $q_{k}$ | 1,0 кН/м2 | Нормативное значение динамической нагрузки |
| $s_{k}$ | 1,0 кН/м2 | Нормативное значение снеговой нагрузки |
| $w_{k}$ 90 007 | -1,0 кН/м2 | Характеристика значение ветровой нагрузки 92}$ |
Материал балки
Во-первых, проектировщику необходимо выбрать между конструкционной древесиной и инженерной древесиной, такой как Glulam (клееный брус) или LVL (ламинированный шпон).
Выбор дизайнера зависит от проекта, пролетов, стоимости и личного вкуса.
Итак, для нашего примера балки мы используем конструкционную древесину C24.
Теперь нам нужно найти свойства этой древесины, и мы можем найти их либо в Еврокоде, либо найти производителя в Интернете, у которого есть таблицы его изделий из древесины. 92}$
Коэффициент модификации $k_{mod}$
Коэффициент модификации $k_{mod}$ учитывает влияние влажности и продолжительности нагрузки на свойства древесины .
Этот коэффициент будет использоваться для расчета расчетных напряжений в деревянных элементах.
Содержание влаги подразделяется на 3 категории или так называемые классы обслуживания.
Эти классы эксплуатации показывают, насколько деревянный элемент подвергается воздействию влаги, а это означает, что элемент, подвергающийся воздействию дождя, может быть отнесен к классу эксплуатации 3, а элемент внутри здания может быть отнесен к классу эксплуатации 1.
Подробное описание можно найти в EN 1995-1-1 2.3.1.3.
Классы длительности нагрузки показывают, как долго нагрузка действует на конструкцию, поскольку чем дольше нагрузка, тем сильнее ухудшаются свойства древесины.
Статическая нагрузка, например, действует на конструкцию постоянно, в то время как ветровая нагрузка действует только в течение короткого времени и поэтому может быть классифицирована как мгновенная нагрузка.
Классы длительности нагрузки можно найти в таблице 2.2 стандарта EN 1995-1-1.
Теперь в нашем случае мы предполагаем, что проектируем плоскую крышу жилого дома. Балки не подвержены влиянию погодных условий. Поэтому у нас есть Класс обслуживания 1 .
Кроме того, мы также можем определить продолжительность нагрузок, действующих на нашу плоскую крышу, в соответствии с таблицей 2.2 стандарта EN 1995-1-1.
| Собственная/собственная нагрузка | Постоянная |
| Постоянная нагрузка, снеговая нагрузка | Среднесрочная |
| ветряная нагрузка | Мгновенный |
Теперь мы можем найти значения $ k_ {mod} $ для конструкционной древесины C24 (сплошная древесина) и наши различные нагрузки в соответствии с En 1995-1-1-1-1-1
| $k_{mod}$ | |||
|---|---|---|---|
| Собственный вес/собственная нагрузка | Постоянное действие | 0,6 | |
| Постоянная нагрузка, снеговая нагрузка | Среднесрочная действие | Класс эксплуатации 1 | 0,8 |
| Ветровая нагрузка | Мгновенное действие | Класс эксплуатации 1 | 1,1 |
Частный множитель
Частный множитель $\gamma_{M}$ учитывает свойства материала в УЛС.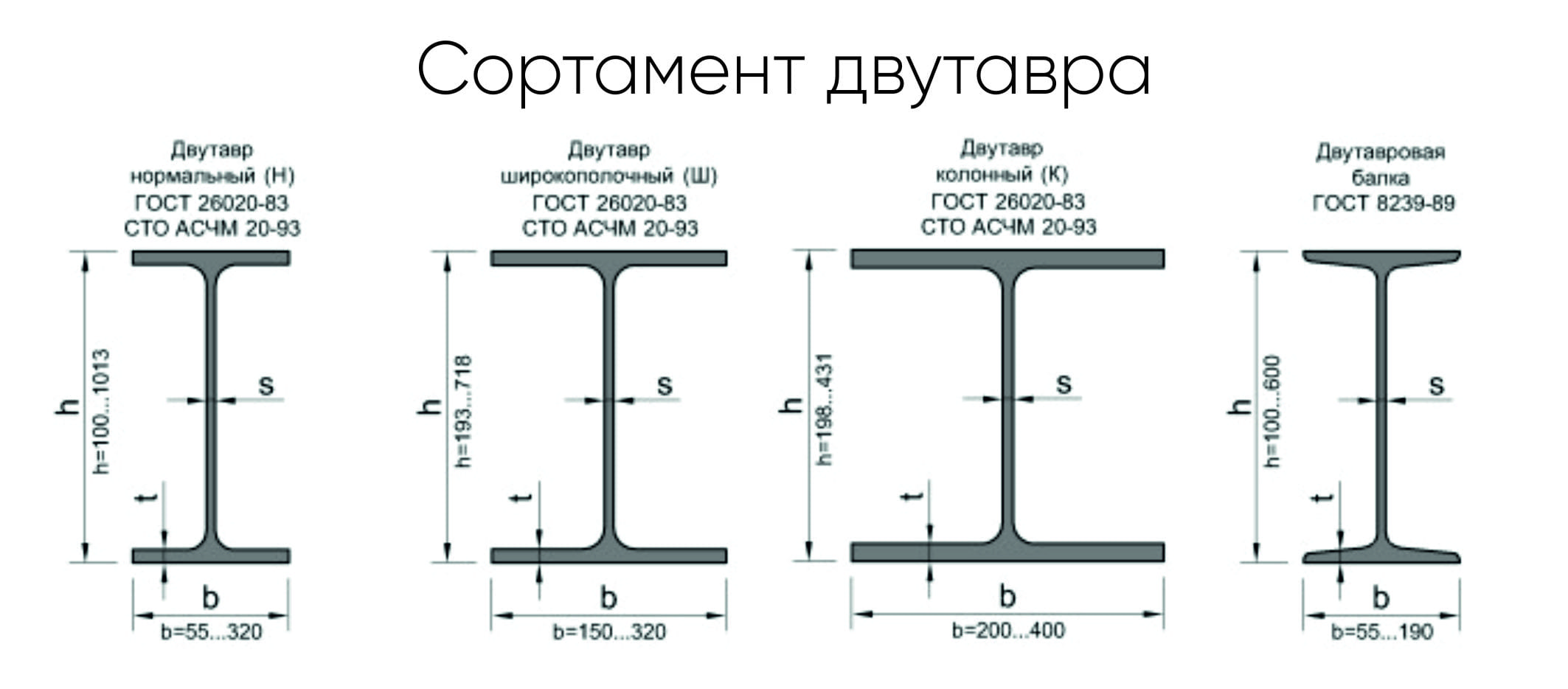
EN 1995-1-1 Таблица 2.3 представляет рекомендуемые частные коэффициенты.
В нашем случае для массивной древесины мы получаем частный коэффициент
$\gamma_{M} = 1,3$
Допущение ширины и высоты балки
Прежде чем мы наконец сможем приступить к проектированию балки, нам нужно определить ширину и высоту поперечного сечения балки. Это основано на опыте дизайнера.
Ознакомьтесь с этой статьей, чтобы оцифровать свои ручные вычисления.
Ширина w = 80 мм
Высота h = 240 мм
Ширина + высота поперечного сечения балки
Зная высоту и ширину поперечного сечения, мы можем рассчитать момент инерции прочной оси, необходимый для рассчитать напряжение из-за изгиба. 92} * 0,8 м $
Теперь эти линейные нагрузки можно применить к нашей статической системе. В качестве примера применим нагрузку LC1.
Изгиб
Из 3 основных комбинаций нагрузок LC1, LC3 и LC5 мы можем рассчитать наиболее критический изгибающий момент.
2}{8}$ 94} * \frac{0,24m}{2} $
Последний шаг, прежде чем мы сможем проверить, может ли поперечное сечение выдержать нагрузки, — это расчет напряжения сопротивления древесины. материал.
$ f_{m.d} = k_{mod} * \frac{f_{m.k}}{\gamma_{m}} $
| LC1 (P-действие) | $k_{mod.P} * \frac{f_{m.k}}{\gamma_{m}} $ | $0,6 * \frac{24 МПа}{1,3} $ | $11,1 МПа $ |
| LC3 (L-действие) | $k_{mod.L} * \frac{f_{m.k}}{\gamma_{m}} $ | $0,8 * \frac{24 МПа}{1,3} $ | $14,77 МПа $ |
| LC5 (I-действие) | $k_{mod.I} * \frac{f_{m.k}}{\gamma_{m}} $ | $1,1 * \frac{24 МПа}{1,3} $ | $20,31 МПа $ |
Наконец, мы можем рассчитать использование поперечного сечения в его наиболее критической точке.
$\eta = \frac{\sigma}{f_{m.d}}$
| LC1 (P-действие) | $\frac{\sigma. P}{f_{m.d.P}} $ | $\frac{4,76 МПа}{11,1 МПа} $ | $ 0,43 $ |
| LC3 (L-действие) | $\frac{13 МПа}{14,77 МПа} $ | $ 0,88 $ | |
| LC5 (I-воздействие) | $\frac{ \sigma.I}{f_{m.d.I}} $ | $\frac{10,1 МПа}{20,31 МПа} $ | $ 0,5 $ |
Сдвиг
9000 2 То же, что и при изгибе от 3 основных сочетаний нагрузок LC1, LC3 и LC5 мы можем продолжить и рассчитать наиболее критическую силу сдвига. Самая высокая сила сдвига в свободно опертая балка находится рядом с двумя опорами и может быть рассчитана по следующей формуле:
$V_{d} = q * \frac{L}{2}$
приложенная нагрузка на балку
Это приводит к следующим силам сдвига из-за LC1, LC3 и LC5
| LC1 (P-действие) | $1,17 \frac{kN }{ м} * \frac{5m}{2} $ | $ 2,93 кН $ |
| LC3 (L-образное действие) | $3,2 \frac{кН}{м} * \frac{5м}{2} $ | $8 кН $ |
| LC5 (I-действие) | $2,48 \frac{кН}{м} * \frac {5 м}{2} $ | $ 6,2 кН $ |
По поперечным силам можно рассчитать напряжение в наиболее критическом поперечном сечении (около опоры свободно опертой балки).
$\tau = \frac{3}{2} * \frac{V_{d}}{w * h} $
| LC1 (P-действие) | $\frac{3}{2 } * \frac{2,93 кН}{0,08 м * 0,24 м} $ | $0,23 МПа $ |
| LC3 (L-действие) | $\frac{3}{2} * \frac{8 кН}{0,08м * 0,24м} $ | $0,63 МПа $ |
| LC5 (I-действие) | $\frac{3}{2} * \frac{6,2 кН}{0,08 м * 0,24 м} $ | $0,48 МПа $ |
Последний шаг перед проверкой выдерживает ли поперечное сечение нагрузки, рассчитывается сопротивление сдвигу деревянного материала.
$f_{v.d} = k_{mod} * \frac{f_{v.k}}{\gamma_{m}}$
| LC1 (P-действие) | $k_{mod.P} * \frac{f_{v.k}}{\gamma_{m}} $ | $0,6 * \frac{4 МПа}{1,3} $ | $1,85 МПа $ |
| LC3 (L-действие) | $k_{mod.L} * \frac{f_{v.k}}{\gamma_{m}} $ | $0,8 * \frac{4 МПа}{1,3} $ | $2,46 МПа $ |
| LC5 (I-действие) | $k_{mod. I} * \frac{f_{v.k}}{\gamma_{m}} $ | $1,1 * \frac{4 МПа}{1,3} $ | $ 3,39 МПа $ |
Наконец, мы можем рассчитать использование поперечного сечения в его наиболее критической точке.
$\eta = \frac{\tau}{f_{v.d.}}$
| LC1 (P-действие) | $\frac{\tau.P}{f_{v.d.P}} $ | $\frac{0,23 МПа}{1,85 МПа} $ | $ 0,124 $ |
| LC3 (L-действие) | $\frac{\tau.L}{f_{v.d.L}} $ | $\frac {0,63 МПа}{2,46 МПа} $ | $ 0,25 $ |
| LC5 (I-действие) | $\frac{\tau.I}{f_{vdI}} $ | $\frac{0,48 МПа}{3,39 МПа} $ | $ 0,14 $ |
Прогиб 9 0900
Прежде чем мы начнем расчет все, что нам нужно, чтобы определить несколько переменных из EN 1995-1-1. деформация ползучести
fin}$ — конечная деформация нетто: $w_{inst} + w_ {ползучесть} – w_{c}$EN 1995-1-1 Таблица 7.2 рекомендует значения для $w_{inst}, w_{net.fin}$ и $w_{fin}$, которые не должны превышаться для свободно опертой балки .
| $w_{inst}$ | $w_{net.fin}$ | $w_{fin}$ |
| $L/300$ до $L/500$ 9000 7 | $L/250 $ до $L/350 $ | $L/150$ до $L/300 $ |
При длине балки (пролете) L=5м мы получаем следующие значения.
| $w_{inst}$ | $w_{net.fin}$ | $w_{fin}$ |
| от 16,67 мм до 10 мм | от 20 мм до 14,3 мм |
Мгновенная деформация $u_{inst}$
$u_{inst}$ (мгновенная деформация) нашей балки может быть рассчитана с нагрузкой характеристического сочетания нагрузок.
