Центр тяжести швеллера и двутавра: Геометрические характеристики плоского поперечного сечения 4 элемента (полоса, двутавр, швеллер уголок) 020
Содержание
Геометрические характеристики плоского поперечного сечения 4 элемента (полоса, двутавр, швеллер уголок) 020
|
|
|
1) Выписываем из таблицы сортамента (ГОСТ 8240-72, ГОСТ 8239-72 и ГОСТ 8509-86) необходимые геометрические характеристики для швеллера, двутавра, уголка и вычисляем по формулам прямоугольника:
а) Полоса (прямоугольник) 300Х24
|
см 2, см 4, см 4, |
б) Швеллер №20
|
см 2, см 4, см 4, см, |
в) Двутавр №24
|
см 2, см 4, см 4, см, |
г) Уголок 140Х9
|
см 2, см 4, см 4, см 4, |
2) Определяем положение центра тяжести сечения относительно начальных осей (осей полосы)
На отдельном листе бумаги в масштабе чертим схему поперечного сечения (рис. 2) и указываем положение центральных осей каждого элемента. Выполняем привязку (указываем расстояния) центров тяжести каждого элемента относительно начальных осей
Координаты центров тяжести элементов в осях
см,
см,
см,
см,
см,
см.
Рис. 2
Площадь поперечного сечения:
см 2,
Координаты центра тяжести сечения:
см,
см.
Откладываем на рисунке координаты и с учетом знаков, обозначаем положение центра тяжести (точка С) и проводим центральные оси
Контролируем достоверность определения положения центра тяжести сложного сечения. Для этого вычисляем координаты центров тяжести элементов сечения в координатных осях и (расстояния между собственными центральными осями отдельных элементов и центральными осями сечения):
|
|
|
и статические моменты площади сечения относительно центральных осей:
см 3,
погрешность:
см 3,
погрешность:
3) На основании формул параллельного перехода вычисляем моменты инерции сечения относительно центральных осей и
— осевые
см 4,
см 4,
— центробежный
см 4.
Понравилась статья! Поддержи проект! Ставь ЛАЙК!
задачи с решением центр тяжести двутавр и швеллер, инфа по теме задачи с решением центр тяжести двутавр и швеллер
|
Что такое центр сдвига — расположение центра сдвига с примерами
🕑 Время чтения: 1 минута
Центр сдвига — это точка на сечении балки, в которой приложение нагрузок не вызывает ее скручивания. Положение центра сдвига зависит от поперечного сечения балки. Например, центр сдвига и центр тяжести совпадают в симметричном сечении, но могут не совпадать с центром тяжести в случае несимметричного сечения.
Положение центра сдвига зависит от поперечного сечения балки. Например, центр сдвига и центр тяжести совпадают в симметричном сечении, но могут не совпадать с центром тяжести в случае несимметричного сечения.
Так, в несимметричных поперечных сечениях внешние силы должны проходить через центр сдвига, а не через центр тяжести сечения, иначе создаваемый изгибающий момент будет сопровождаться скручиванием.
Как вычислить положение центра сдвига?
Рассмотрим сечение канала, как показано на рис. 1. Теперь мы найдем положение плоскости, через которую должны действовать вертикальные нагрузки, чтобы вызвать простой изгиб, с осью x в качестве нейтральной оси.
Рис. 1: Секция швеллера
Можно предположить, что вертикальная сила сдвига F в секции воспринимается только стенкой. Во фланцах будут горизонтальные напряжения сдвига, которые обозначаются как q .
Рассмотрим элемент ‘ abcd ‘, вырезанный из нижней полки двумя соседними поперечными сечениями (дельта z) друг от друга и вертикальной плоскостью, параллельной стенке, на расстоянии ‘ u ‘ (которое является переменным ) от свободного конца нижнего фланца.
Разница в растягивающих усилиях T и T+Delta z должна быть равна поперечной силе на стороне « ad » элемента. Предполагая равномерное распределение касательного напряжения (поскольку толщина мала) по толщине, имеем:
Интегрирование выполняется по части «ab» фланца. Напряжение на единицу длины центральной линии сечения:
Отсюда видно, что q пропорционально u . Максимальное значение q :
На стыке полки и стенки распределение касательного напряжения усложняется, поэтому можно считать, что уравнение 4 справедливо для u = 0 и u = b.
Предположим, что вертикальная поперечная сила F действует через точку ‘ o ’, центр сдвига на расстоянии с от О на осевой линии стенки. Скручивания этой секции можно избежать, если:
указывает положение центра сдвига.
Примечание: Центр сдвига для площадей поперечного сечения, имеющих одну ось симметрии, всегда располагается на оси симметрии. В случае двутавровой балки, симметричной как относительно оси x, так и оси y, центр сдвига совпадает с центром тяжести сечения. Точное расположение центра сдвига для несимметричных сечений сложно и может быть определено осмотром.
В случае двутавровой балки, симметричной как относительно оси x, так и оси y, центр сдвига совпадает с центром тяжести сечения. Точное расположение центра сдвига для несимметричных сечений сложно и может быть определено осмотром.
Пример:
Найдите центр сдвига несимметричного поперечного сечения двутавровой балки, как показано на рисунке ниже:
Здесь,
Принятие момента относительно точки D:
Подробнее: Что такое Стена сдвига?- Ее типы и расположение в зданиях
Момент инерции секции канала
Перейти к
— Калькулятор
— Определения
Содержание
— Калькулятор
— Определения
20003
-Параллельные оси теорема
-Повернутые оси
-Основные оси
-Размеры
-Массовый момент инерции
-Применение
Поделитесь этим
См. Также
МОМО
— Д-р Минас Э. Лемонис, доктор философии — Обновлено: 2 мая 2020 г.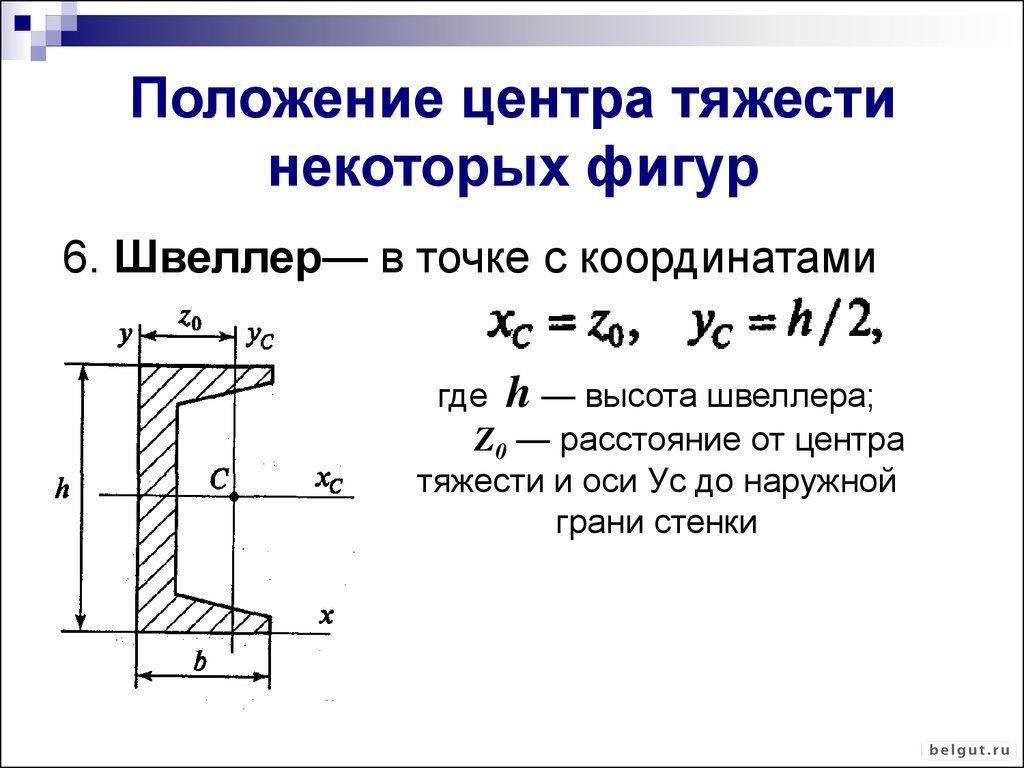 раздел. Фланцы предполагаются равными. Введите размеры формы «h», «b», «t» f ‘и ‘t w ‘ ниже. Вычисленные результаты будут иметь те же единицы измерения, что и введенные вами. Пожалуйста, используйте согласованные единицы для любых входных данных.
раздел. Фланцы предполагаются равными. Введите размеры формы «h», «b», «t» f ‘и ‘t w ‘ ниже. Вычисленные результаты будут иметь те же единицы измерения, что и введенные вами. Пожалуйста, используйте согласованные единицы для любых входных данных.
h = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
b = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
t f = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
t w = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Результаты: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Ищете другую ось?
ADVERTISEMENT |
ADVERTISEMENT
Table of Contents
— Calculator
— Definitions
— Parallel Axes Theorem
— Rotated axes
— Principal оси
— Размеры
— Момент инерции масс
— Приложения
Поделитесь этим
Определения
Момент инерции секции канала можно найти, если разделить общую площадь на три меньшие, A, B, C, как показано на рисунке ниже.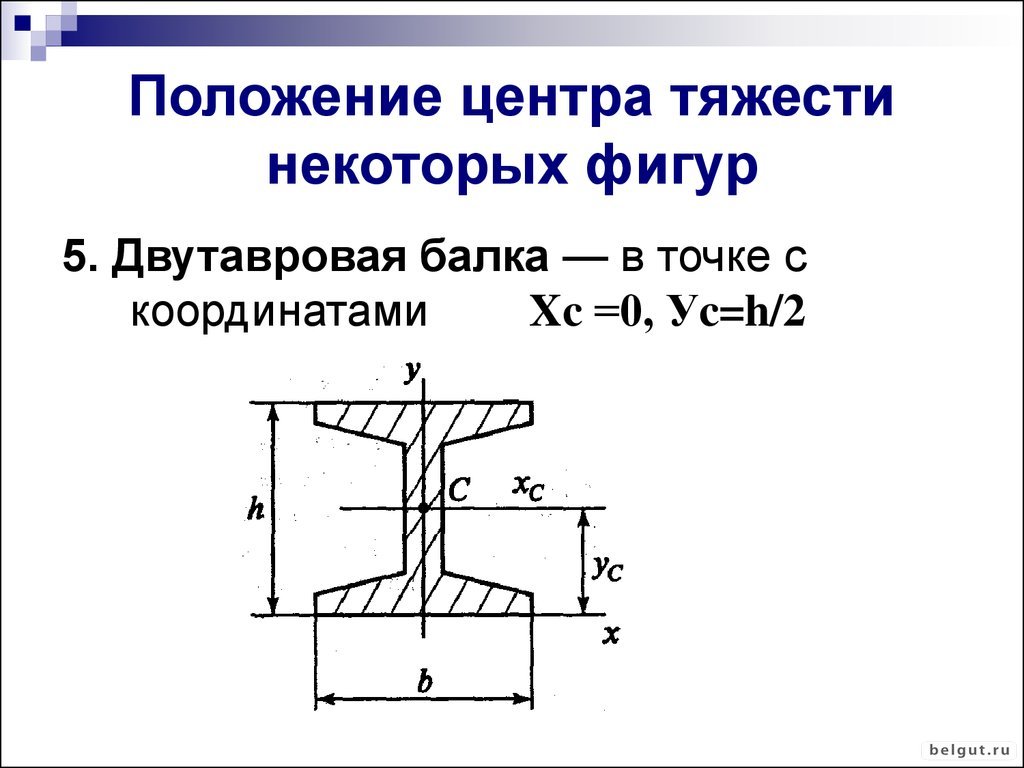 Конечную область можно рассматривать как аддитивную комбинацию A+B+C. Однако, поскольку фланцы равны, более простой комбинацией может быть (A+B+C+V)-V. Следовательно, момент инерции I х сечения канала относительно центральной оси х-х определяется так: 92
Конечную область можно рассматривать как аддитивную комбинацию A+B+C. Однако, поскольку фланцы равны, более простой комбинацией может быть (A+B+C+V)-V. Следовательно, момент инерции I х сечения канала относительно центральной оси х-х определяется так: 92
где I’ — момент инерции относительно произвольной оси, I — момент инерции относительно центральной оси, параллельной первой, d — расстояние между двумя параллельными осями и A — площадь форма, равная 2b t_f + (h-2t_f)t_w , в случае швеллера с равными полками.
Для произведения инерции Ixy теорема о параллельных осях принимает аналогичную форму:
I_{xy’} = I_{xy} + A d_{x}d_{y}
относительно центроидальных осей x,y (=0 для канала из-за симметрии), а Ixy’ — произведение инерции относительно осей, параллельных центроидальным x,y, имеющих смещения от них d_{x} и d_{y} соответственно.
Повернутые оси
Для преобразования моментов инерции от одной системы осей x,y к другой u,v, повернутой на угол φ, используются следующие уравнения:
\begin{split} I_u & = \frac{I_x+I_y}{2} + \frac{I_x-I_y}{2} \cos{2\varphi} -I_{xy} \sin{2\varphi} \\ I_v & = \frac{I_x +I_y}{2} — \frac{I_x-I_y}{2} \cos{2\varphi} +I_{xy} \sin{2\varphi} \\ I_{uv} & = \frac{I_x-I_y }{2} \sin{2\varphi} +I_{xy} \cos{2\varphi} \end{split}
где Ix, Iy — моменты инерции относительно начальных осей, а Ixy — произведение инерции.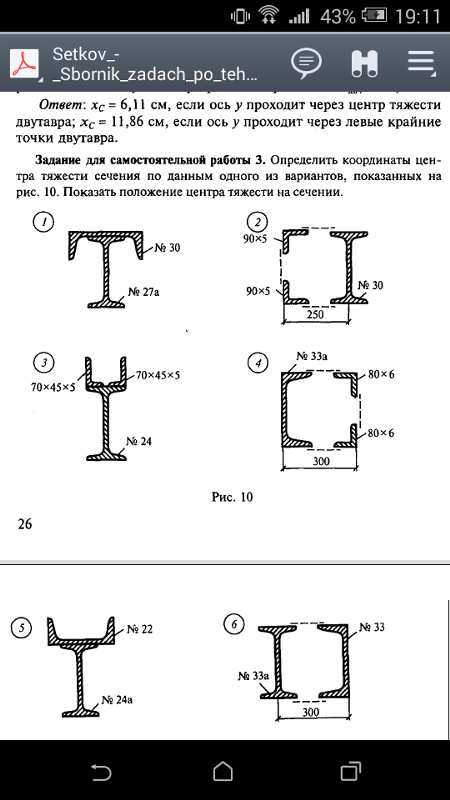 Iu, Iv и Iuv – соответствующие величины для вращающихся осей u,v. Произведение инерции Ixy канала с равными полками относительно центральных осей x,y равно нулю, поскольку x является осями симметрии.
Iu, Iv и Iuv – соответствующие величины для вращающихся осей u,v. Произведение инерции Ixy канала с равными полками относительно центральных осей x,y равно нулю, поскольку x является осями симметрии.
Главные оси
В главных осях, повернутых на угол θ относительно исходных центроидальных осей x,y, произведение инерции становится равным нулю. Из-за этого любая ось симметрии формы также является главной осью. Моменты инерции относительно главных осей I_I, I_{II} называются главными моментами инерции и являются максимальным и минимальным для любого угла поворота системы координат. Для канала с одинаковыми полками x является осью симметрии, и, следовательно, x, y определяют главные оси формы. В результате Ix и Iy являются главными моментами инерции. 94 .
Массовый момент инерции
В физике термин момент инерции имеет другое значение. Это связано с распределением массы объекта (или нескольких объектов) вокруг оси. Это отличается от определения, которое обычно дается в инженерных дисциплинах (также на этой странице) как свойство площади формы, обычно поперечного сечения, вокруг оси.


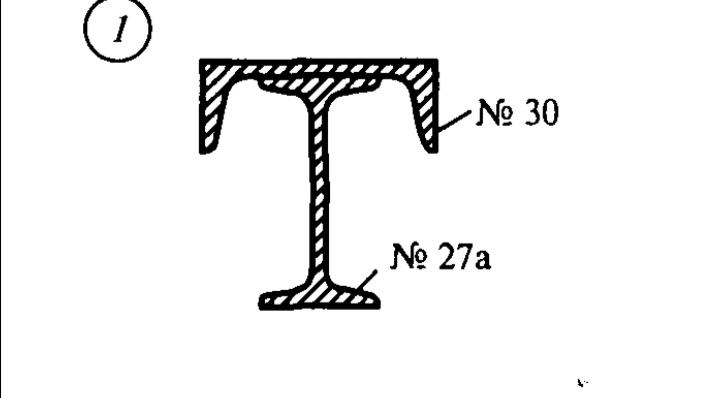
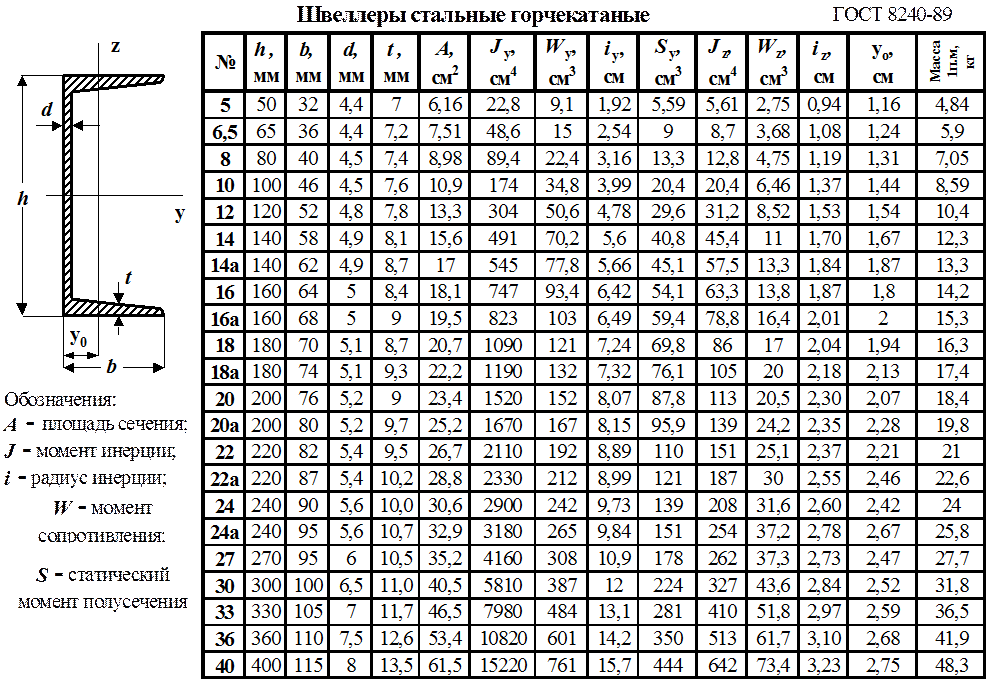
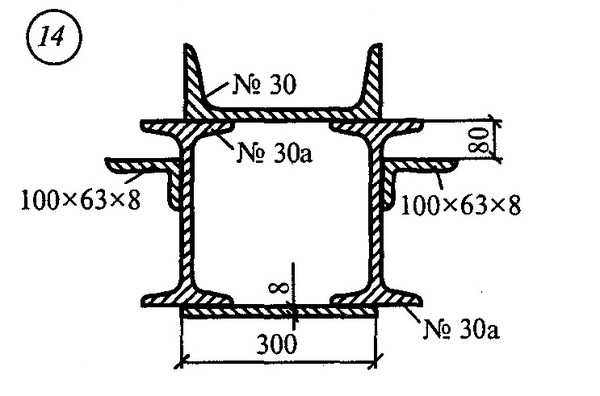 Изобразим сечение в масштабе, укажем центры тяжести …
Изобразим сечение в масштабе, укажем центры тяжести …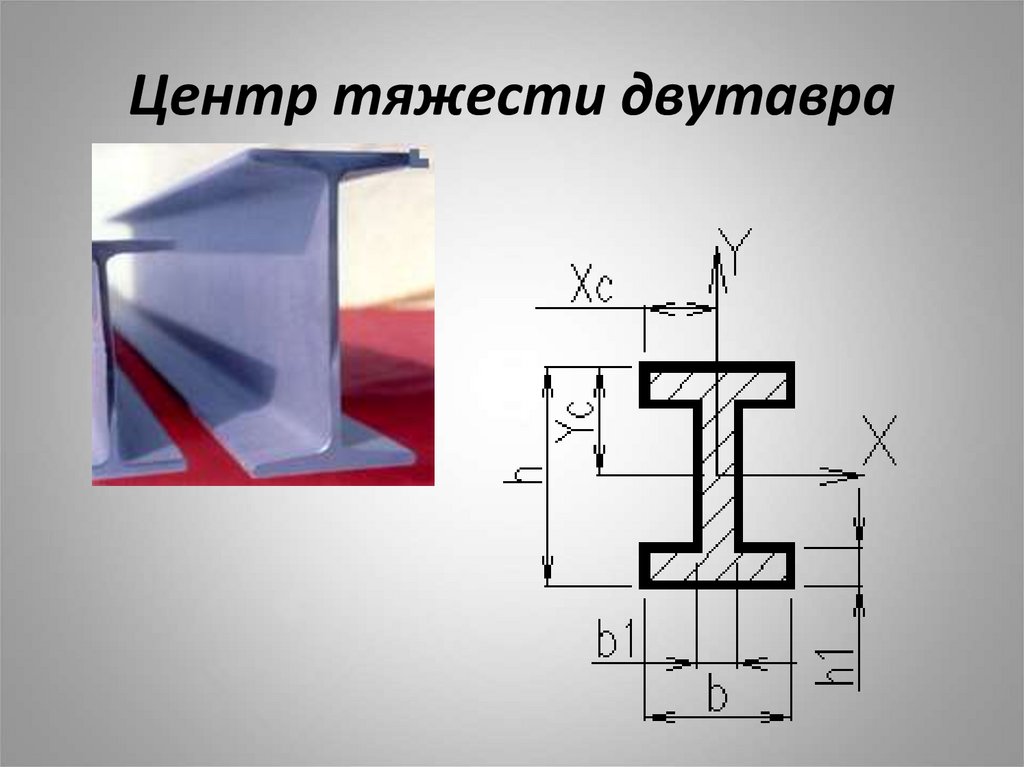 .. Условие задачи: Для заданной схемы сечения требуется определить координаты центра тяжести, … Сечение указано в таблице. Задача 9. Решение .. …
.. Условие задачи: Для заданной схемы сечения требуется определить координаты центра тяжести, … Сечение указано в таблице. Задача 9. Решение .. …