Двутавр нагрузка на изгиб калькулятор: Расчёт металлической балки онлайн (калькулятор)
Содержание
Онлайн калькулятор расчет стойки из швеллера, двутавра, тавра и уголка на прочность, устойчивость и допустимую гибкость
Главная » Онлайн калькуляторы
На чтение 2 мин. Просмотров 9.7k. Обновлено
Калькулятор предназначен для расчёта центрально-нагруженных стоек (колонн) из горячекатаного и другого проката следующей номенклатуры:
- Уголка равнополочного;
- Уголка неравнополочного;
- Швеллера с уклоном и с параллельными гранями полок;
- Двутавров с уклоном полок и с параллельными гранями полок различных модификаций, а также тавровых балок (тавров).
Предлагаем воспользоваться онлайн калькулятором для расчета массы швеллера
| Вид проката Уголок равнополочныйУголок неравнополочныйШвеллер с уклоном полокШвеллер с паралельными гранями полокДвутавр с уклоном полокДвутавр с паралел. гранями полок нормальныйДвутавр с паралел.  гранями полок широкопол.Двутавр с паралел. гранями полок колнныйДвутавр с паралел. гранями полок доп.сери(Д)Тавр с паралелными гранями полок нормальныйТавр с паралел. гранями полок широкополочныйТавр с паралелными гранями полок колнный гранями полок широкопол.Двутавр с паралел. гранями полок колнныйДвутавр с паралел. гранями полок доп.сери(Д)Тавр с паралелными гранями полок нормальныйТавр с паралел. гранями полок широкополочныйТавр с паралелными гранями полок колнный | |||||||||||||||
| Вид и назначение стоек (колонн) Стойки и раскосы передаюшие реакции опорОсновные колонныВторостепенные колонны | |||||||||||||||
| Сталь С235 (Ст3кп2)Сталь С245 (Ст3пс5,Ст3сп5)Сталь С255 (СтГпс,Ст3Гсп)Сталь С285 (Ст3сп,Ст3Гпс,Ст3Гсп)Сталь С345 (12Г2С,09Г2С)Сталь С345К (10ХНДП)Сталь С375 (12Г2С)Сталь С390 (14Г2АФ)Сталь С390Д (14Г2АФД)Сталь С440 (16ГАФ)Сталь С590 (12Г2СМФ) | ||
Если Вашего материала нет в таблице, но Вам известно его расчётное сопротивление, введите его значение в это поле (кг/см2):
| РАЗМЕРЫ ВЫБРАННОГО ПРОФИЛЯ: |
Выберите схему крепления стойки
| Заделка-консоль Заделка-заделка Заделка-шарнир Шарнир-шарнир |
Введите параметры для расчёта
| Длина стойки L, м : | Нагрузка P, кг : |
Размеры проката углового профиля оговариваются ГОСТ 8509-93 и ГОСТ 8510-86; швеллеров ГОСТ 8240-97; двутавров ГОСТ 26020-83; тавров — ТУ 14-2-685-86; (получаемых продольной разрезкой пополам горячекатаных двутавров с параллельными гранями полок по ГОСТ 26020-83).
При проектировании строительных конструкций необходимо принимать схемы, обеспечивающие прочность, устойчивость и пространственную неизменяемость сооружения в целом, а также его отдельных элементов при монтаже и эксплуатации.
Поэтому стойку,находящуюся под действием сжимающей её нагрузки необходимо проверять:
- на прочность;
- устойчивость;
- допустимую гибкость.
Согласно Актуализированной редакция СНиП II-23-81 (CП16.13330, 2011) расчет на прочность элементов из стали при центральном растяжении или сжатии силой P следует выполнять по формуле:
P/Fp*Ry*Yc <= 1, где
- P — действующая нагрузка,
- Fp — плошадь поперечного сечения стойки,
- Ry — расчётное сопротивление материала (стали стойки), выбирается по таблице В5 Приложения «В» того же СНиПа;
- Yc — коэффициент условий работы по таблице 1 СНиПа (0.9-1.1). В соответствии с примечанием к этой таблице (пункт 5) в калькуляторе принято Yc=1.

Проверку на устойчивость элементов сплошного сечения при центральном сжатии силой P следует выполнять по формуле:
P / Fi*Fp*Ry*Yc <= 1, где
Fi — коэффициент продольного изгиба центрально-сжатых элементов.
Коэффициент Fi введён в расчёт в качестве компенсации возможности некоторой не прямолинейности стойки, недостаточной жесткости её крепления и неточности в приложении нагрузки относительно оси стойки. Значение Fi зависит от марки стали и гибкости колонны и часто берётся из таблицы 72 СНиП II-23-81 1990г. исходя из гибкости стойки и расчётного сопротивления выбранной стали сжатию, растяжению и изгибу.
Это несколько упрощает и огрубляет расчёт, так как СНиП II-23-81* предусматривает специальные формулы для определения Fi. Гибкость (Lambda) — некоторая величина, характеризующая свойства рассматриваемого стержня в зависимости от его длины и параметров поперечного сечения, в частности радиуса инерции:
Lambda = Lr / i; здесь
- Lr — расчётная длина стержня;
- i — радиус инерции поперечного сечения стержня (стойки,колонны).

Радиус инерции сечения i равен корню квадратному из выражения I / Fp, где
- I — момент инерции сечения,
- Fp — его площадь.
Lr (расчётная длина) определяется как MuL;
здесь L- длина стойки,а Mu — коэфф., зависящий от схемы её крепления:
- «заделка-консоль»(свободный конец) — Mu = 2;
- «заделка-заделка»-Mu = 0.5;
- «заделка-шарнир» -Mu = 0.7;
- «шарнир-шарнир»-Mu=1.
Следует иметь ввиду,что при наличии у формы поперечного сечения 2-ух радиусов инерции (например, у швеллера, двутавра, тавра — относительно осей x-x и y-y), при расчёте Lambda используется меньший.
Уголки (как равнополочные так, и неравнополочные) имеют минимальный радиус инерции относительно оси z-z, который и используется в расчётах. Кроме того,сама Lambda (гибкость стойки), рассчитанная по формуле Lambda=Lr/i не должна превышать 220-ти в соответствии с табл. 19.СНиП II-23-81*; там же содержатся ограничения на предельную гибкость центрально-сжатых стержней.
Для их использования необходимо сделать выбор в таблице калькулятора «Вид, назначение стоек…». Предельная гибкость стоек, кроме их геометрических параметров, зависит также от коэфф. продольного изгиба (Fi), действующей нагрузки(P), расчётного сопротивления материала стойки (Ry) и условий её работы (Yc).
ПРИМЕЧАНИЕ. Размеры выбранного швеллера, двутавра и тавра указываются в строке «РАЗМЕРЫ ВЫБРАННОГО ПРОФИЛЯ»; размеры полок уголков-в их таблицах; толщина уголков выбирается отдельно после появления возможных толщин выбранного номера уголка в вышеуказанной строке.
Поделиться
Оцените автора
( 3 оценки, среднее 5 из 5 )
Калькулятор балок – расчет для разнотипных конструкций — Школа ремонта
Балки в доме относятся обычно к стропильной системе или перекрытию, и, чтобы получить надежную конструкцию, эксплуатация которой может осуществляться без каких-либо опасений, необходимо использовать калькулятор балок.
На чем строится калькулятор балок
Когда стены уже подведены под второй этаж или под крышу, необходимо сделать перекрытие, во втором случае плавно переходящее в стропильные ноги. При этом материалы нужно подобрать так, чтобы и нагрузка на кирпичные либо бревенчатые стены не превышала допустимую, и прочность конструкции была на должном уровне. Следовательно, если вы собираетесь использовать древесину, нужно правильно подобрать балки из нее, сделать расчеты для выяснения нужной толщины и достаточной длины.
Калькулятор балок
Укажите размеры балок перекрытий и шаг.
| Материал древесины | CоснаЛиственницаЕль | Предельная нагрузка: |
| Пролёт | см | |
| Размеры балки | x мм | |
| Шаг балок | см |
Проседанию или частичному разрушению перекрытия могут послужить разные причины, например, слишком большой шаг между лагами, прогиб поперечин, слишком малая площадь их сечения или дефекты в структуре. Чтобы исключить возможные эксцессы, следует выяснить предполагаемую нагрузку на перекрытие, будь оно цокольное или межэтажное, после чего используем калькулятор балок, учитывая их собственную массу. Последняя может меняться в бетонных перемычках, вес которых зависит от плотности армирования, для дерева и металла при определенной геометрии масса постоянна. Исключением бывает отсыревшая древесина, которую не используют в строительных работах без предварительной сушки.
Чтобы исключить возможные эксцессы, следует выяснить предполагаемую нагрузку на перекрытие, будь оно цокольное или межэтажное, после чего используем калькулятор балок, учитывая их собственную массу. Последняя может меняться в бетонных перемычках, вес которых зависит от плотности армирования, для дерева и металла при определенной геометрии масса постоянна. Исключением бывает отсыревшая древесина, которую не используют в строительных работах без предварительной сушки.
На балочные системы в перекрытиях и стропильных конструкциях оказывают нагрузку силы, действующие на изгиб сечения, на кручение, на прогиб по длине. Для стропил также нужно предусмотреть снеговую и ветровую нагрузку, которые также создают определенные усилия, прилагаемые к балкам. Также нужно точно определить необходимый шаг между перемычками, поскольку слишком большое количество поперечин приведет к лишней массе перекрытия (или кровли), а слишком малое, как было сказано выше, ослабит конструкцию.
Вам также может быть интересна статья о расчёте количества необрезной и обрезной доски в кубе: https://remoskop.
ru/kolichestvo-dosok-v-kube.html
Как рассчитать нагрузку на балку перекрытия
Расстояние между стенами называется пролетом, и в помещении их насчитывается два, причем один пролет обязательно будет меньше другого, если форма комнаты не квадратная. Перемычки межэтажного или чердачного перекрытия следует укладывать по более короткому пролету, оптимальная длина которого – от 3 до 4 метров. При большем расстоянии могут потребоваться балки нестандартных размеров, что приведет к некоторой зыбкости настила. Оптимальным выходом в этом случае будет использование металлических поперечин.
Оптимальным выходом в этом случае будет использование металлических поперечин.
Что касается сечения деревянного бруса, есть определенный стандарт, требующий, чтобы стороны балки соотносились как 7:5, то есть высота делится на 7 частей, и 5 из них должны составить ширину профиля. В этом случае деформация сечения исключается, если же отклониться от вышеуказанных показателей, то при ширине, превышающей высоту, получится прогиб, либо, при обратном несоответствии – загиб в сторону. Чтобы подобное не получилось из-за чрезмерной длины бруса, нужно знать, как рассчитать нагрузку на балку. В частности, допустимый прогиб вычисляется из соотношения к длине перемычки, как 1:200, то есть должен составлять 2 сантиметра на 4 метра.
Чтобы брус не провисал под тяжестью лагов и настила, а также предметов интерьера, можно выточить его снизу на несколько сантиметров, придав форму арки, в этом случае его высота должна иметь соответствующий запас.
Теперь обратимся к формулам. Тот же прогиб, о котором говорилось ранее, рассчитывается так: fнор = L/200, где L – длина пролета, а 200 – допустимое расстояние в сантиметрах на каждую единицу проседания бруса. Для железобетонной балки, распределенная нагрузка q на которую обычно приравнивается 400 кг/м2, расчет предельного изгибающего момента выполняется по формуле Мmax = (q · L2)/8. При этом количество арматуры и ее вес определяется по следующей таблице:
Тот же прогиб, о котором говорилось ранее, рассчитывается так: fнор = L/200, где L – длина пролета, а 200 – допустимое расстояние в сантиметрах на каждую единицу проседания бруса. Для железобетонной балки, распределенная нагрузка q на которую обычно приравнивается 400 кг/м2, расчет предельного изгибающего момента выполняется по формуле Мmax = (q · L2)/8. При этом количество арматуры и ее вес определяется по следующей таблице:
Площади поперечных сечений и масса арматурных стержней
| Диаметр, мм | Площадь поперечного сечения, см2, при числе стержней | Масса 1 пог.м, кг | Диаметр, мм | ||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |||
| Проволочная и стержневая арматура | |||||||||||
| 3 | 0.071 | 0.141 | 0.212 | 0.283 | 0.353 | 0.424 | 0.5 | 0. 565 565 | 0.636 | 0.052 | 3 |
| 4 | 0.126 | 0.25 | 0.38 | 0.5 | 0.68 | 0.75 | 0.88 | 1 | 1.18 | 0.092 | 4 |
| 5 | 0.196 | 0.39 | 0.59 | 0.79 | 0.98 | 1.18 | 1.38 | 1.57 | 1.77 | 0.154 | 5 |
| 6 | 0.283 | 0.57 | 0.85 | 1.13 | 1.42 | 1.7 | 1.98 | 2.26 | 2.55 | 0.222 | 6 |
| 7 | 0.385 | 0.77 | 1.15 | 1.54 | 1.92 | 2.31 | 2.69 | 3.08 | 3.46 | 0.302 | 7 |
| 8 | 0.503 | 1.01 | 1.51 | 2.01 | 2.52 | 3.02 | 3.52 | 4.02 | 4.58 | 0.395 | 8 |
| 9 | 0.636 | 1.27 | 1.91 | 2.54 | 3.18 | 3.82 | 4.45 | 5.09 | 5.72 | 0.499 | 9 |
| 10 | 0. 785 785 | 1.57 | 2.36 | 3.14 | 3.93 | 4.71 | 5.5 | 6.28 | 7.07 | 0.617 | 10 |
| 12 | 1.131 | 2.26 | 3.39 | 4.52 | 5.65 | 6.78 | 7.91 | 9.04 | 10.17 | 0.888 | 12 |
| 14 | 1.539 | 3.08 | 4.61 | 6.15 | 7.69 | 9.23 | 10.77 | 12.3 | 13.87 | 1.208 | 14 |
| 16 | 2.011 | 4.02 | 6.03 | 8.04 | 10.05 | 12.06 | 14.07 | 16.08 | 18.09 | 1.578 | 16 |
| 18 | 2.545 | 5.09 | 7.63 | 10.17 | 12.7 | 15.26 | 17.8 | 20.36 | 22.9 | 1.998 | 18 |
| 20 | 3.142 | 6.28 | 9.41 | 12.56 | 15.7 | 18.84 | 22 | 25.13 | 28.27 | 2.465 | 20 |
| 22 | 3.801 | 7. 6 6 | 11.4 | 15.2 | 19 | 22.81 | 26.61 | 30.41 | 34.21 | 2.984 | 22 |
| 25 | 4.909 | 9.82 | 14.73 | 19.64 | 24.54 | 29.45 | 34.36 | 39.27 | 44.18 | 3.85 | 25 |
| 28 | 6.153 | 12.32 | 18.47 | 24.63 | 30.79 | 36.95 | 43.1 | 49.26 | 55.42 | 4.83 | 28 |
| 32 | 8.043 | 16.09 | 24.18 | 32.17 | 40.21 | 48.26 | 56.3 | 64.34 | 72.38 | 6.31 | 32 |
| 36 | 10.179 | 20.36 | 30.54 | 40.72 | 50.89 | 61.07 | 71.25 | 81.43 | 91.61 | 7.99 | 36 |
| 40 | 12.561 | 25.13 | 37.7 | 50.27 | 62.83 | 75.4 | 87.96 | 100.53 | 113.1 | 9.865 | 40 |
| 45 | 15.904 | 31. 81 81 | 47.71 | 63.62 | 79.52 | 95.42 | 111.33 | 127.23 | 148.13 | 12.49 | 45 |
| 50 | 19.635 | 39.27 | 58.91 | 78.54 | 98.18 | 117.81 | 137.45 | 157.08 | 176.72 | 15.41 | 50 |
| 55 | 23.76 | 47.52 | 71.28 | 95.04 | 118.8 | 142.56 | 166.32 | 190.08 | 213.84 | 18.65 | 55 |
| 60 | 28.27 | 56.54 | 84.81 | 113.08 | 141.35 | 169.62 | 197.89 | 226.16 | 254.43 | 22.19 | 60 |
| 70 | 38.48 | 76.96 | 115.44 | 153.92 | 192.4 | 220.88 | 269.36 | 307.84 | 346.32 | 30.21 | 70 |
| 80 | 50.27 | 100.54 | 150.81 | 201.08 | 251.35 | 301.62 | 351.89 | 402.16 | 452.43 | 39.46 | 80 |
| Семипроволочные канаты класса К-7 | |||||||||||
4. 5 5 | 0.127 | 0.25 | 0.38 | 0.51 | 0.64 | 0.76 | 0.89 | 1.01 | 1.14 | 0.102 | 4.5 |
| 6 | 0.226 | 0.45 | 0.68 | 0.9 | 1.13 | 1.36 | 1.58 | 1.81 | 2.03 | 0.181 | 6 |
| 7.5 | 0.354 | 0.71 | 1.06 | 1.41 | 1.77 | 2.12 | 2.48 | 2.83 | 3.18 | 0.283 | 7.5 |
| 9 | 0.509 | 1.02 | 1.53 | 2.04 | 2.54 | 3.05 | 3.56 | 4.07 | 4.58 | 0.407 | 9 |
| 12 | 0.908 | 1.82 | 2.72 | 3.63 | 4.54 | 5.45 | 6.35 | 7.26 | 8.17 | 0.724 | 12 |
| 15 | 1.415 | 2.83 | 4.24 | 5.66 | 7.07 | 8.49 | 9.9 | 11.32 | 12.73 | 1.132 | 15 |
Нагрузка на любую балку из достаточно однородного материала рассчитывается по ряду формул. Для начала высчитывается момент сопротивления W ≥ М/R. Здесь М – это максимальный изгибающий момент прилагаемой нагрузки, а R – расчетное сопротивление, которое берется из справочников в зависимости от используемого материала. Поскольку чаще всего балки имеют прямоугольную форму, момент сопротивления можно рассчитать иначе: Wz = b · h2 /6, где b является шириной балки, а h – высотой.
Для начала высчитывается момент сопротивления W ≥ М/R. Здесь М – это максимальный изгибающий момент прилагаемой нагрузки, а R – расчетное сопротивление, которое берется из справочников в зависимости от используемого материала. Поскольку чаще всего балки имеют прямоугольную форму, момент сопротивления можно рассчитать иначе: Wz = b · h2 /6, где b является шириной балки, а h – высотой.
Деревянные балкиМеталло-деревянные балкиБалки перекрытия из ОСББалки перекрытия DommaЖелезобетонные балки
Что еще следует знать про нагрузки на балку
Перекрытие, как правило, является заодно и полом следующего этажа и потолком предыдущего.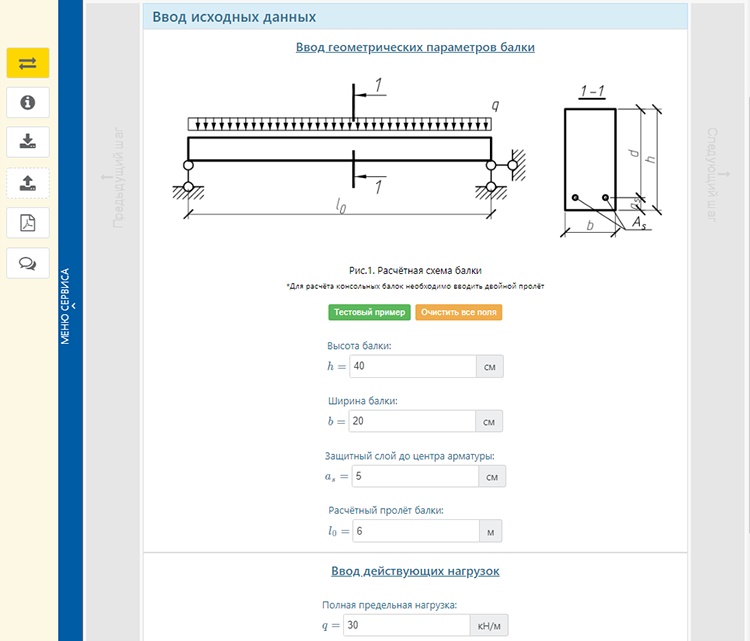 А значит, нужно сделать его таким, чтобы не было риска объединить верхние и нижние помещения путем банального перегруза меблировкой. Особенно такая вероятность возникает при слишком большом шаге между балками и отказе от лагов (дощатые полы настилаются прямо на брус, уложенный в пролеты). В этом случае расстояние между поперечинами напрямую зависит от толщины досок, например, если она составляет 28 миллиметров, то длина доски не должна быть более 50 сантиметров. При наличии лагов минимальный промежуток между балками может достигать 1 метра.
А значит, нужно сделать его таким, чтобы не было риска объединить верхние и нижние помещения путем банального перегруза меблировкой. Особенно такая вероятность возникает при слишком большом шаге между балками и отказе от лагов (дощатые полы настилаются прямо на брус, уложенный в пролеты). В этом случае расстояние между поперечинами напрямую зависит от толщины досок, например, если она составляет 28 миллиметров, то длина доски не должна быть более 50 сантиметров. При наличии лагов минимальный промежуток между балками может достигать 1 метра.
Также обязательно следует учитывать массу утеплителя, используемого для пола. Например, если укладываются маты из минеральной ваты, то квадратный метр цокольного перекрытия будет весить от 90 до 120 килограммов, в зависимости от толщины термоизоляции. Опилкобетон увеличит массу такого же участка в два раза. Использование же керамзита сделает перекрытие еще тяжелее, поскольку на квадратный метр будет приходиться нагрузка в 3 раза больше, чем при укладке минеральной ваты. Далее, не следует забывать про полезную нагрузку, которая для межэтажных перекрытий составляет 150 килограммов на квадратный метр минимум. На чердаке достаточно принять допустимую нагрузку в 75 килограммов на квадрат.
Например, если укладываются маты из минеральной ваты, то квадратный метр цокольного перекрытия будет весить от 90 до 120 килограммов, в зависимости от толщины термоизоляции. Опилкобетон увеличит массу такого же участка в два раза. Использование же керамзита сделает перекрытие еще тяжелее, поскольку на квадратный метр будет приходиться нагрузка в 3 раза больше, чем при укладке минеральной ваты. Далее, не следует забывать про полезную нагрузку, которая для межэтажных перекрытий составляет 150 килограммов на квадратный метр минимум. На чердаке достаточно принять допустимую нагрузку в 75 килограммов на квадрат.
Пример расположение балок и перекрытий для домаДеревянные балкиМежэтажные легкие перекрытияДопустимые пролеты балокФото балок на складе
- Автор: Михаил Малофеев
- Распечатать
Оцените статью:
(13 голосов, среднее: 4 из 5)
Поделитесь с друзьями!
Просто поддерживаемый калькулятор балки | Calcresource
Прыжки до
-калькулятор
-Фон
Соглашение
-Калькулятор
-Фон
-Введение
-Aspuction
-Соглашение
-Символы
-Com равномерная распределенная нагрузка
— Свободно опертая балка с точечной силой в середине
— Свободно опертая балка с точечной силой в произвольном месте
— Свободно опертая балка с точечным моментом
— Свободно опертая балка с треугольной нагрузкой
— Свободно опертая балка с трапециевидной нагрузкой
— Свободно опертая балка с трапециевидным распределением нагрузки плитного типа
— Свободно опертая балка с частично распределенной равномерной нагрузкой load
— Свободно опертая балка с частично распределенной трапециевидной нагрузкой
— Статьи по теме
Поделиться
См. также
также
Калькулятор балки с простой опорой
— Д-р Минас Э. Лемонис, доктор философии — Обновлено: 11 мая 2022 г.
Главная > Статика > Балка с простой опорой
Этот инструмент вычисляет статическую реакцию балки с простой опорой при различных сценариях нагрузки. Инструмент рассчитывает и строит диаграммы для следующих величин:
- реакции
- изгибающие моменты
- поперечные сдвигающие силы
- прогибы
- уклоны
Обратите внимание, что приняты предположения теории балок Эйлера-Бернуля. является упругим, а поперечное сечение постоянным на всем пролете балки (призматическая балка).
- Вместо этого переходите к теории и формулам!
Units: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | 2 | 3 | 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Структура | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
L = | mcmmmydftin | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Рассчитайте момент инерции балок различных сечений с помощью наших специальных калькуляторов. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ADVERTISEMENT |
| 1 | 2 | 3 | 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Imposed loading: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Uniform distributed loadUniform распр. нагрузка (суммарная)Точечная нагрузка (по центру)Точечная нагрузкаТочечный моментТреугольная нагрузкаТрапециевидная нагрузкаТрапециевидная нагрузка (плита)Частичная равномерная нагрузкаЧастичная треугольная нагрузкаЧастичная трапециевидная нагрузка | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Calculate | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | 2 | 3 | 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Results: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Reactions: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
R A = | KNNKGTLBFKIP | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
R B = | KNNKGGIP | KNNKGGIP | KNNKGPKIP | .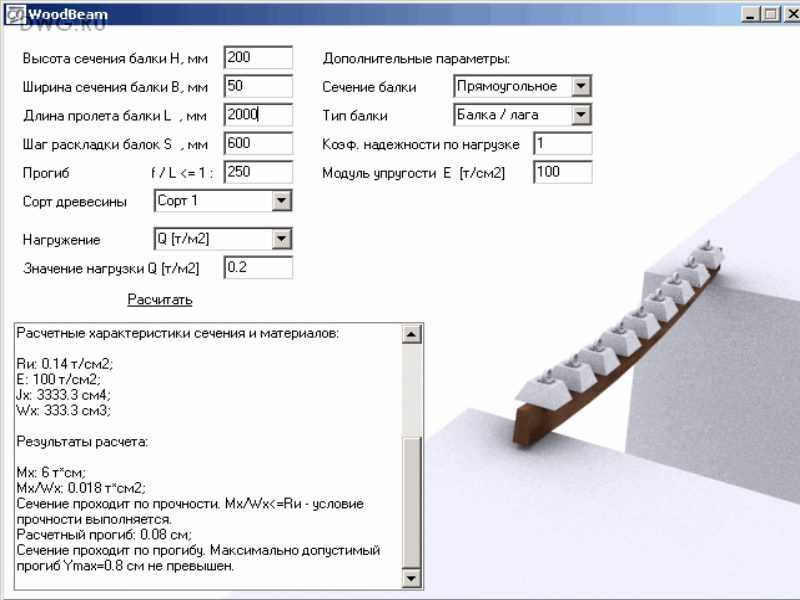 0079 0079 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Bending Moment: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
M u = | kNmNmkg.mt.mlbf.ftlbf.inkip.ftkip.in | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
x m = | McMmmyDftin | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Поперечное сдвиг0081 | mcmmmydftin | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Deflection: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
d u = | mcmmmydftin | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
x d = | mcmmmydftin | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Slopes : | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
θ A = | DEGRADMRAD | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
θ B = | 9999 | 9919 | 9002 B = | θ0086 degradmrad | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | 2 | 3 | 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Request results at a specific point: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
X = | MCMMMYDFTIN | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
M (X) = | KNMNMKG. MT.MLBF.FTLB.INKIP.INKIP.INKIP.INKIP.INKIP.INKIP.INKIP.INKIP.INKIP.INKIP. MT.MLBF.FTLB.INKIP.INKIP.INKIP.INKIP.INKIP.INKIP.INKIP.INKIP.INKIP.INKIP. | .0081 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
V(x) = | kNNkgtlbfkip | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
d(x) = | mcmmmydftin | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
θ(x) = | degradmrad | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| .0003 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| kNmNmkg.mt.mlbf.ftlbf.inkip.ftkip.in | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| kNNkgtlbfkip | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| mcmmmydftin | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| degradmrad | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| kN/mN/mkg/mt/mlbf /ftlbf/inkip/ft | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Реклама
Верхние страницы
Поделитесь этим
Фон
Таблица
-ВВЕДЕНИЕ
-Предложения
-Стои0003
— Обозначения
— Свободно опертая балка с равномерно распределенной нагрузкой
— Свободно опертая балка с точечной силой в середине
— Свободно опертая балка с точечной силой в произвольном положении
— Свободно опертая балка с точечным моментом
— Свободно опертая балка с треугольной нагрузкой
— Свободно опертая балка с трапециевидной нагрузкой
— Свободно опертая балка с трапециевидным распределением нагрузки плитного типа
— Свободно опертая балка с частично распределенной равномерной нагрузкой
— Свободно опертая балка с частично распределенной трапециевидной нагрузкой
— Статьи по теме
Введение
Свободно опертая балка является одной из самых простых конструкций. Он имеет только две опоры, по одной на каждом конце. Одна шарнирная опора и роликовая опора. Оба они препятствуют любому вертикальному движению, позволяя, с другой стороны, свободно вращаться вокруг себя. Роликовая опора также позволяет балке расширяться или сжиматься в осевом направлении, хотя другая опора препятствует свободному горизонтальному движению.
Он имеет только две опоры, по одной на каждом конце. Одна шарнирная опора и роликовая опора. Оба они препятствуют любому вертикальному движению, позволяя, с другой стороны, свободно вращаться вокруг себя. Роликовая опора также позволяет балке расширяться или сжиматься в осевом направлении, хотя другая опора препятствует свободному горизонтальному движению.
Удаление любой из опор или вставка внутреннего шарнира превратит свободно опертую балку в механизм, который будет перемещаться без ограничений в одном или нескольких направлениях. Очевидно, что это нежелательно для несущей конструкции. Таким образом, свободно опертая балка не предлагает избыточности опор. Если произойдет локальный отказ, вся конструкция рухнет. Эти типы структур, которые не предлагают избыточности, называются критическими или детерминантными 9.0574 конструкций. Напротив, конструкция, которая имеет больше опор, чем требуется для ограничения ее свободного движения, называется избыточной или неопределенной конструкцией.
РЕКЛАМА
Допущения
Статический анализ любой несущей конструкции включает оценку ее внутренних сил и моментов, а также ее прогибов. Как правило, для плоской конструкции с плоской нагрузкой интересующими внутренними воздействиями являются осевая сила N, поперечная поперечная сила V и изгибающий момент M. Для свободно опертой балки, которая воспринимает только поперечные нагрузки, осевая сила всегда ноль, поэтому им часто пренебрегают. Расчетные результаты на странице основаны на следующих предположениях:
- Материал однородный и изотропный (другими словами, его характеристики одинаковы во всех точках и направлениях)
- Материал линейно-упругий
- Нагрузки действуют статически (не меняются со временем) )
- Сечение одинаковое по всей длине балки
- Прогибы малы
- Каждое поперечное сечение, изначально плоское и перпендикулярное к продольной оси, остается плоским и нормальным также к отклоненной оси. Это тот случай, когда высота сечения значительно меньше длины балки (в 10 и более раз), а также сечение не многослойное (не сэндвич-сечение).
Последние два предположения удовлетворяют кинематическим требованиям теории балки Эйлера-Бернулли, которая также принимается здесь.
Правила знаков
Для расчета внутренних сил и моментов в любом сечении балки необходимо соблюдать правила знаков. Здесь приняты следующие значения:
- Осевая сила считается положительной, если она вызывает растяжение детали.
- Сила сдвига положительна, когда она вызывает вращение детали по часовой стрелке.
- Изгибающий момент является положительным, когда он вызывает растяжение нижнего волокна балки и сжатие верхнего волокна.
Эти правила хоть и не обязательны, но достаточно универсальны. Другой набор правил, если им следовать последовательно, также приведет к тем же физическим результатам.
Обозначения
- E: модуль упругости материала (модуль Юнга)
- I: момент инерции поперечного сечения вокруг упругой нейтральной оси изгиба
- L: общий пролет балки
- R: опорная реакция
- d: прогиб
- M: изгибающий момент
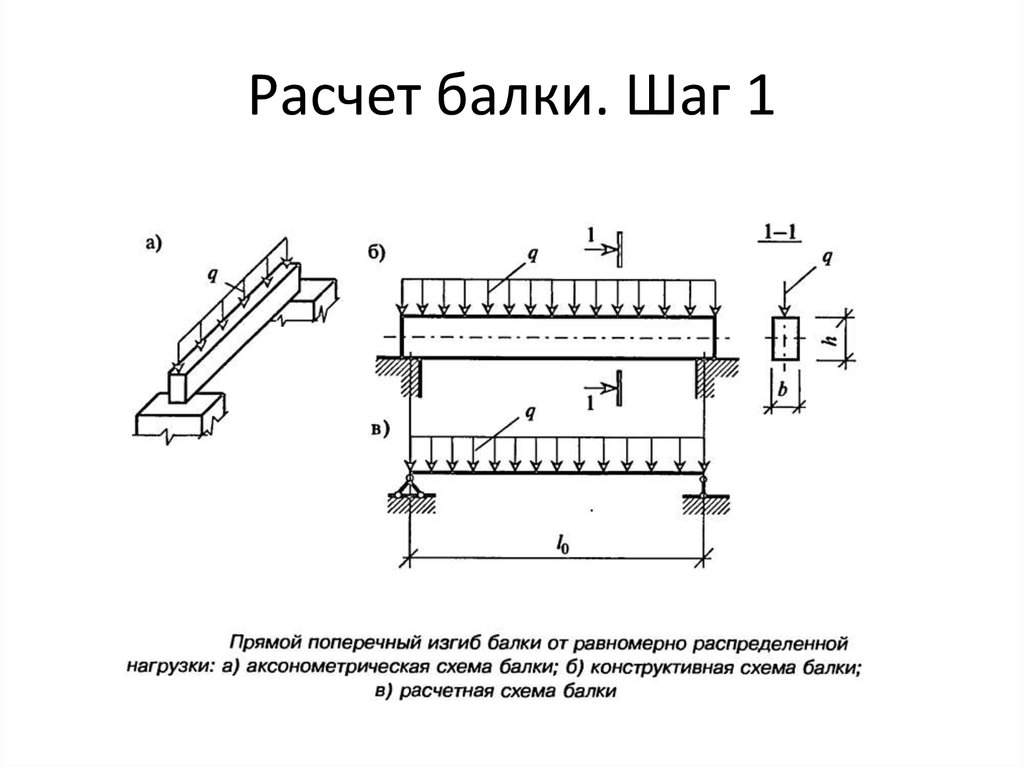
- V: поперечная поперечная сила Нагрузка w распределяется по всему пролету балки, имея постоянную величину и направление.
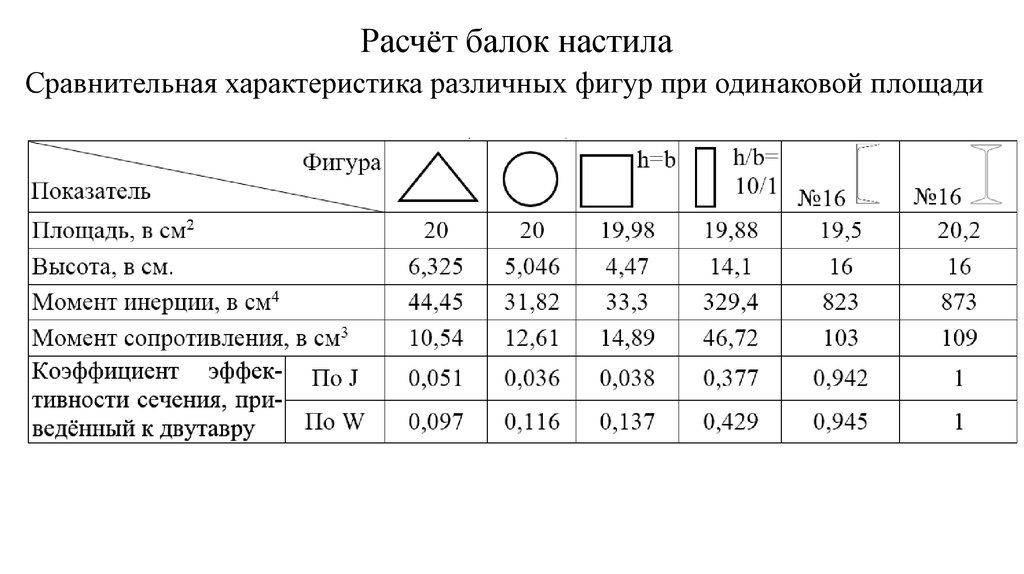 Его размеры представляют собой силу на длину. Суммарная сила, приложенная к балке, равна W=w L, где L — длина пролета. В зависимости от обстоятельств может быть указана либо общая сила W, либо распределенная сила по длине w. 93)}{24 E I}
Его размеры представляют собой силу на длину. Суммарная сила, приложенная к балке, равна W=w L, где L — длина пролета. В зависимости от обстоятельств может быть указана либо общая сила W, либо распределенная сила по длине w. 93)}{24 E I}РЕКЛАМА
Свободно опертая балка с точечной силой посередине
Сила сосредоточена в одной точке, расположенной в середине балки. Однако на практике сила может быть распределена по небольшой площади, хотя размеры этой области должны быть существенно меньше длины пролета балки. В непосредственной близости от приложения силы ожидаются концентрации напряжений, в результате чего реакция, предсказываемая классической балочной теорией, может оказаться неточной. Однако это лишь локальное явление. По мере того, как мы удаляемся от места действия силы, результаты становятся достоверными в силу принципа Сен-Венана. 92)}{16 E I} &, x>L/2 \end{выровнено}\right.
где:
\acute{x}=L-x
Свободно поддерживаемая балка с точечной силой в произвольном месте
Сила сосредоточена в одной точке, в любом месте поперек балки.
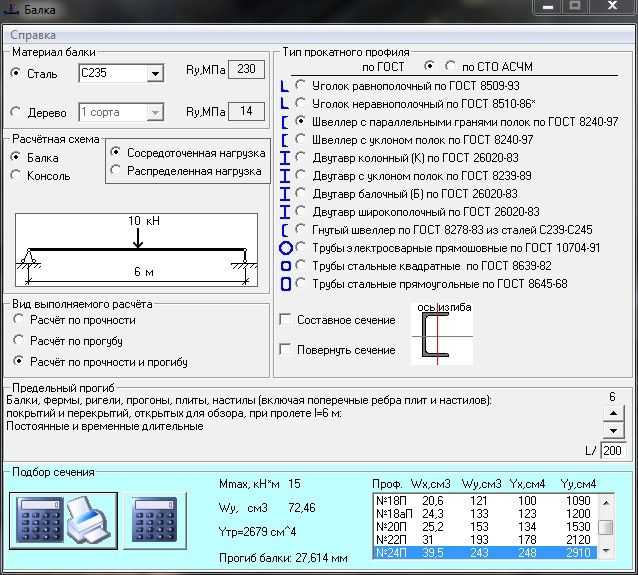 Однако на практике сила может быть распределена по небольшой площади. Однако для того, чтобы считать силу сосредоточенной, размеры области приложения должны быть существенно меньше длины пролета балки. В непосредственной близости от силы ожидаются концентрации напряжений, в результате чего реакция, предсказываемая классической балочной теорией, может оказаться неточной. Однако это лишь локальное явление, и по мере удаления от места действия силы расхождение результатов становится незначительным.
Однако на практике сила может быть распределена по небольшой площади. Однако для того, чтобы считать силу сосредоточенной, размеры области приложения должны быть существенно меньше длины пролета балки. В непосредственной близости от силы ожидаются концентрации напряжений, в результате чего реакция, предсказываемая классической балочной теорией, может оказаться неточной. Однако это лишь локальное явление, и по мере удаления от места действия силы расхождение результатов становится незначительным.В следующей таблице представлены формулы, описывающие статическую реакцию простой балки на сосредоточенную точечную силу P, приложенную на случайном расстоянии a от левого конца.
Просто поддерживаемый луч с точечной нагрузкой в случайном положении
Количество Формула Реакции: 9 2 2 2 2 2 2 2 2 2 2 . 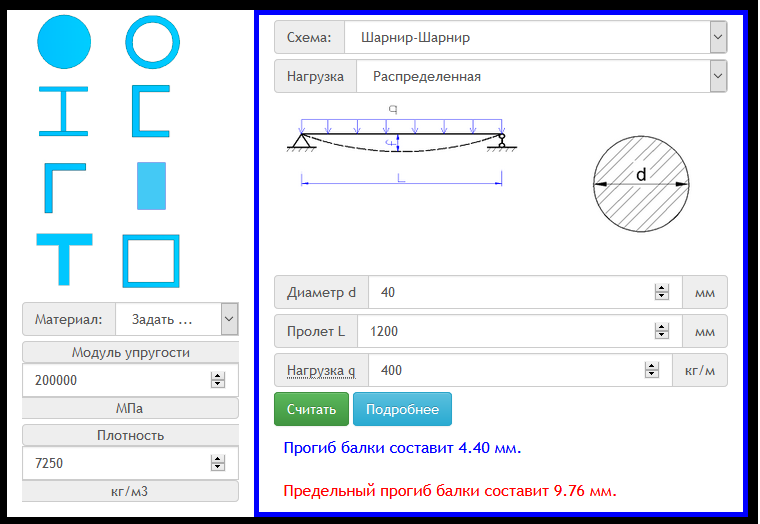 3}{6EI} &, x>a\end{выровнено} \right. 92}{2 E I} &, x>a\end{выровнено} \right.
3}{6EI} &, x>a\end{выровнено} \right. 92}{2 E I} &, x>a\end{выровнено} \right.где:
b=L-a
\acute{x}=L-x
Свободно опертая балка с точечным моментом
, в любом месте на пролете балки. С практической точки зрения это может быть пара сил или элемент при кручении, соединенный вне плоскости и перпендикулярно балке.
В любом случае область приложения момента должна распространяться на небольшую длину балки, чтобы ее можно было успешно идеализировать как сосредоточенный момент в точке. Несмотря на то, что в непосредственной близости от области применения предсказанные результаты с помощью классической теории балок, как ожидается, будут неточными (из-за концентрации напряжений и других локализованных эффектов), по мере удаления предсказанные результаты совершенно достоверны, как заявил Святой — Принцип Венана.
В следующей таблице представлены формулы, описывающие статическую реакцию простой балки на сосредоточенный точечный момент M, приложенный на расстоянии a от левого конца.
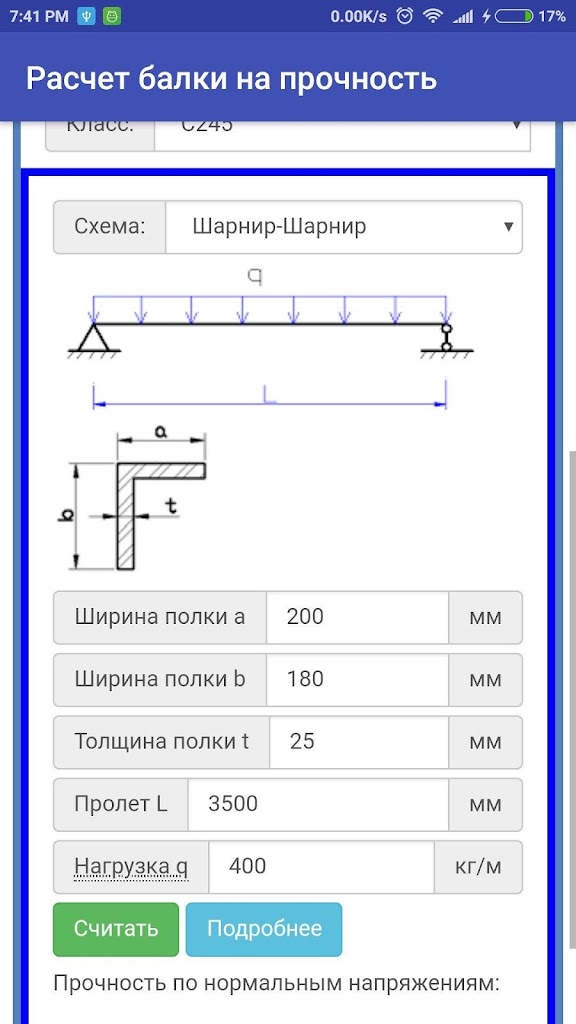
просто поддержанный луч с точечным моментом
Количество Формула Реакции: 9 9 r_2 r_2 r_2 r_2 r_2 r_2 r_2 r_2 r_2 r_2 r_ r_29000 2
. } Концевые уклоны: 92}{2 E I} &, x>a\end{выровнено} \right. где:
b=L-a
\acute{x}=L-x
Просто опертая балка с треугольной нагрузкой, однако, ее величина не распределена по пролету
постоянна, но изменяется линейно, начиная с нуля на левом конце и заканчивая пиковым значением w_1 на правом конце. Размеры w_1 — это сила на длину. Суммарная сила, приложенная к балке, равна W={1\over2}w L, где L — длина пролета.
В следующей таблице представлены формулы, описывающие статическую реакцию простой балки на линейно изменяющуюся (треугольную) распределенную нагрузку, возрастающую слева направо.

Просто поддерживаемый луч с линейной разной распределенной нагрузкой (треугольная)
. 1\over3}w_1L 94} {24EIL} где:
C=\sqrt{15-\sqrt{120}}\left(\sqrt{15}+\sqrt{50}\right)\приблизительно 22,01237
Свободно опертая балка с трапециевидной нагрузкой
Нагрузка распределяется по всему пролету балки и имеет линейно изменяющуюся величину, начиная с w_1 на левом конце и до w_2 на правом конце. Размеры w_1 и w_2 являются силой на длину. Суммарная сила, приложенная к балке, равна W={L\over2}(w_1+w_2), где L — длина пролета.
В следующей таблице представлены формулы, описывающие статическую реакцию простой балки трапециевидной формы на переменную распределенную нагрузку.
Просто поддерживаемый луч с линейно изменяющейся распределенной нагрузкой (трапециевидная)
. 
R_B={(w_1+2w_2)L\over6}
3}{24EI}
где:
w_x=w_1+{(w_2-w_1)x\over L}
Опорная балка с трапециевидным распределением нагрузки характерны для балок по периметру плиты. Распределение имеет трапециевидную форму с максимальной величиной w внутри балки, а на двух ее концах она становится равной нулю. Размеры (\w\) представляют собой силу на длину. Суммарная сила, приложенная к балке, равна W=w (L-a/2-b/2), где L — длина пролета, а a, b — длины левой и правой сторон балки соответственно, где распределение нагрузки переменная (треугольная). 93
Свободно опертая балка с частично распределенной равномерной нагрузкой
Нагрузка распределяется на часть пролета балки с постоянной величиной w, в то время как оставшийся пролет не нагружен. Размеры w представляют собой силу на длину. Суммарная сила, приложенная к балке, равна W=\left(L-a-b\right)w, где L — длина пролета, а a, b — ненагруженные длины левой и правой сторон балки соответственно.

В следующей таблице представлены формулы, описывающие статическую реакцию простой балки на частично распределенную равномерную нагрузку. 92}{2 E I} &,x\ge L-b \end{выровнено}\right.
Где:
\ Острый {x} = L-X
x_a = x-a
L_W = L-A-B
просто поддержанный. пролет балки, имеющий линейно изменяющуюся величину от w_1 до w_2, а оставшийся пролет разгружен. Размеры w_1 и w_2 являются силой на длину. Суммарная сила, приложенная к балке, равна W={L-a-b\over2}(w_1+w_2), где L — длина пролета, а a, b — ненагруженные длины левой и правой сторон балки соответственно.
Это самый общий случай. Формулы для частично распределенных равномерных и треугольных нагрузок могут быть получены путем соответствующей установки значений w_1 и w_2. Кроме того, соответствующие случаи для полностью загруженного пролета могут быть получены путем установки a и b равными нулю.
В следующей таблице представлены формулы, описывающие статическую реакцию простой балки на частично распределенную трапециевидную нагрузку.

Свободно опертая балка с частично распределенной линейно-переменной нагрузкой (трапециевидная) 93
Статьи по теме
Понравилась эта страница? Поделись с друзьями!
РЕКЛАМА
См. также
Формулы напряжения изогнутой двутавровой балки и калькулятор
Связанные ресурсы: калькуляторы
Формулы напряжения изогнутой двутавровой балки и калькулятор с калькулятором прогиба и деформации балки
Формулы напряжения изогнутой двутавровой балки и калькулятор
Изгибающие напряжения в криволинейных балках не изменяются так же линейно, как в прямых балках, из-за различий в длине дуги. Несмотря на то, что для обоих типов используются одни и те же допущения, то есть плоское сечение, перпендикулярное оси балки, остается плоским после изгиба, а напряжение совершенно другое. На рис. 1.0 показано линейное изменение напряжения в прямой балке и гиперболическое распределение напряжения в изогнутой балке.
 Обратите внимание, что напряжение изгиба в изогнутой балке равно нулю в точке, отличной от оси центра тяжести. Также обратите внимание, что нейтральная ось расположена между осью гравитации и центром кривизны: это всегда происходит в криволинейных балках.
Обратите внимание, что напряжение изгиба в изогнутой балке равно нулю в точке, отличной от оси центра тяжести. Также обратите внимание, что нейтральная ось расположена между осью гравитации и центром кривизны: это всегда происходит в криволинейных балках.Предварительный просмотр расчета напряжения изогнутой двутавровой балки
Рисунок 1.0
Рисунок 2.0 Размеры двутавровой балки
Распределение напряжения из-за изгиба определяется по формуле:
Уравнение 1
s = M · γ / ( A · e · ( r n — y ) )Где:
s = изгибающее напряжение, psi
M = изгибающий момент относительно центральной оси, дюйм-фунт
y = расстояние от нейтральной оси до рассматриваемой точки, дюймы (положительно для расстояний до центра кривизны, отрицательно для расстояний от центра кривизны)
A = площадь секции в 2
e = расстояние от оси центра тяжести до нейтральной оси, дюймы
r n = радиус кривизны нейтральной оси, дюймы
значение e, используемое для базового журнала = 2,7182818Изгибающее напряжение внутри волокна определяется по формуле:
Уравнение 2
s = ( M · h i ) / ( A · e · r i )Где:
h i = расстояние от центральной нейтральной оси до внутренней части волокна, дюймы ( h i = r n — r i )
r i04 = радиус кривизны внутри волокна, дюймы
Напряжение изгиба на внешней стороне волокна определяется по формуле:
Уравнение 3
s = ( M · h o ) / ( A · e · r i )Где:
h o = расстояние от центральной нейтральной оси до внутреннего волокна, дюймы ( ч о
= R O — R I )
R O = радиус кривизны на внешнем волокне, дюймы
A = B I I I I I I I I I I I I I I I I I I I I I I I I I I I I I .