Формула площадь двутавра: Площадь поперечного сечения двутавра: параметры расчета

Площадь пояса:

Площадь
стенки:

Отношение:

Определяем
коэффициент с₁
=
1.04.

Равномерно
распределенная нагрузка от собственного
веса балки настила длиной 1 м

Нормативная
нагрузка на балку настила:

Расчетная
нагрузка:

Изгибающий
момент:

Поперечная
сила:

Проверка
несущей способности балки.

Проверка
прочности по нормальным напряжениям в
середине балки:

Проверка
прочности по касательным напряжениям
у опоры:

В
местах приложения локальной нагрузки
к верхнему поясу (рис. 8), а также в опорных
сечениях балки, не укрепленных ребрами
жесткости, стенку следует дополнительно
проверить на местное напряжение σ_loc:

где

t’_f
– расстояние от наружной грани полки
до начала внутреннего закругления
стенки;

где

l_ef
–условная
длина распределения сосредоточенной
нагрузки на стенку вспомогательной
балки;

где

F–
расчетное значение сосредоточенной
силы, равное двум реакциям от балок
настила;

Общую
устойчивость балок настила проверять
не надо, поскольку их сжатые пояса
надежно закреплены в горизонтальном
направлении приваренным к ним стальным
сплошным настилом.

Рис.
6. Схема распределения сосредоточенной
нагрузки

на
стенку прокатной балки

Проверка
жесткости.

Прогибы,
определяемые от нормативных нагрузок,
не должны превышать их предельных
значений, установленных нормами
проектирования. Для однопролетной
балки, нагруженной равномерно
распределенной нагрузкой, проверка
прогиба производится по формуле:

Где

при пролете l
= 9м.

Принятое
сечение не удовлетворяет условиям
прочности и жесткости. В этом случае
необходимо изменить сечение, приняв по
сортаменту следующий номер двутавра
№50Ш1 (W_x
= 2518 см³;
J_x
= 60930 см⁴)
и вновь проверить прочность и жесткость
балки.

Проверка
прочности по нормальным напряжениям в
середине балки:

Недонапряжение
составляет 23. 5%.

Определяем
вес вспомогательной балки на 1м²
рабочей площадки:

5. Расчет железобетонного настила

Расчетный
пролет плиты принимаем l_пл
= а₁
= 2 м.

При
нормативной полезной нагрузке p_n
= 22.8 кН/м²
принимаем толщину плиты t_пл
= 12 см. Нормативная нагрузка от веса
железобетонной плиты (при плотности
железобетона
):

1. Расчет балки настила

Расчетная
схема балки настила представлена на
рис. 7. Пролет балки настила l
= B
= 9 м.

Рис.
7. Расчетная схема балки настила (3-й
вариант)

Определяем
нормативную и расчетную нагрузки.

Нормативная
нагрузка на балку принимается равномерно
распределенной:

Расчетная
нагрузка:

где
_g
= 1,1 – коэффициент надежности по нагрузке
для постоянной нагрузки от железобетонных
плит.

Расчетный
изгибающий момент:

Максимальная
поперечная сила:

Требуемый
момент сопротивления поперечного
сечения балки при работе с учетом
упругопластических деформаций:

По
сортаменту выбираем ближайший номер
двутавра, у которого W_x
> W_n,min.
Принимаем двутавр
№40Ш1,
имеющий момент сопротивления W_x
= 1771 см³;
статический момент полусечения S_x
= 976 см³;
момент инерции сечения J_x
= 34360 см⁴;
площадь сечения А
= 122.4 см²;
ширину пояса b_f
= 300 мм; толщину пояса t_
= 14 мм; толщину стенки t_w
= 9.5 мм; радиус
внутреннего закругления R
= 22 мм;
линейную плотность (массу 1 м пог. ) 78.5
кг/м.

Уточнение
коэффициента с₁,
M
и Q
с учетом собственного веса балки настила.

Построение эпюры касательных напряжений для двутавра

Пример решения задачи на построение эпюры касательных напряжений τ для двутаврового сечения стальной балки.

Предыдущий пункт решения:
Построение эпюры нормальных напряжений.

Задача
Построить эпюру касательных напряжений для двутавра при следующих данных:

• Величина поперечной силы в сечении балки — 58,3 кН
• Двутавровое сечение — №24а

Другие примеры решений >
Помощь с решением задач >

Пример решения

Расчет касательных напряжений в сечении балки ведется по формуле Журавского

Двутавровое сечение по высоте имеет 5 характерных точек: крайние, среднюю и точки, на уровне которых стенка двутавра соединяется с полками.

Обозначим их цифрами и проведем из них горизонтальные линии.

Другие видео

Начнем с крайних точек.

Статический момент в формуле Журавского одним из множителей включает в себя площадь сечения расположенную за рассматриваемой точкой.

Выше точки 1 и ниже точки 5 площадь сечения равна нулю, поэтому касательных напряжений там нет.

Максимальные напряжения следует ожидать в точке 3, потому что относительно нее будет самый большой статический момент. Его принимаем из сортамента.

Чтобы найти напряжения в точках 2 и 4 надо сначала рассчитать статический момент полки двутавра.

Для этого временно заменим её прямоугольником со сторонами b и t, центр тяжести которого, очевидно будет на расстоянии t/2 от точки 1.

Это сильно упрощает расчеты без особого ущерба для правильности вычислений.

Статический момент полки определяется произведением её площади на расстояние от оси x до её центра тяжести.

В этих точках сечение резко меняет свою ширину, поэтому получится скачок напряжений, и нам потребуется найти их величину в стенке и полке.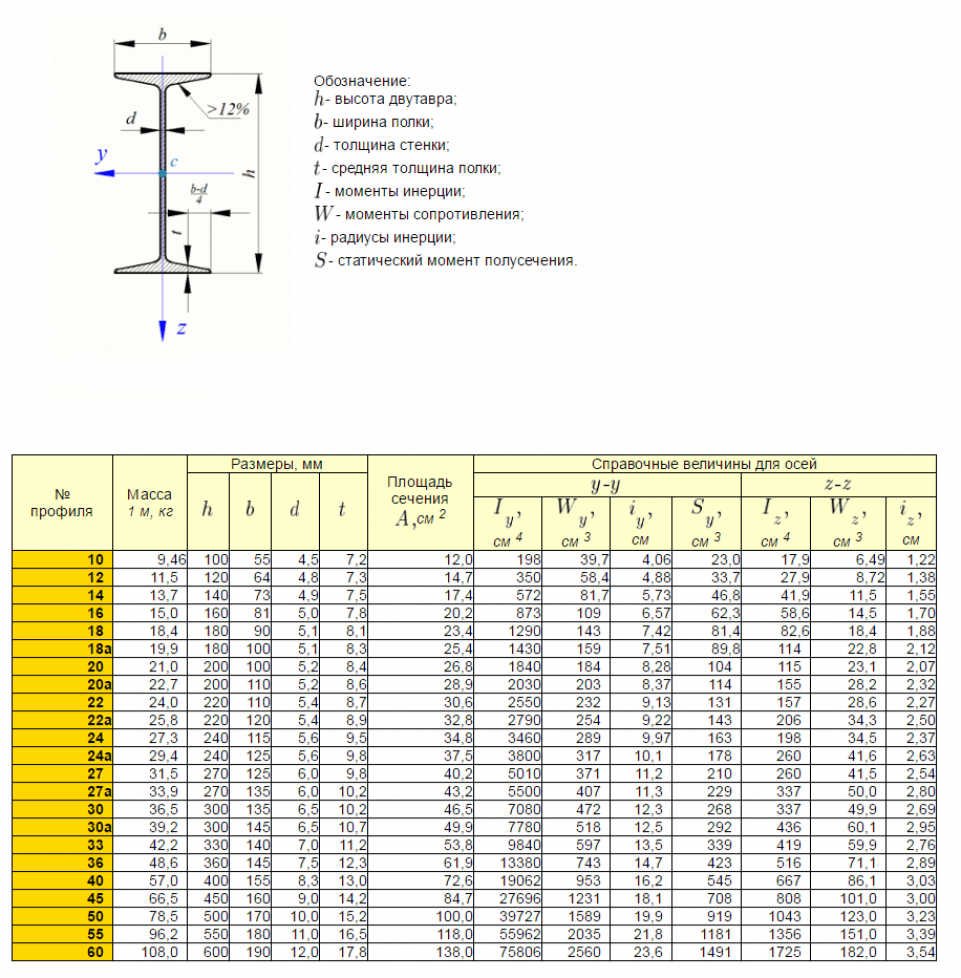

Другие видео

Начнем с полки, то есть сразу выше точки 2. Для этого в знаменатель формулы Журавского подставляем ширину полки b.

При расчете напряжения под точкой 2 подставляем толщину стенки d.

По полученным значениям строим эпюру касательных напряжений

Другие примеры решения задач >

Сохранить или поделиться с друзьями

Вы находитесь тут:

На нашем сайте Вы можете получить решение задач и онлайн помощь

Подробнее

Здесь можно узнать стоимость и заказать решение
задач и выполнение учебных работ для студентов

Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.
Если стоимость устроит вы сможете оформить заказ.

НАБОР СТУДЕНТА ДЛЯ УЧЁБЫ

На нашем сайте можно бесплатно скачать:

— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку

Сохранить или поделиться с друзьями

Заказать решение

Поиск формул и решений задач

Уравнения модуля сечения и калькуляторы Общие формы

Связанные ресурсы: Материаловедение

Уравнения модуля сечения и калькуляторы Общие формы

Сопротивление материалов | Прогиб и напряжение балки

Модуль упругости — это геометрическое свойство заданного поперечного сечения, используемое при расчете балок или изгибаемых элементов. Другие геометрические свойства, используемые в конструкции, включают площадь для растяжения, радиус вращения для сжатия и момент инерции для жесткости. Любая связь между этими свойствами сильно зависит от рассматриваемой формы. Уравнения для модулей сечения обычных форм приведены ниже. Существует два типа модулей сечения: модуль упругого сечения (S) и модуль пластического сечения (Z).

Для общего расчета используется модуль упругого сечения, применяемый до предела текучести для большинства металлов и других распространенных материалов.

Модуль упругого сечения определяется как S = I / y, где I — второй момент площади (или момент инерции), а y — расстояние от нейтральной оси до любого заданного волокна. Об этом часто сообщают, используя y = c, где c — расстояние от нейтральной оси до самого крайнего волокна, как показано в таблице ниже. Его также часто используют для определения момента текучести (M _y ), так что M _y = S × σ _y , где σ _y — предел текучести материала.

Расширенный список: Модуль сечения, Момент инерции площади, Уравнения и калькуляторы

Модуль пластического сечения (PNA)

Модуль пластического сечения используется для материалов, в которых преобладает (необратимое) пластическое поведение. Большинство проектов намеренно не сталкиваются с таким поведением.

Модуль упругости пластического сечения зависит от положения нейтральной оси пластичности (PNA). PNA определяется как ось, которая разделяет поперечное сечение таким образом, что сила сжатия от области, находящейся в состоянии сжатия, равна силе растяжения, создаваемой областью, находящейся в состоянии растяжения. Так, для сечений с постоянным пределом текучести площади над и под ПНА будут равны, а для составных сечений это не обязательно.

Модуль пластического сечения представляет собой сумму площадей поперечного сечения с каждой стороны PNA (которые могут быть равными, а могут и не быть равными), умноженные на расстояние от локальных центров тяжести двух площадей до PNA:

• Уравнения модуля сечения и калькуляторы
• Свойства сечения Радиус инерции Варианты 1–10
• Свойства сечения Радиус инерции Варианты 11–16
• Свойства сечения Радиус инерции Случаи 17 — 22
• Свойства сечения Радиус инерции Случаи 23 — 27
• Свойства сечения Радиус инерции Варианты 28 — 31
• Свойства сечения Радиус инерции Случаи 32 — 34
• Свойства сечения Радиус инерции Случаи 35 — 37

Как рассчитать площадь поперечного сечения

Обновлено 7 февраля 2020 г.

Кевин Бек

Вы можете столкнуться с ситуациями, когда у вас есть трехмерная твердотельная фигура и вам нужно вычислить площадь воображаемой плоскости, вставленной через фигуру и имеющей границы, определяемые границами твердого тела.

Например, если под вашим домом проходит цилиндрическая труба длиной 20 метров (м) и диаметром 0,15 м, вам может понадобиться узнать площадь поперечного сечения трубы.

Поперечные сечения могут быть перпендикулярны оси твердого тела, если таковые существуют. В случае сферы любая секущая плоскость, проходящая через сферу, независимо от ориентации, приведет к диску определенного размера.

Площадь поперечного сечения зависит от формы твердого тела, определяющей границы поперечного сечения, и угла между осью симметрии твердого тела (если она есть) и плоскостью, создающей поперечное сечение.

Площадь поперечного сечения прямоугольного твердого тела

Объем любого прямоугольного твердого тела, включая куб, равен площади его основания (длина, умноженная на ширину), умноженной на его высоту: V = l × w × h.

Следовательно, если поперечное сечение параллельно верхней или нижней части твердого тела, площадь поперечного сечения равна l × w. Если секущая плоскость параллельна одному из двух наборов сторон, площадь поперечного сечения вместо этого определяется как l × h или w × h.

Если поперечное сечение не перпендикулярно какой-либо оси симметрии, созданная форма может быть треугольником (если поместить его через угол твердого тела) или даже шестиугольником.

Пример: Вычислить площадь поперечного сечения плоскости, перпендикулярной основанию куба объемом 27 м ³ .

• Так как для куба l = w = h, длина любого ребра куба должна быть 3 м (поскольку 3

  × 3

  × 3 = 27). Таким образом, поперечное сечение описанного типа представляет собой квадрат со стороной 3 м, что дает площадь 9 м ² .

Площадь поперечного сечения цилиндра

Цилиндр представляет собой твердое тело, образованное путем вытягивания окружности через пространство перпендикулярно ее диаметру. Площадь круга находится по формуле πr ² , где r — радиус. Поэтому имеет смысл, что объем цилиндра будет площадью одной из окружностей, образующих его основание.

Если поперечное сечение параллельно оси симметрии, то площадь поперечного сечения представляет собой просто круг с площадью πr ² . Если секущая плоскость вставляется под другим углом, создается эллипс. Для площади используется соответствующая формула: πab (где a — самое большое расстояние от центра эллипса до края, а b — самое короткое).

Пример: Какова площадь поперечного сечения трубы под вашим домом, описанной во введении?

Площадь поперечного сечения сферы

Любая теоретическая плоскость, проведенная через сферу, даст круг (подумайте об этом несколько минут). Если вы знаете диаметр или длину окружности, образуемой поперечным сечением, вы можете использовать соотношения C = 2πr и A = πr ² для получения решения.