Кинематическая схема фрезерного станка: кинематическая схема токарного и фрезерного станков
|
Конструкции фрезерных станков » Привет Студент!
Конструкции фрезерных станков
0
Фрезерные станки подразделяются на: 1) горизонтально-фрезерные, универсально-фрезерные, 3) вертикально-фрезерные и 4) копировально-фрезерные. Рассмотрим их конструкции.
Рассмотрим их конструкции.
Горизонтально-фрезерный станок. Станки этого типа применяют в механических и инструментальных цехах. На фиг. 486 дан общий вид горизонтально-фрезерного станка. Оправка 1 служит для закрепления фрезы на шпинделе. Деталь закрепляется на столе 2.
На фиг. 487 показана кинематическая схема горизонтально-фрезерного станка. Шпиндель 1 получает вращение от шкива 2 и может работать с перебором 3 и без перебора. Стол 4 получает поступательное движение (движение подачи) от шпинделя 1 через коробку подач 5, универсальный шарнир 6, червяк 7 и червячное зубчатое колесо 8, жестко посаженное на винт продольного самоходного стола.
Универсально-фрезерный станок. Из всех типов фрезерных станков универсально-фрезерные станки получили наиболее широкое распространение; их применяют в ремонтно-механических и инструментальных цехах, а также на заводах с индивидуальным и мелкосерийным производством. Отличительной особенностью этих станков является устройство механизма стола, позволяющее осуществлять поворот стола около вертикальной оси в горизонтальной плоскости. Поворот стола в горизонтальной плоскости (производится вручную) необходим при фрезеровании спиральных канавок (спиральное сверло и т. п.). На фиг. 488 дан общий вид универсально-фрезерного станка. Оправка 1 служит для установки фрез; на столе 2 закрепляют обрабатываемые детали.
Поворот стола в горизонтальной плоскости (производится вручную) необходим при фрезеровании спиральных канавок (спиральное сверло и т. п.). На фиг. 488 дан общий вид универсально-фрезерного станка. Оправка 1 служит для установки фрез; на столе 2 закрепляют обрабатываемые детали.
На фиг. 489 показана кинематическая схема универсально-фрезерного станка. В этом станке фреза, закрепляемая на шпинделе 1, получает вращение от электродвигателя 2 через ременную передачу 3 и коробку скоростей 4. Движение подачи стол 5 получает от вала 6 через систему конических зубчатых колес и коробку подач 7. Стол 5 может иметь три различные направления движения подачи: 1) продольная подача осуществляется ходовым винтом 8, получающим вращение от конического зубчатого колеса 9; 2) вертикальная подача производится винтом 10 через коническое зубчатое колесо 11, жестко посаженное на винте 10; при вращении этого винта он, перемещаясь по гайке 12, опускает или поднимает стол; 3) поперечная подача достигается винтом 13, по которому перемещается жестко связанная со столом гайка 14.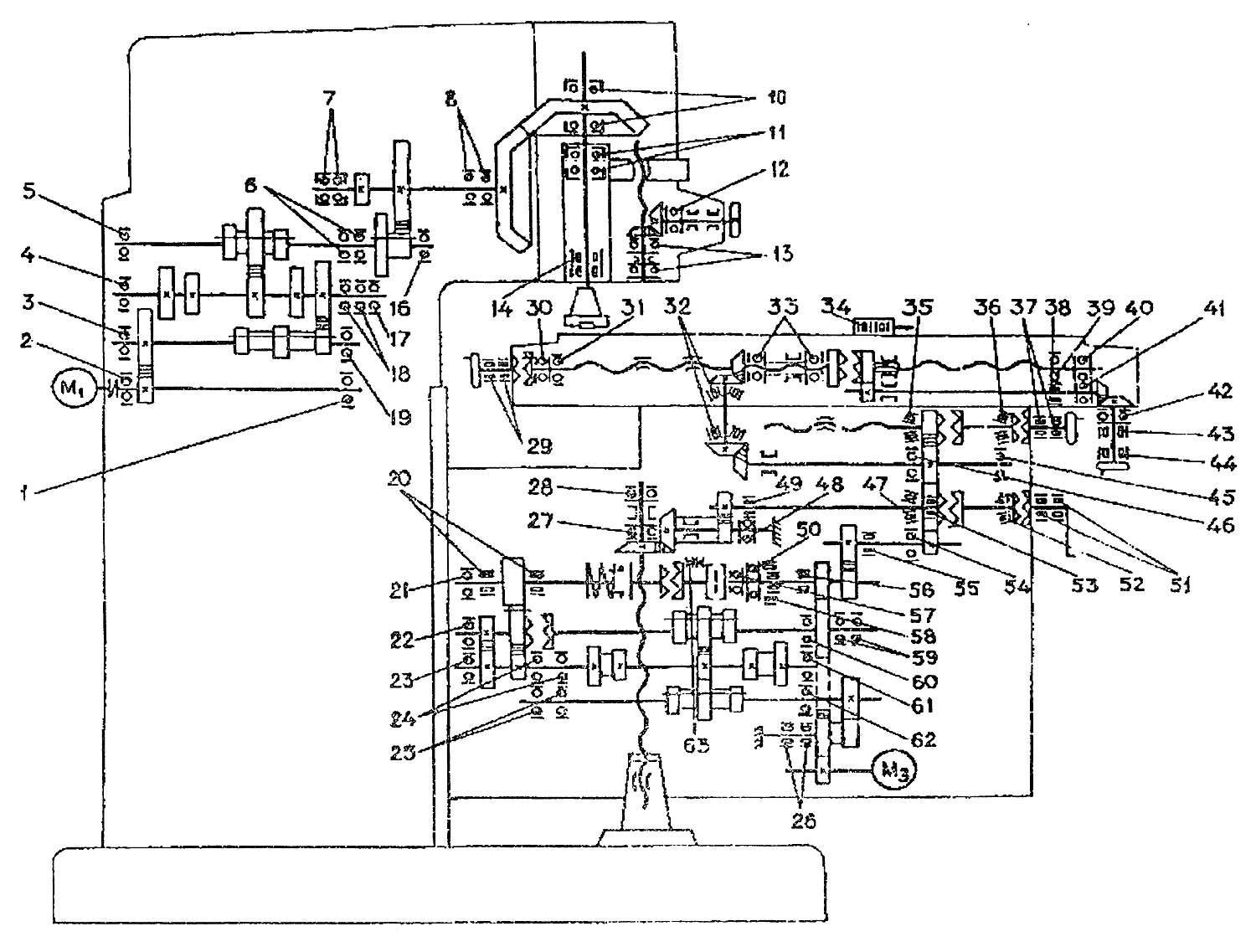
Вертикально-фрезерный станок. В вертикально-фрезерных станках шпиндель занимает вертикальное положение; привод главного движения подобен приводу вертикально-сверлильных станков. Подача в этих станках может быть продольной, поперечной и вертикальной.
Эти станки применяют главным образом для фрезерования шпоночных канавок, JL-образных пазов, пазов типа ласточкина хвоста и т. п.
На фиг. 490 дан общий вид вертикально-фрезерного станка. На столе 1 закрепляется деталь, а фреза крепится на шпинделе 2.
На фиг. 491 показана кинематическая схема вертикально-фрезерного станка, Согласно схеме шпиндель получает вращение от электродвигателя Э1 через шкивы 1 и 2 и далее через зубчатые колеса, расположенные на валах I, II, III, IV, V, VI. Подача в этом станке осуществляется от другого электродвигателя Э2 через коробку подач 3. Продольное перемещение стола (подача) производится винтом 4, поперечная — винтом 5 и вертикальная — винтом 6, полу
чающими движение через соответствующие зубчатые колеса коробки подач, аналогично тому, как это осуществлено в универсально-фрезерном станка (см. кинематическую схему на фиг. 489.
кинематическую схему на фиг. 489.
Продольно-фрезерный станок. Продольно-фрезерные станки применяют при обработке длинных и широких плоскостей, а также фасонных профилей на крупных деталях, например, станины различных станков. Эти станки отличаются высокой производительностью, так как могут работать одновременно несколькими фрезами. На фиг. 492 показан общий вид продольно-фрезерного станка. По направляющим станины может перемещаться в продольном направлении стол с закрепляемой на нем деталью; на вертикальных стойках находятся две фрезерные головки, могущие перемещаться в вертикальном направлении.
Копировально-фрезерный станок. Копировально-фрезерные станки применяют при обработке различных фасонных поверхностей. На фиг. 493 показана схема устройства копировально-фрезерного станка. На вращающемся столе 1 закреплен копир 2 и обрабатываемая деталь 3. Принцип работы станка заключается в том, что копир 2 непрерывно прижимается к ролику 4 под действием груза, не показанного на чертеже, и заставляет стол, на котором укреплена деталь, описывать траекторию, подобную линии очертания копира, а фреза 5 вследствие этого обрабатывает поверхность, очертание которой будет также аналогично с очертанием копира.
Скачать реферат: Konstrukciya-frezernyh-stankov.rar
Пароль на архив: privetstudent.com
Категория: Рефераты / Производство
Уважаемый посетитель, Вы зашли на сайт как незарегистрированный пользователь.
Мы рекомендуем Вам зарегистрироваться либо войти на сайт под своим именем.
Разработка 3-х осевого параллельного кинематического станка для фрезерования древесного материала – Часть 1: Дизайн :: Биоресурсы
Аскар Айылдиз, Э., и Айылдиз, М. (2017). «Разработка 3-осевого параллельного кинематического станка для фрезерования древесного материала. Часть 1: Конструкция», BioRes. 12(4), 9326-9337.
Abstract
Подробно описан 3-осевой параллельный кинематический станок и усовершенствованная система управления с программированием в G-коде для фрезерования древесного материала. Эта параллельная кинематическая машина основана на параллельном механизме 3-PSS (призматическое звено, сферическое звено и сферическое звено). Для этого инструмента была реализована система программирования и управления на базе платформы Windows для ПК реального времени и программного комплекса Mach4. Наконец, было представлено модельное приложение системы программирования, разработанной для линейного треугольного параллельного станка с тремя степенями свободы, и была показана применимость для фрезерования древесного материала (древесноволокнистых плит средней плотности).
Для этого инструмента была реализована система программирования и управления на базе платформы Windows для ПК реального времени и программного комплекса Mach4. Наконец, было представлено модельное приложение системы программирования, разработанной для линейного треугольного параллельного станка с тремя степенями свободы, и была показана применимость для фрезерования древесного материала (древесноволокнистых плит средней плотности).
Загрузить в формате PDF
Статья полностью
Разработка 3-осевого параллельного кинематического станка для фрезерования древесных материалов. Часть 1: Проектирование
Эльмас Ашкар Айылдыз a и Мустафа Айылдыз b, *
Подробно описан 3-осевой параллельный кинематический станок и усовершенствованная система управления с программированием в G-коде для фрезерования древесного материала. Эта параллельная кинематическая машина основана на параллельном механизме 3-PSS (призматическое звено, сферическое звено и сферическое звено). Для этого инструмента была реализована система программирования и управления на базе платформы Windows для ПК реального времени и программного комплекса Mach4. Наконец, было представлено модельное приложение системы программирования, разработанной для линейного треугольного параллельного станка с тремя степенями свободы, и была показана применимость для фрезерования древесного материала (древесноволокнистых плит средней плотности).
Для этого инструмента была реализована система программирования и управления на базе платформы Windows для ПК реального времени и программного комплекса Mach4. Наконец, было представлено модельное приложение системы программирования, разработанной для линейного треугольного параллельного станка с тремя степенями свободы, и была показана применимость для фрезерования древесного материала (древесноволокнистых плит средней плотности).
Ключевые слова: Параллельная кинематическая машина; G-код; Фрезерование древесного материала
Контактная информация: а: Институт науки и технологий Университета Карабюк, Карабюк, Турция; b: Факультет технологии производства технологического факультета Университета Дюздже, Дюздже, Турция; * Автор, ответственный за переписку: [email protected]
ВВЕДЕНИЕ
На обработку древесины сильно влияет текстура древесины. Таким образом, достижение оптимальных условий обработки древесины является очень важной областью исследований (Агилера 9). 0004 и др. 2000). Фрезерование — это операция механической обработки, обычно используемая при изготовлении деталей из дерева. В предыдущей литературе фрезерование металла широко изучалось, но фрезерованию древесноволокнистых плит средней плотности (МДФ) уделялось мало внимания. Многие работы (Aguilera et al. 2000; Gordon and Hillery 2003; Lin et al. 2006; Davim et al. 2009; Vancho et al. 2 017), при сообщении о механической обработке древесного материала, показали, что обрабатываемость зависит от режущего инструмента, механики резания и материала заготовки.
0004 и др. 2000). Фрезерование — это операция механической обработки, обычно используемая при изготовлении деталей из дерева. В предыдущей литературе фрезерование металла широко изучалось, но фрезерованию древесноволокнистых плит средней плотности (МДФ) уделялось мало внимания. Многие работы (Aguilera et al. 2000; Gordon and Hillery 2003; Lin et al. 2006; Davim et al. 2009; Vancho et al. 2 017), при сообщении о механической обработке древесного материала, показали, что обрабатываемость зависит от режущего инструмента, механики резания и материала заготовки.
Параллельные кинематические станки
(PKM) часто используются во многих промышленных приложениях, где требуется высокая точность, требуемая последними достижениями в области технологий. Это связано с тем, что параллельные манипуляторы обладают такими возможностями, как более высокая полезная нагрузка, высокая жесткость и точность, хорошая стабильность, удобство использования в высокоскоростных приложениях, хорошие динамические характеристики и точное позиционирование. ПКМ часто используются в промышленных приложениях, таких как медицинские операции, игровые симуляторы, нефтяные платформы, тяжелый грузовой транспорт, обработка легких металлов, полировка, резка, формование и сборка, а также авиасимуляторы.
ПКМ часто используются в промышленных приложениях, таких как медицинские операции, игровые симуляторы, нефтяные платформы, тяжелый грузовой транспорт, обработка легких металлов, полировка, резка, формование и сборка, а также авиасимуляторы.
Изучив литературу, Гао и др. . (2002) представили дизайн и инновации для новых вариантов параллельных механизмов с 2 степенями свободы (DOF), 3 степенями свободы, 4 степенями свободы и 5 степенями свободы. В своем исследовании Liu et al. (2005 г.) предложил семейство параллельных манипуляторов с 3 степенями свободы с новой высокой скоростью вращения, позволяющей преодолеть возможности низкой скорости существующих параллельных манипуляторов. Будде и др. (2007 г.) представил проблемы проектирования (сингулярность) и оптимизацию линейного дельта-робота (рабочее пространство, жесткость, точность различной длины стержней) и реализовал их модельное применение в поддержку этой работы (Budde и др. 2008).
Стан и др. (2008 г.) представила многокритериальную процедуру оптимального проектирования с учетом характеристик роботов с трехступенчатым и дельта-планированием, таких как границы рабочего пространства, жесткость и индекс качества передачи (характеристики скорости, силы и мощности), которые являются оптимальными критериями проектирования для 3-DOF. параллельные роботы. Корбел и др. (2008) представил проект и оптимизацию параллельного станка путем объединения реального робота с 3 степенями свободы (линейная дельта) с измерительными параллельными роботами с 6 степенями свободы. 9 юаней0004 и др. (2008) предложил оптимальные методы проектирования линейного дельта-робота для получения заданного прямоугольного рабочего пространства.
Келайайа и др. (2012) представлено иллюстративное применение методологии, разработанной для линейного дельта-параллельного робота с 3-степенями свободы. Эта методология включает геометрическую, кинематическую и динамическую модели выбранной конструкции. Он оценивает критерии производительности (рабочее пространство, жесткость, кинематическая и динамическая производительность), определяет границы структуры робота, создает математические формулы задачи оптимизации и использует утилиту генетического алгоритма для решения задачи. Патель и Джордж (2012) сравнили различные критерии, такие как структуры и рабочие пространства, для последовательных и параллельных манипуляторов. Ниу и др. (2013) представили динамику и управление новым параллельным манипулятором с 3 степенями свободы с резервированием срабатывания. Цзэн и др. (2014) представил структуру и дизайн ограничений поступательно-параллельного манипулятора с 3 степенями свободы. Лин и др. (2015) исследовал конструкцию и реализацию дельта-параллельного робота, охватывающего весь мехатронный процесс, включая кинематику, схему управления и методы оптимизации. Се и др. (2016) предложен гибридный механизм с 6 степенями свободы для разработки станка для шлифования турбинных лопаток.
Он оценивает критерии производительности (рабочее пространство, жесткость, кинематическая и динамическая производительность), определяет границы структуры робота, создает математические формулы задачи оптимизации и использует утилиту генетического алгоритма для решения задачи. Патель и Джордж (2012) сравнили различные критерии, такие как структуры и рабочие пространства, для последовательных и параллельных манипуляторов. Ниу и др. (2013) представили динамику и управление новым параллельным манипулятором с 3 степенями свободы с резервированием срабатывания. Цзэн и др. (2014) представил структуру и дизайн ограничений поступательно-параллельного манипулятора с 3 степенями свободы. Лин и др. (2015) исследовал конструкцию и реализацию дельта-параллельного робота, охватывающего весь мехатронный процесс, включая кинематику, схему управления и методы оптимизации. Се и др. (2016) предложен гибридный механизм с 6 степенями свободы для разработки станка для шлифования турбинных лопаток. Представлен концептуальный проект и проанализирована особенность параллельного модуля 3-DOF. Сюй и др. (2017) представил новый гибридный станок с последовательно-параллельной топологической структурой с 6 степенями свободы, используемый в качестве сверхточного полировального оборудования.
Представлен концептуальный проект и проанализирована особенность параллельного модуля 3-DOF. Сюй и др. (2017) представил новый гибридный станок с последовательно-параллельной топологической структурой с 6 степенями свободы, используемый в качестве сверхточного полировального оборудования.
Сегодня большинство университетских лабораторий, научно-исследовательских институтов и предприятий не имеют ПКМ. Это связано с тем, что затраты на образование и обучение для новой технологии, такой как ПКМ, высоки. В литературе встречаются редкие исследования недорогой параллельной кинематической машины с 3 степенями свободы, направленные на то, чтобы внести свой вклад в практический опыт использования ПКМ (Главонич и др. . 2009). Ян и Хонг (2001) разработали программное обеспечение для трехмерной (3D) линейной и круговой интерполяции на основе перехвата в реальном времени для достижения одновременного 3-осевого движения на фрезерном станке PC-NC. Гордон и Хиллери (2005) разработали недорогую систему перемещения X/Y мостового типа. В этой системе контроллер ЧПУ управляется интерфейсом, поддерживающим G-коды, написанные на C++. Канаан и др. (2009) получили уравнения обратной и прямой кинематики для последовательно-параллельного 5-осевого станка, который они назвали станком VERNE. Здесь предлагаются символьные методы для вычисления всех кинематических решений.
В этой системе контроллер ЧПУ управляется интерфейсом, поддерживающим G-коды, написанные на C++. Канаан и др. (2009) получили уравнения обратной и прямой кинематики для последовательно-параллельного 5-осевого станка, который они назвали станком VERNE. Здесь предлагаются символьные методы для вычисления всех кинематических решений.
Го и др. (2012 г.) разработан универсальный программный процессор числового управления (ЧПУ) для систем ЧПУ, предназначенный для обработки различных типов программного обеспечения ЧПУ, поскольку большинство производителей ЧПУ используют свои собственные пользовательские функции в программном обеспечении ЧПУ. В этом исследовании цель состоит в том, чтобы преобразовать G-коды, созданные любым программным обеспечением CAM для управления линейной дельта-параллельной машиной, одной из структур ПКМ, в новую структуру G-кода, интерпретируемую роботом. С этой целью была разработана инверсная кинематическая модель для линейной дельта-параллельной машины, а G-коды были преобразованы в осмысленную кодовую систему для этой конструкции через разработанный интерфейс. Созданные новые коды были последовательно переданы в структуру ПКМ для управления системой.
Созданные новые коды были последовательно переданы в структуру ПКМ для управления системой.
ЭКСПЕРИМЕНТАЛЬНЫЙ
Описание и кинематика механизма
На рис. 1 показаны геометрические характеристики линейной дельта-параллельной машины. Как видно на рис. 2, машина представляет собой параллельный робот с 3 степенями свободы типа 3-PSS (призматическое звено, сферическое звено, сферическое звено) (Gao et al . 2002) . Робот состоит из рук, интегрированных в стационарную платформу, и мобильной платформы. Мобильная платформа и неподвижная платформа связаны друг с другом 3-мя кинематическими цепями, расположенными под углом α и . Каждая кинематическая цепь была соединена с двумя параллельными стержнями длиной L (с дистальным и проксимальным сферическим звеном) и с линейным приводом (Gao et al . 2002).
Мобильная платформа всегда оставалась параллельной неподвижной платформе. Призматическое движение подвижной платформы обеспечивалось совместным движением всех трех исполнительных механизмов. В литературе имеются различные исследования кинематического моделирования линейного дельта-робота (Компани и Пьеро, 2002; Ригеттини, 9).0004 и др. 2002; Лю и др. 2004; Келайайа и др. 2012; Се и др. 2016).
Призматическое движение подвижной платформы обеспечивалось совместным движением всех трех исполнительных механизмов. В литературе имеются различные исследования кинематического моделирования линейного дельта-робота (Компани и Пьеро, 2002; Ригеттини, 9).0004 и др. 2002; Лю и др. 2004; Келайайа и др. 2012; Се и др. 2016).
Рис. 1. Геометрическое определение линейного дельта-робота (Gao et al . 2002)
Геометрические определения линейного дельта-робота приведены ниже (Gao et al . 2002),
{ Р 0 }: ( 0 0 –х 0 , у 0 , z 0 ): « 0 0 ” — система отсчета для неподвижной платформы, центр равностороннего треугольника 0 1 0 2 0 3 , а также центр окружности радиусом 900 04 Р б .
{ R p }: ( P—x n , y n , z n ): « P » система отсчета для мобильной платформы, центр равносторонней треугольник B 1 B 2 B 3 , а также центр окружности радиусом R n .
q 1 , q 2 , q 3 : Связывает переменные для управления ходом 3 линейных приводов.
R b : Радиус окружности с центром в точках 0 0, и расстояние между 0 i и 0 9010 7 0, и
Р n : Радиус круга с центром в P , расстояние между « P», B i и центром мобильной платформы, и.
Кинематическая модель линейного дельта-робота относится к положению и ориентации концевого зажима относительно системы отсчета ( R 0 ) и .
A i B i 2 – L 2 = 0, i = 1, 2, 3 (1)
Координаты B i в системе отсчета для подвижной платформы даны в уравнении. 2,
и координаты A i в системе отсчета для фиксированной платформы даны в уравнении. 3,
3,
Используя уравнение. 1, чтобы построить выражение инверсной кинематической модели, уравнение. 5 было получено.
Чтобы построить прямую кинематическую модель для линейного дельта-робота, уравнение. 6 следует решать относительно X, Y и Z (Стандарт и др. 2008),
где:
Принято решение
Применение приведенных выше уравнений к уравнению. 6 была сформулирована прямая кинематическая модель линейного дельта-робота.
Рис. 2. Схема связи линейного дельта-робота
Структура управления линейной дельта-параллельной машиной
Интегрированные операции системы были обеспечены с помощью системы программного обеспечения, подходящей для управления линейной дельта-параллельной машиной. Интерфейс, разработанный с инверсным кинематическим моделированием линейных дельта и G-кодов, был преобразован в осмысленную кодовую систему для этой структуры. Полученные коды были последовательно переданы в структуру ПКМ для управления системой. На рис. 3 показана структура управления линейной дельта-параллельной машиной.
Полученные коды были последовательно переданы в структуру ПКМ для управления системой. На рис. 3 показана структура управления линейной дельта-параллельной машиной.
Рис. 3. Схема управления линейной дельта-параллельной машиной
На основании рис. 3 можно спланировать орбиту линейной дельта-параллельной машины. При разработке модели любого физического объекта коды сборки объекта создавались с помощью программного обеспечения CAM. Здесь коды сборки, созданные с помощью программного обеспечения CAM, были сформированы в соответствии с декартовым пространством. Адаптируя эти коды в декартовом пространстве к среде сборки, двигатели, связанные с осями X, Y и Z, приводились в движение линейно. Коды, созданные для декартовой структуры, не подходили для подвижной структуры линейной дельта-параллельной структуры машины в рабочей области. Благодаря прямолинейному движению плеч A 1 , A 2 и A 3 линейной дельты, и из-за призматических движений, происходящих на стыке этих плеч, было необходимо преобразование в систему кодирования, интерпретируемую декартовой структурой. Поэтому была создана новая система кодирования на основе соответствующих кодов CAM через интерфейс в соответствии с призматическим движением плеч A 1 , A 2 и A 3 линейным дельта, и с использованием кинематических уравнений для этого состав. Созданные новые коды были запущены в программном обеспечении Mach4 (Валентино и Гольденберг, 2006 г.) для управления линейной дельта-параллельной машиной. Управление линейной дельта-параллельной машиной осуществлялось путем повторения этой последовательности.
Поэтому была создана новая система кодирования на основе соответствующих кодов CAM через интерфейс в соответствии с призматическим движением плеч A 1 , A 2 и A 3 линейным дельта, и с использованием кинематических уравнений для этого состав. Созданные новые коды были запущены в программном обеспечении Mach4 (Валентино и Гольденберг, 2006 г.) для управления линейной дельта-параллельной машиной. Управление линейной дельта-параллельной машиной осуществлялось путем повторения этой последовательности.
РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ
Производство кодов CAM
С помощью программного обеспечения Mastercam X5 (Валентино и Голденберг, 2006 г.) были созданы коды сборки объекта, разработанного в любой программе САПР. При создании кодов сборки с помощью Mastercam X5 был выбран тип станка «По умолчанию». Причина этого в том, что для линейной дельта-параллельной машины не существует типа машины. На рис. 4 показан пример кода, созданного с помощью Mastercam X5.
Рис. 4. Пример кода, созданный с помощью Mastercam X5
Преобразование кода с помощью разработанного интерфейса
Поскольку коды, созданные с помощью Mastercam X5 на рис. 4, подходили для типов машин с декартовой структурой, эти коды были преобразованы в пространство движения параллельной дельта-параллельной машины, имеющей параллельную структуру. Использовались уравнения обратной кинематики. Интерфейс разработан в Visual Studio 2015 (рис. 5).
Рис. 5. Разработан интерфейс
Рис. 6. Блок-схема разработанной системы интерфейса
Блок-схема разработанной системы интерфейса представлена на рис. 6. В этом интерфейсе был разработан алгоритм для кодов G0, G1, G2 и G3. Для кодов G0 и G1 новый код был получен путем выполнения обратного кинематического расчета со значениями X, Y, Z в соответствующей строке. Используя начальную и конечную точки дуги в качестве эталона для кода G2, путь дуги был пикселизирован для линейной интерполяции по часовой стрелке со значениями X, Y, Z и I, J, K. Эти пиксели были рассчитаны на основе найденного угла дуги и гипотенузы. То же самое относится к коду G3. Когда интерфейс распознал коды G2 и G3, алгоритм запустился, и новый код был преобразован в код G1. На рис. 7 показаны параметры круговой интерполяции G2 и G3 (Petrovic и др. 2017).
Эти пиксели были рассчитаны на основе найденного угла дуги и гипотенузы. То же самое относится к коду G3. Когда интерфейс распознал коды G2 и G3, алгоритм запустился, и новый код был преобразован в код G1. На рис. 7 показаны параметры круговой интерполяции G2 и G3 (Petrovic и др. 2017).
Радиус дуг, показанных на рис. 7, дан в уравнении. 16, а углы дуги приведены в уравнениях. 17 и 18 (Петрович и др. 2017),
где x 1 , y 1 , и z 1 — координаты начала дуги, x 2 , y 2 , и z 2 — конец дуги координаты, x c , y c , и z c — центральные координаты круговой интерполяции, r — радиус круговой интерполяции ( o ), α 0 – начальный угол круговой интерполяции ( o ), а α 1 является круговым углом интерполяции ( o ).
Запуск новых кодов с Mach4
Созданные новые коды были запущены с использованием программного обеспечения Mach4. Программное обеспечение Mach4 связывалось с картой управления USB AKZ250 для управления двигателями. На практике было выполнено оконтуривание геометрии квадрата, круга и треугольника. На рис. 8 показано типовое приложение. В таблице 1 показаны G-коды, созданные для декартовой структуры, и новые G-коды, преобразованные в дельта-структуру посредством разработанного интерфейса.
Рис. 8. Контурирование модели для квадрата, круга и треугольника
Таблица 1. G-коды, созданные для декартовой структуры
ВЫВОДЫ
- В этом документе представлена новая конструкция линейного треугольного параллельного станка для фрезерования древесного материала. Разработка машины включала разработку механизма, а также его аппаратного и программного обеспечения.

- Для линейной дельта-параллельной машины была разработана инверсная кинематическая модель, и G-коды были преобразованы в осмысленную систему кодов для этой конструкции через разработанный интерфейс. Полученные новые коды были последовательно переданы в линейную дельта-структуру для управления системой.
- Наконец, путем разработки модельного приложения системы программирования, разработанной для линейного треугольно-параллельного станка с 3 степенями свободы, была продемонстрирована пригодность для фрезерования древесного материала (древесноволокнистых плит средней плотности).
ССЫЛКИ
Агилера, А., Мосоун, П.Дж., и Мартин, П. (2000). «Влияние древесного материала на операции фрезерования: корпус МДФ», евро. Дж. Вуд Вуд Прод. 58(4), 278-283. DOI: 10.1007/s001070050425
Бадде, К., Ласт, П., и Хессельбах, Дж. (2007). «Разработка робота-триплана с увеличенным рабочим пространством», в: Робототехника и автоматизация, 2007 г. , Международная конференция IEEE , Рим, Италия, стр. 543–548.
, Международная конференция IEEE , Рим, Италия, стр. 543–548.
Бадде, К., Роуз, М., Маасс, Дж., и Раат, А. (2008). «Автоматическое определение режима сборки для робота Triglide», в: Robotics and Automation 2008 IEEE International Conference , Пасадена, Калифорния, США, стр. 1568-1575.
Company, О., и Пьеро, Ф. (2002). «Вопросы моделирования и предварительного проектирования 3-осевого параллельного станка», Мех. Мах. Теория 37(11), 1325–1345. DOI: 10.1016/S0094-114X(02)00040-X
Корбель, Д., Компания, О., и Пьеро, Ф. (2008). «Оптимальный дизайн механизма параллельного измерения с 6 степенями свободы, интегрированного в параллельный станок с 3 степенями свободы», в: Intelligent Robots and Systems 2008 IEEE/RSJ International Conference, Nice, France, pp. 1970-1976.
Дэвим, Дж. П., Клементе, В. К., и Сильва, С. (2009). «Аспекты шероховатости поверхности при фрезеровании МДФ (древесноволокнистых плит средней плотности)», Междунар. Дж. Адв. Произв. Тех. 40(1), 49-55. DOI: 10.1007/s00170-007-1318-z
Дж. Адв. Произв. Тех. 40(1), 49-55. DOI: 10.1007/s00170-007-1318-z
Гао Ф., Ли В., Чжао X., Цзинь З. и Чжао Х. (2002). «Новые кинематические структуры для параллельных манипуляторов с 2, 3, 4 и 5 степенями свободы», Mech. Мах. Theory 37(11), 1395-1411.DOI: 10.1016/S0094-114X(02)00044-7
Главонич, М., Милутинович, Д., и Живанович, С. (2009). «Функциональный тренажер 3-осевого параллельного кинематического фрезерного станка», Междунар. Дж. Адв. Произв. Тех. 42(7), 813-821. DOI: 10.1007/s00170-008-1643-x
Гордон С. и Хиллери М. Т. (2003). «Обзор резки композитных материалов», P.I. Mech. англ. Л-Дж. Мат. 217(1), 35-45. DOI: 10.1177/146442070321700105
Гордон С. и Хиллери М. Т. (2005). «Разработка высокоскоростного станка для резки с ЧПУ с использованием линейных двигателей», J. Mater. Процесс. Тех. 166(3), 321-329. DOI: 10.1016/j.jmatprotec.2003.08.009
Го, X., Лю, Ю., Ду, Д., Ямадзаки, К., и Фудзисима, М.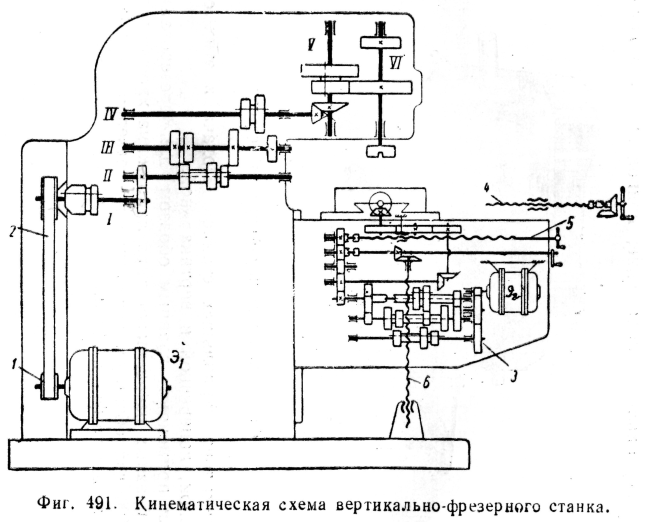 (2012). «Проект универсального программного процессора ЧПУ и реализация прототипа для систем ЧПУ», Междунар. Дж. Адв. Произв. Тех. 60(5), 561-575. DOI: 10.1007/s00170-011-3618-6
(2012). «Проект универсального программного процессора ЧПУ и реализация прототипа для систем ЧПУ», Междунар. Дж. Адв. Произв. Тех. 60(5), 561-575. DOI: 10.1007/s00170-011-3618-6
Канаан, Д., Венгер, П., и Шаблат, Д. (2009). «Кинематический анализ последовательно-параллельного станка: машина Верна», Mech. Мах. Теория 44(2), 487–498. DOI: 10.1016/j.mechmachtheory.2008.03.002
Kelaiaia, R., Company, O., and Zaatri, A. (2012). «Многокритериальная оптимизация линейного дельта-параллельного робота», Mech. Мах. Теория 50, 159–178. DOI: 10.1016/j.mechmachtheory.2011.11.004
Лин, Дж., Луо, С. Х., и Лин, К. Х. (2015). «Проектирование и внедрение нового дельта-параллельного робота на соревнованиях по робототехнике», Int. Дж. Адв. Робот Сист. 12(10), 153-162. DOI: org/10.5772/61744
Лин, Р. Дж., Ван Хаутс, Дж., и Бхаттачарья, Д. (2006). «Исследование обрабатываемости древесноволокнистых плит средней плотности», Holzforschung 60(1), 71-77. DOI: 10.1515/HF.2006.013
DOI: 10.1515/HF.2006.013
Лю, X. Дж., Ван, Дж., и Притшоу, Г. (2005). «Новое семейство пространственных полностью параллельных манипуляторов с тремя степенями свободы и высокой вращательной способностью», Мех. Мах. Теория 40(4), 475–494. DOI: 10.1016/j.mechmachtheory.2004.10.001
Лю, С. Дж., Ван, Дж., О, К. К., и Ким, Дж. (2004). «Новый подход к проектированию дельта-робота с желаемым рабочим пространством», J. Intell. Робот. Сист. 39(2), 209-225. DOI: 10.1023/B:JINT.0000015403.67717.68
Niu, X.M., Gao, G.Q., Liu, X.J., and Bao, Z.D. (2013). «Динамика и управление новым параллельным манипулятором с 3 степенями свободы с резервированием срабатывания», Int. Дж. Автомат. Вычисление . 10(6), 552-562. DOI: org/10.1007/s11633-013-0753-6
Патель, Ю. Д., и Джордж, П. М. (2012). «Приложения параллельных манипуляторов — обзор», Modern Machine Engineering, , 2(3), 57–64. DOI: 10.4236/mme.2012.23008
Петрович А. , Лукич Л., Иванович С. и Павлович А. (2017). «Оптимизация траектории движения инструмента при обработке древесины на станках с ЧПУ», P.I. Mech. англ. CJ. Мех. 231(1), 72–87. DOI: 10.1177/0954406216648715
, Лукич Л., Иванович С. и Павлович А. (2017). «Оптимизация траектории движения инструмента при обработке древесины на станках с ЧПУ», P.I. Mech. англ. CJ. Мех. 231(1), 72–87. DOI: 10.1177/0954406216648715
Ригеттини П., Тасора А. и Гиберти Х. (2002). «Мехатронный дизайн параллельного поступательного манипулятора с тремя степенями свободы», в: 11-й Международный форум по робототехнике в регионе Альпы-Адриа-Дунай , Балатонфюред, Венгрия, стр. 367-372.
Стэн, С. Д., Маник, М., Матиес, В., и Балан, Р. (2008). «Эволюционный подход к оптимальному проектированию экзоскелета с тремя степенями свободы и медицинского параллельного робота», в: «Взаимодействия человеческих систем», 2008 г., конференция , Краков, Польша, стр. 720-725.
Валентино, Дж., и Гольденберг, Дж. (2006). «Пошаговое обучение работе с mastercam x5mill 2d», Industrial Press Inc., Нью-Йорк, США.
Ванчо М., Джамберова З., Барчик Ш., Гафф М., Чековска Х. и Каплан Л. (2017). «Влияние выбранных технических, технологических и материальных факторов на размер щепы молодой древесины тополя, образующейся при торцевом фрезеровании», BioResources 12(3), 4881-4896. DOI: 10.15376.biores./12.3.4881-4896
(2017). «Влияние выбранных технических, технологических и материальных факторов на размер щепы молодой древесины тополя, образующейся при торцевом фрезеровании», BioResources 12(3), 4881-4896. DOI: 10.15376.biores./12.3.4881-4896
Се, Ф., Лю, X. Дж., и Ван, Дж. (2016). «Концептуальное проектирование и оптимизация параллельного механизма с тремя степенями свободы для станка для шлифования лопаток турбины», P.I. Mech. англ. CJ. Мех. 230(3), 406–413. DOI: 10.1177/0954406215589122
Сюй, П., Ли, Б., Чунг, К.Ф., и Чжан, Дж.Ф. (2017). «Моделирование жесткости и оптимизация параллельного робота с тремя степенями свободы в последовательно-параллельной полировальной машине», Int. Дж. Точность. англ. Мужчина. 18(4), 497-507. DOI: org/10.1007/s12541-017-0060-1
Ян, М.Ю., и Хонг, В.П. (2001). «Фрезерный станок ПК-ЧПУ с новым алгоритмом одновременного 3-осевого управления», Int. Дж. Мах. Инструмент. Ману. 41(4), 555-566. DOI: 10. 1016/S0890-6955(00)00091-2
1016/S0890-6955(00)00091-2
Юань, К., Цзи, С., Ван, З., Ван, Г., Ван, Ю. и Чжан, Л. (2008). «Оптимальный дизайн линейного дельта-робота для заданного кубовидного ловкого рабочего пространства на основе диаграммы производительности», в: Материалы международной конференции WSEAS «Математика и компьютеры в науке и технике» (№ 8) Всемирная научно-техническая академия и общество , Ханчжоу, Китай , стр. 35-41.
Цзэн, К., Эйманн, К.Ф., и Цао, Дж. (2014). «Робот с тремя пирамидами: конструкция и кинематический анализ поступательно-параллельного манипулятора с тремя степенями свободы», Вычислительный робот. интегр. Произв. 30(6), 648-657. DOI: org/10.1016/j.rcim.2014.06.002
Статья отправлена: 23 июня 2017 г.; Экспертная оценка завершена: 14 октября 2017 г.; Получена и принята исправленная версия: 18 октября 2017 г. Опубликовано: 25 октября 2017 г.
DOI: 10.15376/biores.12.4.9326-9337
Причина №7 для перехода на TopSolid
Я затронул тему «Кинематическая осведомленность» в посте №10 своей серии. С TopSolid вы начинаете с создания кинематической модели сборки вашего станка.
С TopSolid вы начинаете с создания кинематической модели сборки вашего станка.
(Обратите внимание, что на самом деле вам не «обязано» это делать, вы не «вынуждены» использовать машинное определение во время программирования, но если вы не получаете знания о машине «заранее», вы не Вы не получите всех преимуществ, которые TopSolid может предложить Вам в процессе программирования. Подробнее об этом далее…)
Проще говоря, «кинематическая модель» станка определяет линейные и круговые оси, их пределы перемещения, и их отношения сборки между каждым компонентом. (Что к чему крепится болтами?) Кинематическая модель фиксирует компоновку машины и строится как физическое представление машины в исходном положении машины. Когда вы размещаете обрабатываемую деталь на этой модели, TopSolid «знает», где находятся позиции смены инструмента (мы определяем это), сколько карманов находится в устройстве смены инструмента и позиции рабочих смещений, когда мы загружаем деталь на машинный стол.
Поскольку TopSolid позволяет точно определять кинематические движения вашей машины, разработчики поступили очень умно. Компания Missler Software разработала TopSolid для захвата кинематических возможностей вашего станка и использования этих возможностей при создании траекторий! На самом деле это невероятный подвиг, поскольку на рынке существует около 220 различных конфигураций 5-осевых фрезерных станков.
Я видел исследование, проведенное крупным производителем станков, в котором они провели конкурентный анализ различных станков 5X, представленных на рынке, и конфигурации поворотных/линейных осей каждого из них, включая их собственные. Цель исследования состояла в том, чтобы найти наиболее точный и эффективный метод построения 5-осевой машины. Они придумали 216 или 218 различных конфигураций, откуда я и получил свой номер выше. Если вы остановитесь и задумаетесь об этом на минуту, вы увидите, насколько удивительно сложным становится переход от конфигурации станка с 4 осями к конфигурации с 5 осями. Теперь представьте, что вы имеете дело с 9Осевой, 11-осевой, 13-осевой или более токарно-фрезерный / многозадачный станок, и у вас должна быть мощная и интеллектуальная CAM-система, достаточно эффективная для его запуска. Машины становятся экспоненциально сложными.
Теперь представьте, что вы имеете дело с 9Осевой, 11-осевой, 13-осевой или более токарно-фрезерный / многозадачный станок, и у вас должна быть мощная и интеллектуальная CAM-система, достаточно эффективная для его запуска. Машины становятся экспоненциально сложными.
То, что когда-то было простым вопросом знания нескольких основных G-кодов и M-кодов, меняется, поскольку границы между типами машин продолжают стираться. Теперь у нас есть токарно-фрезерные станки, токарно-фрезерные станки, токарные станки с несколькими револьверными головками, или головками, или задними бабками, или люнетами, или какой-то другой нестандартной вещью, которая отличается от любого другого станка, который там есть. И угадай что? Нет больше такого понятия, как «та же самая машина». В цеху, где я работаю, есть линейка «идентичных» моделей токарно-фрезерных станков. Но в каждом из них различия в переключателях битов параметров радикально меняют поведение машины для разных считываемых кодов. Или кто-то не знает, что 3-я машина была «демонстрационной» моделью, поэтому в ней отсутствует опция, или есть «все опции», и она ведет себя иначе, чем другие машины, стоящие рядом с ней.
Или кто-то не знает, что 3-я машина была «демонстрационной» моделью, поэтому в ней отсутствует опция, или есть «все опции», и она ведет себя иначе, чем другие машины, стоящие рядом с ней.
Поскольку TopSolid собирает информацию о кинематике вашего станка «заранее», они могут использовать «движок» в фоновом режиме, чтобы представить вам доступные параметры для вашего станка во время создания траектории. Почему это важно?
Возьмем то, что на первый взгляд кажется достаточно простым, Фрезерование внешнего контура детали. Вы выбираете траекторию торцевого фрезерования 2D, и вуаля, у вас есть траектория, которая проходит по внешней стороне вашей детали. Теперь вы добираетесь до машины, только чтобы понять, что вы исчерпали ход по оси Y на 0,750 дюйма! (Это сценарий, который случался со мной бесчисленное количество раз за мою карьеру; опция на машине на уровне операции.Может быть, это включение/выключение высокой скорости, или включение координаты или вращения плоскости…) Теперь вы возвращаетесь к чертежной доске и понимаете, что у вас достаточно хода, если вы задействуйте ось C стола. Но как вы это делаете? В большинстве CAM-систем вам нужно выполнить некоторые сложные математические действия, чтобы взять линейные / круговые движения дуги, разбить их на позиции вектора инструмента, а затем подать эти векторы к той части почтового движка, которая вычисляет линейное/поворотное положение.Это сложный процесс, который понимают или умеют реализовать только самые талантливые и склонные к математике программисты.Как только эта логика вписана в ваш пост, это становится простым вопросом установка значения переключателя переменной для включения, но для его реализации требуется, чтобы у вас был отличный разработчик постпроцессора. Вы также вынуждены платить непомерную сумму денег за постпроцессор.
Но как вы это делаете? В большинстве CAM-систем вам нужно выполнить некоторые сложные математические действия, чтобы взять линейные / круговые движения дуги, разбить их на позиции вектора инструмента, а затем подать эти векторы к той части почтового движка, которая вычисляет линейное/поворотное положение.Это сложный процесс, который понимают или умеют реализовать только самые талантливые и склонные к математике программисты.Как только эта логика вписана в ваш пост, это становится простым вопросом установка значения переключателя переменной для включения, но для его реализации требуется, чтобы у вас был отличный разработчик постпроцессора. Вы также вынуждены платить непомерную сумму денег за постпроцессор.
Вот кое-что, что должно вас огорчить в вашем текущем программном обеспечении CAM: Постпроцессоры
дешевые в TopSolid. Это связано с тем, что все математические и вращательные расчеты многоосевой модели уже выполнены: вы уже заплатили за это! TopSolid — это Кинематическая Осведомленность! Зачем платить за расчеты дважды??? Большинство постпроцессоров TopSolid бесплатны с минимальными изменениями. И да, вы также можете редактировать или создавать свои собственные сообщения. Механизм постинга TopSolid написан на C#, современном языке, основанном на Microsoft .NET Framework, и дает вам доступ ко всем современным инструментам программирования для написания постпроцессора.
И да, вы также можете редактировать или создавать свои собственные сообщения. Механизм постинга TopSolid написан на C#, современном языке, основанном на Microsoft .NET Framework, и дает вам доступ ко всем современным инструментам программирования для написания постпроцессора.
Подумайте об этом. Зная, как расположить ваш станок, чтобы прорезать траекторию движения инструмента в материале детали, TopSolid вычисляет фактическую ориентацию инструмента на станке, используя реальные координаты станка. Если траектория позиционируется неправильно, вы фиксируете ее в моделировании, возвращаетесь к траектории инструмента и меняете значение угла/пары для поворотных позиций и при необходимости используете редактор движения Inter-Link для управления отводом/подводом. движется. Это означает, что все движения машины запрограммированы внутри TopSolid, а постпроцессор просто форматирует строки для вывода текста.
TopSolid работает иначе. Поскольку возможности станка известны, вам просто нужно установить флажок, чтобы переключиться с «фрезерного» на «токарный» режим, и это дает вам выход «Ось C», перемещая инструмент только локально по XY, сохраняя касательную фрезу к ваша форма детали по мере того, как вращается стол машины. Это все включено для вас. На самом деле, вы можете перейти к «многоосевым» настройкам для любой 2D- или 3D-траектории инструмента и, по сути, «преобразовать» вывод в сложное 4-кратное или 5-кратное движение. Настоящая красота заключается в том, сколько машинных знаний собрано и доступно вам.
Это все включено для вас. На самом деле, вы можете перейти к «многоосевым» настройкам для любой 2D- или 3D-траектории инструмента и, по сути, «преобразовать» вывод в сложное 4-кратное или 5-кратное движение. Настоящая красота заключается в том, сколько машинных знаний собрано и доступно вам.
Вы можете управлять «ведомой» осью для вращательного движения, включать различные режимы обработки, выбирать начальный/конечный углы для операции, задавать станку другой диапазон перемещения и предел «разворачивания вращения» (это предохраняет кабели от « завернутый» во время обработки) и многое другое. Это знание того, как на самом деле работает ваша машина, предоставляется вам во время программирования. Вы можете увидеть немедленные результаты изменения параметра в интегрированном машинном моделировании. Это дает вам результат «что видишь, то и получаешь» в результате публикации кода NC после запуска его через симуляцию.
Моделирование внутри TopSolid не будет выполнять такие действия, как имитация машинного макроса. Для высокоуровневого моделирования кода ЧПУ и машинных процессов я бы по-прежнему рекомендовал пакет проверки программного обеспечения, такой как Vericut от CGTech, но TopSolid позволит вам получить готовую программу ЧПУ намного быстрее, чем при использовании любой другой CAM-системы на рынке.
Для высокоуровневого моделирования кода ЧПУ и машинных процессов я бы по-прежнему рекомендовал пакет проверки программного обеспечения, такой как Vericut от CGTech, но TopSolid позволит вам получить готовую программу ЧПУ намного быстрее, чем при использовании любой другой CAM-системы на рынке.
Такие функции, как «осведомленность о кинематике» на уровне управления траекторией движения инструмента, ставят TopSolid намного выше любой другой CAM-системы, представленной сегодня на рынке. Использование TopSolid 7 дает мне конкурентное преимущество перед всеми, поскольку я трачу больше времени на программирование траекторий и меньше беспокоюсь об управлении своим станком. Когда мне нужна опция для управления выходом машины, она «прямо здесь». Я продолжаю говорить себе под нос; «Вау, они действительно все продумали!…».
TopSolid позволяет определять невероятно сложные кинематические схемы линейных и круговых осей, а также определять все свойства этих компонентов в интерфейсе TopSolid.

 При обработке небольшой партии деталей управление продольной подачей и быстрым перемещением стола производится вручную.
При обработке небольшой партии деталей управление продольной подачей и быстрым перемещением стола производится вручную.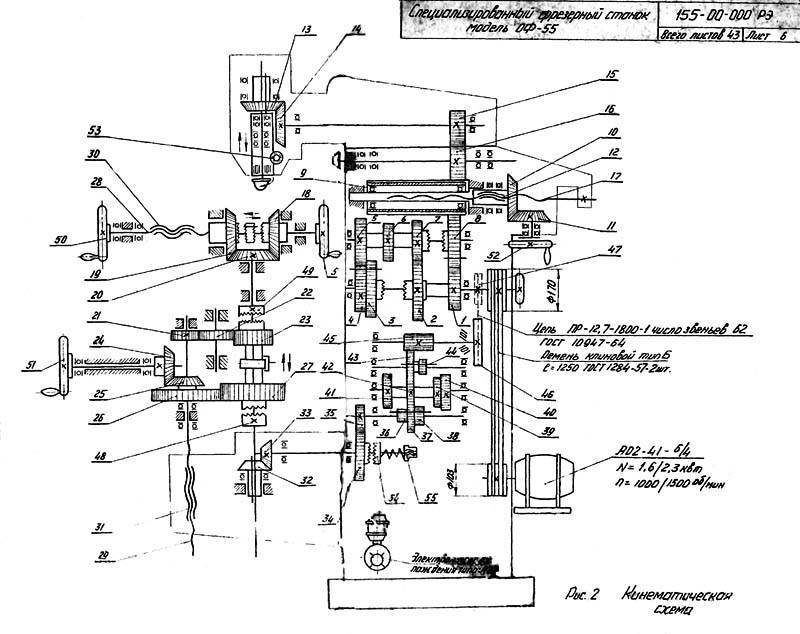 Последний непрерывно совершает замкнутый цикл движений — быстрое перемещение влево, рабочая подача влево, быстрое перемещение вправо, рабочая подача вправо. Снятие обработанной детали и закрепление заготовки производятся рабочим во время фрезерования детали, расположенной на другой стороне стола.
Последний непрерывно совершает замкнутый цикл движений — быстрое перемещение влево, рабочая подача влево, быстрое перемещение вправо, рабочая подача вправо. Снятие обработанной детали и закрепление заготовки производятся рабочим во время фрезерования детали, расположенной на другой стороне стола.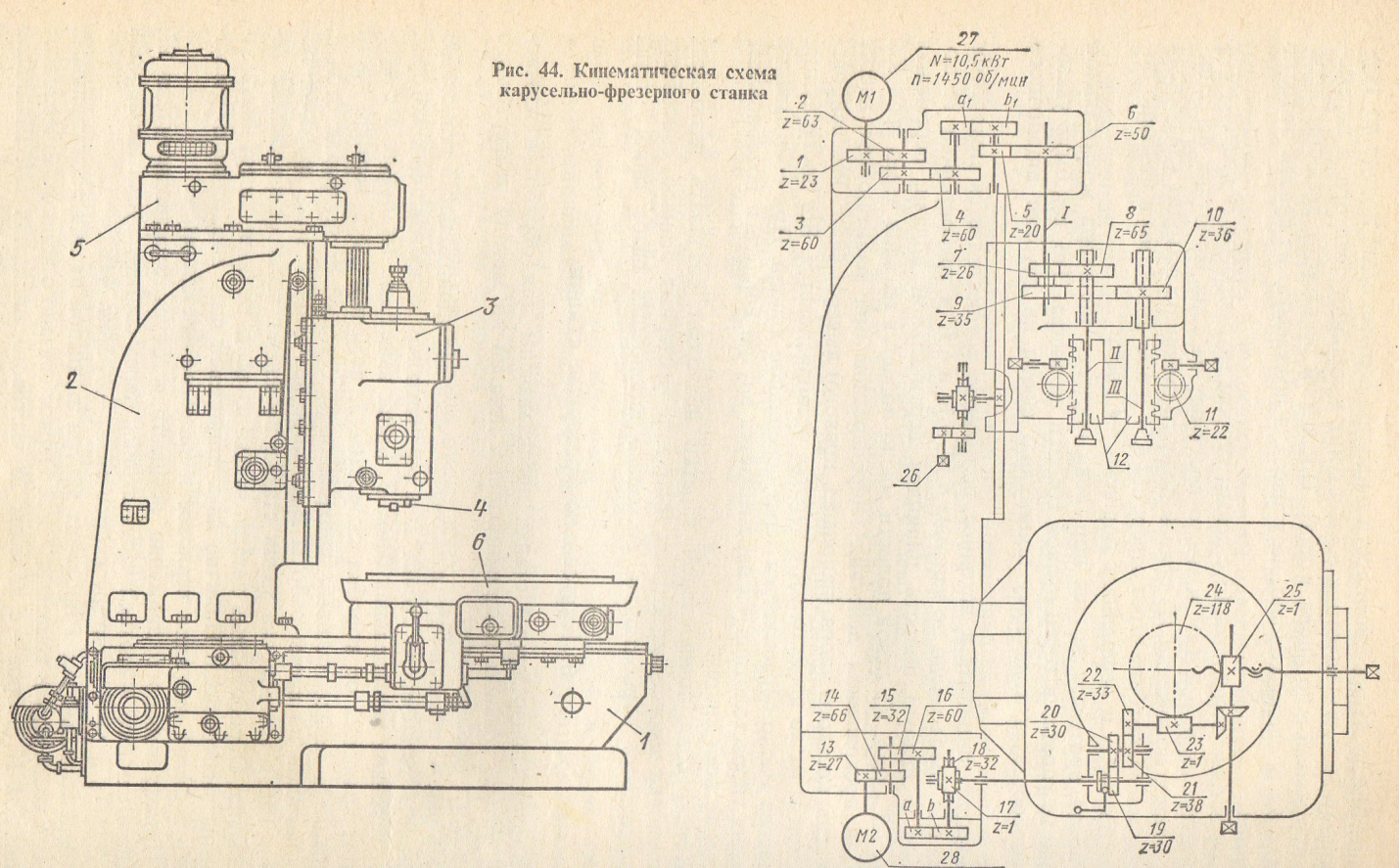 6Р82
6Р82
 Уравнение кинематического баланса имеет вид:
Уравнение кинематического баланса имеет вид:
 Колонна коробчатой формы. Сильно ребристый внутри и дома все приводные механизмы для подачи шпинделя и стола. Передняя вертикальная поверхность колонны точно обработана и имеет с ласточкиным хвостом направляющими способами поддержки колена. Вершина колонны закончена держать за руку, которая простирается наружу в передней части машины.
Колонна коробчатой формы. Сильно ребристый внутри и дома все приводные механизмы для подачи шпинделя и стола. Передняя вертикальная поверхность колонны точно обработана и имеет с ласточкиным хвостом направляющими способами поддержки колена. Вершина колонны закончена держать за руку, которая простирается наружу в передней части машины. Вершина Седло аккуратно обработано для обеспечения направляющих путей к столу.
Вершина Седло аккуратно обработано для обеспечения направляющих путей к столу. передняя скоба имеет прорези для регулировки высоты колена по отношению к над рукой.
передняя скоба имеет прорези для регулировки высоты колена по отношению к над рукой.


 По крайней мере, я ясно вижу, что происходит с обоими показателями. Эти показатели являются относительным чтением. Положите предмет на стол и поверните циферблаты, чтобы обнулить индикаторы. Воткни его в шпиндель.Ваша миссия состоит в том, чтобы вернуть иглы в нулевое положение, постукивая головой так или иначе.
По крайней мере, я ясно вижу, что происходит с обоими показателями. Эти показатели являются относительным чтением. Положите предмет на стол и поверните циферблаты, чтобы обнулить индикаторы. Воткни его в шпиндель.Ваша миссия состоит в том, чтобы вернуть иглы в нулевое положение, постукивая головой так или иначе. Кстати, Indicol — не самая лучшая трамвайная установка.Правильный трамвайный брус был бы более жестким и менее «нервным». Например:
Кстати, Indicol — не самая лучшая трамвайная установка.Правильный трамвайный брус был бы более жестким и менее «нервным». Например:
 Это интересная нить, с весом обеих сторон.Филбур обращается к самому чистому лагерю с таким замечанием:
Это интересная нить, с весом обеих сторон.Филбур обращается к самому чистому лагерю с таким замечанием: Естественно предположить, что у
Естественно предположить, что у  Стенд представляет собой сварную конструкцию
Стенд представляет собой сварную конструкцию  Может случиться так, что с базой все в порядке, и колонна может быть отодвинута, но если вы можете сделать это с базы,
Может случиться так, что с базой все в порядке, и колонна может быть отодвинута, но если вы можете сделать это с базы, 
 Это было легко исправлено небольшим запасом прокладок. Приведя голову в порядок, я продолжил трамбовать это также.
Это было легко исправлено небольшим запасом прокладок. Приведя голову в порядок, я продолжил трамбовать это также.