Натяжка троса между столбами: Как натянуть трос между столбами

Как натянуть трос между столбами

Содержание статьи:

• 
  
  Что такое талреп
  
• 
  
  Порядок крепления троса к столбам
  

Подвесить провода или установить ограду из сетки-рабицы невозможно без туго натянутого стального троса. Решить задачу помогут талрепы для растяжки — простые, но эффективные приспособления для такелажных работ. С помощью этого устройства можно легко отрегулировать натяжение троса, каната и проволоки. Талрепы широко используются в строительстве, промышленности, на морском транспорте. С их помощью прокладывают кабельные сети и даже натягивают канатные ограждения на боксерских рингах. Разберемся в конструкции и особенностях применения устройства.

Что такое талреп

Талрепы часто называют винтовыми стяжками. Ключевые элементы их конструкции — два стержня с разнонаправленной резьбой, ввинченных в корпус прямоугольной или цилиндрической формы. Наружные концы винтов предназначены для крепления троса, они могут быть выполнены в виде петли, крюка или вилки. При монтаже расчалок — тросов или проволоки, оттянутых для соединения элементов конструкций — устройство ставят с вывинченными натяжными болтами. Натяг регулируется вращением корпуса, в результате чего концы винтов смещаются к центру муфты, тем самым устраняя провисание троса.

Чаще применяют талрепы с открытым корпусом, где хорошо видно положение винтов. Закрытые модификации используются на строительных площадках, где пыль, песок или цемент может забиться в муфты и мешать скольжению резьбы. Чаще всего талрепы защищают от коррозии с помощью оцинковки, хотя встречаются модификации, выполненные целиком из нержавейки. Благодаря покрытию такелажные приспособления долго сохраняют свою работоспособность на открытом воздухе.

В перечне эксплуатационных характеристик талрепов обычно указывают:

• предельно допустимую нагрузку;
• длину или диаметр муфты;
• размер устройства при полностью вывинченных натяжных болтах.

Размер, вес и конструкция зависит от области применения устройства. Несущая способность талрепов открытого тип ограничена 6,3 тоннами, закрытые модификации выдерживают до 20 тонн. Модель подбирают по диаметру троса. Как правило, в быту чаще используют талрепы, рассчитанные на небольшие нагрузки.

К содержанию ↑

Порядок крепления троса к столбам

Для натяжения троса между столбами подойдут модификации талрепа типа О+О (кольцо-кольцо). Дополнительно нужно приобрести коуши, зажимы типа «слоник» и крепеж для столбов. Перед монтажом следует проверить работоспособность талрепов, протереть их бензином и нанести смазку. Болты выворачивают, затем в кольцо талрепа вставляют коуш, укладывают в него трос, а конец фиксируют с помощью трех зажимов. При незначительных нагрузках часто используют только один зажим. Операцию повторяют для противоположного конца стального каната.

Свободные кольца талрепов закрепляют на столбах с помощью системы скоба-болт. Затем стяжки последовательно вращают вокруг своей оси, пока трос не будет туго натянут. Силу натяжения можно ослабить, поворачивая корпус талрепа в противоположном направлении. В процессе эксплуатации следует избегать любых нагрузок на конструкцию, за исключением осевой. Периодически необходимо контролировать натяжение и корректировать провисание.

Перед покупкой тщательно проверяйте такелажные приспособления. На талрепах не должно быть трещин, сколов, раковин и других дефектов, которые могут отрицательно сказаться на прочности изделий. Предельно допустимую нагрузку производители обычно указывают на муфте. При правильной эксплуатации срок службы изделий составляет 10-15 лет.

Натяжка проводов и тросов (канатов) ВЛ | Монтаж электрических установок | Архивы

• 6кВ
• 0,4кВ
• кабель
• монтаж
• ВЛ
• подстанция
• 10кВ
• шины и провод
• заземление

Содержание материала

• Монтаж электрических установок
• Маркировка цепей в электрических схемах
• Управление электромонтажным производством
• СПУ
• Организация и подготовка электромонтажных работ
• Производство электромонтажных работ
• Материально техническое-обеспечение бригады
• Бригадный подряд, оплата труда
• Научная организация труда, нормирование
• Материалы для электромонтажных работ
• Электромонтажные изделия
• Опрессовка жил проводов и кабелей
• Сварка жил проводов и кабелей, контактных соединений шин
• Пайка жил проводов и кабелей, контактных соединений шин
• Соединение алюминия с медью, сплав АВ—Е
• Контактные соединения и присоединения к контактным выводам электрооборудования
• Виды сварок в электромонтажном производстве
• Сварка шин в электромонтажном производстве
• Сварка алюминиевых гибких шин
• Сварка стальных заземляющих проводников
• Сварка пластмассовых оболочек кабеля
• Назначение заземляющих устройств
• Заземляющие устройства
• Монтаж заземляющих устройств
• Монтаж распределительных устройств до 1 кВ
• Аппараты распределительных устройств
• Шинопроводы напряжением до 1 кВ
• Монтаж шинопроводов до 1 кВ
• Оборудование распределительных устройств и подстанций выше 1 кВ
• КТП
• ГПП
• ЗРУ
• Силовые выключатели на 6—10 кВ
• Выключатели нагрузки
• Разъединители, предохранители 6, 10 кВ
• Разрядники, измерительные трансформаторы 6, 10 кВ
• Конденсаторы, фильтры, изоляторы 6, 10 кВ
• Монтаж распределительных устройств и подстанций
• Монтаж РЗА и вторичных цепей
• Монтаж токопроводов напряжением выше 1 кВ
• Осветительные установки
• Монтаж осветительных установок
• Устройства для обслуживания светильников, освещение строительных площадок
• Провода и кабели, применяемые в электропроводках
• Общие требования к монтажу электропроводок
• Открытые электропроводки плоскими проводами
• Открытые электропроводки незащищенными изолированными проводами
• Открытые тросовые электропроводки
• Открытые электропроводки защищенными проводами и кабелями
• Скрытые электропроводки
• Электропроводки на лотках и в коробах
• Выбор труб для электропроводок в трубах
• Правила монтажа труб для электропроводок
• Монтаж труб для электропроводок
• Монтаж проводов в трубах
• Электропроводки за подвесными потолками, на чердаках по станкам механизмам и наружные
• Кабельные линии
• Подготовка к прокладке кабелей внутри и вне зданий
• Прокладка кабелей в траншее
• Прокладка кабелей в производственных помещениях
• Прокладка кабелей в кабельных сооружениях
• Прокладка кабеля при низких температурах
• Маркировка кабельных линий после монтажа
• Соединение и оконцевание силовых кабелей
• Удаление изоляции и заполнителей кабеля
• Соединение и оконцевание кабелей с пластмассовом изоляцией
• Соединение кабелей с бумажной изоляцией в свинцовых муфтах
• Оконцевание и монтаж кабелей и муфт
• Подготовительные работы при монтаже ВЛ
• Определения, габариты ВЛ
• Котлованы, фундаменты, опоры ВЛ
• Провода и изоляторы ВЛ
• Защита проводов ВЛ от вибрации (пляски)
• Установка опор ВЛ
• Монтаж изоляторов ВЛ
• Монтаж проводов и тросов ВЛ
• Натяжка проводов и тросов (канатов) ВЛ
• Закрепление проводов и канатов ВЛ
• Заземление опор и траверс ВЛ
• Проверка качества работ при сдаче электроустановок в эксплуатацию
• Сдача электроустановок в эксплуатацию
• Техника безопасности при производстве электромонтажных работ
• Сокращения и использованная литература

Страница 77 из 83

Раскатку проводов и тросов производят, как правило, одновременно. Провес провода, натянутого между двумя опорами (стрела провеса), зависит от массы провода и усилия, с которым он натянут (тяжения провода). Стрелы провеса для данной линии при данных температурах воздуха указывают в проекте.
При натяжке проводов и тросов должны выполняться следующие требования [2]: при визировании проводов и канатов стрелы провеса должны быть установлены согласно рабочим чертежам по монтажным таблицам или кривым в соответствии с температурой провода или каната во время монтажа. При этом фактическая стрела провеса провода или каната не должна отличаться от проектной величины более чем на ±5 % при условии соблюдения требуемых габаритов до земли и пересекаемых объектов; разрегулировка проводов различных фаз и канатов относительно друг друга должна составлять не более 10 % проектной величины стрелы провеса провода или каната; разрегулировка проводов в расщепленной фазе должна быть не более 20 % для ВЛ 330—500 кВ и 10 % для ВЛ 750 кВ; угол разворота проводов в фазе должен быть не более 10°; визирование проводов и канатов ВЛ напряжением выше 1 кВ до 750 кВ включительно следует проводить в пролетах, расположенных в каждой трети анкерного участка при его длине более 3 км. При длине анкерного участка менее 3 км визирование разрешается производить в двух пролетах: наиболее отдаленном и наиболее близком от тягового механизма; отклонение поддерживающих гирлянд вдоль ВЛ от вертикали не должно превышать, мм: 50 — для ВЛ 35 кВ, 100 — для ВЛ 110 кВ, 150 — для ВЛ 150 кВ и 200 — для ВЛ 220 — 750 кВ.

Натяжку проводов ВЛ до 10 кВ производят лебедкой при помощи полиспастов или автомашиной, а линий 35 кВ и выше с большими пролетами — трактором. Провод с алюминиевыми жилами зажимают в монтажном зажиме (рис. 13.38). Натяжку проводов и тросов производят между анкерными опорами.
На линиях 35 кВ и выше обычно производят натяжку нескольких проводов (двух, трех и более). На рис. 13.39 показано приспособление для одновременного натягивания трех проводов.

Рис. 13 38. Зажим монтажный клиновой; 1 — корпус; 2 — планка; 3 — клин

Рис 13 39 Приспособление для одновременного натягивания трех проводов

Оргэнергострой Минэнерго разработал прогрессивный способ монтажа проводов под тяжением с помощью комплекта специальных механизмов и приспособлений. Разработана технология монтажа проводов под тяжением с одновременной раскаткой до трех проводов В комплекте раскатного оборудования использованы серийная базовая техника и комплектующие детали. Навесная тяговая лебедка для перематывания тягового каната сконструирована на базе трактора Т-130Г, лебедка с гидроприводом от трактора для сматывания тягового каната и тормозная установка на три провода — на базе прицепов типа МАЗ, раскаточные устройства для барабанов с проводом — на базе одноосных прицепов. Комплект обеспечивает длину раскатываемых за один цикл проводов до 5 км. Общее тяговое усилие 75 кН, тяговое усилие максимальное: для трех проводов — 60 кН, для одного провода — 40 кН. Применение комплекта механизмов и приспособлений при сооружении ВЛ 500 кВ показало его высокую эффективность [77].
Стрелу провеса проводов и тросов выверяют визированием в соответствии с указанными выше требованиями [2].

Для визирования на опорах визировочных пролетов укрепляют визирные
рейки (рис. 13 40). Высоту установки визирных реек определяют по монтажным кривым или таблицам стрел провеса, приведенным в проекте, с учетом длины поддерживающих гирлянд (или высоты штыревых изоляторов). Таким образом, визирные рейки устанавливают на высоте от земли, соответствующей наинизшей точке провисания провода в пролете для условий монтажного режима. На одну из указанных промежуточных опор поднимается визировщик. По его команде провод сначала перетягивают на 0,3—0,5 м, а затем, выдержав 2 — 3 мин, отпускают до линии визирования. Линия визирования представляет собой прямую линию, проведенную между визирными рейками, установленными на опорах визировочного пролета При горизонтальном расположении проводов вначале обычно визируют средний провод по линии, проходящей через накрест расположенные рейки, после чего визируют крайние провода по рейке и среднему проводу При одновременной натяжке трех проводов визирование производят по верхнему проводу при вертикальном расположении проводов и по среднему проводу — при горизонтальном При плохой видимости стрелу провеса допускается устанавливать по динамометру по тяжению по проводу или тросу, соответствующему монтажному режиму По заданной стреле провеса определяют тяжения Т, Н, по формуле

] — стойка металлической опоры, 2 — окуляр 3 — рейка с уровнем, 4 — струбцина для крепления

Рис 13 40 Приспособление для визирования проводов

где I — длина пролета, м, F — площадь поперечного сечения провода или троса, мм², f — стрела провеса для монтажного режима, м; k — коэффициент, равный для алюминиевых проводов 0,00337, для сталеалюминиевых 0,0044, для стальных проводов и тросов 0,01
По окончании визирования (приема стрелы провеса) на проводе у анкерной опоры, находящейся на противоположном от тягового механизма конце анкерного пролета, наносят метку места установки натяжного зажима После этого провод может быть опущен на землю для удобства монтажа зажима.

Стрелу провеса в анкерном пролете для всех проводов устанавливают одну и ту же. На BЛ до 1 кВ, когда на одной и той же опоре закрепляют провода разных сечений, стрелу провеса для всех проводов также устанавливают одну — по проводу с большим сечением. Стрелы провеса проводов указывают в проектах.
Выше, были указаны наименьшие допустимые расстояния (габариты) от проводов ВЛ до земли, пересекаемых дорог и т. п. В частности, для ВЛ до 1 кВ расстояние от провода до земли должно быть не менее 6 м. Для ВЛ выше 1 кВ и до 110 кВ эти расстояния должны быть не менее: в населенной местности — 7 м; в ненаселенной — 6 м; в труднодоступной — 5 м. Эти расстояния должны быть соблюдены при наивысшей температуре воздуха без учета нагрева провода электрическим током, а также при гололеде, но без ветра [3].

• Назад
• Вперед

• Назад
• Вперед

• Вы здесь:  
• org/ListItem»> Главная
• Книги
• Архивы
• Испытание мощных трансформаторов и реакторов

Читать также:

• Электрические сети промышленных предприятий
• Электромонтажные материалы
• Монтаж сельских электроустановок
• Наладка электроустановок
• Монтаж, эксплуатация и ремонт сельскохозяйственного электрооборудования

Трение веревки вокруг столба | Демонстрация лекций по естественным наукам в Гарварде

ГЛАВНАЯ / ПРЕЗЕНТАЦИИ /

Сила натяжения веревки растет экспоненциально с количеством витков, которые веревка делает вокруг шеста.

Что он показывает:

Многие люди, вероятно, замечали, что, обматывая веревку вокруг столба, человек может сдерживать гораздо большую силу, чем обычно. В этом опыте гибкая толстая веревка наматывается на горизонтальную трубу. Из-за взаимодействия сил трения и натяжения между двумя концами каната может быть значительная разница в натяжении. В демонстрации один конец веревки поддерживает (тяжелый) груз, а другой конец удерживается (небольшой) «удерживающей» силой. Демонстрация моделирует принцип работы шпиля.

Как это работает :

Уравнение Эйлера-Эйтельвейна ⁽¹⁾ связывает натяжение двух концов веревки: — натяжение каната из-за груза, который он поддерживает; T ₁ — натяжение, необходимое для удержания груза без проскальзывания; радианы), сделанные всеми витками веревки (один полный виток равен 2∏ радианам). Сила натяжения увеличивается экспоненциально с коэффициентом трения и количеством витков вокруг трубы. Обратите внимание, что диаметр трубы не имеет значения. Тем не менее, диаметр трубы не может быть слишком маленьким, потому что при сгибании веревки вокруг трубы будет потеряно значительное усилие, особенно если веревка немного жесткая.

Установка :

Прикрепите стальную трубу диаметром 2 дюйма к краю лекционной скамьи двумя С-образными зажимами, как показано на фотографиях. Используйте нейлоновую веревку диаметром 3/8 дюйма. Наш 65-фунтовый шар для разрушения представляет собой впечатляющую тяжелую нагрузку. Привяжите один конец веревки к шару и оберните несколько витков веревки вокруг трубы. Медленно размотав веревку, вы обнаружите, что 4½ оборотов достаточно, чтобы удержать мяч, причем только вес свободной веревки создает «удерживающую» силу. Эта длина свободной веревки весит около 0,11 фунта. При θ=9∏, это говорит о том, что μ≈0,23 (небезосновательное число). За 2½ оборота вы можете легко удерживать мяч пальцами. На 3-м фото показана 100-фунтовая гантель, удерживаемая всего за 4½ витка веревки и пальцами, обеспечивающими натяжение. Используя μ≈0,23, мы оцениваем удерживающую силу пальца в 0,15 фунта.

Комментарии :

Экспоненциальные отношения всегда поражают, и это не исключение. Многие устройства, основанные на трении ремня или обруча, используются в спусках, скалолазании (так называемая верхняя веревка, в которой можно удерживать (страховать) тяжелого человека, чтобы предотвратить падение), парусном спорте и такелаже снаряжения. Вездесущие клиновые ремни и шкивы — еще один пример, искусно усиленный V-образной формой. Соотношение между натяжением натянутой и слабой стороны для клинового ремня аналогично:

T ₂ = T ₁ e ^{μθ/sin(β/2)} , где β — угол V в шкиве (обратите внимание, что при β = 180 градусов мы возвращаемся к плоскому ремню отношение).

сноски :

(1) Уравнение приводится в большинстве учебников по машиностроению. Например: R. Becker, Introduction to Theoretical Mechanics , (McGraw-Hill, NY, 1954), стр. 45-46. Л. Гудман и В. Уорнер, , статика и динамика, , (Уодсворт, Белмонт, Калифорния, 1964) стр. 308–314. См. также Д. Морин, . Введение в классическую механику, , (Cambridge University Press, NY, 2007), стр. 26–27.

См. также: Ньютоновская механика, Второй закон Ньютона, Силы гравитации и трения, Домашняя страница, [M], [t+], [—]

Формула натяжения — DewWool

Натяжение — это сила, действующая по всей длине веревки, струны, проволоки или тросов. Специальной формулы напряжения не существует. Напряжение является разновидностью контактной силы. Основные законы физики можно применить для расчета силы натяжения струны или веревки. Натяжение всегда представляет собой тянущую силу и проявляется в веревке только тогда, когда ее тянет сила. Здесь, в этой статье, мы обсуждаем формулу напряжения в разных сценариях.

При решении числовых величин, связанных с натяжением, мы принимаем во внимание определенные допущения, без которых трудно рассчитать натяжение, используя основные законы физики. Это можно рассматривать как идеальный случай, который не всегда соответствует действительности в сценариях реальной жизни.

• Натяжение одинаково во всех точках веревки.
• Рассматриваемый канат не имеет массы.
• Игнорируйте незначительные эффекты трения, сопротивления воздуха и других нежелательных факторов, если не указано иное.
• Все расчеты сделаны для планеты Земля и значения g (ускорение свободного падения составляет 9,8 м/с ² .

В этой статье мы вычисляем формулу натяжения для следующих 10 сценариев:

1. Натяжение каната, тянущего блоки по горизонтали
2. Натяжение каната, тянущего блоки горизонтально с участием кинетического трения
3. Натяжение веревки во время перетягивания каната
4. Натяжение вертикально подвешенной проволоки с грузом
5. Натяжение веревки, прикрепленной к грузу под углом
6. Напряжение в лифте
7. Человек, идущий по натянутой веревке
8. Натяжение проволоки при круговом движении
9. Натяжение троса шкива
10. Натяжение троса с наклоном и шкивом

Формула для натяжения веревки, тянущей блоки по горизонтали

Натяжение веревки, тянущей блоки по горизонтали

Это наиболее распространенная форма натяжения в задаче о струне. Веревкой тянут два блока, находящихся на расстоянии друг от друга. Блоков может быть n, но натяжение каждой веревки будет разным. Здесь сила F тянет блоки массами M1 и M2 по поверхности без трения (uk=0).

Для всей системы: Fnet(для всей системы) = Общая масса*ускорение => Ускорение(a) = F/(M ₁ +M ₂ )

Используя диаграмму свободного тела как показано выше, мы сосредоточились на двух блоках по отдельности и рассчитали формулу для натяжения.

T = M ₁ *a T = F + M ₂ *a

Оба уравнения можно использовать для определения значения натяжения каната. Значения напряжения будут одинаковыми. Единицей силы натяжения в системе СИ является Ньютон. Вы можете прочитать наш блог о единицах силы для более подробной информации.

Формула для натяжения веревки, тянущей блоки по горизонтали с учетом кинетического трения

Кинетическое трение – это противодействующая сила между двумя телами, находящимися в относительном движении. В идеальном случае проблем с напряжением всегда будет Фактор трения. Обычно мы опускаем его для упрощения вычислений. Статическое трение будет иметь место в случаях, когда сила, приложенная к системе, меньше предельного трения.

Формула для натяжения веревки, тянущей блоки по горизонтали с учетом трения.

Здесь результирующая сила системы будет включать приложенную силу тяги, силу натяжения плюс силу трения в направлении, противоположном приложенной силе. Следует отметить, что сила трения будет применяться к каждому объекту с массой.

Формула трения = μ _k *N => μ _k * (m*g) [где μ _k — коэффициент кинетического трения] Трение всей системы = μ _k ( m1+m2)*g Трение блока1 = m1*g Трение блока2 = m2*g

Используя диаграмму свободного тела, как показано выше,

Блок 1: Сила натяжения и сила трения действуют в противоположных направлениях.

Fnet = T – трение => T = μ _k *m ₁ *g + m ₁ *a

Блок 2: Сила приложена вправо. Натяжение и сила трения действуют в одном направлении.

Fnet = F – T – трение => T = F – μ _k *m ₂ *g – m ₂ *a   

Формула натяжения веревки во время перетягивания каната

В игре «Перетягивание каната» две команды тянут одну веревку навстречу друг другу в противоположных направлениях. Побеждает та команда, которая перетянет противника на свою сторону. Сила команды передается через натяжение веревки, чтобы тянуть противника. Найдем формулу напряженности в таком сценарии.

Формула натяжения каната для перетягивания каната

F = масса x ускорение => F _net = общая масса x a _net => a _net = F _net /общая масса

Ускорение во всей системе будет одинаковым. Используем это значение ускорения в уравнении сил для обоих тел и вычисляем формулу натяжения. Вы можете прочитать здесь для подробного вывода.

T = F1 – [(M ₁ +M ₂ )*ускорение] T = F2 – [(M ₃ +M ₄ )*ускорение]

Формула натяжения вертикально подвешенного троса с грузом

Натяжение вертикально подвешенного троса с грузом груз под углом

Струны не всегда крепятся в вертикальном или горизонтальном положении. Как правило, они крепятся под углом в соответствии с удобством. Например, серийные провода освещения сделаны так, чтобы свободно висеть в елке. Возможно, вы видели линию свешивания ткани, которая никогда не бывает прямой, она изгибается из-за веса. Попробуем рассчитать натяжение струн такого подобного случая.

Натяжение нити, закрепленной под углом

Здесь груз (масса m) подвешен на двух тросах с натяжением T1 и T2. Поскольку задействовано два провода, натяжение может быть разным. Угол, который провода образуют с потолком, обозначен как a и b.

Сначала мы нарисуем диаграмму свободного тела для блока. Силы натяжения разрешаются в горизонтальном и вертикальном направлениях. Сила mg будет действовать вниз за счет гравитационного притяжения, а натяжение будет действовать в противоположном направлении, т.е. вверх.

T1 sin(a) + T2 sin(b) = m*g ———-(1)

T1cos(a) = T2cos(b)———————(2)

Решая уравнения (1) и (2), мы можем получить решение для T1 и T2.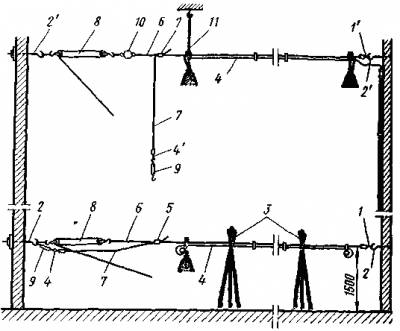 Заметим, что если угол a=b, то натяжение T1 будет равно T2.

Формула натяжения в лифте

Натяжение тросов лифта

Это классическая численная задача физики для определения силы натяжения. Когда кто-нибудь подвешен на веревке в состоянии покоя, тогда натяжение равно весу тела. Но когда веревку тянут вверх или вниз с ускорением, значение натяжения меняется. Напряжение всегда будет выше при подтягивании тела вверх по сравнению с опусканием.

T = m*g [Когда лифт остановлен]

T = m*(g-a) [Когда лифт идет вниз]

T = m*(g+a) [Когда лифт стоит движение вверх]

Человек, идущий по канату

Натяжение каната: Человек массой m, идущий по канату

Возможно, вы видели или слышали о каскадерах, идущих по канату. Эта задача аналогична гире, подвешенной на двух тросах. Вес человека можно принять как блок, свободно подвешенный на двух тросах, образующих угол с потолком. Натяжение будет разным на двух участках веревки, за исключением случаев, когда человек находится точно в середине.

T1 sin(a) + T2 sin(b) = m*g ———-(1)

T1cos(a) = T2cos(b)———————(2)

Формула натяжения проволоки при круговом движении

Натяжение струны при круговом движении

Вы когда-нибудь раскачивали груз, прикрепленный к струне? Вы бы почувствовали натяжение струны в своих руках.

Здесь сила mg груза под действием силы тяжести будет действовать вниз, а натяжение будет действовать к нам, от груза. На груз действует еще одна дополнительная сила. Это называется центростремительной силой. Это сила, которая пытается притянуть объект к центру, т.е. к вам. Итак, на тело действуют три силы: гравитационная, натяжная и центростремительная.

У нас есть три вектора, поэтому мы решаем векторы и находим формулу для натяжения струны.

Натяжение = sqrt[(mg) ² +(mv ² /r) ² ]

Формула натяжения каната шкива

Формула натяжения каната Шкив

Шкив используется для уменьшения усилий при подъеме тяжелых предметов. Он состоит из неподвижного колеса, по которому свободно проходит веревка или веревка. При определении силы натяжения мы предполагаем, что трение между канатом и шкивом равно нулю.

В системе шкивов есть два случая. Веревка может двигаться вверх или вниз с ускорением а. Напряжение в обоих сегментах будет одинаковым. Запишем уравнение для чистой силы в каждом из блоков и рассчитаем натяжение веревки из двух уравнений.

Для блока 1: движение вверх против силы тяжести с ускорением a

м ₁ *a = T – m*g [чистая сила = натяжение – сила тяжести]
T = m ₁ *а + м ₁ *g

Для блока 2: движение вниз под действием силы тяжести с ускорением а T = m ₁ *g – m ₁ *a

Формула натяжения каната с наклоном и шкивом

Натяжение каната с наклоном и шкивом

В реальной жизни, сила, действующая на объект, будет строго горизонтальной или вертикальной. Он всегда будет под углом. Итак, давайте посмотрим на этот пример, где два блока прикреплены к канату шкива. Один блок помещается под наклоном, что также связано с кинетическим трением о поверхность.

На блок m1 будут действовать четыре силы. Вес, нормальная сила, натяжение и кинетическая сила трения. Мы должны решить силы, чтобы составить уравнение в горизонтальном и вертикальном направлениях.

Чистая сила (M₁) = T – m₁gsinθ – трение T = M₁a – M₁gsinθ – μ _k M₁g

На блок m2 будут действовать две силы. Вес и натяжение веревки.

Чистая сила (M₂) = M₂g – натяжение T = M₂g – M₂a

Используя приведенные выше два уравнения, мы можем найти значение силы натяжения.

Исследование силы натяжения:

Натяжение струн в гитаре может влиять на издаваемый ею звук. Натяжение струны регулируется при настройке гитары, чтобы получить определенную ноту.