Расчет балки двутавровой на прочность: Полный расчет балки на прочность и жесткость

Пример расчета балки на изгиб

Содержание

1. Определение опорных реакций
2. Построение эпюр Q и М
3. Подбор сечения двутавровой балки
4. Проверка сечения балки по касательным напряжениям
5. Проверка прочности балки по главным напряжениям
6. Что такое прогиб балки?
7. Метод начальных параметров
8. Расчет прогибов балки
9. Реакции опор
10. Система координат
11. Распределенная нагрузка
12. Учет внешней нагрузки
13. Формулы прогибов
14. Вычисление прогиба

Произвести полный расчет на прочность и проверить жесткость статически определимой двутавровой двухопорной балки (рис. 1) при следующих данных: F=40кН, q=30 кН/м, a=0,8 м, l=4м, допустимые нормальные и касательные напряжения: [ σ ]=160 МПа и [ τ ]=100 МПа, допустимый прогиб балки [f]= l/400

Определение опорных реакций

Подробно, пример определения опорных реакций для балки рассмотрен здесь

А также в нашем видеоуроке:

Построение эпюр Q и М

По этим данным построены эпюры Q и М.

Подбор сечения двутавровой балки

Так как М_mах = 45 кНм, то

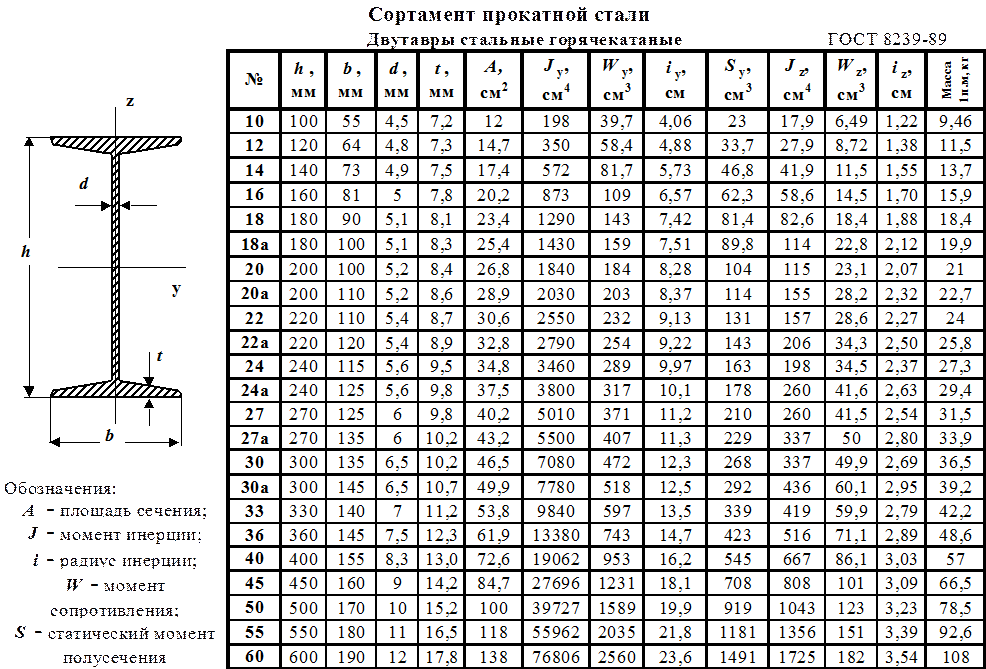
По сортаменту выбираем двутавр № 24, для которого W_x = 289 см 3 , I_x= 3460 см 4 , S_max = 163 см 3 , h = 24 см, b_п = 11,5 см, t = 0,95 см, d = b_c = 0,56 см, h _{= h-2t = 22,1 см.}

Этот двутавр будет работать при максимальном нормальном напряжении в крайнем волокне опасного сечения.

Проверка сечения балки по касательным напряжениям

Так как Q_max = 68 кН, то

Построение эпюр нормальных σ и касательных τ напряжений в неблагоприятном сечении балки:

В отношении главных напряжений неблагоприятным является сечение над левой опорой, в котором:

Значение напряжений в различных точках по высоте двутавра сведены в таблицу 1

Проверка прочности балки по главным напряжениям

Наиболее опасной точкой в неблагоприятном сечении является точка 3.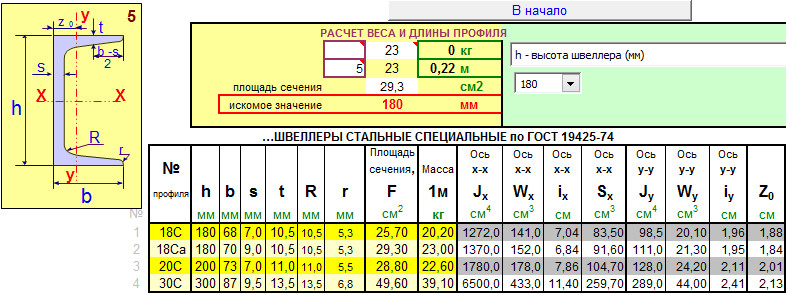 В этой точке σ ₁=118 МПа и σ ₃= -16 МПа. Проверяем прочность в этой точке по третьей гипотезе прочности согласно неравенству σ ₁ — σ ₃≤ [ σ ].

Так как 118 — ( -16) = 134 θ

откуда θ _{= -8,48∙10 -3 радиан.}

Прогиб в пролете при z=l/2=4/2=2 м.

Аналогично определяется прогиб на конце консоли при z = l + a =4+0,8 = 4,8 м.

Для заданной балки двутаврового сечения ( = 210 МПа, Е = 2 х 10 5 МПа) и нагрузок требуется;

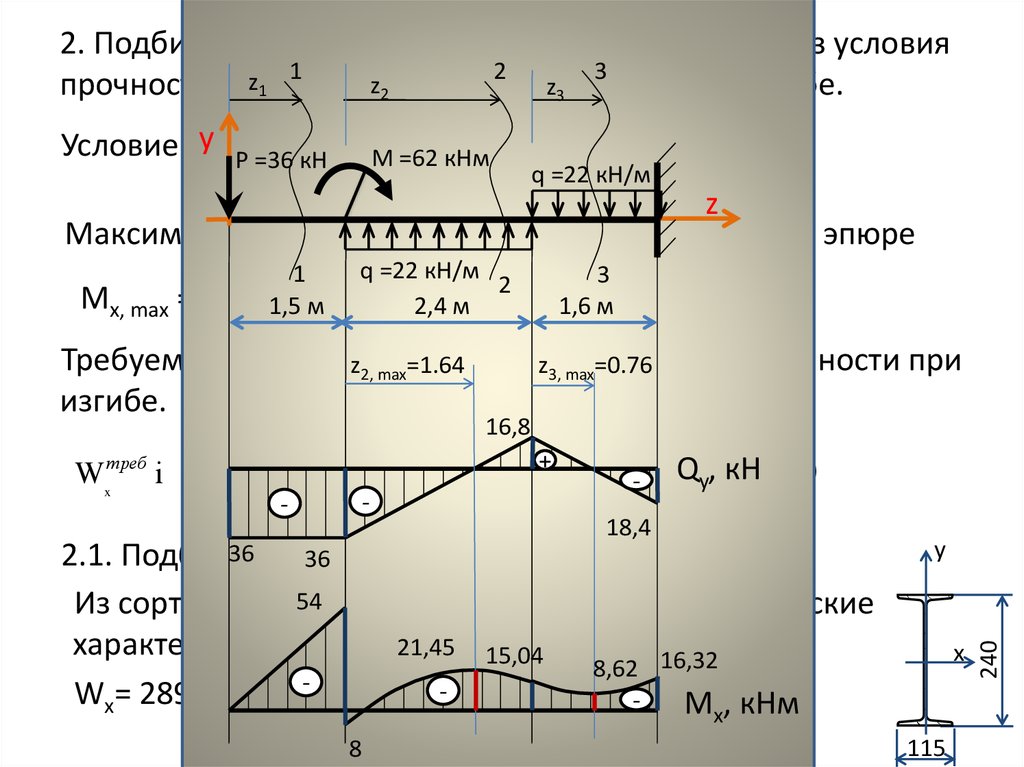
1. Построить эпюры поперечных сил и изгибающих моментов;

2. Определить нормальные и касательные напряжения в сечениях с наибольшим моментом и поперечной силой на расстоянии h/4 от нейтральной оси;

3. Определить прогиб конца балки точки В.

При построении эпюр Q и М необходимо соблюдать правило зна­ков. Положительное направление сил показано на схеме.

1. Определяем опорные реакции

2. Методом сечений определяем ординаты поперечной силы в характерных сечениях. Для этого балку разбиваем на два участка. Границы участков – места изменения нагрузки. Построение эпюры на­чинаем с правого свободного конца балки.

Максимум изгибавшего момента находится в сечении, где поперечная сила равна нулю. Положение этого сечения определяем из условия:

3. Методом сечений определяем изгибающие моменты в характерных сечениях и строим эпюру моментов. Экстремум в т. х = 2 м.

Наиболее нагруженным сечением в балке является сечение А у заделки, где М_max = 120 кН м, Q_mах = – 80 кН.

4. Из условий прочности по нормальным напряжениям определяем требуемый момент сопротивления сечения.

По сортаменту ГОСТ 8509-72 принимаем двутавр № 33.

Максимальные напряжения в опасном сечении будут равны

5. Определяем нормальное напряжение в точке Е сечения на расстоянии h/4 = 8,25 см от нейтральной оси (рис. 4.9.).

Для определения касательного напряжения в точке Е вычислим статический момент отсеченной выше точки Е площади относительно центральной оси Х.

6. Определяем прогиб балки в точке В, используя универсаль­ное уравнение прогибов

Для заданной консольной балки граничные условия будут: угол поворота сечения А ; прогиб сечения А

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: На стипендию можно купить что-нибудь, но не больше. 9122 – | 7289 – или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

В качестве примера, возьмем металлическую балку на двух опорах. Запишем для нее формулу для вычисления прогиба, посчитаем его численное значение. И также в конце этой статьи дам ссылки на другие полезные статьи с примерами определения прогибов для различных расчетных схем.

Что такое прогиб балки?

Под действием внешней нагрузки, поперечные сечения балки перемещаются вертикально (вверх или вниз), эти перемещения называются прогибами. Сопромат позволяет нам определить прогиб балки, зная ее геометрические параметры: длину, размеры поперечного сечения. И также нужно знать материал, из которого изготовлена балка (модуль упругости).

Кстати! Помимо вертикальных перемещений, поперечные сечения балки, поворачиваются на определенный угол. И эти величины также можно определить методом начальных параметров.

ν-прогиб сечения C; θ-угол поворота сечения C.

Прогибы балки необходимо рассчитывать, при расчете на жесткость. Расчётные значения прогибов не должны превышать допустимых значений. Если расчетное значение меньше, чем допустимое, то считают, что условие жесткости элемента конструкции соблюдается. Если же нет, то принимаются меры по повышению жесткости. Например, задаются другим материалом, у которого модуль упругости БОЛЬШЕ. Либо же меняют геометрические параметры балки, чаще всего, поперечное сечение. Например, если балка двутаврового профиля №12, не подходит по жесткости, принимают двутавр №14 и делают перерасчет.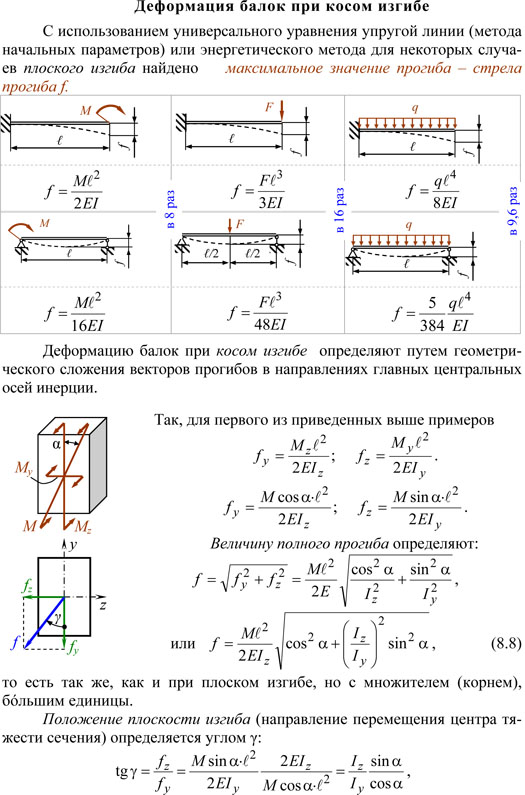 Если потребуется, повторяют подбор, до того момента пока не найдут тот самый – двутавр.

Метод начальных параметров

Метод начальных параметров, является довольно универсальным и простым методом. Используя этот метод можно записывать формулу для вычисления прогиба и угла поворота любого сечения балки постоянной жесткости (с одинаковым поперечным сечением по длине.)

Под начальными параметрами понимаются уже известные перемещения:

• в опорах прогибы равны нулю;
• в жесткой заделке прогиб и угол поворота сечения равен нулю.

Расчет прогибов балки

Посмотрим, как пользоваться методом начальных параметров на примере простой балки, которая загружена всевозможными типами нагрузок, чтобы максимально охватить все тонкости этого метода:

Реакции опор

Для расчета нужно знать все внешние нагрузки, действующие на балку, в том числе и реакции, возникающие в опорах.

Система координат

Далее вводим систему координат, с началом в левой части балки (точка А):

Распределенная нагрузка

Метод начальных параметров, который будем использовать чуть позднее, работает только в том случае, когда распределенная нагрузка доходит до крайнего правого сечения, наиболее удаленного от начала системы координат. Конкретно, в нашем случае, нагрузка обрывается и такая расчетная схема неприемлема для дальнейшего расчета.

Если бы нагрузка была приложена вот таким способом:

То можно было бы сразу приступать к расчету перемещений. Нам же потребуется использовать один хитрый прием – ввести дополнительные нагрузки, одна из которых будет продолжать действующую нагрузку q, другая будет компенсировать это искусственное продолжение. Таким образом, получим эквивалентную расчетную схему, которую уже можно использовать в расчете методом начальных параметров:

Вот, собственно, и все подготовительные этапы, которые нужно сделать перед расчетом.

Приступим непосредственно к самому расчету прогиба балки. Рассмотрим наиболее интересное сечение в середине пролета, очевидно, что это сечение прогнется больше всех и при расчете на жесткость такой балки, рассчитывалось бы именно это сечение. Обзовем его буквой – C:

Относительно системы координат записываем граничные условия.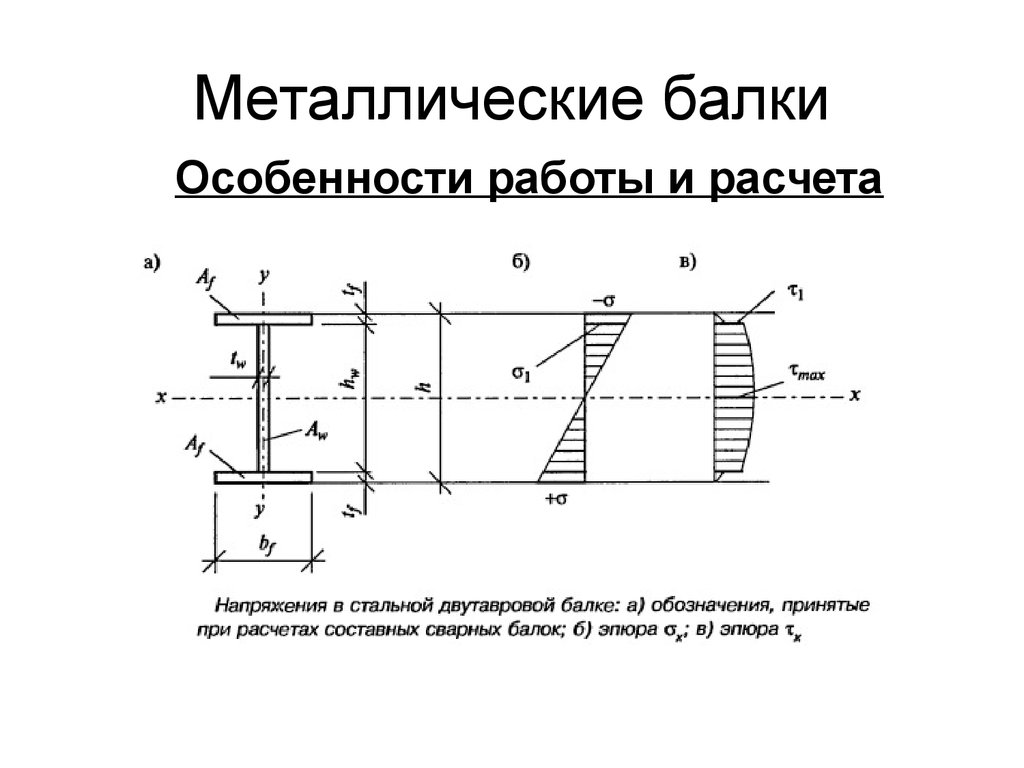 Учитывая способ закрепления балки, фиксируем, что прогибы в точках А и В равны нулю, причем важны расстояния от начала координат до опор:

Записываем уравнение метода начальных параметров для сечения C:

Произведение жесткости балки EI и прогиба сечения C будет складываться из произведения EI и прогиба сечения в начале системы координат, то есть сечения A:

Напомню, E – это модуль упругости первого рода, зависящий от материала из которого изготовлена балка, I – это момент инерции, который зависит от формы и размеров поперечного сечения балки. Также учитывается угол поворота поперечного сечения в начале системы координат, причем угол поворота дополнительно умножается на расстояние от рассматриваемого сечения до начала координат:

Учет внешней нагрузки

И, наконец, нужно учесть внешнюю нагрузку, но только ту, которая находится левее рассматриваемого сечения C. Здесь есть несколько особенностей:

• Сосредоточенные силы и распределенные нагрузки, которые направленны вверх, то есть совпадают с направлением оси y, в уравнении записываются со знаком «плюс». < 3 >>< 6 >]
  • Начало и конец распределенных нагрузок нужно умножать на дробь:

  Формулы прогибов

  С учетом всех вышеописанных правил запишем окончательное уравнение для сечения C:

  В этом уравнении содержится 2 неизвестные величины – искомый прогиб сечения C и угол поворота сечения A.

  Поэтому, чтобы найти прогиб, составим второе уравнение для сечения B, из которого можно определить угол поворота сечения A. Заодно закрепим пройденный материал:

  Выражаем угол поворота:

  Подставляем это значение в наше первое уравнение и находим искомое перемещение:

  Вычисление прогиба

  Значение получили в общем виде, так как изначально не задавались тем, какое поперечное сечение имеет рассчитываемая балка. Представим, что металлическая балка имеет двутавровое поперечное сечение №30. Тогда:

  Таким образом, такая балка прогнется максимально на 2 см. Знак «минус» указывает на то, что сечение переместится вниз.

  Расчет балки на изгиб, прогиб и прочность, включая калькулятор © Геостарт

  Рубрика:

  Строительные материалы

  Одной из важнейших задач для строителя считается расчет балки. Сегодня придумано немало средств, позволяющих решать данную задачу максимально быстро и точно. Наиболее удобными считаются онлайн-калькуляторы, которые за несколько секунд предоставляют необходимое решение. В данной статье мы разберем расчет балки на изгиб, прогиб, прочность с применением калькулятора.

  Как рассчитывать балки на прочность

  Расчет балки на прогиб , калькулятор для которого можно найти в интернете, можно произвести следующими методами:

  • Рассчитать максимальную нагрузку, которую способна выдержать заданная схема;
  • Подобрать сечение;
  • Проверочный перерасчет по максимальным значениям напряжения.

  Для наглядности следует рассмотреть общий принцип подбора сечения двутавра, расположенной на двух опорах. Загрузка происходит равномерно распределенной нагрузкой или сосредоточенной силой.

  Последовательность действий

  Для начала расчета балки на прогиб калькулятором необходимо определить точку, в которой будет максимальное значение момента. Все будет зависеть от того, какая схема представлена в задаче. Наиболее популярны следующие схемы:

  1. Заделка — шарнир;
  2. Заделка — заделка;
  3. Шарнир — шарнир;
  4. Заделка — свободный конец.

  Остальные варианты являются в той или иной степени разновидностями вышеуказанных схем.

  Как только вы нашли изгибающий момент, по таблице ищется момент сопротивления Wx указанного сечения по формулам, которые указываются в соответствующих таблицах. При делении максимального момента изгиба на момент сечения можно отыскать максимальное значение напряжения, которое необходимо сравнить с напряжением, которое максимально выдерживает определяемая конструкция.

  Сравнение полученных напряжений с напряжением материалов

  Онлайн-расчет балки на прочность сопровождается сравнением полученного значения напряжения в сечении с максимально возможным. Здесь необходимо смотреть на таблицу материалов, из которых производятся такие конструкции.

  Если материал пластичен, то максимальное напряжение схемы будет равно пределу текучести материала. К таковым относят алюминий, сталь, иные металлы. Хрупкие же материалы по типу чугуна имеют максимальное значение напряжения, равное пределу прочности. Для каждого конкретного материала имеется свое максимальное значение, которое можно найти в таблицах в специальной литературе.

  Пример расчета

  Предположим, что нам надо проверить на прочность двутавр номер 10. Его длина 2 метра, он жестко заделан в стену, человек массой 90 килограммов решил повиснуть на двутавре. Порядок решения здесь следующий:

  • Выбираем расчетную схему, в этом случае заделка — свободный конец;
  • Максимальное значение находится в заделке, двутавр имеет на всей длине одинаковое сечение. Тогда P = m*g = 90*10=0,9 кН, M = P*I= 1,8 кН*м;
  • Находим по таблице сортаментов для данного двутавра момент сопротивления;
  • Затем находим максимальные напряжения в балке б = M/W = 1,8 / 0. 0000397 = 45,34 Мпа;
  • Сравниваем с максимально допустимым напряжением, равным пределу текучести стали, из которой сделан двутавр. Так как 45,34 Мпа меньше 245 Мпа, то такой двутавр выдержит человека массой 90 килограммов.

  Можно также решить и вторую задачу, связанной с нахождением максимальной массы человека, которую может выдержать данная балка. Здесь приравнивают значения предела текучести и напряжения в сечении балки, найти максимальный момент и затем наибольшую массу. Для более точного результата следует учитывать различные коэффициенты и брать двойной запас прочности.

  Онлайн-калькуляторы

  Расчет прогиба балки онлайн-калькулятором достаточно быстрый и точный. Здесь выбирается одна из схем, затем набираются соответствующие числовые значения и происходит расчет по всем необходимым параметрам.

  Необходимо указать значения моментов, изгибающих сил, длин участков. Итогом станут эпюры моментов и сил. Решение данными программами достаточно точное и позволяет оперативно посчитать силы и моменты для балок на прочность, изгибы и прогибы.

  Преимуществом подобных средств является большой набор схем для расчета, быстрота, точность, простота применения. Однако для уточнения полученного результата надо произвести самостоятельное письменное решение.

  В заключение можно сказать следующее: расчет балки на прочность можно произвести как вручную, так и с применением онлайн-калькуляторов. Их можно комбинировать, использовав один из них для проверки другого метода. Рассчитать балку может понадобиться в разных случаях, особенно актуально это становится при строительстве. Только правильно рассчитанная балка позволит построить или реконструировать сооружение с тем условием, что оно прослужит длительное время.

  Также данный расчет полезен для всех тех, кто учится или имеет дело с техническими науками, ибо прикладная механика является неотъемлемой частью программы любого технического вуза. Удачных расчетов на прочность!

  автор Олейников Константин

  Геодезические измерения: виды, классификация и характеристики.

  Пример заполнения страницы журнала измерения направлений

  Геодезические сети, классификация и способы их развития

  Калькулятор расчета
  цен на кадастровые
  работы

  Расчитать

  Электропроводка в доме своими руками: пошаговая схема

  Подготовка к производству монтажных работ

  Проектирование грунтовой заделки трубчатой моноопоры

  Расчет балок при изгибе на прочность

  Оглавление:

  • В зависимости от поставленной цели расчета на долговечность, расчет балки в момент изгиба на долговечность может быть представлен тремя видами решаемых задач. 1. Проверьте напряжение балок при известных размерах поперечного сечения и заданных прочностных характеристиках материала. 2. Выбор поперечного сечения, то есть определение требуемых размеров поперечного сечения при заданной форме и прочностных

  характеристиках материала (расчетные расчеты). 3. Конечная нагрузка определяется выбранными размерами поперечного сечения и прочностными характеристиками материала. Балка рассчитана с максимальными нормальными, тангенциальными и эквивалентными напряжениями. В данном разделе приведен расчет балок определенного сечения из пластического материала. Расчет прочности по максимальному нормальному напряжению.

  Поскольку балки из пластического материала, как правило, выполнены из
  Людмила Фирмаль

  симметричных сечений, то растягивающие и сжимающие напряжения крайних волокон одинаковы. Опасная часть балки становится участком, где возникает максимальный изгибающий момент Afxm ax, а опасная точка этого участка находится на расстоянии/ / max от нейтральной оси, где условие прочности в опасном участке записывается без учета знака изгибающего момента следующим образом: zmax=l^xmaxl Utak / ^x Ku»(21. x

  Ry, (21.15) где Wx=Jx/h / 2 называется осевым резистивным моментом поперечного сечения. Спецификация момента сопротивления-м3 или см3. Таким образом, момент сопротивления является геометрической характеристикой прочности поперечного сечения балки при изгибе. Чем больше момент сопротивления, тем меньше стресс, который возникает в этой точке опасности. Момент сопротивления высоте h и ширине b прямоугольного сечения Wx = Jx/!/ Max=(bh9 / 12)/(n / 2)=BSC. Момент сопротивления W x радиусу G круглого сечения =Jx / r■ — w* / 4r=LGs. Сопротивление W * раз для наружного радиуса G кольцевого сечения Вт к икс =Jkx/r=n(r4-4r rty. Для профиля качения двутавровой балки канальный момент сопротивления показан в справочниках.

  • Для выбора поперечного сечения балки (расчетный расчет) значение требуемого момента сопротивления определяется по следующей формуле: G xt R>(21.16)Cu Выберите размер этого сечения до полученного значения W x в заданном виде поперечного сечения. Определение предельной нагрузки осуществляется по формуле прочности (21.15). По известным значениям W x и r y вычисляется максимальный изгибающий момент абсолютной величины, который может выдержать данная балка: / Mx m axl=Wx Ry. (21.17) Затем, в соответствии с полученным значением|M x max|, определяется предельное значение внешней нагрузки, действующей на балку. 16-

  480 241 расчет прочности при максимальном касательном напряжении. После расчета балки на нормальное напряжение выполняется проверка на прочность максимального тангенциального напряжения. Балка с определенной шириной поперечного сечения по высоте (прямоугольник, квадрат и др.).), Обычно не рассчитывают на тангенциальное напряжение, определяя его прочность нормальным напряжением. Исключение составляет балка с большой поперечной силой, или балка с резким изменением ширины сечения (двутавровая балка, швеллер и др.).да что с тобой такое? Опасным является поперечное сечение балки, а максимальная поперечная сила действует на Qmax. s»(21.18) s otc-статический момент блокировки части поперечного сечения относительно нейтральной оси;Jx—момент инерции всего
  Людмила Фирмаль

  поперечного сечения относительно нейтральной оси; DST определяется напряжением сдвига; — момент инерции всего поперечного сечения относительно нейтральной оси. Расчет силы эквивалентного напряжения. Расчет эквивалентного напряжения в основном основан на двутавровых балках, каналах,etc.At поскольку любая внешняя нагрузка, максимальный изгибающий момент и максимальная поперечная сила, возникающие сечения, обычно не совпадают, опасным сечением, большим изгибающим моментом и точкой бокового опасного сечения будет точка, в которой эквивалентное напряжение достигает наибольшего значения. Максимальное эквивалентное напряжение поперечного сечения балки создается в точках сопряжения горизонтальной и

  вертикальной стенок. Эквивалентное напряжение при расчете стальных балок рассчитывается по энергетической теории прочности. 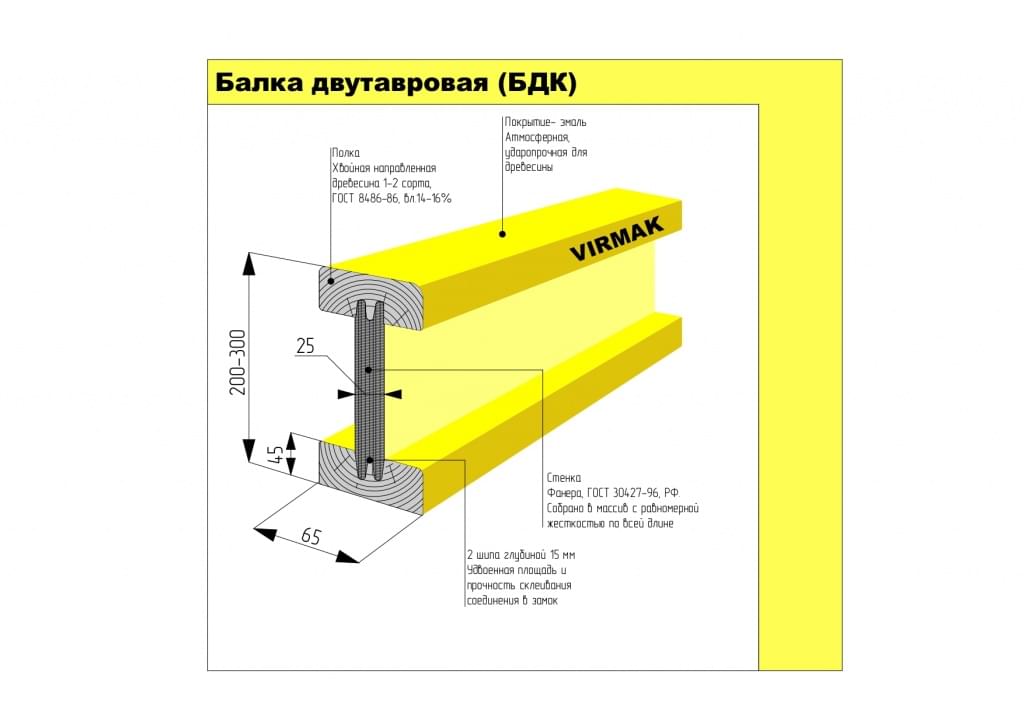Условие прочности описывается следующим образом %kvtah=<1 ‘ 1E*Y(21.19), где Qz-Mxyljx—нормальное напряжение в критической точке;Vpy=qys0tcijxb-касательное напряжение в критической точке;RtJ-расчетное сопротивление стали. Рассмотрим процесс расчета более подробно на примере. 242 гонки 21.20 Например. Может быть. 21.20, а, имеет поперечное сечение в виде двутавровой балки(рис. 21.21,а), ры=2jQ МПа делать расчет на прочность, Ра=121.8 МПа, JX используется — =253.9-ИО-6M4 и АТИ=1209-ИО-6м3. Решение. Из приложенной нагрузки на балку находим опорную реакцию: S z=0;/ / C=0. =504-0, 5+504-4, 5-Rc-5=0; Rc=504kN. ZMc=RB-b— 504-4,5 — 504-0,5 = 0; RB=504kN. Рассчитайте изгибающий момент и боковую силу характерной части балки. Поперечное

  сечение V. MX=0\Qy=Rg=504kN. В разделе D. MX=I 0, 5=252kN-m; Q * eB=504kN; Q » p=0. Раздел К. М,=р, б- 4,5-504-4=252kN-м;м джеб=0;м’*== — 504kN. Секция C. L1x=0; Qy= — 504kN. 1г* 243 согласно этим значениям, графики M и Q(фиг. 21.20, b и C). Расчет самого высокого нормального напряжения. 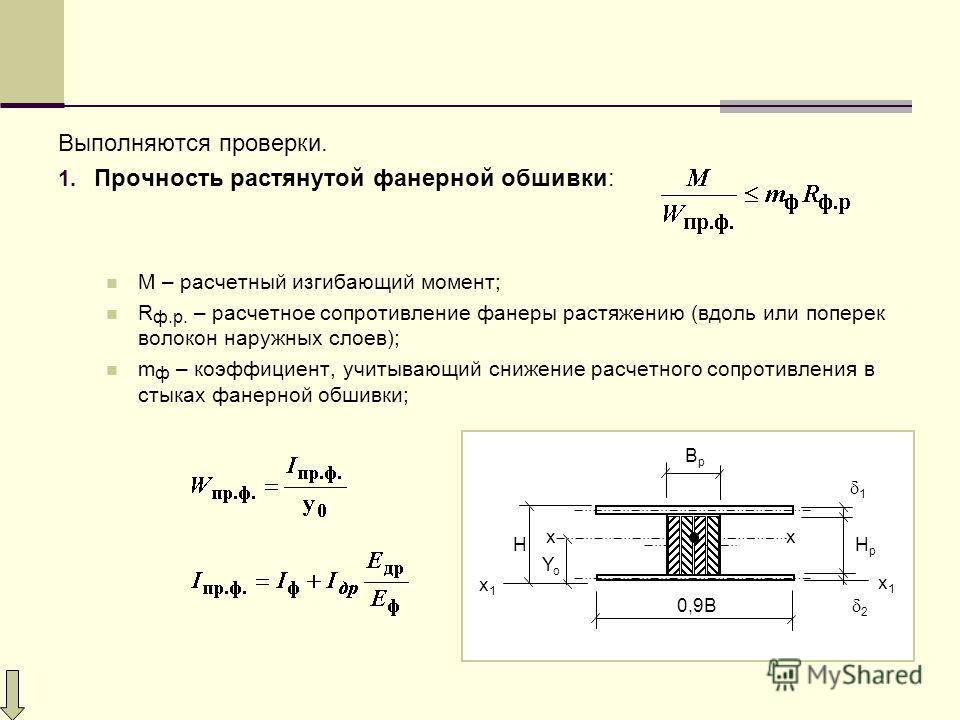x=252-103-2 0.1 0 -2 /2 5 3 ,9 -1 0 -» = 19,85 МПа. Предварительно рассчитанное тангенциальное напряжение в точке 2: Два. = Вычислить эквивалентное напряжение 110,76 МПа: около максимального env= 198,5® + 3-110,76″ = 283,2 МПа. Тэ Макс>1,15/?y или 283.2>241.5. 244балка не соответствует прочностным условиям максимальных тангенциальных и эквивалентных напряжений. Необходимо увеличить размер поперечного сечения.

  Смотрите также:

  Решение задач по технической механике

  ПСК «БАФ-ИНЖИНИРИНГ»

  Высота балки, мм.	Максимальный пролет при нагрузке 400 кг/кв.м.					70х45
  	Шаг 0,3м	Шаг 0,4м	Шаг 0,5м	Шаг 0,6м	Шаг 0,7м	Шаг 0,8м
  200	4,6 м	4,2 м	3,9 м	3,7 м	3,6 м	3,4 м
  250	5,4 м	4,9 м	4,6 м	4,4 м	4,2 м	4,0 м
  300	6,2 м	5,7 м	5,3 м	5 м	4,8 м	4,6 м
  350	7 м	6,4 м	6 м	5,6 м	5,4 м	5,2 м
  400	7,7 м	7,1 м	6,6 м	6,2 м	5,9 м	5,7 м
  450	8,4 м	7,7 м	7,2 м	6,8 м	6,5 м	6,1 м

  Высота балки, мм.	Максимальный пролет при нагрузке 350 кг/кв.м.					70х45
  	Шаг 0,3м	Шаг 0,4м	Шаг 0,5м	Шаг 0,6м	Шаг 0,7м	Шаг 0,8м
  200	4,8 м	4,4 м	4,1 м	3,9 м	3,7 м	3,6 м
  250	5,6 м	5,1 м	4,8 м	4,5 м	4,3 м	4,2 м
  300	6,5 м	5,9 м	5,5 м	5,2 м	5 м	4,8 м
  350	7,3 м	6,7 м	6,2 м	5,9 м	5,6 м	5,4 м
  400	8,1 м	7,4 м	6,9 м	6,5 м	6,2 м	5,9 м
  450	8,8 м	8 м	7,5 м	7,1 м	6,7 м	6,5 м

  Высота балки, мм.	Максимальный пролет при нагрузке 300 кг/кв.м.					70х45
  	Шаг 0,3м	Шаг 0,4м	Шаг 0,5м	Шаг 0,6м	Шаг 0,7м	Шаг 0,8м
  200	5 м	4,6 м	4,3 м	4,1 м	3,9 м	3,7 м
  250	5,9 м	5,4 м	5 м	4,8 м	4,5 м	4,4 м
  300	6,8 м	6,2 м	5,8 м	5,5 м	5,2 м	5 м
  350	7,7 м	7 м	6,5 м	6,1 м	5,9 м	5,6 м
  400	8,5 м	7,7 м	7,2 м	6,8 м	6,5 м	6,2 м
  450	9,3 м	8,4 м	7,9 м	7,4 м	7,1 м	6,8 м

  Высота балки, мм.	Максимальный пролет при нагрузке 250 кг/кв.м.					70х45
  	Шаг 0,3м	Шаг 0,4м	Шаг 0,5м	Шаг 0,6м	Шаг 0,7м	Шаг 0,8м
  200	5,3 м	4,9 м	4,5 м	4,3 м	4,1 м	3,9 м
  250	6,2 м	5,7 м	5,3 м	5 м	4,8 м	4,6 м
  300	7,2 м	6,6 м	6,1 м	5,8 м	5,5 м	5,2 м
  350	8,1 м	7,4 м	6,9 м	6,5 м	6,2 м	6 м
  400	9 м	8,2 м	7,6 м	7,2 м	6,9 м	6,6 м
  450	9,8 м	8,9 м	8,3 м	7,9 м	7,5 м	7,2 м

  Высота балки, мм.	Максимальный пролет при нагрузке 200 кг/кв.м.					70х45
  	Шаг 0,3м	Шаг 0,4м	Шаг 0,5м	Шаг 0,6м	Шаг 0,7м	Шаг 0,8м
  200	5,7 м	5,2 м	4,9 м	4,6 м	4,4 м	4,2 м
  250	6,7 м	6,1 м	5,7  м	5,4 м	5,1 м	4,9 м
  300	7,7 м	7,1 м	6,6 м	6,2 м	5,9 м	5,7 м
  350	8,7 м	7,9 м	7,4 м	7 м	6,7 м	6,4 м
  400	9,6 м	8,8 м	8,2 м	7,7 м	7,4 м	7,1 м
  450	10,5 м	9,6 м	8,9 м	8,4 м	8 м	7,7 м

  Высота балки, мм.	Максимальный пролет при нагрузке 400 кг/кв.м.					89х45
  	Шаг 0,3м	Шаг 0,4м	Шаг 0,5м	Шаг 0,6м	Шаг 0,7м	Шаг 0,8м
  200	5 м	4,6 м	4,3 м	4,1 м	3,9 м	3,7 м
  250	5,9 м	5,4 м	5 м	4,7 м	4,5 м	4,4 м
  300	6,8 м	6,2 м	5,8 м	5,5 м	5,2 м	5 м
  350	7,6 м	6,9 м	6,5 м	6,1 м	5,8 м	5,6 м
  400	8,4 м	7,7 м	7,2 м	6,8 м	6,5 м	6,2 м
  450	9,2 м	8,4 м	7,8 м	7,4 м	7 м	6,8 м

  Высота балки, мм.	Максимальный пролет при нагрузке 350 кг/кв.м.					89х45
  	Шаг 0,3м	Шаг 0,4м	Шаг 0,5м	Шаг 0,6м	Шаг 0,7м	Шаг 0,8м
  200	5,2 м	4,8 м	4,5 м	4,2 м	4 м	3,9 м
  250	6,1 м	5,6 м	5,2 м	4,9 м	4,7 м	4,5 м
  300	7 м	6,4 м	6 м	5,7 м	5,4 м	5,2 м
  350	7,9 м	7,2 м	6,7 м	6,4 м	6,1 м	5,8 м
  400	8,8 м	8 м	7,5 м	7 м	6,7 м	6,4 м
  450	9,6 м	8,7 м	8,1 м	7,7 м	7,3 м	7 м

  Высота балки, мм.	Максимальный пролет при нагрузке 300 кг/кв.м					89х45
  	Шаг 0,3м	Шаг 0,4м	Шаг 0,5м	Шаг 0,6м	Шаг 0,7м	Шаг 0,8м
  200	5,5 м	5 м	4,7 м	4,4 м	4,2 м	4,1 м
  250	6,4 м	5,9 м	5,5 м	5,2 м	4,9 м	4,7 м
  300	7,4 м	6,8 м	6,3 м	6 м	5,7 м	5,5 и
  350	8,3 и	7,6 м	7,1 м	6,7 м	6,4 м	6,1 м
  400	9,2 м	8,4 м	7,8 м	7,4 м	7 м	6,8 м
  450	10 м	9,2 м	8,5 м	8,1 м	7,7 м	7,4 м

  Высота балки, мм.	Максимальный пролет при нагрузке 250 кг/кв.м.					89х45
  	Шаг 0,3м	Шаг 0,4м	Шаг 0,5м	Шаг 0,6м	Шаг 0,7м	Шаг 0,8м
  200	5,8 м	5,3 м	5 м	4,7 м	4,5 м	4,3 м
  250	6,8 м	6,2 м	5,8 м	5,5 м	5,2 м	5 м
  300	7,8 м	7,1 м	6,7 м	6,3 м	6 м	5,8 м
  350	8,8 м	8 м	7,5 м	7,1 м	6,7 м	6,5 м
  400	9,7 м	8,9 м	8,3 м	7,8 м	7,5 м	7,2 м
  450	10,6 м	9,7 м	9 м	8,5 м	8,1 м	7,8 м

  Высота балки, мм.	Максимальный пролет при нагрузке 200 кг/кв.м.					89х45
  	Шаг 0,3м	Шаг 0,4м	Шаг 0,5м	Шаг 0,6м	Шаг 0,7м	Шаг 0,8м
  200	6,2 м	5,7 м	5,3 м	5 м	4,8 м	4,6 м
  250	7,3 м	6,7 м	6,2 м	5,9 м	5,5 м	5,4 м
  300	8,4 м	7,7 м	7,1 м	6,8 м	6,4 м	6,2 м
  350	9,5 м	8,6 м	8 м	7,6 м	7,2 м	6,9 м
  400	10,5 м	9,5 м	8,9 м	8,4 м	8 м	7,7 м
  450	11,4 м	10,4 м	9,7 м	9,2 м	8,7 м	8,4 м

  Высота балки, мм.	Максимальный пролет при нагрузке 400 кг/кв.м.					64х39
  	Шаг 0,3м	Шаг 0,4м	Шаг 0,5м	Шаг 0,6м	Шаг 0,7м	Шаг 0,8м
  200	4,2 м	3,9 м	3,6 м	3,4 м	3,3  м	3,1 м
  250	5 м	4,6 м	4,3 м	4 м	3,9 м	3,7 м
  300	5,8 м	5,3 м	4,9 м	4,6 м	4,4 м	4,2 м
  350	6,5 м	5,9 м	5,5 м	5,2 м	5 м	4,8 м
  400	7,2 м	6,5 м	6,1 м	5,7 м	5,5 м	5,3 м
  450	7,8 м	7,1 м	6,6 м	6,3 м	6 м	5,7 м

  Высота балки, мм.	Максимальный пролет при нагрузке 350 кг/кв.м.					64х39
  	Шаг 0,3м	Шаг 0,4м	Шаг 0,5м	Шаг 0,6м	Шаг 0,7м	Шаг 0,8м
  200	4,4 м	4 м	3,8 м	3,6 м	3,4 м	3,3 м
  250	5,2 м	4,8 м	4,5 м	4,2 м	4 м	3,9 м
  300	6 м	5,5 м	5,1 м	4,8 м	4,6 м	4,4 м
  350	6,8 м	6,2 м	5,7 м	5,4 м	5,2 м	5 м
  400	7,5 м	6,8 м	6,3 м	6 м	5,7 м	5,5 м
  450	8,1 м	7,4 м	6,9 м	6,5 м	6,2 м	6 м

  Высота балки, мм.	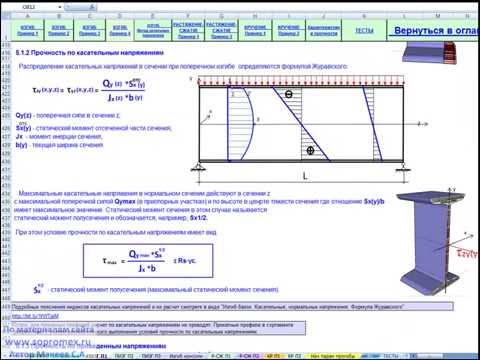Максимальный пролет при нагрузке 300 кг/кв.м					64х39
  	Шаг 0,3м	Шаг 0,4м	Шаг 0,5м	Шаг 0,6м	Шаг 0,7м	Шаг 0,8м
  200	4,6 м	4,2 м	3,9 м	3,7 м	3,6 м	3,4 м
  250	5,5 м	5 м	4,7 м	4,4 м	4,2 м	4 м
  300	6,3 м	5,8 м	5,4 м	5,1 м	4,9 м	4,6 м
  350	7,1 м	6,5 м	6 м	5,7 м	5,4 м	5,2 м
  400	7,8 м	7,2 м	6,7 м	6,3 м	6 м	5,7 м
  450	8,6 м	7,8 м	7,3 м	6,9 м	6,5 м	6,3 м

  Высота балки, мм.	Максимальный пролет при нагрузке 250 кг/кв.м.					64х39
  	Шаг 0,3м	Шаг 0,4м	Шаг 0,5м	Шаг 0,6м	Шаг 0,7м	Шаг 0,8м
  200	4,9 м	4,5 м	4,2 м	3,9 м	3,8 м	3,6 м
  250	5,8 м	5,3 м	5 м	4,7 м	4,5 м	4,3 м
  300	6,7 м	6,1 м	5,7 м	5,4 м	5,1 м	4,9 м
  350	7,5 м	6,9 м	6,4 м	6 м	5,7 м	5,5 м
  400	8,3 м	7,6 м	7,1 м	6,7 м	6,3 м	6,1 м
  450	9,1 м	8,3 м	7,7 м	7,3 м	6,9 м	6,6 м

  Высота балки, мм.	Максимальный пролет при нагрузке 200 кг/кв.м.					64х39
  	Шаг 0,3м	Шаг 0,4м	Шаг 0,5м	Шаг 0,6м	Шаг 0,7м	Шаг 0,8м
  200	5,3 м	4,8 м	4,5 м	4,2 м	4 м	3,9 м
  250	6,3 м	5,7 м	5,3 м	5 м	4,8 м	4,6 м
  300	7,2 м	6,6 м	6,1 м	5,8 м	5,5 м	5,3 м
  350	8,1 м	7,4 м	6,9 м	6,5 м	6,2 м	5,9 м
  400	8,9 м	8 м	7,6 м	7,2 м	6,8 м	6,5 м
  450	9,8 м	8,9 м	8,3 м	7,8 м	7,4 м	7,1 м

  Высота балки, мм.	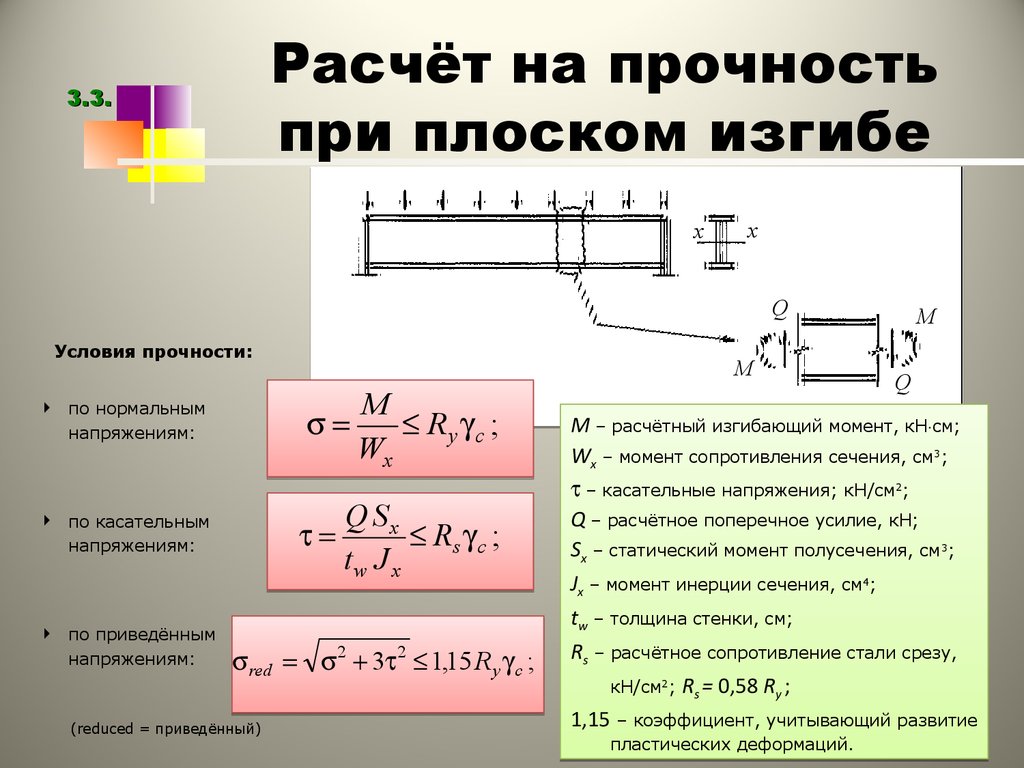Максимальный пролет при нагрузке 400 кг/кв.м.					90х45
  	Шаг 0,3м	Шаг 0,4м	Шаг 0,5м	Шаг 0,6м	Шаг 0,7м	Шаг 0,8м
  200	5 м	4,6 м	4,3 м	4,1 м	3,9 м	3,7 м
  250	5,9 м	5,4 м	5 м	4,8 м	4,5 м	4,4 м
  300	6,8 м	6,2 м	5,8 м	5,5 м	5,2 м	5 м
  350	7,6 м	6,9 м	6,5 м	6,1 м	5,8 м	5,6 м
  400	8,4 м	7,7 м	7,1 м	6,8 м	6,5 м	6,2 м
  450	9,2 м	8,4 м	7,8 м	7,4 м	7 м	6,7 м

  Высота балки, мм.	Максимальный пролет при нагрузке 350 кг/кв.м.					90х45
  	Шаг 0,3м	Шаг 0,4м	Шаг 0,5м	Шаг 0,6м	Шаг 0,7м	Шаг 0,8м
  200	5,2 м	4,8 м	4,5 м	4,2 м	4 м	3,9 м
  250	6,1 м	5,6 м	5,2 м	5 м	4,7 м	4,5 м
  300	7 м	6,4 м	6 м	5,7 м	5,4 м	5,2 м
  350	7,9 м	7,2 м	6,8 м	6,4 м	6,1 м	5,8 м
  400	8,8 м	8 м	7,5 м	7 м	6,7 м	6,5 м
  450	9,5 м	8,7 м	8,2 м	7,7 м	7,3 м	7 м

  Высота балки, мм.	Максимальный пролет при нагрузке 300 кг/кв.м					90х45
  	Шаг 0,3м	Шаг 0,4м	Шаг 0,5м	Шаг 0,6м	Шаг 0,7м	Шаг 0,8м
  200	5,5 м	5 м	4,7 м	4,4 м	4,2 м	4,1 м
  250	6,4 м	5,9 м	5,5 м	5,2 м	5 м	4,8 м
  300	7,4 м	6,8 м	6,3 м	6 м	5,7 м	5,5 м
  350	8,3 м	7,6 м	7,1 м	6,7 м	6,4 м	6,1 м
  400	9,2 м	8,4 м	7,8 м	7,4 м	7 м	6,8 м
  450	10 м	9,2 м	8,5 м	8,1 м	7,7 м	7,4 м

  Высота балки, мм.	Максимальный пролет при нагрузке 250 кг/кв.м.					90х45
  	Шаг 0,3м	Шаг 0,4м	Шаг 0,5м	Шаг 0,6м	Шаг 0,7м	Шаг 0,8м
  200	5,8 м	5,3 м	5 м	4,7 м	4,5 м	4,3 м
  250	6,8 м	6,2 м	5,8 м	5,5 м	5,2 м	5 м
  300	7,8 м	7,2 м	6,7 м	6,3 м	6 м	5,8 м
  350	8,8 м	8 м	7,5 м	7,1 м	6,8 м	6,5 м
  400	9,7 м	8,9 м	8,3 м	7,8 м	7,5 м	7,2 м
  450	10,6 м	9,7 м	9 м	8,5 м	8,1 м	7,8 м

  Высота балки, мм.	Максимальный пролет при нагрузке 200 кг/кв.м.					90х45
  	Шаг 0,3м	Шаг 0,4м	Шаг 0,5м	Шаг 0,6м	Шаг 0,7м	Шаг 0,8м
  200	6,2 м	5,7 м	5,3 м	5 м	4,8 м	4,6 м
  250	7,3 м	6,7 м	6,2 м	5,9 м	5,6 м	5,4 м
  300	8,4 м	7,7 м	7,2 м	6,8 м	6,4 м	6,2 м
  350	9,5 м	8,6 м	8 м	7,6 м	7,2 м	6,9 м
  400	10,5 м	9,5 м	8,9 м	8,4 м	8 м	7,7 м
  450	11,4 м	10,4 м	9,7 м	9,2 м	8,7 м	8,4 м

  Расчет металлической балки перекрытия на прогиб и на жесткость

  11. 07.2016/в Плита перекрытия /от admin

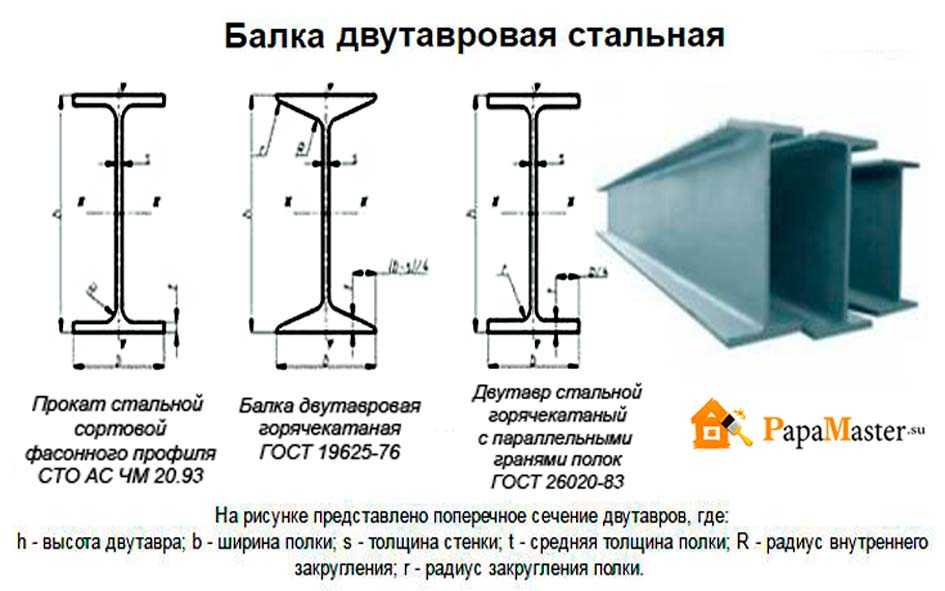
  Металлические балки двутавровые

  Кроме повсеместно ведущегося строительства многоэтажных зданий с большим числом квартир, широкое распространение получило сооружение частных домов, причем не только небольших одноэтажных, но и довольно крупных, с двумя и более этажами, иногда и с мансардой наверху или обитаемым чердаком. Для таких домов уже не подходит каркасный метод; материалом часто служит, вместо дерева, кирпич или железобетон. Возведение крупных частных домов должно вестись по всем правилам строительной науки, так как ошибки при проектировании или воплощении проекта могут привести к нежелательным последствиям.

  Если строящийся дом представляет собой капитальное здание – из бетона, кирпича, шлакоблока, то для потолочных перекрытий, межэтажных и чердачных, целесообразно применить железобетонные плиты. Наиболее подходящий тип каркаса, способный выдержать вес таких перекрытий, – это каркас, элементом которого является металлическая балка двутаврового профиля.

  Именно этот вид проката, установленный своей стенкой вертикально, обладает наибольшей несущей способностью. Естественно, фундамент и стены дома при этом должны быть достаточной прочности, чтобы выдерживать дополнительный вес от 0,5 до 1 тонны – столько металла, в зависимости от количества балок и номера профиля может понадобиться для потолочного перекрытия.

  Чтобы избежать лишних затрат и лишнего веса каркаса потолка, а также не допустить обрушения или значительного прогиба балок, необходимо заранее рассчитать их параметры и по результатам расчета подобрать нужный прокат. Расчет сводится к вычислению следующих величин: требуемого момента сопротивления и минимального момента инерции сечения балки, а исходя из последнего – максимального относительного прогиба.

  Примечание

  Расчет ведется по двум характеристикам – на прочность и на жесткость. По полученным значениям момента сопротивления и момента инерции в таблицах ГОСТ находят требуемый номер проката.

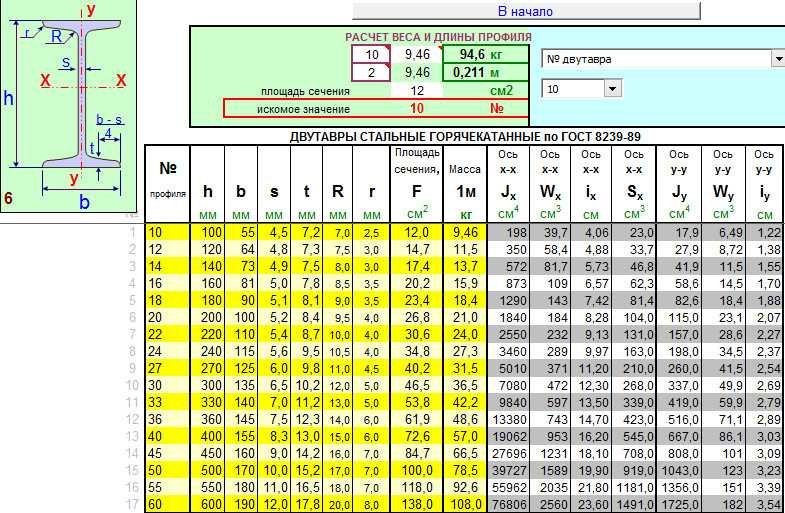
  Исходные данные для расчетов

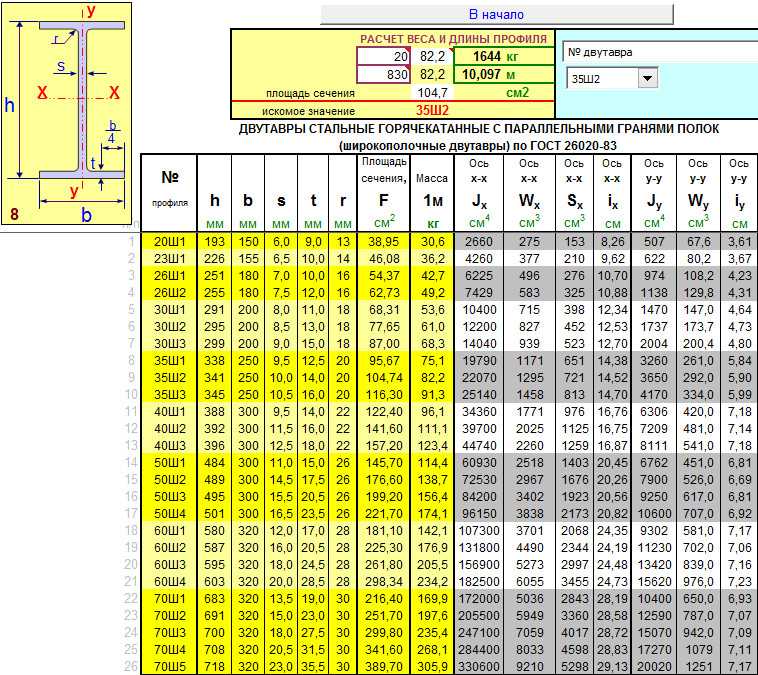
  Для каркаса потолочных перекрытий малогабаритных частных домов обычно используется двутавр 10 – 20 номеров. Характеристики этих профилей приводятся в ГОСТ 8239-72 – их линейные размеры, площади сечения, максимальные моменты сопротивления по вертикали W_y и минимальные моменты инерции J_y.

  Необходимо знать тип плит, которые будут опираться на балочный каркас, а также размеры несущего периметра дома. Можно применить пустотные железобетонные плиты ПК-12-10-8 (1180 х 990 мм, масса 380 кг), а размеры дома взять 4,5 х 6 м. Балки укладываются вдоль короткой стены; шаг укладки при таком размере плит равен 1000 мм (стыки плит совпадают с продольными осями балок, при минимальном зазоре 1 см). Это потребуется для расчета распределенной нагрузки, и исходя из нее – линейной нагрузки на балку, вес самой балки по сравнению с распределенной нагрузкой мал, и при вычислении линейной нагрузки им можно пренебречь.

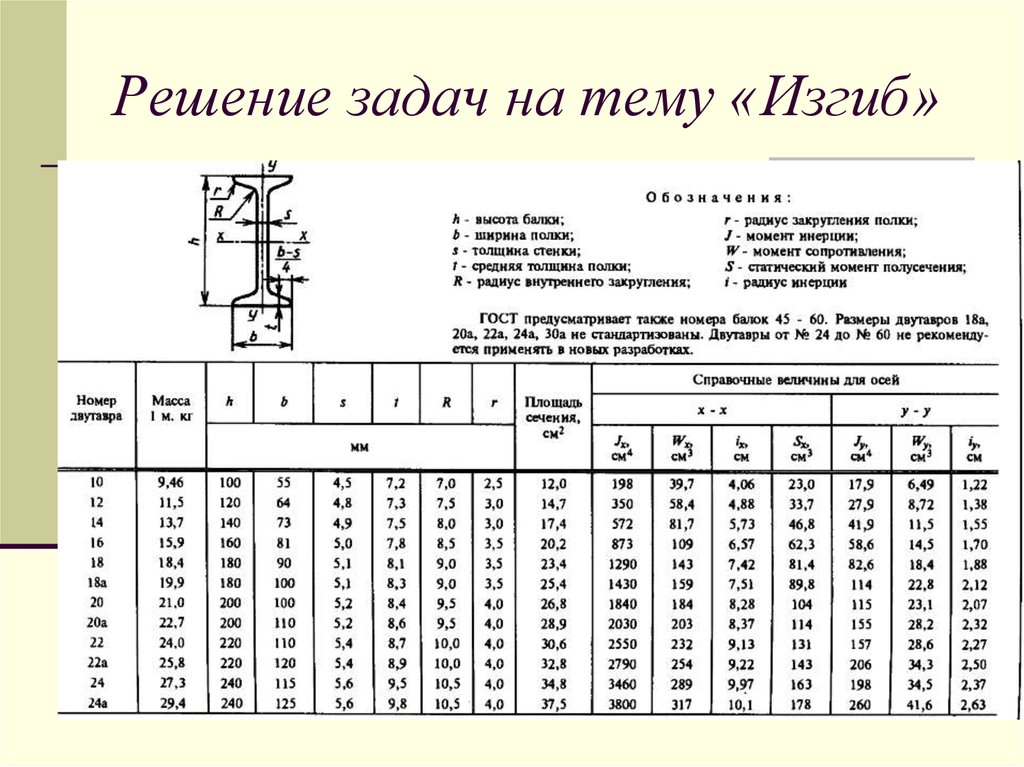
  Распределенная нагрузка при таком типе плит будет равна 325 кгс / м². К этому надо добавить нагрузку возможных перегородок на верхней стороне перекрытия (75 кгс / м²) и возможную временную нагрузку (200 кгс / м²). В итоге нагрузка, распределенная по площади:

  Q = 325 + 75 + 200 = 600 кгс / м²,

  а линейная нагрузка

  q = Q * p = 600 кгс / м = 6 кгс / см.

  Эта величина используется в дальнейших расчетах.

  Расчет на прогиб

  Изгибающий момент для каждой балки вычисляется, исходя из величины линейной нагрузки q, шага укладки балок p и длины перекрываемого пролета L. Так как балки укладываются вдоль короткой стороны, то L = 4,5 м = 450 см (конечно, сами балки длиннее – около 5 м, так как опираются на стены, но шарнирными опорами для них служат именно внутренние края стен).

  Искомая величина момента, в таком случае:

  M_y = (q * L²) / 8 = 6 * 450² / 8 = 151875 кгс * см.

  Максимальный момент сопротивления сечения балки можно рассчитать, разделив изгибающий момент на расчетное сопротивление стали – например, марки С235, равное 2150 кгс / см²:

  W_y = 151875 / 2150 = 70,6 см³.

  Это полученное значение надо сравнить с величиной момента сопротивления сечения двутавровой балки. Из таблицы ГОСТ 8239-72 видно, что вычисленный показатель  примерно соответствует (с запасом) моменту сопротивления для профиля 14 (81,7 см³⁾. Следовательно, этот номер проката будет удовлетворять требованиям к прочности балок.

  Расчет на жесткость

  Жесткость балок характеризуется максимальной величиной прогиба при заданных исходных параметрах. В случае распределенной нагрузки прогиб вычисляется по формуле:

  f = 5 * q * L⁴ / (384 * E * J_y), где

  • q – линейная нагрузка на балку;
  • L – длина пролета;
  • E – модуль упругости материала, для стали С235 равный 2,1 * 10⁶ кгс / см²;
  • J_y – минимальный момент инерции для данного профиля.

  Для принятых ранее исходных данных, с учетом того, что из расчета на прочность наиболее подходящим профилем оказался № 14, для которого J_y, по табличным значениям ГОСТ, равен 572 см⁴, можно получить:

  f = 2,6 см,

  а в относительной мере, с учетом того, что длина пролета 450 см – 1 / 172. Это превышает максимально допустимый прогиб, принятый равным 1 / 250.

  Поэтому расчет приходится повторить и вычислить прогиб для другого номера проката. Для № 16, у которого момент инерции равен 873 см⁴, абсолютный прогиб получается 1,74 см, а относительный – 1 / 256, что является приемлемым.

  Расчеты металлической балки перекрытия на прочность и прогиб, онлайн-калькулятор

  Несмотря на бушующий в мире экономический кризис, который, к сожалению, затронул и нашу страну, строительство объектов различной важности продолжает производиться. При этом, в последнее время получило новый толчок развития именно промышленное строительство, однако, потребность жителей страны в жилых квадратных метрах не уменьшилось.

  • Описание ↓
  • Область применения ↓
  • Расчет ↓
  • Онлайн ↓
  • Пример расчета ↓

  Сегодня в строительстве промышленных и гражданских объектов повсеместно применяются металлические балки перекрытия, которые повышают несущую способность всей конструкции.

  Описание

  Стальные балки перекрытия представляют собой металлический брус определённой длины и определённой формы поперечного сечения. Как правило, металлические балки исполняются из высокопрочной стали марки Ст 5 с формой поперечного сечения типа двутавр и швеллер.

  Балки производятся именно в таких формах поперечного сечения, потому что расчёт показывает, что такая форма является более экономически выгодной по сравнению с другими геометрическими фигурами.

  Кроме того, расчёты показывают, что балка именно двутаврогого сечения лучше всего воспринимает давление и такие нагрузки, как изгиб, кручение и их совместное действие.

  Продолжая перечислять преимущества двутавровых балок, можно отметить немаловажный факт того, что такая форма сечения помогает уменьшить вес конструкции.

  Это помогает снизить нагрузку, например, на стены и фундамент здания, если в межэтажном перекрытии использовать металлические балки перекрытия. Также, из преимуществ можно отметить простоту монтажа любой конструкции из балок, скорость выполнения работ.

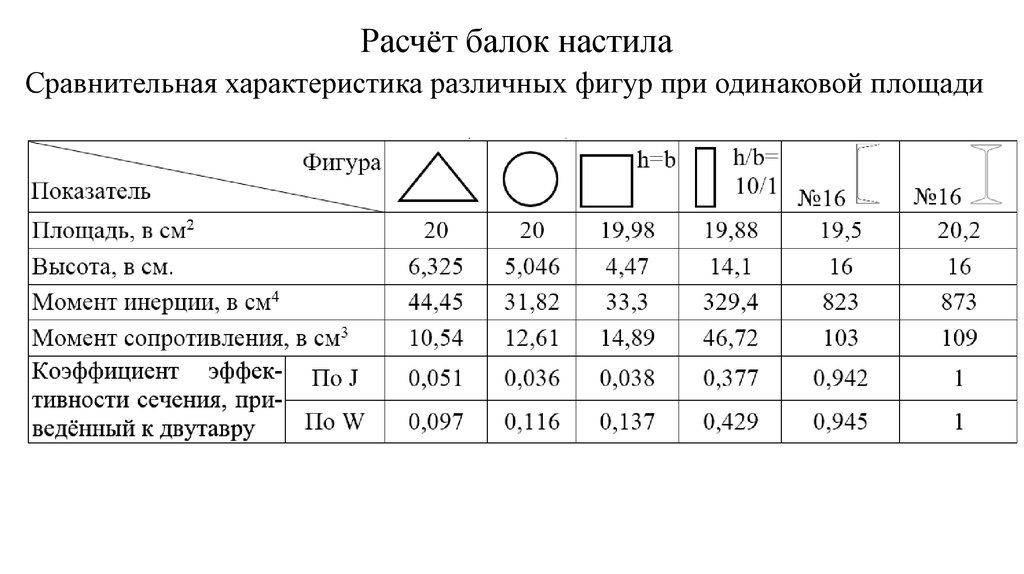
  Для большей экономии использования металла и для облегчения всей конструкции существует сортамент балок двутаврового и швеллерного поперечного сечения. Площадь сечения изменяется от минимальной равной 12 кв. см до максимальной 234 кв. см, соответственно, для номеров профиля 10 и 70б.

  Все значения площадей и массы профиля представлены в таблицах ГОСТ 8239-72. Чтобы её произвести, необходимо произвести расчёт профиля по прочностным характеристикам и вычислить подходящую площадь. Точная методика представлена ниже.

  Таким образом, видно, что в качестве бруса перекрытия стоит использовать именно стальные балки, так как они во многом выигрывают по сравнению с конкурирующими материалами.

  Область применения

  Чаще всего, двутавровые балки применяются в промышленном строительстве, а именно, в случае возведения зданий с большими пролётами между опорами.

  Благодаря своим механическим характеристикам и стойкости к динамическим воздействиям, металлический брус используют при возведении дорог и мостов и в других случаях необходимости возведения конструкций, выдерживающих большие нагрузки подобного характера.

  В последнее время, стальные двутавровые балки стали применять в качестве элемента декора в квартирах и офисах. После покраски, металлическая балка может выглядеть эстетично и иметь практическое применение в бытовом хозяйстве.

  Расчет

  Чтобы произвести выбор металлического бруса для той или иной конструкции, которая будет нести определённую нагрузку, необходимо произвести расчёт балки на прочность при изгибе. Это можно сделать, рассчитав все параметры самостоятельно по известной методике или воспользоваться онлайн-калькулятором.

  Для выбора балки перекрытия, делают проверку из условия на прочность, где максимальная прочность стали должна быть больше суммы отношений максимального изгибающего момента в точке действия той или иной нагрузки к осевому моменту, и поперечных сил и площади поперечного сечения в максимально нагруженной точке.

  Для определения всех неизвестных параметров этого условия, вычисления проводят поочерёдно.

  Сначала определяют максимально нагруженный участок балки. Для этого, строят эпюру поперечных сил и изгибающих моментов. Чтобы построить эпюру, необходимо вычислить все суммарные изгибающие моменты и поперечные силы, действующие на балку, по участкам.

  Как правило, в случае металлического бруса перекрытия, расчётную схему заменяют балкой, лежащей на двух шарнирных опорах. В этих опорах возникают реакции сопротивления, у которых необходимо определить их условия:

  Когда реакции определены, балку разбивают на участки по опорам. Первый участок находится от одного конца балки до опоры, второй участок располагается между опорами, третий за последней опорой и так далее. Необходимо знать, что если на одном участке имеется точка изменения нагрузки, то её нужно выделить в отдельный участок.

  После того, как участки определены, строятся эпюры поперечных сил и изгибающий моментов, и определяется нагруженный участок. Далее, вычисляется осевой момент сопротивления сечения:

  По вычисленному параметру производят выбор номера двутавра из сортамента. На этом расчёт балки считается оконченным.

  Онлайн

  Рассчитывать металлическую балку и производить её выбор вручную довольно трудоёмко и занимает время, которое не всегда можно выделить занятому человеку. Поэтому, стоит довериться расчётам профессионалов.

  Но, если заказчик строительства сомневается в экономической целесообразности произведённого строителями расчёта, можно произвести быстрый автоматический расчёт при помощи сайтов, предлагающих данный товар.

  Одним из примеров такого калькулятора может быть портал http://svoydomtoday.ru/building-onlayn-calculators/111-raschet-metallicheskoy-balki-perekritiya.html, который предлагает, находясь на сайте, рассчитать расход материала и выбрать балку из сортамента.

  Данный калькулятор требует введения следующих исходных данных:

  1. Сначала нужно ввести условия эксплуатации металлической балки.
  2. После этого характеристики предварительно выбранной металлической балки.
  3. Указать нормативную и расчётную нагрузку на балку и произвести расчёт.

  В результате, получается минимально возможный при заданных условиях момент сопротивления балки. Из полученного момента можно выбрать балку по таблице сортамента.

  Так же определяется минимально допустимый момент инерции, по которому можно выбрать номер профиля из сортамента. Если для строительства в первую очередь важно не допустить прогиб балки, тогда стоит выбирать балку исходя из полученного момента инерции.

  Пример расчета

  Металлической балки перекрытия:

  Расчет несущей способности:

  1. Чтобы рассчитать несущую способность одной балки нужно из таблицы сортамента выбрать момент осевого сопротивления и по формуле вычислить максимально допустимый изгибающий момент:
  2. Отсюда можно вычислить максимально допустимую равнораспределённую нагрузку на однопролётную балку.

  Расчет сечения металлических балок:

  1. Для расчёта необходимого сечения металлической балки можно воспользоваться формулой расчёта момента сопротивления сечения.
  2. После вычисления результата, определить площадь сечения нужно по сортаменту фасонного профиля, выбрав при этом номер двутавра с ближайшим большим значением момента сопротивления.

  При расчёте металлической балки пролёта необходимо отнестись ко всему ответственно и внимательно, потому что от расчёта зависит срок эксплуатации здания и его возможная нагрузка. Здания, построенные по ошибочным расчётам, могут разрушиться в любой момент, унеся за собой много жизней.

  Статья была полезна?

  0,00 (оценок: 0)

  Расчет нагрузок на перемычки и балки — Строительные технологии

  Обратите внимание: Эта старая статья нашего бывшего преподавателя остается доступной на нашем сайте для архивных целей. Некоторая информация, содержащаяся в нем, может быть устаревшей.

  Понимание того, как нагрузки передаются через конструкцию и действуют на элементы конструкции, является первым шагом к определению размеров коллекторов и балок.0003 Большинство строителей автоматически выбирают двойные перемычки -2 x 8 или -2 x 10 для обрамления окон и дверей в каждом доме, который они строят. Эти заголовки работают, чтобы выдерживать большинство жилых нагрузок и, по совпадению, удерживают верхние части окон на одинаковой высоте. Изящное решение, но является ли это эффективным и экономичным использованием материала? То же самое относится и к балкам, таким как коньковые балки и центральные балки. Слишком часто строители собирают 2-дюймовые пиломатериалы для поддержки нагрузки на крышу и пол, не рассматривая другие варианты. Вы не можете превзойти пиломатериалы для большинства небольших оконных переплетов, но по мере увеличения пролетов и нагрузок более прочные материалы являются лучшим выбором. Пиломатериалы ограничивают возможности дизайна, а в некоторых случаях просто не работают. Parallam, Timberstrand, Laminated Veneer Lumber и Anthony Power Beam являются примерами альтернативных материалов, которые предоставляют строителям интересный выбор.

  В этой серии статей, состоящей из двух частей, мы рассмотрим, как пиломатериалы и эти конструкционные материалы используются в качестве перемычек и балок. Часть I покажет вам, как проследить структурные нагрузки на коллекторы и балки. В части II будут рассмотрены процедуры определения размеров, характеристики и стоимость этих материалов для нескольких применений (см. «Определение размеров спроектированных балок и коллекторов» для части 2).

  Выполнение работы

  Работа коллекторов и балок проста. Они передают нагрузки сверху на фундамент снизу через сеть конструктивных элементов. Идея определения размеров коллекторов и балок проста: сложите вместе все временные и постоянные нагрузки, действующие на стержень, а затем выберите материал, который выдержит эту нагрузку. Балка должна быть достаточно прочной, чтобы не сломаться (значение Fb), и достаточно жесткой, чтобы не прогибаться под нагрузкой (значение E). Однако процесс определения размеров этих структурных элементов может быть сложным, если вы не инженер. Вот упрощенный подход, который поможет вам указать подходящий материал для многих приложений.

  Первый шаг одинаков для пиломатериалов и конструктивных деревянных материалов: сложите все нагрузки, действующие на жатку или балку, а затем переведите эту нагрузку в термины , какую нагрузку будет ощущать каждый линейный фут жатки или балки . На языке луча вы говорите: этот заголовок должен нести Х-фунтов на линейный фут. Этот перевод является ключом к любой проблеме определения размеров конструкции. Вооружившись этой информацией, вы можете определить минимальный размер, пролет или прочность балки (кредит Хулио). Размеры компонентов из инженерной древесины определяются с помощью таблиц пролетов, которые сопоставляют различные пролеты с фунтами на фут балки. Для пиломатериалов необходимо выполнить математические расчеты.

  Нагрузки считаются либо распределенными , либо точечными нагрузками. Слой песка, равномерно распределенный по поверхности, является примером чистой распределенной нагрузки. Каждый квадратный метр поверхности испытывает одинаковую нагрузку. Живые и статические нагрузки, указанные в строительных нормах и правилах для крыш и полов, являются приближенными значениями распределенных нагрузок. Точечные нагрузки возникают, когда вес возлагается на одно место в конструкции, например на колонну. Нагрузка не распределяется поровну между опорной конструкцией. Анализ точечной нагрузки лучше оставить инженерам. Мы будем рассматривать только распределенные нагрузки. Это позволит нам подобрать размеры балок для наиболее распространенных применений.

  Рисунок 1

  Проследим распределенные нагрузки для нескольких разных домов. Предположим, что все они расположены в одном и том же климате, но имеют разные пути загрузки из-за того, как они построены. Эти примеры иллюстрируют, как распределенные нагрузки назначаются конструктивным элементам. Наши образцы домов находятся в районе, где снеговая нагрузка составляет 50 фунтов на квадратный фут площади крыши (рассматривайте снег как динамическую нагрузку). Само собой разумеется, что в более теплом климате снеговая нагрузка, вероятно, будет меньше, поэтому вам необходимо проверить свою кодовую книгу на наличие постоянных и постоянных нагрузок в вашем регионе. Все нагрузки указаны в фунтах на квадратный фут горизонтальной проекции (площади опоры). (СМ. РИСУНОК 1)

  Коллекторы

  Рисунок 2

  Пример № 1 коллектора

  Здесь каждый квадратный фут системы крыши выдерживает 50 фунтов динамической нагрузки и 15 фунтов общей постоянной нагрузки система поддержки. Помните, эти нагрузки распределяются равномерно по всей поверхности крыши. Внешняя стена (и перемычки внутри) будут нести все нагрузки от середины дома (между опорными стенами) к внешней стороне дома (включая свес крыши). Расстояние в этом случае составляет 12 футов + 2 фута = 14 футов. Таким образом, каждый линейный фут стены должен нести нагрузки, создаваемые полосой шириной 1 фут в этой области 14 футов. С технической точки зрения, ширина притока стены составляет 14 футов. Из этого мы можем легко увидеть, что каждый линейный фут стены поддерживает:

  Условия:

  динамическая нагрузка (снег):	50 фунтов на квадратный фут x 14 футов = 700 фунтов на линейный фут
  Статическая нагрузка на крышу:	15 фунтов на квадратный фут x 14 футов = 210 фунтов на линейный фут
  общая загрузка:	= 910 фунтов на погонный фут

  Важно перечислять динамическую нагрузку, стационарную нагрузку и общую нагрузку отдельно, поскольку динамическая нагрузка используется для расчета жесткости, а общая нагрузка используется для расчета прочности.

  Рисунок 3

  Пример #2

  Этот дом идентичен нашему первому примеру, за исключением того, что он построен из палочек. В результате динамическая нагрузка, статическая нагрузка и распределение усилий различны. В отличие от стропильной крыши, временная и статическая нагрузки стропил и потолочных балок должны учитываться как отдельные системы. Поскольку чердак можно использовать для хранения, временная нагрузка на мансардный этаж устанавливается в соответствии с нормами 20 фунтов на квадратный фут.

  Условия:

  динамическая нагрузка (снег):	50 фунтов на квадратный фут x 14 футов = 700 фунтов на линейный фут
  Статическая нагрузка на крышу:	10 фунтов на квадратный фут x 14 футов = 140 фунтов на линейный фут
  динамическая нагрузка потолка:	20 фунтов на квадратный фут x 6 футов = 120 фунтов на линейный фут
  статическая нагрузка на потолок:	10 фунтов на квадратный фут x 6 футов = 60 фунтов на линейный фут
  общая загрузка:	= 1020 фунтов на погонный фут

  Рисунок 4

  Пример верхнего колонтитула №3

  Опять же, этот дом имеет такую ​​же ширину, но имеет 2 уровня. На нижний коллектор действуют нагрузки от кровли, верхних стен и системы второго этажа. В Стандартах архитектурной графики вес внешней стены 2×6 указан как 16 фунтов на фут 9 .0177 2 . Таким образом, стена высотой 8 футов весит 8 футов x 16 фунтов/фут ² = 128 фунтов на линейный фут. Грузы, доставленные в жатку:

  Условия:

  динамическая нагрузка (снег):	50 фунтов на квадратный фут x 14 футов = 700 фунтов на линейный фут
  Статическая нагрузка на крышу:	15 фунтов на квадратный фут x 14 футов = 210 фунтов на линейный фут
  стена верхнего уровня:	= 128 фунтов на линейный фут
  Временная нагрузка на 2-й этаж:	30 фунтов на квадратный фут x 6 футов = 180 фунтов на линейный фут
  Статическая нагрузка 2-го этажа:	10 фунтов на квадратный фут x 6 футов = 60 фунтов на линейный фут
  общая загрузка:	= 1278 фунтов на погонный фут

  Балки

  Пример коньковой балки

  Рисунок 5. На этом рисунке показаны 2 элемента конструкции: коньковая балка и центральная балка. Оба имеют площадь притока 12 футов 0 дюймов. Нагрузка на фут балки определяется так же, как и для жаток.

  Условия коньковой балки

  динамическая нагрузка (снег):	50 фунтов на квадратный фут x 12 футов = 600 фунтов на линейный фут
  статическая нагрузка на крышу:	10 фунтов на квадратный фут x 12 футов = 120 фунтов на линейный фут
  общая загрузка:	= 720 фунтов на линейный фут

  Пример балки

  Центральная балка несет половину нагрузки на перекрытие, нагрузку на перегородку и половину нагрузки на второй этаж. Живая и статическая нагрузки указаны в строительных нормах. Вес перегородки указан в Стандартах архитектурной графики как 10 фунтов на квадратный фут.

  B) Состояние балки первого этажа

  Временная нагрузка 1-го этажа:	40 фунтов на квадратный фут x 12 футов = 480 фунтов на линейный фут
  Статическая нагрузка 1-го этажа:	10 фунтов на квадратный фут x 12 футов = 120 фунтов на линейный фут
  Перегородка высотой 8 футов:	= 80 фунтов на линейный фут
  Временная нагрузка на 2-й этаж:	30 фунтов на квадратный фут x 12 футов = 360 фунтов на линейный фут
  Статическая нагрузка 2-го этажа:	10 фунтов на квадратный фут x 12 футов = 120 фунтов на линейный фут
  общая загрузка:	= 1160 фунтов на погонный фут

  Вкратце

  Эти примеры являются типичными для типов расчетов, которые вам придется выполнять для определения равномерной нагрузки, распределяемой на балку или перемычку. Вы должны установить, какую нагрузку получает каждый линейный фут жатки или балки. Следующим шагом является использование технической литературы любой из компаний, производящих инженерные деревянные компоненты, для определения размера пролета и балки. Все они соотносят допустимые пролеты для нагрузки на фут балки. Списки пролетов основаны на допустимом отклонении, динамической нагрузке и статической нагрузке, которые перечислены в вашей книге строительных норм и правил. В части 2 «Определение размеров инженерных перекрытий и балок» мы сравниваем стоимость и характеристики некоторых изделий из инженерной древесины с пиломатериалами.

  Все иллюстрации предоставлены Journal of Light Construction.

  Поиск:

  Исследование в BCT

  • ОСНОВНОЕ В BCT (BS)
  • ПРОФЕССИОНАЛЬНЫЙ МС
  • ИССЛЕДОВАНИЯ MS И PHD
  • ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАНИЕ
  • СВИДЕТЕЛЬСТВО О ВЫПУСКЕ

  Присоединяйтесь к нашим информационным сессиям

  Новости BCT

  Подписаться на новости по электронной почте

  Введите свой адрес электронной почты, чтобы подписаться на наши новости и получать уведомления.

  Что такое расчет балки? (с картинками)

  `;

  Д. Пупон

  
  Дата последнего изменения: 13 сентября 2022 г.

  Расчет балки — это измерение напряжения и прогиба конструкционной балки при приложении к ней заданной нагрузки. На способность балки сопротивляться изгибу влияют многие факторы, такие как характеристики балки, нагрузка и опоры. Вычисление смещения нагрузки одиночной балки с использованием уравнения балки Эйлера-Бернулли несложно, но в большинстве практических приложений используется программное обеспечение балки. Расчеты луча используются для обеспечения безопасности и предотвращения чрезмерной застройки в различных дисциплинах, таких как строительство и аэронавтика.

  Необходимо рассчитать несущую способность балки, чтобы построить конструкции из самых легких и недорогих материалов, при этом выполняя требования безопасности и сохраняя эстетические качества конструкции. Вся дисциплина строительной инженерии посвящена этому анализу и проектированию, гарантируя, что крыши не рухнут под тяжестью снега, что подземные гаражи будут безопасны, когда движение транспорта над головой и что небоскребы, построенные вдоль линий разлома, отвечают требованиям сейсмостойкости. Расчет балок также имеет применение в машиностроении при проверке сопротивления отдельных частей машины нагрузкам, например нагрузке, которую может выдержать крыло самолета до развития потенциально опасных напряжений. Наконец, архитекторы должны учитывать деформацию балок при строительстве и ремонте домов из стоек и балок, а также при рассмотрении визуального воздействия провисающих полов, крыш и балконов.

  Одним из наиболее важных факторов при расчете несущей способности балки является выбор материалов. Обычно балки изготавливаются из дерева, стали, железобетона или алюминия. Каждый материал имеет различную склонность к упругой деформации, называемую модулем упругости, который относится к способности материала возвращаться на место. В пределе текучести материал будет пластически деформироваться, сохраняя деформацию после снятия приложенной силы.

  Форма поперечного сечения балки — вторая характеристика, учитываемая при расчете балки. Балки могут быть прямоугольными, круглыми или полыми, а также иметь множество типов боковых сторон, таких как двутавровые, Z-образные или тавровые балки. Каждая форма имеет свой момент инерции, также известный как второй момент площади, который предсказывает жесткость балки.

  Усилие на единицу длины — это еще один параметр, используемый при расчете балки, и он зависит от типа нагрузки. Постоянные нагрузки — это просто вес конструкции, а вынужденные или временные нагрузки — это силы, которым конструкция будет периодически подвергаться, например снег, движение транспорта или ветер. Большинство нагрузок являются статическими, но особое внимание следует уделять динамическим нагрузкам, землетрясениям, волнам и ураганам, которые повторяются в течение длительного времени. Нагрузка может быть распределена, как правило, равномерно или асимметрично, например, снегопад или куча грязи. Он также может быть сконцентрирован в точке, в центре или с различными интервалами.

  Граничные условия для расчета балки зависят от типа опоры балки. Балка может просто поддерживаться с обоих концов, как балка пола между двумя несущими стенами. Он может быть консольным или поддерживаться на одном конце, как балкон или крыло самолета. Граничные условия применяются ко всем точкам по длине балки.

  Связь между прогибом балки и статической нагрузкой описывается уравнением Эйлера-Бернулли для балки. Другое уравнение, уравнение балки Эйлера-Лагранжа, описывает это соотношение для динамической нагрузки, но из-за сложности его применения обычно используются статические приближения. Можно рассчитать прогиб, изгибающие моменты и поперечную силу балки с учетом приложенной нагрузки. На практике для обобщения этой информации используются диаграммы нагрузки, в которых перечислены распространенные материалы, отвечающие требованиям безопасности для известной нагрузки. Для более сложных приложений калькуляторы балок легко доступны на веб-сайтах компаний и в качестве надстроек для программного обеспечения автоматизированного проектирования (САПР).

  Расчет и анализ конструкционных балок

  Расчет балок является неотъемлемой частью строительства. Архитекторы и инженеры-строители должны сбалансировать затраты, строительные нормы и требования клиентов в своих проектах. Таким образом, конструкция балки требует тщательного изучения. В этом посте мы рассмотрим материалы балки и примеры конструкции балки, а также расскажем, как выполнить трехэтапный анализ балки.

  Материалы и конструкции балок

  Большинство конструкционных балок изготавливаются из дерева, клееного бруса, предварительно напряженного бетона, монолитного бетона, железа или композитных материалов. Каждый из этих строительных материалов по-разному реагирует на нагрузку, и у каждого есть свои уникальные преимущества.

  Деревянные балки

  Деревянные балки широко используются в жилых домах. Деревянные балки могут быть надрезаны или соединены вместе для дополнительной прочности. Деревянные балки недороги и их легко изменить в соответствии со спецификациями строителя. Однако они также подвержены гниению и заражению насекомыми. В настоящее время доступны специально обработанные деревянные балки, которые устойчивы к разложению, влаге и насекомым, что делает их привлекательным материалом для изготовления балок для большинства домовладельцев.

  Перекладины

  Перекладины представляют собой балки специальной конструкции, которые соединяют стальной лист с соседними деревянными панелями, образуя одну составную конструкционную балку. Перекладины прочные, но менее дорогие и легкие, чем сплошные стальные балки. Добавление деревянных элементов позволяет прибить балки к существующим деревянным конструкциям. Конструкция лафетной балки приводит к уменьшению габаритных размеров балки. Они используются для поддержки тяжелых вертикальных нагрузок при сохранении строгого бюджета строительства. Перекидные балки также очень полезны при добавлении дополнительной несущей способности к существующей балке.

  Стальные двутавровые балки

  Одним из очень распространенных типов стальных балок являются двутавровые балки. I-образная балка имеет форму заглавной буквы I, хотя эту конструкцию также иногда называют W-образной. Конструкция двутавровой балки является наиболее эффективным использованием конструкционной стали, поскольку она перемещает основную часть стали в части балки, фактически сопротивляющиеся нагрузкам. Двутавровые балки также прочны и доступны по цене. Стальные балки могут быть обработаны для предотвращения коррозии и окисления, особенно при использовании вблизи или под водой. В результате стальные двутавровые балки очень популярны в строительстве, но их можно использовать и в жилых домах.

  Бетонные балки

  Бетонные балки чаще всего используются в коммерческом строительстве, например, при возведении многоуровневых парковок, больниц и крупных отелей. Бетонные балки также широко используются в качестве опор для мостов и автомагистралей. Некоторые бетонные балки используются в сочетании со стальными балками для обеспечения дополнительной прочности. Более новые бетонные балки могут также содержать гибридный материал традиционного бетона, смешанный с полимером, армированным стекловолокном (GFRP) или углеродным FRP.

  Бетон — прочный строительный материал, но он подвержен разрушению водой и растрескиванию. В балки часто включают железные стержни, чтобы добавить прочности и устойчивости в местах, подверженных большим нагрузкам. Бетонные балки также желательны из-за их способности поглощать звук и вибрацию.

  Консольные балки

  Консольные балки создают эффект подвески. Эти балки позволяют создать эркер, балконы и некоторые мосты. В конструкциях с консольными балками весовая нагрузка распределяется обратно на основные балки конструкции, позволяя части конструкции выходить за поддерживаемые периметры фундамента конструкции.

  Вальмовые балки

  Вальмовые балки популярны в кровельных конструкциях. Вальмовая балка обеспечивает поддержку других несущих балок, ответвляющихся под симметричными углами. Такая конструкция часто используется в жилом строительстве.

  Как выполнить анализ балки в 3 этапа

  Процесс, используемый для определения пригодности деревянной, стальной или даже бетонной балки, практически одинаков. После выбора балки используется следующий метод:

  1. Определение нагрузок
  2. Расчет напряжений
  3. Проверка допустимых напряжений по отношению к фактическим напряжениям.

  1 – Определение нагрузок

  Первым шагом в расчете конструкции балки является определение величины нагрузки или веса, который балка будет воспринимать. Есть две основные категории нагрузок:

  Временные нагрузки. Временная нагрузка — это тип нагрузки, временно воздействующей на конструкцию (например, нагрузки от снега, ветра, транспортных средств и т. д.). Величина временных нагрузок будет определена или указана в местных строительных нормах.

  Постоянные нагрузки — Постоянные нагрузки постоянно прикреплены к конструкции (например, нагрузки от строительных материалов, мебели и т. д.). Иногда вес материалов точно известен и может быть сложен для определения общей статической нагрузки. Чаще всего предполагается статическая нагрузка и дается приблизительный вес.

  2 – Расчет напряжений

  Существует два типа напряжений, которые обычно рассчитываются при расчете балки: напряжение изгиба и напряжение сдвига. Более полное определение напряжения изгиба и напряжения сдвига можно найти здесь.

  Чтобы рассчитать напряжения изгиба и сдвига, необходимо сначала рассчитать максимальный изгибающий момент и максимальный сдвиг, возникающие в балке. Максимальный момент и сдвиг, скорее всего, произойдут в разных местах. Высококачественное программное обеспечение для проектирования конструкционных балок может рассчитать возможности в данной конструкции балки, сравнивая значения напряжения изгиба и сдвига с известными инженерными значениями конструкции, чтобы обеспечить целостность конструкции.

  Двумя другими элементами информации, необходимыми для определения напряжений, будут модуль сечения и площадь поперечного сечения используемой балки. Модуль сечения и площадь поперечного сечения можно рассчитать или, в большинстве случаев, найти в таблицах (например, в Национальной спецификации проектирования (NDS) для деревянных балок или в Руководстве AISC по стали для стальных балок). После того, как вся информация будет сведена в таблицу, определите номинальное максимальное напряжение изгиба и номинальное максимальное напряжение сдвига.

  3 – Сравните фактические напряжения с допустимыми напряжениями

  В большинстве случаев допустимые напряжения приведены в таблицах в каком-либо руководстве по проектированию (например, в NDS для дерева или в Руководстве AISC по стали для стали). После того, как допустимые напряжения определены, определение адекватности балки — это просто вопрос сравнения фактических напряжений с допустимыми напряжениями.

  Расчет прогиба балки

  Одним из важных моментов, не обсуждаемых в этой статье, является прогиб или провисание балки. Балка может быть достаточно прочной конструктивно, но все же прогибаться так сильно, что это влияет на фактическую работу балки. Прогиб является очень важным расчетом и будет рассмотрен в отдельной статье.

  Экономьте время и деньги с помощью программного обеспечения для расчета конструкционных балок

  Проектирование балок может быть сложным процессом. Опытный строитель может знать, какой тип балки используется для достижения желаемого визуального стиля конструкции, но способна ли эта балка адекватно выдерживать нагрузку конструкции? Оставляет ли это возможность дальнейшего расширения структуры? Существует ли более дешевая балка, которая соответствовала бы конструкции конструкции?

  Программное обеспечение для проектирования конструкций, такое как Vitruvius, может помочь избавить процесс проектирования от догадок. Программное обеспечение для проектирования конструкционных балок учитывает жесткость, прочность и размер желаемой балки. Затем рассчитывается потенциальная несущая нагрузка проектируемой балки. Расчеты, основанные на желаемых качествах, раскрывают все жизнеспособные возможности конструкции балки. Также могут быть выполнены расчеты, показывающие экономическую эффективность каждого варианта конструкции балки.

  Программное обеспечение для проектирования конструкционных балок также предоставляет список возможных материалов балок, которые помогут создать устойчивую конструкцию без превышения заданного бюджета строительства. Вам нужна сплошная балка или можно использовать пустотелую балку? Вам нужна двутавровая конструкция или прямоугольная балка? Программное обеспечение для проектирования несущих балок может помочь вам разобраться во всех вариантах.

  Программное обеспечение для проектирования несущих балок является разумным вложением средств для любого инженера-строителя, строительного подрядчика или индивидуального строителя нового дома. Это устраняет возможные ошибки при проектировании конструкции, а также обеспечивает сохранение целостности конструкции при внесении последних изменений в планы строительства.

  Не все программы для расчета балок одинаковы

  Не все программы для расчета несущих балок являются высококачественными. Обязательно изучите функции, предлагаемые программным обеспечением для проектирования несущих балок, включая поддержку, доступную в программе, прежде чем выбирать пакет программного обеспечения для проектирования несущих балок. Если вы хотите попробовать Vitruvius, мы предлагаем бесплатную 30-дневную пробную версию.

  Расчет нагрузки на балку, как для рамы прицепа — механические элементы

  В качестве упрощенного введения в нагрузку на балку в этой статье обсуждаются сложности расчета напряжений и прогиба. Несмотря на то, что рассчитать нагрузку на балку для простых теоретических случаев довольно легко, очень немногие балки на самом деле являются простыми. Рама прицепа, например, представляет собой ряд простых балок, но когда мы собираем их все вместе, она становится намного сложнее.

  Сравнительный анализ: сталь и алюминий для рам прицепов и крановых балок

  Даже балки, которые кажутся простыми, например верхняя балка козлового крана, не так уж и просты. Изображение из предыдущей статьи, посвященной сравнению стали и алюминия. На нем видно, что напряжение увеличивается вблизи концов главной балки, где простая теория говорит, что напряжение снижается. Дополнительная нагрузка возникает из-за того, что прогиб верхней балки пытается согнуть ногу. Хотя связь достаточно проста, она, безусловно, усложняет точный полный анализ.

  Не расстраивайтесь. Даже со всеми сложностями реальности есть способы подобраться «достаточно близко», и в большинстве случаев это «достаточно хорошо».

  Начните с концепции нагрузки на балку

  Подчеркнем, что это упрощенное введение. Хотя реальность обычно сложна, базовые теоретические концепции по-прежнему применимы, поэтому мы начнем с основ расчета нагрузки на балку. Мы коснулись многих из этих концепций в других статьях, поэтому перейдите по ссылкам для получения дополнительных объяснений.

  Нагрузка

  Во-первых, разберитесь с нагрузками на балку. Какие силы «пытаются» воздействовать на балку? В то время как обсуждение находится в разделе «Выбор лучшего материала для рамы прицепа», это изображение изгиба, сдвига и скручивания показывает концепции. Чтобы начать расчет нагрузки на балку, нужно знать силы и их направления. Они «изгибают» луч? Перекрутить луч? Или попробовать «подстричь» его? Часто это комбинация.

  Форма

  Во-вторых, что делает форма балки, чтобы сопротивляться силам. Как и в обсуждении «Формы балок для строительства», форма имеет большое значение в том, как она справляется с силами.

  Один пример. Двутавровая балка широко известна своей прочностью, и это правильно. Это инженерная форма, позволяющая выдерживать большие нагрузки при меньшем общем весе. ОДНАКО, это утверждение вводит в заблуждение. Двутавровая балка действительно очень хорошо справляется с изгибающими нагрузками (в вертикальном направлении, если смотреть на это изображение), но не так хорошо справляется с боковыми нагрузками (горизонтальными на изображении) или скручивающими нагрузками. Направление и тип нагрузки имеют значение для каждой формы.

  Материал

  Свойства материала одинаковы для данного материала независимо от размера или формы луча. Для расчета нагрузки на балку мы используем эти свойства, определяемые в математических терминах физикой материала. 93. Это означает, что стальной блок размером 1 метр на 1 метр на 1 метр весит 7800 кг. Блок алюминия того же размера весит около 2700 кг. Магния больше похоже на 1700 кг. Плотность — это свойство материала, и это просто так.

  «Модуль упругости» — это свойство, которое мы используем при нагружении балки для расчета прогиба (изгиба). Мы часто видим его как «Е» в уравнениях. Чтобы сравнить жесткость материалов, мы смотрим на это число. Например, «модуль упругости» стали составляет примерно 30 000 000 фунтов на квадратный дюйм. Алюминий примерно 10 000 000 фунтов на квадратный дюйм. Магний составляет 6 500 000 фунтов на квадратный дюйм. (Английские единицы.) В этих статьях, посвященных сравнению «Сравнить: сталь и алюминий» и особенно в «– Часть 2», показано, как прогиб является важной частью расчета нагрузки на балку.

  Прочность

  Мы выражаем механическую «прочность» через «напряжение». Силы, воздействующие на балку, создают реакцию, которую мы рассчитываем как напряжение. Если напряжение превышает прочность, то форма материала изменяется. Иногда это хорошо, например, если мы изготавливаем кронштейны и нам нужна новая форма, но иногда это плохо, например, когда балка выходит из строя. (См. эти проблемы с отказом крана.)

  Свойства материала (выше) не меняются в зависимости от размера или формы. Они также не сильно меняются с различными сплавами. Например, необработанная сталь имеет примерно такую ​​же плотность, как высокопрочная инструментальная сталь. То же самое для алюминиевых сплавов. С другой стороны, прочность у разных сплавов сильно различается. Он также меняется в зависимости от состояния — мы обсуждали ослабление материала вблизи сварного шва.

  Чтобы рассчитать нагрузку на балку, нам нужно знать прочность материала и, в частности, прочность, которая важна для нашей ситуации с нагрузкой. Например, предел прочности или предел прочности при растяжении не так важен при анализе рамы прицепа. Элементы рамы будут изгибаться задолго до того, как сломаются, поэтому ключевым моментом является знание предела текучести (изгибной прочности).

  Еще одна сила, «Усталость», со временем становится важной. К сожалению, показатели усталости не публикуются, поскольку они зависят от многих факторов, помимо самой балки или материала. Хотя мы должны знать об этом, расчет усталости выходит за рамки этой статьи.

  Размер

  Это может показаться очевидным. Размер важен для расчета напряжения нагрузки на балку, и он взаимодействует с формой .

  Итак, как определить размер для расчетов? Мы делаем это с 2 свойствами.

  Первое и самое простое для понимания — это «у» или расстояние от нейтральной оси. Для изгибающих нагрузок, характерных для рамы прицепа, можно использовать это изображение (из статьи о сварке кронштейнов рессор). Глядя на стрелки силы (красная и синяя), мы видим, что центр балки не имеет изгибающей нагрузки. В этом луче, поскольку он симметричен, «нейтральная ось» является центром луча. Это не всегда так, и уголки — хороший тому пример.

  «y» (в некоторых источниках используется другая переменная) — это расстояние от нейтральной оси до точки анализа. Поскольку самые высокие силы находятся в самой дальней точке (если смотреть на сечение балки), мы обычно анализируем там. Мы называем это «у-макс».

  Во-вторых, это «момент инерции площади», или иногда называемый «секундным моментом площади». Часто в уравнениях мы видим его как «I» (заглавная i). Мы не будем вдаваться в подробности (вы можете найти математические подробности здесь), потому что это сложно, но это связано с количеством материала и его расстоянием от нейтральной оси.

  Для двутавровой балки основная часть материала находится на крайних точках (около y-max), что придает форме большую букву «I» для ее общего веса и размера.

  Помните, это сочетание формы и размера. Ширина тоже имеет значение, толщина тоже. Кроме того, если вы складываете лучи, «момент инерции площади» изменяется, чтобы принять полный стек.

  Простые инженерные уравнения

  Теперь рассмотрим расчет нагрузки на балку. У нас есть немного знаний о нагрузке, свойствах материала, прочности, размере и форме.

  Поскольку для начала лучше всего использовать простое, мы будем использовать сплошную балку на простых концевых опорах. Затем одна центральная нагрузка. В верхней части рисунка показаны балка и нагрузки.

  Графика включает некоторые уравнения для расчета нагрузки на балку. График сдвига (синий) показывает, как мы представляем, что происходит с силами вдоль балки.

  На следующем графике представлены моменты или изгибающие силы вдоль балки.

  Наконец, график отклонения. (Между расчетами моментов и отклонениями есть несколько шагов, но они здесь не рассматриваются.)

  Это очень простой случай. На самом деле слишком просто для большинства реальных жизненных ситуаций, но дает представление. Итак, что это значит? Если эта балка изготовлена ​​из титана, сплошная 1 ″ x 1 ″ (25,4 мм x 25,4 мм), длиной 6 футов (~ 2 м) и имеет предел текучести 35 000 фунтов на квадратный дюйм (241 МПа), то она выдержит нагрузку 324 фунта. (147 кг) перед постоянным сгибанием. Центр будет отклоняться чуть более чем на 1,7 дюйма (43 мм) до выхода из строя. Это, конечно, теоретическое, потому что оно основано на опубликованных цифрах. На самом деле это может быть немного больше или немного меньше, потому что вещи никогда не бывают идеальными, но это близко.

  Конечно, простые основы не учитывают движения, подпрыгивания или аномалии, которые случаются в реальной жизни.

  Расчет нагрузки на балку рамы прицепа

  Теперь вопрос, который нам задают довольно часто. Как рассчитать нагрузку на балку прицепа?

  Для простоты воспользуемся примером из статьи «Куда идет ось», так как в ней уже есть уравнения для расчета сил и положения. Вот обзор.

  Сводка загрузки:

  Длина дышла = 42 дюйма
  Длина станины = 96 дюймов
  Вес рамы = 450 фунтов
  Распределенная нагрузка = 2250 фунтов
  Вес ящика для инструментов = 300 фунтов

  Нагрузка на дышло = 360 фунтов (12%) Нагрузка на ось = 2640 фунтов. ″ из мяча.

  Подробная информация по этим номерам находится в статье «Куда идет ось».

  Итак, это состояние нагрузки. Теперь, вот график (ниже), показывающий, как указанная выше нагрузка применяется к прицепу. Это похоже на графики загрузки выше, но здесь 3 графика вместе с масштабированием, поэтому их легко сравнивать от строки к строке.

  Для краткости мы пропустим уравнения для этих графиков. Они похожи на приведенные выше уравнения, но с большей сложностью, с несколькими нагрузками, различными типами нагрузок, а не только на концах.

  На этом втором графике мы не показываем отклонение, но показываем «Напряжение» для рамы прицепа. Линия Stress выделяет области перехода, например, место, где дека встречается с языком. Поскольку напряжение зависит от размера и формы балки, на этом графике уже учтены балки. Тем не менее, это шаг вперед.

  На самом деле мы используем силы и моменты для выбора балок. Применяя свойства балки и материала, мы можем выбрать балки, которые будут выдерживать нагрузки. Строка «Стресс» предназначена для балок в этом примере, но процесс выбора не так прост и поэтому выходит за рамки этой статьи.

  Понимание техники

  Приведенные выше расчеты являются началом. Начнем с графика нагрузки, показывающего силы. Силы ВВЕРХ должны быть равны силам ВНИЗ. (См. диаграмму сдвига.) Силы также должны суммироваться с НУЛЕМ при расчете силы на соответствующем расстоянии. (См. расчеты в статье о положении оси.) Мы называем это суммированием моментов. Если эти два условия выполняются, то, вероятно, мы все сделали правильно, и остальные расчеты сработают.

  Далее идет сила сдвига. Это своего рода проверка правильности расчета нагрузки. (Синяя линия на графике.) Использование графика — это простой способ увидеть относительную величину сил, и он является хорошим ориентиром при анализе загрузки прицепа.

  Затем график моментов. (Зеленая линия) Вы можете думать об этом как о сгибании, но это не совсем так. Для таких балок, как на прицепе, изгиб является основным условием, поэтому мы должны быть очень внимательны. Хотя заманчиво просто посмотреть на высокие точки, области, где нагрузка переходит от одного набора лучей к другому, очень важны. Например, место, где заканчивается кровать, а продолжается язык. По нашему опыту, это самое слабое место для большинства прицепов.

  Хотя приведенное выше — хороший способ взглянуть на силы, на самом деле все гораздо сложнее. Даже при загрузке, потому что пример статичен (не двигается). Когда все движется, динамика действительно меняет игру.

  Еще для расчета нагрузки на балку

  Все вышеперечисленное является первым шагом к выбору балок рамы прицепа. Мы сказали, что следующим шагом будет выбор подходящих лучей, но это не совсем так. Следующим шагом является повторение этого процесса для всех возможных условий нагрузки. Мы сделали простую статическую равномерно распределенную нагрузку — например, заполнив прицеп водой, когда нагрузка равномерно распределяется по всей платформе. Это интересно, но не так реалистично. Даже когда вы перевозите песок, обычно в середине есть горб, из-за которого нагрузка распределяется не совсем равномерно.

  А как насчет перевозки RZR? Маленький трактор? Или квадроцикл? Поскольку шины соприкасаются с платформой прицепа только в 4 точках, это создает очень разные силы. Мы должны рассчитать нагрузку на балку и для этого случая. Если он загоняет его на прицеп, весь вес приходится на заднюю часть, а это еще один случай нагрузки. Нам нужно сделать еще один расчет нагрузки на балку.

  Список загрузки можно продолжить. Как насчет того, чтобы в передней части трейлера стоял холодильник, а рядом с ним стиральная машина и сушилка? (Ничего сзади.) Ага, еще один набор расчетов.

  Когда расчеты завершены, следующим шагом будет подумать о том, насколько они реалистичны и какие модификаторы применяются. Например, при перевозке песка вы, скорее всего, наткнетесь на кочку во время движения по дороге. Нам нужно компенсировать динамическими расчетами. Мы, вероятно, не наткнемся на кочку при загрузке квадроцикла. Однако, вероятно, есть некоторый отскок, поэтому наши динамические расчеты для этого отличаются.

  Еще один момент: приведенный выше анализ представляет собой 2D-анализ, но большинство трейлеров — 3D  . . . Надеюсь, вы уловили идею.

  Выбор балок

  Как бы нам не хотелось, чтобы это было просто, это не так. К сожалению, именно поэтому многие производители прицепов не занимаются проектированием. Да, это правда. Большинство просто соединяют балки вместе, основываясь на опыте, копировании и том, что «чувствует» себя хорошо. Это работает для большинства, пока это не работает.

  Как инженер, занимающийся этим долгое время, я, вероятно, вижу худшее из этого. Люди связываются со мной, поэтому я это вижу, но мало что могу сделать. Как только балка изгибается или сварной шов рвется, время для проектирования уже давно прошло. Что подчеркивает необходимость действительно убедиться, что он достаточно силен в первую очередь.

  В общем, мы отклонились от темы. Выбор балки включает в себя объединение всех загружений с соответствующей динамикой и ситуационными модификациями. Да, факторы безопасности также имеют значение. Все это устанавливает потребности, затем мы можем выбрать балки. По сути, мы рассчитываем напряжение любой заданной балки (форма, размер, материал), а затем сравниваем напряжение с прочностью материала. Если напряжение ниже прочности, то, наверное, сработает. Если прогнозируемое напряжение выше, балка может выйти из строя.

  В этом суть расчета нагрузки на балку. В то время как для простых балок и единичных вариантов использования это достаточно просто, сложности возникают быстро, когда накладываются динамические и загруженные варианты.

  Оптимизация для упрощения

  Одно предостережение. Частой целью при проектировании прицепов является минимизация веса. Это хорошая цель, но она обманчива. Если варианты использования хорошо определены, то целесообразна большая оптимизация. Однако оптимизация для одного варианта использования оставит уязвимыми другие области. Я видел много «слишком легких» трейлеров, которые не были сняты. Если вы ищете легкий вес, убедитесь, что вы не жертвуете функциональностью ради восприятия «легкости». Есть способы достичь цели, не прибегая к коротким путям.

  Также подумайте о реальных преимуществах. Довольно легко увлечься цифрами, такими как вес, в дизайне. Спросите себя о ценности, например, какова ценность 50 фунтов? Если в этом разница между рамой, в которой вы уверены, и «легкой» рамой, которая может показаться схематичной, то стоит ли это 50 фунтов? А 100 фунтов? Для прицепа, предназначенного для перевозки 3500 фунтов, небольшое увеличение веса рамы незначительно по сравнению со стоимостью неисправной рамы.

  Я предлагаю дизайн для решения сложных задач, которые неизбежно возникнут. Всегда есть практический баланс, так что имейте это в виду, если вам нужен легкий вес.

  Пусть компьютер рассчитает нагрузку на балку

  Приведенные здесь примеры простые и двумерные. На самом деле анализ рамы прицепа намного сложнее, поэтому мы используем специальные инструменты САПР.

  Иногда на нашем сайте можно увидеть такие цветные изображения. Они получены из FEA, анализа методом конечных элементов, который выполняет для нас все сложные расчеты балки. К сожалению, это загружается одновременно, поэтому полный анализ занимает много времени, особенно с учетом итераций для оптимизации.

  Большим преимуществом является то, что он позволяет рассчитать нагрузку на балку так, как не могут рассчитать вышеописанные методы. Это делает сложное легким. Хотя это отличный инструмент, у него есть один существенный недостаток — мусор на входе равен мусору на выходе. Это легко даст красивые картинки, но входные данные должны быть правильными, иначе выходные данные будут мусором. Просто пища для размышлений.

  Используя инструменты и инженерные знания, мы производим лучшие чертежи прицепов на рынке. Мы делаем это для планов трейлеров на этом сайте, потому что это правильный способ проектирования. Мы делаем это и для всех нестандартных прицепов, которые мы проектируем. Это одна из ценностей, которую вы получаете в Mechanical Elements.

  Кстати, один из наших конкурентов утверждает, что у них есть «единственные» спроектированные чертежи трейлеров — теперь вы знаете правду. Они продаются на нескольких сайтах, но это все одни и те же планы. Я не буду бить инженеров других, но скажем так, эти планы не соответствуют моим стандартам.

  Стройте уверенно, вот что мы говорим. Удачи вам в ваших дизайнерских начинаниях.

  Расчет прочности и жесткости сварной двутавровой балки

  а – изменение поперечного сечения по длине балки; б – сечение балки и диаграммы напряжений.

  Задача: Проверка режима «Сопротивление сечений» в постпроцессоре «Сталь» SCAD

  Задача: Проверка расчетного сечения сварного двутавра для главных балок с пролетом 18 м в обычной системе коротких балок. Верхний пояс основных балок удерживается стрингерами, расположенными с шагом 1125 м.

  Источник: Металлоконструкции: Учебник / [Кудишин Ю.И., Беленя Е.И., Игнатьева В.С и др.] — 13-е изд. обр. — М.: Издательский центр «Академия», 2011. 19 с.5.

  Соответствие кодам: СНиП II-23-81*, СП 16.13330.2011, ДБН В.2.6-163:2010.

  Файл исходных данных:

  4.1 SectionResistance_Example_4.1.spr; Отчет
  — 4.1 SectionResistance_Example_4.1.doc

  Исходные данные:

  Параметры SCAD. СТАЛЬ Постпроцессор:

  [Элемент №1] Силы

  907:35

  M _k
  Макс. 0 T*m
  Привязка 0 м

  Макс. 0 T*m
  Привязка 0 м

  N Макс. 0 Т Защелка 0 м Макс. 0 Т Защелка 0 м	M y Макс. 0 T*m Привязка 0 м Макс. 353,65 Т*м Защелка 3,75 м	M z Макс. 0 T*m Привязка 0 м Макс. 0 T*m Привязка 0 м
  Q z Макс. 94,31 Т Защелка 0 м	Q y Макс. 0 Т Защелка 0 м Макс. 0 Т Защелка 0 м
  	Длина стержня 3,75 м Длина гибкой части 3,75 м Загрузка L1

  Расчет соответствует СНиП II-23-81*
  Элемент конструкции Сечение

  Сталь: C255

  Длина элемента 3,75 м
  Предел гибкости на сжатие
  элементов на сжатие2 для элементов натяжение: 300
  Коэффициент эксплуатации 1
  Коэффициент значимости 1
  Коэффициент полезной длины в плоскости XoY 1,125 м
  Коэффициент полезной длины в плоскости XoZ 18 м
  Длина между внешними ограничениями 1,125 м внутренние поверхности фланцев ГОСТ 8239-89 24

  Результаты	Чек	Коэффициент использования
  Раздел 5. 12	Прочность под действием изгибающего момента M y	0,99
  Раздел 5.12,5.18	Прочность под действием боковой силы Q z	0,41
  Раздел 5.24,5.25	Прочность при совместном действии продольной силы и изгибающих моментов, без пластичности	0,99
  сек. 5,14*	Прочность по приведенным напряжениям при одновременном действии изгибающего момента и поперечной силы	0,86
  Раздел 5.15	Устойчивость к плоскостному изгибу	0,99
  Раздел 6.15,6.16	Предельная гибкость в плоскости XoY	0,09
  Раздел 6.15,6.16	Предельная гибкость в плоскости XoZ	0,09

   

  Коэффициент использования 0,99 — Прочность под действием изгибающего момента M 9{2} \]

  4. Гибкость стержня в плоскости момента:

  \[ \lambda_{y} =\frac{\mu l}{i_{y} }=\frac{18\cdot 100} {63 715}=28 2508. \]

  5. Гибкость стержня вне плоскости момента:

  \[ \lambda_{y} =\frac{\mu l}{i_{y} }=\frac{1,125\cdot 100}{4,265 }=26,3775. \]

   

  Сравнение решений:

  907:35

  0,088

  Фактор	Расчет вручную	СКАД	Отклонение, %
  Прочность под действием изгибающего момента М у	15083,826/15187,794 = 0,993	0,993	0,0
  Прочность под действием боковой силы Q z	5,4388/13,3 = 0,4089	0,408	0,0
  Прочность при приведенных напряжениях	22,7715/1,15/23 = 0,861	0,86	0,0
  Прочность при совместном действии продольной силы и изгибающих моментов, без пластичности	–	0,993	0,0
  Устойчивость к плоскостному изгибу	–	0,993	0,0
  Предельная гибкость в плоскости XoY	26,3775/300 = 0,088	0,0
  Предельная гибкость в плоскости XoZ	28,2508/300 = 0,094	0,094	0,0

  (Модуль сечения — TotalConstructionHelp)

  (Модуль сечения — TotalConstructionHelp)

  Модуль упругости сечения При проектировании балки используется еще одно свойство: Модуль упругости сечения (Z) , также известный как Sx . Момент сопротивления формы поперечного сечения имеет большое значение при проектировании балок. Это прямая мера прочности балки. Балка с большим модулем сечения, чем другая, будет прочнее и способна выдерживать большие нагрузки. Он включает идею о том, что большую часть работы при изгибе выполняют крайние волокна балки, т.е. верхнее и нижнее волокна сечения. Поэтому при расчете учитывается расстояние от волокон сверху донизу. Модуль упругости обозначается Z или Sx . Чтобы рассчитать Z, необходимо найти расстояние (y) до крайних волокон от центра тяжести (или нейтральной оси), поскольку именно здесь максимальное напряжение может привести к отказу. В проектировании конструкций модуль сечения балки представляет собой отношение второго момента площади поперечного сечения к расстоянию от нейтральной оси до предельно сжатого волокна. Для симметричных секций это будет означать, что Zx max и Zx min равны. Для несимметричных сечений (например, тавровой балки) используемый модуль сопротивления сечения будет отличаться в зависимости от того, происходит ли сжатие в стенке или полке сечения. Модуль сопротивления напрямую связан с прочностью соответствующей балки. Он выражается в единицах объема, например, в дюймах 3 , в м 3 , в мм 3 . Для общего расчета используется модуль упругого сечения, применяемый до предела текучести для большинства металлов и других распространенных материалов. Показанные балки представляют собой деревянные и стальные балки.

  ---

  Ниже приведены некоторые типовые сечения и уравнения для некоторых из наиболее распространенных элементов: Предположим, что квадратная форма имеет размеры 6 x 6 дюймов, поэтому, чтобы найти сечение Модуль (Sx): Sх = д 3 / 6 = 6 3 / 6 = 36 дюймов 3 , за хх через Центр. Как только мы узнаем модуль сечения, момент инерции можно рассчитать с помощью компьютера. уравнение: Ix = Sx x c = 36 x 3 = 108 дюймов 4 или уравнение Ix = d 4 / 12 можно использовать. или Sх = д 3 / 3 = 6 3 / 3 = 72 дюйма 3 , для xx через нижний край. Предположим, что квадратная фигура имеет размеры 4 дюйма в ширину и 6 дюймов в высоту, поэтому, чтобы найти Модуль упругости сечения (Sx): Sх = бд 2 / 6 = 4 х 6 2 / 6 = 24 дюйма 3 , за хх через Центр. Как только мы узнаем модуль сечения, момент инерции можно рассчитать с помощью компьютера. уравнение: Ix = Sx x c = 24 x 3 = 72 дюйма 4 или уравнение Ix = bd 3 / 12 можно использовать. или Sх = бд 2 / 3 = 4 х 6 2 / 3 = 48 дюймов 3 , для xx через нижний край. Published by admin View all posts by admin