Расчет двутавра на изгиб: Расчёт металлической балки онлайн (калькулятор)
Содержание
Расчет уголка на прогиб
Главная » Разное » Расчет уголка на прогиб
Расчет уголка на прогиб и изгиб
Данный онлайн-калькулятор предназначен для того, чтобы Вы могли легко и быстро подобрать размеры уголка в зависимости от приходящейся на него нагрузки. Особенность его в том, что на одной странице возможно сравнение равнополочных (ГОСТ 8509-93) и неравнополочных (ГОСТ 8510-86) уголков. Последние, в свою очередь, можно подбирать в зависимости от расположения его в пространстве, т.е. в зависимости от того, как он будет ориентирован относительно нагрузки.
Содержание:
1. Калькулятор
2. Инструкция к калькулятору
Расчет уголков производится на изгиб и прогиб (по прочности и по деформациям) для следующих расчетных схем:
- Тип 1 — однопролетная шарнирно-опертая балка с равномерно распределенной нагрузкой. Пример: перемычка из уголка, которая несет плиты перекрытия и небольшую высоту кладки.
 (Подробнее о расчете перемычек из уголка см. этот калькулятор).
(Подробнее о расчете перемычек из уголка см. этот калькулятор).
- Тип 2 — консольная балка с жесткой заделкой с равномерно распределенной нагрузкой. Пример: железобетонный козырек, выполненный с применением уголка, который жестко (с применением ребер жесткости, ограничивающих любые повороты) приварен к железобетонной стене.
- Тип 3 — однопролетная шарнирно-опертая балка с консолью с равномерно распределенной нагрузкой. Пример: тот же козырек, что и в предыдущей схеме, только здесь уголок с одной стороны заводится в стену, а с другой опирается на раскос (на рисунке синий).
- Тип 4 — однопролетная шарнирно-опертая балка с одной сосредоточенной силой. Пример: перемычка, на которую опирается одна балка перекрытия.
- Тип 5 — однопролетная шарнирно-опертая балка с двумя сосредоточенными силами. Пример: перемычка, на которую опираются две сосредоточенные силы.
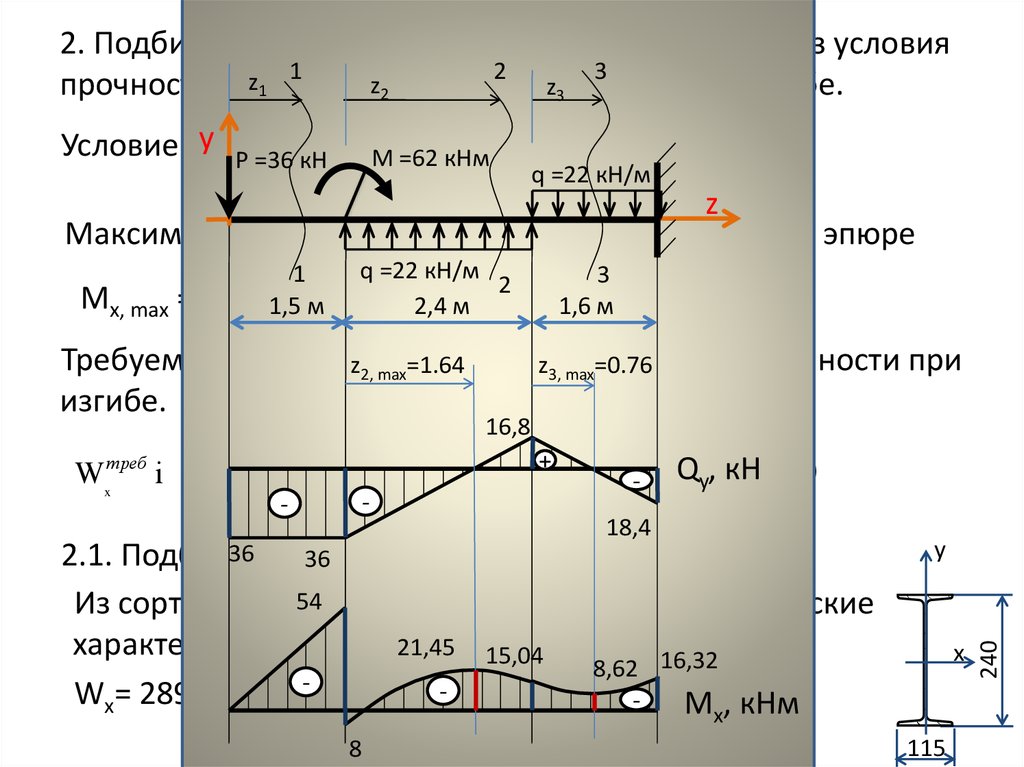
- Тип 6 — консольная балка с одной сосредоточенной силой. Пример: козырек дома с кирпичной стенкой на нем, построенного в африканской республике (где никогда не выпадает снег) по фантазии африканского архитектора. Уголки этого козырька жестко заделаны в стену, так как описано во второй схеме.
Примечание: рассчитываемый уголок на рисунках с примерами окрашен в красный цвет.
Калькулятор
Расчет прогиба балки онлайн калькулятор. Площадь поперечного сечения профиля. Расчет на прочность.
Описание
При выборе схемы с распределенной нагрузкой, приложенная «Нагрузка Q» указывается как относительная «килограмм на метр». Определяется она по формуле Q = [общяя нагрузка, кг]/[общая длина, м].
Использование калькулятора «Расчет прогиба балки онлайн» значительно сократит время и послужит залогом надежных инженерных конструкций.
Калькулятор разработан исключительно по формулам Сопромата и справочным данным для каждого типа материала и сечения балки. Расчет прогиба сечения является теоретическим, следовательно практические значения могут быть отличными от расчетных и зависеть от множества условий.
Расчет прогиба сечения является теоретическим, следовательно практические значения могут быть отличными от расчетных и зависеть от множества условий.
Однако значения полученные в данном калькуляторе будут невероятно полезными и послужат основой для расчета необходимой конструкции.
Для быстрого доступа к расчетам необходимого профиля добавьте калькулятор в избранное (CTRL+D на ПК или значек «звездочка» справа вверху браузера)
Пример расчета уголка, швеллера и двутавра на прогиб и изгиб
На данной странице представлен пример расчета швеллера. Что касается расчетов уголка и двутавра, то они производится аналогичным образом. Другими словами, данный пример является полезным для следующих калькуляторов:
В примере будут описаны несколько действий, которые должны выполняться последовательно.
Дано.
Район строительства — Нижний Новгород.
Расчетная схема — Тип 1.
Необходимо подобрать швеллер, который будет воспринимать нагрузку от снега.
Действие 1. Внесение исходных данных.
Расчетная нагрузка = 240 кг/м2 — так как город Н.Новгород находится в IV снеговом районе (в соответствии с табл. 10.1 и картой 1 СП 20.13330.2011 «Нагрузки и воздействия» [1]).
Fmax = 1/200 — так как пролет балки равен 5 м (пункт 2 табл. E1 [1]).
Расположение — по оси Х (швеллер воспринимает нагрузку вертикально).
Расчетное сопротивление Ry=210 МПа — берется как наихудший вариант для стали.
Действие 2. Выбор предполагающих номеров профилей.
Предположим, что мы рассматриваем два вида профилей: с параллельными гранями и с уклоном полок. Поэтому для первоначального расчета выбираются швеллеры размером 8П И 8У.
После произведенного расчета видно, что в графе «Запас» в том и другом случае стоят отрицательные значения. Это означает, что выбранные швеллеры не способны воспринимать приложенную на них нагрузку. Следовательно, необходимо выбирать профили большего размера.
Следовательно, необходимо выбирать профили большего размера.
Действие 3. Корректирующий расчет.
При увеличении профилей до 10П и 10У ситуация аналогичная. Но после того, как профили были увеличены до 12П и 12У в графах «Запас» появились положительные значения. Следовательно, в качестве балки перекрытия можно принять тот или иной профиль (имеется в виду 12П или 12У).
| Вид проката Уголок равнополочныйУголок неравнополочныйШвеллер с уклоном полокШвеллер с паралельными гранями полокДвутавр с уклоном полокДвутавр с паралел. гранями полок нормальныйДвутавр с паралел. гранями полок широкопол.Двутавр с паралел. гранями полок колнныйДвутавр с паралел. гранями полок доп.сери(Д)Тавр с паралелными гранями полок нормальныйТавр с паралел. гранями полок широкополочныйТавр с паралелными гранями полок колнный | Вид и назначение стоек (колонн) Стойки и раскосы передаюшие реакции опорОсновные колонныВторостепенные колонны |
| Сталь С235 (Ст3кп2)Сталь С245 (Ст3пс5,Ст3сп5)Сталь С255 (СтГпс,Ст3Гсп)Сталь С285 (Ст3сп,Ст3Гпс,Ст3Гсп)Сталь С345 (12Г2С,09Г2С)Сталь С345К (10ХНДП)Сталь С375 (12Г2С)Сталь С390 (14Г2АФ)Сталь С390Д (14Г2АФД)Сталь С440 (16ГАФ)Сталь С590 (12Г2СМФ) |
Если Вашего материала нет в таблице, но Вам известно его расчётное сопротивление, введите его значение в это поле (кг/см2):
| РАЗМЕРЫ ВЫБРАННОГО ПРОФИЛЯ: |
Выберите схему крепления стойки Введите параметры для расчёта
Размеры проката углового профиля оговариваются ГОСТ 8509-93 и ГОСТ 8510-86; швеллеров ГОСТ 8240-97; двутавров ГОСТ 26020-83; тавров – ТУ 14-2-685-86; (получаемых продольной разрезкой пополам горячекатаных двутавров с параллельными гранями полок по ГОСТ 26020-83).
При проектировании строительных конструкций необходимо принимать схемы, обеспечивающие прочность, устойчивость и пространственную неизменяемость сооружения в целом, а также его отдельных элементов при монтаже и эксплуатации.
Поэтому стойку,находящуюся под действием сжимающей её нагрузки необходимо проверять:
- на прочность;
- устойчивость;
- допустимую гибкость.
Согласно Актуализированной редакция СНиП II-23-81 (CП16.13330, 2011) расчет на прочность элементов из стали при центральном растяжении или сжатии силой P следует выполнять по формуле:
P/Fp*Ry*Yc <= 1, где
- P – действующая нагрузка,
- Fp – плошадь поперечного сечения стойки,
- Ry – расчётное сопротивление материала (стали стойки), выбирается по таблице В5 Приложения “В” того же СНиПа;
- Yc – коэффициент условий работы по таблице 1 СНиПа (0.9-1.1). В соответствии с примечанием к этой таблице (пункт 5) в калькуляторе принято Yc=1.
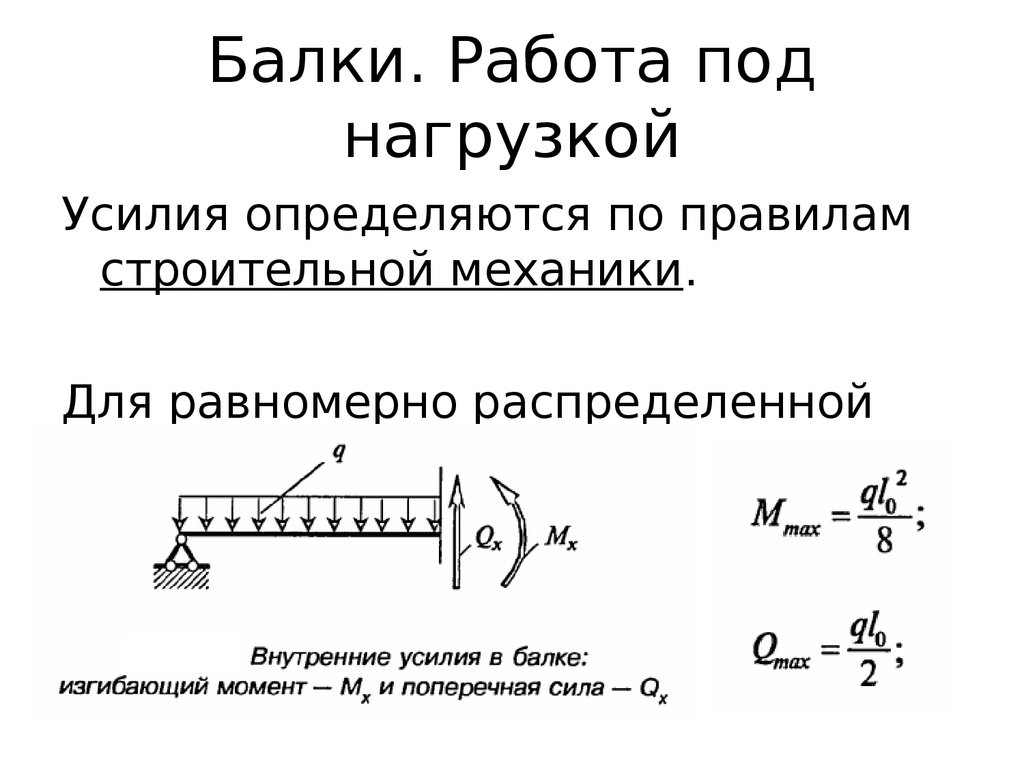
Проверку на устойчивость элементов сплошного сечения при центральном сжатии силой P следует выполнять по формуле:
P / Fi*Fp*Ry*Yc <= 1, где
Fi – коэффициент продольного изгиба центрально-сжатых элементов.
Коэффициент Fi введён в расчёт в качестве компенсации возможности некоторой не прямолинейности стойки, недостаточной жесткости её крепления и неточности в приложении нагрузки относительно оси стойки. Значение Fi зависит от марки стали и гибкости колонны и часто берётся из таблицы 72 СНиП II-23-81 1990г. исходя из гибкости стойки и расчётного сопротивления выбранной стали сжатию, растяжению и изгибу.
Это несколько упрощает и огрубляет расчёт, так как СНиП II-23-81* предусматривает специальные формулы для определения Fi. Гибкость (Lambda) – некоторая величина, характеризующая свойства рассматриваемого стержня в зависимости от его длины и параметров поперечного сечения, в частности радиуса инерции:
Lambda = Lr / i; здесь
- Lr – расчётная длина стержня;
- i – радиус инерции поперечного сечения стержня (стойки,колонны).

Радиус инерции сечения i равен корню квадратному из выражения I / Fp, где
- I – момент инерции сечения,
- Fp – его площадь.
Lr (расчётная длина) определяется как MuL;
здесь L- длина стойки,а Mu – коэфф., зависящий от схемы её крепления:
- “заделка-консоль”(свободный конец) – Mu = 2;
- “заделка-заделка”-Mu = 0.5;
- “заделка-шарнир” -Mu = 0.7;
- “шарнир-шарнир”-Mu=1.
Следует иметь ввиду,что при наличии у формы поперечного сечения 2-ух радиусов инерции (например, у швеллера, двутавра, тавра – относительно осей x-x и y-y), при расчёте Lambda используется меньший.
Уголки (как равнополочные так, и неравнополочные) имеют минимальный радиус инерции относительно оси z-z, который и используется в расчётах. Кроме того,сама Lambda (гибкость стойки), рассчитанная по формуле Lambda=Lr/i не должна превышать 220-ти в соответствии с табл. 19.СНиП II-23-81*; там же содержатся ограничения на предельную гибкость центрально-сжатых стержней.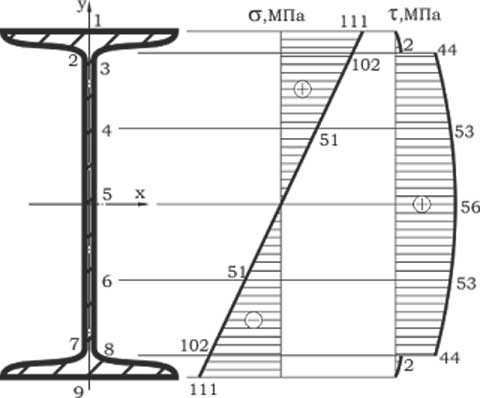
Для их использования необходимо сделать выбор в таблице калькулятора “Вид, назначение стоек…”. Предельная гибкость стоек, кроме их геометрических параметров, зависит также от коэфф. продольного изгиба (Fi), действующей нагрузки(P), расчётного сопротивления материала стойки (Ry) и условий её работы (Yc).
ПРИМЕЧАНИЕ. Размеры выбранного швеллера, двутавра и тавра указываются в строке “РАЗМЕРЫ ВЫБРАННОГО ПРОФИЛЯ”; размеры полок уголков-в их таблицах; толщина уголков выбирается отдельно после появления возможных толщин выбранного номера уголка в вышеуказанной строке.
Расчет металлической балки на прогиб: учимся составлять формулы
Приветствую тебя, читатель экспресс-курса — «сопромат для чайников» на сайте – SoproMats.ru. Меня зовут Константин Вавилов, я являюсь автором статей по сопромату и других материалов данного ресурса. В этой статье, будем рассматривать универсальную методику расчета прогибов балки — метод начальных параметров. Как и любая другая статья для чайников, на нашем проекте, этот материал будет изложен максимально просто, лаконично и без лишних заумных терминов.
Как и любая другая статья для чайников, на нашем проекте, этот материал будет изложен максимально просто, лаконично и без лишних заумных терминов.
В качестве примера, возьмем металлическую балку на двух опорах. Запишем для нее формулу для вычисления прогиба, посчитаем его численное значение. И также в конце этой статьи дам ссылки на другие полезные статьи с примерами определения прогибов для различных расчетных схем.
Что такое прогиб балки?
Под действием внешней нагрузки, поперечные сечения балки перемещаются вертикально (вверх или вниз), эти перемещения называются прогибами. Сопромат позволяет нам определить прогиб балки, зная ее геометрические параметры: длину, размеры поперечного сечения. И также нужно знать материал, из которого изготовлена балка (модуль упругости).
Кстати! Помимо вертикальных перемещений, поперечные сечения балки, поворачиваются на определенный угол. И эти величины также можно определить методом начальных параметров.
ν-прогиб сечения C; θ-угол поворота сечения C.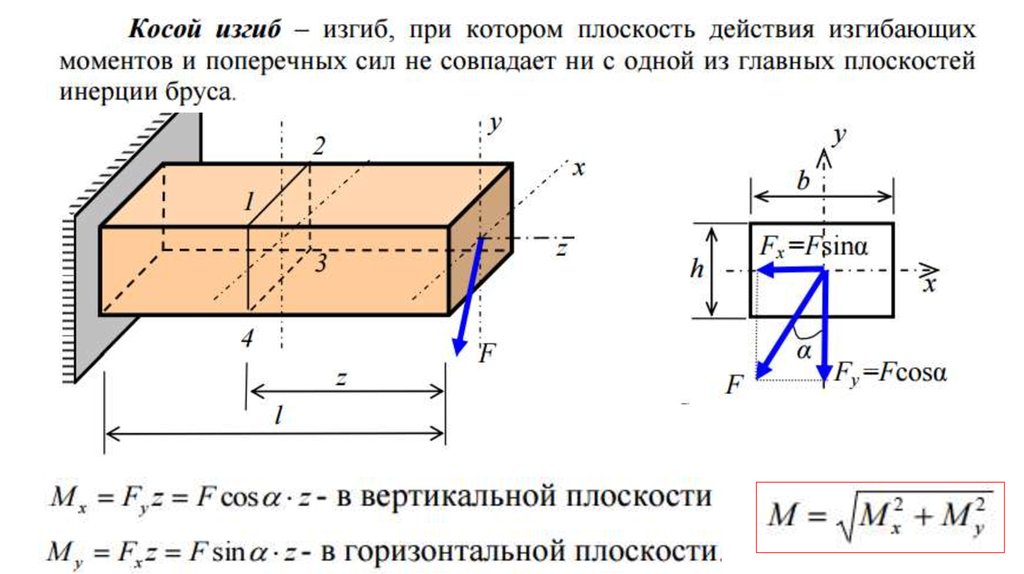
Прогибы балки необходимо рассчитывать, при расчете на жесткость. Расчётные значения прогибов не должны превышать допустимых значений. Если расчетное значение меньше, чем допустимое, то считают, что условие жесткости элемента конструкции соблюдается. Если же нет, то принимаются меры по повышению жесткости. Например, задаются другим материалом, у которого модуль упругости БОЛЬШЕ. Либо же меняют геометрические параметры балки, чаще всего, поперечное сечение. Например, если балка двутаврового профиля №12, не подходит по жесткости, принимают двутавр №14 и делают перерасчет. Если потребуется, повторяют подбор, до того момента пока не найдут тот самый – двутавр.
Метод начальных параметров
Метод начальных параметров, является довольно универсальным и простым методом. Используя этот метод можно записывать формулу для вычисления прогиба и угла поворота любого сечения балки постоянной жесткости (с одинаковым поперечным сечением по длине.)
Под начальными параметрами понимаются уже известные перемещения:
- в опорах прогибы равны нулю;
- в жесткой заделке прогиб и угол поворота сечения равен нулю.

Учитывая эти хитрости, их называют еще граничными условиями, определяются перемещения в других частях балки.
Расчет прогибов балки
Посмотрим, как пользоваться методом начальных параметров на примере простой балки, которая загружена всевозможными типами нагрузок, чтобы максимально охватить все тонкости этого метода:
Реакции опор
Для расчета нужно знать все внешние нагрузки, действующие на балку, в том числе и реакции, возникающие в опорах.
Если ты не знаешь, как определять реакции, то рекомендую изучить данный материал, где я как раз рассказываю, как они определяются на примере этой балки:
Система координат
Далее вводим систему координат, с началом в левой части балки (точка А):
Распределенная нагрузка
Метод начальных параметров, который будем использовать чуть позднее, работает только в том случае, когда распределенная нагрузка доходит до крайнего правого сечения, наиболее удаленного от начала системы координат. Конкретно, в нашем случае, нагрузка обрывается и такая расчетная схема неприемлема для дальнейшего расчета.
Конкретно, в нашем случае, нагрузка обрывается и такая расчетная схема неприемлема для дальнейшего расчета.
Если бы нагрузка была приложена вот таким способом:
То можно было бы сразу приступать к расчету перемещений. Нам же потребуется использовать один хитрый прием – ввести дополнительные нагрузки, одна из которых будет продолжать действующую нагрузку q, другая будет компенсировать это искусственное продолжение. Таким образом, получим эквивалентную расчетную схему, которую уже можно использовать в расчете методом начальных параметров:
Вот, собственно, и все подготовительные этапы, которые нужно сделать перед расчетом.
Приступим непосредственно к самому расчету прогиба балки. Рассмотрим наиболее интересное сечение в середине пролета, очевидно, что это сечение прогнется больше всех и при расчете на жесткость такой балки, рассчитывалось бы именно это сечение. Обзовем его буквой – C:
Относительно системы координат записываем граничные условия. Учитывая способ закрепления балки, фиксируем, что прогибы в точках А и В равны нулю, причем важны расстояния от начала координат до опор:
Учитывая способ закрепления балки, фиксируем, что прогибы в точках А и В равны нулю, причем важны расстояния от начала координат до опор:
\[ { V }_{ A }=0\quad при\quad x=0 \]
\[ { V }_{ B }=0\quad при\quad x=8м \]
Записываем уравнение метода начальных параметров для сечения C:
\[ E{ I }_{ z }{ V }_{ C }=… \]
Произведение жесткости балки EI и прогиба сечения C будет складываться из произведения EI и прогиба сечения в начале системы координат, то есть сечения A:
\[ E{ I }_{ z }{ V }_{ C }=E{ I }_{ z }{ V }_{ A }+ … \]
Напомню, E – это модуль упругости первого рода, зависящий от материала из которого изготовлена балка, I – это момент инерции, который зависит от формы и размеров поперечного сечения балки. Также учитывается угол поворота поперечного сечения в начале системы координат, причем угол поворота дополнительно умножается на расстояние от рассматриваемого сечения до начала координат:
\[ E{ I }_{ z }{ V }_{C }=E{ I }_{ z }{ V }_{ A }+E{ I }_{ z }{ \theta }_{ A }\cdot 4+… \]
Учет внешней нагрузки
И, наконец, нужно учесть внешнюю нагрузку, но только ту, которая находится левее рассматриваемого сечения C. { 4 } } =-2см \]
{ 4 } } =-2см \]
Таким образом, такая балка прогнется максимально на 2 см. Знак «минус» указывает на то, что сечение переместится вниз.
На этом, пожалуй, закончу данный урок. Если у вас возникли какие-либо вопросы по представленным материалам, задавайте вопросы в комментариях к этой статье. А также рекомендую вам посмотреть другие примеры определение прогибов этим методом. Там вы найдете более сложные задачи, определение углов поворотов, примеры расчета консольных балок (с жесткой заделкой).
Расчёт балки, рамы бесплатно онлайн
Лимит расчётов:
|
Добро пожаловать! Данный онлайн-калькулятор предназначен для расчёта балки или рамы и
позволит построить эпюры внутренних силовых факторов (изгибающих моментов, поперечных и
осевых или продольных сил), рассчитать реакции в опорах. В итоге формируется отчёт с
готовым решением.
| |
| КАЛЬКУЛЯТОРЫ КОМПРЕССИОННЫХ ЧЛЕНОВ | |
| Калькулятор | Определение |
| Расчет элементов сжатия (продольного изгиба) | |
| ПРОСТО ОПОРНАЯ БАЛКА КАЛЬКУЛЯТОРЫ ПРОГИБА | |
| Балка с простой опорой и множественными точечными / распределенными нагрузками и моментами | |
| Балка с простой опорой и сосредоточенной нагрузкой в любой точке | |
| Просто поддерживаемая балка с двумя Точечные нагрузки | |
| Балка с простой опорой и частично распределенной промежуточной нагрузкой | |
| Балка с простой опорой и двумя частично распределенными промежуточными нагрузками | |
| Балка с простой опорой и моментом | |
| Балка с простой опорой и двумя моментами | |
| КАНТИЛЬНАЯ БАЛКА КАЛЬКУЛЯТОРЫ ПРОГИБА | |
| Консольная балка с множественными точечными / распределенными нагрузками и моментами | |
| Консольная балка с одинарной нагрузкой | |
| Распределенная нагрузка консольной балки | |
.
% PDF-1.6 % 104 0 объект > endobj xref 104 52 0000000016 00000 н. 0000002216 00000 н. 0000002377 00000 н. 0000002421 00000 н. 0000002547 00000 н. 0000002902 00000 н. 0000003045 00000 н. 0000003182 00000 п. 0000003324 00000 н. 0000003351 00000 п. 0000003418 00000 н. 0000003955 00000 н. 0000004444 00000 н. 0000004471 00000 н. 0000005149 00000 п. 0000005176 00000 п. 0000005771 00000 п. 0000006307 00000 н. 0000006764 00000 н. 0000007200 00000 н. 0000007333 00000 н. 0000007360 00000 п. 0000007733 00000 н. 0000008258 00000 н. 0000008758 00000 н. 0000009241 00000 п. 0000009643 00000 п. 0000009713 00000 н. 0000009908 00000 н. 0000046337 00000 п. 0000046548 00000 п. 0000046941 00000 п. 0000047011 00000 п. 0000047272 00000 п. 0000106092 00000 н. 0000106298 00000 п. 0000106421 00000 н. 0000117145 00000 н. 0000117340 00000 н. 0000117547 00000 н. 0000117617 00000 н. 0000117799 00000 н. 0000156281 00000 н. 0000156483 00000 н. 0000156859 00000 н. 0000156929 00000 н. 0000157517 00000 н. 0000157588 00000 н. 0000157704 00000 н. 0000157824 00000 н. 0000157913 00000 н. 0000001336 00000 н. трейлер ] / Назад 1604346 >> startxref 0 %% EOF 155 0 объект > поток hb«`b«ce`c«`f @
0000157588 00000 н. 0000157704 00000 н. 0000157824 00000 н. 0000157913 00000 н. 0000001336 00000 н. трейлер ] / Назад 1604346 >> startxref 0 %% EOF 155 0 объект > поток hb«`b«ce`c«`f @
.
Калькулятор для инженеров — момент инерции площади, центр тяжести, модуль упругости углового сечения
Дополнительные ссылки
Викторина по гражданскому строительству
Проверьте свои знания по различным темам гражданского строительства
Статически неопределенные структуры
Определение и методы решения
Решенных примеров
Расчет сил стержня фермы
методом соединений и методом секций
Сила сдвига и изгибающий момент
Иллюстрированные решенные примеры для построения диаграмм силы сдвига и изгибающего момента
Наклон и прогиб балки и фермы
Иллюстрированные решенные примеры для определения наклона и прогиба балки и фермы
Решение неопределенных конструкций
Отклонение откоса, распределение момента и т. Д.
Д.
Балка железобетонная
Решенные примеры для определения прочности и других параметров
Другие полезные ссылки
Небоскребы мира
Высокие здания мира
Профиль инженеров-строителей
Познакомьтесь с выдающимися инженерами-строителями
Профессиональные общества
Международные профессиональные общества инженеров-строителей
Расскажите о нас друзьям
Поищите на нашем сайте больше…
.
Что такое прогиб? | Программное обеспечение SkyCiv Cloud для структурного анализа
перейти к содержанию
Искать:
- Программное обеспечение
- SkyCiv Structural 3D: Программное обеспечение для структурного анализа
- SkyCiv Beam
- SkyCiv Section Builder
- SkyCiv Connection Design
- SkyCiv RC Design
- SkyCiv Foundation Design
- SkyCiv8 Модуль нагрузки на ветер
SkyCiv8 Интеграции и надстройки
.
Угол возвышения Солнца (на год) Калькулятор
- Цель использования
- различные солнечные приложения, конечно, но в основном просто для того, чтобы быть проинформированным о моем физическом окружении.
- Комментарий / запрос
- Я мог бы быть более поучительным, если бы время наблюдения имело вариант местного кажущегося полудня, когда солнце находится на самом высоком уровне. Поскольку вы запрашиваете долготу наблюдателя, это должно быть просто.
[1] 2020/12/20 04:17 Мужчина / 60 лет и старше / Пенсионер / Полезно /
- Цель использования
- Расчет максимальной высоты дерева относительно расположения солнечных панелей.
- Комментарий / запрос
- Вычисление корректировки времени от GMT с использованием долготы было бы полезным и простым.
[2] 2020/12/07 03:31 Мужчина / 60 лет и старше / Инженер / Очень /
- Цель использования
- Размещение солнечных панелей
- Комментарий / запрос
- Arigatou gozaimasu!
[3] 2020/12/07 03:25 Мужской / 40-летний уровень / Средняя школа / Университет / аспирант / Очень /
- Цель использования
- Я хочу построить пассивную теплицу на севере ( Северный Квебек), и я хотел знать, под каким углом поставить стену, чтобы максимально эффективно использовать солнце в зимние месяцы
[4] 2020/12/01 22:20 Мужчина / Уровень 50 лет / Офисный работник / Государственный служащий / Полезный /
- Цель использования
- Определение того, в какое время года, в какое время суток и в каком направлении можно видеть радугу в моем местоположении (солнце должно быть ниже 42 градусов над горизонтом).

- Комментарий / запрос
- Я знаю, как узнать мою широту и долготу, поэтому мог бы использовать этот сайт, но если бы была возможность печатать в ближайшем городе, даже если это было бы менее точно, гораздо больше людей уметь его использовать.
[5] 2020/11/16 15:41 Женщина / 60 лет или старше / Пенсионер / Полезно /
- Цель использования
- Анализ выходной мощности солнечной батареи в зависимости от высоты Солнца
- Комментарий / Запрос
- Отличный калькулятор
[6] 2020/11/05 00:16 Мужчина / 60 лет и старше / Учитель / Исследователь / Очень /
- Цель использования
- Проверка тени на крыше для установка PV
- Отчет об ошибке
- По сравнению с диаграммой, углы которой указаны в таблице, азимут и углы возвышения не имеют никакого смысла.Как может полуденное солнце находиться только по азимуту (азимуту) между 39 и 67 градусами? Я мог бы понять эти углы, если бы они были даны от восточной оси.
 Тогда азимут будет в районе 129–157 градусов, то есть примерно в юго-восточном направлении. Кроме того, как солнце может быть выше в зимнее время, чем в летние месяцы? Возможно, если бы эти углы были измерены от вертикальной оси (Зинет), они имели бы больше смысла. Извините, но, на мой взгляд, приведенная здесь информация неверна.
Тогда азимут будет в районе 129–157 градусов, то есть примерно в юго-восточном направлении. Кроме того, как солнце может быть выше в зимнее время, чем в летние месяцы? Возможно, если бы эти углы были измерены от вертикальной оси (Зинет), они имели бы больше смысла. Извините, но, на мой взгляд, приведенная здесь информация неверна.
[7] 2020/11/04 20:42 Мужчина / 60 лет и старше / Инженер / Совсем нет /
- Цель использования
- Я фотограф, выясняю положение солнца в определенные дни в месяц, чтобы я мог делать красивые фотографии в «контролируемой» обстановке.
- Комментарий / запрос
- Спасибо. Продолжайте в том же духе!
[8] 2020/11/04 18:11 Женский / 50-летний уровень / Самозанятые / Полезные /
- Цель использования
- ИСПОЛЬЗОВАНИЕ СОЛНЕЧНОЙ ЭНЕРГИИ
- Комментарий / запрос
- ДУМАЯ О СОЛНЦЕ ПАНЕЛИ
[9] 2020/10/20 04:13 Мужчина / 60 лет и старше / Пенсионер / Очень /
- Цель использования
- Самообразование
[10] 2020/10/19 18:32 Мужчина / 60 лет и старше / Пенсионер / Очень /
.
Расчёт металлической балки онлайн (калькулятор).
Калькулятор предусматривает расчёт балок на изгиб и прогиб, из горячекатаного и другого проката следующей номенклатуры:
- уголка равнополочного;
- уголка неравнополочного;
- швеллера с уклоном и с параллельными гранями полок;
- двутавров с уклоном полок и с параллел. гранями полок различных модификаций, а также тавровых балок (тавров).
Размеры проката углового профиля оговариваются ГОСТ 8509-93 и 8510-86; швеллеров — 8240-97; двутавров — 26020-83; тавров — ТУ 14-2-685-86; (получаемых продольным разрезом пополам горячекатаных двутавров с парал-ыми гранями полок по ГОСТ 26020-83) — смотрите калькулятор веса двутавра.
При вычислении массы 1 метра длины проката плотность стали в этих стандартах принята равной 7,85 г/см3 (7.85 кг/дм3 или 7850кг/м3).
ПРИМЕЧАНИЕ. Размеры выбранного швеллера, двутавра и тавра указываются в строке «РАЗМЕРЫ ВЫБРАННОГО ПРОФИЛЯ»; размеры полок уголков в их таблицах; толщина уголков выбирается отдельно после появления возможных толщин выбранного номера уголка в вышеуказанной строке.
Швеллер в наличии на складе в Москве
Швеллер является продукцией прокатного производства, которая имеет U-образное поперечное сечение. В зависимости от технологии производства, швеллеры бывают горячекатаные и гнутые.
Размеры и форма г/к швеллеров общего назначения регламентируются стандартом ГОСТ 8240-97. Ширина проката согласно указанному нормативному документу может быть от 32 до 115 мм, а высота 50 — 400 мм.
В обозначении номера профиля зашифрована высота швеллера в сантиметрах (цифра) и серия или тип профиля (буква).
Размеры гнутого швеллера регламентируются стандартом ГОСТ 8278-83. В соответствии этому документу высота профиля может принимать значение от 25 до 410 мм, толщина швеллера — от 2 до 8 мм, и ширина может быть 26 — 160 мм.
В соответствии этому документу высота профиля может принимать значение от 25 до 410 мм, толщина швеллера — от 2 до 8 мм, и ширина может быть 26 — 160 мм.
В APEX L вы сможете приобрести швеллер наиболее востребованных размеров из стали марок Ст3 и 09Г2С:
- серии П с параллельными гранями — типоразмеры профиля 5П — 30П;
- серии У с уклоном граней — типоразмеры профиля 6,5У — 30У;
- гнутый швеллер с размерами от 50х40х3 до 250х125х6.
Значения высоты и ширины полки, ширины и толщины стенки по ГОСТ 8240-97 смотрите на странице — Как правильно расшифровать условное обозначение швеллера.
youtube.com/embed/06EiyhXiMuY?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>
Виды перекрытий
По назначению перекрытия можно разделить на:
- цокольные — отделяют первый этаж здания от цокольного этажа или подвала
- межэтажные — направлены на разделение между собой этажей здания
- чердачные. Первые . Из названия второго вида следует, что они . Последние отделяют чердачное помещение от жилого здания.
В зависимости от конструктивных особенностей перекрытия их можно разделить на плиточные и балочные:
- Плиточные перекрытия чаще всего монтируют в крупногабаритных каменных домах с использованием железобетонных плит.
- Балочные перекрытия используются при строительстве малоэтажных жилых домов. Для их монтажа могут применяться металлические или деревянные балки.
Основные способы усиления швеллера
Можно встретить различные ситуации, когда необходимо провести мероприятия по усилению той или иной конструкции, выполненной из швеллера или другого вида проката. Существует множество различных способов, которые можно применить для усиления швеллера. Среди них можно выделить несколько типовых ситуаций.
Существует множество различных способов, которые можно применить для усиления швеллера. Среди них можно выделить несколько типовых ситуаций.
1. На этапе проектирования можно подобрать швеллер большего размера; изготовленный из более прочной марки стали. Если же размеры балки по высоте строго или частично ограничены, то можно использовать швеллер усиленный (серия С горячекатаных швеллеров, которая при совпадающих номерах профиля, обладает большими значениями площади и моментов сопротивления/инерции), составное сечение балки/стержня, которое можно выполнить из двух швеллеров, либо швеллер+полоса/уголок и т.д.
2. В случае, если необходимо усилить уже существующую конструкцию, то можно провести следующие мероприятия. 1) Увеличение сечения швеллера, которое можно осуществить приваркой полосы, уголка, швеллера либо к полкам, либо к стенкам, и этим самым, либо изменить площадь и сопротивление сечения, либо снизить нагрузку, воспринимаемую одним швеллером. 2) Организацией дополнительных распорок, связей ребер, диафрагм с целью увеличения местной или общей устойчивости швеллера и конструкции. 3) Монтаж дополнительных элементов, которые изменяют схему конструкции (шпренгельные элементы, подкосы и т.д.). 4) Бетонирование конструкции — позволяет повысить жесткость и несущую способность колонн и стоек из швеллера и прочего проката.
3) Монтаж дополнительных элементов, которые изменяют схему конструкции (шпренгельные элементы, подкосы и т.д.). 4) Бетонирование конструкции — позволяет повысить жесткость и несущую способность колонн и стоек из швеллера и прочего проката.
3. В случае, если элемент конструкции находится в предаварийном состоянии, то усиливать его не стоит, а следует произвести замену.
Конструктивные особенности
Швеллеры 2 вида:
- П-образного сечения прокат горячекатаный;
- П-образного сечения прокат гнутый.
Конструктивное исполнение швеллера с 2 полками в 1 сторону располагает главную ось инерции к стенке со смещением усилий, накладываемых к изделию. Оно работает на косой изгиб. Лёгким и прочным каркас из швеллера получится, когда швеллер модернизировать. Сделать из него коробчатые стойки. Электрической дуговой сваркой с прерывистым швом соединить швеллеры полками внутрь конструкции. Усиление шва через 1,2-1,5 м упрочняет сборное изделие.
Балке из двутавра не требуется дополнительное усиление. Она выдерживает нагрузки.
Она выдерживает нагрузки.
Расчет металлической балки перекрытия на прогиб и на жесткость
Металлические балки двутавровые
Кроме повсеместно ведущегося строительства многоэтажных зданий с большим числом квартир, широкое распространение получило сооружение частных домов, причем не только небольших одноэтажных, но и довольно крупных, с двумя и более этажами, иногда и с мансардой наверху или обитаемым чердаком. Для таких домов уже не подходит каркасный метод; материалом часто служит, вместо дерева, кирпич или железобетон. Возведение крупных частных домов должно вестись по всем правилам строительной науки, так как ошибки при проектировании или воплощении проекта могут привести к нежелательным последствиям.
Если строящийся дом представляет собой капитальное здание – из бетона, кирпича, шлакоблока, то для потолочных перекрытий, межэтажных и чердачных, целесообразно применить железобетонные плиты.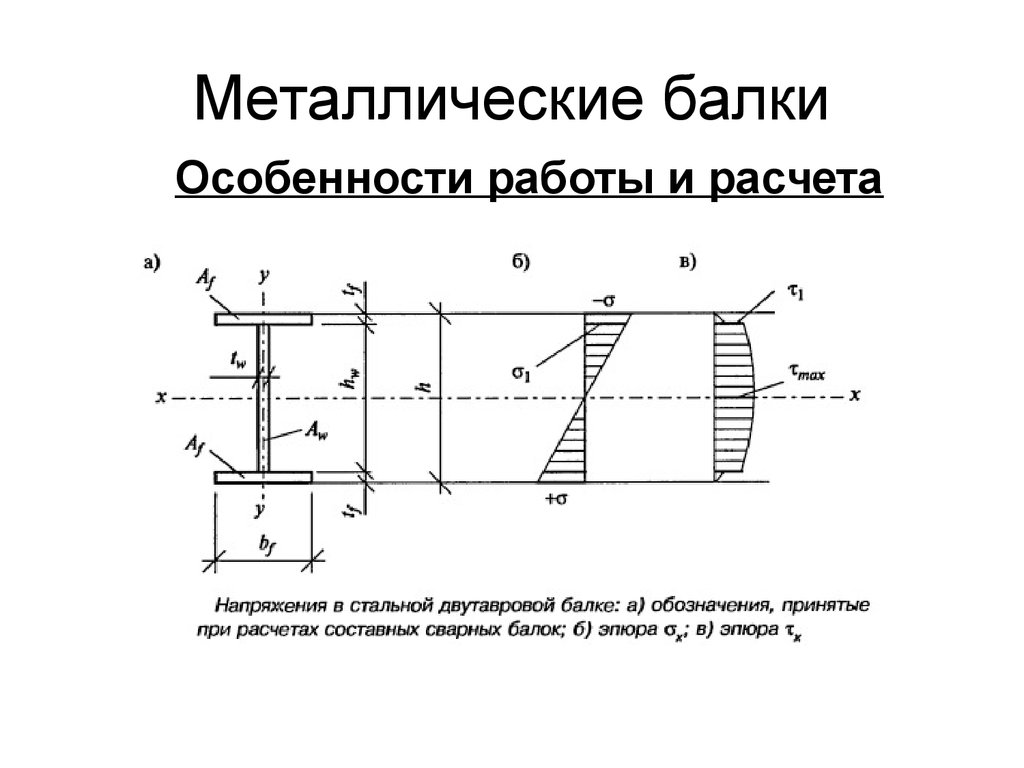 Наиболее подходящий тип каркаса, способный выдержать вес таких перекрытий, – это каркас, элементом которого является металлическая балка двутаврового профиля.
Наиболее подходящий тип каркаса, способный выдержать вес таких перекрытий, – это каркас, элементом которого является металлическая балка двутаврового профиля.
Именно этот вид проката, установленный своей стенкой вертикально, обладает наибольшей несущей способностью. Естественно, фундамент и стены дома при этом должны быть достаточной прочности, чтобы выдерживать дополнительный вес от 0,5 до 1 тонны – столько металла, в зависимости от количества балок и номера профиля может понадобиться для потолочного перекрытия.
Чтобы избежать лишних затрат и лишнего веса каркаса потолка, а также не допустить обрушения или значительного прогиба балок, необходимо заранее рассчитать их параметры и по результатам расчета подобрать нужный прокат. Расчет сводится к вычислению следующих величин: требуемого момента сопротивления и минимального момента инерции сечения балки, а исходя из последнего – максимального относительного прогиба.
Примечание Расчет ведется по двум характеристикам – на прочность и на жесткость.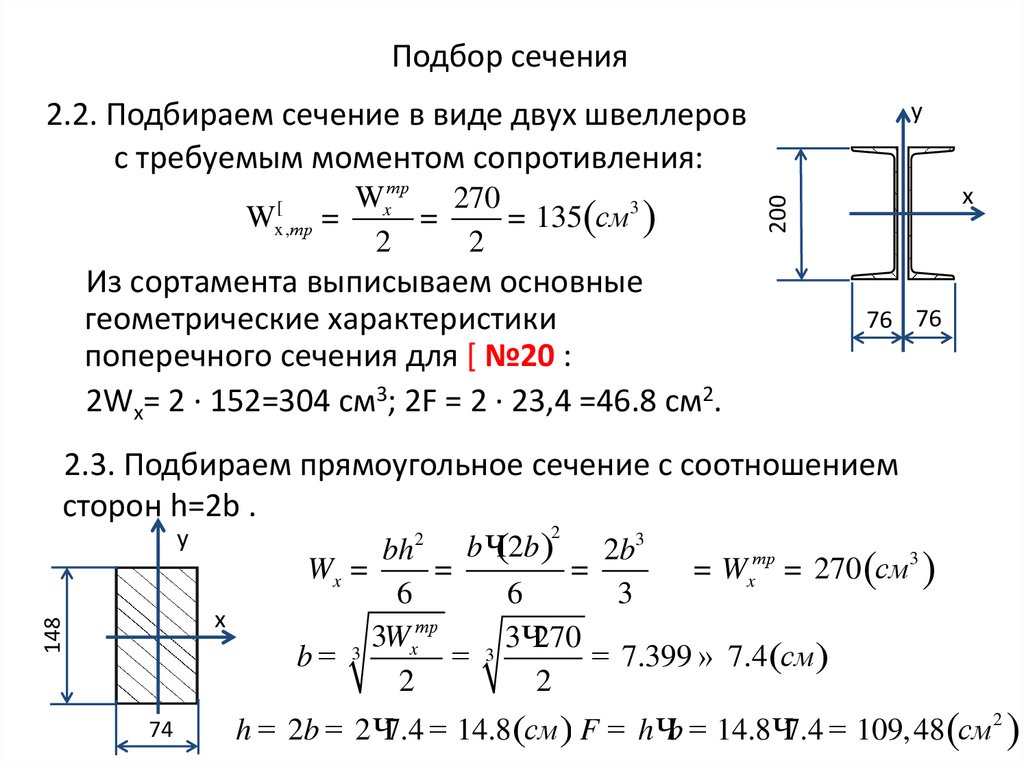 По полученным значениям момента сопротивления и момента инерции в таблицах ГОСТ находят требуемый номер проката.
По полученным значениям момента сопротивления и момента инерции в таблицах ГОСТ находят требуемый номер проката.
Исходные данные для расчетов
Для каркаса потолочных перекрытий малогабаритных частных домов обычно используется двутавр 10 – 20 номеров. Характеристики этих профилей приводятся в ГОСТ 8239-72 – их линейные размеры, площади сечения, максимальные моменты сопротивления по вертикали Wy и минимальные моменты инерции Jy.
Необходимо знать тип плит, которые будут опираться на балочный каркас, а также размеры несущего периметра дома. Можно применить пустотные железобетонные плиты ПК-12-10-8 (1180 х 990 мм, масса 380 кг), а размеры дома взять 4,5 х 6 м. Балки укладываются вдоль короткой стены; шаг укладки при таком размере плит равен 1000 мм (стыки плит совпадают с продольными осями балок, при минимальном зазоре 1 см). Это потребуется для расчета распределенной нагрузки, и исходя из нее – линейной нагрузки на балку, вес самой балки по сравнению с распределенной нагрузкой мал, и при вычислении линейной нагрузки им можно пренебречь.
Распределенная нагрузка при таком типе плит будет равна 325 кгс / м2. К этому надо добавить нагрузку возможных перегородок на верхней стороне перекрытия (75 кгс / м2) и возможную временную нагрузку (200 кгс / м2). В итоге нагрузка, распределенная по площади:
Q = 325 + 75 + 200 = 600 кгс / м2,
а линейная нагрузка
q = Q * p = 600 кгс / м = 6 кгс / см.
Эта величина используется в дальнейших расчетах.
Как подобрать форму сечения двутавровой балки, в зависимости от назначения?
Горячекатаный металлопрокат с параллельными внутренними полками граней бывает следующих групп, согласно ГОСТу 26020-83:
- «Б» – нормальная. Диапазон номеров – 10-60. Толщина стенки составляет до 1/58 ее высоты. Металлопродукция применяется при монтаже перекрытий путепроводов, возведении мостов и эстакад.
«Ш» – широкополочная. Подразделяется на разрезную и неразрезную продукцию.
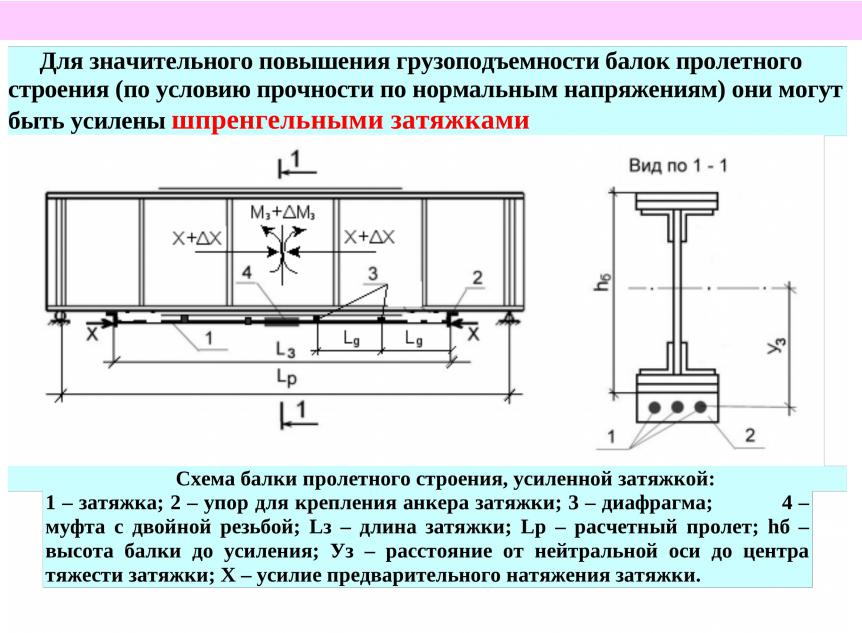 Разрезные изделия, позволяющие получать две тавровые балки, применяют для укладки на один пролет, неразрезные – на один или несколько. Производство таких металлоизделий требует увеличенного (на 10-12%) расхода металла, что можно считать минусом. Плюсы: возможность установки в качестве самостоятельного элемента без дополнительных деталей, что существенно сокращает скорость проведения работ.
Разрезные изделия, позволяющие получать две тавровые балки, применяют для укладки на один пролет, неразрезные – на один или несколько. Производство таких металлоизделий требует увеличенного (на 10-12%) расхода металла, что можно считать минусом. Плюсы: возможность установки в качестве самостоятельного элемента без дополнительных деталей, что существенно сокращает скорость проведения работ.«К» – колонная. Особенность сечения этого вида двутавра – увеличенная толщина полок. Продукция выполняет функции несущих элементов строений, применяется для устройства больших пролетов, способна выдерживать значительные крановые нагрузки. В сортаменте это самые тяжелые и износостойкие профили.
Расчет на прогиб
Изгибающий момент для каждой балки вычисляется, исходя из величины линейной нагрузки q, шага укладки балок p и длины перекрываемого пролета L. Так как балки укладываются вдоль короткой стороны, то L = 4,5 м = 450 см (конечно, сами балки длиннее – около 5 м, так как опираются на стены, но шарнирными опорами для них служат именно внутренние края стен).
Искомая величина момента, в таком случае:
My = (q * L2) / 8 = 6 * 4502 / 8 = 151875 кгс * см.
Максимальный момент сопротивления сечения балки можно рассчитать, разделив изгибающий момент на расчетное сопротивление стали – например, марки С235, равное 2150 кгс / см2:
Wy = 151875 / 2150 = 70,6 см3.
Это полученное значение надо сравнить с величиной момента сопротивления сечения двутавровой балки. Из таблицы ГОСТ 8239-72 видно, что вычисленный показатель примерно соответствует (с запасом) моменту сопротивления для профиля 14 (81,7 см3). Следовательно, этот номер проката будет удовлетворять требованиям к прочности балок.
Выбор сечения двутавра – другие виды изделий
Подбор сечения профиля для специального горячекатаного профиля будет отличаться. Во многом это определяется уклоном внутренних граней полок. ГОСТ 19425-74 еще ГОСТом Р 57837-2017 заменить гениальная мысль не пришла в головы (шутка). Если кратко, то существует два основных вида специальной двутавровой балки.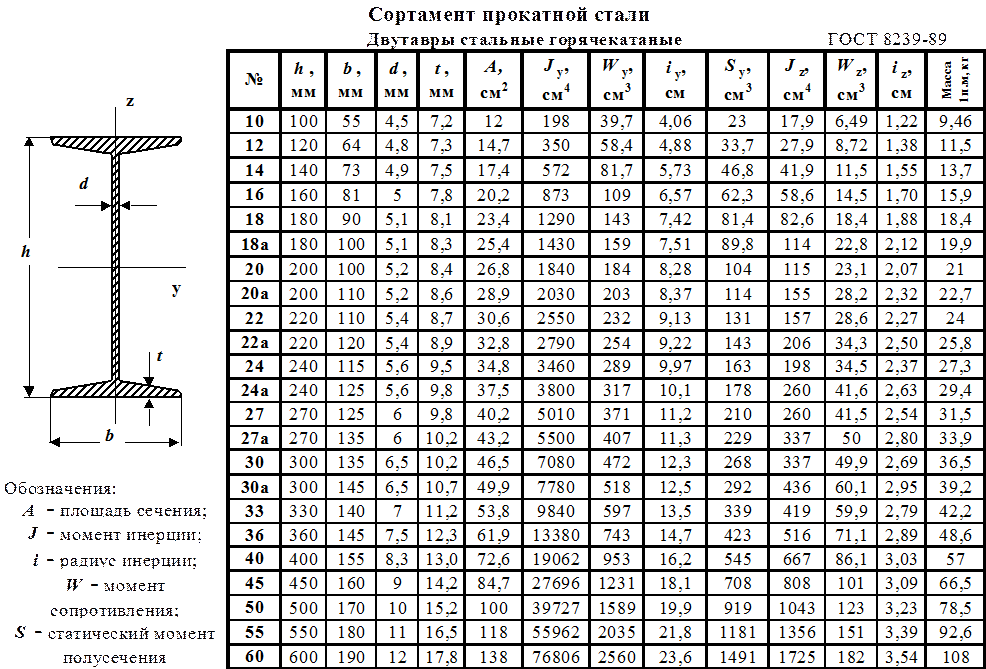 Первый – М (подвесная, монорельсовая). Соотношение основания двутавра к ширине полок примерно 2/1 или 3/1. С – для армирования стволов шахт. Сечение отличается значительным уклоном внутренних граней полок.
Первый – М (подвесная, монорельсовая). Соотношение основания двутавра к ширине полок примерно 2/1 или 3/1. С – для армирования стволов шахт. Сечение отличается значительным уклоном внутренних граней полок.
Обращайте внимание что все еще есть на рынке и двутавровая балка У. Буква указывает на то что это узкополочный прокат. Характерная черта сечения – узкие полки.
И последний тип горячекатаного двутавра – Д. Это обозначает дополнительный. По ГОСТ Р 57837-2017 маркируется как ДК и ДБ. Изготавливается по требованиям заказчика. Какое нужно сечение, такое и сделают под заказ. Особенно актуально когда стоит сложная, нетривиальная инженерная задача при проектировании уникальных металлоконструкций. Среди характерных черт сечения – ширина полки. Она меньше чем ширина полки у широкополочного двутавра. Но при этом ширина полки двутавра Д меньше чем ширина полки у двутавра нормального типа. Хотя бывают и исключения.
Подводя итог скажем так. Подбор сечения двутавра определяется сложными расчетами. Форма профиля зависит от основных параметров проката и определяет его тип. Иногда характеристики типа определяют вид сечения. С особой тщательностью надо выполнять выбор сечения двутавра для нагруженных конструкций. Остались вопросы? Требуется двутавровая балка? Обращайтесь!
Форма профиля зависит от основных параметров проката и определяет его тип. Иногда характеристики типа определяют вид сечения. С особой тщательностью надо выполнять выбор сечения двутавра для нагруженных конструкций. Остались вопросы? Требуется двутавровая балка? Обращайтесь!
Расчет на жесткость
Жесткость балок характеризуется максимальной величиной прогиба при заданных исходных параметрах. В случае распределенной нагрузки прогиб вычисляется по формуле:
f = 5 * q * L4 / (384 * E * Jy), где
- q – линейная нагрузка на балку;
- L – длина пролета;
- E – модуль упругости материала, для стали С235 равный 2,1 * 106 кгс / см2;
- Jy – минимальный момент инерции для данного профиля.
Для принятых ранее исходных данных, с учетом того, что из расчета на прочность наиболее подходящим профилем оказался № 14, для которого Jy, по табличным значениям ГОСТ, равен 572 см4, можно получить:
f = 2,6 см,
а в относительной мере, с учетом того, что длина пролета 450 см – 1 / 172. Это превышает максимально допустимый прогиб, принятый равным 1 / 250.
Это превышает максимально допустимый прогиб, принятый равным 1 / 250.
Поэтому расчет приходится повторить и вычислить прогиб для другого номера проката. Для № 16, у которого момент инерции равен 873 см4, абсолютный прогиб получается 1,74 см, а относительный – 1 / 256, что является приемлемым.
Требования
Все требования, предъявляемые к балкам из металла, четко обозначены в ГОСТах и СНиПах. Основными требованиями являются:
- Прочность. В зависимости от типа материала, используемого при изготовлении изделия, показатели прочности могут отличаться, но они должны соответствовать значениям, указанным в нормативных документах.
- Период эксплуатации. Металлические конструкции, согласно ГОСТ, должны прослужить минимум 80 лет.
- Устойчивость к коррозии. Готовые элементы должны быть дополнительно обработаны составами, предотвращающими образование коррозии.
Итоги расчета
Итак, для помещения размером 4,5 х 6 м каркас потолочного перекрытия из железобетонных плит ПК-12-10-8 с распределенной нагрузкой 600 кгс / м2 может быть устроен из двутавровых балок профиля № 16 стали марки С235, расположенных вдоль короткой стороны с шагом 1 м. Можно рассчитать, что для такого здания понадобится 7 таких балок длиной по 5 м, и, зная массу и цену погонного метра, вычислить общую массу балочного каркаса и его стоимость.
Можно рассчитать, что для такого здания понадобится 7 таких балок длиной по 5 м, и, зная массу и цену погонного метра, вычислить общую массу балочного каркаса и его стоимость.
Так, для приведенного примера общее количество погонных метров – 35; масса балочного каркаса из профиля № 16 – 525 кг.
Особенности процесса монтажа
Процедура устройства перекрытий с использованием металлических балок имеет определенные особенности, которые необходимо знать и четко соблюдать.
Обязательно наличие четкой схемы постройки с произведенными расчетами на прочность и изгиб изделий.
- К боковым граням балок крепятся бруски сечением 60х60, после чего размещается накат из досок.
- Накат накрывается слоем утеплителя, выполняющего функции звуко и теплоизоляции.
- Шаг между стальными балками не должен превышать 150 см, оптимальное расстояние – 100 см.
- Глубина опирания концов металлических конструкций на стены – максимум 25 см.
- Чтобы добиться большей звукоизоляции можно использовать не обычные, а пружинные скобы.

Плюсы и минусы применения в зданиях
Конструкции из металла обладают рядом преимуществ, благодаря которым материал широко используется:
- повышенной прочностью;
- огнестойкостью;
- устойчивостью к внешним факторам;
- повышенной надежностью;
- большим периодом эксплуатации;
- возможностью усилить уже построенное здание;
- увеличенной несущей способностью.
Однако такие балки имеют и свои недостатки, которые также следует учитывать:
- сложность проведения строительных работ;
- необходимость задействовать тяжелую технику;
- металл может подвергаться коррозии;
- требуется производить сложные подсчеты, с чем у новичка могут возникнуть серьезные сложности.
Двутавры стальные горячекатаные с параллельными гранями полок по ГОСТ 26020-83
| Наименование профиля двутавра | Высота (h), мм | Ширина полки (b), мм | Толщина стенки (s), мм | Средняя толщина полки (t), мм | Масса 1 м балки, кг | Метров балки в тонне |
| Нормальные двутавры | ||||||
| Балка 10Б1 | 100 | 55 | 4. 1 1 | 8.1 | 123.46 | |
| Балка 12Б1 | 117.6 | 64 | 3.8 | 8.7 | 114.94 | |
| Балка 12Б2 | 120 | 64 | 4.4 | 10.4 | 96.15 | |
| Балка 14Б1 | 137.4 | 73 | 3.8 | 10.5 | 95.24 | |
| Балка 14Б2 | 140 | 73 | 4.7 | 12.9 | 77.52 | |
| Балка 16Б1 | 157 | 82 | 4 | 12.7 | 78.74 | |
| Балка 16Б2 | 160 | 82 | 5 | 15.8 | 63.29 | |
| Балка 18Б1 | 177 | 91 | 4.3 | 15.4 | 64.94 | |
| Балка 18Б2 | 180 | 91 | 5.3 | 18.8 | 53.19 | |
| Балка 20Б1 | 200 | 100 | 5.6 | 22.4 | 44.64 | |
| Балка 23Б1 | 230 | 110 | 5.6 | 25.8 | 38.76 | |
| Балка 26Б1 | 258 | 120 | 5.8 | 28 | 35. 71 71 | |
| Балка 26Б2 | 261 | 120 | 6 | 31.2 | 32.05 | |
| Балка 30Б1 | 296 | 140 | 5.8 | 32.9 | 30.4 | |
| Балка 30Б2 | 299 | 140 | 6 | 36.6 | 27.32 | |
| Балка 35Б1 | 346 | 155 | 6.2 | 38.9 | 25.71 | |
| Балка 35Б2 | 349 | 155 | 6.5 | 43.3 | 23.09 | |
| Балка 40Б1 | 392 | 165 | 7 | 48.1 | 20.79 | |
| Балка 40Б2 | 396 | 165 | 7.5 | 54.7 | 18.28 | |
| Балка 45Б1 | 443 | 180 | 7.8 | 59.8 | 16.72 | |
| Балка 45Б2 | 447 | 180 | 8.4 | 67.5 | 14.81 | |
| Балка 50Б1 | 492 | 200 | 8.8 | 73 | 13.7 | |
| Балка 50Б2 | 496 | 200 | 9.2 | 80.7 | 12.39 | |
| Балка 55Б1 | 543 | 220 | 9. 5 5 | 89 | 11.24 | |
| Балка 55Б2 | 547 | 220 | 10 | 97.9 | 10.21 | |
| Балка 60Б1 | 593 | 230 | 10.5 | 106.2 | 9.42 | |
| Балка 60Б2 | 597 | 230 | 11 | 115.6 | 8.65 | |
| Балка 70Б1 | 691 | 260 | 12 | 129.3 | 7.73 | |
| Балка 70Б2 | 697 | 260 | 12.5 | 144.2 | 6.93 | |
| Балка 80Б1 | 791 | 280 | 13.5 | 159.5 | 6.27 | |
| Балка 80Б2 | 798 | 280 | 14 | 177.9 | 5.62 | |
| Балка 90Б1 | 893 | 300 | 15 | 194 | 5.15 | |
| Балка 90Б2 | 900 | 300 | 15.5 | 213.8 | 4.68 | |
| Балка 100Б1 | 990 | 320 | 16 | 230.6 | 4.34 | |
| Балка 100Б2 | 998 | 320 | 17 | 258. 2 2 | 3.87 | |
| Балка 100Б3 | 1006 | 320 | 18 | 285.7 | 3.5 | |
| Балка 100Б4 | 1013 | 320 | 19.5 | 314.5 | 3.18 | |
| Широкополочные двутавры | ||||||
| Балка 20Ш1 | 193 | 150 | 6 | 30.6 | 32.68 | |
| Балка 23Ш1 | 226 | 155 | 6.5 | 36.2 | 27.62 | |
| Балка 26Ш1 | 251 | 180 | 7 | 42.7 | 23.42 | |
| Балка 26Ш2 | 255 | 180 | 7.5 | 49.2 | 20.33 | |
| Балка 30Ш1 | 291 | 200 | 8 | 53.6 | 18.66 | |
| Балка 30Ш2 | 295 | 200 | 8.5 | 61 | 16.39 | |
| Балка 30Ш3 | 299 | 200 | 9 | 68.3 | 14.64 | |
| Балка 35Ш1 | 338 | 250 | 9.5 | 75.1 | 13.32 | |
| Балка 35Ш2 | 341 | 250 | 10 | 82. 2 2 | 12.17 | |
| Балка 35Ш3 | 345 | 250 | 10.5 | 91.3 | 10.95 | |
| Балка 40Ш1 | 388 | 300 | 9.5 | 96.1 | 10.41 | |
| Балка 40Ш2 | 392 | 300 | 11.5 | 111.1 | 9 | |
| Балка 40Ш3 | 396 | 300 | 12.5 | 123.4 | 8.1 | |
| Балка 50Ш1 | 484 | 300 | 11 | 114.4 | 8.74 | |
| Балка 50Ш2 | 489 | 300 | 14.5 | 138.7 | 7.21 | |
| Балка 50Ш3 | 495 | 300 | 15.5 | 156.4 | 6.39 | |
| Балка 50Ш4 | 501 | 300 | 16.5 | 174.1 | 5.74 | |
| Балка 60Ш1 | 580 | 320 | 12 | 142.1 | 7.04 | |
| Балка 60Ш2 | 587 | 320 | 16 | 176.9 | 5.65 | |
| Балка 60Ш3 | 596 | 320 | 18 | 205.5 | 4. 87 87 | |
| Балка 60Ш4 | 603 | 320 | 20 | 234.2 | 4.27 | |
| Балка 70Ш1 | 683 | 320 | 13.5 | 169.9 | 5.89 | |
| Балка 70Ш2 | 691 | 320 | 15 | 197.6 | 5.06 | |
| Балка 70Ш3 | 700 | 320 | 18 | 235.4 | 4.25 | |
| Балка 70Ш4 | 708 | 320 | 20.5 | 268.1 | 3.73 | |
| Балка 70Ш5 | 718 | 320 | 23 | 305.9 | 3.27 | |
| Колонные двутавры | ||||||
| Балка 20К1 | 195 | 200 | 6.5 | 41.5 | 24.1 | |
| Балка 20К2 | 198 | 200 | 7 | 46.9 | 21.32 | |
| Балка 23К1 | 227 | 240 | 7 | 52.2 | 19.16 | |
| Балка 23К2 | 230 | 240 | 8 | 59.5 | 16.81 | |
| Балка 26K1 | 255 | 260 | 8 | 65. 2 2 | 15.34 | |
| Балка 26K2 | 258 | 260 | 9 | 73.2 | 13.66 | |
| Балка 26K3 | 262 | 260 | 10 | 83.1 | 12.03 | |
| Балка 30К1 | 296 | 300 | 9 | 84.8 | 11.79 | |
| Балка 30К2 | 304 | 300 | 10 | 96.3 | 10.38 | |
| Балка 30К3 | 300 | 300 | 11.5 | 108.9 | 9.18 | |
| Балка 35К1 | 343 | 350 | 10 | 109.7 | 9.12 | |
| Балка 35К2 | 348 | 350 | 11 | 125.9 | 7.94 | |
| Балка 35К3 | 353 | 350 | 13 | 144.5 | 6.92 | |
| Балка 40К1 | 393 | 400 | 11 | 138 | 7.25 | |
| Балка 40К2 | 400 | 400 | 13 | 165.6 | 6.04 | |
| Балка 40К3 | 409 | 400 | 16 | 202.3 | 4. 94 94 | |
| Балка 40К4 | 419 | 400 | 19 | 242.2 | 4.13 | |
| Балка 40К5 | 431 | 400 | 23 | 291.2 | 3.43 | |
| Двутавры дополнительной серии (Д) | ||||||
| Балка 24ДБ1 | 239 | 115 | 5.5 | 27.8 | 35.97 | |
| Балка 27ДБ1 | 269 | 125 | 6 | 31.9 | 31.35 | |
| Балка 36ДБ1 | 360 | 145 | 7.2 | 49.1 | 20.37 | |
| Балка 35ДБ1 | 349 | 127 | 5.8 | 33.6 | 29.76 | |
| Балка 40ДБ1 | 399 | 139 | 6.2 | 39.7 | 25.19 | |
| Балка 45ДБ1 | 450 | 152 | 7.4 | 52.6 | 19.01 | |
| Балка 45ДБ2 | 450 | 180 | 7.6 | 65 | 15.38 | |
| Балка 30ДШ1 | 300.6 | 201.9 | 9.4 | 72.7 | 13.76 | |
| Балка 40ДШ1 | 397. 6 6 | 302 | 11.5 | 124 | 8.06 | |
| Балка 50ДШ1 | 496.2 | 303.8 | 14.2 | 155 | 6.45 |
Если на двутавр существуют ГОСТ ы, то изготовление тавровой балки осуществляется по ТУ 14-2-685-86
Обозначение здесь такое же, как и у двутавровой балки.
Тавры колонные и Тавры ШТ по ТУ 14-2-685-86 имеют следующие размеры
Тавры ШТ по ТУ 14-2-685-86. Наименование профиля, вес.
Расчет балок на прочность.
Расчет по допускаемым напряжениям
на прочность при изгибе.
– при |
Проверка прочности по предельным состояниям.

– максимальный изгибающий момент от
расчетных нагрузок.
Рр=Рн×n
n
– коэффициент перегрузки.
– нормативная нагрузка.
Рр
– расчетная нагрузка.
– коэффициент условия работы.
Если материал работает неодинаково на
растяжение и сжатие, то прочность
проверяется по формулам:
где Rp
и Rсж
– расчетное
сопротивление на растяжение и сжатие
Расчет по несущей способности и учетом пластической деформации.
В предыдущих методах расчета прочность
проверяется по максимальны напряжениям
в верхних и нижних волокнах балки. При
этом средние волокна оказываются
недогруженными.
Оказывается, если нагрузку
увеличивать дальше, то в крайних волокнах
напряжение дойдет до предела текучести
σт( в пластичных
материалах), и до предела прочности σnч( в хрупких материалах).
При дальнейшем увеличении нагрузки
хрупкие материалы разрушатся, а в
пластичных материалах напряжения в
крайних волокнах далее не возрастают,
а растут во внутренних волокнах. (см.
рис.)
Несущая способность балки
исчерпывается, когда по всему сечению
напряжения достигнут σт.
W W — статический момент растянутой и Мпред где где R | |||
— проверка | |||
Для прямоугольного сечения:
W пл=S1+S2=bh2 W W W |
Примечание: для прокатных
профилей (швеллер и двутавр) пластический
момент Wnл=(1. 1÷1,17)×W
1÷1,17)×W
Касательные
напряжения при изгибе балки прямоугольного
сечения. Формула Журавcкого.
Так как момент в сечении 2
больше момента в сечении 1, то напряжение
σ2>σ1=>N2>N1.
В этом случае элемент abcd
должен переместиться влево. Этому
перемещению препятствуют касательные
напряжения τ
на площадке cd.
— уравнение равновесия,
после преобразования которого получается
формула для определения τ:
— Формула Журавского
где Q Sотс J-момент |
Распределение
касательных напряжений в балках
прямоугольного, круглого и двутаврового
сечений.
1.
Прямоугольное сечение:
— формула для сечения |
2.Круглое сечение.
— — формула для сечения |
3. Двутавровое сечение.
Для стенки двутавра касательные напряжения вычисляют по формуле: | ||||
Для полки: условно вертикальные | ||||
В | ||||
На рисунке | ||||
Главные напряжения при изгибе.
Проверка прочности балок.
Выделим из балки участок, Наиболее опасными точками Прочность проверяется по напряжениям На практике обычно |
[σсж]
Примечание: при расчете
по предельным состояниям вместо [σсж]
и [σр]
в формулы
ставятся
Rcж
и Rp
–
расчетные сопротивления материала при
сжатии и растяжении.
Если же балка короткая, то
проверяют точку Б:
где
Rсрез
– расчетное
сопротивление материала на срез.
В точке D
на элемент действует нормальные и
касательные напряжения, поэтому в
некоторых случаях их совместное действие
вызывает опасность для прочности. В
этом случае элемент D
проверяют на прочность используя главные
напряжения.
В нашем случае: ,
следовательно:
Используя σ
1и
σ2
по теории прочности проверяют элемент
D.
По теории наибольших
касательных напряжений имеем: σ
1 —
σ2≤R
Примечание: точку D
следует брать по длине балки там, где
одновременно действуют большие M
и Q.
По высоте балки выбираем
такое место, где одновременно действуют
значения σ
и
τ.
Из эпюр
видно:
1. В балках прямоугольного
и круглого сечения отсутствуют точки,
в которых одновременно действуют большие
σ
и τ.
Поэтому в таких балках проверка точки
D
не делается.
2. В балках двутаврового
сечения на границе пересечения полки
со стенкой (т. А) одновременно действуют
большие σ
и τ.
Поэтому они проверяются на прочность
в этой точке.
Примечание:
В прокатных двутаврах и
швеллерах в зоне пересечения полки со
стенкой сделаны плавные переходы
(закругления). Стенка и полка подобраны
так, что точка A
оказывается в благоприятных условиях
работы и проверка прочности не требуется.В составных (сварных)
двутавровых балках проверка точки А
необходима.
Простая гибка балки | Инженерная библиотека
На этой странице представлены разделы о простом изгибе балки из «Руководства по анализу напряжений», Лаборатория динамики полета ВВС, октябрь 1986 г.
Другие связанные главы из «Руководства по анализу стресса» ВВС можно увидеть справа.
| А | = | площадь поперечного сечения |
| б | = | ширина секции |
| с | = | расстояние от нейтральной оси до крайнего волокна |
| Е | = | модуль упругости |
| Ф ти | = | предел текучести при растяжении |
| е б | = | расчетное первичное напряжение изгиба |
| ф кр | = | расчетное критическое напряжение сжатия |
| Г | = | модуль упругости при сдвиге |
| ч | = | высота или глубина |
| я | = | момент инерции |
| Дж | = | постоянная кручения |
| Л | = | длина |
| Л’ | = | эффективная длина балки |
| М | = | приложенный изгибающий момент |
| М кр | = | критический момент |
| М фп | = | полностью пластиковый изгибающий момент |
| М у | = | изгибающий момент в начале текучести |
| П | = | приложенная сосредоточенная нагрузка |
| В | = | статический момент поперечного сечения, \( \int_{A_1} y ~dA \) |
| к | = | сдвиговое течение |
| с | = | расстояние от центральной оси до точки приложения нагрузки |
| т ж | = | толщина фланца |
| т ш | = | толщина стенки |
| В | = | поперечная сила |
| х, у, з | = | прямоугольные координаты |
| у | = | прогиб балки из-за изгиба |
| р | = | радиус вращения |
| θ | = | наклон балки |
1.
 3.1 Простые балки на изгибе
3.1 Простые балки на изгибе
Простые балки при упругом и пластическом изгибе рассматриваются в разделах 1.3.1.1 и 1.3.1.3 соответственно, а возможность поперечной неустойчивости глубоких балок при изгибе рассматривается в разделе 1.3.1.5.
1.3.1.1 Простые балки при упругом изгибе
В этом разделе рассматриваются простые балки при изгибе, для которых максимальное напряжение остается в области упругости.
Максимальное изгибающее напряжение в такой балке находится по формуле
$$ f_b = {Mc \над I} $$
(1-1)
в то время как сдвиговый поток определяется выражением
$$ q = { VQ \над I } $$
(1-2)
где \( Q = \int_{A_1} y~dA \). Использование этих уравнений показано в разделе 1.3.2.2.
Вертикальные и угловые перемещения простой балки при упругом изгибе задаются уравнениями (1-3) и (1-4) соответственно, где А и В — константы интегрирования.
92 + Ах + В $$
(1-3)
$$ \theta = {dy \over dx} = \int {M \over EI}~ dx + A $$
(1-4)
Нужен калькулятор луча?
Попробуйте этот калькулятор луча.
- Расчет напряжений и прогибов в прямых балках
- Построение диаграмм сдвига и моментов
- Можно указать любую конфигурацию ограничений, сосредоточенных сил и распределенных сил
1.3.1.2 Пример задачи — простая балка при упругом изгибе
Дано : Консольная балка, показанная на рис. 1-1.
Найти : Максимальные напряжения изгиба и сдвига.
Решение : Из уравнений статики можно получить диаграммы сдвига и момента на рисунке 1-2.
Поскольку c и I постоянны вдоль балки, максимальное изгибающее напряжение возникает в точке максимального изгибающего момента; и из уравнения (1-1),
92 $$
Нужен калькулятор луча?
Попробуйте этот калькулятор луча.
- Расчет напряжений и прогибов в прямых балках
- Построение диаграмм сдвига и моментов
- Можно указать любую конфигурацию ограничений, сосредоточенных сил и распределенных сил
1.
 3.1.3 Простые балки при гибке пластика
3.1.3 Простые балки при гибке пластика
В некоторых случаях допустима деформация балки при изгибе. Если материал балки можно считать упруго-идеально пластичным, изгибающий момент при разрушении определяется выражением
$$ M_{fp} = K ~M_y $$
(1-5)
где M y — это момент, вызывающий начальную деформацию крайних волокон, а K — коэффициент формы, указанный в Таблице 1-1.
| Раздел | |||||||
| К | 1,0 93 }\справа) $$ |
1.3.1.4 Пример задачи — простая балка при пластическом изгибе
Дано : Свободно опертая балка, показанная на рис. 1-4.
Найти : Нагрузка P, вызывающая полностью пластический изгиб.
Решение : Преобразование уравнения (1-1) и замена изгибающего напряжения пределом текучести дает
$$ M_y = { F_y ~I \over c } = { 55000 (0,666) \over 1,0 } = 36 600 ~\text{in/lb} $$
Вставка значения K из таблицы 1-1 в уравнение (1-5) дает
$$ M_{fp} = K ~M_y = 1,5 (36 600) = 54 900 ~\text{дюйм/фунт} $$
Из статики максимальный момент на перекладине 10П. Таким образом, при полностью пластическом изгибе
Таким образом, при полностью пластическом изгибе
$$ P = {M_{fp} \over 10} = 5490 ~\text{фунт} $$
1.3.1.5 Введение в поперечную неустойчивость глубоких балок при изгибе
Балки при изгибе при определенных условиях нагрузки и ограничения могут выйти из строя из-за поперечного выпячивания таким же образом, как и у колонн, нагруженных осевым сжатием. Однако консервативно получать изгибающую нагрузку, рассматривая сжатую сторону балки как колонну, поскольку этот подход не учитывает жесткость балки при кручении.
В общем, критический изгибающий момент для поперечной неустойчивости глубокой балки, как показано на рисунке 1-5, может быть выражен как
$$ M_{cr} = { K \sqrt{ E I_y GJ } \over L } $$
(1-6)
где J — постоянная кручения балки, а K — постоянная, зависящая от типа нагрузки и торцевого крепления. Таким образом, критическое сжимающее напряжение определяется выражением
$$ f_{cr} = { M_{cr} ~c \over I_x } $$
(1-7)
где с — расстояние от центральной оси до волокон крайней степени сжатия. Если это сжимающее напряжение попадает в пластический диапазон, коэффициент эквивалентной гибкости можно рассчитать как
Если это сжимающее напряжение попадает в пластический диапазон, коэффициент эквивалентной гибкости можно рассчитать как
$$ \left({ L’ \over \rho }\right) = \pi \sqrt{ E \over f_{cr} } $$
(1-8)
Фактическое критическое напряжение можно затем найти, введя кривые столбца главы 2 при этом значении (L’/ρ). Это значение напряжения не является истинным сжимающим напряжением в балке, но является достаточно точным, чтобы его можно было использовать в качестве ориентира при проектировании.
Нужен калькулятор луча?
Попробуйте этот калькулятор луча.
- Расчет напряжений и прогибов в прямых балках
- Построение диаграмм сдвига и моментов
- Можно указать любую конфигурацию ограничений, сосредоточенных сил и распределенных сил
1.3.1.6 Боковая неустойчивость глубоких прямоугольных балок при изгибе
Критический момент для глубоких прямоугольных балок, нагруженных в диапазоне упругости, нагруженных вдоль центральной оси, определяется выражением
92 \над L ч }\справа) $$
(1-10)
где K u представлен в табл. 1-2.
1-2.
Если балка не нагружена вдоль центральной оси, как показано на рисунке 1-6, вместо K f в уравнении (1-10) используется скорректированное значение K’ f . Этот фактор выражается как
$$ K_f’ = K_f ~(1-n) \left({s \over L}\right) $$
(1-11)
где n — константа, определенная ниже:
- Для свободно опертых балок с сосредоточенной нагрузкой в середине пролета n = 2,84.
- Для консольных балок с сосредоточенной торцевой нагрузкой n = 0,816.
- Для свободно опертых балок при равномерной нагрузке n = 2,52.
- Для консольных балок при равномерной нагрузке n = 0,725.
Нужен калькулятор луча?
Попробуйте этот калькулятор луча.
- Расчет напряжений и прогибов в прямых балках
- Построение диаграмм сдвига и моментов
- Можно указать любую конфигурацию ограничений, сосредоточенных сил и распределенных сил 93) $$
(1-14)
Этот метод может применяться только в том случае, если нагрузка приложена к центральной оси.

Механика материалов: изгиб – нормальное напряжение » Механика гибких конструкций
исследования
человек
курсы
77 200029 блог
902
Моменты площадиЧтобы рассчитать напряжение (и, следовательно, деформацию), вызванное изгибом, нам нужно понять, где находится нейтральная ось балки, и как рассчитать второй момент площади для данного поперечного сечения.
Давайте начнем с представления произвольного поперечного сечения — чего-то не круглого, не прямоугольного и т. д.
На изображении выше произвольная форма имеет площадь, обозначенную A . Мы можем посмотреть на небольшую дифференциальную область дА , которая существует на расстоянии x и y от начала координат. Мы можем посмотреть на первый момент площади в каждом направлении из следующих формул:
Первый момент площади — это интеграл длины по площади — это означает, что он будет иметь единицы длины в кубе [L 3 ].
 Это важно, потому что помогает нам найти центр тяжести объекта. Центроид определяется как «среднее x (или y ) положение области». Математически это утверждение выглядит так:
Это важно, потому что помогает нам найти центр тяжести объекта. Центроид определяется как «среднее x (или y ) положение области». Математически это утверждение выглядит так:Крайняя правая часть приведенных выше уравнений будет очень полезна в этом курсе — она позволяет нам разбить сложную фигуру на простые формы с известными площадями и известным расположением центроидов. В большинстве инженерных сооружений есть хотя бы одна ось симметрии — и это позволяет значительно упростить нахождение центроида. Центроид должен располагаться на оси симметрии . Например:
Для поперечного сечения слева мы знаем, что центроид должен лежать на оси симметрии, поэтому нам нужно найти только центроид вдоль оси y . Поперечное сечение справа еще проще — поскольку центроид должен совпадать с осями симметрии, он должен быть в центре объекта.
Теперь, когда мы знаем, как найти центр тяжести, мы можем обратить внимание на второй момент площади.
 Как вы, возможно, помните из предыдущего раздела о кручении, это определяется как:
Как вы, возможно, помните из предыдущего раздела о кручении, это определяется как:И, наконец, иногда нам нужно будет определить второй момент площади относительно произвольной оси x или y , которая не соответствует центроиду. В этом случае мы можем использовать теорему о параллельных осях для его вычисления. В этом случае мы используем второй момент площади относительно центроида плюс термин, который включает расстояния между двумя осями.
Это уравнение называется теоремой о параллельных осях . Это будет очень полезно на протяжении всего курса. Как описано во вступительном видео к этому разделу, вычисление второго момента площади простой формы может быть простым. Для более сложных форм нам потребуется вычислить I путем вычисления отдельных I для каждой простой формы и объединения их вместе с использованием теоремы о параллельных осях.
Диаграммы сдвига и момента
Поперечная нагрузка относится к силам, которые перпендикулярны длинной оси конструкции.
 Эти поперечные нагрузки вызовут изгибающий момент M , который вызывает нормальное напряжение , и поперечную силу V , которая вызывает касательное напряжение . Эти силы могут и будут варьироваться по длине балки, и мы будем использовать диаграммы сдвига и момента (диаграмма VM) для извлечения наиболее подходящих значений. Построение этих диаграмм должно быть вам знакомо по статике , но мы рассмотрим их здесь. При исследовании балки с поперечной нагрузкой необходимо учитывать два важных момента:
Эти поперечные нагрузки вызовут изгибающий момент M , который вызывает нормальное напряжение , и поперечную силу V , которая вызывает касательное напряжение . Эти силы могут и будут варьироваться по длине балки, и мы будем использовать диаграммы сдвига и момента (диаграмма VM) для извлечения наиболее подходящих значений. Построение этих диаграмм должно быть вам знакомо по статике , но мы рассмотрим их здесь. При исследовании балки с поперечной нагрузкой необходимо учитывать два важных момента:- Как балка нагружена?
- точечная нагрузка, распределенная нагрузка (равномерная или переменная), комбинация нагрузок…
- Как балка поддерживается?
- свободно опертый, консольный, нависающий, статически неопределимый…
Знание нагрузок и опор позволит вам нарисовать качественную диаграмму V-M, а затем статический анализ свободного тела поможет вам определить количественное описание кривых.
 Начнем с того, что вспомним наши соглашения о знаках .
Начнем с того, что вспомним наши соглашения о знаках .Эти соглашения о знаках должны быть знакомы. Если сдвиг вызывает вращение против часовой стрелки, он положительный. Если момент изгибает луч таким образом, что луч изгибается в «улыбку» или U-образную форму, он положительный. Лучший способ вспомнить эти диаграммы — это проработать пример. Начните с этой консольной балки — отсюда вы можете переходить к более сложным нагрузкам.
Нормальное напряжение при изгибе
Во многих отношениях изгиб и кручение очень похожи. Изгиб возникает из-за приложенной пары или изгибающего момента M . Как и при кручении, при чистом изгибе в материале есть ось, на которой напряжение и деформация равны нулю.
 Это называется нейтральной осью . И, как и при кручении, напряжение уже не одинаково по сечению конструкции — оно меняется. Давайте начнем с того, что рассмотрим момент о z — ось изгибает конструкцию. В данном случае мы не будем ограничиваться круглыми сечениями – на рисунке ниже рассмотрим призматическое сечение.
Это называется нейтральной осью . И, как и при кручении, напряжение уже не одинаково по сечению конструкции — оно меняется. Давайте начнем с того, что рассмотрим момент о z — ось изгибает конструкцию. В данном случае мы не будем ограничиваться круглыми сечениями – на рисунке ниже рассмотрим призматическое сечение.Прежде чем мы углубимся в математику изгиба, давайте попробуем понять его концептуально. Возможно, лучший способ увидеть, что происходит, — наложить изогнутую балку поверх оригинальной прямой балки.
Теперь вы можете заметить, что нижняя поверхность луча стала длиннее, а верхняя поверхность луча стала короче. Также по центру луча длина вообще не изменилась – соответствует нейтральной оси. Повторяя это язык этого класса, мы можем сказать, что нижняя поверхность находится под напряжением, а верхняя поверхность находится под сжатием. Кое-что, что является немного более тонким, но все еще можно наблюдать из наложенного выше изображения, заключается в том, что смещение луча изменяется линейно сверху вниз, проходя через ноль на нейтральной оси.
 Помните, это именно то, что мы видели и при кручении — напряжение линейно менялось от центра к центру. Мы можем посмотреть на это распределение напряжений по поперечному сечению балки немного более явно:
Помните, это именно то, что мы видели и при кручении — напряжение линейно менялось от центра к центру. Мы можем посмотреть на это распределение напряжений по поперечному сечению балки немного более явно:Теперь мы можем найти математическую связь между приложенным моментом и напряжением внутри балки. Мы уже упоминали, что балка деформируется линейно от одного края к другому — это означает, что деформация в направлении x увеличивается линейно с расстоянием вдоль оси y- (или по толщине балки). Таким образом, деформация будет максимальной при растяжении при y = -c (поскольку y=0 находится на нейтральной оси, в данном случае в центре балки), и будет максимальной при сжатии при y=c . Мы можем записать это математически следующим образом:
Теперь это говорит нам кое-что о деформации, что мы можем сказать о максимальных значениях напряжения? Начнем с умножения обеих частей уравнения на E , модуль упругости Юнга. Теперь наше уравнение выглядит так:
Используя закон Гука, мы можем связать эти величины с фигурными скобками под ними с напряжением в направлении x и максимальным напряжением.
 Что дает нам это уравнение для напряжения в направлении x-:
Что дает нам это уравнение для напряжения в направлении x-:Наш последний шаг в этом процессе — понять, как изгибающий момент связан с напряжением. Для этого вспомним, что момент — это произведение силы на расстояние. Если мы можем представить себе, что смотрим только на очень маленький элемент в луче, дифференциальный элемент, то мы можем записать это математически как:
Поскольку в нашем уравнении есть дифференциалы, мы можем определить момент M , действующий на площадь поперечного сечения балки, путем интегрирования обеих частей уравнения. И если мы вспомним наше определение напряжения как силы на единицу площади, мы можем написать:
Последний член в последнем уравнении — интеграл по y в квадрате — представляет второй момент площади относительно оси z (из-за того, как мы определили наши координаты). В декартовых координатах этот второй момент площади обозначается I (в цилиндрических координатах, помните, обозначался J ).
 Теперь мы можем, наконец, записать наше уравнение для максимального напряжения и, следовательно, напряжения в любой точке вдоль оси y , как:
Теперь мы можем, наконец, записать наше уравнение для максимального напряжения и, следовательно, напряжения в любой точке вдоль оси y , как:Важно отметить, что нижние индексы в этом уравнении и направление вдоль поперечного сечения (здесь оно измеряется вдоль y ) будут меняться в зависимости от характера проблемы, то есть направления момента — по какой оси находится луч. сгибаясь? Мы основывали наши обозначения на изображении изогнутой балки на первом изображении этого урока.
Помните, в начале раздела я упомянул, что изгиб и кручение на самом деле очень похожи? На самом деле мы очень ясно видим это в последнем уравнении. В обоих случаях напряжение (нормальное для изгиба и сдвиговое для кручения) равно пар/момент ( M для изгиба и T для кручения), умноженных на положение вдоль поперечного сечения. , , потому что напряжение неравномерно по поперечному сечению (с декартовыми координатами для изгиба и цилиндрическими координатами для кручения), все делится на секундный момент площади сечения.
Сводка
На этом уроке мы узнали о моментах площади и диаграммах момента сдвига . Из первого момента площади поперечного сечения мы можем вычислить центроид . Мы узнали, как вычислить секундный момент площади в декартовых и полярных координатах, и мы узнали, как теорема о параллельной оси позволяет нам вычислить второй момент площади относительно центра тяжести объекта — это полезно для разделения сложного поперечного сечения на несколько простых фигур и объединение их вместе. Мы пересмотрели концепцию диаграммы сдвига и момента из статики. Эти диаграммы будут необходимы для определения максимальной силы сдвига и изгибающего момента вдоль сложно нагруженной балки, что, в свою очередь, потребуется для расчета напряжений и прогнозирования разрушения. Наконец, мы узнали о нормальном напряжении от изгиба балки. И напряжение, и деформация изменяются по поперечному сечению балки, при этом одна поверхность растягивается, а другая сжимается.
 Плоскость, проходящая через центр тяжести, образует нейтральную ось — вдоль нейтральной оси нет напряжений или деформаций. Напряжение является функцией приложенного момента и второго момента площади относительно оси, вокруг которой находится момент.
Плоскость, проходящая через центр тяжести, образует нейтральную ось — вдоль нейтральной оси нет напряжений или деформаций. Напряжение является функцией приложенного момента и второго момента площади относительно оси, вокруг которой находится момент.Этот материал основан на работе, поддержанной Национальным научным фондом в рамках гранта № 1454153. Любые мнения, выводы и выводы или рекомендации, выраженные в этом материале, принадлежат авторам и не обязательно отражают точку зрения Национальный научный фонд.
Изгибающий момент: лучшие уравнения, которые нужно знать (бесплатный калькулятор)
В этой статье мы обсудим концепции, связанные с изгибающим моментом. Мы также предоставляем уравнения и калькуляторы для распространенных конфигураций балок.
Почему важен изгибающий момент?
Конструкция конструкций учитывает воздействие нагрузки. Поэтому для сохранения устойчивости конструкций решающее значение имеет сопротивление изгибающему моменту .
 Примерами нагрузок могут быть, например, динамическая нагрузка (люди или объекты в здании), статическая нагрузка (вес самой конструкции) и нагрузки от окружающей среды (снеговая нагрузка, ветровая нагрузка и землетрясения). Повреждение может произойти из-за изгиба, когда напряжение изгиба превышает предел прочности элемента.
Примерами нагрузок могут быть, например, динамическая нагрузка (люди или объекты в здании), статическая нагрузка (вес самой конструкции) и нагрузки от окружающей среды (снеговая нагрузка, ветровая нагрузка и землетрясения). Повреждение может произойти из-за изгиба, когда напряжение изгиба превышает предел прочности элемента.Грузоподъемность в зависимости от спроса
Постоянные и временные нагрузки действуют на конструкции одновременно, изменяя взаимодействие всех их компонентов. В результате, проектируя структуру для обеспечения оптимальной устойчивости, инженеры должны учитывать и то, и другое. Способность балки выдерживать нагрузку — это вычисление, которое помогает определить общую прочность конструкции здания. Поскольку ни один материал не может выдержать бесконечную нагрузку, инженеры рассчитывают «изгибающий момент» с учетом внешних сил .
Внешние силы
Три силы влияют на расчетные параметры нагрузки:
- Сжатие происходит, когда частицы вещества прижимаются друг к другу, укорачивая или сжимая их.
 Сжатие обычно применяется сверху конструкции. Узнайте больше о сжатии и его последствиях в этой статье: Потеря устойчивости колонны
Сжатие обычно применяется сверху конструкции. Узнайте больше о сжатии и его последствиях в этой статье: Потеря устойчивости колонны - Растяжение — это полная противоположность сжатия; при растяжении материал тянется силами тяги. Балка находится под растягивающей нагрузкой, когда балка выходит из строя в верхней части.
- Сила скручивания, действующая на конструктивную часть, известна как кручение.
Вышеупомянутые три напряжения всегда присутствуют в конструкциях. Например, предположим, что вы прогуливаетесь по второму этажу дома. Затем ваш вес будет сжимать балки, поддерживающие пол. Следовательно, балки вверху сжимаются, а внизу растягиваются. Это создает изгибающий момент. Кроме того, срезное полотно удерживает балки вместе. В заключение, структура дома должна быть в состоянии сбалансировать все эти нагрузки, чтобы сохранить структурную целостность.
Что такое изгибающий момент?
Мера эффекта изгиба из-за приложенной к элементу конструкции поперечной силы называется изгибающим моментом.
 Таким образом, в проектировании конструкций изгибающий момент является важным элементом при проектировании конструкций. В противном случае было бы трудно понять поведение элементов конструкции при приложении поперечной нагрузки. Как упоминалось ранее, конструкция конструкции удерживает максимальные пределы изгиба конструкции в допустимых пределах. Однако при превышении пределов изгиба или сдвига конструкция не сможет сохранить свою устойчивость и в конечном итоге приведет к ее разрушению.
Таким образом, в проектировании конструкций изгибающий момент является важным элементом при проектировании конструкций. В противном случае было бы трудно понять поведение элементов конструкции при приложении поперечной нагрузки. Как упоминалось ранее, конструкция конструкции удерживает максимальные пределы изгиба конструкции в допустимых пределах. Однако при превышении пределов изгиба или сдвига конструкция не сможет сохранить свою устойчивость и в конечном итоге приведет к ее разрушению.Визуализация изгибающих моментов на балке, подвергнутой двухосному изгибу.
Как рассчитывается изгибающий момент
Когда поперечная сила прикладывается к секции балки, возникающие напряжения называются напряжениями изгиба. Следовательно, приложенные силы вызывают изгибающий момент, который обычно измеряется как сила x расстояние (кН-м). При измерении изгиба сила должна быть перпендикулярна плечу момента . Балка является наиболее распространенным конструктивным элементом, подверженным изгибающим моментам, так как под нагрузкой она может изгибаться в любой точке по своей длине.
 Несмотря на различия в процессах, балка может разрушиться из-за касательных напряжений до разрушения изгиба. В этом случае изгибающая сила заставит балку вращаться вокруг точки поворота, если точка поворота не ограничена должным образом. Таким образом, точка, в которой возникает максимальный изгибающий момент, важна для расчета конструкции на изгиб.
Несмотря на различия в процессах, балка может разрушиться из-за касательных напряжений до разрушения изгиба. В этом случае изгибающая сила заставит балку вращаться вокруг точки поворота, если точка поворота не ограничена должным образом. Таким образом, точка, в которой возникает максимальный изгибающий момент, важна для расчета конструкции на изгиб.Вывод уравнения изгибающего момента
Чтобы полностью понять контекст изгибающих моментов, мы должны изучить поперечное сечение балки при изгибе.
Дискретная полоса напряжения изгиба
Иллюстрация распределения напряжения по сечению при изгибе. Источник: Университет Аризоны
Из рисунка видно, что внутренние напряжения статически эквивалентны внешним силам и моментам. Во-первых, рассмотрим силу дФ , действующую на полосу площадью дА . Развиваемое напряжение σ будет равно
Следовательно, момент M будет задан как
Здесь y — расстояние силы от нейтральной оси (т.
 на луче). Впоследствии, чтобы получить максимальное напряжение в крайней волокне, fb , мы можем использовать тригонометрический прием:
на луче). Впоследствии, чтобы получить максимальное напряжение в крайней волокне, fb , мы можем использовать тригонометрический прием:Напряжения изгибающего момента, возникающие в поперечном сечении.
Из подобия треугольников на рисунке выше мы можем получить
Преобразование приведенного выше уравнения
Где c — расстояние от нейтральной оси до вершины поперечного сечения, fbmax — максимальное напряжение на краю волокна, а σ — изгибные напряжения на полосе на расстоянии.
Интегрирование напряжения изгиба
Теперь мы можем подставить это в первое уравнение. Однако в начале вывода уравнения предполагалась одна полоса поперечного сечения. Чтобы включить все сечение, берется интегрирование;
Здесь мы определяем, что определение второго момента площади I можно использовать для упрощения уравнения.
Переставить для fbmax (Напряжение при изгибе)
Таким образом, напряжение fb на любом расстоянии, y от нейтральной оси будет
Мы также можем написать
Раздел S Y .

Допущения
Обратите внимание, что приведенный выше вывод уравнений изгибающего момента основан на следующих допущениях:
- Во-первых, балка является линейной и имеет однородную площадь поперечного сечения до приложения напряжений.
- Во-вторых, изгибающий момент возникает внутри продольной плоскости симметрии балки.
- В-третьих, балка подвергается чистому изгибу (изгибающий момент не изменяется по длине).
- Наконец, материал, используемый в балке, является однородным и изотропным.
Вам понравился этот пост? Подпишитесь, и каждый месяц мы будем присылать вам еще больше таких замечательных постов.
Уравнения изгибающего момента
Разделы ниже содержат конфигурацию балки вместе с приложенной нагрузкой и формулами для расчета максимального изгибающего момента .
Консоли
В этом подразделе мы рассмотрим различные конфигурации нагрузки консольных балок.
Консоль – Точечная нагрузка на конце
Защемленная балка с вертикальной точечной нагрузкой на конце будет иметь максимальный момент на опоре.
 Чтобы проиллюстрировать это, см. диаграмму моментов и уравнение ниже.
Чтобы проиллюстрировать это, см. диаграмму моментов и уравнение ниже.Уравнение и диаграмма
Диаграмма изгибающего момента консоли – точечная нагрузка на конце
Калькулятор
Следуя приведенному выше уравнению, используйте этот калькулятор для расчета максимального момента консольной балки длиной L , подвергаемой точечной нагрузке P в конце.
Консоль – равномерно распределенная нагрузка
Как и в приведенной выше конфигурации, защемленная балка с равномерно распределенной нагрузкой будет иметь максимальный момент на опоре. Чтобы проиллюстрировать это, см. диаграмму моментов и уравнение ниже.
Уравнение и диаграмма
Диаграмма изгибающего момента консоли — равномерно распределенная нагрузка
Калькулятор
Следуя приведенному выше уравнению, используйте этот калькулятор для расчета максимального момента консольной балки длиной L , подвергаемой точечной равномерно распределенной нагрузке д .

Консоль – треугольная распределенная нагрузка
Как и в приведенной выше конфигурации, защемленная балка с треугольной распределенной нагрузкой будет иметь максимальный момент на опоре. Чтобы проиллюстрировать это, см. диаграмму моментов и уравнение ниже.
Уравнение и диаграмма
Диаграмма изгибающего момента консоли – треугольная распределенная нагрузка
Калькулятор
Следуя приведенному выше уравнению, используйте этот калькулятор для расчета максимального момента консольной балки длиной L , подвергаемой точечной треугольной распределенной нагрузке д .
Консоль – конечный момент
Защемленная балка с моментной нагрузкой на конце будет иметь постоянный момент по всей балке. Чтобы проиллюстрировать это, см. диаграмму моментов и уравнение ниже.
Уравнение и диаграмма
Диаграмма изгибающего момента Консоль – конечный момент
Калькулятор
Следуя приведенному выше уравнению, используйте этот калькулятор для расчета максимального момента консольной балки длиной L , подвергаемой мгновенной нагрузке M0 в конец.

Просто поддерживаемые балки
В этом подразделе мы рассмотрим различные конфигурации нагрузки свободно опертых балок. Другими словами, балки с одним концом на штифтах, а другой конец на ролике.
Просто поддерживаемая — промежуточная нагрузка
Теперь, если мы посмотрим на свободно опертые балки, общая конфигурация — это конфигурация с точечной нагрузкой на расстоянии a от первой опоры.
Уравнение и диаграмма
Диаграмма изгибающего момента Просто опертая – промежуточная нагрузка
Калькулятор
Следуя приведенному выше уравнению, используйте этот калькулятор для расчета максимального момента свободно опертой балки общей длиной a + b , подверженной точечная нагрузка P расположен на расстоянии a от опоры.
П: а: б: Простая опора – нагрузка в центре
Простая балка с точечной нагрузкой в центре.
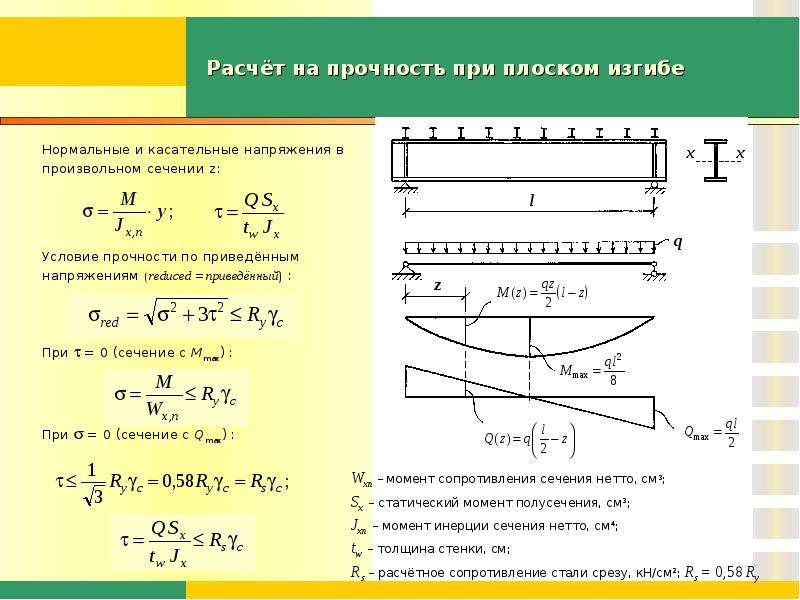 Максимальный момент возникает там, где приложена точечная нагрузка.
Максимальный момент возникает там, где приложена точечная нагрузка.Уравнение и диаграмма
Диаграмма изгибающего момента Свободно опертый — нагрузка в центре
Калькулятор
Следуя приведенному выше уравнению, используйте этот калькулятор для расчета максимального момента свободно опертой балки длиной L , подвергаемой точечной нагрузке P в центре.
Просто опертая – две точечные нагрузки на равном расстоянии от опор
Просто опертая балка с двумя точечными нагрузками на равном расстоянии от опор. Максимальный момент возникает между двумя точечными нагрузками.
Уравнение и диаграмма
Диаграмма изгибающего момента для свободно опертой балки — две точечные нагрузки на равном расстоянии от опор
Калькулятор
Следуя приведенному выше уравнению, используйте этот калькулятор для расчета максимального момента свободно опертой балки длиной L две точечные нагрузки на равном расстоянии и от опор.
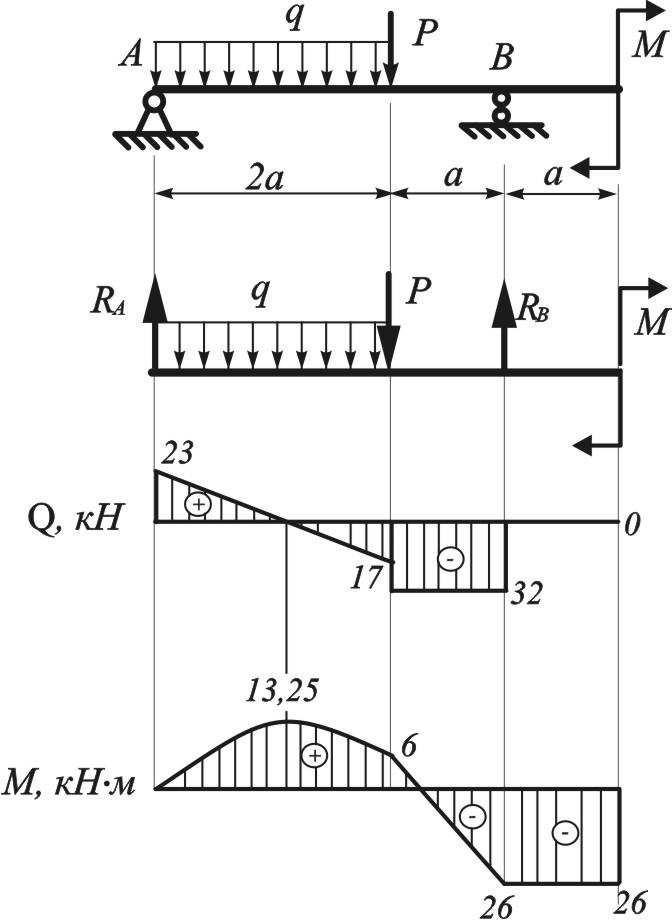
Просто опертая – равномерно распределенная нагрузка
Просто опертая балка с равномерно распределенной нагрузкой. Максимальный момент возникает в центре балки.
Уравнение и диаграмма
Диаграмма изгибающего момента Просто опертая – равномерно распределенная нагрузка
Калькулятор
Следуя приведенному выше уравнению, используйте этот калькулятор для расчета максимального момента свободно опертой балки длиной L , подверженной равномерно распределенной нагрузке нагрузка q .
Просто опертая – момент на каждой опоре
Просто опертая балка с двухточечной моментной нагрузкой на каждом конце. Момент постоянен по длине балки.
Уравнение и диаграмма
Диаграмма изгибающего момента Просто опертая – момент на каждой опоре
Калькулятор
Следуя приведенному выше уравнению, используйте этот калькулятор для расчета максимального момента свободно опертой балки длиной L , подверженной действию двух моментов нагрузки M0 на концах.

Просто опертая – момент на одной опоре
Просто опертая балка с моментной нагрузкой на одну опору. Диаграмма момента имеет треугольную форму, где максимальный момент возникает там, где приложен момент.
Уравнение и диаграмма
Диаграмма изгибающего момента Просто опертая – момент на одной опоре
Калькулятор
Следуя приведенному выше уравнению, используйте этот калькулятор для расчета максимального момента свободно опертой балки длиной L , подверженной одному моменту нагрузка M0 на одном конце.
Свободно опертая, момент в средней точке
Свободно опертая балка с моментной нагрузкой, приложенной в центре. Максимальный момент будет в центре.
Уравнение и диаграмма
Диаграмма изгибающего момента Просто опертая, момент в средней точке
Калькулятор
Следуя приведенному выше уравнению, используйте этот калькулятор для расчета максимального момента свободно опертой балки длиной L , подверженной одному моменту нагрузки M0 в центре.

Заключение по изгибающему моменту
В заключение, изгибающий момент — это реакция, возникающая в элементе конструкции, когда на него действует внешняя сила или момент, вызывающий его изгиб. Балка является наиболее типичным или простейшим элементом конструкции, подверженным действию изгибающих моментов.
Чтобы проиллюстрировать это далее, рассмотрим момент (силу) на локте. Как упоминалось ранее в статье, момент прямо пропорционален плечу рычага. Точно так же он играет важную роль в определении параметров конструкции консольных конструкций. Если момент превышает расчетную прочность конструкции или любого другого компонента из-за чрезмерной нагрузки, она может разрушиться. Разрушение башен Всемирного торгового центра произошло из-за увеличения количества соединений, вызванных сильным жаром пожаров. При изменении моментов в конструкции передача усилий на другие элементы, соединения и узлы общей системы становится неуправляемой, что может привести к отказу.
Наконец, в наши дни инженеры проектируют конструкции с помощью программного обеспечения для получения точных и быстрых результатов.
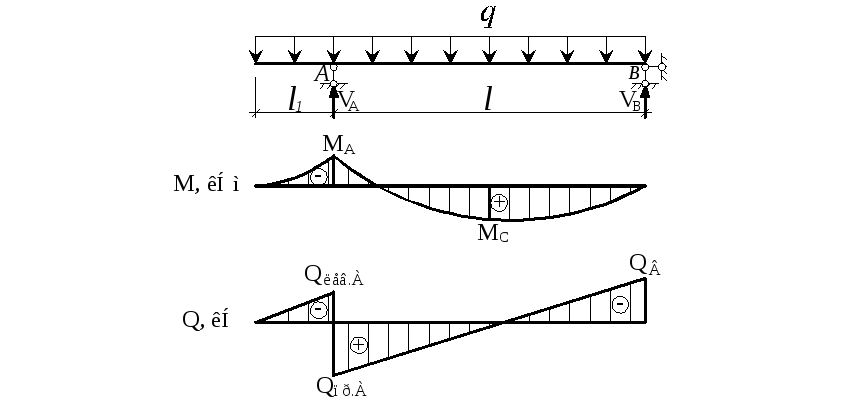 Например, Tribby3d — облачное программное обеспечение для загрузки конструкций. Используя tribby3d, инженеры могут легко рассчитать площади притоков и нагрузку на элементы различных типов, таких как колонны и стены. Затем результаты можно экспортировать в различные выходные файлы, такие как Excel и AutoCAD.
Например, Tribby3d — облачное программное обеспечение для загрузки конструкций. Используя tribby3d, инженеры могут легко рассчитать площади притоков и нагрузку на элементы различных типов, таких как колонны и стены. Затем результаты можно экспортировать в различные выходные файлы, такие как Excel и AutoCAD.Tribby3d — это облачное инженерное программное обеспечение, которое может вычислять загрузку элементов.
Похожие статьи
Изгиб балки
Введение
На этой странице рассматривается классическая теория изгиба балки, которая
является важным фактором почти во всех структурных проектах и
анализы. Хотя это менее очевидно, это также относится к изгибу колонны.
также. И это на самом деле второй мотив этого
страницу, чтобы заложить основу для предстоящего обсуждения теории потери устойчивости колонны.Цель здесь не в том, чтобы охватить все аспекты изгиба балки. Особенно,
такие темы, как определение нейтральной оси, теорема о параллельной оси и
расчет отклонений балки не рассматривается.
Радиус кривизны
Радиус кривизны является основным для изгиба балки, поэтому он будет
рассмотрел здесь. Обычно обозначается греческой буквой \(\rho\),
и может рассматриваться как радиус круга, имеющего ту же кривизну, что и
часть графика, кривая дороги или любой другой путь.
Когда путь прямой, \(\rho\) бесконечен, а когда путь имеет острый
кривая в нем, \(\rho\) мала.Нам понадобится аналитическое выражение для радиуса кривизны,
поэтому он будет развиваться здесь. Начните с любой функции \(y = y(x)\), как
показано на рисунке. Напомним, что длина дуги \(s\) связана с
\(\rho\) через \(\rho \, \theta = s\), где \(\theta\) — угол
дуги. В дифференциальной форме это \(\rho\, d\theta = ds\).
Теперь разделите обе части на \(dx\).
9{3/2} }
\]
Любопытно, что любое выражение, включающее радиус кривизны, кажется, всегда содержит
появляются в знаменателе. И это не исключение, даже если это
определяющее уравнение.Также интересен тот факт, что многие механические приложения связаны с изгибом,
но в малых масштабах. Обсуждаемый здесь изгиб балки не является исключением. В таких случаях,
Обсуждаемый здесь изгиб балки не является исключением. В таких случаях,
наилучший подход состоит в том, чтобы определить ось x вдоль луча таким образом, чтобы
\(y\) отклонения и, что более важно, деформированный наклон, \(y’\), будут
оба быть маленькими. Если \(y’ \lt \lt 1\), то \(y’\) можно пренебречь в приведенном выше уравнении.
Это дает гораздо более простое выражение.
93}
\]
, где \({\bf v}\) — вектор, определяемый параметрически как \({\bf v} = {\bf v}(x(t), y(t), z(t))\),
\({\bf v’}\) — его первая производная, \({\bf v»}\) — его вторая производная, и
\(|…|\) представляет длину вектора, т. е. квадратный корень из суммы
квадраты его компонентов.Деформация изгиба
Напомним, что длина дуги \(L\) связана с радиусом кривизны \(\rho\) через
\(L = \rho\, \theta\), где \(\theta\) — угол.Все становится сложнее, когда принимается во внимание толщина.
На рисунке ниже объект начальной длины \(L_o\) изогнут
как показано. Поскольку он имеет конечную толщину, различные его части растягиваются,
Поскольку он имеет конечную толщину, различные его части растягиваются,
или сжатые, разные количества. Внешняя часть балки
растянута больше всего, потому что находится дальше всего от
тот центр. Математически все части согнуты под одним и тем же углом \(\theta\),
но \(\rho\) варьируется по толщине, поэтому количество \(\rho\, \theta\)
тоже меняется, а значит, и \(L\) меняется.Следующий шаг — принять сознательное решение, чтобы избежать путаницы, связанной с наличием множества
различные радиусы кривизны по толщине изогнутого объекта. Это
осуществляется в два этапа.Сначала найдите тот \(\rho\), который удовлетворяет \(\rho \, \theta = L_o\). Обратите внимание, что
\(\rho\) — это вычисляемый результат, а \(\theta\) и \(L_o\) — входные данные.
Обратите также внимание, что длина в уравнении равна \(L_o\), исходной, недеформированной длине,
не деформированный. Этот шаг устанавливает одно уникальное значение \(\rho\) для
поперечное сечение, а не иметь несколько значений, что может привести к большой путанице.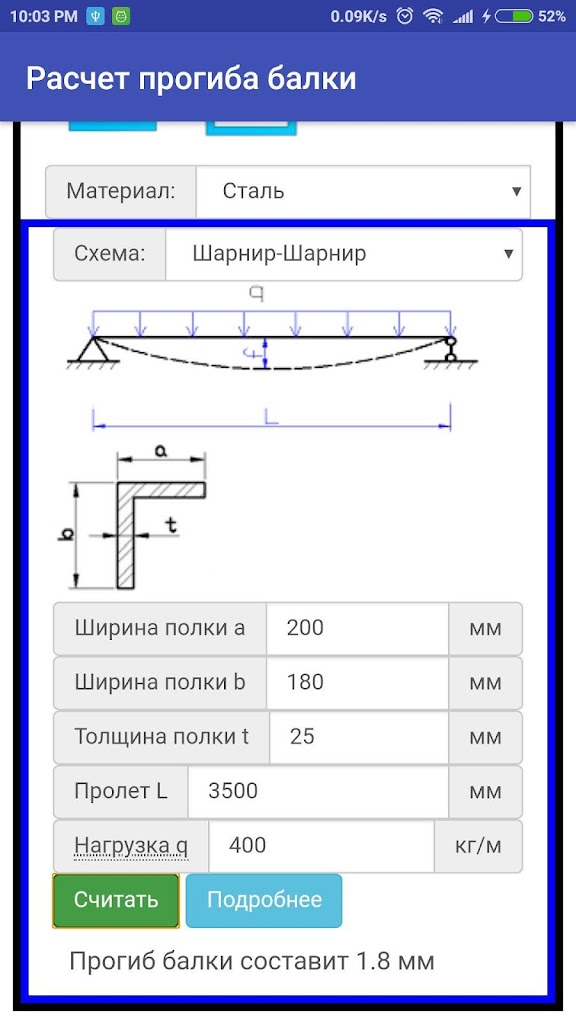
Нейтральная ось
Место в поперечном сечении, где \(\rho\, \theta = L_o\) известно
как нейтральная ось . Это единственное место, где окончательная деформированная длина
такая же, как исходная недеформированная длина, поэтому растяжения не происходит…
из-за изгиба. Не предполагайте, что нейтральная ось должна быть посередине.
поперечного сечения объекта. Это не обязательно так, особенно
если объект состоит из разных материалов с разными
жесткость.Оговорка «из-за изгиба» в предыдущем абзаце присутствует, потому что объект
также может быть одновременно нагружен растяжением (или сжатием), что растягивает его
пока каждая точка в его поперечном сечении не станет длиннее (или короче, если сжато), чем
исходная длина, \(L_o\).Второй шаг состоит в том, чтобы ввести переменную \(y\) как расстояние от нейтральной оси
до любого другого радиуса в поперечном сечении, как показано на рисунке ниже.
В результате радиус кривизны при любом
\(y\) равно \((\rho — y)\), а окончательная длина в любой точке \(y\) определяется выражением\[
L = (\rho — y) \тета
\]
Напомним, что \(L_o = \rho \, \theta\). Теперь деформация \(\эпсилон\) может быть выражена как\[
\epsilon_x = {L — L_o \over L_o} = { (\rho — y) \theta — \rho \, \theta \over \rho \, \theta}
\]
, который упрощается до\[
\epsilon_x = — {y \over \rho}
\]
Это ключевой результат деформации объекта. Он показывает, что деформация равна нулю при \(y=0\),
нейтральной оси и линейно изменяется от нее. Если объект толстый, то \(y\) может принимать
на больших значениях, а на тонких объектах — нет. Именно поэтому толстые объекты
обладают большей жесткостью на изгиб, чем тонкие предметы.Кроме того, радиус кривизны в знаменателе объясняет многие эффекты изгиба.
Когда объект не согнут, то \(\rho\) бесконечно, и деформации, естественно, равны нулю.
Когда объект изгибается, \(\rho\) уменьшается, и уравнение показывает, что деформации будут увеличиваться.
Наконец, обратите внимание, что деформация нормальная деформация и на самом деле является продольной,
по длине балки. Обычно ось \(x\) выравнивают вдоль
длина балки, создающая деформацию \(\epsilon_x\).Напряжение при изгибе
Теперь, когда у нас есть выражение для напряжения, разработка выражения для напряжения уже невозможна.
будь проще. Умножьте деформацию на \(E\), модуль упругости,
чтобы получить стресс, \(\sigma_x\).\[
\sigma_x = — {E \, y \over \rho}
\]
Хотя этот шаг был невероятно простым, на самом деле он довольно глубок в том, что
пренебрегали простотой. Напомним со страницы на
Закон Гука, согласно которому каждый компонент нормального напряжения
зависит от всех трех компонентов нормальной деформации. Но здесь у нас просто
умножил деформацию на \(E\), чтобы получить напряжение. Этот шаг имеет ключевое предположение
встроены в него… что на балку не действуют боковые нагрузки/напряжения.
В таких случаях уравнения «срабатывают» так, что \(\sigma_x = E \, \epsilon_x\), как в
одноосное растяжение. Это происходит в большинстве балок, потому что они тонкие по сравнению с
их длина.92) } \epsilon_x
\]
, где \(\nu\) — коэффициент Пуассона материалов. Понятно, что напряжение для данного
деформация в этом случае выше, чем при классическом одноосном растяжении.Изгибающие моменты и напряжения
Изгибающий момент \(M_z\) в поперечном сечении из-за поля напряжений вычисляется по формуле
\[
М_з \; знак равно \int_A r \times dF \; знак равно — \int_A y \, \sigma_x dA
\]
, где \(y\) — плечо момента, а \(\sigma_x dA\) — сила.92 дА
\]
Всегда помните, что значения \(y\) отсчитываются от нейтральной оси, что
соответствует \(y = 0\).Уравнение изгибающего момента теперь можно записать в виде
\[
M_z = {E \, I_{zz} \over \rho}
\]
, что является очень важным уравнением.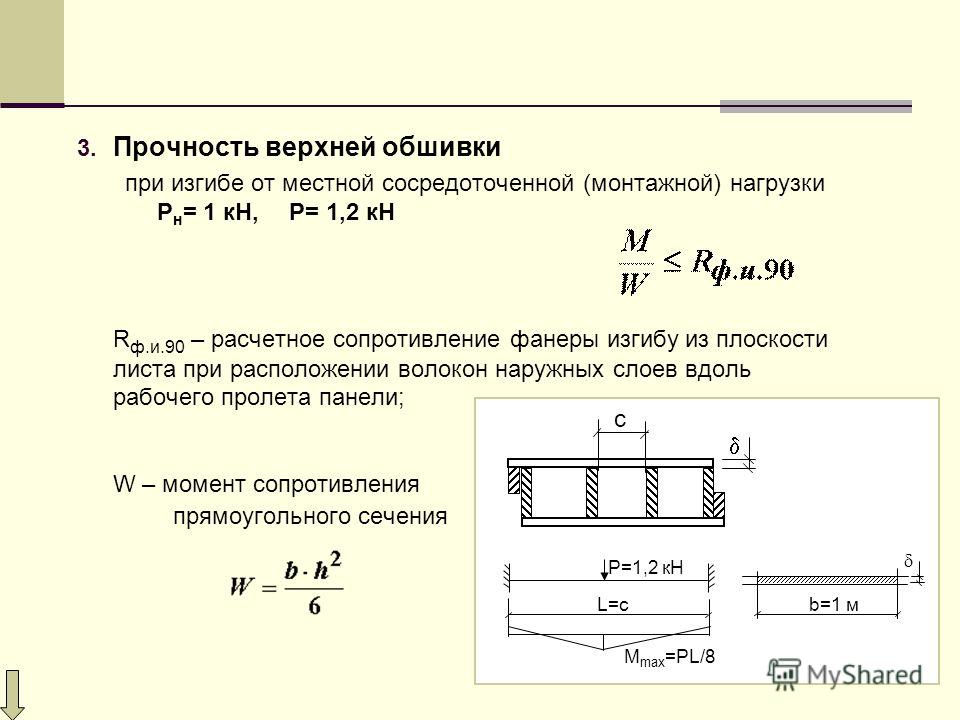
Малый изгиб Приблизительно
Напомним, что мы обсуждали ранее, что
когда уровень изгиба мал и \(y’ \lt \lt 1\), то \(\rho\) может быть близко
аппроксимируется \(y»\). Это дает\[
M_z = E \, I_{zz} y» \qquad (\text{когда} \;\; y’ \lt \lt 1)
\]
, что является еще одним очень важным и полезным уравнением.Теперь… вернитесь к этим двум уравнениям
\[
M_z = {E \, I_{zz} \over \rho} \qquad \qquad \text{and} \qquad \qquad \sigma_x = — {E \, y \over \rho}
\]
и узнайте, что оба содержат \( E / \rho\). Решение каждого уравнения для этого отношения дает\[
{E \over \rho} = {M_z \over I_{zz} } \qquad \qquad \text{and} \qquad \qquad {E \over \rho} = -{y \over \sigma_x}
\]
Итак, приравняйте два уравнения, чтобы получить одно из самых известных уравнений в машиностроении.\[
\sigma_x = — {M_z \, y \over \; I_{zz} }
\]Трехмерная гибка
Полный трехмерный изгиб включает в себя отклонения в двух направлениях, \(y\) и \(z\).
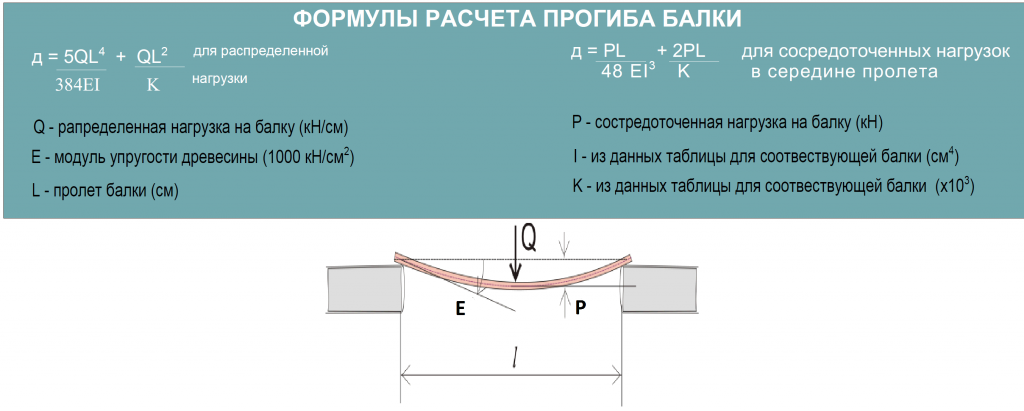 Напряжение,
Напряжение,
\(\epsilon_x\), теперь зависит от обеих координат.\[
\epsilon_x = {z \over \rho_y} — {y \over \rho_z}
\]
Умножьте на \(E\), чтобы получить напряжение.\[
\sigma_x = {E \, z \над \rho_y} — {E \, y \над \rho_z}
\]
92 dA — {E \over \rho_y} \int_A y \, z \, dA
\\
\\
\\
& & & = & {E \over \rho_z} I_{zz} — {E \over \rho_y} I_{yz}
\end{эквнаррай}
\]
Уравнения можно компактно записать в матричной форме как\[
\оставил\{
\матрица {
Мой
\\
\\
M_z
}
\Правильно\}
знак равно
\оставил[
\матрица {
\; I_{yy} и -I_{yz} \\
\\
-I_{yz} & \; I_{zz}
}
\Правильно]
\оставил\{
\матрица {
Е / \rho_y
\\
\\
E / \rho_z
}
\Правильно\}
\]
Это показывает, что момент инерции на самом деле является тензором.
92\).Наконец, если \(I_{yz} = 0\), все значительно упрощается до
\[
\sigma_x = {M_y \, z \над I_{yy} } — {M_z \, y \над I_{zz} }
\]Простой калькулятор луча | Calcresource
Прыжки до
-Калькулятор
-Фон
Соглашение
-Калькулятор
-Фон
-Введение
-Aspuction
-Согласование.
 равномерная распределенная нагрузка
равномерная распределенная нагрузка— Свободно опертая балка с точечной силой в середине
— Свободно опертая балка с точечной силой в произвольном положении
— Свободно опертая балка с точечным моментом
— Свободно опертая балка с треугольной нагрузкой
— Свободно опертая балка с трапецеидальная нагрузка
— Свободно опертая балка с распределением трапециевидной нагрузки в виде плиты
— Свободно опертая балка с частично распределенной равномерной нагрузкой
— Свободно опертая балка с частично распределенной трапециевидной нагрузкой
— Статьи по теме
Поделитесь этим
См. также
Калькулятор балки с простой опорой
— Д-р Минас Э. Лемонис, доктор философии — Обновлено: 11 мая 2022 г.
Инструмент рассчитывает статическую реакцию свободно опертых балок при различных сценариях нагружения. Инструмент рассчитывает и строит диаграммы для следующих величин:
- реакции
- изгибающие моменты
- поперечные силы сдвига
- прогибы
- уклоны
Учтите, что приняты допущения теории балки Эйлера-Бернулли, материал упругий и поперечное сечение постоянно на всем пролете балки (призматическая балка).
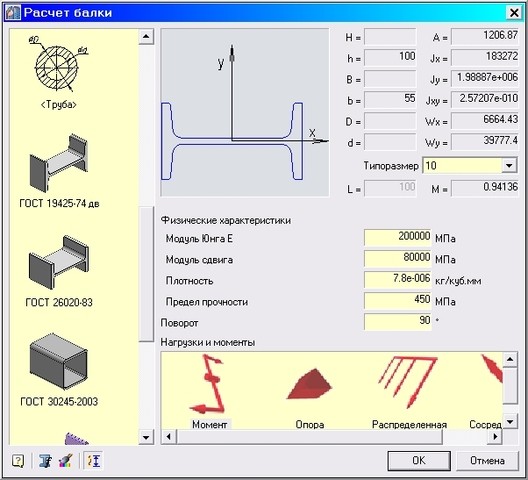
- Вместо этого переходите к теории и формулам!
Единицы:
Imperial
Метрика
0015
1 2 3 4 Structure
L =
mcmmmydftin Optional properties, required только для результатов отклонения/наклона:
E =
PakPaMPaGPapsiksiMpsi I3 =
4
Рассчитайте момент инерции балок различных сечений с помощью наших специальных калькуляторов.
ADVERTISEMENT
1 2 3 4 Imposed loading:
Uniform distributed loadUniform распр.  нагрузка (суммарная)Точечная нагрузка (по центру)Точечная нагрузкаТочечный моментТреугольная нагрузкаТрапециевидная нагрузкаТрапециевидная нагрузка (плита)Частичная равномерная нагрузкаЧастичная треугольная нагрузкаЧастичная трапециевидная нагрузка
нагрузка (суммарная)Точечная нагрузка (по центру)Точечная нагрузкаТочечный моментТреугольная нагрузкаТрапециевидная нагрузкаТрапециевидная нагрузка (плита)Частичная равномерная нагрузкаЧастичная треугольная нагрузкаЧастичная трапециевидная нагрузкаCalculate
1 2 3 4 Results:
Reactions:
R A =
KNNKGTLBFKIP R B =
KNNKGTLBFKIP KNNKGTLBFKIP .0015 Bending Moment:
M u =
kNmNmkg.mt.mlbf.ftlbf.inkip.ftkip.in x m =
McMmmydftin Поперечное сдвиг1403
mcmmmydftin Deflection:
d u =
mcmmmydftin x d =
mcmmmydftin Slopes
θ A =
Degradmrad θ B =
θ B =
θ B =
θ B0009 degradmrad
1 2 3 4 Request results at a specific point:
x =
mcmmmydftin M(x) =
kNmNmkg. 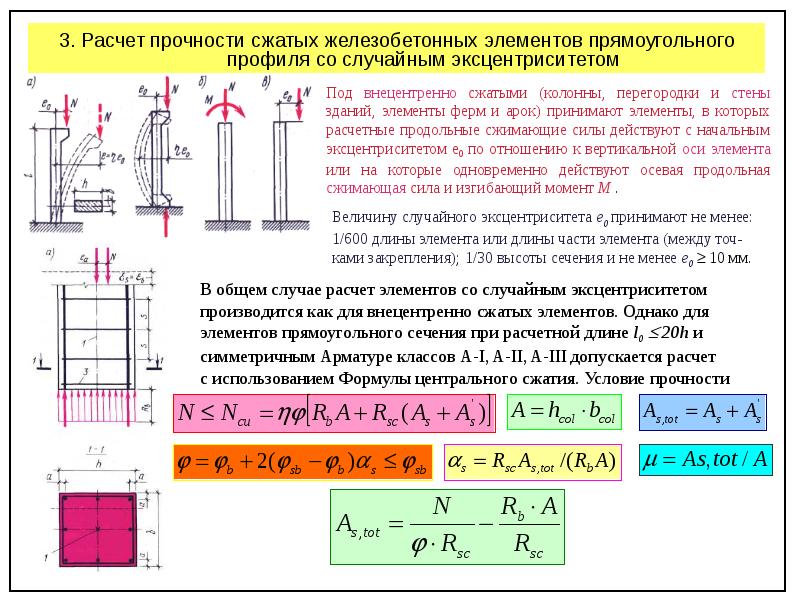 mt.mlbf.ftlbf.inkip.ftkip.in
mt.mlbf.ftlbf.inkip.ftkip.inV(x) =
kNNkgtlbfkip d(x) =
mcmmmydftin θ(x) =
degradmrad ADVERTISEMENT
1 2 Diagrams
kNmNmkg.mt.mlbf.ftlbf.inkip.ftkip.in kNNkgtlbfkip mcmmmydftin degradmrad kN/mN/mkg/mt/mlbf /ftlbf/inkip/ft Реклама
Верхние страницы
Поделитесь этим
Фон
Таблица Содержимо0003
— Обозначения
— Свободно опертая балка с равномерно распределенной нагрузкой
— Свободно опертая балка с точечной силой в середине
— Свободно опертая балка с точечной силой в произвольном положении
— Свободно опертая балка с точечным моментом
— Свободно опертая балка с треугольной нагрузкой
— Свободно опертая балка с трапециевидной нагрузкой
— Свободно опертая балка с трапециевидным распределением нагрузки плитного типа
— Свободно опертая балка с частично распределенной равномерной нагрузкой
— Свободно опертая балка с частично распределенной трапециевидной нагрузкой
— Статьи по теме
Введение
Свободно опертая балка является одной из самых простых конструкций.
 Он имеет только две опоры, по одной на каждом конце. Одна шарнирная опора и роликовая опора. Оба они препятствуют любому вертикальному движению, позволяя, с другой стороны, свободно вращаться вокруг себя. Роликовая опора также позволяет балке расширяться или сжиматься в осевом направлении, хотя другая опора препятствует свободному горизонтальному движению.
Он имеет только две опоры, по одной на каждом конце. Одна шарнирная опора и роликовая опора. Оба они препятствуют любому вертикальному движению, позволяя, с другой стороны, свободно вращаться вокруг себя. Роликовая опора также позволяет балке расширяться или сжиматься в осевом направлении, хотя другая опора препятствует свободному горизонтальному движению.Удаление любой из опор или вставка внутреннего шарнира превратит свободно опертую балку в механизм, который будет перемещаться без ограничений в одном или нескольких направлениях. Очевидно, что это нежелательно для несущей конструкции. Таким образом, свободно опертая балка не предлагает избыточности опор. Если произойдет локальный отказ, вся конструкция рухнет. Эти типы структур, которые не предлагают избыточности, называются критическими или определяющими 9.0580 конструкций. Напротив, конструкция, которая имеет больше опор, чем требуется для ограничения ее свободного движения, называется избыточной или неопределенной конструкцией.

РЕКЛАМА
Допущения
Статический анализ любой несущей конструкции включает оценку ее внутренних сил и моментов, а также ее прогибов. Как правило, для плоской конструкции с плоской нагрузкой интересующими внутренними воздействиями являются осевая сила N, поперечная поперечная сила V и изгибающий момент M. Для свободно опертой балки, которая воспринимает только поперечные нагрузки, осевая сила всегда ноль, поэтому им часто пренебрегают. Расчетные результаты на странице основаны на следующих предположениях: 9
- Материал линейно упругий )
- Сечение одинаковое по всей длине балки
- Прогибы малы
- Каждое поперечное сечение, изначально плоское и перпендикулярное к продольной оси, остается плоским и нормальным также к отклоненной оси. Это тот случай, когда высота сечения значительно меньше длины балки (в 10 и более раз), а также сечение не многослойное (не сэндвич-сечение).
Последние два предположения удовлетворяют кинематическим требованиям теории балки Эйлера-Бернулли, которая также принята здесь.
Правила знаков
Для расчета внутренних сил и моментов в любом сечении балки необходимо соблюдать правила знаков. Здесь приняты следующие значения:
- Осевая сила считается положительной, если она вызывает растяжение детали.
- Сила сдвига положительна, если она вызывает вращение детали по часовой стрелке.
- Изгибающий момент является положительным, когда он вызывает растяжение нижнего волокна балки и сжатие верхнего волокна.
Эти правила хоть и не обязательны, но достаточно универсальны. Другой набор правил, если им следовать последовательно, также приведет к тем же физическим результатам.
Символы
- E: модуль упругости материала (модуль Юнга)
- I: момент инерции поперечного сечения вокруг упругой нейтральной оси изгиба
- L: общий пролет балки
- R: опорная реакция
- d: прогиб
- M: изгибающий момент
- V: поперечная поперечная сила
- \theta: уклон
Свободно опертая балка с равномерной нагрузкой Нагрузка w распределяется по всему пролету балки, имея постоянную величину и направление.
 Его размеры представляют собой силу на длину. Суммарная сила, приложенная к балке, равна W=w L, где L — длина пролета. В зависимости от обстоятельств может быть указана либо общая сила W, либо распределенная сила по длине w. 93)}{24 E I}
Его размеры представляют собой силу на длину. Суммарная сила, приложенная к балке, равна W=w L, где L — длина пролета. В зависимости от обстоятельств может быть указана либо общая сила W, либо распределенная сила по длине w. 93)}{24 E I}
РЕКЛАМА
Свободно опертая балка с точечной силой посередине
Сила сосредоточена в одной точке, расположенной в середине балки. Однако на практике сила может быть распределена по небольшой площади, хотя размеры этой области должны быть существенно меньше длины пролета балки. В непосредственной близости от приложения силы ожидаются концентрации напряжений, в результате чего реакция, предсказываемая классической балочной теорией, может оказаться неточной. Однако это лишь локальное явление. По мере того, как мы удаляемся от места действия силы, результаты становятся достоверными в силу принципа Сен-Венана. 92)}{16 E I} &, x>L/2 \end{выровнено}\right.
где:
\acute{x}=L-x
Свободно поддерживаемая балка с точечной силой в произвольном месте
Сила сосредоточена в одной точке в любом месте поперек пролета балки. Однако на практике сила может быть распределена по небольшой площади. Однако для того, чтобы считать силу сосредоточенной, размеры области приложения должны быть существенно меньше длины пролета балки. В непосредственной близости от силы ожидаются концентрации напряжений, в результате чего реакция, предсказываемая классической балочной теорией, может оказаться неточной. Однако это лишь локальное явление, и по мере удаления от места действия силы расхождение результатов становится незначительным.
Однако на практике сила может быть распределена по небольшой площади. Однако для того, чтобы считать силу сосредоточенной, размеры области приложения должны быть существенно меньше длины пролета балки. В непосредственной близости от силы ожидаются концентрации напряжений, в результате чего реакция, предсказываемая классической балочной теорией, может оказаться неточной. Однако это лишь локальное явление, и по мере удаления от места действия силы расхождение результатов становится незначительным.
В следующей таблице представлены формулы, описывающие статическую реакцию простой балки на сосредоточенную точечную силу P, приложенную на случайном расстоянии a от левого конца.
Просто поддерживаемый луч с точечной нагрузкой в случайной позиции | |
|---|---|
| Количество | Формула |
| Реакции: | |
| . более L} | |
где: b=L-a \acute{x}=L-x | |
Свободно опертая балка с точечным моментом
, в любом месте на пролете балки. С практической точки зрения это может быть пара сил или элемент при кручении, соединенный вне плоскости и перпендикулярно балке.
В любом случае область приложения момента должна распространяться на небольшую длину балки, чтобы ее можно было успешно идеализировать как сосредоточенный момент в точке. Несмотря на то, что в непосредственной близости от области применения предсказанные результаты с помощью классической теории балок, как ожидается, будут неточными (из-за концентрации напряжений и других локализованных эффектов), по мере удаления предсказанные результаты совершенно достоверны, как заявил Святой — Принцип Венана.
В следующей таблице представлены формулы, описывающие статическую реакцию простой балки на сосредоточенный точечный момент M, приложенный на расстоянии a от левого конца.
просто поддерживается луч с точкой момента | |
|---|---|
| Количество | Формула |
| Реакции: | r_A rauds over ud over ud overs ud overs rabripe rauds rauds rauds rauds rauds rauds rauds rauds rauds rauds rauds rauds rauds rauds rauds rauds rauds 9000 9000 9000 9000 9000 9000 } |
| Концевые уклоны: 92}{2 E I} &, x>a\end{выровнено} \right. | |
где: b=L-a \acute{x}=L-x | |
Просто опертая балка с треугольной нагрузкой, однако, ее нагрузка не распределена по всему пролету
постоянна, но изменяется линейно, начиная с нуля на левом конце и заканчивая пиковым значением w_1 на правом конце. Размеры w_1 — это сила на длину. Суммарная сила, приложенная к балке, равна W={1\over2}w L, где L — длина пролета.
В следующей таблице представлены формулы, описывающие статическую реакцию простой балки на линейно изменяющуюся (треугольную) распределенную нагрузку, возрастающую слева направо.
Simply supported beam with linearly varying distributed load (triangular) | |
|---|---|
| Quantity | Formula |
| Reactions: | R_A={1\over6}w_1L R_B={ 1\over3}w_1L 94}{24EIL} |
где: C=\sqrt{15-\sqrt{120}}\left(\sqrt{15}+\sqrt{50}\right)\приблизительно 22,01237 | |
Свободно опертая балка с трапециевидной нагрузкой
Нагрузка распределяется по всему пролету балки и имеет линейно изменяющуюся величину, начиная с w_1 на левом конце и до w_2 на правом конце. Размеры w_1 и w_2 являются силой на длину. Суммарная сила, приложенная к балке, равна W={L\over2}(w_1+w_2), где L — длина пролета.
В следующей таблице представлены формулы, описывающие статическую реакцию простой балки трапециевидной формы на переменную распределенную нагрузку.
Simply supported beam with linearly varying distributed load (trapezoidal) | |
|---|---|
| Quantity | Formula |
| Reactions: | R_A={(2w_1+w_2)L\over6} R_B={(w_1+2w_2)L\over6} |
где: w_x=w_1+{(w_2-w_1)x\over L} | |
Опорная балка с трапециевидным распределением нагрузки характерны для балок по периметру плиты.
 Распределение имеет трапециевидную форму с максимальной величиной w внутри балки, а на двух ее концах она становится равной нулю. Размеры (\w\) представляют собой силу на длину. Суммарная сила, приложенная к балке, равна W=w (L-a/2-b/2), где L — длина пролета, а a, b — длины левой и правой сторон балки соответственно, где распределение нагрузки переменная (треугольная). 93
Распределение имеет трапециевидную форму с максимальной величиной w внутри балки, а на двух ее концах она становится равной нулю. Размеры (\w\) представляют собой силу на длину. Суммарная сила, приложенная к балке, равна W=w (L-a/2-b/2), где L — длина пролета, а a, b — длины левой и правой сторон балки соответственно, где распределение нагрузки переменная (треугольная). 93
Свободно опертая балка с частично распределенной равномерной нагрузкой
Нагрузка распределяется на часть пролета балки с постоянной величиной w, в то время как оставшийся пролет не нагружен. Размеры w представляют собой силу на длину. Суммарная сила, приложенная к балке, равна W=\left(L-a-b\right)w, где L — длина пролета, а a, b — ненагруженные длины левой и правой сторон балки соответственно.
В следующей таблице представлены формулы, описывающие статическую реакцию простой балки на частично распределенную равномерную нагрузку. 92}{2 E I} &,x\ge L-b \end{выровнено}\right.
Где:
\ aste {x} = L-X
X_A = X-A
L_W = L-A-B
. Проще говоря, с частично распределенной нагрузкой
. пролет балки, имеющий линейно изменяющуюся величину от w_1 до w_2, а оставшийся пролет разгружен. Размеры w_1 и w_2 являются силой на длину. Суммарная сила, приложенная к балке, равна W={L-a-b\over2}(w_1+w_2), где L — длина пролета, а a, b — ненагруженные длины левой и правой сторон балки соответственно.
Это самый общий случай. Формулы для частично распределенных равномерных и треугольных нагрузок могут быть получены путем соответствующей установки значений w_1 и w_2. Кроме того, соответствующие случаи для полностью загруженного пролета могут быть получены путем установки a и b равными нулю.
В следующей таблице представлены формулы, описывающие статическую реакцию простой балки на частично распределенную трапециевидную нагрузку.
Свободно опертая балка с частично распределенной линейно-переменной нагрузкой (трапециевидная) 93 |
|---|
Статьи по теме
Понравилась эта страница? Поделись с друзьями!
РЕКЛАМА
См. также
также
Бесплатный онлайн калькулятор луча | Civils.ai
Создание диаграмм изгибающих моментов, диаграмм поперечной силы и измерение прогиба для неопределенного пролета балки.
Рассчитайте изгибающий момент, поперечную силу, силы реакции и прогиб, используя свойства реального стального сечения.
Этот инструмент оптимизирован для настольного использования
Длина балки: 10,0 м
Второй момент площади: 473,0 см 4
Модуль Юнга: 210,0 ГПа
Загрузка…
Условия крепления неудовлетворительны, добавьте еще одно крепление.
Загрузка…
Макс. БМ:
Мин. BM:
Макс. SF:
Мин. SF:
Макс. отклонение:
Мин. отклонение:
Как работает этот анализ?
Введение
Балки бывают самых разных форм и размеров, понимание того, как рассчитать силы, действующие на конструкционную балку, может быть затруднено. Но здесь мы дадим вам краткое введение в теорию того, как они устроены. Начиная с теории напряжения балки .
Но здесь мы дадим вам краткое введение в теорию того, как они устроены. Начиная с теории напряжения балки .
Что такое напряжение балки и как рассчитать напряжение балки?
Когда мы прикладываем силу где-то вдоль пролета балки, мы создаем внутренние напряжения. Возникают два типа стресса:
- Нормальное напряжение: Возникает от сил, действующих по длине балки при сжатии или растяжении.
- Касательное напряжение: Возникает из-за сил, действующих параллельно направлению нагрузки.
Происхождение этих двух компонентов напряжения можно разделить на два компонента силы, которые мы называем Изгибающий момент и Поперечное усилие .
Виды внешней нагрузки
Простейшие нагрузки, прикладываемые к балке, можно разделить на три категории:
- Точечные нагрузки: Это сила, приложенная к одной точке балки.

- Распределенные нагрузки: Эта сила распределяется по определенной длине и действует как форма давления.
- Сосредоточенный момент: Это чистый момент, действующий на балку в заданном положении.
Типы опор
Простейшие опоры балки можно разделить на три категории:
- Штифтовая опора: Удерживает балку как в горизонтальном, так и в вертикальном направлениях, не ограничивая ее вращение.
- Роликовая опора: Опора, обеспечиваемая балке только в одном направлении, без ограничения изгиба или вращения.
- Фиксированная опора: Эти опоры обеспечивают фиксацию балки во всех направлениях и препятствуют вращению.
Диаграмма силы свободного тела
Чтобы найти силы, действующие на балку, мы должны следовать процессу построения диаграммы сил свободного тела.
Как рассчитать силы реакции опор на пролет балки?
Сначала мы рисуем балку в масштабе с указанием силовых составляющих приложенных нагрузок, а затем рассчитываем силы реакции опоры.
Для расчета реакций необходимо использовать уравнения равновесия для разрешения внешних сил:
- Σ Приложенные вертикальные силы = 0 кН
- Σ Приложенные горизонтальные силы = 0 кН
- Σ Прикладываемые моменты = 0 кНм
Существует два типа случаев при разрешении внешних условий балки:
- Статически определяемые: Где количество уравнений равно количеству неизвестных, и расчеты могут быть решены с помощью ручных вычислений в закрытой форме.
- Статически неопределимое: Когда количество неизвестных превышает количество уравнений, необходимо использовать более продвинутые методы, такие как теория сопротивления момента.
Как нарисовать диаграмму поперечной силы?
Чтобы создать диаграмму поперечной силы, вы работаете слева направо поперек балки, суммируя приложенные силы и реакции в каждой точке приложения.

 Удачи!
Удачи!
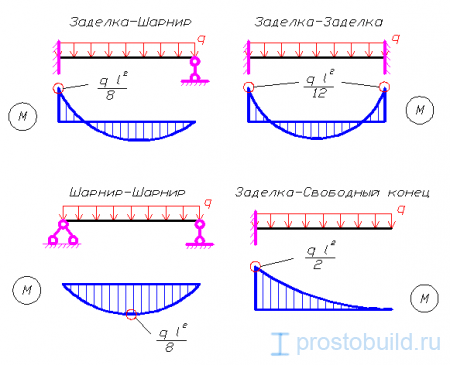

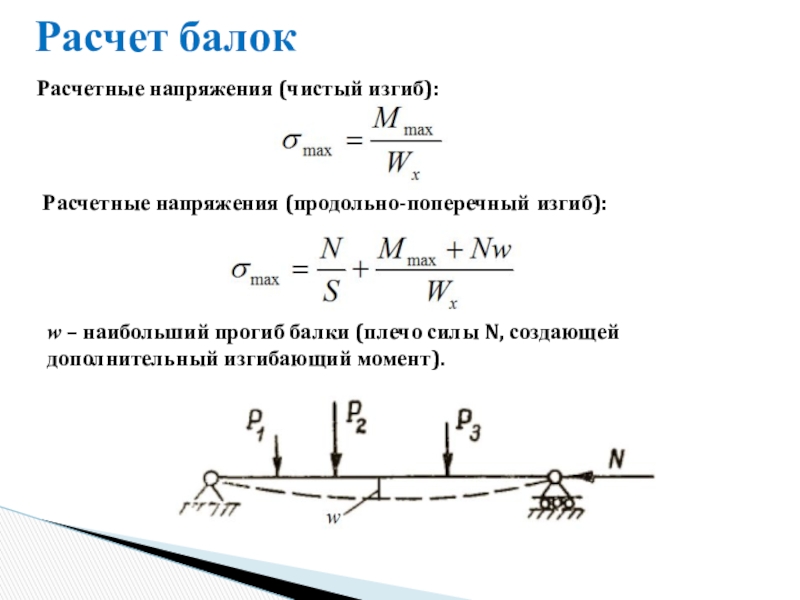 3}{6EI} &, x>a\end{выровнено} \right. 92}{2 E I} &, x>a\end{выровнено} \right.
3}{6EI} &, x>a\end{выровнено} \right. 92}{2 E I} &, x>a\end{выровнено} \right.