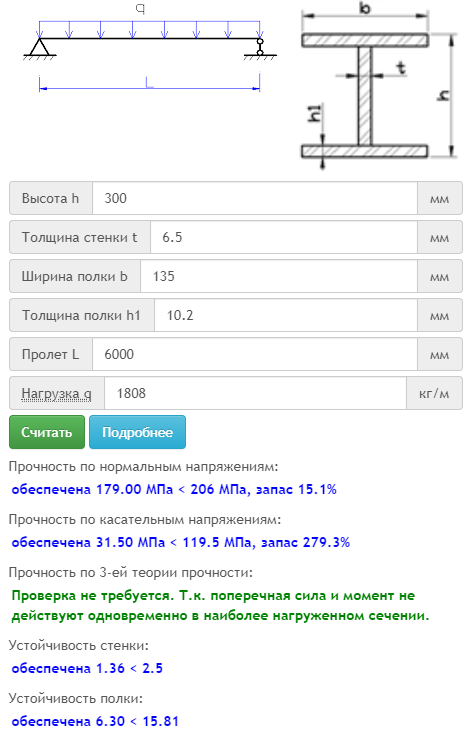
Расчет двутавра на прогиб калькулятор: Расчёт металлической балки онлайн (калькулятор)
Содержание
Калькулятор расчета деревянных балок перекрытия и стропильной системы!
Как пользоваться онлайн калькулятором расчета балок перекрытия и стропил
Чтобы правильно произвести прочностной расчет балки перекрытия и подобрать необходимый тип двутавровой балки, вы можете воспользоваться онлайн-калькулятором. На основе полученных вычислений можно точно рассчитать количество, необходимое для устройства стропильной системы или укладки лаг. Расчет деревянных балок перекрытия возможен только после того, как будет известно расстояние между стенами (расчетная длина балки). Кроме того, необходимо знание величины предполагаемой нагрузки на всю конструкцию.
Для межэтажных перекрытий, в том числе цокольного, используйте значение 400 кг/м2; для чердачного — 200 кг/м2 (или 250 кг/м2, если нагрузка от стропильной системы передается непосредственно на чердачное перекрытие). Для стропильной системы 220 кг/м2 для Московского региона, для других регионов принимайте значения в зависимости от снегового района.
Заказать бесплатный расчет балок по проекту или проконсультироваться у специалистов нашей компании можно по телефону
+7(495)105-91-63
+7(812)425-65-03
+7(843)207-04-92
+7(4722)77-73-16
+7(800)333-79-86
+7(421)240-08-29
+7(818)246-42-27
+7(861)212-30-63
+7(800)333-37-59
Так же Вы можете прислать чертежи для расчета на [email protected]
Онлайн калькулятор расчета деревянных балок перекрытия и стропил
Где используются балки
ПерекрытиеСтропила
Вам необходимо выбрать конструкцию, для которой вы будете использовать балки: будет ли это расчет перекрытий (применяются в качестве лаг) или стропильной системы (используются в качестве стропил).
Расчетная длина балки (м)
Длина при расчете перекрытия – это наибольший пролет, т.е. наибольшее расстояние между соседними стенами «в свету», на которые опирается балка.
Длина при расчете стропильной системы – это расстояние по скату кровли между двумя опорами.
Например, в двускатной кровле расчетной длиной будет считаться расстояние по скату от конька до мауэрлата (опоры на стену).
Измеряется в метрах (пример: 7.8 м).
Шаг балки (0.2 м – 1.2 м)
Шаг (понятие, используемое при расчете) – это межцентровое расстояние между балками. В перекрытии дома с черновым полом (настилом) из плитных материалов, таких как OSB-3, ЦСП, мы рекомендуем использовать шаг в 0.4 м (40 см). Это связано с прогибом самого плитного материала при большем шаге балок. При более сложном «пироге» перекрытия можно использовать любой другой шаг.
Измеряется в метрах (пример: 0.4 м).
Расчетная нагрузка (кг/м2)
Расчетной нагрузкой называется сумма временной и постоянной нагрузок. В СНиПе «Нагрузки и воздействия» расчетная нагрузка на перекрытие равна 400 кг/м2, на стропильную систему — 220 кг/м2. В частных случаях можно использовать другие значения.
Измеряется в килограммах на квадратный метр (пример: 400 кг/м2).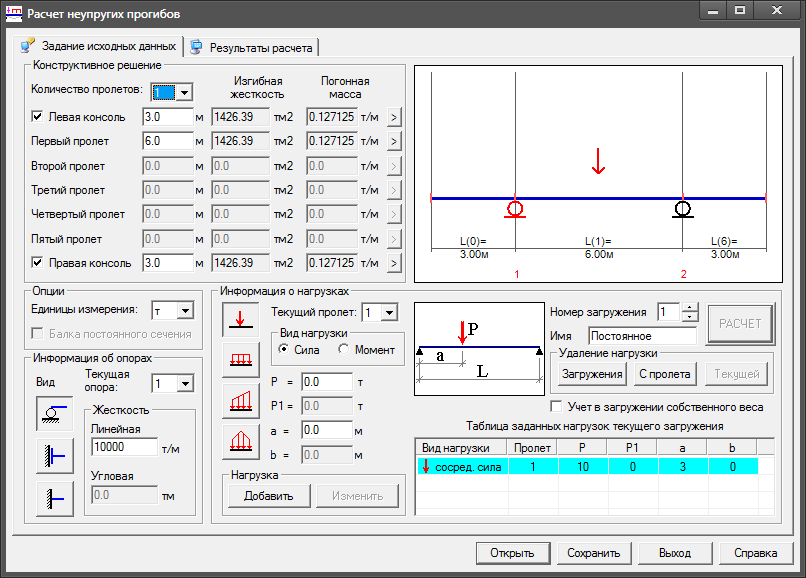
Отправить чертежи на бесплатный расчет
Узнать
цены на балки
Заказать
обратный звонок
Компания «ИнтерСити» производит износоустойчивые деревянные двутавры. Благодаря отличным эксплуатационным свойствам, изделия могут использоваться в различных конструкциях. Однако нужно помнить, что самостоятельно производить расчет балки перекрытия «на глаз» не следует. Ошибка может привести к прогибу конструкции под нагрузкой и, как следствие, потере возможности дальнейшей эксплуатации. Последующий ремонт или замена балок — очень трудоемкий и дорогой процесс. Отнеситесь серьезно к подбору и расчету конструкции перекрытий и стропил; излишняя экономия и подбор без расчета по принципу «всегда так строили» может привести к серьезным проблемам.
Онлайн калькулятор расчет стойки из швеллера, двутавра, тавра и уголка на прочность, устойчивость и допустимую гибкость
Главная » Онлайн калькуляторы
На чтение 2 мин. Просмотров 10.5k. Обновлено
Калькулятор предназначен для расчёта центрально-нагруженных стоек (колонн) из горячекатаного и другого проката следующей номенклатуры:
- Уголка равнополочного;
- Уголка неравнополочного;
- Швеллера с уклоном и с параллельными гранями полок;
- Двутавров с уклоном полок и с параллельными гранями полок различных модификаций, а также тавровых балок (тавров).
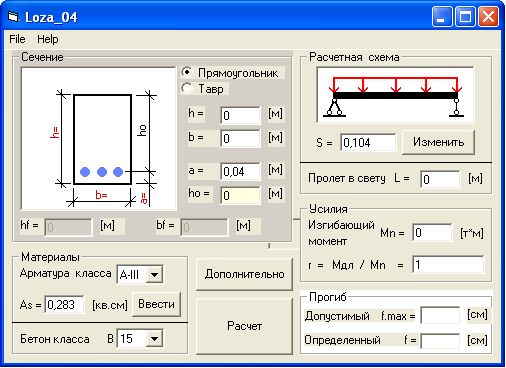
Предлагаем воспользоваться онлайн калькулятором для расчета массы швеллера
| Вид проката Уголок равнополочныйУголок неравнополочныйШвеллер с уклоном полокШвеллер с паралельными гранями полокДвутавр с уклоном полокДвутавр с паралел. гранями полок нормальныйДвутавр с паралел. гранями полок широкопол.Двутавр с паралел. гранями полок колнныйДвутавр с паралел. гранями полок доп.сери(Д)Тавр с паралелными гранями полок нормальныйТавр с паралел. гранями полок широкополочныйТавр с паралелными гранями полок колнный | |||||||||||||||
| Вид и назначение стоек (колонн) Стойки и раскосы передаюшие реакции опорОсновные колонныВторостепенные колонны | |||||||||||||||
| Сталь С235 (Ст3кп2)Сталь С245 (Ст3пс5,Ст3сп5)Сталь С255 (СтГпс,Ст3Гсп)Сталь С285 (Ст3сп,Ст3Гпс,Ст3Гсп)Сталь С345 (12Г2С,09Г2С)Сталь С345К (10ХНДП)Сталь С375 (12Г2С)Сталь С390 (14Г2АФ)Сталь С390Д (14Г2АФД)Сталь С440 (16ГАФ)Сталь С590 (12Г2СМФ) | ||
Если Вашего материала нет в таблице, но Вам известно его расчётное сопротивление, введите его значение в это поле (кг/см2):
| РАЗМЕРЫ ВЫБРАННОГО ПРОФИЛЯ: |
Выберите схему крепления стойки
| Заделка-консоль Заделка-заделка Заделка-шарнир Шарнир-шарнир |
Введите параметры для расчёта
| Длина стойки L, м : | Нагрузка P, кг : |
Размеры проката углового профиля оговариваются ГОСТ 8509-93 и ГОСТ 8510-86; швеллеров ГОСТ 8240-97; двутавров ГОСТ 26020-83; тавров — ТУ 14-2-685-86; (получаемых продольной разрезкой пополам горячекатаных двутавров с параллельными гранями полок по ГОСТ 26020-83).
При проектировании строительных конструкций необходимо принимать схемы, обеспечивающие прочность, устойчивость и пространственную неизменяемость сооружения в целом, а также его отдельных элементов при монтаже и эксплуатации.
Поэтому стойку,находящуюся под действием сжимающей её нагрузки необходимо проверять:
- на прочность;
- устойчивость;
- допустимую гибкость.
Согласно Актуализированной редакция СНиП II-23-81 (CП16.13330, 2011) расчет на прочность элементов из стали при центральном растяжении или сжатии силой P следует выполнять по формуле:
P/Fp*Ry*Yc <= 1, где
- P — действующая нагрузка,
- Fp — плошадь поперечного сечения стойки,
- Ry — расчётное сопротивление материала (стали стойки), выбирается по таблице В5 Приложения «В» того же СНиПа;
- Yc — коэффициент условий работы по таблице 1 СНиПа (0.9-1.1). В соответствии с примечанием к этой таблице (пункт 5) в калькуляторе принято Yc=1.
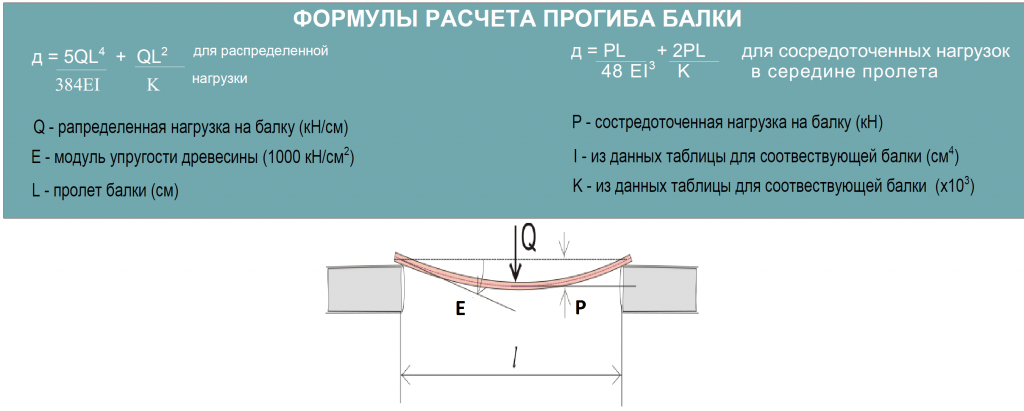
Проверку на устойчивость элементов сплошного сечения при центральном сжатии силой P следует выполнять по формуле:
P / Fi*Fp*Ry*Yc <= 1, где
Fi — коэффициент продольного изгиба центрально-сжатых элементов.
Коэффициент Fi введён в расчёт в качестве компенсации возможности некоторой не прямолинейности стойки, недостаточной жесткости её крепления и неточности в приложении нагрузки относительно оси стойки. Значение Fi зависит от марки стали и гибкости колонны и часто берётся из таблицы 72 СНиП II-23-81 1990г. исходя из гибкости стойки и расчётного сопротивления выбранной стали сжатию, растяжению и изгибу.
Это несколько упрощает и огрубляет расчёт, так как СНиП II-23-81* предусматривает специальные формулы для определения Fi. Гибкость (Lambda) — некоторая величина, характеризующая свойства рассматриваемого стержня в зависимости от его длины и параметров поперечного сечения, в частности радиуса инерции:
Lambda = Lr / i; здесь
- Lr — расчётная длина стержня;
- i — радиус инерции поперечного сечения стержня (стойки,колонны).
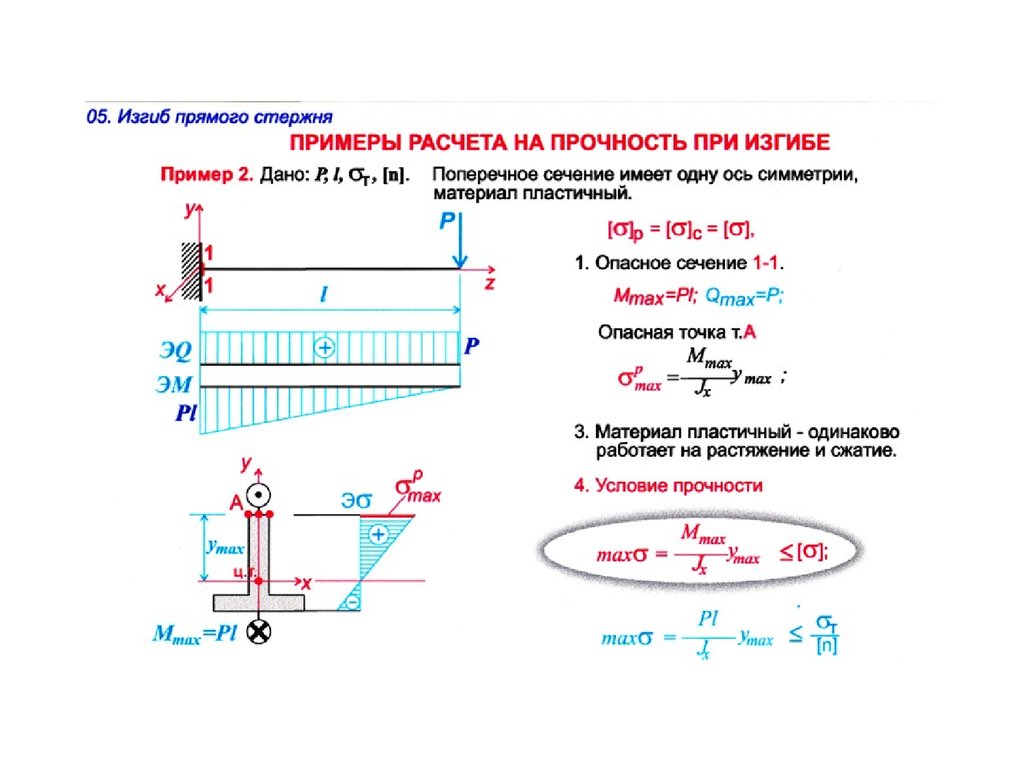
Радиус инерции сечения i равен корню квадратному из выражения I / Fp, где
- I — момент инерции сечения,
- Fp — его площадь.
Lr (расчётная длина) определяется как MuL;
здесь L- длина стойки,а Mu — коэфф., зависящий от схемы её крепления:
- «заделка-консоль»(свободный конец) — Mu = 2;
- «заделка-заделка»-Mu = 0.5;
- «заделка-шарнир» -Mu = 0.7;
- «шарнир-шарнир»-Mu=1.
Следует иметь ввиду,что при наличии у формы поперечного сечения 2-ух радиусов инерции (например, у швеллера, двутавра, тавра — относительно осей x-x и y-y), при расчёте Lambda используется меньший.
Уголки (как равнополочные так, и неравнополочные) имеют минимальный радиус инерции относительно оси z-z, который и используется в расчётах. Кроме того,сама Lambda (гибкость стойки), рассчитанная по формуле Lambda=Lr/i не должна превышать 220-ти в соответствии с табл. 19.СНиП II-23-81*; там же содержатся ограничения на предельную гибкость центрально-сжатых стержней.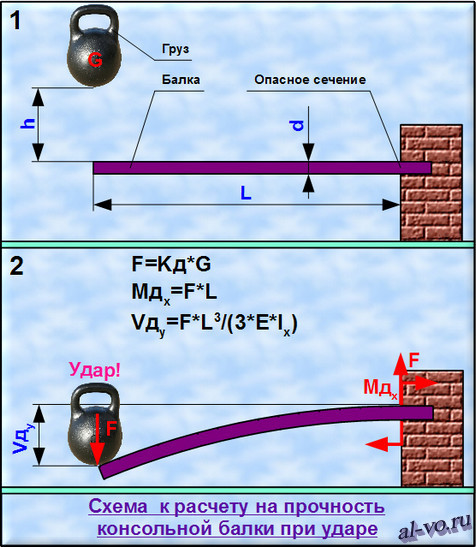
Для их использования необходимо сделать выбор в таблице калькулятора «Вид, назначение стоек…». Предельная гибкость стоек, кроме их геометрических параметров, зависит также от коэфф. продольного изгиба (Fi), действующей нагрузки(P), расчётного сопротивления материала стойки (Ry) и условий её работы (Yc).
ПРИМЕЧАНИЕ. Размеры выбранного швеллера, двутавра и тавра указываются в строке «РАЗМЕРЫ ВЫБРАННОГО ПРОФИЛЯ»; размеры полок уголков-в их таблицах; толщина уголков выбирается отдельно после появления возможных толщин выбранного номера уголка в вышеуказанной строке.
Поделиться
Оцените автора
( 3 оценки, среднее 5 из 5 )
Калькуляторы прогиба балки
— EngineerExcel
Расчет прогиба балки применим к нескольким сценариям проектирования конструкций. Например, расчет отклонения консольной балки может определить силы, действующие на крыло самолета.
Калькуляторы прогиба балки
Самый простой способ определить прогиб балки под действием силы или момента — использовать калькулятор и параметры балочной системы. В зависимости от балочной системы, консольной, просто поддерживаемой или неподвижно-фиксированной, были оценены различные случаи, чтобы получить уравнение для расчета отклонения балки как функции расстояния вдоль балки.
Калькуляторы прогиба консольной балки
Существует пять общих случаев для учета прогиба консольной балки.
Консольная балка с конечным усилием
Первый – это прогиб под действием силы на свободном конце балки, как показано ниже:
Прогиб балки можно рассчитать с помощью следующего уравнения:
где:
- F сила, приложенная к концу балки (Н)
- х — позиция вдоль балки, где оценивается прогиб (м)
- E — модуль Юнга материала балки (Па)
- I – момент инерции площади (м4)
- L общая длина балки (м)
Консольная балка с нагрузкой в любой точке
Второе отклонение консольной балки — это отклонение из-за силы, приложенной в какой-либо точке, отличной от конца, как показано ниже:
Прогиб балки можно рассчитать с помощью следующих уравнений:
где a — расстояние от поддерживаемого конца до места действия силы (м).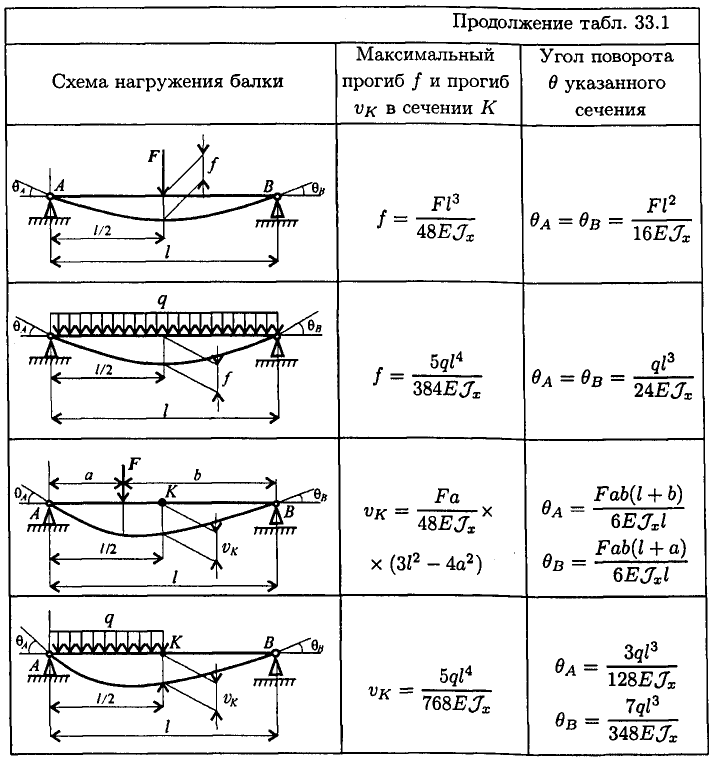
Консольная балка с равномерно распределенной нагрузкой
Третье отклонение консольной балки представляет собой отклонение из-за силы, приложенной равномерно по длине балки, как показано ниже:
Прогиб балки можно рассчитать с помощью следующего уравнения:
где w равномерная нагрузка (Н/м).
Консольная балка с треугольной распределенной нагрузкой
Четвертый прогиб консольной балки представляет собой прогиб из-за треугольной распределенной силы, приложенной по длине балки, как показано ниже:
Прогиб балки можно рассчитать с помощью следующего уравнения :
где w 1 максимальное значение силы (Н).
Консольная балка с конечным моментом
Конечным прогибом консольной балки является прогиб из-за момента на свободном конце балки, как показано ниже:
Прогиб балки можно рассчитать по следующему уравнению:
где M 0 — момент, приложенный к свободному концу (Н∙м).
Калькуляторы прогиба свободно опертой балки
Просто опертая балка с нагрузкой в любой точке
Существует семь общих случаев для рассмотрения прогиба свободно опертой балки. Первый – это отклонение из-за промежуточной силы, как показано ниже:
Отклонение балки можно рассчитать с помощью следующего уравнения:
, где a и b — расстояния по обе стороны от приложенной силы (м).
Свободно опертая балка с нагрузкой в середине пролета
Второй прогиб свободно опертой балки — это прогиб из-за силы, приложенной к центру балки, как показано ниже:
Прогиб балки можно рассчитать с помощью Следующее уравнение:
Свободно опертая балка с равномерно распределенной нагрузкой
Третье отклонение свободно опертой балки — это отклонение из-за равномерно распределенной силы, как показано ниже:
Прогиб балки можно рассчитать с помощью следующего уравнения:
Свободно опертая балка с моментом на каждом конце
Четвертый прогиб свободно опертой балки — это прогиб из-за моментов на обеих опорах, как показано ниже:
прогиб можно рассчитать по следующему уравнению:
Свободно опертая балка с моментом на одном конце
Пятый прогиб свободно опертой балки — это прогиб из-за момента на одной опоре, как показано ниже:
Прогиб балки можно рассчитать по следующему уравнению:
Свободно опертая балка с моментом в центре
Окончательный прогиб свободно опертой балки — это прогиб из-за момента в центре балки, как показано ниже :
Прогиб балки можно рассчитать с помощью следующего уравнения:
Калькуляторы прогиба фиксированной-фиксированной балки
Фиксированная-фиксированная балка с нагрузкой в середине пролета отклонение луча.
Первый — это отклонение из-за силы в центре, как показано ниже:
Прогиб балки можно рассчитать с помощью следующего уравнения:
Неподвижно-неподвижная балка с равномерно распределенной нагрузкой
Другое фиксированно-неподвижное отклонение балки представляет собой отклонение из-за равномерно распределенной силы, как показано ниже:
Прогиб балки можно рассчитать с помощью следующего уравнения:
Дифференциальный расчет прогиба балки
Другой метод расчета прогиба балки включает использование дифференциального уравнения кривой прогиба для оценки поведения балки при изгибе. Здесь представлен обзор этого метода, однако конкретные детали выходят за рамки этого введения.
В этом методе используется общее уравнение, и его можно применять к любой комбинации сил и моментов, действующих в любой точке балки. Используемое уравнение:
где:
- v — прогиб балки (м)
- d 2 v/dx 2 — вторая производная прогиба относительно положения вдоль балки
- M — изгибающий момент вдоль балки в зависимости от положения (Н∙м)
Изгибающий момент в каждом сечении балки рассчитывается как функция x .
Затем каждая функция дважды интегрируется для решения EIv . Системные ограничения используются для создания системы уравнений, решение которой позволяет определить константы интегрирования. Наконец, отдельные уравнения могут быть использованы для определения отклонения v как функции x .
Применение прогиба балки
Путем расчета прогиба балки под действием силы или момента можно выбрать подходящий материал для конкретного применения. Форма балки будет определять момент инерции ее поперечного сечения. Используя это с модулем Юнга материала и требованиями к изгибу, балочную систему можно оптимизировать.
WebStructural — Расчет балки
Экстремальные значения
| Максимальное смещение | @ | ||
|---|---|---|---|
| Максимальная сдвиговая нагрузка | @ | ||
| Максимальный момент | @ |
