Расчет двутавра на прогиб: Расчёт металлической балки онлайн (калькулятор)
Содержание
Расчет квадратной трубы на прогиб и изгиб
Калькулятор
| Пример расчета |
Калькуляторы по теме:
- Сбор нагрузок на балки перекрытия онлайн.
- Расчет прямоугольной трубы
- Расчет двутавра
- Расчет швеллера
- Расчет уголка
- Расчет деревянной балки
Свойства и особенности профильных трубных изделий
Профильными принято назвать трубы, сечение которых отличается от круглого. Наиболее распространённые варианты – это квадратные и прямоугольные изделия. Особую популярность им придаёт тот факт, что созданная на их основе конечная конструкция имеет относительно небольшой вес. Более того! Благодаря специфической форме, крепление трубных элементов к различным поверхностям и друг к другу значительно упрощается.
Более того! Благодаря специфической форме, крепление трубных элементов к различным поверхностям и друг к другу значительно упрощается.
Данные строительные изделия производятся из широкого спектра сплавов и металлов. Однако чаще всего используются профильные трубы из низколегированной и углеродистой стали. Каждому металлу характерно такое природное качество, как точка сопротивления. Она бывает как максимальной, так и минимальной. Первая, в частности, служит причиной деформации построенных сооружений, приводит к перегибам, следствием которых могут быть изломы.
Выполняя загиб, важно принимать во внимание такие характеристики, как вид изделия и его плотность, сечение, размер, а также гибкость материала и его жёсткость. Зная все эти свойства металла, исполнитель сможет понять, как поведёт себя конструкция в процессе эксплуатации.
Кроме того, следует помнить, что при сгибании изделия его внутренние части подвергаются сжатию, что ведёт к увеличению их плотности и уменьшению размеров. Длина наружного слоя соответственно возрастает, он становится более растянутым, но менее плотным. При этом даже по завершении процесса изначальные характеристики срединных участков сохраняются.
Длина наружного слоя соответственно возрастает, он становится более растянутым, но менее плотным. При этом даже по завершении процесса изначальные характеристики срединных участков сохраняются.
При сгибании трубы нужно учитывать свойства материала, из которого она изготовлена, ее размеры и толщину стенок
Важно! Напряжение при сгибании трубного профиля будет обязательно возникать даже на максимально удаленных от нейтральной зоны сегментах изделия. Особо высокое давление будут испытывать слои, расположенные в непосредственной близости от вышеуказанной нейтральной зоны.
Инструкция к калькулятору
Обращаю ваше внимание, что в нецелых числах необходимо ставить точку, а не запятую, то есть, например, 5.7 м, а не 5,7. Также, если что-то не понятно, задавайте свои вопросы через форму комментариев, расположенную в самом низу.
Исходные данные
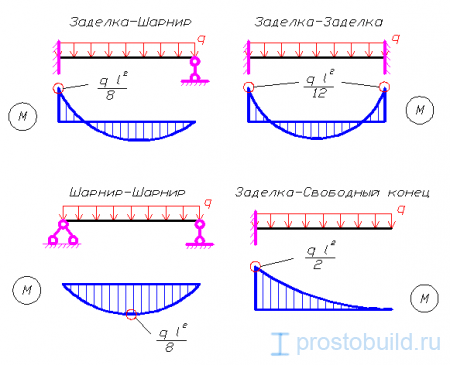
Расчетная схема:
Длина пролета (L) — пролет через который переброшена балка или длина консоли.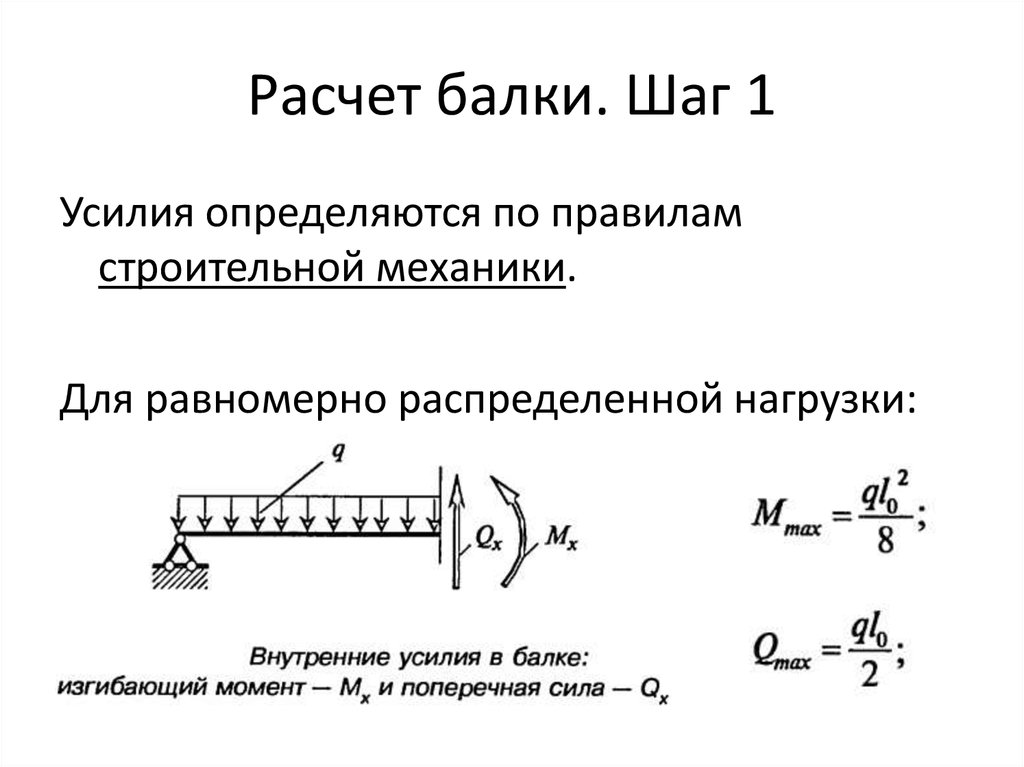
Расстояния (A и B) — расстояния от опор до мест приложения нагрузок. Для 3 схемы А равна длине консоли балки, опирающейся на 2 опоры.
Нормативная и расчетная нагрузки — нагрузки, на которые рассчитывается квадратная труба. Рассчитать их можно с помощью следующих материалов:
- калькулятор по сбору нагрузок на балку перекрытия;
- пример сбора нагрузок на балку перекрытия;
- пример сбора нагрузок на стропила.
Fmax — максимально допустимый прогиб, подбираемой по таблице E.1 СНиПа «Нагрузки и воздействия», в зависимости от вида конструкции. Некоторые значения этого показателя приведены в таблице 1.
Таблица 1. Максимальный прогиб для некоторых конструкций согласно СНиП.
| Вид балки | Длина пролета | Требования | Fmax |
| Балки перекрытий, покрытий, крыши | L ≤ 1 м | Эстетико-психологические, то есть такие, при которых прогиб балки не будет «бросаться в глаза» | 1/120 (1/60) |
| L = 3 м | 1/150 (1/75) | ||
| L = 6 м | 1/200 (1/100) | ||
| L = 12 м | 1/250 (1/125) | ||
| Балки покрытий и перекрытий при наличии на них элементов, подверженных растрескиванию (стяжек, полов, перегородок) | любая | Конструктивные | 1/150 (1/75) |
| Перемычки | любая | Конструктивные | 1/200 |
| Примечания: 1. 2. В случае промежуточных значений длины пролета L максимальный прогиб Fmax находится по линейной интерполяции. | |||
Количество труб — обычно указывается одна балка, но если есть желание ее усилить и положить рядом еще одну такую же балку, то следует выбрать в графе «две».
Расчетное сопротивление Ry— данный параметр зависит от марки стали. Основные значения этого показателя приведены в таблице 2.
Таблица 2. Расчетное сопротивление стали по ГОСТ 27772-88.
| Марка стали | Аналог | Толщина проката | Расчетное сопротивление, Ry |
| Неизвестно | — | любая | 210 МПа |
| C235 | Ст3кп2 по ГОСТ 535-2005 | 2 — 20 мм | 230 МПа |
| 20,1 — 40 мм | 220 МПа | ||
| С245 | Ст3пс5, Ст3сп5 по ГОСТ 535-2005 | 2 — 20 мм | 240 МПа |
| 20,1 — 30 мм | 230 МПа | ||
| С255 | Ст3Гпс, Ст3Гсп по ГОСТ 535-2005 | 4 — 10 мм | 250 МПа |
| 10,1 — 20 мм | 240 МПа | ||
| 20,1 — 44 мм | 230 МПа | ||
| С275 | Ст3пс по ГОСТ 535-2005 | 2 — 20 мм | 270 МПа |
| С285 | Ст3сп, Ст3Гпс, Ст3Гсп по ГОСТ 535-2005 | 4 — 10 мм | 280 МПа |
| 10,1 — 20 мм | 270 МПа | ||
| С345 | 12Г2С, 09Г2С по ГОСТ 19281-2014 | 2 — 10 мм | 335 МПа |
| 10,1 — 20 мм | 315 МПа | ||
| 20,1 — 40 мм | 300 МПа | ||
| С345К | 10ХНДП по ГОСТ 19281-2014 | 4 -10 мм | 335 МПа |
Размер трубы — здесь необходимо выбрать тот размер трубы, который вы хотите проверить на заданные нагрузки.
Показатели массы и нагрузки на изгиб
При расчете профильной трубы: масса и изгиб являются основными показателями. Знать вес погонного метра проката нужно, чтобы не ошибиться в прочностных значениях создаваемой конструкции. Метод определения направлен на подбор оптимального сечения трубного проката при разной его длине. Наглядный пример соотношений этих двух показателей представлен в таблицах ниже.
Табл.№1. Значения для изделий квадратного сечения:
Табл. №2. Значения для изделий прямоугольного сечения:
Технологический процесс изгиба
Любая деформация приводит к уменьшению несущей способности профильной трубы и сопровождается возникновением длительных напряжений на её стенках. На внутреннем слое из-за сжатия металла плотность увеличивается, а на внешней части растяжение, наоборот, уменьшает значение данного показателя. Форма сечения при этом также ожидаемо меняется. Совокупность данных факторов приводит к тому, что несущая способность конструкции в месте изгиба заметно уменьшается.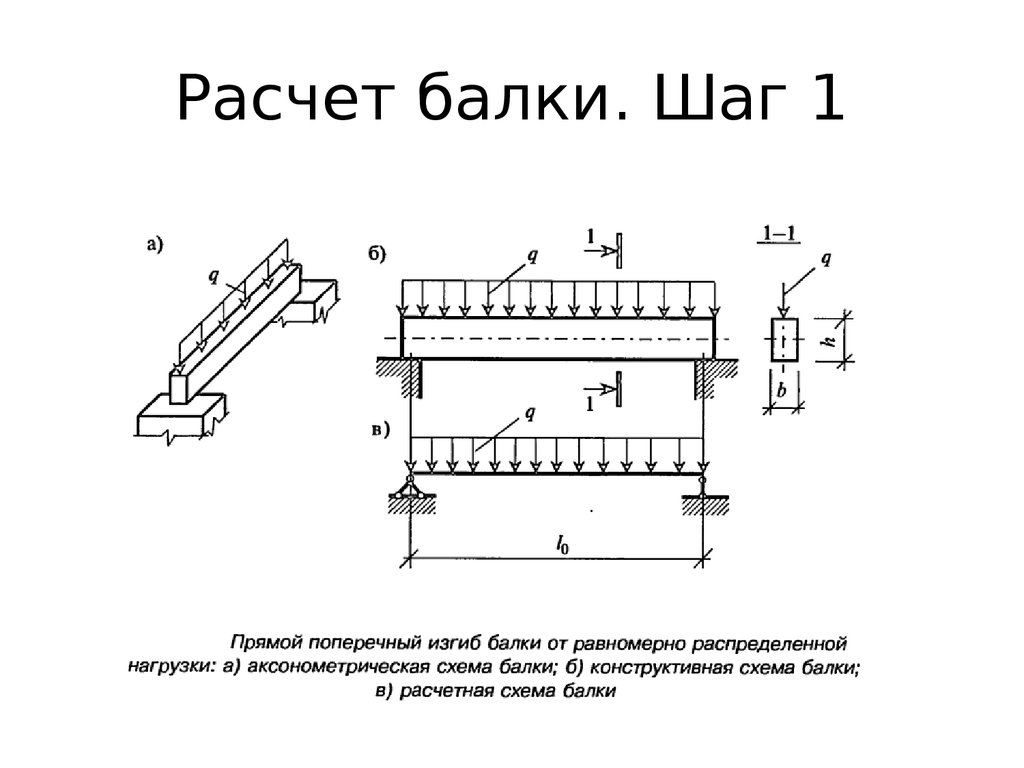 Это актуально для круглой трубы, а также для прямоугольного и квадратного трубного изделия. Причём, для последних двух подобное явление не столь выражено, нежели для трубы с круглым сечением.
Это актуально для круглой трубы, а также для прямоугольного и квадратного трубного изделия. Причём, для последних двух подобное явление не столь выражено, нежели для трубы с круглым сечением.
Однако в любом случае требуется внимательный подход к оценке степени прикладываемой нагрузки при изгибе заготовки. Тогда на ней не появятся ненужные разломы и искривления. С точки зрения функционального предназначения касается это, прежде всего круглых труб, из которых изготавливаются отводы для систем водоснабжения.
Полезно знать! Образуемые складки приводят к возникновению засоров, повышают сопротивление транспортируемой жидкости и снижают проходимость рабочей среды.
Поэтому степень овальной деформации для детали диаметром до 20 мм не должна превышать 15 процентов. При увеличении диаметра значение данного показателя уменьшается до отметки 12,5 процентов. Эти же цифры применяются и при определении оптимальной нагрузки на прогиб трубы с профильным сечением, а вышеуказанные значения диаметров относятся к вписанной/описанной в/вокруг прямоугольник(а) или квадрат(а) окружности.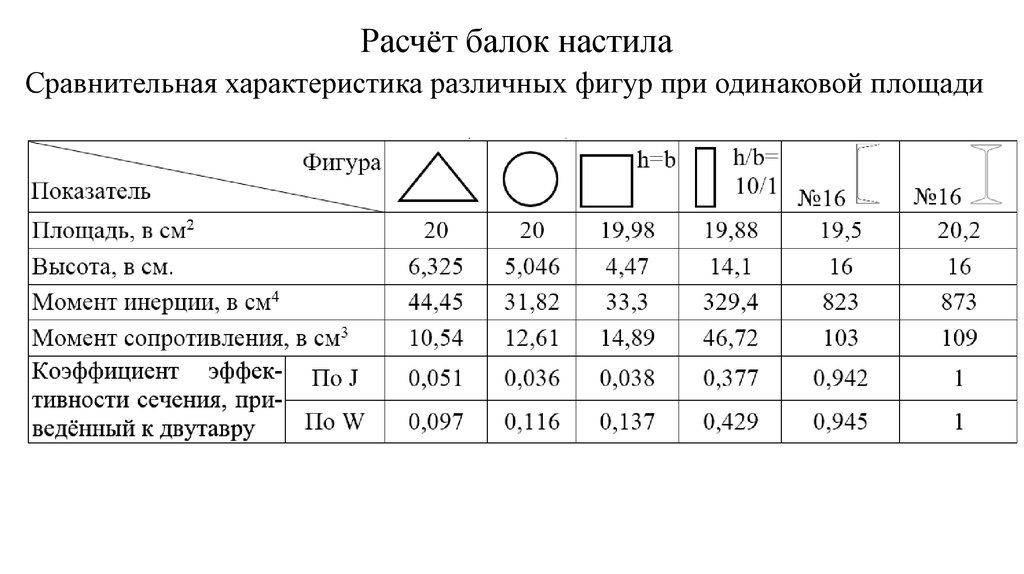
Примеры расчетов изгиба труб
При проектировании и изготовлении конструкций из металла и других материалов очень важно соблюдать и выполнять физико-механические расчеты на прочность, одним из которых является расчет балок на изгиб (прогиб). Выполнять расчет прогиба балки онлайн — очень удобно и быстро. Поэтому специалисты нашего предприятия подготовили онлайн калькулятор для расчетов.
Расчет прогиба балки онлайн
Площадь поперечного сечения профиля:
Расчетный вес профиля (балки):
Описание
При выборе схемы с распределенной нагрузкой, приложенная «Нагрузка Q» указывается как относительная «килограмм на метр». Определяется она по формуле Q = [общяя нагрузка, кг]/[общая длина, м].
Использование калькулятора «Расчет прогиба балки онлайн» значительно сократит время и послужит залогом надежных инженерных конструкций.
Калькулятор разработан исключительно по формулам Сопромата и справочным данным для каждого типа материала и сечения балки. Расчет прогиба сечения является теоретическим, следовательно практические значения могут быть отличными от расчетных и зависеть от множества условий. Однако значения полученные в данном калькуляторе будут невероятно полезными и послужат основой для расчета необходимой конструкции.
Расчет прогиба сечения является теоретическим, следовательно практические значения могут быть отличными от расчетных и зависеть от множества условий. Однако значения полученные в данном калькуляторе будут невероятно полезными и послужат основой для расчета необходимой конструкции.
Для быстрого доступа к расчетам необходимого профиля добавьте калькулятор в избранное (CTRL+D на ПК или значек «звездочка» справа вверху браузера)
Как правильно рассчитать нагрузку на профильную трубу, используя таблицы
Профильные стальные изделия востребованы в современном строительстве благодаря продолжительному сроку эксплуатации и простотой монтажа. Перед покупкой труб необходимо произвести расчеты нагрузки и прочности на изгиб, чтобы определиться с видом и количеством материалов.
Особенности профильных изделий
Профильные трубы, которые широко используются в монтаже различных конструкций и прокладке коммуникаций, представляют собой полый продолговатый металлический брусок с сечением квадратной или прямоугольной формы.
Материалом для изготовления профильных изделий является высокоуглеродистая сталь различных марок.
Профилированная стальная труба служит материалом для сооружения каркасов различный конструкций:
- теплиц;
- павильонов и остановок;
- рекламных конструкций;
- перегородок;
- лестниц;
- мебели и т. д.
Также стальная труба может использоваться в качестве перекрытия или балки.
Зачем нужны расчеты
Стальные профили, собранные в конструкцию, испытывают нагрузку других материалов или веществ, а также испытывают напряжение в металле при изгибе. Превышение максимально допустимой нагрузки влечет деформацию трубопрокатных изделий или их разрыв.
Неверно рассчитанная нагрузка повлечет за собой неустойчивость конструкции, невозможность сборки или разрушение в последующем. Это чревато лишними финансовыми затратами на ремонт, приобретение материалов и восстановление конструкции.
В процессе эксплуатации труб под нагрузкой происходит ряд изменений в структуре металла, которые необходимо учесть при подборе изделий.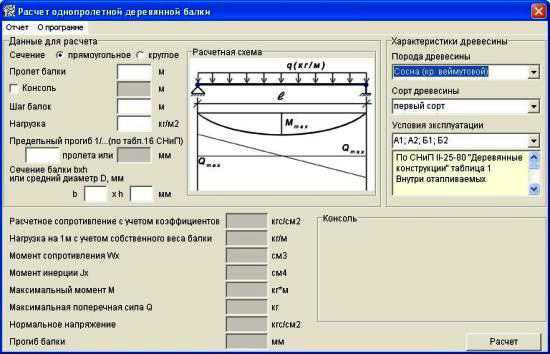 При внешнем воздействии на изделие или его изгибе в металле возникает напряжение, т.е происходит неравномерная деформация, при которой отмечается сжатие внутренних связей между молекулами и одновременное растяжение наружного слоя. При этом внутренние части металла увеличиваются в плотности, а наружные уменьшаются за счет уплотнения в месте воздействия.
При внешнем воздействии на изделие или его изгибе в металле возникает напряжение, т.е происходит неравномерная деформация, при которой отмечается сжатие внутренних связей между молекулами и одновременное растяжение наружного слоя. При этом внутренние части металла увеличиваются в плотности, а наружные уменьшаются за счет уплотнения в месте воздействия.
Какие параметры нужны для расчета нагрузки
При подборе трубных профилей для строительства конструкций необходимо получить информацию о состоянии трубопрокатных профилей для анализа условий и возможностей изделия в процессе эксплуатации.
Данные, которые необходимы для этого:
- размеры профиля, мм;
- форма сечения;
- параметры напряжения конструкции;
- показатели прочности материала;
- вид нагрузки на профиль.
Таким образом, принимаются в расчет точки сопротивления для каждого вида материала. При этом учитываются предельно максимальные и минимальные значения:
- Минимум показателей предполагают нулевую нагрузку.

- Максимальные – с изгибом изделия до состояния разрыва в металле. Учет данных значений позволит правильно рассчитать устойчивость и подобрать трубы соответствующих параметров, чтобы увеличить срок эксплуатации конструкции.
Как рассчитать нагрузку с помощью таблиц
С учетом различных параметров произведены общепринятые математические расчеты, которые сведены в единые таблицы.
Каждый желающий по стандартам и правилам может произвести расчет допустимой нагрузки по справочным общедоступным таблицам и выбрать вид металлического профиля.
Обратите внимание! Значения в справочных материалах получены учеными и расчетными бюро при использовании теории сопротивлений материалов и законов физики.
Методика расчета нагрузок на металлопрофиль по утвержденным таблицам более точна в связи с учетом в них:
- вида опор;
- наличия креплений;
- типа нагрузок.
В проектах используют данные справочных таблиц из документа СП 20. 13330.2011.
13330.2011.
В случаях, когда конструкция не имеет нагрузки, берутся значения из таблицы 1 утвержденного стандарта.
Например, для перильных или декоративных конструкций. Таблицы 2 и 3 содержат показатели максимальной нагрузки на трубный профиль, когда материал может деформироваться, но без разрыва и при прекращении воздействия металлический элемент примет исходную форму и состояние.
При увеличении максимальной нагрузки конструкция может сломаться или разрушиться.
Это важно! Рекомендуется приобретать стальные профили с запасом прочности минимум в 2 раза больше предельно допустимого.
Какую нагрузку способны выдержать профильные трубы
Согласно утвержденным стандартам нагрузка по времени воздействия классифицируется на четыре группы:
- Постоянная. На профиль оказывается воздействие без изменений показателей. Это могут быть другие материалы, грунт и т. д.;
- Временно длительная. На профильную конструкцию оказывается нагрузка в течение продолжительного времени.
 Например, при возведении гипсокартонных перегородок, постройке лестниц в частных домах и т. д.;
Например, при возведении гипсокартонных перегородок, постройке лестниц в частных домах и т. д.; - Кратковременная. Трубопрокат испытывает сезонные или временные нагрузки. Например, тяжесть снега, сильного ветра или напора дождя, вес мебели и посетителей и т. д.;
- Особенная. Нагрузка на случай стихийных бедствий или чрезвычайных ситуаций. Например, во время землетрясения, столкновения транспорта и т. д.
Обратите внимание! Во время расчета нагрузки на металлический профиль для возведения навеса важно помнить, что изделие является несущей конструкцией.
Для вычисления силы воздействия на каркас из металлопрофиля следует учесть следующие типы нагрузок:
- вес и вид материала навеса;
- тип снежного покрова и его высота;
- сила ветра;
- возможность повреждения конструкции транспортными средствами.
Другие виды расчетов
Существуют другие методы расчета нагрузки на конструкции:
- по формуле расчета напряжения изгиба металлической трубы: расчет напряжения при изгибе = изгибающий момент силы / сопротивление
В этой формуле используется закон Гука о пропорциональности силы упругости к показателю деформации.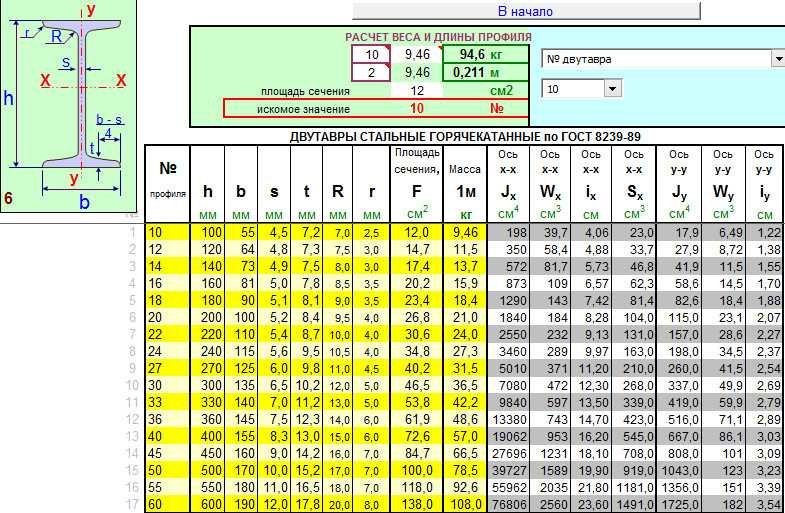
- с помощью специальных готовых калькуляторов.
Обратите внимание! Следует помнить, что использование собственных расчетов по разработанным формулам может быть чревато ошибками и погрешностями. Будьте внимательны при учете всех показателей.
Максимальные нагрузки
Чтобы правильно подобрать трубу для использования, надо знать предельный вес, который должна выдерживать балка или опора в данном месторасположении.
Эта величина выражается в виде сосредоточенной силы, приложенной в центре пролета.
Под давлением указанной силы балка прогнется, но после окончания воздействия возвратится в прежнее состояние (на фото). Превышение наибольшего значения сломает несущую.
В бытовой практике часто встречается распределенная нагрузка, равномерно воздействующая на всю длину балки.
Профильная или круглая труба
Лучшим основанием являются металлические трубы для забора – прочные, технологичные в монтаже и долговечные. На металлическом каркасе можно без проблем закрепить любой ограждающий материал – древесину, профилированный стальной лист, сетку, сотовый поликарбонат, асбесто или цементно — стружечные листы. Бюджетных застройщиков часто останавливает высокая цена металла. Однако, сравнив срок эксплуатации металлического ограждения с деревянным, вы убедитесь в обратном.
На металлическом каркасе можно без проблем закрепить любой ограждающий материал – древесину, профилированный стальной лист, сетку, сотовый поликарбонат, асбесто или цементно — стружечные листы. Бюджетных застройщиков часто останавливает высокая цена металла. Однако, сравнив срок эксплуатации металлического ограждения с деревянным, вы убедитесь в обратном.
Металлические столбы и прожилины простоят минимум 50 лет в то время, как деревянный каркас забора за этот период вам придется заменить 3-4 раза со всеми вытекающими расходами. С точки зрения науки, изучающей сопротивление материалов (сопромат), наиболее выгодным является круглое сечение трубы. При минимуме материала оно обеспечивает максимальную жесткость. Если учесть удобства монтажа, то круглые трубы уступают профильным.
Прямоугольные стойки и прогоны удобнее резать и стыковать с помощью сварки. Плоская поверхность контакта позволяет плотнее и жестче фиксировать все элементы забора, чем круглая. Как мы уже говорили, круглая труба при одинаковом весе прочнее профильной на изгиб. Поэтому, решив купить для забора стойки круглого сечения, вы сэкономите за счет уменьшения веса металла. Кроме этого, в мягкий грунт круглую трубу удобнее ставить методом вкручивания с помощью ворота.
Поэтому, решив купить для забора стойки круглого сечения, вы сэкономите за счет уменьшения веса металла. Кроме этого, в мягкий грунт круглую трубу удобнее ставить методом вкручивания с помощью ворота.
Надежность всей конструкции забора напрямую зависит от материала несущего каркаса. Поставьте деревянные столбики, и ограждение на вашей участке простоит не более 10 лет. Древесина, даже антисептированная, подвержена гниению. Бетон – вариант более надежный. Но при монтаже такой конструкции возникают трудности с креплением прогонов. Сверлить армированный столб непросто, а качественно установить в нем закладные могут далеко не все застройщики. Большое значение имеет шаг стоек забора.
Оптимальный — 2,5 метра. В районе с сильными порывистыми ветрами его нужно уменьшить до 2 метров. Для невысоких заборов (менее 1,5 метра) может быть использована квадратная труба 40х40х2 мм или 60х60х2 мм с прожилинами сечением 30х20х2 мм или 40х20х2 мм.
Немного о прямоугольной трубе ГОСТ Р 54157-2010 «Трубы стальные профильные для металлоконструкций», настоящий стандарт распространяется на круглые, квадратные, прямоугольные, овальные и плоскоовальные трубы для металлоконструкций из углеродистой и низколегированной стали.
Размеры прямоугольных профильных труб:– 20х10, 28х25, 30х15, 30х20, 40х25, 40х28, 50х20, 50х25, 50х30, 50х40– 60х30, 60х40, 80х40, 80х60, 100х50, 100х60, 100х80, 120х60, 120х80– 140х60, 150х100, 160х120, 160х80, 180х125, 200х100Большим плюсом стальных прямоугольных труб является эффективная способность к взаимодействию с плоскостями симметричной поверхности, что позволяет значительно расширить области использования в целом.
Прямоугольное сечение труб увеличивает спектр функциональной направленности продукта конечного сырья, но стоит сразу исключить те области, в которых не используют трубы с подобным сечением и это, прежде всего транспортировка газообразных веществ, водопроводные и прочие системы. Основные сферы и области применения:– Мелкомасштабное строительство (реже — крупномасштабное)– Машиностроение– Монтажные работы, как наружного, так и внутреннего типа– Металлоконструкции широкого профиля– Производство товаров народного потребления
Методы сгибания труб по радиусу
Процесс сгибания стальных труб по радиусу позволяет придавать им частичную или полную изогнуто-плавную конфигурацию, которая не зависит от формы сечения профиля.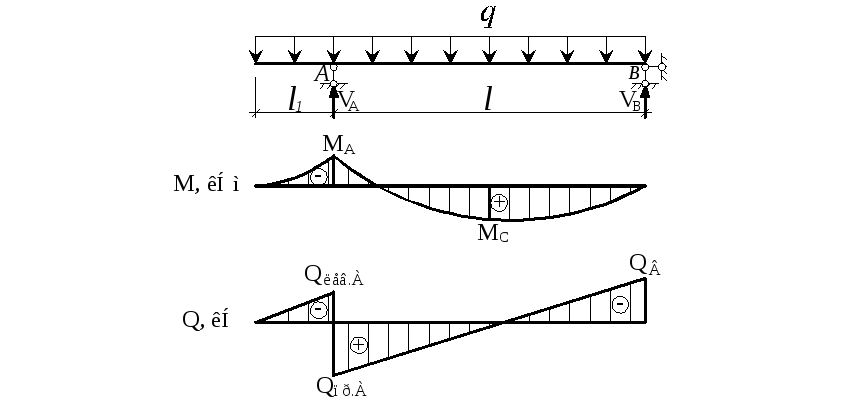 Так, при сгибании полого профиля на стальную заготовку, одновременно действует сила, сжимающая ее по внутренней стенке и усилие, растягивающее по внешнему радиусу. Специфика такого процесса состоит в том, что:
Так, при сгибании полого профиля на стальную заготовку, одновременно действует сила, сжимающая ее по внутренней стенке и усилие, растягивающее по внешнему радиусу. Специфика такого процесса состоит в том, что:
- профиль в момент придания ему формы загиба может получить искривление, при котором трубой будет утрачена соосность;
- при растяжении наружной стенки трубы на участке максимального радиуса может произойти разрыв стенки за счет воздействия радиальной силы;
- сдавливаемая внутренняя часть трубы при неравномерном сокращении будет сминаться складками в виде гофры от приложения тангенциальных сил.
Поэтому существуют два основных способа, при которых производиться гибка трубы по радиусу, а именно:
- непосредственно на холодной трубе,
- при разогреве места сгиба.
Холодный способ используют в основном для труб с малым диаметром, но в этом случае необходимо четко знать минимальный радиус гиба трубы по осевой линии.
При разогреве места сгибания создаются более благоприятные условия для процесса заданной деформации, так как металл приобретает достаточную пластичность, снижая вероятность образования различных дефектов. Горячие способы сгибания трубы по радиусу применяют в основном для заготовок большого диаметра, так как эта методика является более затратной и требует большего времени для осуществления единичного гиба.
При использовании обоих способов необходимо знать технологический процесс, который позволит обеспечить равномерное сечение металлической трубы на всем протяжении радиуса искривления и полное отсутствие на стенках трещин и складок.
Онлайн калькулятор
| Круглая | Квадратная | Прямоугольн._1 | Прямоугольн._2 |
| Выбор материала |
Если Вашего материала нет в таблице, но Вам известно допускаемое напряжение при изгибе для этого материала, ведите его значение в это поле (кг/см2): Выберите схему крепления балки и нагрузки на неё
| Схема_1 | Схема_2 | Схема_3 | Схема_4 | Схема_5 | Схема_6 |
| Схема_7 | Схема_8 | Схема_9 | Схема_10 | Схема_11 | Схема_12 |
| Схема_13 | Схема_14 | Схема_15 | Схема_16 | Схема_17 | Схема_18 |
| Схема_19 | Схема_20 | Схема_21 | Схема_22 | Схема_23 | Схема_24 |
Введите параметры для расчёта
| Диаметр D или сторона A,мм | Распределённая нагрузка q,кг/м |
| Сторона B,мм | Длина балки L,м |
| Толщина стенки S,мм | Размер а,м |
| Сосредоточенная нагрузка P,кг | Размер b,м |
Данная страница не существует!
О центре
История
Структура
Совет Директоров
Руководство
Специалисты
Помним
Дирекция специальных проектов
Дирекция научно-технических проектов и экспертиз
Вакансии
Научные школы
Партнеры
Технологическая платформа «Строительство и архитектура»
Членство в организациях
Лицензии
Раскрытие информации
Отчетность 2019
Непрофильные активы
Противодействие коррупции
Социальная ответственность
Услуги
В сфере подземного строительства
Геологические изыскания
Инженерные изыскания
В сфере бетонного строительства
В высотном и уникальном строительстве
Проектирование
Управление проектами
Проект реконструкции
Экспертиза
Обследование зданий
Технологический и ценовой аудит (ТЦА)
Галерея проектов
Ультразвуковой контроль сплошности свай и ультразвуковой контроль сплошности стен в грунте
Акустическое обследование фундаментных плит
Сейсмоакустический контроль сплошности свай
Сейсмоакустический контроль сплошности фундаментов и плит, поиск дефектов и пустот
Динамические испытания свай по волновой теории удара
Статические испытания свай
Теплоконтроль сейсмичности при бетонировании свай
Новости
Новости Центра
Новости отрасли
Календарь мероприятий
СМИ о нас
Отзывы организаций
Закупки
Центр
сертификацииЗаказчику
Оборудование
Контакты
Научно —
техническая
деятельностьНаучные и инновационные разработки в области строительства и их внедрение
Научно-исследовательские (теоретические, поисковые и прикладные) работы
Научно-технический совет (НТС)
Научно-техническое сопровождение
Нормативно-технические документы
Разработка СТУ
Сотрудничество
BIM-технологии
Интеллектуальная собственность
Корпоративные издания
Научно —
образовательная
деятельностьСведения об образовательной деятельности
Диссертационный совет
Информация о защитах диссертаций
Аспирантура
Подготовка диссертаций без освоения программы подготовки научно-педагогических кадров в аспирантуре
Прикрепление для сдачи кандидатских экзаменов
Докторантура
Повышение квалификации
Учебные программы Центра информационного моделирования
Психология личностного роста в профессиональной деятельности
ПК СТАРКОН.
 Обучение.
Обучение.Кафедра Иностранных языков и кафедра Философии
Кафедра Строительные сооружения, конструкции и материалы
Вакансии
Контакты
Обратная связь
Проверка стальной балки на прогиб
БЛОГ
PROJECT TUTORIAL
Прогиб балки является одной из проверок, которые должны выполняться при проектировании предельных состояний эксплуатационной пригодности. Прогиб — это смещение элемента конструкции под действием нагрузок, без учета смещения остальной части конструкции.
Прогиб — это смещение элемента конструкции под действием нагрузок, без учета смещения остальной части конструкции.
Рис. 1. Ограничение прогиба
Рис. 2. Предлагаемые пределы прогиба для элементов конструкции (Сравнение результатов анализа и результатов проектирования)
SW не просто использует результаты анализа, потому что прогиб в результате анализа представляет собой величину, включающую деформацию соседних элементов.
Результат проектирования консольной балки
Рисунок 3. Результаты проверки отклонения
Рисунок 4. Результаты анализа и конструкции
Как вычислять это по мотильному? (Пример — консоль)
Вычисление вручную дает приблизительное значение, поэтому ручное значение и значение результата Gen не могут совпадать.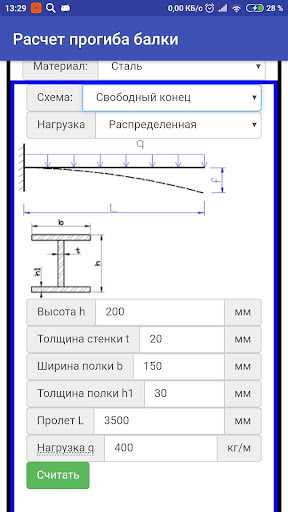
Пожалуйста, обратитесь только к расчетной концепции и способу.
Рисунок 5. Пример кантилевера модели
Как вычислить деформацию кантилевера по ручным (единица: мм) — Пример
Δ = (Δ E 595
Δ = (Δ . E 5
. –Δ C ) -θ 1 * L (добавьте это, чтобы удалить эффект по деформации столбца)
= (0,846566 -(-0,039507)) -0,000473 * 1981,2
= -0,0510 мм
= -0,0510 мм
= -0,0510 мм
= -0,0510 мм
0007
Результаты проверки отклонения
Рисунок 6. Результаты проверки отклонения — 1
Как рассчитать его по общению? (Пример — консольный)
Рисунок 7. Пример модели кантилевера с узелом A
θ 1 : роскошь по деформации столбца
0002 θ 2 : Угол линии, которая связывает деформированные точки
BEAM COLUND и первого узла, когда L разделяется на
100 100 равный.
Δ E : деформация конца луча (деформация на одном конце луча)
Δ C Δ C Δ C Δ C Δ C .0153
beam)
Node A : the first internal node when L is divided into 100 equal
parts
L : Length of beam
Как рассчитать деформацию кантилевера в мидасе Gen (единица измерения: мм)
Gen использует θ 2 рассчитывается внутренне. θ 2 означает угол линии, соединяющей узлы колонны и ближайший к колонне деформированный узел при разделении балки на 100 равных частей и
θ 2 = ( DZ AT Узел A = DZ AT NODE 1) / (100) DZ AT NODE 1) / (100) DZ AT NODE 1) / (100) DZ AT NODE 1) / (100) DZ . ) / (1981.2/100)
) / (1981.2/100)
= 0.000425
δ = ( δ E – δ C ) – θ 2 *L
= (0.846566 – (-0.039507)) – 0.000425* 1981.2
= — 0.0436 mm
Deflection checking results
Рисунок 6. Результаты проверки отклонения – 1
Dz в узле A = -0,031082
Поскольку это внутреннее значение, оно не выводится отдельно.
Как рассчитать? (Example -Continous Beam)
Figure 8. Continuous Beam Example Model
δ 1 : Deformation at One end of beam
δ 2 : Деформация на другом конце балки
δ м : Деформация в средней точке балки
How to calculate the deformation of the cantilever by manual (unit : mm)
δ = δ m – ( δ 1 – δ 2 )/2
= 0. 845448 – (0.039507 – 0.000) / 2
845448 – (0.039507 – 0.000) / 2
= 0.8257 mm
Результаты проверки отклонения
Рисунок 9. Результаты проверки отклонения -2
Рекомендуйте прочитать эту статью », нагрузка на ветер согласно AS 7-16 для Склад с односкатной крышей».
- Последние
- Популярные
Подписаться на новостную рассылку S.O.S
Лучшее руководство по определению прогиба в балках переменного сечения — инженер-наставник
Таблицы балок дают информацию и предполагают, что прогиб
Расчет основан на постоянном поперечном сечении. Итак, что мы делаем, если наш луч имеет крест
сечение, изменяющееся по длине балки?
Для определения величины отклонения в
балка переменного сечения, необходимо интегрировать формулу прогиба балки
с моментом инерции, являющимся переменной по отношению к длине и
применять граничные условия.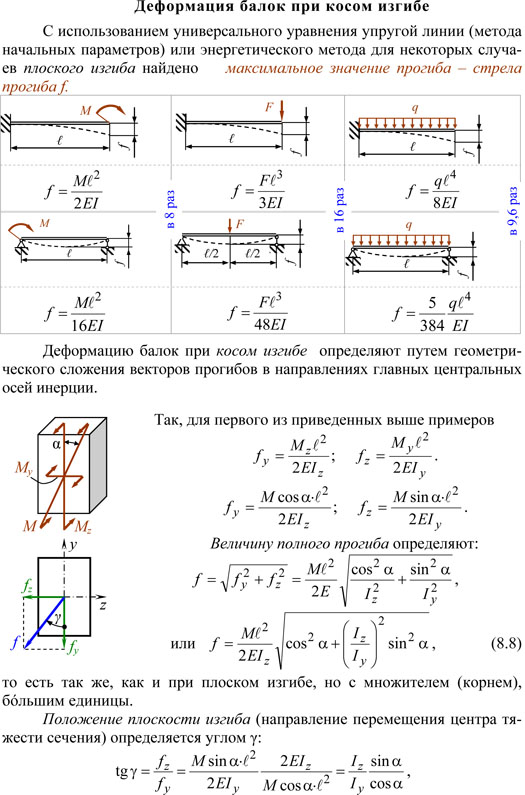 Луч
Луч
формула отклонения: v’’ = M(x)/[E*I(x)].
Непрерывная или дискретная – Существует два типа секций балки: непрерывная и дискретная. Большинство балок представляют собой непрерывные балки и имеют либо постоянное сечение, либо сечение, которое постепенно изменяется по длине балки. Балки крыши в больших стальных зданиях являются отличным примером непрерывной переменной балки. Балка относительно короткая по высоте на концах и очень высокая в середине.
Дискретные лучи являются лучами
которые имеют внезапные разрывы в разрезе. Хотите верьте, хотите нет, иногда это проще
для расчета, потому что дискретные сечения обычно постоянны, что приводит к
более легкий расчет.
Формула отклонения луча является универсальной
формула, которая позволяет настраивать несколько нагрузок и балок
разделы. Я предупрежу вас, что чем больше
точным должен быть ваш расчет, тем сложнее будет сделать математику. Упрощение здесь сэкономит много времени
Упрощение здесь сэкономит много времени
и усилие. Как упоминалось перед
формула:
v’’
= M(x)/[E*I(x)]
ускорение отклонения), M — момент, который обычно является функцией
положение по длине балки, х.
E — модуль упругости, I — момент инерции площади.
луч. Все табличные лучи будут
считать это константой, и поэтому ни одна из формул отклонения
может быть использован.
Теперь, когда мы проинтегрируем приведенное выше уравнение, мы получим
выполнение неопределенного интеграла, что означает, что мы должны добавить константу, C n,
к многочлену каждый раз, когда мы интегрируем.
Поскольку мы будем интегрировать уравнение два раза, мы получим
две константы. Если у нас есть дискретный
случае у нас будет два или более уравнений.
Граничные условия
требования, которым должна соответствовать формула отклонения луча, когда она
находится в окончательном виде. Окончательная форма
приходит только тогда, когда мы используем граничные условия для решения констант
образован неопределенным интегралом. Общий
Общий
случаи, когда концы свободно опертой балки должны быть 0 (дюймы, мм и т. д.) или
наклон консольной балки должен быть 0 радиан.
В этой статье мы рассмотрим три примера обычных балок переменного сечения.
- Двухсекционная консольная балка с точечной нагрузкой на конце.
- Двухсекционная свободно опертая балка под собственным весом.
- Постоянно меняющаяся неразрезная свободно опертая балка с постоянной распределенной нагрузкой.
https://mentoredengineer.com/the-best-guide-to-solving-statically-indeterminate-beams/
Пример 1: Двухсекционная консольная балка с точечной нагрузкой на конце. 94.
Теперь определим момент и дважды проинтегрируем уравнение прогиба балки, каждый раз добавляя переменную для неопределенного интеграла. Я выбрал, чтобы моя система координат (переменная x) начиналась с основания. Это немного усложняет интегрирование, но переменные C 1 и C 2 взаимно компенсируются из-за граничных условий 1 и 2. Через секунду вы увидите.
Через секунду вы увидите.
Мне нужно только сделать интеграцию для одного из разделов, а затем изменить I 1 по I 2 в уравнениях. Я также сохранил переменную «v» как отклонение балки, но изменил первую производную отклонения на переменную «s», чтобы указать наклон. Я также указал переменные.
Теперь, когда проблема определена, давайте настроим граничные условия. Нам нужно, чтобы положение и наклон на фиксированном конце балки были равны 0 дюймов и 0 радиан. Также нам потребуются еще два граничных условия на стыке отрезков. Наклон и положение в этом положении должны быть одинаковыми.
Найдем граничные условия 1 и 2
Как упоминалось выше, я предвидел, что переменные C1 и C2
будет равно 0, если я решу, чтобы система координат начиналась с
база.
Далее мы рассмотрим граничные условия 3 и 4. Они немного сложнее.
Обратите внимание на галочку, которую я поставил в блоке «Найти», чтобы
чтобы мы могли убедиться, что v 1 = v 2 и s 1 =
s 2 на 50 дюймов.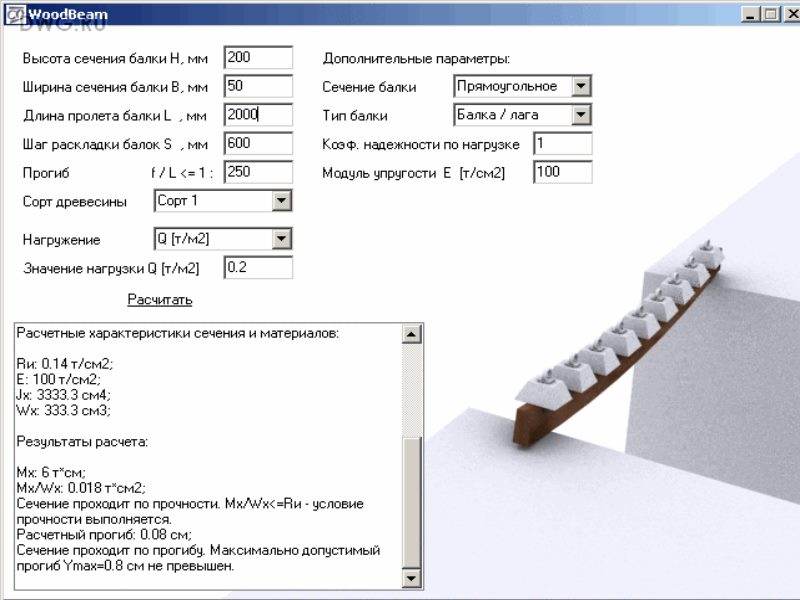 Это подтверждает
Это подтверждает
что положение и наклон будут непрерывными в этой точке.
Следующим шагом является проверка результатов. Это делается в два этапа. Во-первых, построить каждый сегмент по всей длине. Мы ищем четыре граничных условия, которые должны быть выполнены. Как видите, линии пересекаются и касаются друг друга на расстоянии 50 дюймов. Кроме того, v 1 не имеет отклонения или наклона в основании.
Наконец, мы объединим два графика вместе, сформировав окончательное уравнение для отклонения нашей консольной балки.
Как вы можете видеть, отклонение быстро увеличивается после 50 дюймов от основания. Это ясно видно на обоих графиках. 94.
Теперь определим момент и проинтегрируем
уравнение отклонения луча дважды каждый раз добавляя переменную. Я выбрал две системы координат. Координата x идет слева направо и
координата y идет справа налево.
Они связаны:
г
= L-x
Я выбрал эту систему координат так, что C 2
и C 4 сокращаются, когда мы находим граничные условия 1 и 2.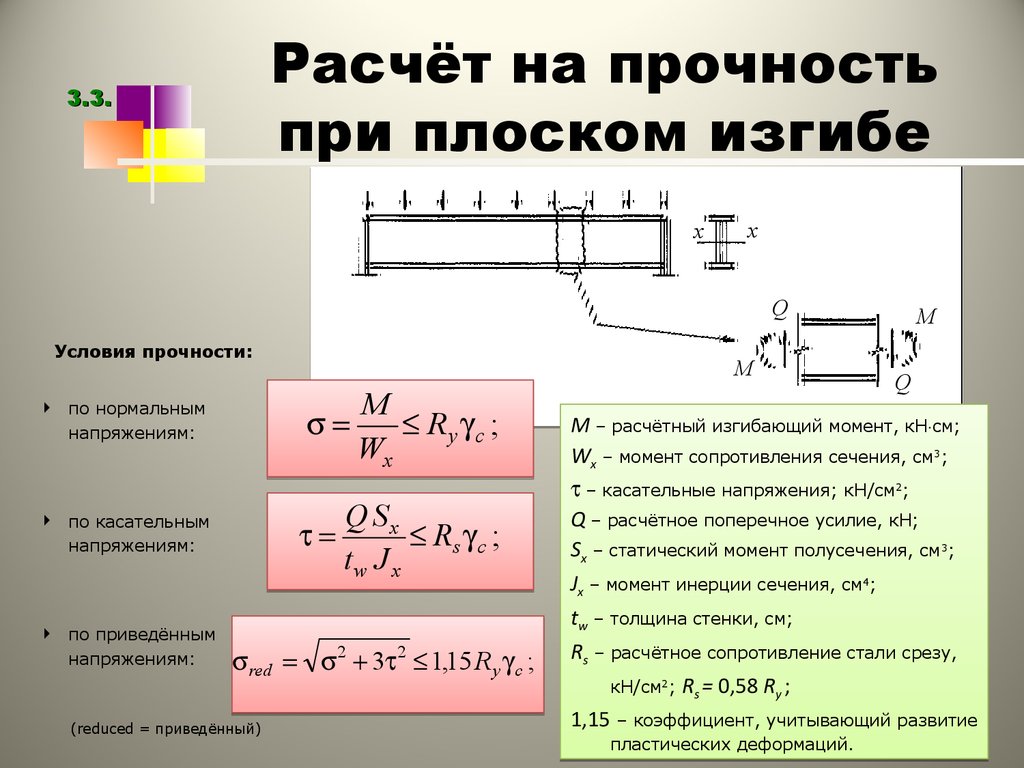 Это также упрощает математику.
Это также упрощает математику.
чрезвычайно. Вы увидите через секунду.
Мне нужно выполнить интегрирование только для одного из разделов, а затем изменить I 1 на I 2 и w 1 на w 2 в уравнениях. В уравнениях правого сечения я также заменю «у» на «х». Я также сохранил переменную «v» как отклонение балки, но изменил первую производную отклонения на переменную «s», чтобы указать наклон. Я также указал переменные.
Теперь, когда проблема определена, давайте настроим граничные условия. Нам нужно, чтобы концы балки имели отклонение 0 дюймов (BC 1 и 2). Также нам потребуются еще два граничных условия на стыке отрезков. Наклон и положение в этом месте должны быть одинаковыми в месте соединения сегментов.
Найдем граничные условия 1 и 2
Как упоминалось выше, я предвидел, что переменные C 2
и C 4 будет равно 0, когда я выберу координату
запуск системы на базе.
Далее мы рассмотрим граничные условия 3 и 4. Они немного сложнее.
Они немного сложнее.
Обратите внимание на галочку, которую я поставил в блоке «Найти», чтобы
чтобы мы могли убедиться, что v 1 = v 2 и s 1 =
с 2 на 200 дюймов. Это подтверждает
что положение и наклон будут непрерывными в этой точке.
Следующим шагом является проверка результатов. Это делается в два этапа. Во-первых, построить каждый сегмент по всей длине. Мы ищем четыре граничных условия, которые должны быть выполнены.
О-о, что случилось!?
Линии определенно пересекаются на расстоянии 200 дюймов, и каждый конец имеет 0 дюймов длины.
отклонение, но они не касаются в месте пересечения. Я не только иллюстрирую силу
построение графика решения для точности, а также демонстрация того, что использование двух
различные системы координат представляли собой проблему.
Согласно уравнениям, склоны приближаются к месту
узел на нисходящем склоне равный по величине. Однако сделать эту работу одним из склонов
на самом деле должен подойти.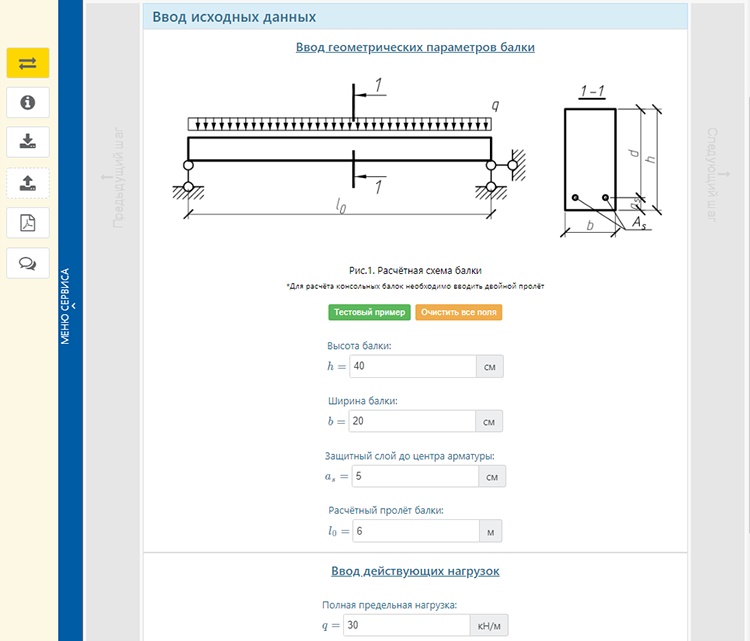 Мы можем
Мы можем
устраните эту проблему, внеся одно небольшое изменение.
с 1
= -s 2
Давайте внесем это изменение и приступим к решению.
Да, намного лучше! Наконец, мы объединим два графика вместе, сформировав окончательное уравнение для отклонения нашей консольной балки.
Как и ожидалось, более длинная и жесткая секция меньше прогибается.
Как рассчитать данные балки, если вашего случая нет в таблице
Пример 3: постоянно меняющаяся, непрерывная, свободно опертая балка с постоянной распределенной нагрузкой.
Эта задача состоит из свободно опертой стальной балки длиной 300 дюймов с распределенной нагрузкой 1000 фунтов/дюйм поперек балки. Секция начинается с высоты 10 дюймов и линейно увеличивается к центру, где достигает высоты 24 дюймов. Затем он сужается до 10 дюймов.
Чтобы определить, как изменяется момент инерции относительно x, мы будем моделировать в Solidworks и брать сечения через каждые 30 дюймов. Мы сведем эти данные в таблицу и подгоним к ним строку.
Мы сведем эти данные в таблицу и подгоним к ним строку.
Вы, наверное, заметили, что я составил таблицу только для значений от 0 до 150 дюймов. Это потому, что я собираюсь использовать симметрию, чтобы упростить эту сложную задачу. Мы можем использовать симметрию, потому что и нагрузка, и сечение балки симметричны относительно середины балки. Из-за симметрии нам нужно, чтобы конечная точка имела отклонение 0 дюймов, а наклон в середине луча был 0 градусов. Затем мы можем отразить это, чтобы получить непрерывное отклонение луча. В этом случае у нас будет координата x слева направо.
Здесь можно увидеть, что рассчитанные значения I(x) близко соответствуют значениям, указанным в таблице выше. Я назвал вторую производную от положения «а1» (ускорение). Как видите, с верхней и нижней частью, имеющей переменную «x», будет очень весело интегрировать это. Итак, есть одна вещь, которую вам нужно знать обо мне. У меня есть ограничения в том, что я не буду делать. Интеграция — одна из таких вещей. Вот почему у нас есть MathCAD!
Вот почему у нас есть MathCAD!
Как видите, очень кропотливая работа по интеграции
был замазан, и мы смогли напрямую решить для нашей границы
условия. В уравнениях s(x) и
v(x), на самом деле были натуральные бревна и каким-то образом появился арктангенс
(не показаны). я до сих пор не жалею
позволяя MathCAD делать всю работу.
Следующим шагом является проверка результатов. Это делается в два этапа. Во-первых, построить каждый сегмент по всей длине. Мы ищем, чтобы наши граничные условия были выполнены. Как видите, отклонение при x = 0 дюймов составляет 0 дюймов, а наклон кажется плоским при x = 150 дюймов.
Наконец, мы зеркально отразим графики вместе, образуя окончательное уравнение для отклонения нашей консольной балки.
Как видите, отклонение составляет 0 дюймов в конечных точках и имеет максимальное отклонение в центре.
Лучшее руководство по расчету статически неопределимых балок
Заключение
В этой статье рассматриваются три популярных варианта нагружения, в которых балка имеет переменное поперечное сечение.

 Без скобок Fmax указан для пролета, в скобках — для консоли.
Без скобок Fmax указан для пролета, в скобках — для консоли.