Расчет на изгиб двутавра: Расчёт металлической балки онлайн (калькулятор)

Расчет балки на прочность онлайн калькулятор

Балка длиной L загружена равномерно распределенной нагрузкой q либо сосредоточенной силой P, которые необходимо будет задать
(как собрать нагрузки на балку можно получить тут Сбор нагрузок (калькулятор).

Все геометрические размеры сечения можно задать самому, поэтому в калькуляторе реализован огромный выбор самых различных балок: труба,
швеллер, профильная труба, двутавр, уголок, пластина и др.

Расчет проходит по нормальным и касательным напряжениям, которые возникают из-за поперечной силы.

Касательные напряжения получаем по формуле Журавского и производим проверку с использованием главных напряжений по 3-ей теории прочности.

В онлайн расчет входят такие материалы, как сталь нескольких классов (С235, С245, С255, С345) и дерево трех сортов.

Для расчета вам необходимо:

1. Выбрать форму поперечного сечения (труба, швеллер, профильная труба, двутавр, уголок, пластина и др. )

2. Выбрать материал (сталь, дерево)

3. Выбрать необходимую расчетную схему

4. Выбрать вид нагрузки (распределенная по длине балки либо сосредоточенная)

5. Указать геометрические размеры, указанные на картинках

6. Задать нагрузку (нагрузку можно рассчитать онлайн здесь)

Материал:

СтальДерево

Класс:

С235С245С255С345

Схема:
Шарнир-ШарнирЗаделка-ШарнирЗаделка-ЗаделкаСвободный конец

Нагрузка
РаспределеннаяСосредоточенная

Диаметр d

мм

Пролет L

мм

«>Нагрузка q

кг/м

Прочность по нормальным напряжениям:Прочность по касательным напряжениям:

Схема:
Шарнир-ШарнирЗаделка-ШарнирЗаделка-ЗаделкаСвободный конец

Нагрузка
РаспределеннаяСосредоточенная

Диаметр d

мм

Толщина стенки t

мм

Пролет L

мм

Нагрузка q

кг/м

Прочность по нормальным напряжениям:Прочность по касательным напряжениям:

Схема:
Шарнир-ШарнирЗаделка-ШарнирЗаделка-ЗаделкаСвободный конец

Нагрузка
РаспределеннаяСосредоточенная

Высота h

мм

Толщина стенки t

мм

Ширина полки b

мм

Толщина полки h2

мм

Пролет L

мм

«>Нагрузка q

кг/м

Прочность по нормальным напряжениям:Прочность по касательным напряжениям:Прочность по 3-ей теории прочности:Устойчивость стенки:Устойчивость полки:

Схема:
Шарнир-ШарнирЗаделка-ШарнирЗаделка-ЗаделкаСвободный конец

Нагрузка
РаспределеннаяСосредоточенная

швеллер горизонтально

Высота h

мм

Толщина стенки s

мм

Толщина полки t

мм

Ширина полки b

мм

Пролет L

мм

«>Нагрузка q

кг/м

Прочность по нормальным напряжениям:Прочность по касательным напряжениям:Прочность по 3-ей теории прочности:Устойчивость стенки:Устойчивость полки:

Схема:
Шарнир-ШарнирЗаделка-ШарнирЗаделка-ЗаделкаСвободный конец

Нагрузка
РаспределеннаяСосредоточенная

Ширина полки а

мм

Ширина полки b

мм

Толщина полки t

мм

Пролет L

мм

Нагрузка q

кг/м

Прочность по нормальным напряжениям:Прочность по касательным напряжениям:Прочность по 3-ей теории прочности:Устойчивость стенки:Устойчивость полки:

Схема:
Шарнир-ШарнирЗаделка-ШарнирЗаделка-ЗаделкаСвободный конец

Нагрузка
РаспределеннаяСосредоточенная

Высота h

мм

Толщина t

мм

Пролет L

мм

«>Нагрузка q

кг/м

Прочность по нормальным напряжениям:Прочность по касательным напряжениям:

Схема:
Шарнир-ШарнирЗаделка-ШарнирЗаделка-ЗаделкаСвободный конец

Нагрузка
РаспределеннаяСосредоточенная

Высота h

мм

Пролет L

мм

Нагрузка q

кг/м

Прочность по нормальным напряжениям:Прочность по касательным напряжениям:

Схема:
Шарнир-ШарнирЗаделка-ШарнирЗаделка-ЗаделкаСвободный конец

Нагрузка
РаспределеннаяСосредоточенная

Высота h

мм

Ширина b

мм

Толщина стенки t

мм

Пролет L

мм

«>Нагрузка q

кг/м

Прочность по нормальным напряжениям:Прочность по касательным напряжениям:Прочность по 3-ей теории прочности:Устойчивость стенки:Устойчивость полки:

Также есть возможность выбора расчетной схемы: шарнир-шарнир, заделка-шарнир, заделка-заделка, свободный конец балки.


Коэффициенты поправки расчетного сопротивления дерева на изгиб приняты следующие:

Mдл = 0.66 — совместное действие постоянной и кратковременной снеговой нагрузок

Mв = 0.9 — нормальные условия эксплуатации дерева (влажность менее 12%)

Mт = 0.8 — эксплуатация дерева при температуре 50 градусов

Mсс = 0.9 — срок эксплуатации конструкции 75 лет

При расчете уже учитывается собственный вес конструкции.

Последние изменения
1. Добавлена возможность расчета балки при сосредоточенной нагрузке

— Добавлена проверка устойчивости стенки и полки двутавра, швеллера, уголка, профильной трубы

— Исправлено расчетное сопротивление дерева на изгиб согласно СП 64. 13330.2017 «Деревянные конструкции»

— Исправлены расчетные сопротивления стали

— Исправлено допустимое эквивалентное напряжение при действии нормальных и касательных напряжений

— Добавлена возможность поворота швеллера

Если данный калькулятор оказался Вам полезен – не забывайте делиться им с друзьями и коллегами ссылкой в соц.сети, а также посмотреть другие
строительные калькуляторы онлайн, они простые, но здорово облегчают жизнь строителям и тем, кто решил сам строить свой дом с нуля.

Расчет балки на изгиб: adcitymag — LiveJournal

Рассчитывать балку на изгиб можно несколькими вариантами:

1. Расчет максимальной нагрузки, которую она выдержит

2. Подбор сечения этой балки

3. Расчет по максимальным допустимым напряжениям (для проверки)

Давайте рассмотрим общий принцип подбора сечения балки на двух опорах загруженной равномерно распределенной нагрузкой или сосредоточенной силой.

Для начала, вам необходимо будет найти точку (сечение), в которой будет максимальный момент.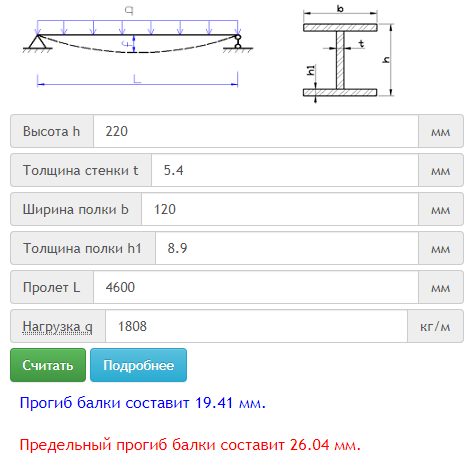 Это зависит от опирания балки или же ее заделки. Снизу приведены эпюры изгибающих моментов для схем, которые встречаются чаще всего.

После нахождения изгибающего момента мы должны найти момент сопротивления Wx этого сечения по формуле приведенной в таблице:

Далее, при делении максимального изгибающего момента на момент сопротивления в данном сечении, мы получаем максимальное напряжение в балке и это напряжение мы должны сравнить с напряжением, которое вообще сможет выдержать наша балка из заданного материала.

Для пластичных материалов (сталь, алюминий и т.п.) максимальное напряжение будет равно пределу текучести материала, а для хрупких (чугун) – пределу прочности. Предел текучести и предел прочности мы можем найти по таблицам ниже.

Давайте рассмотрим пару примеров:

1. Вы хотите проверить, выдержит ли вас двутавр №10 (сталь Ст3сп5) длиной 2 метра жестко заделанного в стену, если вы на нем повисните. Ваша масса пусть будет 90 кг.

Для начала нам необходимо выбрать расчетную схему.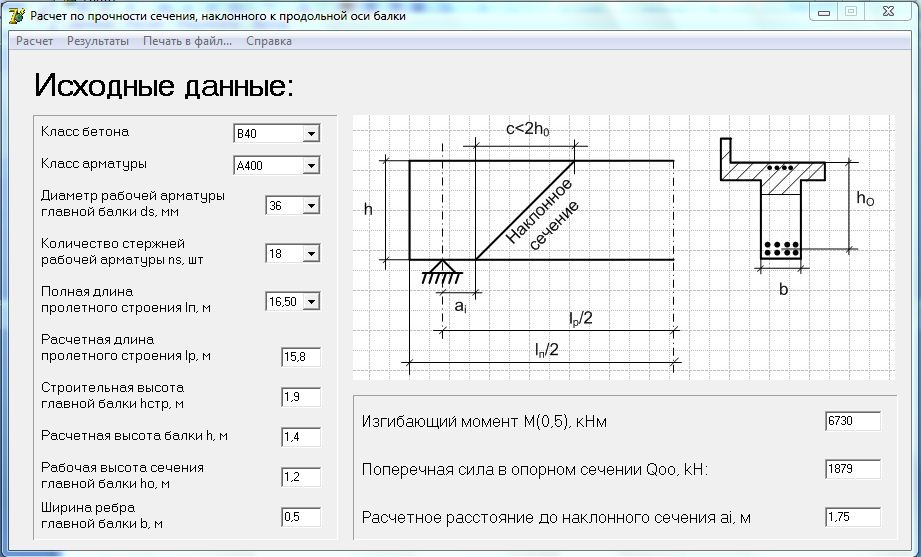

На данной схеме видно, что максимальный момент будет в заделке, а поскольку наш двутавр имеет одинаковое сечение по всей длине, то и максимальное напряжение будет в заделке. Давайте найдем его:

P = m * g = 90 * 10 = 900 Н = 0.9 кН

М = P * l = 0.9 кН * 2 м = 1.8 кН*м

По таблице сортамента двутавров находим момент сопротивления двутавра №10.

Он будет равен 39.7 см3. Переведем в кубические метры и получим 0.0000397 м3.

Далее по формуле находим максимальные напряжения, которые у нас возникают в балке.

б = М / W = 1.8 кН/м / 0.0000397 м3 = 45340 кН/м2 = 45.34 МПа

После того, как мы нашли максимальное напряжение, которое возникает в балке, то мы его может сравнить с максимально допустимым напряжением равным пределу текучести стали Ст3сп5 – 245 МПа.

45.34 МПа < 245 МПа – верно, значит данный двутавр выдержит массу 90 кг.

2. Поскольку у нас получился доволи-таки большой запас, то решим вторую задачу, в которой найдем максимально возможную массу, которую выдержит все тот же двутавр №10 длиной 2 метра.

Если мы хотим найти максимальную массу, то значения предела текучести и напряжения, которое будет возникать в балке, мы должны приравнять (б=245 Мпа = 245 000 кН*м2).

Далее по формуле б = М / W, находим максимальный момент.

М = б * W = 245 000 * 0.0000397 = 9.73 кН * м

Тогда по формуле M = P * L найдем P:

P = 9,73 кН/м / 2м = 4,87 кН = 487 кг

Итак, максимальная масса, которую выдержит двутавр №10 – 487 кг. Число это грубое, поскольку для простоты расчета мы не учитывали различные коэффициенты запаса, поэтому, чтобы подстраховаться, возьмите некий двукратный запас по прочности.

#БАЛКИ, #Изгиб, #На, #Расчет

Механика материалов: изгиб – нормальное напряжение » Механика гибких конструкций

исследования

человек

курсы

блог

Моменты площади

Чтобы рассчитать напряжение (и, следовательно, деформацию), вызванное изгибом, нам нужно понять, где находится нейтральная ось балки, и как рассчитать второй момент площади для данного поперечного сечения.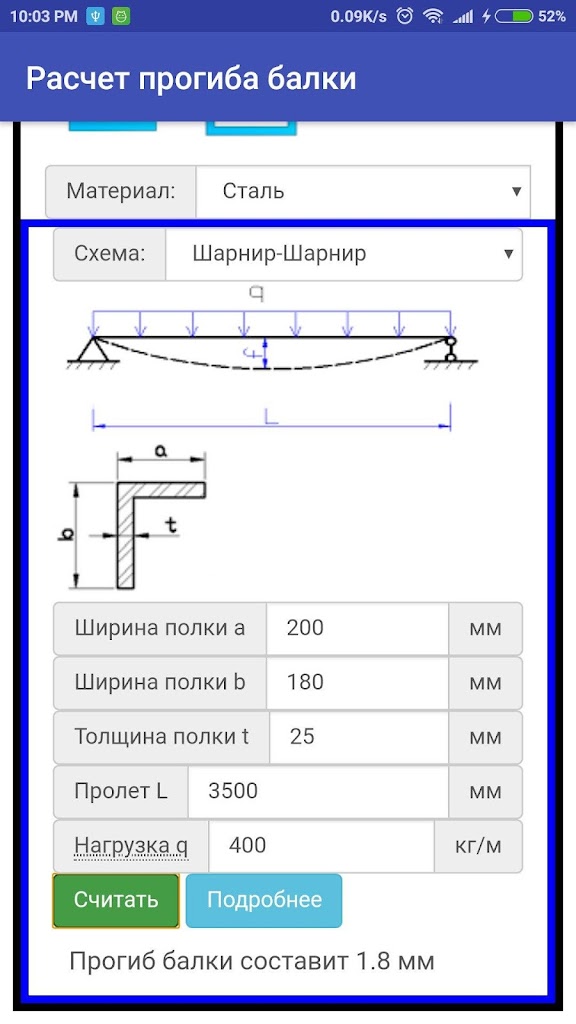

Начнем с того, что представим себе произвольное поперечное сечение — что-то не круглое, не прямоугольное и т. д. 

На изображении выше произвольная форма имеет площадь, обозначенную A . Мы можем посмотреть на небольшую дифференциальную область дА , которая существует на расстоянии x и y от начала координат. Мы можем посмотреть на первый момент площади в каждом направлении по следующим формулам:

Первый момент площади — это интеграл длины по площади — это означает, что он будет иметь единицы длины в кубе [L ³ ]. Это важно, потому что помогает нам найти центр тяжести объекта. Центроид определяется как «среднее  9 0023 x (или y ) позиции области». Математически это утверждение выглядит так:

Крайняя правая часть приведенных выше уравнений будет очень полезна в этом курсе — она позволяет нам разбить сложную фигуру на простые формы с известными площадями и известным расположением центроидов. В большинстве инженерных сооружений есть хотя бы одна ось симметрии — и это позволяет значительно упростить нахождение центроида. Центроид должен располагаться на оси симметрии . Например: 

Для поперечного сечения слева мы знаем, что центроид должен лежать на оси симметрии, поэтому нам нужно найти только центроид вдоль оси y . Поперечное сечение справа еще проще — поскольку центроид должен совпадать с осями симметрии, он должен быть в центре объекта.

Теперь, когда мы знаем, как найти центр тяжести, мы можем обратить внимание на второй момент площади. Как вы, возможно, помните из предыдущего раздела о кручении, это определяется как:

И, наконец, иногда нам нужно будет определить второй момент площади относительно произвольной оси x или y , которая не соответствует центроиду. В этом случае мы можем использовать теорему о параллельных осях для его вычисления. В этом случае мы используем второй момент площади относительно центроида плюс термин, который включает расстояния между двумя осями.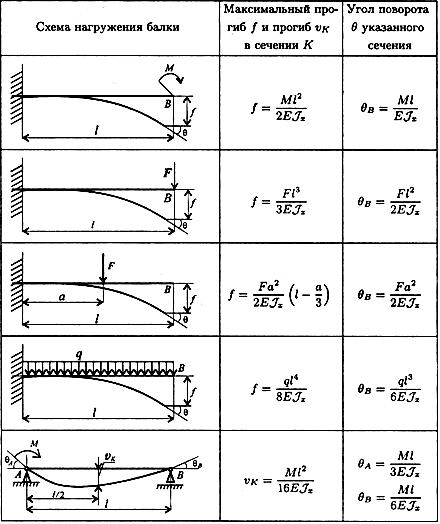

Это уравнение называется теоремой о параллельных осях . Это будет очень полезно на протяжении всего курса. Как описано во вступительном видео к этому разделу, вычисление второго момента площади простой формы может быть простым. Для более сложных форм нам потребуется вычислить I путем вычисления отдельных I для каждой простой формы и объединения их вместе с использованием теоремы о параллельных осях.

Диаграммы сдвига и момента

Поперечная нагрузка относится к силам, которые перпендикулярны длинной оси конструкции. Эти поперечных нагрузок вызовут изгибающий момент M  , который вызывает нормальное напряжение , и поперечную силу  V , которая вызывает касательное напряжение . Эти силы могут и будут варьироваться по длине балки, и мы будем использовать диаграммы сдвига и момента (диаграмма VM) для извлечения наиболее подходящих значений. Построение этих диаграмм должно быть вам знакомо по статике , но мы рассмотрим их здесь. При исследовании балки с поперечной нагрузкой необходимо учитывать два важных момента:

1. Как балка нагружена?

• точечная нагрузка, распределенная нагрузка (равномерная или переменная), комбинация нагрузок…

1. Как балка поддерживается?

• свободно опертый, консольный, нависающий, статически неопределимый…

Знание нагрузок и опор позволит вам начертить качественную диаграмму V-M, а затем статический анализ свободного тела поможет вам определить количественное описание кривых. Начнем с того, что вспомним наши соглашений о знаках .

Эти соглашения о знаках должны быть знакомы. Если сдвиг вызывает вращение против часовой стрелки, он положительный. Если момент изгибает луч таким образом, что луч изгибается в «улыбку» или U-образную форму, он положительный. Лучший способ вспомнить эти диаграммы — это проработать пример. Начните с этой консольной балки — отсюда вы можете переходить к более сложным нагрузкам.

Нормальное напряжение при изгибе

Во многих отношениях изгиб и кручение очень похожи. Изгиб возникает из-за приложенной пары или изгибающего момента   M . Как и при кручении, при чистом изгибе в материале есть ось, на которой напряжение и деформация равны нулю. Это называется нейтральной осью . И, как и при кручении, напряжение уже не одинаково по сечению конструкции — оно меняется. Давайте начнем с того, что рассмотрим момент о z — ось изгибает конструкцию. В данном случае мы не будем ограничиваться круглыми сечениями – на рисунке ниже рассмотрим призматическое сечение.

Прежде чем мы углубимся в математику изгиба, давайте попробуем понять его концептуально. Возможно, лучший способ увидеть, что происходит, — наложить изогнутую балку поверх оригинальной прямой балки.

Теперь вы можете заметить, что нижняя поверхность луча стала длиннее, а верхняя поверхность луча стала короче. Также по центру луча длина вообще не изменилась – соответствует нейтральной оси. Повторяя это язык этого класса, мы можем сказать, что нижняя поверхность находится под напряжением, а верхняя поверхность находится под сжатием. Кое-что, что является немного более тонким, но все еще можно наблюдать из наложенного выше изображения, заключается в том, что смещение луча изменяется линейно сверху вниз, проходя через ноль на нейтральной оси. Помните, это именно то, что мы видели и при кручении — напряжение линейно менялось от центра к центру. Мы можем посмотреть на это распределение напряжений по поперечному сечению балки немного более явно:

Теперь мы можем найти математическую связь между приложенным моментом и напряжением внутри балки.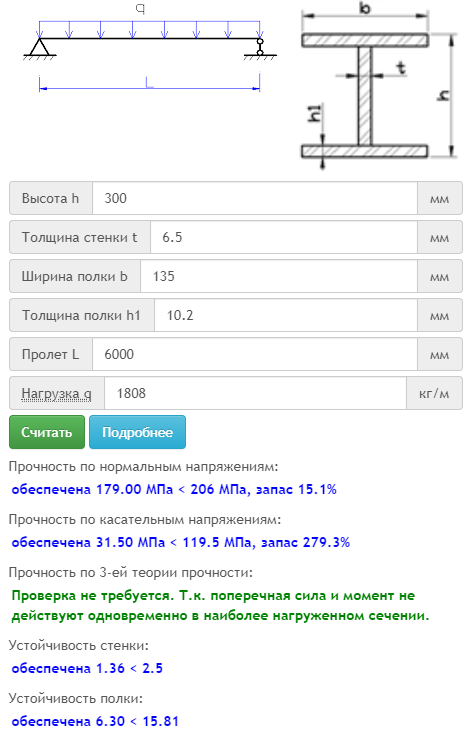 Мы уже упоминали, что балка деформируется линейно от одного края к другому — это означает, что деформация в направлении x увеличивается линейно с расстоянием вдоль оси y- (или по толщине балки). Таким образом, деформация будет максимальной при растяжении при y = -c (поскольку y=0 находится на нейтральной оси, в данном случае в центре балки), и будет максимальной при сжатии при y=c . Мы можем записать это математически следующим образом:

Теперь это говорит нам кое-что о деформации, что мы можем сказать о максимальных значениях напряжения? Начнем с умножения обеих частей уравнения на E , модуль упругости Юнга. Теперь наше уравнение выглядит так:

Используя закон Гука, мы можем связать эти величины с фигурными скобками под ними с напряжением в направлении x и максимальным напряжением. Что дает нам это уравнение для напряжения в направлении x-:

Наш последний шаг в этом процессе — понять, как изгибающий момент связан с напряжением.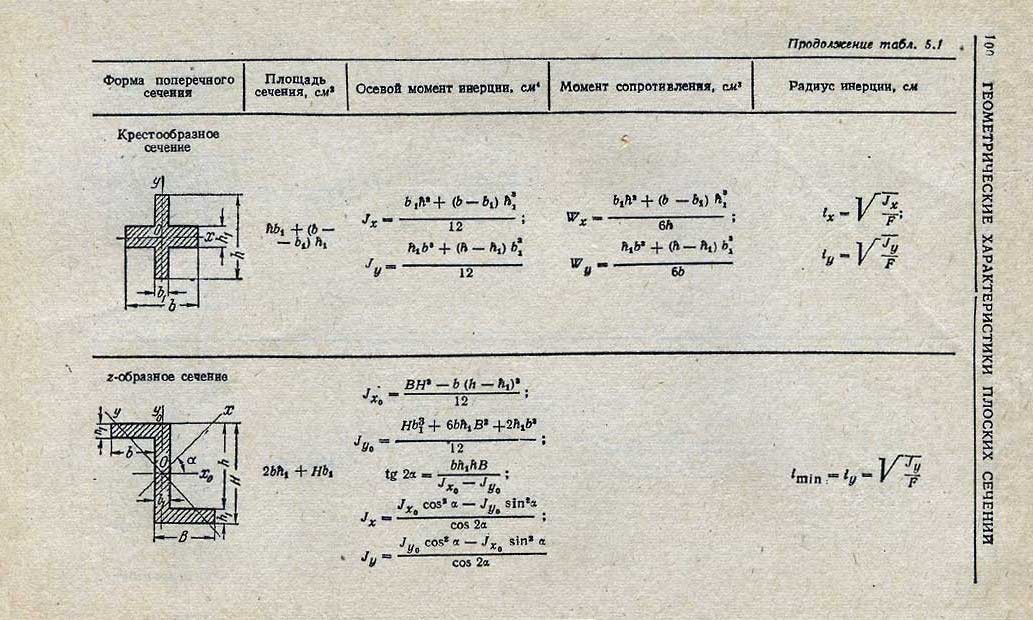 Для этого вспомним, что момент — это произведение силы на расстояние. Если мы можем представить себе, что смотрим только на очень маленький элемент в луче, дифференциальный элемент, то мы можем записать это математически как:

Поскольку в нашем уравнении есть дифференциалы, мы можем определить момент M , действующий по площади поперечного сечения балки, путем интегрирования обеих частей уравнения. И, если мы вспомним наше определение напряжения как силы на единицу площади, мы можем написать:

Последний член в последнем уравнении — интеграл по y в квадрате — представляет второй момент площади относительно оси z (из-за того, как мы определили наши координаты). В декартовых координатах этот второй момент площади обозначается I (в цилиндрических координатах, помните, обозначался J ). Теперь мы можем, наконец, записать наше уравнение для максимального напряжения и, следовательно, напряжения в любой точке вдоль оси y , как:

Важно отметить, что нижние индексы в этом уравнении и направление вдоль поперечного сечения (здесь оно измеряется вдоль y ) будут меняться в зависимости от характера проблемы, то есть направления момента — по какой оси находится луч. сгибаясь? Мы основывали наши обозначения на изображении изогнутой балки на первом изображении этого урока.

Помните, в начале раздела я упомянул, что изгиб и кручение на самом деле очень похожи? На самом деле мы очень ясно видим это в последнем уравнении. В обоих случаях напряжение (нормальное для изгиба и сдвиговое для кручения) равно пар/момент ( M для изгиба и T для кручения), умноженных на положение вдоль поперечного сечения. , , потому что напряжение неравномерно по поперечному сечению  (с декартовыми координатами для изгиба и цилиндрическими координатами для кручения), все делится на второй момент площади поперечного сечения.

Сводка

На этом уроке мы узнали о моментах площади и диаграммах момента сдвига . Из первого момента площади поперечного сечения мы можем вычислить центроид .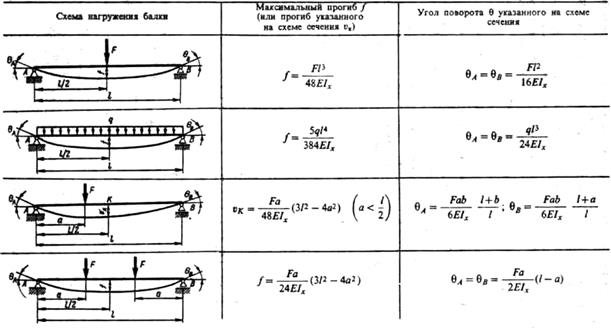 Мы узнали, как вычислить секундный момент площади в декартовых и полярных координатах, и мы узнали, как теорема о параллельных осях позволяет нам вычислить второй момент площади относительно центра тяжести объекта — это полезно для разбиения сложного поперечного сечения на несколько простых фигур и объединение их вместе. Мы пересмотрели концепцию 9Диаграммы сдвига и момента 0015 из статики. Эти диаграммы будут необходимы для определения максимальной силы сдвига и изгибающего момента вдоль сложно нагруженной балки, что, в свою очередь, потребуется для расчета напряжений и прогнозирования разрушения. Наконец, мы узнали о нормальном напряжении от изгиба балки. И напряжение, и деформация изменяются по поперечному сечению балки, при этом одна поверхность растягивается, а другая сжимается. Плоскость, проходящая через центр тяжести, образует нейтральную ось — вдоль нейтральной оси нет напряжений или деформаций. Напряжение является функцией приложенного момента и второго момента площади относительно оси, вокруг которой находится момент.

Этот материал основан на работе, поддержанной Национальным научным фондом в рамках гранта № 1454153. Любые мнения, выводы и выводы или рекомендации, выраженные в этом материале, принадлежат авторам и не обязательно отражают точку зрения Национальный научный фонд.

Изгиб балки

Введение

На этой странице рассматривается классическая теория изгиба балки, которая
является важным фактором почти во всех структурных проектах и
анализы. Хотя это менее очевидно, это также относится к изгибу колонны.
также. И это на самом деле второй мотив этого
страницу, чтобы заложить основу для предстоящего обсуждения теории потери устойчивости колонны.

Цель здесь не в том, чтобы охватить все аспекты изгиба балки. В частности,
такие темы, как определение нейтральной оси, теорема о параллельной оси и
расчет отклонений балки не рассматривается.

Радиус кривизны

Радиус кривизны является основным для изгиба балки, поэтому он будет
рассмотрел здесь. Обычно обозначается греческой буквой \(\rho\),
и может рассматриваться как радиус круга, имеющего ту же кривизну, что и
часть графика, кривая дороги или любой другой путь.
Когда путь прямой, \(\rho\) бесконечен, а когда путь имеет острый
кривая в нем, \(\rho\) мала.

В конечном итоге нам понадобится аналитическое выражение для радиуса кривизны,
поэтому он будет развиваться здесь. Начните с любой функции \(y = y(x)\), как
показано на рисунке. Напомним, что длина дуги \(s\) связана с
\(\rho\) через \(\rho \, \theta = s\), где \(\theta\) — угол
дуги. В дифференциальной форме это \(\rho\, d\theta = ds\).
Теперь разделите обе части на \(dx\).

\[
\rho {d \ theta \ над dx} = {ds \ над dx}
\]

Нам нужны выражения для \(d \theta \over dx\) и \(ds \over dx\). Начиная с
\(d \theta \over dx\), напомним, что
9{3/2} }
\]

Интересно, что любое выражение, включающее радиус кривизны, кажется, всегда имеет его
появляются в знаменателе. И это не исключение, даже если это
определяющее уравнение.

Также интересен тот факт, что многие механические приложения связаны с изгибом,
но в малых масштабах. Обсуждаемый здесь изгиб балки не является исключением. В таких случаях,
наилучший подход состоит в том, чтобы определить ось x вдоль луча таким образом, чтобы
\(y\) отклонения и, что более важно, деформированный наклон, \(y’\), будут
оба быть маленькими. Если \(y’ \lt \lt 1\), то \(y’\) можно пренебречь в приведенном выше уравнении.
Это дает гораздо более простое выражение.
93}
\]

, где \({\bf v}\) — вектор, определяемый параметрически как \({\bf v} = {\bf v}(x(t), y(t), z(t))\),
\({\bf v’}\) — его первая производная, \({\bf v»}\) — его вторая производная, и
\(|…|\) представляет длину вектора, т. е. квадратный корень из суммы
квадраты его компонентов.

Деформация изгиба

Напомним, что длина дуги \(L\) связана с радиусом кривизны \(\rho\) через
\(L = \rho\, \theta\), где \(\theta\) — угол.

Все становится сложнее, когда принимается во внимание толщина.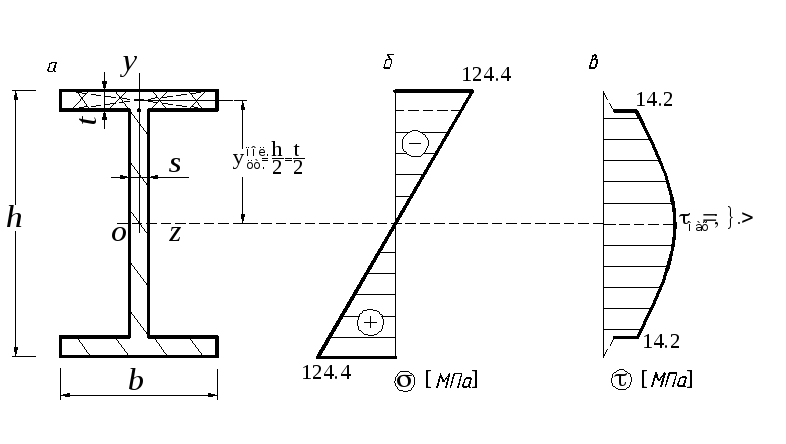
На рисунке ниже объект начальной длины \(L_o\) изогнут
как показано. Поскольку он имеет конечную толщину, различные его части растягиваются,
или сжатые, разные количества. Внешняя часть балки
растянута больше всего, потому что находится дальше всего от
тот центр. Математически все части согнуты под одним и тем же углом \(\theta\),
но \(\rho\) варьируется по толщине, поэтому количество \(\rho\, \theta\)
тоже меняется, а значит, и \(L\) меняется.

Следующий шаг — принять сознательное решение, чтобы избежать путаницы, связанной с наличием множества
различные радиусы кривизны по толщине изогнутого объекта. Это
осуществляется в два этапа.

Сначала найдите тот \(\rho\), который удовлетворяет \(\rho \, \theta = L_o\). Обратите внимание, что
\(\rho\) — это вычисляемый результат, а \(\theta\) и \(L_o\) — входные данные.
Обратите также внимание, что длина в уравнении равна \(L_o\), исходной, недеформированной длине,
не деформированный. Этот шаг устанавливает одно уникальное значение \(\rho\) для
поперечное сечение, а не иметь несколько значений, что может привести к большой путанице.

Нейтральная ось

Место в поперечном сечении, где \(\rho\, \theta = L_o\) известно
как нейтральная ось . Это единственное место, где окончательная деформированная длина
такая же, как исходная недеформированная длина, поэтому растяжения не происходит…
из-за изгиба. Не предполагайте, что нейтральная ось должна быть посередине.
поперечного сечения объекта. Это не обязательно так, особенно
если объект состоит из разных материалов с разными
жесткость.

Оговорка «из-за изгиба» в предыдущем абзаце присутствует, потому что объект
также может быть одновременно нагружен растяжением (или сжатием), что растягивает его
пока каждая точка в его поперечном сечении не станет длиннее (или короче, если сжато), чем
исходная длина, \(L_o\).

Второй шаг состоит в том, чтобы ввести переменную \(y\) как расстояние от нейтральной оси
до любого другого радиуса в поперечном сечении, как показано на рисунке ниже.
В результате радиус кривизны при любом
\(y\) равно \((\rho — y)\), а окончательная длина в любой точке \(y\) определяется выражением

\[
L = (\rho — y) \тета
\]

Напомним, что \(L_o = \rho \, \theta\). Теперь деформация \(\эпсилон\) может быть выражена как

\[
\epsilon_x = {L — L_o \over L_o} = { (\rho — y) \theta — \rho \, \theta \over \rho \, \theta}
\]

, который упрощается до

\[
\epsilon_x = — {y \over \rho}
\]

Это ключевой результат деформации объекта. Он показывает, что деформация равна нулю при \(y=0\),
нейтральной оси и линейно изменяется от нее. Если объект толстый, то \(y\) может принимать
на больших значениях, а на тонких объектах — нет. Именно поэтому толстые объекты
обладают большей жесткостью на изгиб, чем тонкие предметы.

Кроме того, радиус кривизны в знаменателе объясняет многие эффекты изгиба.
Когда объект не согнут, то \(\rho\) бесконечно, и деформации, естественно, равны нулю.
Когда объект изгибается, \(\rho\) уменьшается, и уравнение показывает, что деформации будут увеличиваться.

Наконец, обратите внимание, что деформация является нормальной деформацией и на самом деле является продольной,
по длине балки. Обычно ось \(x\) выравнивают вдоль
длина балки, создающая деформацию \(\epsilon_x\).

Напряжение при изгибе

Теперь, когда у нас есть выражение для напряжения, разработка выражения для напряжения уже невозможна.
будь проще. Умножьте деформацию на \(E\), модуль упругости,
чтобы получить стресс, \(\sigma_x\).

\[
\sigma_x = — {E \, y \over \rho}
\]

Хотя этот шаг был невероятно простым, на самом деле он довольно глубок в том, что
пренебрегали простотой. Напомним со страницы на
Закон Гука, согласно которому каждый компонент нормального напряжения
зависит от всех трех компонентов нормальной деформации. Но здесь у нас просто
умножил деформацию на \(E\), чтобы получить напряжение. Этот шаг имеет ключевое предположение
встроены в него… что на балку не действуют боковые нагрузки/напряжения.
В таких случаях уравнения «срабатывают» так, что \(\sigma_x = E \, \epsilon_x\), как в
одноосное растяжение. Это происходит в большинстве балок, потому что они тонкие по сравнению с
их длина.

92) } \epsilon_x
\]

, где \(\nu\) — коэффициент Пуассона материалов. Понятно, что напряжение для данного
деформация в этом случае выше, чем при классическом одноосном растяжении.

Изгибающие моменты и напряжения

Изгибающий момент \(M_z\) в поперечном сечении из-за поля напряжений вычисляется по формуле

\[
М_з \; «=» \int_A r \times dF \; «=» — \int_A y \, \sigma_x dA
\]

, где \(y\) — плечо момента, а \(\sigma_x dA\) — сила.

92 дА
\]

Всегда помните, что значения \(y\) отсчитываются от нейтральной оси, что
соответствует \(y = 0\).

Уравнение изгибающего момента теперь можно записать в виде

\[
M_z = {E \, I_{zz} \over \rho}
\]

, что является очень важным уравнением.

Малый изгиб Приблизительно

Напомним, что мы обсуждали ранее, что
когда уровень изгиба мал и \(y’ \lt \lt 1\), то \(\rho\) может быть близко
аппроксимируется \(y»\). Это дает

\[
M_z = E \, I_{zz} y» \qquad (\text{когда} \;\; y’ \lt \lt 1)
\]

, что является еще одним очень важным и полезным уравнением.

Теперь… вернитесь к этим двум уравнениям

\[
M_z = {E \, I_{zz} \over \rho} \qquad \qquad \text{and} \qquad \qquad \sigma_x = — {E \, y \over \rho}
\]

и узнайте, что оба содержат \( E / \rho\). Решение каждого уравнения для этого отношения дает

\[
{E \over \rho} = {M_z \over I_{zz} } \qquad \qquad \text{and} \qquad \qquad {E \over \rho} = -{y \over \sigma_x}
\]

Итак, приравняйте два, чтобы получить одно из самых известных уравнений в машиностроении.

\[
\sigma_x = — {M_z \, y \over \; I_{zz} }
\]

Трехмерная гибка

Полный трехмерный изгиб включает в себя отклонения в двух направлениях, \(y\) и \(z\). Напряжение,
\(\epsilon_x\), теперь зависит от обеих координат.

\[
\epsilon_x = {z \over \rho_y} — {y \over \rho_z}
\]

Умножьте на \(E\), чтобы получить напряжение.