Расчет на прогиб двутавровой балки: Расчёт металлической балки онлайн (калькулятор)
Содержание
Расчет балок на прогиб. Максимальный прогиб балки: формула расчета
Балка – элемент в инженерии, представляющий собой стержень, который нагружают силы, действующие в направлении, перпендикулярном стержню. Деятельность инженеров зачастую включает в себя необходимость расчета прогиба балки под нагрузкой. Этой действие выполняется для того, чтобы ограничить максимальный прогиб балки.
Типы
На сегодняшний день в строительстве могут использоваться балки, изготовленные из разных материалов. Это может быть металл или дерево. Каждый конкретный случай подразумевает под собой разные балки. При этом расчет балок на прогиб может иметь некоторые отличия, которые возникают по принципу разницы в строении и используемых материалов.
Деревянные балки
Сегодняшнее индивидуальное строительство подразумевает под собой широкое применение балок, изготовленных из дерева. Практически каждое строение содержит в себе деревянные перекрытия. Балки из дерева могут использоваться как несущие элементы, их применяют при изготовлении полов, а также в качестве опор для перекрытий между этажами.
Ни для кого не секрет, что деревянная, так же как и стальная балка, имеет свойство прогибаться под воздействием нагрузочных сил. Стрелка прогиба зависит от того, какой материал используется, геометрических характеристик конструкции, в которой используется балка, и характера нагрузок.
Допустимый прогиб балки формируется из двух факторов:
- Соответствие прогиба и допустимых значений.
- Возможность эксплуатации здания с учетом прогиба.
Проводимые при строительстве расчеты на прочность и жесткость позволяют максимально эффективно оценить то, какие нагрузки сможет выдерживать здание в ходе эксплуатации. Также эти расчеты позволяют узнать, какой именно будет деформация элементов конструкции в каждом конкретном случае. Пожалуй, никто не будет спорить с тем, что подробные и максимально точные расчеты – это часть обязанностей инженеров-строителей, однако с использованием нескольких формул и навыка математических вычислений можно рассчитать все необходимые величины самостоятельно.
Для того чтобы произвести правильный расчет прогиба балки, нужно также брать во внимание тот факт, что в строительстве понятия жесткости и прочности являются неразрывными. Опираясь на данные расчета прочности, можно приступать к дальнейшим расчетам относительно жесткости. Стоит отметить, что расчет прогиба балки – один из незаменимых элементов расчета жесткости.
Обратите ваше внимание на то, что для проведения таких вычислений самостоятельно лучше всего использовать укрупненные расчеты, прибегая при этом к достаточно простым схемам. При этом также рекомендуется делать небольшой запас в большую сторону. Особенно если расчет касается несущих элементов.
Расчет балок на прогиб. Алгоритм работы
На самом деле алгоритм, по которому делается подобный расчет, достаточно прост. В качестве примера рассмотрим несколько упрощенную схему проведения расчета, при этом опустив некоторые специфические термины и формулы. Для того чтобы произвести расчет балок на прогиб, необходимо выполнить ряд действий в определенном порядке. Алгоритм проведения расчетов следующий:
Алгоритм проведения расчетов следующий:
- Составляется расчетная схема.
- Определяются геометрические характеристики балки.
- Вычисляется максимальную нагрузку на данный элемент.
- В случае возникновения необходимости проверяется прочность бруса по изгибающему моменту.
- Производится вычисление максимального прогиба.
Как видите, все действия достаточно просты и вполне выполнимы.
Составление расчетной схемы балки
Для того чтобы составить расчетную схему, не требуется больших знаний. Для этого достаточно знать размер и форму поперечного сечения элемента, пролет между опорами и способ опирания. Пролетом является расстояние между двумя опорами. К примеру, вы используете балки как опорные брусья перекрытия для несущих стен дома, между которыми 4 м, то величина пролета будет равна 4 м.
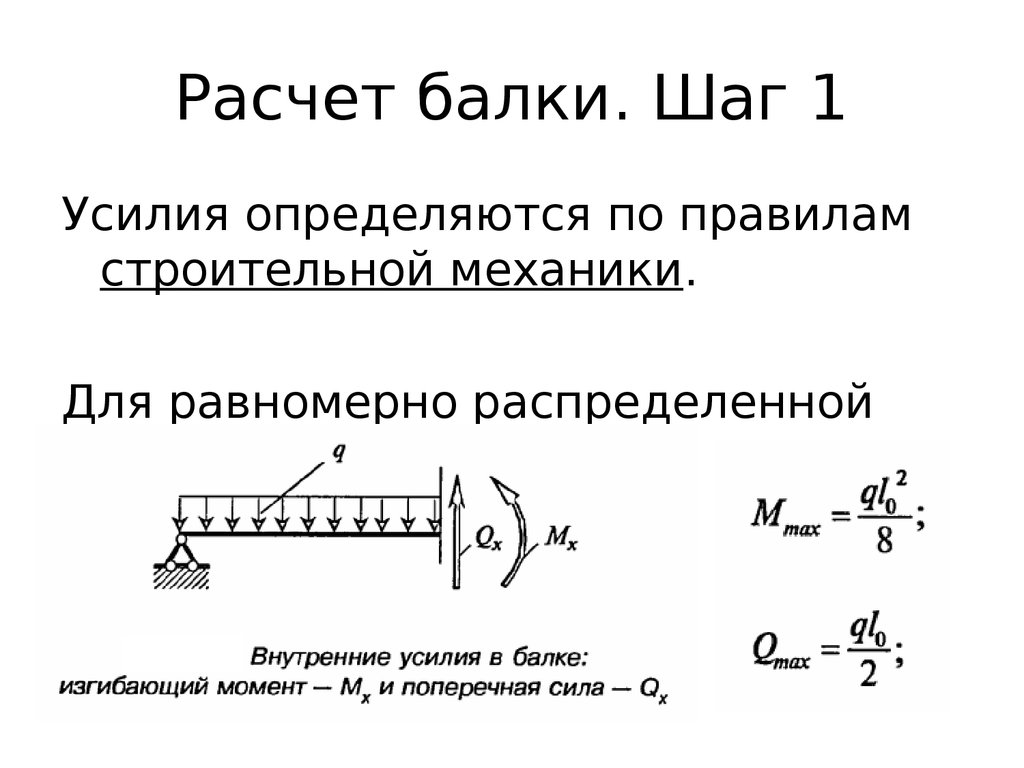
Вычисляя прогиб деревянной балки, их считают свободно опертыми элементами конструкции. В случае балки перекрытия для расчета принимается схема с нагрузкой, которая распределена равномерно. Обозначается она символом q. Если же нагрузка несет сосредоточенный характер, то берется схема с сосредоточенной нагрузкой, обозначаемой F. Величина этой нагрузки равна весу, который будет оказывать давление на конструкцию.
Обозначается она символом q. Если же нагрузка несет сосредоточенный характер, то берется схема с сосредоточенной нагрузкой, обозначаемой F. Величина этой нагрузки равна весу, который будет оказывать давление на конструкцию.
Момент инерции
Геометрическая характеристика, которая получила название момент инерции, важна при проведении расчетов на прогиб балки. Формула позволяет вычислить эту величину, мы приведем ее немного ниже.
При вычислении момента инерции нужно обращать внимание на то, что размер этой характеристики зависит от того, какова ориентация элемента в пространстве. При этом наблюдается обратно пропорциональная зависимость между моментом инерции и величиной прогиба. Чем меньше значение момента инерции, тем больше будет значение прогиба и наоборот. Эту зависимость достаточно легко отследить на практике. Каждый человек знает, что доска, положенная на ребро, прогибается гораздо меньше, чем аналогичная доска, находящаяся в нормальном положении.
Подсчет момента инерции для балки с прямоугольным сечением производится по формуле:
J=b*h^3/12, где:
b – ширина сечения;
h – высота сечения балки.
Вычисления максимального уровня нагрузки
Определение максимальной нагрузки на элемент конструкции производится с учетом целого ряда факторов и показателей. Обычно при вычислении уровня нагрузки берут во внимание вес 1 погонного метра балки, вес 1 квадратного метра перекрытия, нагрузку на перекрытие временного характера и нагрузку от перегородок на 1 квадратный метр перекрытия. Также учитывается расстояние между балками, измеренное в метрах. Для примера вычисления максимальной нагрузки на деревянную балку примем усредненные значения, согласно которым вес перекрытия составляет 60 кг/м², временная нагрузка на перекрытие равна 250 кг/м², перегородки будут весить 75 кг/м². Вес самой балки очень просто вычислить, зная ее объем и плотность. Предположим, что используется деревянная балка сечением 0,15х0,2 м. В этом случае ее вес будет составлять 18 кг/пог.м. Также для примера примем расстояние между брусьями перекрытия равным 600 мм. В этом случае нужный нам коэффициент составит 0,6.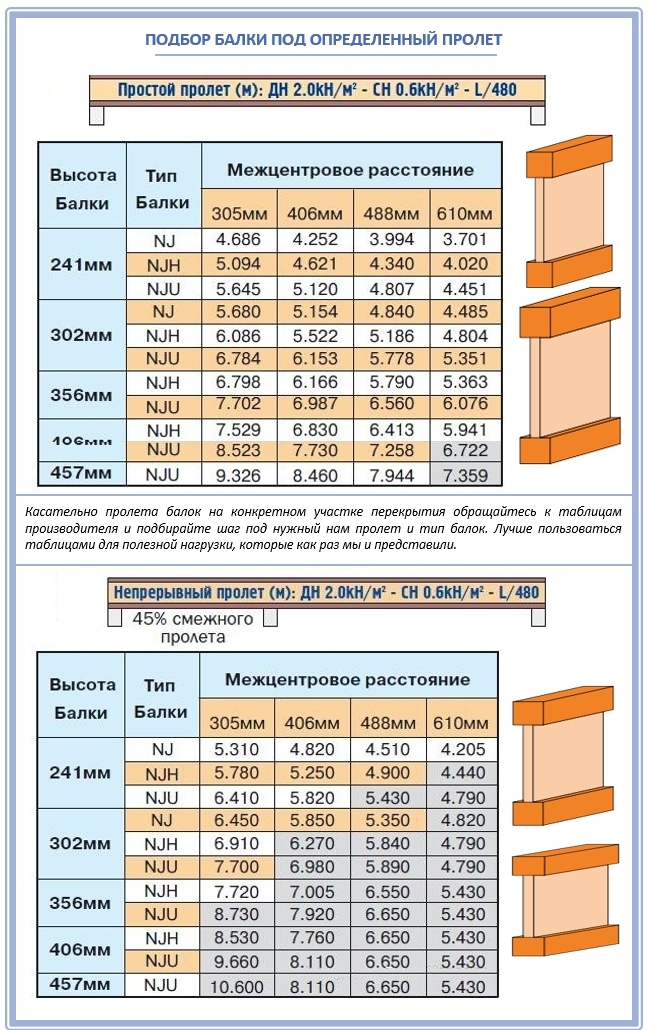 3/48*E*J, где:
3/48*E*J, где:
F – сила давления на брус.
Также обращаем внимание на то, что значение модуля упругости, используемое в расчетах, может различаться для разных видов древесины. Влияние оказывают не только порода дерева, но и вид бруса. Поэтому цельная балка из дерева, клееный брус или оцилиндрованное бревно будут иметь разные модули упругости, а значит, и разные значения максимального прогиба.
Вы можете преследовать разные цели, совершая расчет балок на прогиб. Если вы хотите узнать пределы деформации элементов конструкции, то по завершении расчета стрелки прогиба вы можете остановиться. Если же ваша цель – установить уровень соответствия найденных показателей строительным нормам, то их нужно сравнить с данными, которые размещены в специальных документах нормативного характера.
Двутавровая балка
Обратите внимание на то, что балки из двутавра применяются несколько реже в силу их формы. Однако также не стоит забывать, что такой элемент конструкции выдерживает гораздо большие нагрузки, чем уголок или швеллер, альтернативой которых может стать двутавровая балка.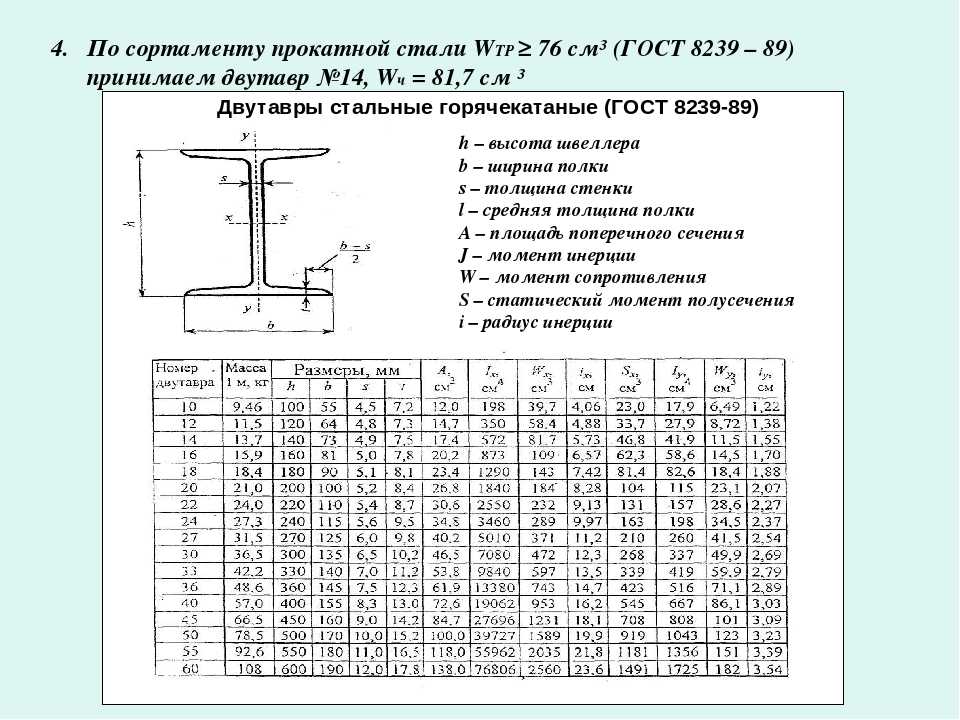
Расчет прогиба двутавровой балки стоит производить в том случае, если вы собираетесь использовать ее в качестве мощного элемента конструкции.
Также обращаем ваше внимание на то, что не для всех типов балок из двутавра можно производить расчет прогиба. В каких же случаях разрешено рассчитать прогиб двутавровой балки? Всего таких случаев 6, которые соответствуют шести типам двутавровых балок. Эти типы следующие:
- Балка однопролетного типа с равномерно распределенной нагрузкой.
- Консоль с жесткой заделкой на одном конце и равномерно распределенной нагрузкой.
- Балка из одного пролета с консолью с одной стороны, к которой прикладывается равномерно распределенная нагрузка.
- Однопролетная балка с шарнирным типом опирания с сосредоточенной силой.
- Однопролетная шарнирно опертая балка с двумя сосредоточенными силами.
- Консоль с жесткой заделкой и сосредоточенной силой.
Металлические балки
Расчет максимального прогиба одинаковый, будь это стальная балка или же элемент из другого материала. Главное — помнить о тех величинах, которые специфические и постоянные, как к примеру модуль упругости материала. При работе с металлическими балками, важно помнить, что они могут быть изготовлены из стали или же из двутавра. Прогиб металлической балки, изготовленной из стали, вычисляется с учетом, что константа Е в данном случае составляет 2·105Мпа. Все остальные элементы, вроде момента инерции, вычисляются по алгоритмам, описанным выше.
Главное — помнить о тех величинах, которые специфические и постоянные, как к примеру модуль упругости материала. При работе с металлическими балками, важно помнить, что они могут быть изготовлены из стали или же из двутавра. Прогиб металлической балки, изготовленной из стали, вычисляется с учетом, что константа Е в данном случае составляет 2·105Мпа. Все остальные элементы, вроде момента инерции, вычисляются по алгоритмам, описанным выше.
Расчет максимального прогиба для балки с двумя опорами
В качестве примера рассмотрим схему, в которой балка находится на двух опорах, а к ней прикладывается сосредоточенная сила в произвольной точке. До момента прикладывания силы балка представляла собой прямую линию, однако под воздействием силы изменила свой вид и вследствие деформации стала кривой.
Предположим, что плоскость ХУ является плоскостью симметрии балки на двух опорах. Все нагрузки действуют на балку в этой плоскости. В этом случае фактом будет то, что кривая, полученная в результате действия силы, также будет находиться в этой плоскости. Данная кривая получила название упругой линии балки или же линии прогибов балки. Алгебраически решить упругую линию балки и рассчитать прогиб балки, формула которого будет постоянной для балок с двумя опорами, можно следующим образом.
Данная кривая получила название упругой линии балки или же линии прогибов балки. Алгебраически решить упругую линию балки и рассчитать прогиб балки, формула которого будет постоянной для балок с двумя опорами, можно следующим образом.
Прогиб на расстоянии z от левой опоры балки при 0 ≤ z ≤ a
F(z)=(P*a2*b2)/(6E*J*l)*(2*z/a+z/b-z3/a2*b)
Прогиб балки на двух опорах на расстоянии z от левой опоры при а ≤ z ≤l
f(z)=(-P*a2*b2)/(6E*J*l)*(2*(l-z)/b+(l-z)/a-(l-z)3/a+b2), где Р – прикладываемая сила, Е – модуль упругости материала, J – осевой момент инерции.
В случае балки с двумя опорами момент инерции вычисляется следующим образом:
J=b1h13/12, где b1 и h1 – значения ширины и высоты сечения используемой балки соответственно.
Заключение
В заключение можно сделать вывод о том, что самстоятельно вычислить величину максимального прогиба балки разных типов достаточно просто. Как было показано в этой статье, главное — знать некоторые характеристики, которые зависят от материала и его геометрических характеристик, а также провести вычисления по нескольким формулам, в которых каждый параметр имеет свое объяснение и не берется из ниоткуда.
Как было показано в этой статье, главное — знать некоторые характеристики, которые зависят от материала и его геометрических характеристик, а также провести вычисления по нескольким формулам, в которых каждый параметр имеет свое объяснение и не берется из ниоткуда.
Расчет балки на прогиб
вернуться в раздел РАСЧЕТЫ КМ И КЖ
Здесь представлены формулы расчета для нахождения значений изгибающих моментов и прогибов для различных балок.
| Однопролетные балки на двух шарнирных опорах | ||
| 1 | Расчет балки на двух шарнирных опорах при одной сосредоточенной нагрузке | Смотреть расчет |
| 2 | Расчет балки на двух шарнирных опорах при двух сосредоточенных нагрузках | Смотреть расчет |
| 3 | Расчет балки на двух шарнирных опорах при одной равномерно-распределенной нагрузке | Смотреть расчет |
| 4 | Расчет балки на двух шарнирных опорах при одной неравномерно-распределенной нагрузке | Смотреть расчет |
| 5 | Расчет балки на двух шарнирных опорах при действии изгибающего момента | Смотреть расчет |
| Балки с жестким защемлением на двух опорах | ||
| 6 | Расчет балки с жестким защемлением на опорах при одной сосредоточенной нагрузке | Смотреть расчет |
| 7 | Расчет балки с жестким защемлением на опорах при двух сосредоточенных нагрузках | Смотреть расчет |
| 8 | Расчет балки с жестким защемлением на опорах при одной равномерно-распределенной нагрузке | Смотреть расчет |
| 9 | Расчет балки с жестким защемлением на опорах при одной неравномерно-распределенной нагрузке | Смотреть расчет |
| 10 | Расчет балки с жестким защемлением на опорах при действии изгибающего момента | Смотреть расчет |
| Балки с жестким защемлением на одной опоре (консольные) | ||
| 11 | Расчет однопролетной балки с жестким защемлением на одной опоре при одной сосредоточенной нагрузке | Смотреть расчет |
| 12 | Расчет однопролетной балки с жестким защемлением на одной опоре при одной равномерно-распределенной нагрузке | Смотреть расчет |
| 13 | Расчет однопролетной балки с жестким защемлением на одной опоре при одной неравномерно-распределенной нагрузке | Смотреть расчет |
| 14 | Расчет однопролетной балки с жестким защемлением на одной опоре при действии изгибающего момента | Смотреть расчет |
| Балки двухпролетные | ||
| 15 | Расчет двухпролетной с шарнирными опорами при одной сосредоточенной нагрузке | Смотреть |
| 16 | Расчет двухпролетной с шарнирными опорами при двух сосредоточенных нагрузках | Смотреть |
| 17 | Расчет двухпролетной с шарнирными опорами при одной равномерно-распределенной нагрузке | Смотреть |
| 18 | Расчет двухпролетной с шарнирными опорами при одной неравномерно-распределенной нагрузке | Смотреть |
| 19 | Расчет двухпролетной с шарнирными опорами при одной неравномерно-распределенной нагрузке | Смотреть |
Прогиб балки – Дополнение по сопротивлению материалов для энергетики
Перейти к содержимому
Основной корпус
Прогиб
Цели обучения
По завершении этой главы вы должны быть в состоянии вычислить:
- Радиус кривизны отклоненной балки, используя теоретические соотношения
- Максимальный прогиб свободно опертой балки
- Максимальный прогиб различных балок с использованием метода формул и приложений учебника
Упругие свойства материалов количественно определяются их модулем упругости. Все материалы в той или иной степени эластичны, например сталь Е ≈ 210 ГПа, чугун Е ≈ 160 ГПа, алюминий Е ≈ 70 ГПа, бетон Е ≈ 40 ГПа. В реальных ситуациях балки, подверженные внешним нагрузкам, будут прогибаться пропорционально изгибающему моменту и обратно пропорционально их жесткости. Общая жесткость балки может быть выражена как E×I c , где E можно рассматривать как жесткость материала, а I c — как поперечную или геометрическую жесткость.
Все материалы в той или иной степени эластичны, например сталь Е ≈ 210 ГПа, чугун Е ≈ 160 ГПа, алюминий Е ≈ 70 ГПа, бетон Е ≈ 40 ГПа. В реальных ситуациях балки, подверженные внешним нагрузкам, будут прогибаться пропорционально изгибающему моменту и обратно пропорционально их жесткости. Общая жесткость балки может быть выражена как E×I c , где E можно рассматривать как жесткость материала, а I c — как поперечную или геометрическую жесткость.
Радиус кривизны
Ознакомьтесь с выводом прогиба балки, подробно описанным в главе 10 учебника. В практических ситуациях деформация балки очень мала по сравнению с ее длиной, и в результате радиус кривизны относительно велик.
Этот радиус кривизны можно рассчитать с помощью
где:
- E — модуль упругости (сопротивление, обусловленное свойствами материала)
- I c — момент инерции относительно центральной оси (сопротивление из-за геометрии сечения)
- M — изгибающий момент в интересующем сечении
Если балка нагружена таким образом, что изгибающий момент постоянен в сечении балки (горизонтальная линия на диаграмме BM), то отклонение представляет собой дугу окружности, а радиус кривизны постоянен.
Найдите минутку и проанализируйте приведенную выше формулу… увеличение жесткости балки (E×I c ) уменьшит прогиб (большой R), в то время как больший изгибающий момент приводит к меньшему радиусу кривизны (большему прогибу/провисанию).
Прогиб балки
Рассмотрим свободно опертую балку, как показано на рисунке выше. Как только радиус кривизны найден, максимальное отклонение (в середине пролета) можно легко рассчитать геометрически следующим образом:
Метод формулы для простых случаев
Формула радиуса кривизны действительна только для случаев, когда изгибающий момент постоянен. В других случаях для определения отклонения балки используются геометрические методы или методы, основанные на интегрировании. Результаты этих расчетов, представленные в алгебраической форме, приведены в инженерном справочнике формул. Наиболее распространенные случаи обобщены в Приложении F к учебнику
.
При использовании готовых формул необходимо сначала согласовать геометрию балки и нагрузку с одним из заданных случаев. Если вы имеете дело с более сложной нагрузкой, такой как точечные нагрузки, накладываемые на распределенную нагрузку, вы можете проанализировать две нагрузки по отдельности, а для общего прогиба просто добавить составляющие.
| # | Корпус: | Загрузка и размеры | Форма и материал |
| Проблема 1 |
|
| |
| Проблема 2 |
|
| |
| Проблема 3 |
|
| |
| Проблема 4 |
|
|
Проблема 5: Порекомендуйте одно улучшение в этой главе.
Как легко рассчитать допустимый прогиб :: Weyerhaeuser
Как легко рассчитать допустимый прогиб
1 сентября 2022 г. в Wood Products — #software
#технический разговор
#трус балка
Автор Дэвид Микнхаймер, профессиональный инженер компании Weyerhaeuser
Вычисление величины отклонения элемента и его соответствия минимальным нормам является сложным инженерным процессом. ForteWEB®, наше программное решение для определения размеров стержней, может помочь упростить этот процесс без использования формул отклонения балки. Но сначала, что такое отклонение?
Что такое отклонение?
Прогиб – это изгиб или «прогиб», вызванный нагрузкой. Все элементы конструкции будут прогибаться или изгибаться под нагрузкой. Величина изгиба зависит от величины приложенной нагрузки, размаха элемента и жесткости элемента. Как правило, минимальный прогиб желателен для более качественных полов.
Как правило, минимальный прогиб желателен для более качественных полов.
Максимально допустимый прогиб
Глава 3 Международного жилищного кодекса (IRC) определяет максимально допустимый прогиб для данного элемента конструкции (пола, крыши, стены и т. д.). См. таблицу ниже. Допустимый прогиб обычно выражается в долях пролета. Большее число внизу дроби представляет собой более строгое ограничение. Например, допустимый прогиб балки перекрытия с гипсом длиной 12 футов (L/360) составляет 0,4 дюйма (12 футов, деленное на 360). Если у той же балки был гипсокартонный потолок (L/240), допустимый прогиб составляет 0,6 дюйма.
Таблица R301.7 Допустимый прогиб элементов конструкции
Элемент конструкции | Допустимое отклонение |
|---|---|
Стропила с уклоном более 3:12 без готового потолка, прикрепленного к стропилам | л / 180 |
Внутренние стены и перегородки | Г / 180 |
Полы и оштукатуренные потолки | л / 360 |
Все остальные элементы конструкции | л / 240 |
Наружные стены со штукатуркой или лепниной | ч / 360 |
Наружные стены-ветровые нагрузки с хрупкой отделкой | Н/240 |
Наружные стены-ветровые нагрузки с гибкой отделкой | л / 120 |
Перемычки, поддерживающие стены из каменной кладки | л / 600 |
L: длина пролета H: высота пролета
Расчет допустимого прогиба без уравнений прогиба
Программное обеспечение ForteWEB упрощает расчет допустимого прогиба. Вы можете указать собственный предел отклонения для своего проекта или использовать минимум кода. Здесь вы можете увидеть балку длиной 24 фута, 5 1/4” x 16” 2.0E Parallam® PSL заподлицо с перекрытием с шириной притока 5 футов. При нагрузке постоянной нагрузкой 12 фунтов на квадратный фут и динамической нагрузкой 40 фунтов на квадратный фут эта балка имеет прогиб при динамической нагрузке L/640 и общий прогиб под нагрузкой L/447. Эти отклонения легко соответствуют минимальным требованиям IRC.
Вы можете указать собственный предел отклонения для своего проекта или использовать минимум кода. Здесь вы можете увидеть балку длиной 24 фута, 5 1/4” x 16” 2.0E Parallam® PSL заподлицо с перекрытием с шириной притока 5 футов. При нагрузке постоянной нагрузкой 12 фунтов на квадратный фут и динамической нагрузкой 40 фунтов на квадратный фут эта балка имеет прогиб при динамической нагрузке L/640 и общий прогиб под нагрузкой L/447. Эти отклонения легко соответствуют минимальным требованиям IRC.
Если у вас есть дополнительные вопросы об участниках PSL Parallam®, обратитесь в службу технической поддержки Weyerhaeuser или обратитесь к руководствам наших спецификаторов.
Дополнительную информацию можно найти на этих ресурсах.
- 2018 Международный жилищный кодекс для одно- и двухквартирных домов
- Программное обеспечение ForteWeb — критерии отклонения
ИНФОРМАЦИОННЫЙ БЮЛЛЕТЕНЬ
Получайте самые последние новости о продуктах Weyerhaeuser, а также технические статьи, написанные нашими профессиональными инженерами здесь, в Weyerhaeuser, чтобы помочь вам в проектировании, спецификации и сборке для обеспечения качества, производительности и экономии.
Электронная почта
Необходимый
Я хочу получать информационный бюллетень Insights
Необходимый
ДаНет
Заинтересованы в получении электронной почты об этих продуктах:
Трус Балка
ОСБ
Распределение
Пиломатериал
Программное обеспечение
Штат США или провинция Канады
Алабама, ALAlaska, AKAризона, AZArkansas, ARCalifornia, CAColorado, COConnecticut, CTDelaware, DEFlorida, FLGeorgia, GAHawaii, HIIdaho, IDIllinois, ILIndiana, INIowa, IAKansas, KSKentucky, KYLouisiana, LAMaine, MEMaryland, MDMassachusetts, MAMichip, MIMissota, MIMinnesota MOMontana, MTNebraska, NENevada, NVNew Hampshire, NHNew Jersey, NJNew Mexico, NMNew York, NYNorth Carolina, NCNorth Dakota, NDOhio, OHOklahoma, OKOregon, ORPennsylvania, PARhode Island, RISouth Carolina, SCSouth Dakota, SDTennessee, TNTexas, TXUTah, UTVermont, VTVirginia , VAWashington, WAWWest Virginia, WVWisconsin, WIWyoming, WYWashington D.