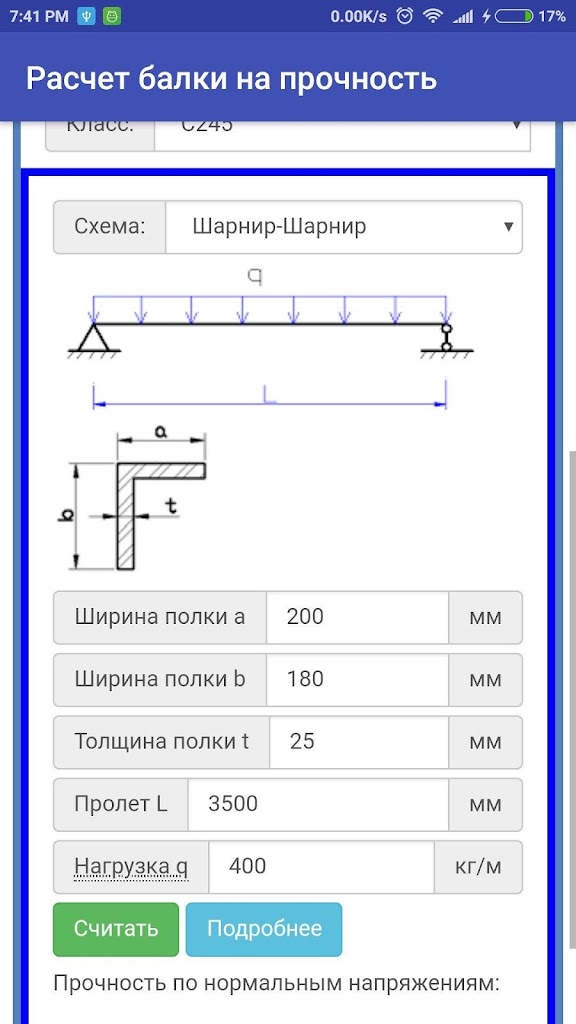
Расчет нагрузки на двутавровую балку: Расчёт металлической балки онлайн (калькулятор)
Содержание
Расчет динамической нагрузки(удара) — пример решения задачи
Ниже приведено условие и решение задачи. Закачка решения в формате doc начнется автоматически через 10 секунд.
На двутавровую балку с высоты H падает груз F.
Требуется :
1) Определить наибольшие нормальные напряжения в балке ;
2) Вычислить наибольшие напряжения в балке при условии, что правая опора заменена пружиной, податливость которой (т.е. осадка от груза 1 кН) равна α ;
3) Сравнить полученные результаты.
Дано : номер двутавра 36 ; L=3 м ; F=11 кН ; α=3 мм/кН ; H=L/5 (высота падения не задана, поэтому принимаем самостоятельно).
Решение.
Балка подвергается поперечному (изгибающему) удару.
Условие прочности балки :
Наибольшее напряжение в балки от статического действия груза :
где Mx – максимальный момент в сечении балки (определяется по эпюре) ; Wx – момент сопротивления сечения при изгибе, для двутавра № 36 : Wx=743 cм3 (определяется по таблицам сортамента прокатной стали).
Построим эпюру изгибающих моментов. Определим реакции опор :
ΣmC=-RAL+0.8FL=0 , откуда
RA=0.8F=0.8×11=8.8 кН
ΣmA=RCL-0.2FL=0 , откуда
RC=0.2F=0.2×11=2.2 кН
Балка имеет два участка. Обозначим zi расстояние от левого (правого) конца балки до некоторого её сечения. Найдём изгибающие моменты в характерных сечениях балки.
MA=0 ; MBл=0.2RAL=0.2×8.8×3=5.28 кН·м ; MBпр=0.8RCL=0.8×2.2×3=5.28 кН·м ; MC=0.
Эпюра изгибающих моментов построена на рисунке, со стороны растянутых волокон.
Тогда, при Mx=5.28 кН∙м (в сечении B) наибольшее напряжение в балке от статического действия груза :
=7.1×106 Па=7.1 МПа
Для определения динамического коэффициента вычислим величину прогиба в точке приложения груза от статического действия его.
Воспользуемся методом начальных параметров. Начало отсчёта абсциссы z примем на опоре A, где y0=0. В точке удара :
В точке удара :
EJyB=
Неизвестный начальный параметр ν0 найдём, составив уравнения для сечения С, где yC=0 :
EJyC=
Откуда : ν0=
Тогда, при найденном выражении для ν0, получим :
EJyB=
EJyB=
Откуда yB==-9.5×10-5 м=-0.095 мм
где Е=2×1011 Па – модуль упругости ; J=Jx=13380 см4 – момент инерции (по таблице сортамента прокатной стали).
Находим динамический коэффициент :
kd==113.4
Находим динамическое напряжение :
МПа
Находим прогиб от динамического действия груза F в точке удара :
yd=kdyst=kdyB=113.4×0.095=10.8 мм.
Вычислим наибольшее напряжение в балке при условии, что правая опора заменена пружиной.
В случае опирания правого конца балки на пружину при действии на балку статической силы F пружина под влиянием опорной реакции RC=2. 2 кН, укоротится на длину a=RCα=
2 кН, укоротится на длину a=RCα=
=2.2×3=6.6 мм. Правый конец балки при этом опустится на величину a, а сечение B балки – на величину yBст=0.2a=0.2×6.6=1.32 мм.
Полное вертикальное перемещение от статического действия силы F в сечении под силой (в сечении B) равно сумме величин прогиба, найденной при расчёте балки без пружины, и перемещения, вызванного сжатием пружины, т.е. :
Δст=yB+yBст=0.095+1.32=1.415 мм.
Находим динамический коэффициент :
kd==30.1
Находим динамическое напряжение :
МПа
Находим прогиб от динамического действия груза F в точке удара :
yd=kdyst=kdΔст=30.1×1.415=42.6 мм.
Таким образом, установка пружины под правым концом балки уменьшила динамические напряжения в 805.14/213.71=3.8 раза.
Задачи на динамические нагрузки | ПроСопромат.ру
На двутавровую балку (№ 20)длиной l=9м, свободно лежащую на двух жестких опорах , с высоты h=5 см падает груз Q=1200Н.
Требуется: найти наибольшее нормальное напряжение в балке и определить прогиб балки в месте падения груза.
1) Рассчитываем балку на действие статической нагрузки. Прикладываем силу Q и строим эпюру изгибающих моментов МF. Для этого определяем реакции:
Максимальный момент будет равен:
2) В место падения груза прикладываем единичную силу и строим единичную эпюру (эпюру моментов от единичной нагрузки).
Максимальный момент будет равен:
3) Определяем максимальный прогиб балки в месте падения груза при статическом действии нагрузки по любому изученному методу определения перемещений. Например, по правилу Верещагина:
4) Определяем динамический коэффициент:
5) Наибольшее нормальное напряжение в балке при ударе
6) Наибольший прогиб при ударе:
Запись опубликована автором admin в рубрике Задачи на динамические нагрузки.
Консольная балка из двутавра №22 подверглась удару при падении груза F=10кН в сечении С. Высота падения Н=2см.
Найти прогиб свободного конца балки.
Решение:
Здесь придется дважды определить прогибы от статического действия силы веса падающего груза: прогиб в точке С для определения динамического коэффициентаи прогиб конца консоли для ответа на поставленный в задаче вопрос:
«Перемножением» эпюр находим:
Динамический коэффициент при ударе
Тогда динамический прогиб конца консоли будет:
Запись опубликована автором admin в рубрике Задачи на динамические нагрузки.
Пусть груз F=10кН падает с высоты H=10см на двутавровую стойку длиной ℓ=4м.
Определить:
1) максимальное нормальное напряжение
2) наибольшее укорочение стойки при ударе.
Считать, что стойка не теряет устойчивости.
Решение.
Расчетными формулами при ударе являются:
где динамический коэффициент при ударе
— эти параметры соответствуют статическому способу приложения силы веса падающего груза, то есть:
Запись опубликована автором admin в рубрике Задачи на динамические нагрузки.
На двутавровой балке установлен электродвигатель весом G=5кН, при работе которого из-за дисбаланса вращающихся частей возникает вертикальная центробежная сила при скорости вращения n=300 об/мин.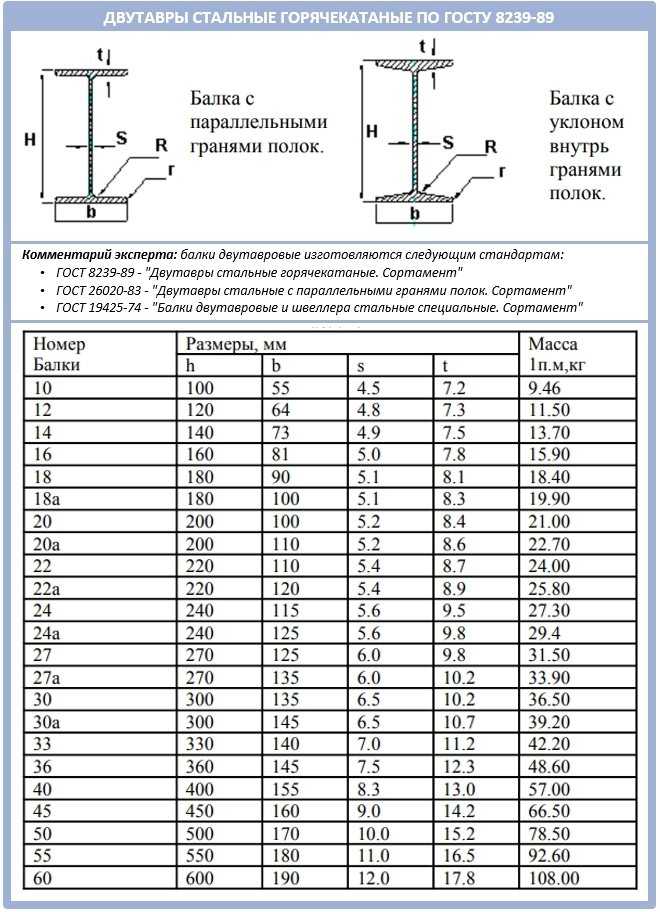
Определить наибольшие нормальные напряжения и прогиб.
Решение:
Балка находится под действием двух нагрузок: под действием статической нагрузки – веса двигателя G и под действием динамической (вибрационной) нагрузки F. Поэтому все параметры складываются из статической и динамической составляющих:
Статические составляющие от силы G найдем как обычно при статическом расчете:
Наибольшее статическое напряжение в среднем сечении балки будет:
Для определения статического прогиба среднего сечения выберем вспомогательное состояние и построим эпюру :
Прогиб от статической нагрузки G будет:
Динамические значения параметров от действия вибрационной нагрузки определяются с помощью динамического коэффициента следующим образом:
В формулу динамического коэффициента вибрационной нагрузки входит величина ω – круговая частота собственных (свободных) колебаний, определяемая по формуле:
где: g=9,81м/сек2 –ускорение свободного падения,
Δст – перемещение точки расположения колеблющейся массы (в данном случае двигателя) от собственного веса.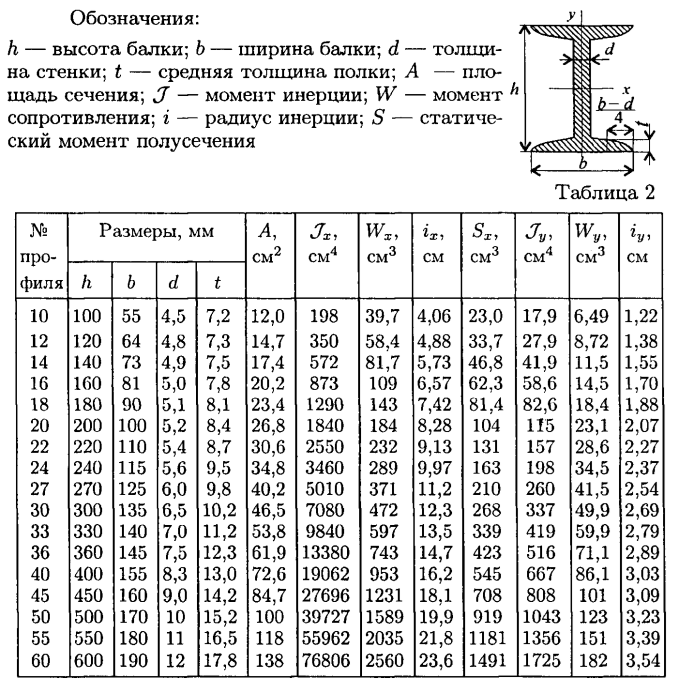
Тогда значение динамического коэффициента вибрационной нагрузки будет:
Здесь круговая частота действия самой вибрационной нагрузки
Далее находим , для чего к балке прикладывается наибольшая величина вибрационной нагрузки статическим образом:
Прогиб середины пролета в балке на двух опорах можно вычислить и по известной формуле:
Тогда динамические значения искомых параметров будут:
представляет собой амплитуду колебаний массы (двигателя), то есть наибольшее отклонение от положения статического равновесия. Поэтому наибольшее значение прогиба складывается из статического смещения и амплитуды колебаний
Наибольшее нормальное напряжение
Запись опубликована автором admin в рубрике Задачи на динамические нагрузки.
Как загрузить расчет для колонн, балок, стен и перекрытий | Расчет конструкции колонны | Расчет нагрузки на балку | Расчет нагрузки на стену
Важный момент
Что такое колонна?
Сжимающий элемент, т. е. колонна, является важным элементом каждой железобетонной конструкции . Они используются для безопасной передачи нагрузки от надстройки на фундамент.
В качестве сжимающих элементов в зданиях, мостах, опорных системах резервуаров, заводов и многих других подобных сооружений используются в основном колонны, стойки и пьедесталы.
Колонна определяется как элемент вертикального сжатия, который в основном подвергается действию эффективной длины и осевых нагрузок , которые в три раза превышают его наименьший поперечный размер.
Сжимаемый элемент, эффективная длина которого меньше, чем в три раза его наименьшего поперечного размера, называется пьедесталом.
Элемент сжатия, который наклонен или горизонтален и подвергается осевым нагрузкам, называется распоркой. Распорки используются в фермах.
Функция колонн — передавать нагрузку конструкции вертикально вниз, чтобы передать ее на фундамент. Кроме того, стена выполняет следующие функции:
- Ограждает помещения здания на различные отсеки и обеспечивает конфиденциальность.
- Обеспечивает защиту от взлома и насекомых.
- Сохраняет тепло в здании зимой и летом.
№
Также читайте: Что такое Pier Foundation | Типы буровых пирсов | Преимущества и недостатки буронабивных фундаментов
Что такое луч?
Балка – элемент конструкции, противостоящий изгибу. В основном балка несет вертикальные гравитационные силы, но также тянет на нее горизонтальные нагрузки.
Балка называется стеновой плитой или плитой порога , которая несет передачи и нагружает их на балки, колонны или стены. Он прилагается с.
Он прилагается с.
В первые века древесина была наиболее предпочтительным материалом для использования в качестве балки для этой структурной опоры, теперь, чтобы выдерживать силу наряду с переносом вертикальной силы тяжести, теперь они состоят из алюминия, стали или другого подобного материала. материалы.
В действительности балки представляют собой конструкционные материалы, которые воспринимают абсолютную силу нагрузки и изгибающий момент.
Чтобы выдерживать большее напряжение и нагрузку, в настоящее время в фундаментах мостов и других подобных огромных сооружений широко используются предварительно напряженные бетонные балки.
Поддерживаются несколько известных балок, используемых в настоящее время: Балка, Фиксированная балка, Консольная балка, Непрерывная балка, Нависающая балка.
Что такое стена?
Стена – конструктивный элемент, разделяющий пространство (помещение) на два пространства (комнаты), а также обеспечивающий безопасность и укрытие. Как правило, стены делятся на два типа: внешние стены и внутренние стены.
Как правило, стены делятся на два типа: внешние стены и внутренние стены.
Внешние стены служат ограждением дома для укрытия, а внутренние стены помогают разделить ограждение на необходимое количество комнат. Внутренние стены также называют перегородками.
Стены строятся для разделения жилого помещения на разные части. Они обеспечивают конфиденциальность и защиту от температуры, дождя и кражи.
Также читайте: Что такое гипс | Тип гипса | Дефекты штукатурки
Что такое плита?
Плита сконструирована для обеспечения плоских поверхностей, обычно горизонтальных, при строительстве крыш, полов, мостов и других типов конструкций . Плита может поддерживаться стенами , железобетонными балками, обычно , монолитно отлитыми с плитой, балками из конструкционной стали, колоннами или землей.
Плита представляет собой пластинчатый элемент, глубина (D) которого очень мала по сравнению с его длиной и шириной. Плита используется в качестве пола или крыши в зданиях, равномерно распределяет нагрузку.
Плита используется в качестве пола или крыши в зданиях, равномерно распределяет нагрузку.
Плита Может быть
- Просто поддерживается.
- Непрерывный.
- Консольный.
Расчет различных нагрузок на колонну, балку, стену и перекрытие
- Колонна = собственный вес x количество этажей
- Балки = собственный вес на погонный метр
- Нагрузка на стену на погонный метр
- Суммарная нагрузка на плиту (постоянная нагрузка + временная нагрузка + ветровая нагрузка + собственный вес)
Помимо вышеуказанной нагрузки, на колонны также действуют изгибающие моменты, которые необходимо учитывать при окончательном расчете. Эти инструменты уменьшают трудоемкий и трудоемкий метод ручных расчетов при проектировании конструкций, что в настоящее время настоятельно рекомендуется в этой области.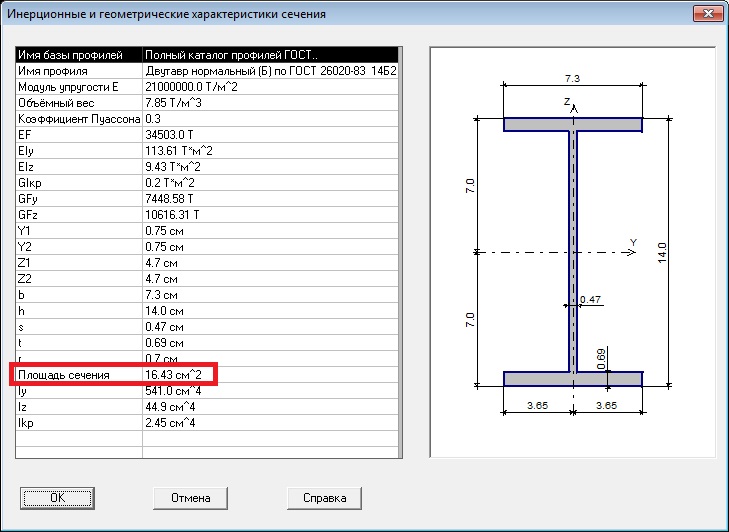
Наиболее эффективным методом проектирования конструкции является использование современного программного обеспечения для проектирования конструкций, такого как STAAD Pro или ETABS. Для профессиональной практики проектирования конструкций существуют некоторые основные допущения, которые мы используем для расчетов несущей способности конструкции.
Также читайте: Введение Козловой балки | Нагрузка на портальный желоб | Тип нагрузки на портальный желоб
Расчет нагрузки на колонну:
Мы знаем, что собственный вес бетона составляет около 2400 кг/м 3 , , что эквивалентно 24,54 4 м кн/4 и собственный вес стали около 7850 кг/м 3 . (Примечание: 1 килоньютон равен 101,9716 килограмма)
Итак, если мы предположим, что размер столбца равен 300 мм x 600 мм с 1% стали и 2,55 ( почему 2,55 так, высота колонны 3 м — размер балки ) метров стандартная высота, собственный вес колонны около 1000 кг на этаж , что id равно 10 кН.
Как загрузить расчет в столбец?
- Размер колонны Высота 2,55 м, длина = 300 мм, ширина = 600 мм
- Объем бетона = 0,30 x 0,60 x 2,55 = 0,459 м³
- Вес бетона = 0,459 x 2400 = 1101,60 кг
- Вес стали (1%) в бетоне = 0,459 x 1% x 7850 = 36,03 кг
- Общий вес колонны = 1101,60 + 36,03 = 1137,63 кг = 11,12 кН
При выполнении расчетов мы предполагаем, что собственный вес колонн составляет от 10 до 12 кН на этаж.
Расчет нагрузки на балку:
Мы применяем тот же метод расчета и для балки.
мы предполагаем, что каждый метр балки имеет размеры 300 мм x 600 мм без учета толщины плиты.
Предположим, что каждый (1 м) метр балки имеет размеры
Как
Расчет нагрузки на балку ?
- 300 мм x 600 мм без плиты.
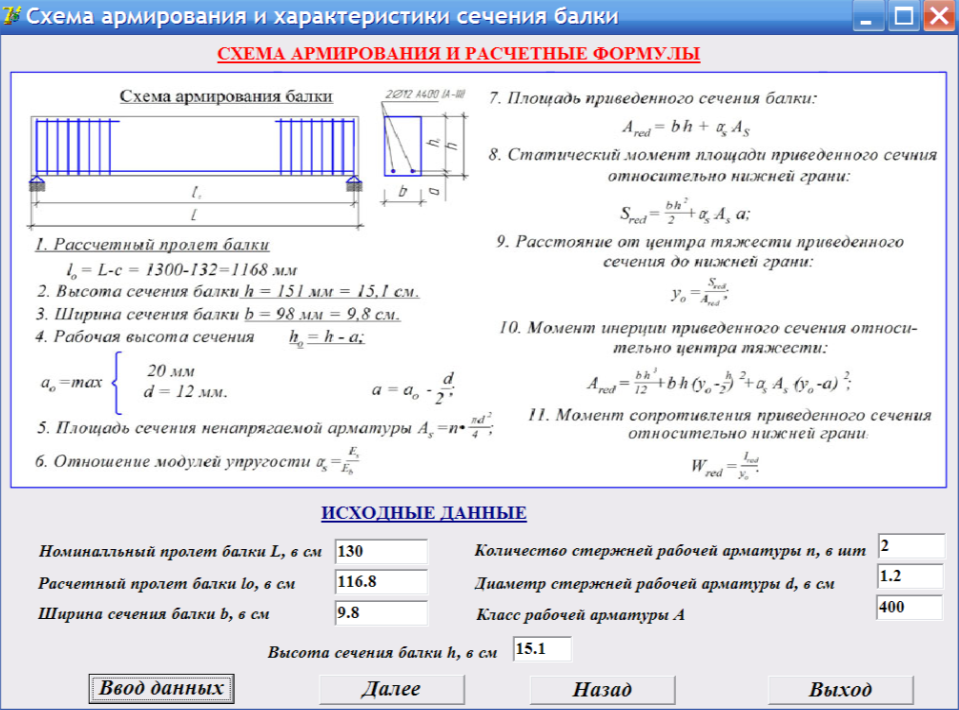
- Объем бетона = 0,30 x 0,60 x 1 = 0,18 м³
- Вес бетона = 0,18 x 2400 = 432 кг
- Вес стали (2%) в бетоне = 0,18 x 2% x 7850 = 28,26 кг
- Общий вес колонны = 432 + 28,26 = 460,26 кг/м = 4,51 кН/м
Таким образом, собственный вес составит около 4,51 кН на погонный метр.
Также читайте: Разница между битумом и дегтем | Что такое битум | Что такое Tar
Как рассчитать нагрузку на стену :
Мы знаем, что плотность кирпича варьируется от 1800 до 2000 кг/м 3 .
Для кирпичной стены толщиной 9 дюймов (230 мм), высотой 2,55 м и длиной 1 м ,
Нагрузка на погонный метр должна быть равна ,
, что эквивалентно 11,50 кН/метр.
Этот метод можно использовать для расчета нагрузки кирпича на погонный метр для любого типа кирпича с использованием этого метода.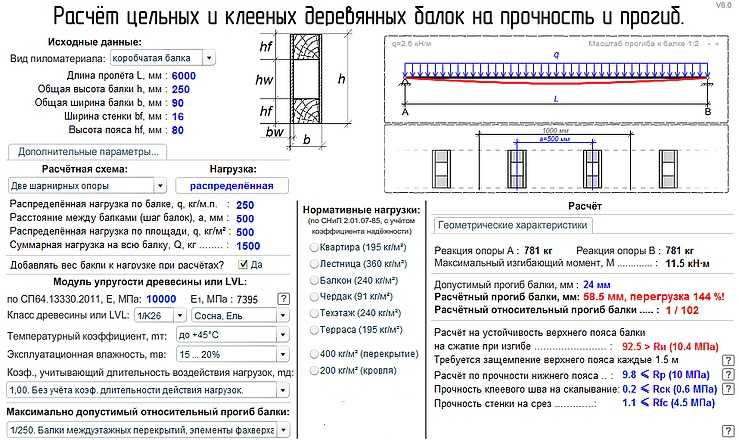
Для газобетонных блоков и блоков из автоклавного бетона (ACC), таких как Aerocon или Siporex, вес на кубический метр составляет от от 550 до 650 кг за кубический метр.
Нагрузка на погонный метр должна быть равна 0,230 x 1 x 2,55 x 650 = 381,23 кг. , использование этого блока позволяет значительно удешевить проект.
Расчет нагрузки на плиту :
Допустим, толщина плиты 150 мм.
Таким образом, собственный вес каждого квадратного метра плиты будет равен
Расчет нагрузки плиты = 0,150 x 1 x 2400 = 360 кг, что эквивалентно 3,53 кН.
Теперь, если принять во внимание, что нагрузка на отделку пола составляет 1 кН на метр , наложенная временная нагрузка составляет 2 кН на метр, а ветровая нагрузка согласно Is 875 Около 2 кН на метр .
Таким образом, исходя из приведенных выше данных, мы можем оценить нагрузку на плиту примерно от 8 до 9 кН на квадратный метр.
Как загрузить расчет Колонковой стенки. Стенная плита луча
FAQ
Расчет нагрузки на столбце:
- Торг бетон = 0,23 x 0,60 x 3 = 0,414M=
- Вес бетона = 0,414 x 2400 = 993,6 кг
- Вес стали (1%) в бетоне = 0,414x 0,01 x 8000 = 33 кг
- Общий вес колонны = 994 + 33 = 1026 кг = 10КН
.
Расчет нагрузки на стену
- Плотность кирпича стены с раствором составляет примерно 1600-2200 кг/м 3 . Таким образом, мы считаем собственный вес кирпича стены равным 2200 кг/м 3 в этом расчете .
- Объем кирпичной стены: Объем кирпичной стены = l × b × h, длина = 1 метр, ширина = 0,152 мм, высота стены = 2,5 метра, объем = 1 м × 0,152 м × 2,5 м, объем кирпичной стены = 0,38 м 3
- Собственная нагрузка кирпичной стены: Вес = объем × плотность, Собственная нагрузка = 0,38 м 3 × 2200 кг/м 3 , Собственная нагрузка = 836 кг/м
- Переведем в килоньютоны, разделив на 100, получим 8,36 кН/м
- Таким образом, статическая нагрузка кирпичной стены составляет около 8,36 кН/м, действующая на колонну.

Расчет нагрузки на балку
- 300 мм x 600 мм без учета толщины плиты.
- Объем бетона = 0,30 x 0,60 x 1 = 0,18 м³
- Вес бетона = 0,18 x 2400 = 432 кг
- Вес стали (2%) в бетоне = 0,18 x 2% x 7850 = 28,26 кг
- Общий вес колонны = 432 + 28,26 = 460,26 кг/м = 4,51 кН/м
Нагрузка на колонну
Колонна является важным конструктивным элементом конструкции RCC, который помогает передавать нагрузку надстройки от надстройки на фундамент. Это элемент вертикального сжатия, подвергающийся прямому осевому нагрузки и его эффективная длина в три раза больше, чем его наименьший поперечный размер.
Расчет статической нагрузки для здания
Статическая нагрузка = объем элемента x удельный вес материалов.
Путем расчета объема каждого элемента и умножения на единицу веса материалов, из которых он состоит, можно определить точную статическую нагрузку для каждого компонента.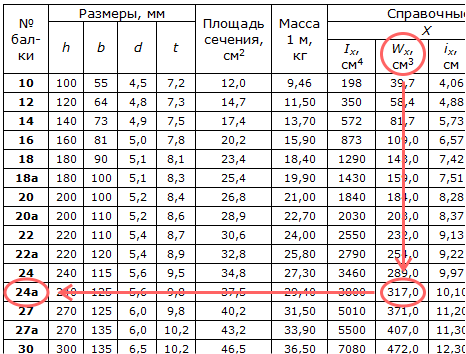
Расчет конструкции колонны
- Объем бетона = 0,23 x 0,60 x 3 = 0,414 м³
- Вес бетона = 0,414 x 2400 = 993,6 кг
- Вес стали (1%) в бетоне = 0,414x 0,01 x 8000 = 33 кг
- Общий вес колонны = 994 + 33 = 1026 кг = 10 кН
Расчет нагрузки на фундамент
Для стены толщиной 6 дюймов, высотой 3 метра и длиной 1 метр нагрузка может быть измерена на погонный метр, что эквивалентно 0,150 x 1 x 3 x 2000 = 900 кг, что эквивалентно 9 кН/метр . Нагрузку на погонный метр можно измерить для любого типа кирпича, следуя этому методу.
Расчет нагрузки на бетонную плиту
- Размер плиты Длина 3 м x 2 м Толщина 0,150 м
- Объем бетона = 3 x 2 x 0,15 = 0,9 м³
- Вес бетона = 0,9 х 2400 = 2160 кг.
Расчет нагрузки на сталь
- Размер плиты Длина 3 м x 2 м Толщина 0,150 м
- Объем бетона = 3 x 2 x 0,15 = 0,9м³
- Вес бетона = 0,9 х 2400 = 2160 кг.
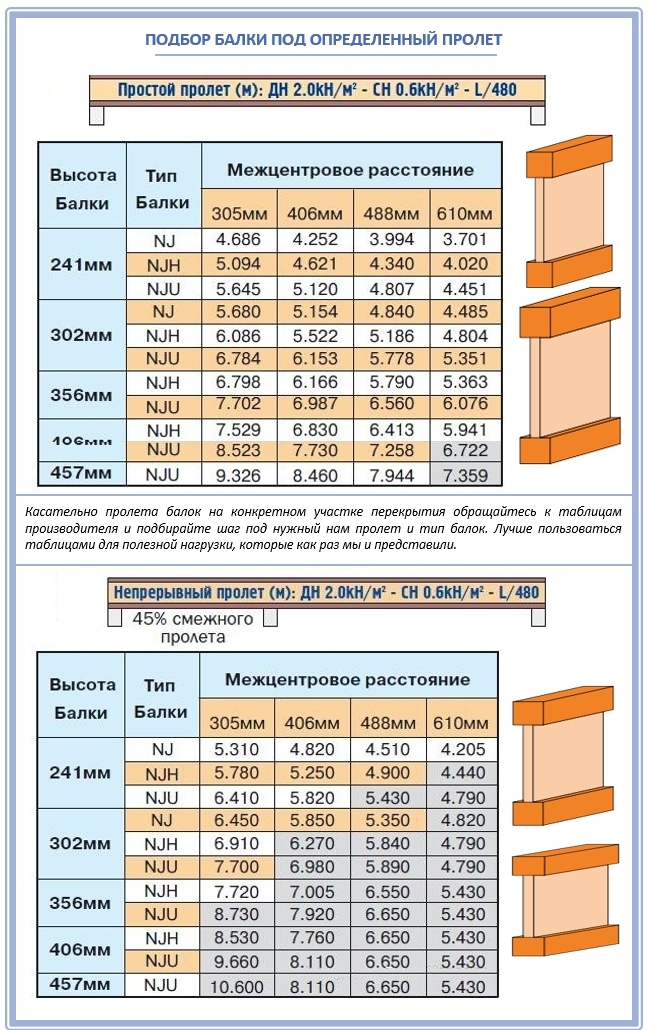
- Вес стали (1%) в бетоне = 0,9 x 0,01 x 7850 = 70,38 кг.
- Общий вес колонны = 2160 + 70,38 = 2230,38 кг/м = 21,87 кН/м.
Как рассчитать нагрузку на балку
- 300 мм x 600 мм без плиты.
- Объем бетона = 0,30 x 0,60 x 1 = 0,18 м³
- Вес бетона = 0,18 x 2400 = 432 кг
- Вес стали (2%) в бетоне = 0,18 x 2% x 7850 = 28,26 кг
- Общий вес колонны = 432 + 28,26 = 460,26 кг/м = 4,51 кН/м
Как рассчитать нагрузку на балку
Простой взгляд вокруг покажет нам простой, но интересный факт, что каждый объект, живой или неживой, постоянно прикладывает определенную нагрузку к определенному основанию и одновременно подвергается действию равной и противоположной величины силы со стороны поддерживаемого основания.
Автомобиль, припаркованный над местом, оказывает на землю силу или оказывает нагрузку, которая может быть равна его весу; однако земля также оказывает равную, но противоположную силу на автомобиль, так что он остается на месте неповрежденным.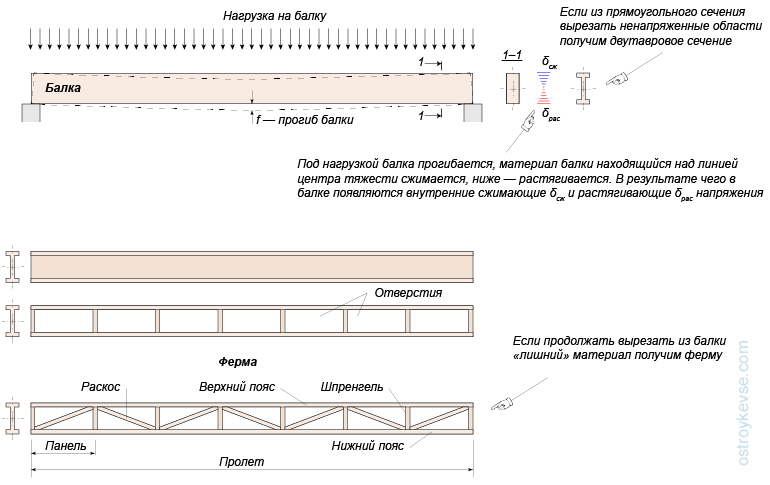 Поскольку автомобиль удерживается в одном постоянном положении, это означает, что две силы должны быть равны и действовать в противоположных направлениях.
Поскольку автомобиль удерживается в одном постоянном положении, это означает, что две силы должны быть равны и действовать в противоположных направлениях.
Обычно на любой объект, представляющий собой нагрузку, обычно действуют следующие две силы:
- Вес объекта, действующий на землю
- Реакция земли или основания, действующая на объект вверх
Прежде чем мы Чтобы перейти к деталям расчета нагрузки на балку, важно сначала узнать о типах нагрузок, которые могут действовать на балку, поддерживаемую на ее концах.
Нагрузку можно разделить на следующие важные типы:
- Точечная нагрузка, резко ограниченная одной точкой,
- Равномерно или равномерно распределенная нагрузка и,
- Равномерно изменяющаяся нагрузка.
Давайте разберем их по порядку.
Точечная нагрузка: Нагрузка или вес, воздействующий на точечную площадь, называется точечной нагрузкой . Однако с математической точки зрения точечная нагрузка не выглядит осуществимой просто потому, что любая нагрузка должна иметь определенную площадь удара и не может балансировать в точке, но если площадь удара слишком мала по сравнению с длиной балки, может приниматься как определено.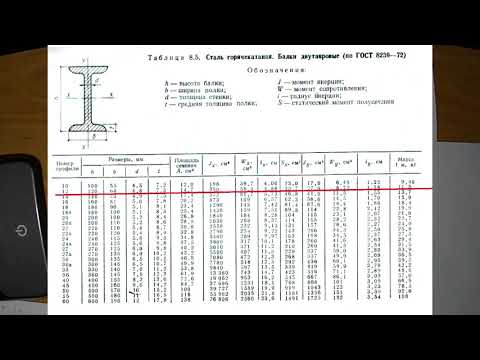
Равномерно распределенная нагрузка: Как следует из названия, нагрузка, равномерно распределенная по всей балке, называется равномерно распределенной нагрузкой .
Равномерно изменяющаяся нагрузка: Нагрузки, распределенные по балке, которые создают равномерно увеличивающийся градиент нагрузки по всей балке от конца до конца, называются равномерно изменяющейся нагрузкой .
Балка может быть подвергнута одной из вышеуказанных нагрузок или их комбинациям.
Лучевые реакции
На следующем простом рисунке мы познакомимся с формулами, относящимися к расчету нагрузки на балку или, точнее, реакции балки: буквами А и В соответственно.
Пусть на балку действуют точечные нагрузки в точках, отмеченных как W1, W2 и W3.
Также пусть,
RA = Реакция на конце A балки.
RB = Реакция на конце B балки.
В основном существует пара сил (эффект поворота), которые действуют на концы балки A и B, а именно.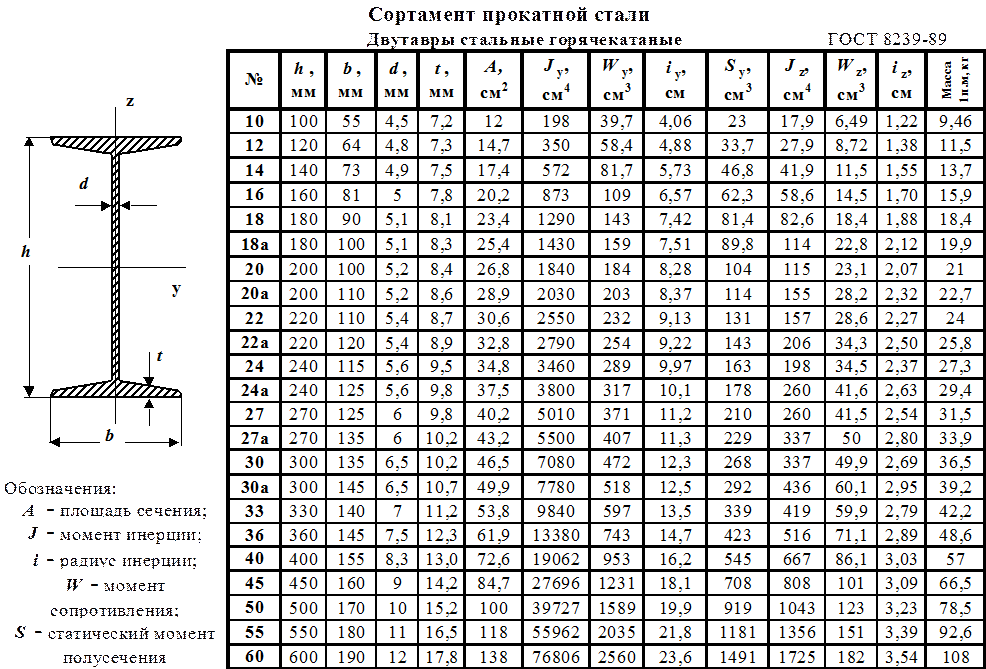 по часовой стрелке и против часовой стрелки момент силы.
по часовой стрелке и против часовой стрелки момент силы.
Поскольку момент силы, действующей на опорную балку, равен произведению Силы (здесь веса) на ее расстояние от опоры или оси вращения, общий момент по часовой стрелке, действующий в точке A, может быть равен:
W1. a + W2.b + W3.c,
Также против часовой стрелки момент силы, действующей на точку B, должен быть:
RB.1
Теперь, поскольку балка находится в равновесии, подразумевается, что два вышеупомянутых момента силы должны быть равны по величине, поэтому приравнивание двух выражений дает:
W1.a + W2.b + W3.c = RB.l
RB = W1.a + W2.b + W3.c / l
Равновесие с балкой также означает, что:
RA + RB = W1.a + W2.b + W3.c
RA = ( W1.a + W2.b + W3.c) — RB
Теперь, согласно условиям равновесия, алгебраическая сумма всех горизонтальных компонент в приведенное выше выражение становится несущественным и может быть обнулено (ƩH = 0. )
)
Следовательно, окончательное уравнение принимает вид
RA = (W1 + W2 + W3) — RB
Приведенную выше формулу можно использовать для определения реакции нагруженной балки относительно ее концевых опор.
Расчет поперечной силы и изгибающего момента
При расчете нагрузки на балку также используются два важных параметра: поперечная сила (SF) и изгибающий момент (BM).
Выведем их с помощью следующей простой иллюстрации:
Ссылаясь на рисунок рядом, рассмотрим балку, нагруженную равномерно распределенной нагрузкой Вт на единицу длины. Также рассмотрим некоторый участок балки RS, имеющий длину δx на расстоянии x от левой опоры балки.
Нагрузка, действующая на сечение RS балки, будет равна Вт. δx ( момент Силы).
Теперь предположим, что сила сдвига в точке R равна = F,
Тогда в точке S она будет равна F + δF .
Кроме того, если изгибающий момент при R = M , то при S он становится M + δM.
Так как балка находится в равновесии, то приложенный момент также должен подчиняться законам равновесия, поэтому приравнивая два неуравновешенных выражения при S получаем:
Или δF/δx = W,
Приведенные выше выражения показывают, что скорость изменения силы сдвига равна давлению нагрузки или интенсивности.
Аналогично моменты в S можно приравнять как:
M – F.δx – Wδx2/2 = M + δM
Или δM = – F.δx, (без учета тривиальной величины δx2)
Получаем , δM/δx = – F
Приведенное выше соотношение показывает, что скорость изменения изгибающего момента равна поперечной силе сечения RS.
Данные (формула реакции, отношение поперечной силы и изгибающего момента), приведенные в этой статье, могут использоваться при расчете нагрузки на балку для дальнейшего определения качества и типа материала, который будет использоваться для безопасной нагрузки на балку.