Расчет прогиба балки двутавровой балки: Расчёт металлической балки онлайн (калькулятор)

Содержание

Расчет прочности и жесткости прокатной балки двутаврового сечения

1 – балка настила

Цель: Проверка режима расчета сопротивления сечений

Задача: Проверить расчетное сечение прокатного двутаврового профиля для балок настила пролетом 6 м в балочной клетке нормального типа. Верхний пояс балок настила непрерывно раскреплен настилом.

Источник: Металлические конструкции: учебник для студ. Учреждений высш. проф. Образования / [Ю. И. Кудишин, Е. И. Беленя, В. С. Игнатьева и др.]; под. Ред. Ю. И. Кудишина. — 13-е изд., испр. — М. : Издательский центр «Академия», 2011. С 183.

Соответствие нормативным документам: СНиП II-23-81*, СП 16.13330, ДБН В.2.6-163:2010.

Имя файла с исходными данными:

4.2.sav;
отчет — Kristall4.2.doc

Исходные данные:

а = 1,125 мШаг балок настила;
Ry = 23 кН/cм2,Сталь марки C235;
M = 125,55 кНмРасчетный изгибающий момент;
γc = 1Коэффициент условий работы;
l = 6 мПролет балки;
сx = 1,1Коэффициент для учета пластических деформаций;
Wx = 597 см3
iy = 13,524см, iz = 2,791 см.		Принятый двутавр №33 по ГОСТ 8239-89;

 

Параметры КРИСТАЛЛ:

 

Сталь: C235

Группа конструкций по таблице 50* СНиП II-23-81* 4
Коэффициент надежности по ответственности  γn = 1
Коэффициент надежности по ответственности (2-е предельное состояние)  = 1
Коэффициент условий работы 1

Конструктивное решение

Закрепления от поперечных смещений и поворотов

 

Слева

Справа

Смещение вдоль Y

Закреплено

Закреплено

Смещение вдоль Z

Закреплено

Закреплено

Поворот вокруг Y

 

 

Поворот вокруг Z

 

 

 

Сплошное закрепление сжатого пояса из плоскости изгиба

Сечение

Профиль: Двутавp с уклоном полок по ГОСТ 8239-89  33

 

Ручной расчет (СНиП II-23-81*):

 

1.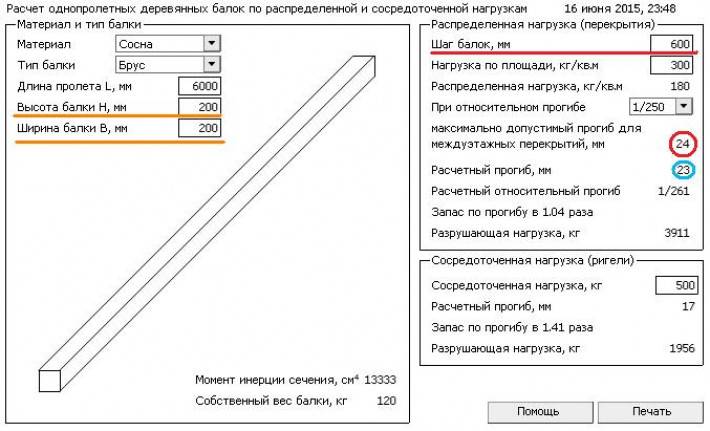 {3}. \]

2. Гибкость элемента в плоскости действия момента:

\[ \lambda_{y} =\frac{\mu l}{i_{y} }=\frac{6\cdot 100}{13,524}=44,3656. \]

3. Гибкость элемента из плоскости действия момента:

\[ \lambda_{z} =\frac{l_{ef,z} }{i_{z} }=\frac{6\cdot 100}{2,791}=214,9767. \]

Сравнение решений:

Фактор

Источник

Ручной счет

КРИСТАЛЛ

Отклонение от ручного счета, %

Прочность при действии изгибающего момента Му

0,83

545,8696/597 = 0,914

0,915

0,0

Прочность при совместном действии продольной силы и изгибающих моментов без учета пластики

–

545,8696/597 = 0,914

0,915

0,0

Устойчивость плоской формы изгиба

–

545,8696/1/597 = 0,914

0,915

0,0

Предельная гибкость в плоскости XoY

–

214,9767/250 = 0,86

0,86

0,0

Предельная гибкость в плоскости XoZ

–

44,3656/250 = 0,177

0,177

0,0

Комментарии:

  1. В источнике проверка прочности балки выполнялась с учетом развития ограниченных пластических деформаций.
  2. Проверка прочности балки с учетом развития ограниченных пластических деформаций при ручном счете не выполнялась, поскольку согласно норм такой расчет возможен только при соответствующем оребрении стенки балки. В исходных данных примера балка настила задавалась без промежуточных ребер жесткости.

Расчет несущей способности и прогиба деревянных балок

Чтобы построить деревянный дом необходимо провести расчёт несущей способности деревянной балки. Также особое значение в строительной терминологии имеет определение  прогиба.

Без качественного математического анализа всех параметров просто невозможно построить дом из бруса. Именно поэтому перед тем как начать строительство крайне важно правильно рассчитать прогиб деревянных балок. Данные расчёты послужат залогом вашей уверенности в качестве и надёжности постройки.

Что нужно для того чтобы сделать правильный расчёт

Расчёт несущей способности и прогиба деревянных балок не такая простая задача, как может показаться на первый взгляд. Чтобы определить, сколько досок вам нужно, а также, какой у них должен быть размер необходимо потратить немало времени, или же вы просто можете воспользоваться нашим калькулятором.

Во-первых, нужно замерить пролёт, который вы собираетесь перекрыть деревянными балками. Во-вторых, уделите повышенное внимание методу крепления. Крайне важно, насколько глубоко фиксирующие элементы будут заходить в стену. Только после этого вы сможете сделать расчёт несущей способности вместе с прогибом и ряда других не менее важных параметров.

Длина

Перед тем как рассчитать несущую способность и прогиб, нужно узнать длину каждой деревянной доски. Данный параметр определяется длиной пролёта. Тем не менее это не всё. Вы должны провести расчёт с некоторым запасом.

Важно! Если деревянные балки заделываться в стены — это напрямую влияет на их длину и все дальнейшие расчёты.

При подсчёте особое значение имеет материал, из которого сделан дом. Если это кирпич, доски будут монтироваться внутрь гнёзд. Приблизительная глубина около 100—150 мм.

Когда речь идёт о деревянных постройках параметры согласно СНиПам сильно меняются. Теперь достаточно глубины в 70—90 мм. Естественно, что из-за этого  также изменится конечная несущая способность.

Если в процессе монтажа применяются хомуты или кронштейны, то длина брёвен или досок соответствует проёму. Проще говоря, высчитайте расстояние от стены до стены и в итоге сможете узнать несущую способность всей конструкции.

Важно! При формировании ската крыши брёвна выносятся за стены на 30—50 сантиметров. Это нужно учесть при подсчёте способности конструкции противостоять нагрузкам.

К сожалению, далеко не всё зависит от фантазии архитектора, когда дело касается исключительно математики. Для обрезной доски максимальная длина шесть метров. В противном случае несущая способность уменьшается, а прогиб становится больше.

Само собой, что сейчас не редкость дома, у которых пролёт достигает 10—12 метров. В таком случае используется клееный брус. Он может быть двутавровым или же прямоугольным. Также для большей надёжности можно использовать опоры. В их качестве идеально подходят дополнительные стены или колоны.

Совет! Многие строители при необходимости перекрыть длинный пролёт используют фермы.

Общая информация по методологии расчёта

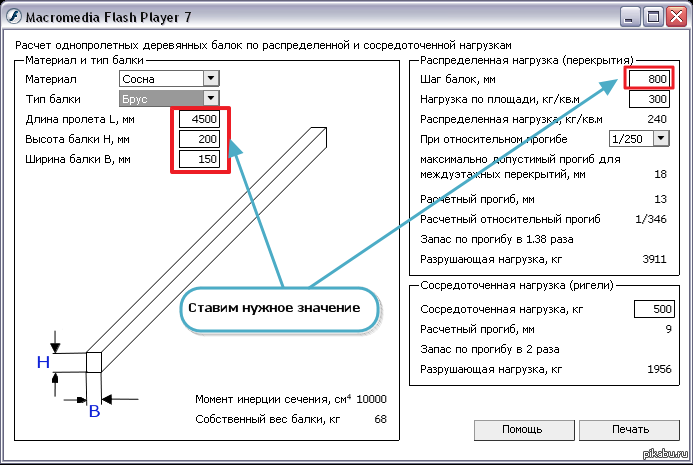
В большинстве случаев в малоэтажном строительстве применяются однопролётные балки. Они могут быть в виде брёвен, досок или брусьев. Длина элементов может варьироваться в большом диапазоне. В большинстве случаев она напрямую зависит от параметров строения, которые вы собираетесь возвести.

Внимание! Представленный в конце странички калькулятор расчета балок на прогиб позволит вам просчитать все значения с минимальными затратами времени. Чтобы воспользоваться программой, достаточно ввести базовые данные.

Роль несущих элементов в конструкции выполняют деревянные бруски, высота сечения которых составляет от 140 до 250 мм, толщина лежит в диапазоне 55—155 мм. Это наиболее часто используемые параметры при расчёте несущей способности деревянных балок.

Очень часто профессиональные строители для того чтобы усилить конструкцию используют перекрёстную схему монтажа балок. Именно эта методика даёт наилучший результат при минимальных затратах времени и материалов.

Если рассматривать длину оптимального пролёта при расчёте несущей способности деревянных балок, то лучше всего ограничить фантазию архитектора в диапазоне от двух с половиной до четырёх метров.

Внимание! Лучшим сечением для деревянных балок считается площадь, у которой высота и ширина соотносятся как 1,5 к 1.

Как рассчитать несущую способность и прогиб

Стоит признать, что за множество лет практики в строительном ремесле был выработан некий канон, который чаще всего используют для того, чтобы провести расчёт несущей способности:

M/W<=Rд

Расшифруем значение каждой переменной в формуле:

  • Буква М вначале формулы указывает на изгибающий момент. Он исчисляется в кгс*м.
  • W обозначает момент сопротивления. Единицы измерения см3.

Расчёт прогиба деревянной балки является частью, представленной выше формулы. Буква М указывает нам на данный показатель. Чтобы узнать параметр применяется следующая формула:

M=(ql2)/8

В формуле расчёта прогиба есть всего две переменных, но именно они в наибольшей степени определяют, какой в конечном итоге будет несущая способность деревянной балки:

  • Символ q показывает нагрузку, которую способна выдержать доска.
  • В свою очередь буква l — это длина одной деревянной балки.

Внимание! Результат расчёт несущей способности и прогиба зависит от материала из которого сделана балка, а также от способа его обработки.

Насколько важно правильно рассчитать прогиб

Этот параметр крайне важен для прочности всей конструкции. Дело в том, что одной стойкости бруса недостаточно для долгой и надёжной службы, ведь со временем его прогиб под нагрузкой может увеличиваться.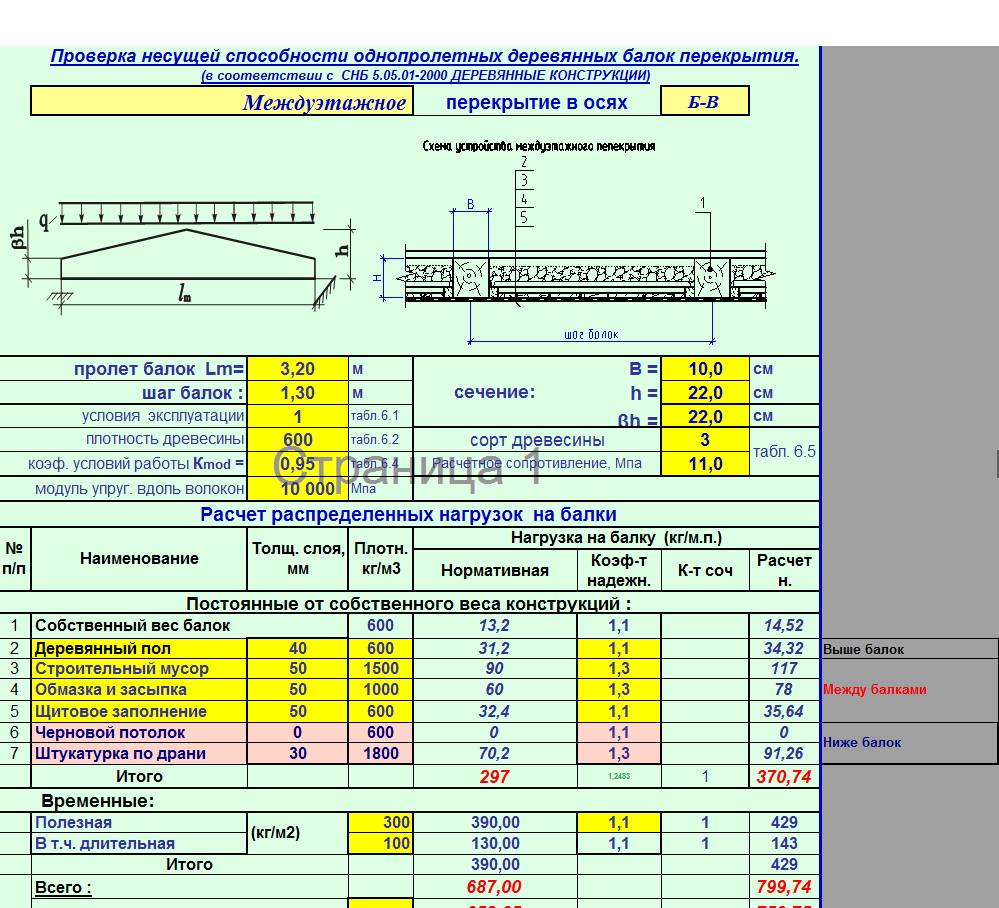

Прогиб не просто портит эстетичный вид перекрытия. Если данный параметр превысит показатель в 1/250 от общей длины элемента перекрытия, то вероятность возникновения аварийной ситуации возрастёт в десятки раз.

Так зачем нужен калькулятор

Представленный ниже калькулятор позволит вам моментально просчитать прогиб, несущую способность и многие другие параметры без использования формул и подсчётов. Всего несколько секунд и данные по вашему будущему дому будут готовы.

Калькулятор уравнений прогиба и напряжения для балки, опирающейся на оба конца при равномерной нагрузке

Калькулятор уравнений изгиба, прогиба и напряжения для балки, опираемой на оба конца при равномерной нагрузке

Прогиб балки, формула напряжения и калькуляторы

Уравнения момента инерции & Калькуляторы

Уравнения прогиба балки, напряжения, изгиба и калькулятор для балки с опорой на обоих концах при равномерной нагрузке Уравнения напряжения и прогиба и калькулятор.

Балки равномерного поперечного сечения, загруженного поперечно

Общая нагрузка («W»)

или

Нагрузка на давление (P)

Open
. Деталение луча, расщепление напряженного погрузки

9914 . Определение напряжения. Напряжение балки в любой точке

Напряжение балки в центре постоянного поперечного сечения

Прогиб балки в любой заданной точке

Максимальный прогиб балки в центре

С общей нагрузкой «Вт»

или

Максимальное отклонение балки в центре

С линейной нагрузкой давления «p»

Где:

5

9

0

Модуль упругости фунтов на квадратный дюйм

(Н/мм 2)

Я = Момент инерции в 4 (мм 4)
л = Длина балки дюймов (мм)
Ш = Общая нагрузка на балку фунтов (Н)
р = С линейной нагрузкой давления фунтов на квадратный дюйм (Н/мм)
с = Напряжение в оцениваемом поперечном сечении фунт/дюйм 2 (Н/мм 2)
г = Прогиб балки дюймов (мм)
х = Некоторое расстояние, указанное дюймов (мм)
Z = модуль поперечного сечения балки = I/z в 3 (мм 3)
г = расстояние от нейтральной оси до крайнего волокна (края) дюймов (мм)
  • Обратите внимание, буква « l » (строчная буква «L») отличается от буквы «I» (момент инерции).
  • Прогибы относятся только к постоянным поперечным сечениям по всей длине.

Ссылки:

  1. Справочник по любому оборудованию, опубликованный с 1931 года или
  2. Справочник по машинному оборудованию, 21-е издание, стр. 404 или
  3. Справочник по машинному оборудованию, 23-е издание, стр. 260 или
  4. Справочник по машинному оборудованию, 27-е издание, стр. 261 или

    5. Стандартный справочник

  5. Marks для инженеров-механиков, десятое издание, 1996 г., стр. 297 (таблица 5.2.2)
  6. Справочник инженера-механика, под редакцией Майера Куца, John Wiley & Sons, Inc., 1986, стр. 414
  7. Эшбак, Справочник по инженерным основам, третье издание, серия инженерных справочников Wiley, 1974 г., стр. 518
  8. Механика материалов, Фердинанд П. Бир и Э. Рассел Джонстон-младший ISBN0-07-004291-8

Сопутствующие товары

  • Уравнения прогиба балки, сдвига и напряжений и калькулятор для балки с опорой на один конец, консольно с реверсивной ограниченной конической нагрузкой
  • Балка с опорой на один конец, штифт на противоположный конец и частичная распределенная нагрузка Уравнения прогиба, сдвига и напряжения и калькулятор
  • Балка поддерживается одним концом, штифтом на противоположном конце и двумя отдельными частями с распределенной нагрузкой.
  • Теории хрупкого разрушения Вычисление коэффициентов запаса Калькулятор электронных таблиц Excel
  • Уравнения и калькулятор для балки, поддерживаемой одним концом, штифтом на противоположном конце и одной конической распределенной нагрузкой
  • Уравнения прогиба балки, сдвига и напряжений и калькулятор для балки, поддерживаемой одним концом, штифтом на противоположном конце и двумя коническими распределенными нагрузками
  • Усиление железобетонных балок на изгиб ламинатами FRP Калькулятор электронных таблиц
  • Уравнения сдвига и напряжений и калькулятор для балки с опорой на один конец, штифтом на противоположном конце и треугольной распределенной нагрузкой
  • Калькулятор для балки с опорой на один конец, штифтом на противоположном конце и одиночным моментом на конце
  • Уравнения напряжения и калькулятор для балки с опорой на один конец, консольной в определенном месте и одинарной нагрузкой на конце

    11 Таблицы формул прогиба балки |

    11 Таблицы формул прогиба балки

    Формулы прогиба балки

    Содержание

    Уравнения изгиба и прогиба

    При проектировании балок (бетонных, стальных или деревянных) способность к изгибу и сдвигу проверяется в соответствии с применяемой теорией изгиба.

    Приложенная сила заставляет элемент изгибаться, и он подвергается изгибающим моментам, а концы реагируют на сдвигающие нагрузки.

    Профиль изгиба и сдвига балки/элемента зависит от типа опоры балки (т. е. шарнирные, фиксированные и свободные концы).

    Формула упругого прогиба балки

    \(\frac{M}{I}=\frac{\sigma}{y}=\frac{E}{R}\)

    • M — приложенный момент
    • I — момент инерции сечения
    • \(\sigma\) — напряжение изгиба волокна 92\))
    • W — общая нагрузка (ВДС х длина)
    • w — УДС (усилие на единицу длины, кН/м)

    В таблицах ниже приведены формулы прогиба балки для свободно опертой, неподвижной балки и консолей для различных конечных условий и нагрузок.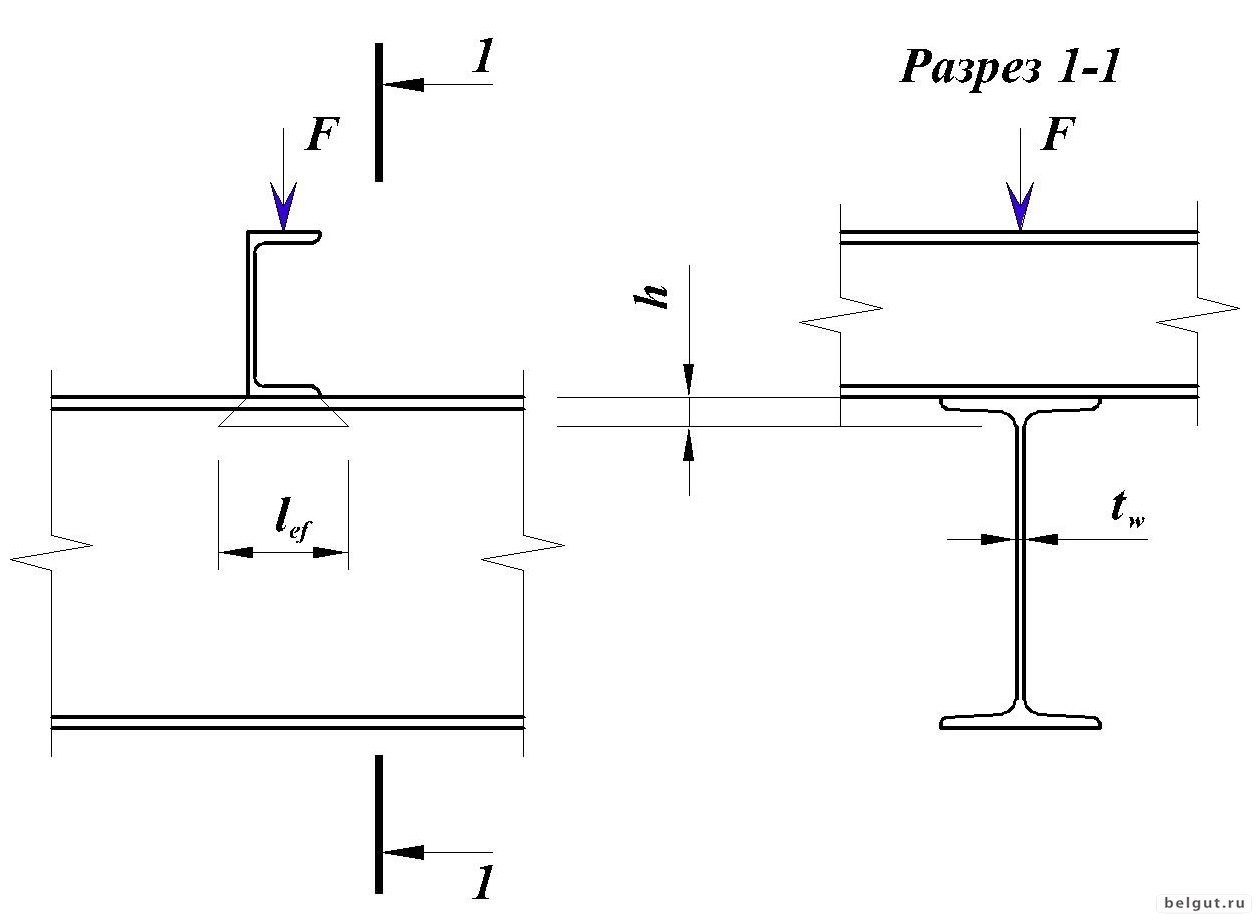

    Таблицы формул прогиба балки

    Прогиб балки с простой опорой и формула

    Простая балка с опорой при одноточечной нагрузке – (2 штыревых соединения на каждом конце) 93}{48EI}\)

    Сила сдвига и реакция:

    \(R_A=R_B=\frac{P}{2}\)

    Балки с простой опорой под одной точечной нагрузкой, расположенной в любом месте балки – (2 штыревых соединения на каждом конце)

     

    Балка с простой опорой – точечная нагрузка

    Момент:

    \(M_{C} = \frac {Pab}{L}\)

    Уравнение отклонения балки:

    , когда a>b,

    \(\delta_x = \frac{Pab(L+b)}{27EIL} \sqrt{3a(L+ б)}\)

    в \(x=\sqrt{\frac{a(L+b)}{3}}\) from A

    Сила сдвига и реакция:

    \(R_A= \frac{Pb} {L}\)

    \(R_B= \frac{Pa}{L}\)

    Простые опорные балки под 2-точечной нагрузкой – (2 штыревых соединения на каждом конце)

     

    Просто поддерживаемая балка – 2-точечная нагрузка

    Момент:

    \(M_{C} = Pa\)

    \ (M = \frac{PL}{3}\)

    Уравнение прогиба балки:

    , когда a>b, 94}{384EI}\)

    Сила сдвига и реакция:

    \(R_A  = R_B \frac{wL}{2}\)

    \(R_A  = R_B \frac{wL}{2} \)

    Фиксированный конец и штифт с UDL – (1 фиксированный конец и штифтовое соединение на каждом конце).

    Примечание – штифтовые опоры не принимают моментов, поэтому изгиб у опоры равен нулю.

    Примечание. Неподвижные опоры сопротивляются моменту, поэтому они создают момент 

    Фиксированная балка и простая опора — UDL

    93}{8EI}

    Сила сдвига и реакция:

    \(R_A  = W\)

     

    Лучшие сообщения

    Площадь поверхности пирамиды – примеры расчетов

    Площадь поверхности пирамиды Пирамида представляет собой трехмерную структуру с плоским основанием, соединенным на вершине, которая называется вершиной. Там

    Подробнее »

    Формула объема обычных фигур

    Формула объема фигур Формула объема фигуры, твердого тела или трехмерного объекта определяет, сколько места он может занимать, т.е.

    Подробнее »

    Методы улучшения грунта

    Методы улучшения грунта Что такое улучшение грунта Методы улучшения грунта используются для подготовки строительных площадок перед возведением любого фундамента или надстройки.

Published by admin