Швеллер типоразмеры: Таблица размеров швеллера: размеры швеллера 12,10,16

Слияние размеров канала и ширины канавки диктует скользкую гидродинамику в рифленых гидрофобных ограничениях. Int J Numer Methods Fluids 57:453–472

Статья
МАТЕМАТИКА

Google Scholar

  • Brackbill JU, Kothe DB, Zemach C (1992) Континуальный метод моделирования поверхностного натяжения. J Вычислительная физика 100: 335–354

    Артикул
    MathSciNet
    МАТЕМАТИКА

    Google Scholar

  • Чакраборти С. (2007) На пути к обобщенному представлению поверхностных эффектов на поток жидкости под давлением в микроканалах. Appl Phys Lett 90:034108

    Статья

    Google Scholar

  • Чакраборти Д., Дингари Н.Н., Чакраборти С. (2012) Комбинированное влияние шероховатости поверхности и характеристик смачивания на подвижную контактную линию в микроканальных потоках. Ленгмюр 28: 16701–16710

    Артикул

    Google Scholar

  • Чакраборти С. , Чаттерджи Д., Бакли С. (2013) Нелинейное усиление при электрокинетической накачке в наноканалах при наличии гидрофобных взаимодействий. Phys Rev Lett 110:184503

    Статья

    Google Scholar

  • Chen H, Li L, Zhang T, Qiao Z, Tang J, Zhou J (2018) Транслокация белка через нанопору MoS2: исследование молекулярной динамики. J Phys Chem C 122:2070–2080

    Артикул

    Google Scholar

  • Cheng Y, Teo C, Khoo B (2009) Потоки в микроканалах с супергидрофобными поверхностями: влияние числа Рейнольдса и отношения ширины узора к высоте канала. Phys Fluids 21:122004

    Статья
    МАТЕМАТИКА

    Google Scholar

  • Cheng Y, Xu J, Sui Y (2015) Численное исследование снижения сопротивления и повышения теплопередачи в микроканалах с супергидрофобными поверхностями для электронного охлаждения. Appl Therm Eng 88: 71–81

    Артикул

    Google Scholar

  • Choi C-H, Kim C-J (2006) Большое скольжение потока водной жидкости по наноинженерной супергидрофобной поверхности. Phys Rev Lett 96:066001

    Статья

    Google Scholar

  • Cummins SJ, Francois MM, Kothe DB (2005) Оценка кривизны по объемным долям. Comput Struct 83:425–434

    Статья

    Google Scholar

  • Das A, Bhaumik SK (2018) Изготовление цилиндрических супергидрофобных микроканалов путем воспроизведения структур листьев лотоса на внутренних стенках. J Micromech Microeng 28:045011

    Артикул

    Google Scholar

  • Davies J, Maynes D, Webb B, Woolford B (2006) Ламинарный поток в микроканале с супергидрофобными стенками, имеющими поперечные ребра. Phys Fluids 18:087110

    Артикул

    Google Scholar

  • Дей П., Саха С.К., Чакраборти С. (2018) Геометрия микроканавок определяет скользкую гидродинамику на супергидрофобных субстратах. Phys Fluids 30:122007

    Статья

    Google Scholar

  • Франсуа М. М., Камминс С.Дж., Денди Э.Д., Коте Д.Б., Сицилиан Дж.М., Уильямс М.В. (2006) Алгоритм сбалансированной силы для непрерывных и резких моделей межфазного поверхностного натяжения в рамках отслеживания объема. J Вычислительная физика 213: 141–173

    Артикул
    МАТЕМАТИКА

    Google Scholar

  • Fürstner R, Barthlott W, Neinhuis C, Walzel P (2005) Смачивающие и самоочищающиеся свойства искусственных супергидрофобных поверхностей. Ленгмюр 21:956–961

    Статья

    Google Scholar

  • Гаддам А., Агравал А., Джоши С.С., Томпсон М. (2015) Использование полостного вихря для задержки перехода смачивания в одномерных структурированных микроканалах. Ленгмюр 31: 13373–13384

    Артикул

    Google Scholar

  • Genzer J, Efimenko K (2006) Последние разработки в области супергидрофобных поверхностей и их значение для морского обрастания: обзор. Биообрастание 22:339–360

    Статья

    Google Scholar

  • Гогте С., Воробьев П., Трусделл Р., Маммоли А., ван Свол Ф., Шах П., Бринкер С.Дж. (2005) Эффективное скольжение на текстурированных супергидрофобных поверхностях. Физ-флюиды 17:051701

    Артикул
    МАТЕМАТИКА

    Google Scholar

  • Greenshields CJ (2015) OpenFOAM: набор инструментов CFD с открытым исходным кодом, руководство пользователя OpenFOAM Foundation Ltd

  • Hirt CW, Nichols BD (1981) Метод объема жидкости (VOF) для динамики свободных границ. J Comput Phys 39:201–225

    Статья
    МАТЕМАТИКА

    Google Scholar

  • Holt JK et al (2006) Быстрый перенос массы через углеродные нанотрубки размером менее 2 нанометров. Наука 312:1034–1037

    Артикул

    Google Scholar

  • Holzmann T (2016) Математика, числовые расчеты, производные и OpenFOAM ® Loeben. Holzmann CFD, Германия

    Google Scholar

  • Jung YC, Bhushan B (2009) Смачивание капель воды и масла на трехфазных границах раздела для гидрофобности/фильности и олеофобности/фильности. Ленгмюр 25:14165–14173

    Статья

    Google Scholar

  • Kim TJ, Hidrovo C (2012) Влияние давления и частичного смачивания на снижение супергидрофобного трения в микроканальном потоке. Phys Fluids 24:112003

    Статья

    Google Scholar

  • Лауга Э., Стоун Х.А. (2003) Эффективное скольжение в потоке Стокса, управляемом давлением. J Fluid Mech 489:55–77

    Статья
    MathSciNet
    МАТЕМАТИКА

    Google Scholar

  • Lee C, Choi C-H (2008) Структурированные поверхности для гигантского проскальзывания жидкости. Phys Rev Lett 101:064501

    Статья

    Google Scholar

  • Li C, Zhang S, Xue Q, Ye X (2016) Моделирование снижения сопротивления в супергидрофобных микроканалах на основе параболических границ раздела газ-жидкость. Phys Fluids 28:102004

    Статья

    Google Scholar

  • Liu T, Kim CJ (2014) Превращение поверхности в суперрепеллент даже для полностью смачивающих жидкостей. Наука 346 (6213): 1096–1100

    Артикул

    Google Scholar

  • Malik M, Fan ESC, Bussmann M (2007) Адаптивный VOF с уточнением кривизны. Int J Numer Meth Fluids 55:693–712

    Статья
    МАТЕМАТИКА

    Google Scholar

  • Мейнс Д., Джеффс К., Вулфорд Б., Уэбб Б. (2007) Ламинарный поток в микроканале с гидрофобными поверхностными микроребрами, ориентированными параллельно направлению потока. Физические жидкости 19:093603

    Артикул
    МАТЕМАТИКА

    Google Scholar

  • Макхейл Г., Рубатклифф Н., Эванс С., Ньютон М. (2009) Измерения предельной скорости и снижения сопротивления на супергидрофобных сферах. Appl Phys Lett 94:064104

    Статья

    Google Scholar

  • Мотамеди М., Чанг С.И., Рафей М., Хьеррильд Н., Цзян Ф., Ку Х., Тейлор А., Тейлор Р.А. (2019) Экспериментальные испытания гидрофобных микроканалов с наножидкостями и без них для солнечных фотоэлектрических / тепловых коллекторов. Энергии 12:3036

    Артикул

    Google Scholar

  • Ng CO, Wang C (2009) Сдвиговое течение Стокса по решетке: значение для супергидрофобного скольжения. Phys Fluids 21:087105

    Артикул
    МАТЕМАТИКА

    Google Scholar

  • Носоновский М., Бхушан Б. (2009) Супергидрофобные поверхности и новые области применения: неприлипание, энергетика, экологическая инженерия. Curr Opin Colloid Interf Sci 14:270–280

    Артикул

    Google Scholar

  • Ou J, Rothstein JP (2005) Прямые измерения скорости потока, проходящего мимо ультрагидрофобных поверхностей, снижающих сопротивление. Phys Fluids 17:103606

    Артикул
    МАТЕМАТИКА

    Google Scholar

  • Ou J, Perot B, Rothstein JP (2004) Уменьшение ламинарного сопротивления в микроканалах с использованием ультрагидрофобных поверхностей. Phys Fluids 16:4635–4643

    Статья
    МАТЕМАТИКА

    Google Scholar

  • Rusche H (2003) Вычислительная гидродинамика дисперсных двухфазных потоков при высоких фракциях фаз. Имперский колледж Лондона (Лондонский университет)

  • Самаха М.А., Вахеди Тафреши Х., Гад-эль-Хак М. (2011) Моделирование снижения сопротивления и стабильности мениска супергидрофобных поверхностей, состоящих из случайных шероховатостей. Phys Fluids 23:012001

    Статья

    Google Scholar

  • Шеффель Д., Койнов К., Фоллмер Д., Батт Х-Дж., Шенекер С. (2016) Локальное поле течения и длина скольжения супергидрофобных поверхностей. Phys Rev Lett 116: 134501

    Артикул

    Google Scholar

  • Song D, Song B, Hu H, Du X, Du P, Choi C-H, Rothstein JP (2018) Влияние градиента поверхностного натяжения на скользящее течение вдоль супергидрофобной поверхности раздела воздух-вода. Phys Rev Fluids 3:033303

    Статья

    Google Scholar

  • Sussman M (2003) Совместный набор уровня второго порядка и метод объема жидкости для расчета роста и схлопывания пузырьков пара. J Вычислительная физика 187: 110–136

    Артикул
    MathSciNet
    МАТЕМАТИКА

    Google Scholar

  • Teo CJ, Khoo BC (2010) Обтекание супергидрофобных поверхностей, содержащих продольные канавки: эффекты кривизны интерфейса. Microfluid Nanofluid 9:499–511

    Артикул

    Google Scholar

  • Teo C, Khoo B (2014) Влияние кривизны интерфейса на течение Пуазейля через микроканалы и микротрубки, содержащие супергидрофобные поверхности с поперечными канавками и ребрами. Микрожидкость Наножидкость 17:891–905

    Артикул

    Google Scholar

  • Цай П., Петерс А.М., Пират С., Весслинг М., Ламмертинк Р.Г., Лозе Д. (2009) Количественная оценка эффективной длины скольжения по гидрофобным поверхностям с микроузором. Phys Fluids 21:112002

    Статья
    МАТЕМАТИКА

    Google Scholar

  • Ван Леер Б. (1977) К окончательной консервативной разностной схеме III. Конечно-разностные схемы с центром вверх по потоку для идеального сжимаемого потока. J Вычислительная физика 23: 263–275

    Артикул
    МАТЕМАТИКА

    Google Scholar

  • Ван Леер Б. (1979) К окончательной консервативной разностной схеме. V. Второе продолжение метода Годунова. J Comput Phys 32:101–136

    Статья
    МАТЕМАТИКА

    Google Scholar

  • Weller H (1993) Разработка новой модели горения по площади пламени с использованием условного усреднения Отчет по разделу теплоносителей TF 9307

  • Weller HG (2008) Новый подход к методам захвата интерфейса на основе VOF для несжимаемых и сжимаемых потоков OpenCFD Ltd, Report TR/HGW 4

  • Woolford B, Jeffs K, Maynes D, Webb B (2005 ) Ламинарное полностью развитое течение в микроканале с узорчатыми ультрагидрофобными стенками. В: Летняя конференция ASME 2005 по теплопередаче, совместно с Технической конференцией и выставкой ASME 2005 Pacific Rim по интеграции и компоновке МЭМС, НЭМС и электронных систем, 2005 г. Американское общество инженеров-механиков, стр. 481–488

  • Чжао С., Сюэ Дж., Кан В. (2013)Ионный отбор больших нанопор с модифицированным зарядом в листе графена. J Chem Phys 139:114702

    Статья

    Google Scholar

    • Швеллеры с параллельными фланцами — Rainham Steel

    9 0381 2,06

    90 381 196

    9 0381 103

    91 5,1

    90 381 2,3

    9038 1 11,7

    903 81 2,82

    90 381 151

    Серийный размер Масса на метр
    кг/м    		 Глубина
    секции D мм    		 Ширина
    секции B мм    		 Толщина
    перемычка t мм    		 Толщина полки
    T мм    		 Расстояние
    Cy см    		 Радиус основания
    r мм    		 Глубина между галтелями
    d мм    		 Соотношения для местной
    потери устойчивости Фланец B/2T    		 Соотношения для местного изгиба
    Перемычка d /t    		 Второй момент
    площадь Ось x-x см4    		 Второй момент
    площадь Ось y-y см4    		 Радиус вращения
    Ось x-x см    		 Радиус вращения
    Ось г-г см    		 Модуль упругости
    Ось x-x см3    		 Модуль упругости
    Ось y-y см3    		 Модуль пластичности
    Ось x-x см3    		 Модуль пластичности
    Ось y-y см3 9030 1

    		 Потеря устойчивости
    параметр u    		 Крутильная
    индекс x    		 Деформация
    константа H dm6    		 Крутящая
    постоянная Дж см4    		 Площадь сечения
    см2    		 Ориентировочные значения для
    S355 Сталь Mcx кНм    		 Ориентировочные значения для S355 Сталь
    Pcy* для L e =3,5 м кН
    100x50x10 10,2 100 50 5 8,5 903 82

    		 1,73 9 65 5,88 13 208 32,3 4 9 0382

    		 1,58 41,5 9,9 48,9 17,6 0,942 10 0,0005 2. 53 13 17,4 46,7
    125x65x15 14,8 125 65 5,5 9,5 2 .25 12 82 6,84 14,9 483 80 5,07 77,3 18,8 89,9 33,5 0,942 11,1 0,0019 4,72 18,8 31,9 110
    150x75x18 17,9 150 75 5,5 10 2,58 12 106 7,5 19,3 861 131 6,15 2,4 115 9038 2

    		 26,6 132 47,3 0,946 13,1 0,0047 6,1 22,8 4 6,9 174
    150x90x24 23,9 150 90 6,5 12 3,3 12 102 7,5 1 5,7 1162 253 6,18 2,89 155 44,4 179 903 82

    		 77 0,936 10,8 0,0089 11,8 30,4 63,5 317
    180x75x20 20,3 180 75 6 10,5 2,41 12 135 7,14 22,5 1370 146 7,27 2,38 152 28,8 176 52 0,9 46 15,3 0,0075 7,34 25,9 62,5 195
    180x90x26 26,1 180 90 6,5 12,5 3,17 12 131 7,2 20,2 1817 277 7.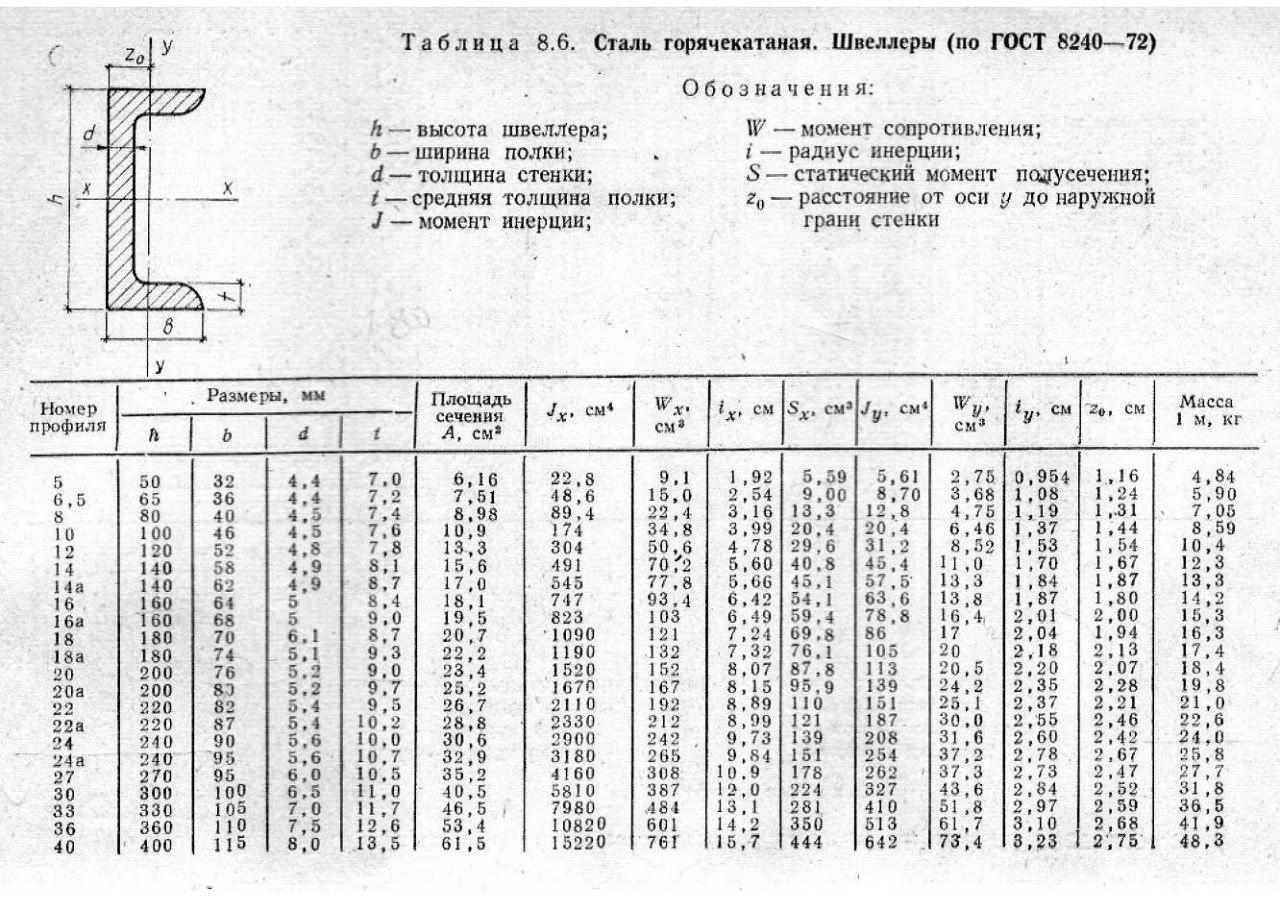 4 2,89 202 47,4 232 83,5 0,949 12,8 903 82

    		 0,0141 13,3 33,2 82,4 347
    200x75x23 23,4 200 75 6 12,5 2. 48 12 151 6 25,2 1963 170 8,11 2,39 33,8 227 60,8 0,956 14,8 0,0107 11,1 29,9 80,6 227
    200x90x30 29,7 200 90 7 14 3,12 12 148 6,43 21,1 2523 314 8,16 2,88 252 53,4 291 94,6 0,954 12,9 0,0197 18,3 37,9 394
    230x75x26 25,7 230 75 6,5 12,5 2,3 12 181 6 27,8 2748 181 9,17 2,35 239 34,8 278 63,2 0,947 17,3 0,0153 11,8 32,7 98,7 241
    230x90x32 32,2 230 90 7,5 14 2. 92 12 178 6,43 23,7 3518 334 0,0279 19,3 41 126 421
    260x75x28 27,6 260 75 7 12 2,1 12 212 6,25 30,3 3619 185 10,1 278 34,4 328 62 0,932 20,5 0,0203 35,1 116 249
    260x90x35 34,8 260 90 8 14 2,74 12 208 6,43 26 4728 353 10,3 364 56,3 425 102 0,942 17,2 0,0379 20,6 44,4 445
    300x90x41 41,4 300 90 9 15,5 2.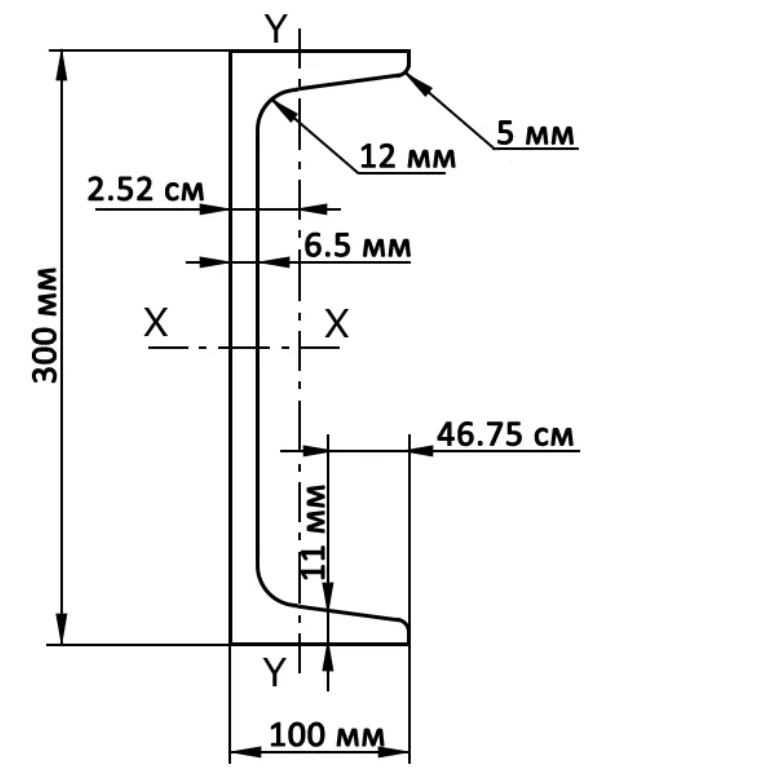 6 12 245 5,81 27,2 7218 404 11,7 2,77 481 63,1 568 114 0,934 18,4 0,0581 28,8 52,7 202 513 90 382
    300x100x46 45,5 300 100 9 16,5 3,05 15 237 6,06 26,3 8229 568 11,9 903 82

    		 3,13 549 81,7 641 148 0,944 17 0,0813 36,8 58 221 681
    380x100x54 54 380 100 9,5 17,5 2,79 15 315 5,71 33,2 15034 643 14,8 90 382

    		 3,06 791 89,2 933 161 0,932 21,2 0,15 45,7 68,7 322 779
    430x100x64 64,4 430 100 11 19 2 .

    Published by admin