16К20 габариты: Токарный станок 16К20 – технические характеристики, ремонт + Видео
Содержание
16к20 технические характеристики | Станок токарный винторезный
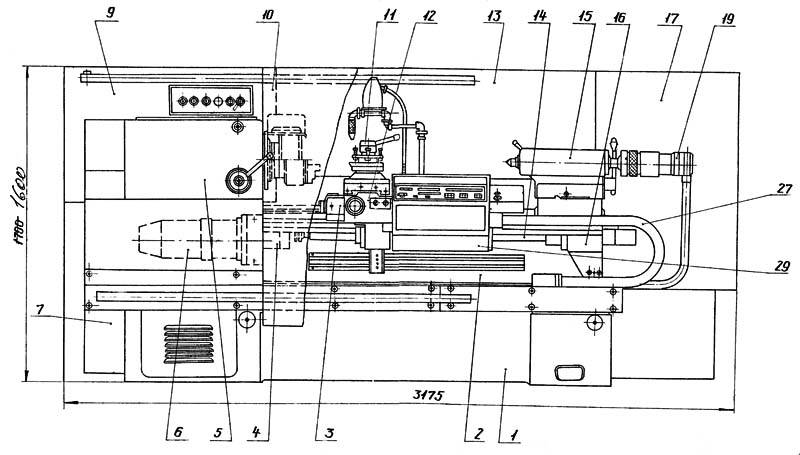
Технические характеристики станка 16к20 позволяют выполнять различные токарные операции как нормальной, так и повышенной точности (в зависимости от исполнения). Все модификации станка выполнены на базе модели 16к20, максимально унифицированы и имеют схожую конструкцию.
Наименование параметра | Единица измерения | Величины параметра | |||
|
| 16К20 | 16К20П | 16К20Г | 16К25 |
Основные данные | |||||
Наибольшая длина обрабатываемого изделия: | |||||
| мм | 710 | |||
| мм | 1000 | |||
| мм | 1400 | — | 1400 | |
| мм | 2000 | — | 2000 | |
Высота оси центров над плоскими направляющими станины | мм | 215 | 250 | ||
Пределы чисел оборотов шпинделя: | |||||
Основное исполнение | об/ мин | 12,5-1600 | 12,5—1600 | ||
По особому заказу | об/мин | 16—2000 | 10-1250 | ||
Пределы подач: | |||||
Продольных | мм/об | 0,05-2,8 | |||
Поперечных | мм/об | 0,025—1,4 | |||
Наибольшее усилие допускаемое механизмом подач: | |||||
продольное |
|
| |||
на упоре | кгс (н) | 800 (7845) | |||
на резце | кгс (н) | 600 (5884) | |||
поперечное |
|
| |||
на упоре | кгс (н) | 460 (4510) | |||
на резце | кгс (н) | 360 (3530) | |||
Мощность электродвигателя главного привода: | |||||
основное исполнение | кВт | 11 | |||
по особому заказу | кВт | 7,5 | |||
Габариты и масса | |||||
Габарит станка: | |||||
длина | мм | 3195 | 2505 | 3195 | |
| мм | 3795 | 2795 | 3795 | |
ширина | мм | 1190 | 1240 | ||
высота | мм | 1500 | |||
Масса станка: | |||||
| кг | 2835 | 2835 | 2945 | 2925 |
| кг | 3005 | 3010 | 3110 | 3095 |
| кг | 3225 | — | 3335 | 3315 |
| кг | 3685 | — | 3695 | 3775 |
Параметры обрабатываемой детали | |||||
Наибольший диаметр изделия, устанавливаемого над станиной | мм | 400 | 500 | ||
Наибольший диаметр обработки над поперечными салазками суппорта | мм | 220 | 290 | ||
Наибольший диаметр изделия, устанавливаемого над выемкой в станине | мм | — | 630 | ||
Наибольший диаметр прутка, проходящего через отверстие в шпинделе | мм | 53 | |||
Наибольшая длина обтачивания: | |||||
| мм | 645 | |||
| мм | 935 | |||
| мм | 1335 | — | 1335 | |
| мм | 1935 | — | 1935 | |
Расстояние от торца фланца шпинделя до правого края выемки | мм | — | 298 | — | |
Длина выемки | мм | — | 305 | — | |
Пределы шагов нарезаемых резьб: | |||||
метрических | мм | 0,5—112 | |||
модульных | модуль | 0,5—112 | |||
дюймовых | число ниток на 1″ | 56—0,5 | |||
питчевых | питч | 56—0,5 | |||
Максимально допустимая масса изделия устанавливаемого: |
|
| |||
в патроне | кт | 200 | |||
в центрах | кт | 460 | |||
| кг | 650 | |||
| кг | 900 | |||
| кг | 1300 | |||
Шпиндель | |||||
Конец шпинделя по ГОСТ 12593—72 |
| 6К | |||
Диаметр шпиндельного фланца | мм | 170 | |||
Коническое отверстие ГОСТ 2847—67 |
| Морзе № 6 | |||
Диаметр сквозного отверстия | мм | 52 | |||
Суппорт | |||||
Наибольшая длина продольного перемещения | мм | 645, 935, 1335, 1935 | |||
Наибольшая длина поперечного перемещения | мм | 300 | |||
Скорость быстрых перемещений: |
|
| |||
продольных | мм/мин | 3800 | |||
поперечных | мм/мин | 1900 | |||
Максимально допустимая скорость перемещений при работе по упорам | мм/мин | 250 | |||
Минимально допустимая скорость перемещения каретки | мм/мин | 10 | |||
Цена одного деления лимба: |
|
| |||
продольного перемещения | мм | 1 | |||
поперечного перемещения | мм | 0,05 на диаметр обрабатываемого изделия | |||
Резцовые салазки | |||||
Шкала угла поворота | град | ±90 | |||
Цена одного деления шкалы поворота | град | 1 | |||
Наибольшая длина перемещения | мм | 150 | |||
Цена одного деления лимба | мм | 0,05 | |||
Индексируемая резцовая головка | |||||
Количество фиксированных позиций |
| 4 | |||
Число резцов, одновременно устанавливаемых в резцедержателе |
| 4 | |||
Наибольшее сечение державки резца | мм | 25×25 | |||
Высота от опорной поверхности резца до оси центров | мм | 25 | |||
Задняя бабка | |||||
Коническое отверстие в пииоли ГОСТ 2847—67 |
| Морзе № 5 | |||
Наибольшее перемещение пиноли | мм | 150 | |||
Цена одного деления лимба перемещения пиноли | мм | 0,1 | |||
Величина, поперечного смещения корпуса | мм | ±15 | |||
Рисунок — эскиз шпинделя
Рисунок — 16к20 эскиз суппорта
16К20 (РМЦ 1000 мм) комплект лінійок та ПЦІ Ditron для токарного верстата на осі 3
Цена с НДС
Під замовлення16К20, 3 осі, РМЦ 1000 мм. , 1 мкм., комплект лінійок та ПЦІ Ditron на токарний верстат
, 1 мкм., комплект лінійок та ПЦІ Ditron на токарний верстат
25 694 ₴/комплект
Купити
Купити з
+380 (98) 753-31-67
Київстар
+380 (95) 811-30-72
МТС
+380 (56) 767-39-45
Опис
Характеристики
Інформація для замовлення
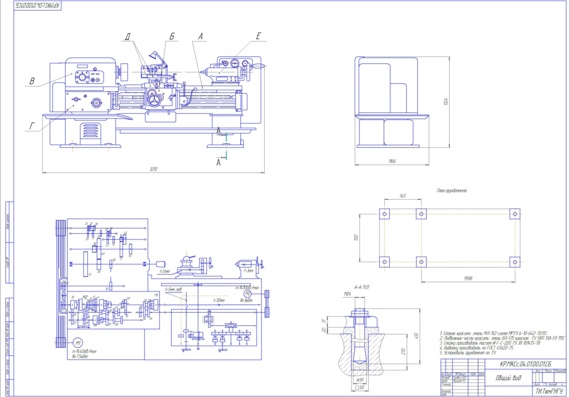
Комплект для універсального токарно-гвинторізного верстата типу 16К20 (РМЦ 1000 мм. ) включає в себе:
) включає в себе:
- DC11-250 — оптична лінійка з довжиною вимірювання 250 мм, дискретністю 1 мкм., для контролю переміщень поперечних салазок супорта (вісь X)
- DC11-320 — оптична лінійка з довжиною вимірювання 320 мм., дискретністю 1 мкм., для контролю поздовжнього переміщення каретки супорта (вісь Z)
- DC11-1100 — оптична лінійка з довжиною вимірювання 1100 мм., дискретністю 1 мкм., для контролю переміщення різцевих салазок (суппортка (вісь U)
- D60-3 три-координатний пристрій цифрової індикації, повнорозмірний ПЦІ в металевому корпусі, з розширеним функціоналом, оснащений повноцінною клавіатурою та 7-ми розрядним РК-дисплеєм зеленого світіння
- Кронштейни та кріпильні елементи для встановлення лінійок та ПЦІ
- Інструкція з монтажу та посібник користувача.
Ви можете самостійно встановити цей комплект на своє обладнання або замовити установку, заповнивши форму за посиланням.
Фахівці ТОВ «ТПП «Станкоресурс» у стислі терміни виконають якісний монтаж, підключення та налаштування цього комплекту.
Ознайомитись з короткою відеоінструкцією з монтажу лінійних перетворювачів Ви можете у розділі «Статті» нашого сайту або перейшовши за цим посиланням
Важливо!
Перед покупкою комплекту обов’язково проконсультуйтеся з нашими фахівцями, або самостійно переконайтеся в тому, що межі переміщень виконавчих органів верстата не перевищують межі довжин вимірювання лінійок, які вказані в даній пропозиції, а габарити місця встановлення дозволяють закріпити корпус лінійки згідно інструкції!!
Существенная размерность простых алгебр с инволюциями | Бюллетень Лондонского математического общества
Фильтр поиска панели навигации
Бюллетень Лондонского математического обществаЭтот выпускLMS JournalsMathematicsBooksJournalsOxford Academic
Мобильный телефон Введите поисковый запрос
Закрыть
Фильтр поиска панели навигации
Бюллетень Лондонского математического обществаЭтот выпускLMS JournalsMathematicsBooksJournalsOxford Academic
Введите поисковый запрос
Расширенный поиск
Журнальная статья
Получить доступ
Санхун Пэк
Санхун Пэк
Ищите другие работы этого автора на:
Оксфордский академический
Google Scholar
Бюллетень Лондонского математического общества , том 44, выпуск 3, июнь 2012 г. , страницы 578–590, https://doi.org/10.1112/blms/bdr120
, страницы 578–590, https://doi.org/10.1112/blms/bdr120
Опубликовано:
8 декабря 2011 г.
История статьи
Получено:
25 января 2011 г.
Получена редакция:
12 сентября 2011 г.
Опубликовано:
08 декабря 2011 г.
Фильтр поиска панели навигации
Бюллетень Лондонского математического обществаЭтот выпускLMS JournalsMathematicsBooksJournalsOxford Academic
Мобильный телефон Введите поисковый запрос
Закрыть
Фильтр поиска панели навигации
Бюллетень Лондонского математического обществаЭтот выпускLMS JournalsMathematicsBooksJournalsOxford Academic
Введите поисковый запрос
Advanced Search
Abstract
Пусть 1≤ m ≤ n — целые числа, где m | n и Alg n , м класс центральных простых алгебр степени n и показателя, делящего m . В этой статье мы находим новые, улучшенные верхние оценки существенной размерности и двумерности Alg n , 2 . В частности, мы показываем, что ed 2 (Alg 16, 2 )=24 над полем F характеристики, отличной от 2.
В этой статье мы находим новые, улучшенные верхние оценки существенной размерности и двумерности Alg n , 2 . В частности, мы показываем, что ed 2 (Alg 16, 2 )=24 над полем F характеристики, отличной от 2.
Этот контент доступен только в формате PDF.
© 2011 Лондонское математическое общество
Отдел выдачи:
Бумаги
В настоящее время у вас нет доступа к этой статье.
Скачать все слайды
Войти
Получить помощь с доступом
Получить помощь с доступом
Доступ для учреждений
Доступ к контенту в Oxford Academic часто предоставляется посредством институциональных подписок и покупок. Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:
Доступ на основе IP
Как правило, доступ предоставляется через институциональную сеть к диапазону IP-адресов. Эта аутентификация происходит автоматически, и невозможно выйти из учетной записи с IP-аутентификацией.
Эта аутентификация происходит автоматически, и невозможно выйти из учетной записи с IP-аутентификацией.
Войдите через свое учреждение
Выберите этот вариант, чтобы получить удаленный доступ за пределами вашего учреждения. Технология Shibboleth/Open Athens используется для обеспечения единого входа между веб-сайтом вашего учебного заведения и Oxford Academic.
- Нажмите Войти через свое учреждение.
- Выберите свое учреждение из предоставленного списка, после чего вы перейдете на веб-сайт вашего учреждения для входа.
- Находясь на сайте учреждения, используйте учетные данные, предоставленные вашим учреждением. Не используйте личную учетную запись Oxford Academic.
- После успешного входа вы вернетесь в Oxford Academic.
Если вашего учреждения нет в списке или вы не можете войти на веб-сайт своего учреждения, обратитесь к своему библиотекарю или администратору.
Войти с помощью читательского билета
Введите номер своего читательского билета, чтобы войти в систему. Если вы не можете войти в систему, обратитесь к своему библиотекарю.
Члены общества
Доступ члена общества к журналу достигается одним из следующих способов:
Войти через сайт сообщества
Многие общества предлагают единый вход между веб-сайтом общества и Oxford Academic. Если вы видите «Войти через сайт сообщества» на панели входа в журнале:
- Щелкните Войти через сайт сообщества.
- При посещении сайта общества используйте учетные данные, предоставленные этим обществом. Не используйте личную учетную запись Oxford Academic.
- После успешного входа вы вернетесь в Oxford Academic.
Если у вас нет учетной записи сообщества или вы забыли свое имя пользователя или пароль, обратитесь в свое общество.
Вход через личный кабинет
Некоторые общества используют личные учетные записи Oxford Academic для предоставления доступа своим членам. См. ниже.
Личный кабинет
Личную учетную запись можно использовать для получения оповещений по электронной почте, сохранения результатов поиска, покупки контента и активации подписок.
Некоторые общества используют личные учетные записи Oxford Academic для предоставления доступа своим членам.
Просмотр учетных записей, вошедших в систему
Щелкните значок учетной записи в правом верхнем углу, чтобы:
- Просмотр личной учетной записи, в которой выполнен вход, и доступ к функциям управления учетной записью.
- Просмотр институциональных учетных записей, предоставляющих доступ.
Выполнен вход, но нет доступа к содержимому
Oxford Academic предлагает широкий ассортимент продукции. Подписка учреждения может не распространяться на контент, к которому вы пытаетесь получить доступ. Если вы считаете, что у вас должен быть доступ к этому контенту, обратитесь к своему библиотекарю.
Подписка учреждения может не распространяться на контент, к которому вы пытаетесь получить доступ. Если вы считаете, что у вас должен быть доступ к этому контенту, обратитесь к своему библиотекарю.
Ведение счетов организаций
Для библиотекарей и администраторов ваша личная учетная запись также предоставляет доступ к управлению институциональной учетной записью. Здесь вы найдете параметры для просмотра и активации подписок, управления институциональными настройками и параметрами доступа, доступа к статистике использования и т. д.
Реклама
Реклама
16-ХХ | г Ассоциативные кольца и алгебры {Для коммутативного случая см. 13-ХХ} |
| 16-00 | Общие справочные издания (справочники, словари, библиографии и т.д.) |
| 16-01 | Учебная экспозиция (учебники, учебные пособия и т. д.) д.) |
| 16-02 | Научная экспозиция (монографии, обзорные статьи) |
| 16-03 | Исторические {!также должен быть присвоен хотя бы один классификационный номер из раздела 01} |
| 16-04 | Явные машинные вычисления и программы (не теория вычислений или программирование) |
| 16-06 | Труды, конференции, сборники и т.д. |
16Bxx | Общее и разное |
| 16Б50 | Категорийные методы и результаты {!за исключением 16Д90, 16E10} [Смотрите также |
| 16Б70 | Приложения логики [Смотрите также 03Cxx] |
| 16B99 | Ничего из вышеперечисленного, но в этом разделе |
16Dxx | Модули, бимодули и идеалы |
| 16Д10 | Общая теория модулей |
| 16Д20 | Бимодули |
| 16Д25 | Идеалы |
| 16Д30 | Бесконечномерные простые кольца (кроме как в 16кхх) |
| 16Д40 | Свободные, проективные и плоские модули и идеалы [Смотрите также 19А13] |
| 16Д50 | Инъективные модули, самоинъективные кольца [Смотрите также 16L60] |
| 16Д60 | Простые и полупростые модули, примитивные кольца и идеалы |
| 16Д70 | Структура и классификация {!кроме как в 16Gxx}, прямое разложение суммы, сокращение |
| 16Д80 | Другие классы модулей и идеалов [Смотрите также 16G60] |
| 16Д90 | Категории модулей [Смотрите также 16Gxx, 16С90]; |
| 16Д99 | Ничего из вышеперечисленного, но в этом разделе |
16Exx | Гомологические методы {О коммутативных кольцах см.  13Dxx; общие категории см. 18Gxx} |
| 16E05 | Сизигии, разрешения, комплексы |
| 16E10 | Гомологическая размерность |
| 16E20 | группы Гротендика, $K$-теория и т.д. [Смотрите также 18Ф30, 19Axx, 19Д50] |
| 16E30 | Гомологические функторы на модулях (Tor, Ext и др.) |
| 16Е40 | (Ко)гомологии колец и алгебр (например, гохшильдовские, циклические, диэдральные и т. д.) |
| 16Э45 | Дифференциально-градуированные алгебры и приложения |
| 16Е50 | Регулярные кольца фон Неймана и их обобщения |
| 16Е60 | Полунаследственные и наследственные кольца, свободные идеальные кольца, кольца Сильвестра и др.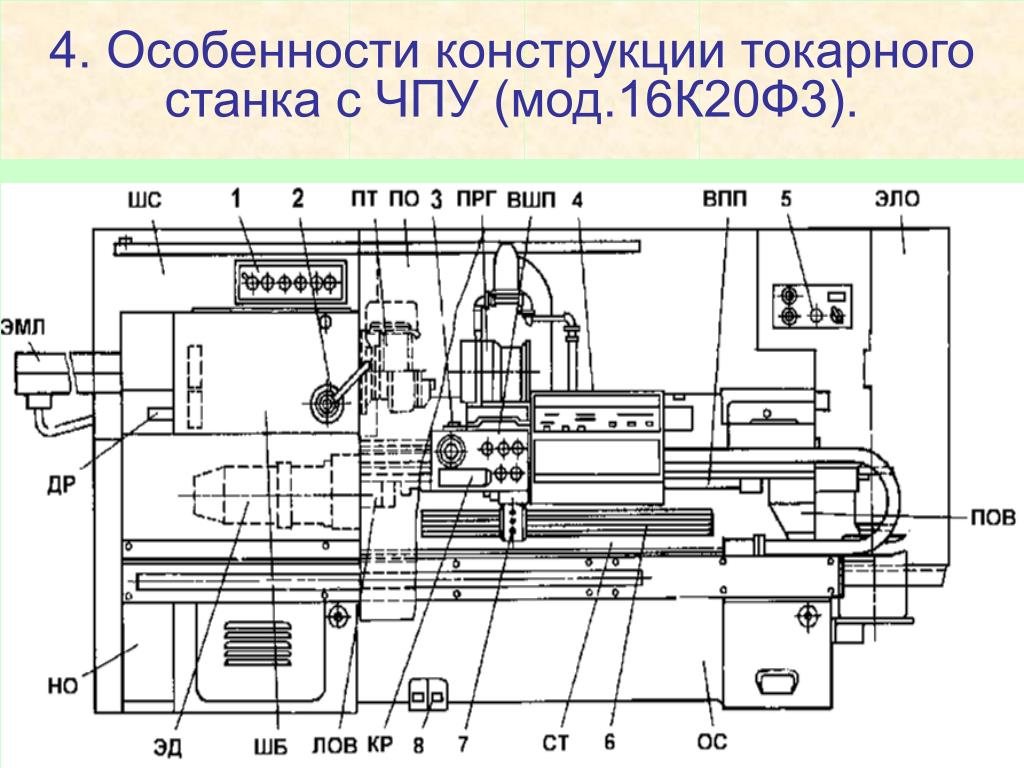 |
| 16Е65 | Гомологические условия на кольцах (обобщения регулярных колец Горенштейна, колец Коэна-Маколея и др.) |
| 16Е99 | Ничего из вышеперечисленного, но в этом разделе |
16Gxx | Теория представлений колец и алгебр |
| 16G10 | Представления артиновых колец |
| 16G20 | Представления колчанов и частично упорядоченных множеств |
| 16Г30 | Представления порядков, решеток, алгебр над коммутативными кольцами [Смотрите также 16H05] |
| 16Г50 | Модули Коэна-Маколея |
| 16G60 | Тип представления (конечный, ручной, дикий и т.д.) |
| 16G70 | Последовательности Auslander-Reiten (почти разделенные последовательности) и колчаны Auslander-Reiten |
| 16G99 | Ничего из вышеперечисленного, но в этом разделе |
| 16H05 | Порядки и арифметика, сепарабельные алгебры, алгебры Адзумая [Смотрите также 11Р52, 11Р54, 11С45] |
16кхх | Кольца с делением и полупростые кольца Артина [Смотрите также 12Е15, 15А30] |
| 16К20 | конечномерный {Для скрещенных продуктов см.  16С35} |
| 16К40 | Бесконечномерный и общий |
| 16К50 | группы Брауэра [Смотрите также 12G05, 14F22] |
| 16К99 | Ничего из вышеперечисленного, но в этом разделе |
16Lxx | Локальные кольца и обобщения |
| 16Л30 | Некоммутативные локальные и полулокальные кольца, совершенные кольца |
| 16Л60 | Кольца квазифробениуса [Смотрите также 16Д50] |
| 16Л99 | Ничего из вышеперечисленного, но в этом разделе |
16Nxx | Радикалы и радикальные свойства колец |
| 16Н20 | Радикал Джекобсона, квазиумножение |
| 16Н40 | Ниль- и нильпотентные радикалы, множества, идеалы, кольца |
| 16Н60 | Первичные и полупервичные кольца [Смотрите также 16Д60, 16U10] |
| 16Н80 | Общие радикалы и кольца {О радикалах в категориях модулей см.  16С90} |
| 16Н99 | Ничего из вышеперечисленного, но в этом разделе |
16Pxx | Цепные условия, условия роста и другие формы конечности |
| 16П10 | Конечные кольца и конечномерные алгебры {Для полупростых см. 16К20; для коммутативного см. 11Txx, 13Мхх} |
| 16П20 | Артиновы кольца и модули |
| 16П40 | Нётеровы кольца и модули |
| 16П50 | Локализация и нётеровы кольца [Смотрите также 16U20] |
| 16П60 | Цепные условия на аннуляторах и слагаемых: условия типа Голди [Смотрите также 16У20], Измерение Крулля |
| 16П70 | Цепные условия на другие классы подмодулей, идеалов, подколец и т.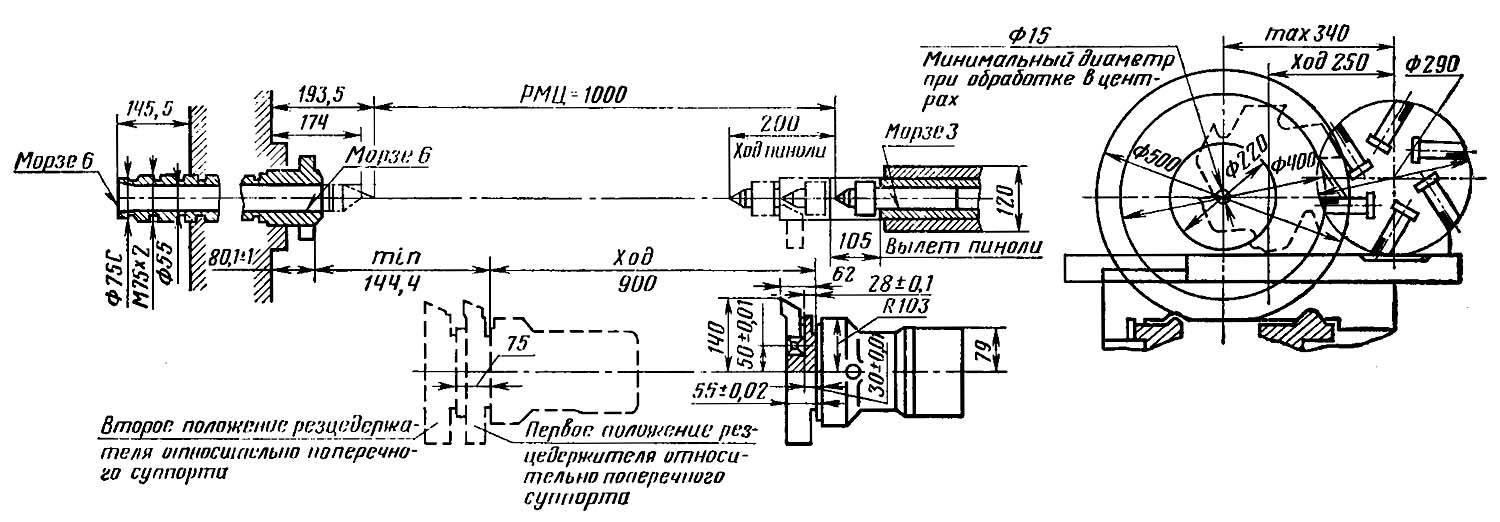 д.; когерентность д.; когерентность |
| 16П90 | Скорость роста, размерность Гельфанда-Кириллова |
| 16П99 | Ничего из вышеперечисленного, но в этом разделе |
16Rxx | Кольца с полиномиальной идентичностью |
| 16R10 | $T$-идеалы, тождества, многообразия колец и алгебр |
| 16R20 | Полупростой пи.и. Кольца, кольца, вложимые в матрицы над коммутативными кольцами |
| 16R30 | Кольца следов и теория инвариантов |
| 16Р40 | Тождества, отличные от тождеств матриц над коммутативными кольцами |
| 16Р50 | Другие виды тождеств (обобщенные полиномиальные, рациональные, инволюционные) |
| 16Р99 | Ничего из вышеперечисленного, но в этом разделе |
16схх | Кольца и алгебры, возникающие при различных конструкциях |
| 16С10 | Кольца, определяемые универсальными свойствами (свободные алгебры, копроизведения, присоединение обратных и т. д.) д.) |
| 16С15 | Конечное порождение, конечная представимость, нормальные формы (алмазная лемма, переписывание терминов) |
| 16С20 | Централизация и нормализация расширений |
| 16С30 | Универсальные обертывающие алгебры алгебр Ли [См. в основном 17В35] |
| 16С32 | Кольца дифференциальных операторов [Смотрите также 13Н10, 32С38] |
| 16С34 | Групповые кольца [Смотрите также 20С05, 20С07], |
| 16С35 | Скрученные и косые групповые кольца, скрещенные произведения |
| 16С36 | Обыкновенные и косые кольца полиномов и полугрупповые кольца [Смотрите также 20М25] |
| 16С37 | Квадратичные алгебры и алгебры Кошуля |
| 16С38 | Кольца, возникающие из некоммутативной алгебраической геометрии |
| 16С40 | Разбейте продукты общего действия Хопфа [Смотрите также 16W30] |
| 16С50 | Кольца эндоморфизмов; матричные кольца [Смотрите также 15-ХХ] |
| 16С60 | Кольца функций, подпрямые произведения, пучки колец. |
| 16С70 | Расширения колец идеалами |
| 16С80 | Деформации колец [Смотрите также 13Д10, 14Д15] |
| 16С90 | Максимальное кольцо частных, теории кручения, радикалы на модульных категориях [Смотрите также 13Д30, 18Э40] {О радикалах колец см. |
| 16С99 | Ничего из вышеперечисленного, но в этом разделе |
16Uxx | Условия для элементов |
| 16U10 | Интегральные домены |
| 16U20 | \Рудные кольца, мультипликативные множества, \Рудная локализация |
| 16У30 | Делимость, некоммутативные UFD |
| 16У60 | Юниты, группы юнитов |
| 16У70 | Центр, нормализатор (инвариантные элементы) |
| 16У80 | Обобщения коммутативности |
| 16U99 | Ничего из вышеперечисленного, но в этом разделе |
16Wxx | Кольца и алгебры с дополнительной структурой |
| 16W10 | Кольца с инволюцией: Ли, Жордан и другие неассоциативные структуры [Смотрите также 17Б60, 17С50, 46Kxx] |
| 16W20 | Автоморфизмы и эндоморфизмы |
| 16W22 | Действия групп и полугрупп; теория инвариантов |
| 16W25 | Выводы, действия алгебр Ли |
| 16W30 | Коалгебры, биалгебры, алгебры Хопфа [Смотрите также 57Т05, 16С30, 16С40]; |
| 16W35 | Кольцевые аспекты квантовых групп [Смотрите также 17Б37, 20Г42, 81R50] |
| 16W50 | Градуированные кольца и модули |
| 16W55 | «Супер» (или «косая») структура [Смотрите также 17А70, 17С70] {О внешних алгебрах см. 15А66} |
| 16W60 | Оценки, дополнения, формальные степенные ряды и связанные с ними построения [Смотрите также 13Jxx] |
| 16W70 | Фильтрованные кольца; фильтрационные и градуированные методы |
| 16W80 | Топологические и упорядоченные кольца и модули [Смотрите также 13Jxx] |
| 16W99 | Ничего из вышеперечисленного, но в этом разделе |
16Yxx | Обобщения {О неассоциативных кольцах см. 
|

 , страницы 578–590, https://doi.org/10.1112/blms/bdr120
, страницы 578–590, https://doi.org/10.1112/blms/bdr120 д.
д.