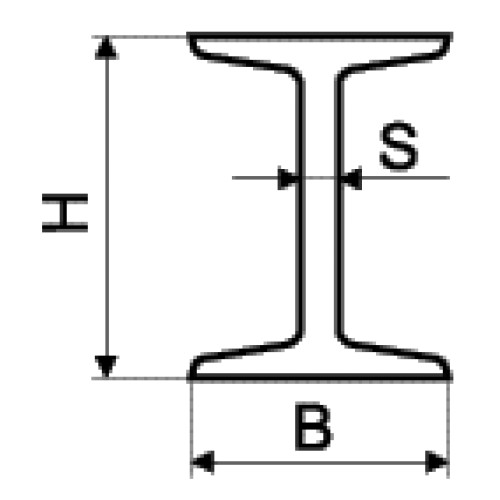
Центр тяжести двутавра и швеллера: Геометрические характеристики плоского поперечного сечения 4 элемента (полоса, двутавр, швеллер уголок) 020
Содержание
Примеры определения центров тяжести составных фигур, образованных из простых сечений и прокатных профилей
Пример 6.3. Определить положение центра тяжести плоской фигуры, представленной на рис.6.14. Размеры даны в сантиметрах.
Решение. Вычерчиваем в масштабе заданную плоскую фигуру и разделяем её на три прямоугольника. Центры их тяжести находятся в точках пересечения диагоналей. Обозначим эти центры буквами C1, С2 и С3.
Выбираем систему координат 0yz как показано на рис.6.14 и вычисляем координаты точек C1, С2 , С3.:
y1 = 5 см, y2 = I см , y3 = 3 см
z1= I см, z2 = 3,5 см, z3 = 6 см .
Вычисляем площади каждого прямоугольника:
A1 = 10∙2 = 20 см2, A2 = 2∙3 = 6 см2, A3 = 2∙6 = 12 см2.
По формулам (6.24) определяем координаты центра тяжести всей плоской фигуры:
, ,
,
Таким образом, центр тяжести площади заданной фигуры находится в точке С (3,73; 2,97) по отношению к осям y и z .
Примечание: Решение задачи можно упростить, если выбрать другую систему координат, оси которой проходят через центры тяжести отдельных частей заданной фигуры.
Рис. 6.14
На рис.6.14 показаны положения осей и , которые позволяют определить координаты центра тяжести С, выполнив меньшее число арифметических операций, так как при этом z1= 0 и y2 = 0 .
Пример 6.4. Определить положение центра тяжести площади сечения, составленного из прокатных профилей: равнополочного уголка № 5,6 (ГОСТ 8509-57) и двутавра №12 (ГОСТ 8239-56). Расположение элементов сечения и размеры в сантиметрах показаны на рис. 6.15.
6.15.
Рис.6.15
Решение. Рассматриваемое сечение состоит из двух элементов, площади которых находим из таблиц (таблиц сортамента прокатной стали):
A1= 16,5 см2 — площадь сечения двутавра №12 ;
A2 = 5,41 см2 — площадь сечения уголка № 5,6.
Из тех же таблиц находим все необходимые размеры, определяющие заданные сечения и положения их собственных центров тяжести С1 и С2 соответственно.
Выбираем систему координат Oy1z1cначалом в центре тяжести двутавра. Тогда точки С1 и С2 будут иметь следующие координаты: С1(0 ; 0) , С2(2,18 ; 7,57).
Определяем координаты центра тяжести всего сечения по формулам (6.24).
,
,
Отложим от начала О вдоль координатных осей отрезки, равные вычисленным значениям ycи zc в принятом масштабе. Из полученных точек восстановим перпендикуляры к осям и продолжим их до взаимного пересечения в точке С — центре тяжести площади всего сечения.
Из полученных точек восстановим перпендикуляры к осям и продолжим их до взаимного пересечения в точке С — центре тяжести площади всего сечения.
Если площадь сечения составлена из двух простых фигур, то общий центр тяжести располагается на прямой, соединяющей их центры тяжести и делит эту прямую на части, обратно пропорциональные площадям, т.е: C1C : СC2= A2: A1.
Вопросы для самоконтроля полученных знаний
1) Что такое пространственная система сил?
2) В каком случае систему пространственных сил называют сходящейся?
3) Как определяется равнодействующая пространственной системы сходящихся сил?
4) Сколько и какие условия равновесия должны выполняться для пространственной системы сходящихся сил?
5) Что такое момент силы относительно оси? Как он определяется и в каком случае он имеет знак плюс и знак минус?
6) В каких случаях момент силы относительно оси равен нулю?
7) Как приводится к центру произвольная система пространственных сил?
8) Что такое главный вектор системы пространственных сил? Чем отличается он от равнодействующей и чему он равен?
9) Какие составляющие имеет главный вектор?
10) Что такое главный момент системы пространственных сил? Как он определяется?
11) Какие составляющие имеет главный момент?
12) Сколько и какие условия равновесия должны выполняться, чтобы пространственная система сил находилась в равновесии?
13) Как определяется равнодействующая системы параллельных сил в пространстве?
14) Сколько и какие условия равновесия должны выполняться, чтобы пространственная система параллельных сил находилась в равновесии?
15) Что такое центр тяжести твердого однородного тела? Как определяются координаты центра тяжести?
16) Что такое центр тяжести плоской фигуры? Как определяются его координаты?
РАЗДЕЛ II
Дата добавления: 2018-11-26; просмотров: 2430; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
2.
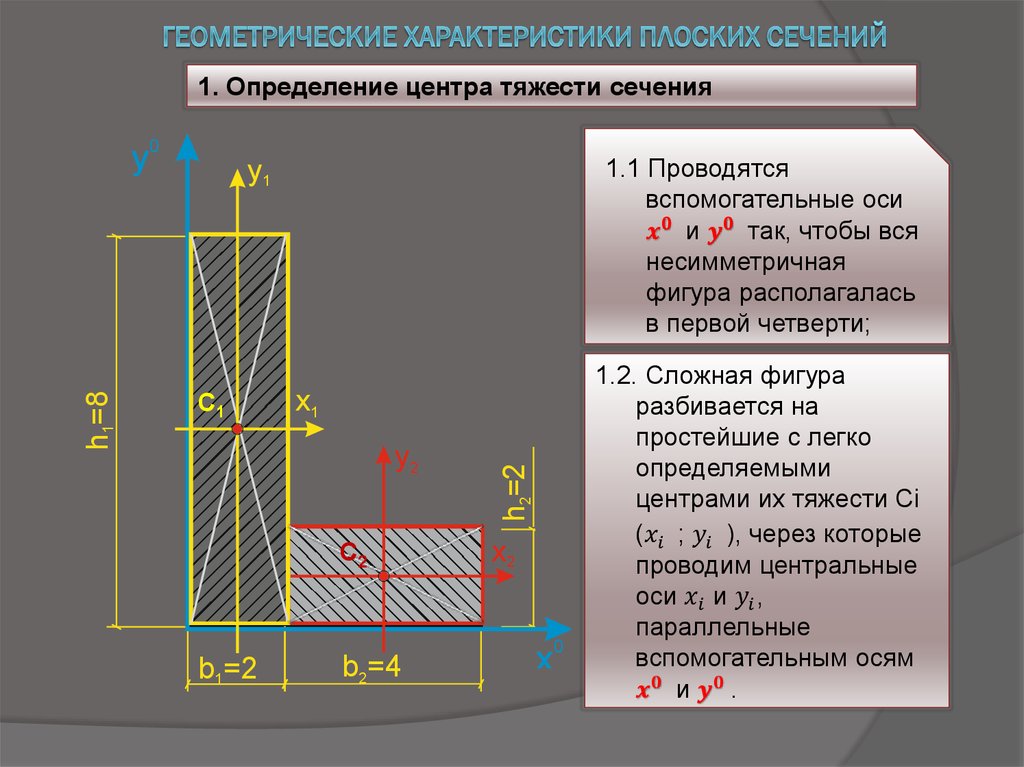
 1. Нахождение центра тяжести составного сечения.
1. Нахождение центра тяжести составного сечения.
Выберем произвольную
систему координат x0y0
(пусть она
совпадает с собственными осями бруса),
относительно которой будем искать центр
тяжести сечения. Координаты центра
тяжести определяются по формулам
;
,
где
,
– статические моменты относительно
осей x0
и y0
соответственно каждой фигуры, входящей
в сечение;
–
площадь отдельной фигуры.
Площади сечений
неравнобокого уголка, швеллера и двутавра
взяты из таблиц сортаментов ([3],
с.342-354, табл. 1, 2, 4).
Таблица 2.2
Номер фигуры | Тип сечения | А, см2 | , | , |
1. | Неравнобокий | 22,2 | 444 | 146 |
2. | Швеллер | 13,3 | 304 | 31,2 |
3. | Двутавр | 14,7 | 350 | 27,9 |
Длина бруса
мм.
Площадь сечения
бруса найдем по формуле
см2
.
Статические
моменты фигуры вычисляются по формулам
;
,
где А
– площадь фигуры;
,
– расстояния от центра тяжести фигуры
до осей x0
и y0
соответственно.
см3;
см3;
см3;
см3;
см3;
см3;
см3;
см3.
Таким образом,
координаты центра тяжести равны:
см;
см.
2.2. Нахождение момента инерции относительно центральных осей.
Вычислим моменты
инерции относительно осей, проходящих
через центр тяжести сечения. Введем
центральные оси составного сечения x
и
y.
Согласно
теореме о переносе осей (теореме
Гюйгенса-Штейнера) момент инерции
каждой фигуры относительно центральной
оси будет складываться из собственного
и переносного моментов инерции:
;
,
где
,
– моменты инерции относительно
собственных осей фигуры; А
– площадь фигуры; a,
b
– расстояние между собственной осью
фигуры и центральной осью составного
сечения (соответственно x
и y).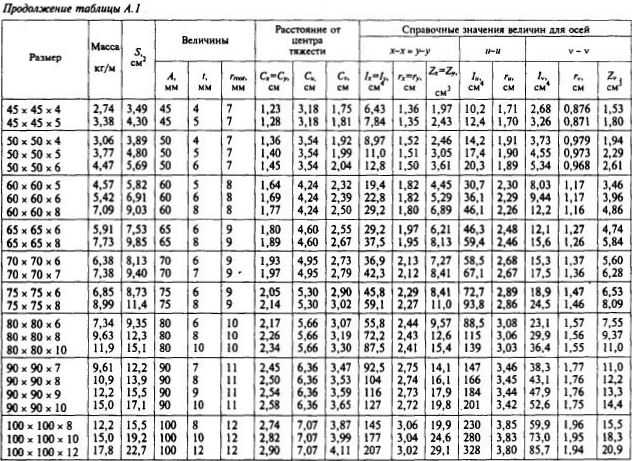
Собственные
моменты инерции неравнобокого уголка,
швеллера и двутавра взяты по сортаменту
(см. табл. 2.2).
Собственные
моменты инерции бруса определяются по
формулам
см4;
см4.
Таким образом,
моменты инерции фигур в составе сечения
относительно центральных осей составного
сечения будут иметь вид:
см4;
см4;
см4;
см4;
см4;
см4;
см4;
см4;
Момент инерции
составного сечения относительно оси
x:
см4;
относительно оси
y:
см4.
Задача 3
Р асчет прочно-плотного заклепочного шва
Рассчитать
продольный прочно-плотный шов для котла
с внутренним давлением q,
диаметром D,
выполненного из стали, а также определить
напряжения на наклонной площадке
элемента стенки котла.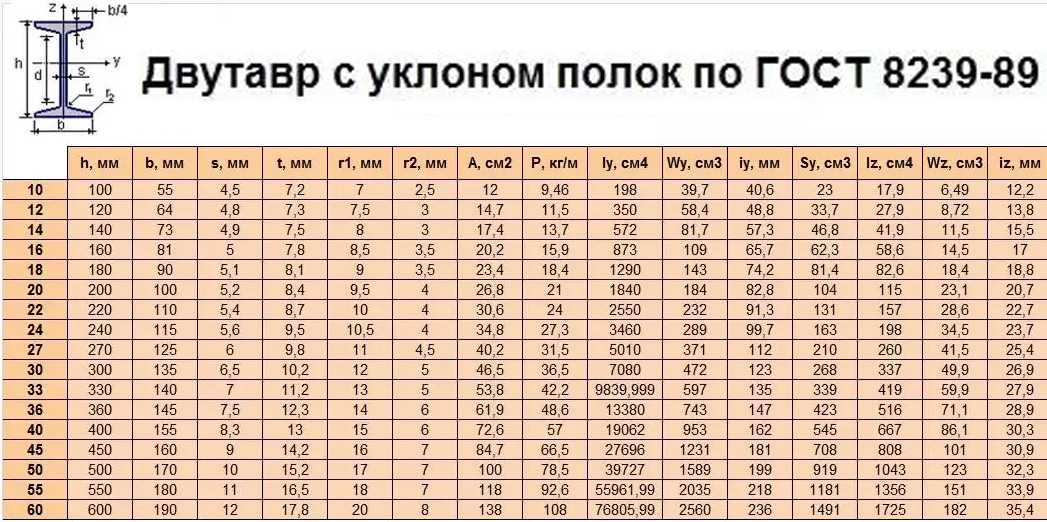 Исходные данные
Исходные данные
указаны в табл. 3.1.
Таблица 3.1
№ п/п | Диаметр котла D, | Температура стенки | Внутреннее q, | Материал листов котла, | Угол наклона площадки, | Вид элемента |
14 | 1,2 | 180 | 0,8 | Сталь 15пс | 15 |
Рис. 3.1.
3.1.
Решение
3.1 Определение толщины δ стенки котла.
Условие прочности
на растяжение для тонкостенного сосуда
имеет вид:
,
где
– допускаемое напряжение при растяжении;
[S]
– допускаемый коэффициент прочности
шва.
Температура
нагрева стенки котла 180°С < 250°С, поэтому
вычислим по формуле:
,
где
– предел прочности при растяжении
материала листов стенки котла;
– коэффициент запаса прочности,
соответствующий
;
.
Для стали марки
15пс
МПа ([2], с.
50).
Исходя из соотношения
МПа∙м, примем тип шва – двухрядный
стыковой. Допускаемый коэффициент
прочности для такого типа шва ([м.у.],
табл. 2.1):
.
В качестве
максимального напряжения примем
как наиболее опасное:
.
Таким образом,
условие прочности примет вид:
;
.
м
мм.
С учетом добавки
на коррозию металла
мм принимаем значение:
мм.
ЗАДАЧА 3 — Студопедия
Поделись
Для заданных сечений, состоящих из прокатных профилей и полосы bЧh, определить положение центра тяжести.
| Вариант | Двутавр | b, см | h, м | Швеллер |
| 20,0 | 1,2 | |||
| 18,0 | 1,5 | |||
| 24,0 | 1,8 | |||
| 28,0 | 2,0 | 18а | ||
| 24,0 | 1,8 | 22а | ||
| 20,0 | 1,5 | 24а | ||
| 15,0 | 1,2 | |||
| 24а | 12,0 | 1,0 | ||
| 18а | 24,0 | 2,0 | ||
| 22а | 21,0 | 2,4 |
ПРИМЕР 3.
Определить координаты центра тяжести сечения. Сечение состоит из двутавра № 18, швеллера № 18 и пластины 200*60 (рисунок-6)
Рисунок — 6
1 Разобьем сечение на профили проката. Оно состоит из двутавра № 18, швеллера № 18 и пластины 200*60. обозначим их 1, 2, 3.
2 Укажем центры тяжести каждого профиля, используя таблицу приложения, и обозначим их С1, С2, С3, проведем через них оси Х1, Х2, Х3.
3 Выберем систему координатных осей. Ось Y совместим с осью симметрии, а ось Х проведем через центр тяжести двутавра.
4 Определим центр тяжести всего сечения. Так как ось Y совпадает с осью симметрии, то она проходит через центр тяжести сечения, потому Хс=0. Координату Yс определим по формуле:
Пользуясь таблицами ГОСТ 8239-89, ГОСТ 8240-89, ГОСТ 8510-86, ГОСТ 8509-86, определим координаты центров тяжести
А1 = 20,7 см2 7,57 см
А2 = 23,4 см2y2 = 0
А3 = 20*6 = 120 см2 -12 см
Координата у2 равна нулю, так как ось Х проходит через центр тяжести двутавра. Подставим полученные значения в формулу для определения уС:
Подставим полученные значения в формулу для определения уС:
-7,82 см
1 Укажем центр тяжести сечения на рисунке и обозначим его буквой С. Покажем расстояние уС = -7,82 см от оси Х до точки С.
2 Определим расстояние между точками С и С1, С и С2, С и С3, обозначим их а1, а2, а3:
а1 = у1 + уС = 7,57 + 7,82 = 15,39 см
а2 = уС = 7,82 см
а1 = у3 — уС = 12 — 7,82 = 4,18 см
3 Выполним проверку. Для этого ось Х проведем по нижнему краю пластины. Ось Y оставим, как в первом решении. Формулы для определения хС и уС не изменятся:
хС = 0,
Площади профилей останутся такими же, а координаты центров тяжести двутавра, швеллера и пластины изменятся.
А1 = 20,7 см2 22,57 см
А2 = 23,4 см2 15 см
А3 = 20*6 = 120 см2 3 см
Находим координату центра тяжести:
7,18 см
По найденным координатам хС и уС наносим на рисунок точку С.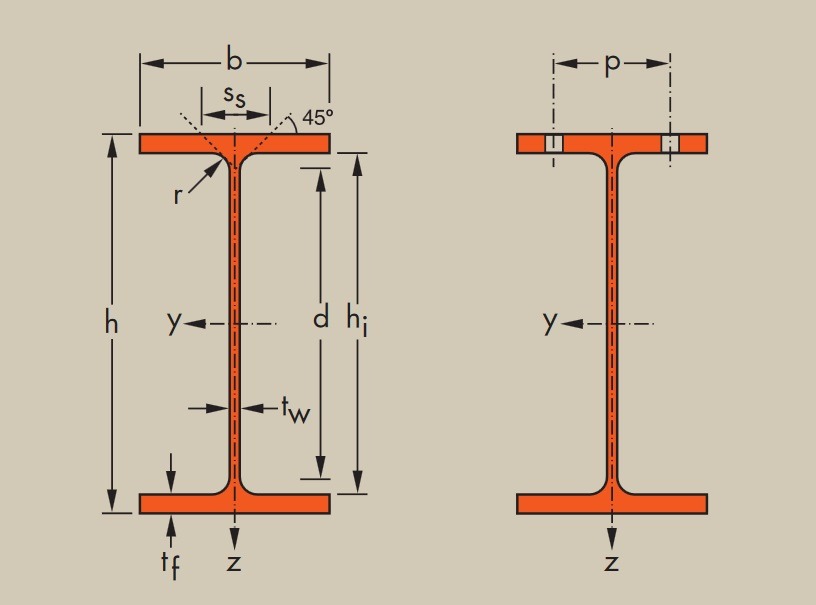 Найденное двумя способами положение центра тяжести находится в одной и той же точке. Сумма координат уС, найденных при первом и втором решении: 7,82 + 7,18 = 15 см
Найденное двумя способами положение центра тяжести находится в одной и той же точке. Сумма координат уС, найденных при первом и втором решении: 7,82 + 7,18 = 15 см
Это равно расстоянию между осями Х при первом и втором решении:
18/2 + 6 = 15 см.
ЗАДАЧА 4
По оси ступенчатого бруса приложены силы и . Необходимо построить эпюры продольных сил и нормальных напряжений, определить абсолютную деформацию бруса. Принять Е = 2,1 * 105 МПа.
| Вариант | F1, кН | F2, кН | l1, м | l2, м | l3, м | А, см2 |
| 1,0 | 1,2 | 1,4 | 4,0 | |||
| 1,2 | 1,4 | 1,6 | 6,0 | |||
| 1,4 | 1,6 | 1,8 | 3,5 | |||
| 1,6 | 1,8 | 2,0 | 4,5 | |||
| 1,8 | 1,6 | 1,4 | 4,0 | |||
| 2,0 | 1,4 | 1,2 | 6,5 | |||
| 1,8 | 2,0 | 2,4 | 7,5 | |||
| 1,6 | 1,4 | 1,2 | 6,0 | |||
| 1,4 | 1,2 | 1,0 | 5,0 | |||
| 1,2 | 1,4 | 1,6 | 4,0 |
ПРИМЕР 4
Для данного ступенчатого бруса построить эпюры продольных сил и нормальных напряжений. Определить абсолютное удлинение (укорочение) бруса (рисунок 7)
Определить абсолютное удлинение (укорочение) бруса (рисунок 7)
Дано:
, , м, м, м, А=3,2 см 2, Е=2,1*105 МПа
Рисунок — 7
Решение
1 Проводим ось Z в сторону свободного конца бруса и определяем реакцию заделки :
2 Разбиваем брус на участки, границы которых определяются сечениями, где изменяется площадь поперечного сечения или приложены внешние силы. На каждом из участков проводим характерные сечения 1-1, 2-2, 3-3. С помощью метода сечений определяем продольные силы на каждом из участков бруса: мысленно рассекаем брус в пределах первого участка сечения 1-1, отбрасываем верхнюю часть бруса и заменяем ее действие продольной силой N1 (рисунок 7) для оставшейся части составляем уравнение равновесия:
Аналогично находим N2 и N3:
сечение 2-2 (рисунок 7)
;
сечение 3-3 (рисунок 7)
.
По найденным значениям продольной силы строим соответствующую эпюру.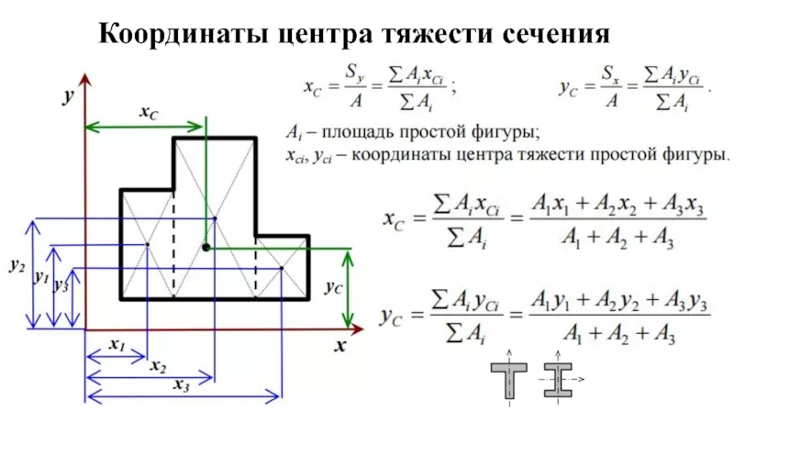 Для этого параллельно оси бруса проведем базовую (нулевую) линию. Левее ее откладываем отрицательные значения N, соответствующие сжатому участку, а правее – положительные значения N, соответствующие растянутому участку (рисунок — 7).
Для этого параллельно оси бруса проведем базовую (нулевую) линию. Левее ее откладываем отрицательные значения N, соответствующие сжатому участку, а правее – положительные значения N, соответствующие растянутому участку (рисунок — 7).
Определяем нормальные напряжения в характерных сечениях бруса по формуле:
;
.
Строим соответствующую найденным значениям эпюру σ (рисунок — 7)
4 Определяем абсолютное удлинение бруса.
В соответствии с законом Гука:
где Е=2,1*105 МПа – модуль продольной упругости для стали.
Складывая удлинение участков, получим:
Учитывая, что I м=103мм, будем иметь:
(87,5*2,4+43,75*2,2-112,5*2,0)=0,39 мм.
Таким образом, абсолютное удлинение бруса = 0,39 мм.
ЗАДАЧА 5
По данным задачи 2 для двухопорной балки построить эпюры поперечных сил Qу и изгибающих моментов Мх. Подобрать сечение стального двутавра, приняв
[σ] = 160 МПа.
ПРИМЕР 5
Для двухопорной балки построить эпюры поперечных сил Q и изгибающих моментов М. Подобрать сечение стального двутавра, приняв [σ] = 160 МПа.
Дано: F1=24 kH; F2=36 кН; m1=18 кНм;
m2=24 кНм; =2.0 м; м; м.
Рисунок — 8
Решение
1 Составляем уравнение равновесия параллельной системы сил, из которых определяем опорные реакции балки:
(6)
Из уравнения (6) находим RAУ:
Из уравнения (5) находим В:
Проверяем правильность определения опорных реакций, составляя сумму проекций всех сил на ось У:
то есть реакции определены верно.
2 Определяем значения поперечной силы Q в характерных сечениях балки, которые обозначим цифрами 1, 2, 3, 4 (рисунок 8 а)
Q1=Q2лев=F1=24 кН;
Q2прав=Q3лев=F1+RАУ=24-13=11 кН;
Q32прав=Q4=F1+RАУ-F2= -RВУ= -25 кН.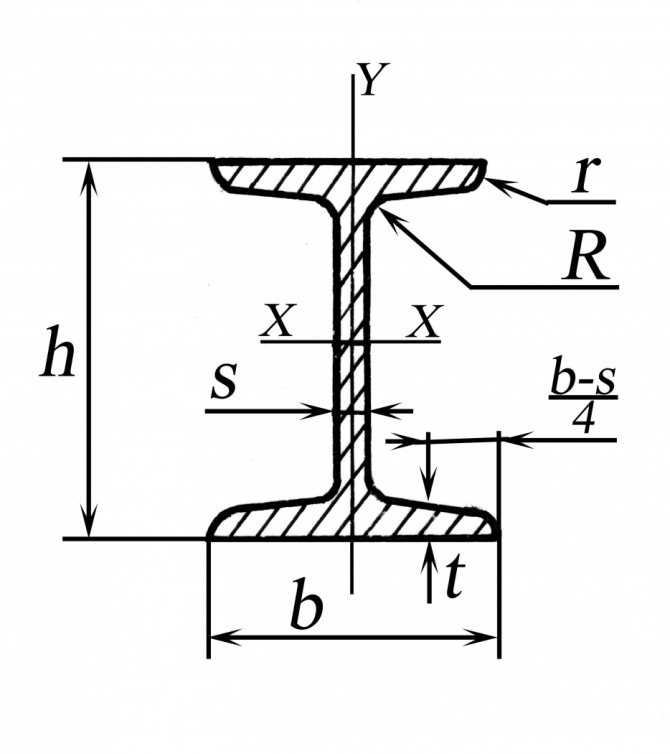
По найденным значениям строим эпюру, поперечных сил Q (рисунок 8 б).
3 Аналогично определяем значения изгибающего момента М в характерных сечениях балки:
М1=0;
М2лев=F1*2.0=48 кНм
М2прав=М2лев+m1=48+18=66 кНм;
М3=F1*5.0+m1+RАУ*3,0=120+18-39=99 кНм;
М4=m2=24 кНм.
По найденным значениям строим эпюру изгибающих моментов М (рисунок 8 в).
4 По эпюре изгибающих моментов определяем положение опасного сечения балки (сечение, в котором изгибающий момент имеет наибольшее по абсолютной величине значение). В нашем случае – это сечение 3, где М3=Мmaх=99 кНм. Из условия прочности балки на изгиб вычисляем необходимый осевой момент сопротивления:
.
В соответствии с ГОСТ 8239-89 принимаем сечение из стального двутавра № 33 с Wх=597 см3. Имеем перенапряжение:
что находится в разрешенных пределах (менее 5%).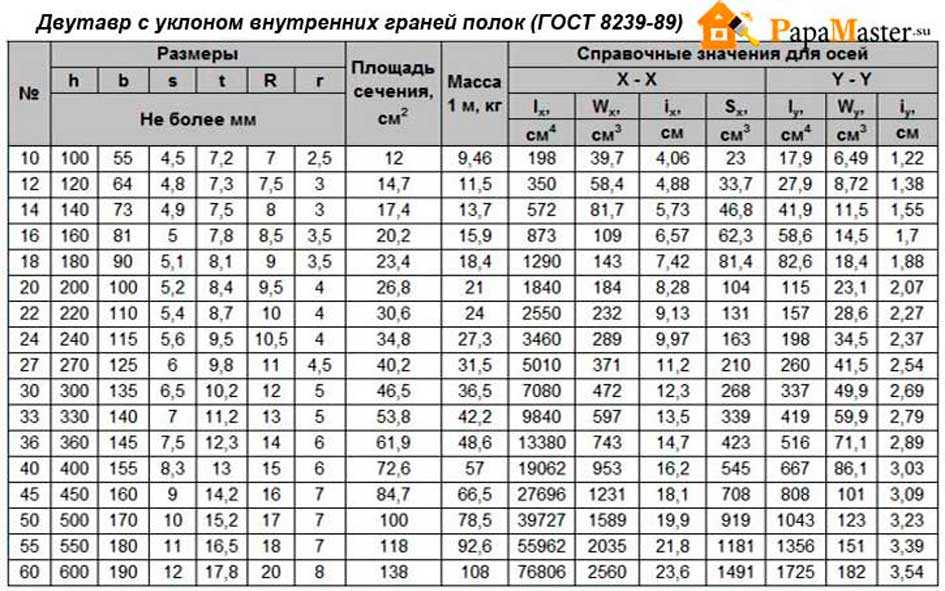
Ответ: сечение балки двутавр № 33.
Свойства сечения швеллера (U) | Calcresource
Соглашение
-Геометрия
-Момент инерции
-Почему момент инерции полезен
-Полярный момент инерции
-Эластичный сечение ось
— Вокруг оси Y
— Радиус вращения
— Формулы сечения U
— Связанные страницы
Геометрия
U-образное сечение (также называемое швеллером) является довольно распространенной формой сечения, обычно используемой в стальных конструкциях. Однако U-образные поперечные сечения могут быть изготовлены и из других материалов (например, из бетона, алюминия, пластика и т. д.). На следующем рисунке показаны основные размеры U-образного сечения, а также широко распространенные обозначения его компонентов. В частности, U-образное сечение определяется двумя полками и стенкой. На этой странице предполагается, что два фланца идентичны, что приводит к симметричной U-образной форме. 92 \справа)
92 \справа)
Мы пришли к последнему уравнению, разобрав U-образный профиль на более простые компоненты (полки и стенку), а затем найдя статический момент каждого из них, от оси, направленной к внешнему краю стенки. . Если вам нужна дополнительная информация об этой технике, вы можете прочитать нашу статью о поиске центроида составных областей здесь.
Момент инерции
Момент инерции секции канала можно найти, если всю площадь разделить на три меньшие части, A, B, C, как показано на рисунке ниже. Конечную область можно рассматривать как аддитивную комбинацию A+B+C. Однако, поскольку фланцы равны, более простой комбинацией может быть (A+B+C+V)-V (это разница между двумя прямоугольными областями). Следовательно, момент инерции I_x сечения канала вокруг центральной оси x определяется следующим образом: 93}{12}
где h высота канала, b ширина полки, t_f толщина полки и t_w толщина стенки. Обратите внимание, что нет необходимости применять теорему о параллельных осях для любой из двух прямоугольных областей (V и A+B+C+V), потому что их центроиды лежат над исследуемой осью x. 3\over3. Тогда получается следующая формула: 92
3\over3. Тогда получается следующая формула: 92
Зачем нужен момент инерции
Момент инерции (второй момент или площадь) используется в теории балок для описания жесткости балки при изгибе. Изгибающий момент M, приложенный к поперечному сечению, связан с его моментом инерции следующим уравнением:
M = E\times I \times \kappa
где E — модуль Юнга, свойство материала, и \kappa кривизна балки из-за приложенной нагрузки. Таким образом, из предыдущего уравнения видно, что при приложении определенного изгибающего момента M к поперечному сечению балки развиваемая кривизна обратно пропорциональна моменту инерции I.
Полярный момент инерции
Полярный момент инерции описывает жесткость поперечного сечения по отношению к крутящему моменту, так же как плоские моменты инерции, описанные выше, связаны с изгибом. Расчет полярного момента инерции I_z вокруг оси z (перпендикулярной сечению) можно выполнить с помощью теоремы о перпендикулярных осях:
I_z = I_x + I_y
, где I_{x} и I_{y} равны моменты инерции вокруг осей x и y, которые взаимно перпендикулярны оси z и сходятся в одном начале координат. 94 .
94 .
РЕКЛАМА
Модуль упругости сечения
Модуль упругости сечения S_x любого поперечного сечения вокруг оси x (центроидальной) описывает реакцию сечения на упругий изгиб вокруг той же оси. Он определяется как:
S_x = \frac{I_x}{Y}
где I_{x} — момент инерции сечения вокруг оси x, а Y — расстояние от центра тяжести волокна данного сечения ( параллельно оси). Как правило, для этого расчета используется более удаленное волокно, что приводит к минимальному модулю упругости сечения. Если поперечное сечение симметрично относительно оси (как U-образное сечение вокруг оси x) и его размер, перпендикулярный этой оси, равен h, то самое удаленное волокно лежит на расстоянии Y=h/2 от оси. Следовательно, последняя формула принимает вид:
S_x = \frac{2 I_x}{h}
Для модуля упругости сечения S_y вокруг оси y можно определить два значения: одно для левого волокна сечения (расстояние x_c от центра тяжести) и одно для правые волокна, являющиеся концами фланцев (на расстоянии b-x_c от центра тяжести):
\begin{split} & S_{y,max} & = \frac{I_y}{x_c} \\ & S_ {y,min} & = \frac{I_y}{b-x_c} \end{split}
, где обозначение max/min основано на предположении, что x_c \lt b-x_c , что справедливо для любого участка канала . Обычно требуется только минимальный модуль сечения (см. следующий абзац, почему).
Обычно требуется только минимальный модуль сечения (см. следующий абзац, почему).
Если к оси x приложен изгибающий момент M_x, сечение будет реагировать нормальными напряжениями, линейно изменяющимися с расстоянием от нейтральной оси (которая в упругом режиме совпадает с центроидальной осью x-x). Вдоль нейтральной оси напряжения равны нулю. Абсолютный максимум \sigma будет иметь место на самом удаленном волокне, величина которого определяется формулой: свойство, аналогичное поперечному сечению А, для осевой нагрузки. Для последнего нормальным напряжением является F/A. 93 .
Модуль пластического сечения
Модуль пластического сечения аналогичен упругому, но определяется в предположении полной пластической текучести поперечного сечения при изгибе. В этом случае все сечение разделено на две части, одну на растяжение и одну на сжатие, каждая из которых находится под однородным полем напряжений. Для материалов с равными напряжениями текучести при растяжении и сжатии это приводит к разделению сечения на две равные области, A_t при растяжении и A_c при сжатии, разделенные нейтральной осью. Это результат уравновешивания внутренних сил в поперечном сечении при пластическом изгибе. В самом деле, сжимающая сила, реализуемая по всей сжимаемой площади, будет равна A_cf_y, если предположить условия пластичности (т. е. материал будет деформироваться везде) и что предел текучести при сжатии равен f_y. Точно так же растягивающая сила будет равна A_t f_y, если использовать те же предположения. Обеспечение равновесия:
Это результат уравновешивания внутренних сил в поперечном сечении при пластическом изгибе. В самом деле, сжимающая сила, реализуемая по всей сжимаемой площади, будет равна A_cf_y, если предположить условия пластичности (т. е. материал будет деформироваться везде) и что предел текучести при сжатии равен f_y. Точно так же растягивающая сила будет равна A_t f_y, если использовать те же предположения. Обеспечение равновесия:
A_cf_y = A_t f_y\Rightarrow
A_c= A_t
Ось называется пластической нейтральной осью , а для несимметричных сечений не совпадает с упругой нейтральной осью (которая опять же является центроидальной). Модуль пластического сечения задается общей формулой:
Z = A_c Y_c + A_t Y_t
, где Y_c — расстояние от центра тяжести области сжатия A_c до нейтральной пластической оси, а Y_t — соответствующее расстояние от центра тяжести зоны растяжения. площадь А_т.
Вокруг оси x
В случае U-образного сечения существует симметрия относительно оси, параллельной полкам. Другими словами, центральная ось x также является осью симметрии. В таком случае пластическая нейтральная ось, которая делит всю площадь на две равные части, также должна быть центроидальной. Из-за симметрии Y_c=Y_t и применение последнего уравнения приводит к следующей формуле для модуля пластического сечения поперечного сечения канала при изгибе x-x:
Другими словами, центральная ось x также является осью симметрии. В таком случае пластическая нейтральная ось, которая делит всю площадь на две равные части, также должна быть центроидальной. Из-за симметрии Y_c=Y_t и применение последнего уравнения приводит к следующей формуле для модуля пластического сечения поперечного сечения канала при изгибе x-x:
Z_x = 2 A_c Y_c
Найти центроид области сжатия несложно. Как показано на следующем рисунке, площадь сжатия считается эквивалентной разнице между большим прямоугольником с размерами b и h/2 и меньшим прямоугольником (синего цвета). Затем рассчитывается расстояние Y_c с учетом статических моментов этих участков, например:
Y_c = \frac{1}{A_c} \left(\frac{bh}{2}\frac{h}{4 } -(b-t_w) ({h\over2}-t_f)\frac{ ({h\over2}-t_f)}{2} \right) \Rightarrow 92}{4}
РЕКЛАМА
Вокруг оси Y
U-образное сечение не имеет симметрии, вокруг оси, параллельной перемычке. Если это так, пластическая нейтральная ось не видна только при осмотре и должна быть определена в первую очередь.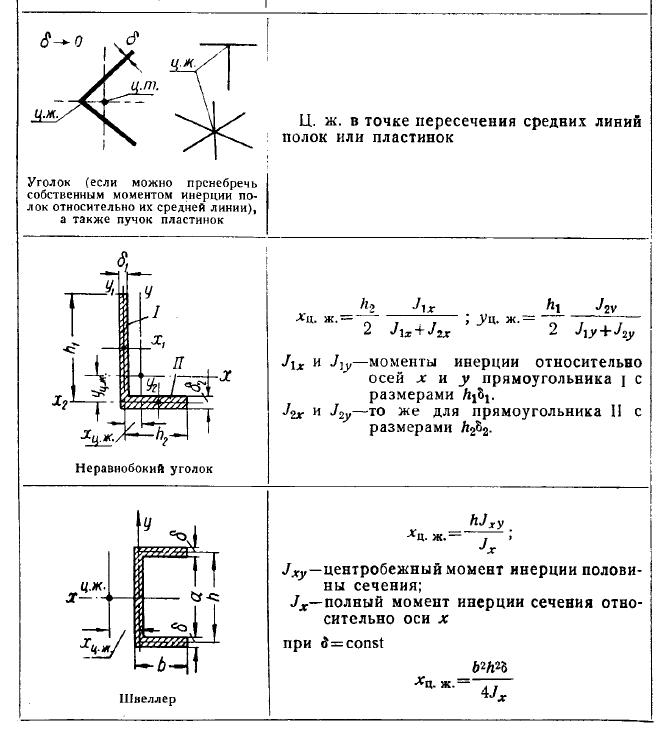 Можно использовать свойство пластической нейтральной оси делить все сечение на две равные области. В частности, для U-образного сечения получаются следующие два уравнения изгиба вокруг оси y:
Можно использовать свойство пластической нейтральной оси делить все сечение на две равные области. В частности, для U-образного сечения получаются следующие два уравнения изгиба вокруг оси y:
\left \{ \begin{array}{ll} 2(b-x_{pna})t_f = \frac{A {2} & \text{ , если } x_{pna} \ge t_w \\ x_{pna} h = \frac{A}{2} & \text{ , если } x_{pna} \lt t_w \\ \end{массив} \right.
, который становится следующим:
x_{pna} =\left \{ \begin{array}{ll} b- \frac{A}{4t_f} & \text{ , если: } t_w \le {A\over2 h } \\ \frac{A}{2h} & \text{ , если: } t_w \gt {A\over2 h} \\ \end{массив} \right.
где x_\textit{pna} — расстояние нейтральной оси пластика от внешнего края стенки (левый край на рисунке). Первое уравнение справедливо, когда пластическая нейтральная ось пересекает две полки, а второе — когда она пересекает стенку. Как правило, нельзя заранее знать, какое уравнение является релевантным. 92) — 4bt_f h_wt_w \right) \quad , t_w \gt {A\over2 h}
где: h_w=h-2t_f .
Радиус вращения
Радиус вращения R_g поперечного сечения относительно оси определяется по формуле:
R_g = \sqrt{\frac{I}{A}}
где I момент инерции поперечного сечения вокруг той же оси и A его площади.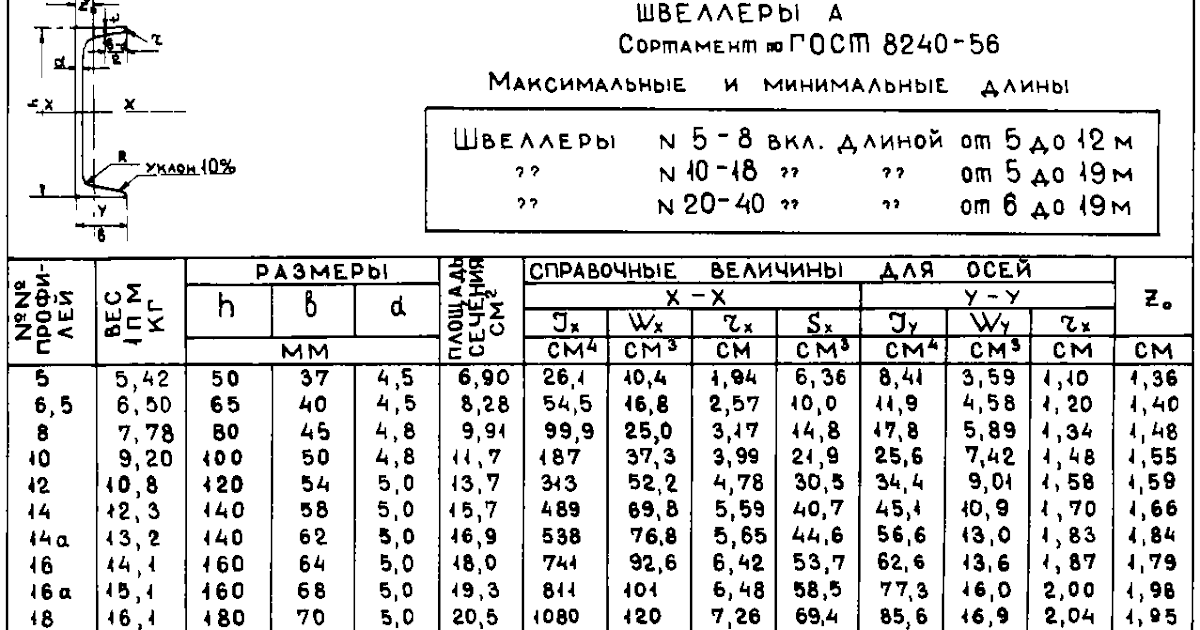 3}{ 3}
3}{ 3}
Связанные страницы
Понравилась эта страница? Поделись с друзьями!
Момент инерции площади — типичные поперечные сечения I
Момент инерции площади или Момент инерции площади — , также известный как Второй момент площади — I , является свойством формы, которое используется для прогнозирования прогиба, изгиба и напряжения в балках.
Площадь Момент инерции — Имперские единицы
- inches 4
Area Moment of Inertia — Metric units
- mm 4
- cm 4
- m 4
Converting between Units
- 1 cm 4 = 10 -8 m 4 = 10 4 mm 4
- 1 in 4 = 4.16×10 5 mm 4 = 41,6 см 4
Пример — преобразовать между площадью
9240 CM 4 может быть обращено в 9240 CM 4 .
(9240 см 4 ) 10 4 = 9,24 10 7 мм 4
Область.0027
Для изгиба вокруг оси x можно выразить как
I x = ∫ y 2 Да (1)
, где
I
. до оси x ( м 4 , мм 4 , дюймов 4 )
y = расстояние элемента от оси x 2,9dA 9 мinches )
dA = an elemental area ( m 2 , mm 2 , inches 2 )
The Moment of Inertia for Изгибание вокруг оси Y может быть выражено как
I Y = ∫ x 2 Да (2)
, где
I Y = зона. M 4 , мм 4 , дюймы 4 )
x = Perpenduld Distecat
Момент инерции площади для типичных сечений I
- Момент инерции площади для типовых сечений II быть рассчитано как
I x = a 4 / 12 (2)
where
a = side (mm, m, in.
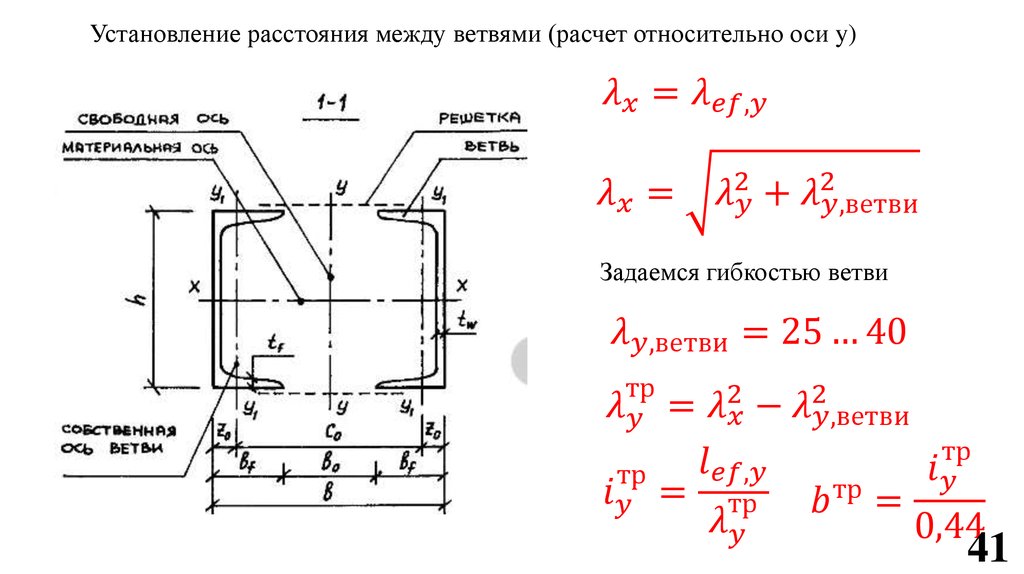 .)
.)
I y = A 4 /12 (2B)
Сплошная прямоугольная сечение
Момент области инициации для прямоугольной секции может быть рассчитано как
I x = B 9029.9 3 /12 (3)
, где
B = ширина
H = высота
I
I
9
I
I
I
I
.
Сплошное круглое поперечное сечение
Момент инерции площади для сплошного цилиндрического сечения можно рассчитать как
I x = π r 4 / 4
= π d 4 / 64 (4)
where
r = radius
d = diameter
I y = π r 4 /4
= π D 4 /64 (4B)
Полово цилиндрический сечение
Область инерции для полой цилиндрической секции может быть вычислен в виде
.
 0005
0005I x = π (d o 4 — d i 4 ) / 64 (5)
where
d o = cylinder outside diameter
d i = cylinder inside diameter
I y = π (d o 4 — d i 4 ) / 64 (5b)
квадратная секция — Диагональные моменты
Диагональные моменты инерции для квадратной секции можно рассчитать как
I x = I Y = A 4 /12 (6) 696996 = A 4 /12 (6) 6969696 = A 4 /12 (6) 695 = 4 /12 (6) 696 .
Прямоугольное сечение – Моменты площади на любой линии, проходящей через центр тяжести
Прямоугольное сечение и площадь момента на линии, проходящей через центр тяжести, можно рассчитать как
I x = (B H / 12) (H 2 COS 2 A + B 2 SIN 2 A) (7)
Симметричная форма
Оберный момент для Inertia для симметричных снимков Symtritical Shapeed Symtrical Symtrical Symtrical Symtrical Symtrical Symtrical Symtrical Symtrical Symtrical Symtrical Symetrical Shaped Symtrical Symtrical Symtrical Symtrical Symtrical.
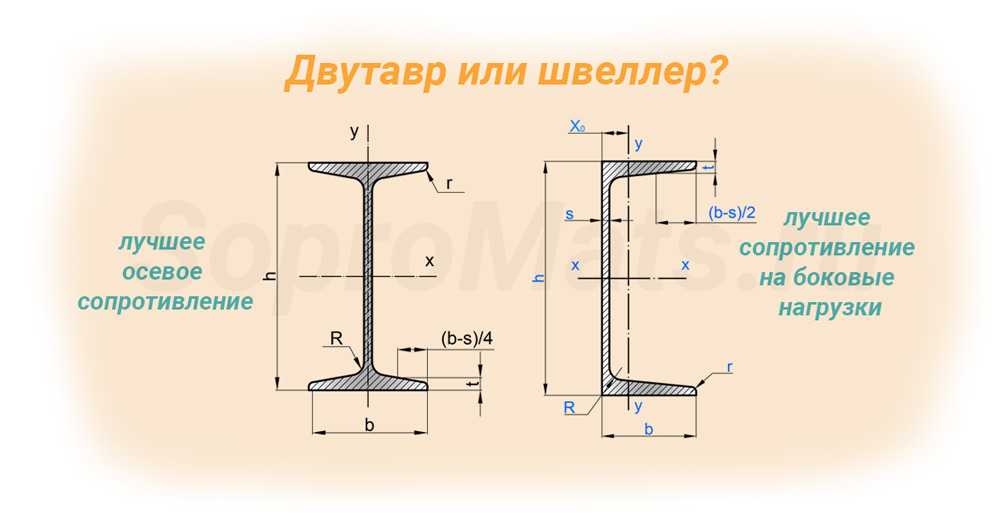 section can be calculated as
section can be calculated asI x = (a h 3 / 12) + (b / 12) (H 3 — h 3 ) (8)
I y = (a 3 h / 12) + (b 3 / 12) (H — h) (8b)
Nonsymmetrical Shape
Area Moment of Inertia for a non symmetrical shaped section can be calculated as
I x = (1 / 3) (B y b 3 — B 1 H B 3 + B Y T 3 — B1 H T 3 ) (9)
- область в области. Полярный момент инерции против момента инерции
- «Момент инерции площади» — это свойство формы, которое используется для прогнозирования прогиба, изгиба и напряжения в балках. скручивание балки под действием крутящего момента
- «Момент инерции» является мерой сопротивления объекта изменению направления вращения.
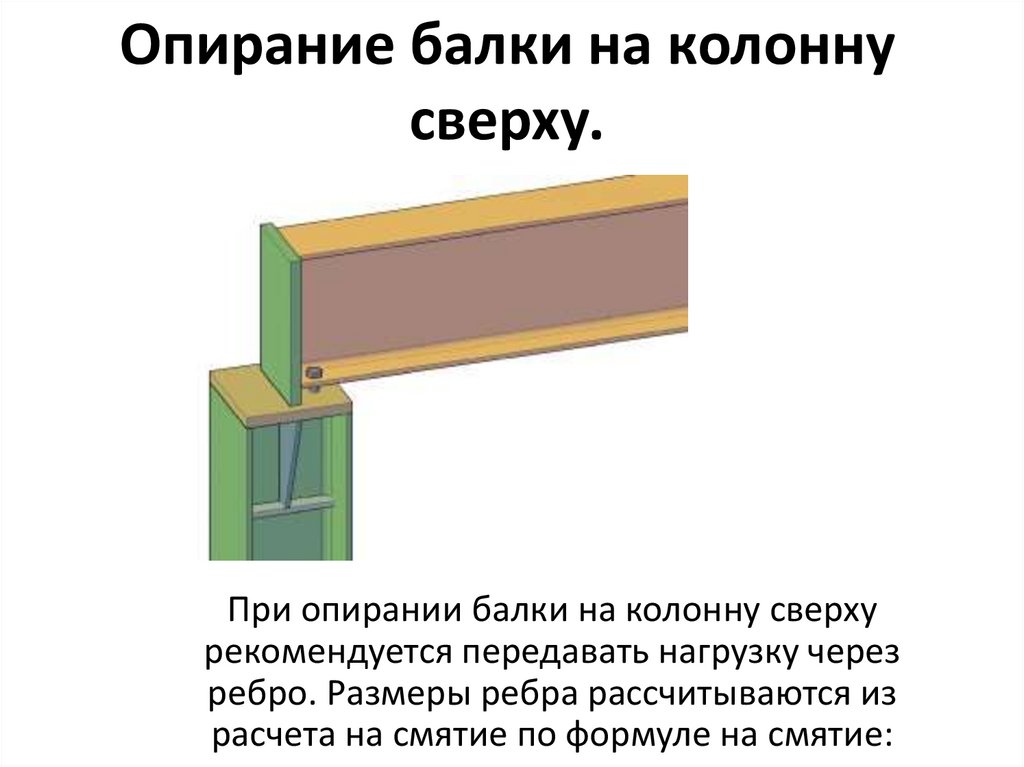
Модуль упругости сечения
- «Модуль сечения» определяется как W = I / y , где I — момент инерции площади, а y — расстояние от нейтральной оси до любого заданного волокна
Экспериментальное исследование четырехточечного изгиба тонкостенной стальной балки открытого сечения, нагруженной и установленной в центре сдвига
Реферат
Тонкостенные холоднодеформированные конструкции были и остаются очень популярными конструкционными элементами, используемыми в машиностроении. Современные технологии и прогресс в области материаловедения позволяют изготавливать тонкостенные холодноформованные детали различной формы. Таким образом, комбинации между технологическими возможностями, свойствами материалов, нагрузками и техническими требованиями являются широкими и неограниченными для тонкостенных компонентов. Целью данной статьи является проведение экспериментального исследования холодногнутых стальных балок с С-образным профилем под действием четырехточечной изгибающей нагрузки на основе явлений глобального и местного выпучивания.
 Был разработан испытательный стенд со специально разработанной системой поддержки, чтобы подвергать тонкостенные стальные балки четырехточечной изгибающей нагрузке, где опора и нагрузки прикладывались к центру сдвига стальной балки открытого сечения. Показано, что полностью исключить моментную нагрузку на тонкостенную балку с открытым сечением, где нагрузка и опора приложены в центре сдвига, не представляется возможным, поскольку исследуемые балки выполнены не идеально. Тонкостенные балки открытого сечения очень чувствительны к граничным условиям и геометрической точности. Сила тяжести тоже работает. Представленная методика исследования может быть усовершенствована и испытана на других тонкостенных балках открытого сечения.
Был разработан испытательный стенд со специально разработанной системой поддержки, чтобы подвергать тонкостенные стальные балки четырехточечной изгибающей нагрузке, где опора и нагрузки прикладывались к центру сдвига стальной балки открытого сечения. Показано, что полностью исключить моментную нагрузку на тонкостенную балку с открытым сечением, где нагрузка и опора приложены в центре сдвига, не представляется возможным, поскольку исследуемые балки выполнены не идеально. Тонкостенные балки открытого сечения очень чувствительны к граничным условиям и геометрической точности. Сила тяжести тоже работает. Представленная методика исследования может быть усовершенствована и испытана на других тонкостенных балках открытого сечения.Введение
Преимущества тонкостенных холодногнутых конструкций по сравнению с классическими металлургическими профилями заключаются в том, что конструкции с аналогичными прочностными характеристиками намного легче. Кроме того, тонкостенные детали холодной штамповки имеют меньше ограничений с точки зрения процесса формования.
 Прошлогоднее технологическое развитие дало возможность практически любой холодной штамповки стальных деталей. Аналитические методы с тонкостенными стержнями и балками открытого сечения были разработаны во Власове (1940) теория, где допущения малых перемещений и линейные свойства между напряжениями и деформациями составляют основу для сформулированных математических зависимостей. Теория тонкостенных балок открытого сечения основана на предположениях теории длинных оболочек и пластин, где жесткость конструкции, глобальная и местная устойчивость играют ключевую роль при проектировании. Введение для теоретической устойчивости стержней, оболочек, пластин и других конструкций описано Тимошенко и Гере 1 . В настоящее время существует множество научных работ, в которых прочность и устойчивость тонкостенных конструкций представляют интерес для инженеров и ученых.
Прошлогоднее технологическое развитие дало возможность практически любой холодной штамповки стальных деталей. Аналитические методы с тонкостенными стержнями и балками открытого сечения были разработаны во Власове (1940) теория, где допущения малых перемещений и линейные свойства между напряжениями и деформациями составляют основу для сформулированных математических зависимостей. Теория тонкостенных балок открытого сечения основана на предположениях теории длинных оболочек и пластин, где жесткость конструкции, глобальная и местная устойчивость играют ключевую роль при проектировании. Введение для теоретической устойчивости стержней, оболочек, пластин и других конструкций описано Тимошенко и Гере 1 . В настоящее время существует множество научных работ, в которых прочность и устойчивость тонкостенных конструкций представляют интерес для инженеров и ученых.Устойчивость тонкостенных балок открытого сечения изучалась Magnucki et al. и Magnucka-Blandzi и Zając 2 .
 Магнуки и др. 3 в своей монографии описали вопросы устойчивости в задачах прикладной механики. Они описали устойчивость основных структурных моделей, таких как стержни, балки и связанные системы структурных стержней. Они подробно представили устойчивость тонких прямоугольных или круглых пластин и вращающихся оболочек. В их работе есть глава об устойчивости тонкостенных балок с открытыми сечениями. Авторы применили энергетические методы к аналитическим исследованиям, представив практическую проблему для стальных резервуаров. Они представили практические примеры применения метода конечных элементов и современные эксперименты по тестированию стабильности. Тему устойчивости тонкостенных конструкций также проанализировал Анбарасу 9.0299 4, 5 . Он представил результаты изучения потери устойчивости холодногнутого стального тонкостенного канала с кромкой. Разработан экспериментальный и расчетный метод исследования. Взаимодействие исследуемых форм потери устойчивости, таких как местная, деформационная, боковая, крутильная, было подвергнуто численной модели.
Магнуки и др. 3 в своей монографии описали вопросы устойчивости в задачах прикладной механики. Они описали устойчивость основных структурных моделей, таких как стержни, балки и связанные системы структурных стержней. Они подробно представили устойчивость тонких прямоугольных или круглых пластин и вращающихся оболочек. В их работе есть глава об устойчивости тонкостенных балок с открытыми сечениями. Авторы применили энергетические методы к аналитическим исследованиям, представив практическую проблему для стальных резервуаров. Они представили практические примеры применения метода конечных элементов и современные эксперименты по тестированию стабильности. Тему устойчивости тонкостенных конструкций также проанализировал Анбарасу 9.0299 4, 5 . Он представил результаты изучения потери устойчивости холодногнутого стального тонкостенного канала с кромкой. Разработан экспериментальный и расчетный метод исследования. Взаимодействие исследуемых форм потери устойчивости, таких как местная, деформационная, боковая, крутильная, было подвергнуто численной модели. Оценивали предельное сопротивление и достаточный изгибающий момент. Anbarasu 5 в своем исследовании игнорировал остаточные напряжения и применил модель упруго-совершенного пластического материала без деформационного упрочнения. Предлагаемая аналитическая формула, в которой оценивалось взаимодействие между формами потери устойчивости, может быть интересным инструментом проектирования для инженеров.
Оценивали предельное сопротивление и достаточный изгибающий момент. Anbarasu 5 в своем исследовании игнорировал остаточные напряжения и применил модель упруго-совершенного пластического материала без деформационного упрочнения. Предлагаемая аналитическая формула, в которой оценивалось взаимодействие между формами потери устойчивости, может быть интересным инструментом проектирования для инженеров.Анбарасу по адресу ул. 6 и Dar at al. 7 представлены результаты экспериментального исследования тонкостенных стальных балок, выполненных из швеллеров, полки которых имеют изгиб в виде полосы, так называемых швеллеров с выступами, расположенных ребрами друг относительно друга с определенным дистанционные и стальные пластины, соединенные с фланцами швеллера саморезами с шайбами. Испытываемые балки подвергались 3- и 4-точечному изгибу. Испытываемые балки, состоящие из стальных швеллеров и плоских полок, представляли собой симметричную систему, в которой как направление сил реакции, так и статическая нагрузка пересекались с центром тяжести сечения и центром поперечных сил.
 К концам балок были приварены стальные пластины, чтобы предотвратить коробление сечения во время испытаний. Авторы указали на локальное выпучивание, которое характеризует тонкостенные конструкции, обозначенные как CFS. В другой статье 8 авторы представили результаты серии экспериментальных испытаний прямоугольных сталежелезобетонных балок из КФС с полкой на сжатие, показавшие более высокую жесткость этих конструкций по сравнению с традиционными решениями. Еще одно экспериментальное исследование 9 тонкостенных конструкций из КФС, усиленных уголками для увеличения жесткости конструкции и несущей способности балки. Были исследованы балки как с открытым, так и с закрытым сечением в конфигурации четырехточечного изгиба для различных систем жесткости. В работе отмечается, что правильный подбор элементов жесткости увеличивает несущую способность и жесткость балки, изготовленной по технологии CFS, с 85 до 100 %. В следующей статье Амбарансу 10 представлены результаты имитационного исследования балок замкнутого сечения, изготовленных по технологии CFS.
К концам балок были приварены стальные пластины, чтобы предотвратить коробление сечения во время испытаний. Авторы указали на локальное выпучивание, которое характеризует тонкостенные конструкции, обозначенные как CFS. В другой статье 8 авторы представили результаты серии экспериментальных испытаний прямоугольных сталежелезобетонных балок из КФС с полкой на сжатие, показавшие более высокую жесткость этих конструкций по сравнению с традиционными решениями. Еще одно экспериментальное исследование 9 тонкостенных конструкций из КФС, усиленных уголками для увеличения жесткости конструкции и несущей способности балки. Были исследованы балки как с открытым, так и с закрытым сечением в конфигурации четырехточечного изгиба для различных систем жесткости. В работе отмечается, что правильный подбор элементов жесткости увеличивает несущую способность и жесткость балки, изготовленной по технологии CFS, с 85 до 100 %. В следующей статье Амбарансу 10 представлены результаты имитационного исследования балок замкнутого сечения, изготовленных по технологии CFS. Ссылаясь на литературные данные экспериментальных исследований, он провел валидацию имитационной модели в программе Abaqus. Испытания проводились для различных форм поперечного сечения балок и различной толщины вставных элементов стальных балок КФС.
Ссылаясь на литературные данные экспериментальных исследований, он провел валидацию имитационной модели в программе Abaqus. Испытания проводились для различных форм поперечного сечения балок и различной толщины вставных элементов стальных балок КФС.Экспериментальное исследование проблем потери устойчивости для балок асимметричного двутаврового сечения было проведено Balasubramanian et al. 11 . Полученные результаты были проверены методом МКЭ. Представленная экспериментальная методика апробирована для деталей различного поперечного сечения при четырехточечном изгибе силами нагрузки в две точки в плоскости полки. Определена критическая нагрузка для каждого испытанного элемента. Белингарди и др. 12 экспериментально исследованы стальные тонкостенные цилиндрические балки, в которых между соединяемыми деталями применялись клеевые соединения. Под нагрузкой использовался трехточечный изгиб. Было исследовано поведение трех типов участников. В качестве прослойки между образцом и тонкостенным элементом во время испытаний использовалась пластина из композитного ламината.
 Взаимодействие между режимами потери устойчивости балки при четырехточечном изгибе было разработано Shokouhian et al. 13 экспериментально, аналитически и методом конечных элементов. Потеря устойчивости и последующая потеря устойчивости тонкостенных решетчатых алюминиевых колонн под действием сжимающих усилий была исследована Ziółkowski et al. 14 . Во время экспериментальных испытаний новым исследовательским предложением было управление перемещением сил сжатия. Образцы из алюминия, используемые для экспериментальных испытаний, были изготовлены с очень высокой геометрической точностью, что оказалось очень важным фактором в экспериментальных исследованиях тонкостенных конструкций. Точно также были определены механические свойства алюминиевых колонн с изменением оценки коэффициента Пуассона. В ходе эксперимента авторы использовали тестовые тензометрические датчики, приклеенные в критических местах для обозначения пластического выпучивания. В результате экспериментального выпучивания алюминиевых колонн материал пластически поддается выпучиванию, упругому и неупругому выпучиванию.
Взаимодействие между режимами потери устойчивости балки при четырехточечном изгибе было разработано Shokouhian et al. 13 экспериментально, аналитически и методом конечных элементов. Потеря устойчивости и последующая потеря устойчивости тонкостенных решетчатых алюминиевых колонн под действием сжимающих усилий была исследована Ziółkowski et al. 14 . Во время экспериментальных испытаний новым исследовательским предложением было управление перемещением сил сжатия. Образцы из алюминия, используемые для экспериментальных испытаний, были изготовлены с очень высокой геометрической точностью, что оказалось очень важным фактором в экспериментальных исследованиях тонкостенных конструкций. Точно также были определены механические свойства алюминиевых колонн с изменением оценки коэффициента Пуассона. В ходе эксперимента авторы использовали тестовые тензометрические датчики, приклеенные в критических местах для обозначения пластического выпучивания. В результате экспериментального выпучивания алюминиевых колонн материал пластически поддается выпучиванию, упругому и неупругому выпучиванию. Авторы разделили рассматриваемые образцы в зависимости от их гибкости и механизма коробления.
Авторы разделили рассматриваемые образцы в зависимости от их гибкости и механизма коробления.Интересная статья Rusiński et al. 15 описывает проблемы устойчивости тонкостенных конструкций, где стальные листовые детали тонкостенной конструкции соединялись точечной сваркой. Авторы экспериментально и расчетно методом МКЭ исследовали тонкостенные детали замкнутого сечения под действием осевых сжимающих нагрузок. Диаметр сварного шва и шаг сварного шва контролировались по величине поглощения энергии. Все элементы конструкции фиксируются различными техниками. Применяемый способ соединения, технология и условия эксплуатации могут иметь ключевую роль с точки зрения энергопоглощающих характеристик статической и динамической устойчивости тонкостенных конструкций. Тонкостенные конструкции имеют дополнительные практические преимущества рассеивания механической энергии. Экспериментальное исследование тонкостенных холодногнутых стальных балок, подвергающихся монотонному и циклическому нагружению, было проведено Calderoni et al.
 16 . Динамические экспериментальные исследования основывались на изменении амплитуды перемещений. В ходе монотонных испытаний измерялись силы реакции и смещения образца. На основании полученных характеристик силы и зависимостей перемещений были выделены отдельные фазы. Можно было наблюдать фазу стабильного состояния, критическую силу из-за локальной потери устойчивости и нестабильное состояние из-за обрушения тестируемого участка. При циклическом испытании было отмечено, что поведение исследуемых балок характеризовалось прогрессивным снижением несущей способности. Как правило, локальные коробления фланцев приводят к разрушению детали.
16 . Динамические экспериментальные исследования основывались на изменении амплитуды перемещений. В ходе монотонных испытаний измерялись силы реакции и смещения образца. На основании полученных характеристик силы и зависимостей перемещений были выделены отдельные фазы. Можно было наблюдать фазу стабильного состояния, критическую силу из-за локальной потери устойчивости и нестабильное состояние из-за обрушения тестируемого участка. При циклическом испытании было отмечено, что поведение исследуемых балок характеризовалось прогрессивным снижением несущей способности. Как правило, локальные коробления фланцев приводят к разрушению детали.В статье He et al. 17 тонкостенные балки открытого сечения были исследованы на предмет потери устойчивости. Для анализа элементов трех различных форм поперечного сечения использовались два метода: полуаналитический метод матрицы переноса с конечной полосой и метод матрицы переноса. Полученные результаты сравнивались с моделированием методом конечных элементов.
 Авторы широко описали эволюцию численных методов и различных концепций, которые применялись при анализе потери устойчивости. Исследуемые элементы: асимметричное Е-образное сечение, симметричное двутавровое сечение и X-образное сечение, предложенные стратегии и результаты потери устойчивости сравниваются и обсуждаются. Влияние несовершенства на перфорированную тонкостенную холодноформованную конструкцию исследовали Ungureanu et al. 18 . Экспериментальные исследования были дополнены авторами численным моделированием с использованием метода конечных элементов. Авторы пришли к выводу, что для обеспечения устойчивости тонкостенных холоднодеформированных конструкций необходимо дополнительно проводить анализ надежности, способный дать результаты при заданной вероятности отказа. Экспериментальное исследование эффекта Баушингера в тонком стальном листе толщиной 1 мм, подвергнутом испытаниям на растяжение и четырехточечный изгиб, было проведено Kato et al. 19 . Испытание на растяжение применяли для определения остаточных напряжений в образцах, затем применяли проволочные тензорезисторы при экспериментальных исследованиях и нагрузках на изгиб.
Авторы широко описали эволюцию численных методов и различных концепций, которые применялись при анализе потери устойчивости. Исследуемые элементы: асимметричное Е-образное сечение, симметричное двутавровое сечение и X-образное сечение, предложенные стратегии и результаты потери устойчивости сравниваются и обсуждаются. Влияние несовершенства на перфорированную тонкостенную холодноформованную конструкцию исследовали Ungureanu et al. 18 . Экспериментальные исследования были дополнены авторами численным моделированием с использованием метода конечных элементов. Авторы пришли к выводу, что для обеспечения устойчивости тонкостенных холоднодеформированных конструкций необходимо дополнительно проводить анализ надежности, способный дать результаты при заданной вероятности отказа. Экспериментальное исследование эффекта Баушингера в тонком стальном листе толщиной 1 мм, подвергнутом испытаниям на растяжение и четырехточечный изгиб, было проведено Kato et al. 19 . Испытание на растяжение применяли для определения остаточных напряжений в образцах, затем применяли проволочные тензорезисторы при экспериментальных исследованиях и нагрузках на изгиб. В результате уровень напряжений и остаточных деформаций может быть важен для инженеров по тонкостенным конструкциям, когда динамические нагрузки или циклические нагрузки и разгрузки являются условиями эксплуатации.
В результате уровень напряжений и остаточных деформаций может быть важен для инженеров по тонкостенным конструкциям, когда динамические нагрузки или циклические нагрузки и разгрузки являются условиями эксплуатации.Следует отметить, что приведенные выше исследования представляют собой лишь малую часть исследований, касающихся области использования тонкостенных балок открытого сечения в качестве энергопоглощающих элементов барьеров безопасности. Тонкостенные балки также используются в качестве энергопоглощающих элементов в конструкции транспортных средств в качестве пассивной защиты. Авторы статьи Vignjevic et al. 20 представил результаты исследования проблем устойчивости конструкций в безопасности транспортных средств. Холодноформованные тонкостенные конструкции обычно применяются в конструкциях автомобильных кузовов. Кузов современных автомобилей проектируется с акцентом на пассивную безопасность автомобиля. При аварии нагрузки имеют разное направление, интенсивность и место приложения.
 Первой стадией разрушения конструкции является линейная упругая деформация, затем пластическая деформация и потеря устойчивости, разрыв материала и разрушение соединений. Автор Вигевич 20 заметил, что жесткость тонкостенной конструкции кузова снижается при ударной нагрузке. Ценное наблюдение является ограничением теории балок, поскольку деформация тонкостенной динамической конструкции напрямую зависит от свойств материала, производственного процесса и конструкции. В статье Vignjevic 20 основное внимание уделяется поглощению энергии тонкостенными конструкциями, такими как прямоугольные балки, при одноосном и двухосном разрушении на глубокий изгиб. Динамические исследования тонкостенных конструкций представляются необходимой областью исследований.
Первой стадией разрушения конструкции является линейная упругая деформация, затем пластическая деформация и потеря устойчивости, разрыв материала и разрушение соединений. Автор Вигевич 20 заметил, что жесткость тонкостенной конструкции кузова снижается при ударной нагрузке. Ценное наблюдение является ограничением теории балок, поскольку деформация тонкостенной динамической конструкции напрямую зависит от свойств материала, производственного процесса и конструкции. В статье Vignjevic 20 основное внимание уделяется поглощению энергии тонкостенными конструкциями, такими как прямоугольные балки, при одноосном и двухосном разрушении на глубокий изгиб. Динамические исследования тонкостенных конструкций представляются необходимой областью исследований.Авторы Obst et al. 21 экспериментально и аналитически исследованы стальные тонкостенные балки открытого сечения, точки заложения и нагрузки которых находились в плоскости стенки и применялись дополнительные диафрагмы.
 В другой статье авторы Obst et al. 22 также представил исследование устойчивости тонкостенной балки открытого сечения, подвергнутой четырехточечному изгибу. Граничные условия играют ключевую роль в устойчивости тонкостенных конструкций. Исследуемые балки при четырехточечном изгибе были нагружены и установлены в центре тяжести поперечного сечения балки.
В другой статье авторы Obst et al. 22 также представил исследование устойчивости тонкостенной балки открытого сечения, подвергнутой четырехточечному изгибу. Граничные условия играют ключевую роль в устойчивости тонкостенных конструкций. Исследуемые балки при четырехточечном изгибе были нагружены и установлены в центре тяжести поперечного сечения балки.В работе представлены результаты экспериментальных исследований трех типов стальных С-образных балок открытого сечения, которые поддерживались и нагружались в центре сдвига специальными ручками. Рукоятки, использованные при проведении экспериментальных исследований, состояли из: цилиндрического штифта, кольца, прикрепленного к штифту, и скобы, привинченной к стенке балки. Расстояние между центром кольца и стенкой балки определяло положение расчетного центра сдвига для заданной формы поперечного сечения. На рис. 1, 2, 3 видны ручки.
Рисунок 1
Жесткие стальные пластины стенки и шарнир, которые позволяют устанавливать и нагружать балку в центре сдвига.
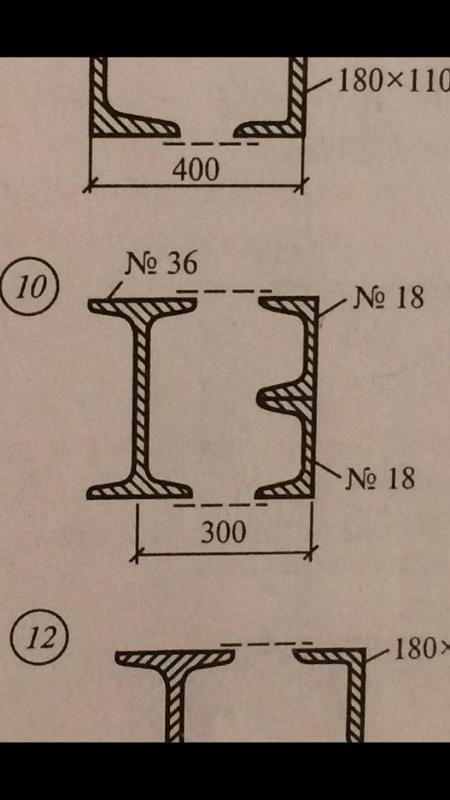
Полноразмерное изображение
Рисунок 2
Изгиб.
Изображение полного размера
Рис. 3
Схема размещения тензодатчиков (A1, A2, A3) и датчиков перемещения (B).
Изображение в полный размер
Методы
Для экспериментальных исследований использовались три холодногнутые стальные балки С-образного сечения, как показано на рис. 4. Во время эксперимента образец балки устанавливался специальной системой поддержки, в которой четыре применялся точечный изгиб. Дополнительно к центру сдвига испытуемой тонкостенной балки прикладывались заданные значения и точки силы. Экспериментальные исследования были подготовлены для балок со следующими поперечными и продольными размерами (таблица 1).
Рисунок 4
Размеры поперечного сечения балки.
Таблица 1 Размеры поперечных сечений балок.
Полноразмерный стол
Схема нагружения балки и ее размеры приведены на рис.
 5. Точки установки и точки нагрузки на образцы балок были установлены специальным устройством, закрепленным на стенке балки жесткими стальными пластинами и винтами, представленными на рис. 1. Простое регулирование дало возможность зафиксировать положение в центре сдвига балок образца открытого сечения. Экспериментальные исследования были подготовлены для двух систем настройки: без диафрагмы и с диафрагмой, что показано на рис. 2.
5. Точки установки и точки нагрузки на образцы балок были установлены специальным устройством, закрепленным на стенке балки жесткими стальными пластинами и винтами, представленными на рис. 1. Простое регулирование дало возможность зафиксировать положение в центре сдвига балок образца открытого сечения. Экспериментальные исследования были подготовлены для двух систем настройки: без диафрагмы и с диафрагмой, что показано на рис. 2.Рисунок 5
Схема нагружения и продольные размеры балки.
Увеличить
Экспериментальные испытания были подготовлены и проведены на разрывной машине Zwick Z100, оснащенной дополнительной системой жестких балок и настройкой, позволяющей реализовать четырехточечный изгиб тонкостенного образца с граничными условиями центра сдвига. Каждый испытанный образец балки был снабжен тензодатчиками, соединенными с углом и центром стенки (рис. 3, 6) и с центром полки балки.
Рисунок 6
Тензометрические датчики, прикрепленные к стенке образца и фланцу.

Увеличенное изображение
Дополнительно к стенке образца были установлены индуктивные датчики перемещения, которые измеряли смещение в четырех точках углов жесткой стальной пластины стенки, как показано на рис. 3 и 7.
Рис. 7
Датчики смещения, установленные в четырех точках жестких стальных пластин.
Изображение полного размера
Датчики смещения, нанесенные на жесткие пластины стенки образца, использовались для анализа поворота поперечного сечения образца при подъеме груза. Исследуемые балки, нагруженные и установленные в центре сдвига, должны испытывать чистый изгибающий момент, что трудно реализовать в реальных экспериментальных условиях.
Результаты
В ходе экспериментальных испытаний были исследованы три балки различной формы поперечного сечения. Скорость перемещения машины при растяжении составила \(5\ {\text{мм/мин}}\), а начальное усилие равно \(0,5\ {\text{кН}}\). Все образцы поддерживались и нагружались в центре сдвига специальной рукояткой.
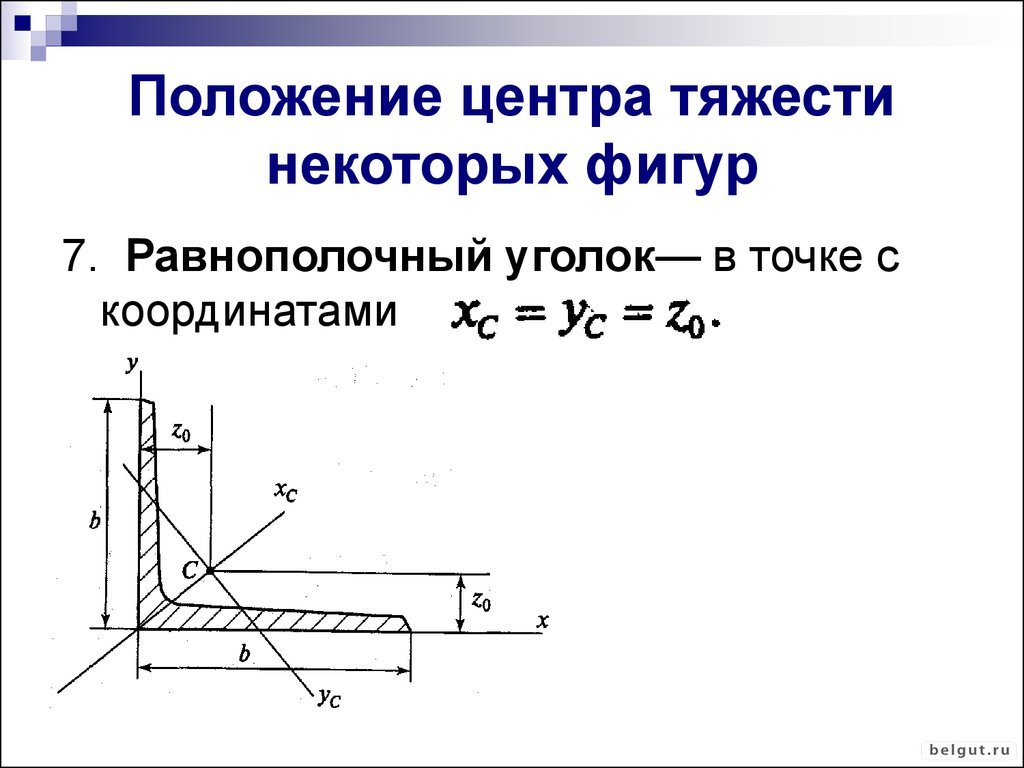 Расстояние центра сдвига от стенки определялось аналитически для заданного сечения тонкостенной балки. Положение центра сдвига измерялось с точностью \(0,1\ {\text{мм}}\). Ошибка физического позиционирования центра сдвига существует и является результатом точности измерения расстояния от стенки, а также точности изготовления балки, т.е. продольная прямолинейность балки. Испытываемый образец изгибался в четырех точках, как показано на рис. 2а. Статические возрастающие нагрузки, приложенные на машине для испытаний на растяжение Zwick Z100, от нуля до точки потери устойчивости до разрушения балок. Было замечено начало коробления и разрушения при изгибе, когда нижние полки начинают сморщиваться, как показано на рис. 8. Кручение балок наблюдалось во время испытания и показано на рис. 9..
Расстояние центра сдвига от стенки определялось аналитически для заданного сечения тонкостенной балки. Положение центра сдвига измерялось с точностью \(0,1\ {\text{мм}}\). Ошибка физического позиционирования центра сдвига существует и является результатом точности измерения расстояния от стенки, а также точности изготовления балки, т.е. продольная прямолинейность балки. Испытываемый образец изгибался в четырех точках, как показано на рис. 2а. Статические возрастающие нагрузки, приложенные на машине для испытаний на растяжение Zwick Z100, от нуля до точки потери устойчивости до разрушения балок. Было замечено начало коробления и разрушения при изгибе, когда нижние полки начинают сморщиваться, как показано на рис. 8. Кручение балок наблюдалось во время испытания и показано на рис. 9..Рис. 8
C-образная форма без усиления, с двойной коробчатой полкой и одной коробчатой балкой после потери устойчивости.
Увеличить
Рис.
 9
9 Деформация поперечного сечения балки при эксперименте на четырехточечный изгиб.
Увеличить
В ходе экспериментальных исследований были исследованы три тонкостенные балки различного сечения, подвергнутые чистому изгибу. При статических испытаниях на четырехточечный изгиб, сдвигающие центральные нагрузки и деформации должен быть реализован чистый изгиб. К сожалению, идеального чистого изгиба получить не удалось. При монотонном росте нагрузки можно было наблюдать небольшое искривление балок при кручении. Механические свойства стали образцов балок определяли при испытаниях на растяжение плоских образцов, вырезанных из материала балок. Измеренные свойства: модуль Юнга \(E = 185\ {\text{ГПа}}\), коэффициент Пуассона \(\nu = 0,3\), предел текучести \(R_{eH} = 330\ {\text{МПа }}\), предел прочности при растяжении \(R_m = 380\ {\text{МПа}}\). На основе экспериментальной проверки должны были быть получены следующие результаты (рис. 10).
На рис. 11а можно наблюдать соотношение между смещением точек измерения.
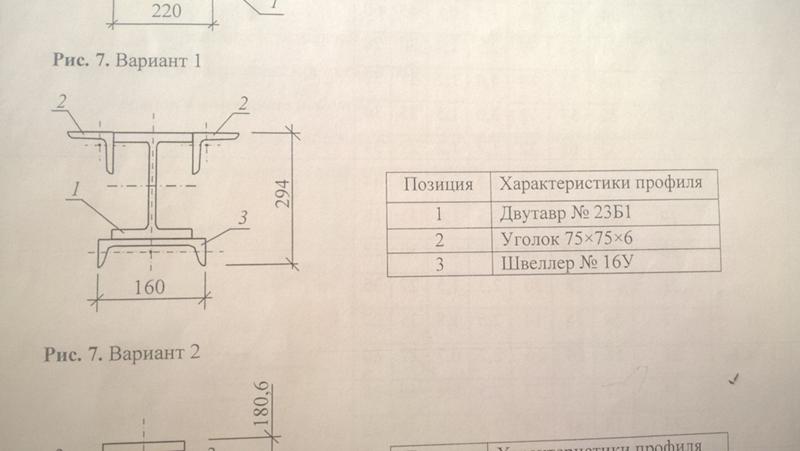 Представленные результаты можно интерпретировать как вращение поперечного сечения балки вокруг продольной оси x. Балка С-образного сечения под действием приложенной нагрузки вращается даже при малых нагрузках. Причиной такой ситуации являются технологические и материальные несовершенства. Накладные ручки являются основой представленной ситуации. Экспериментальная методология также может быть причиной описанной проблемы. На основании экспериментальных характеристик рис. 10 можно найти критическую силу для локальной и общей потери устойчивости соответственно: \(F_{Lcr}=0,6\ {\text{кН}}\), \(F_{Gcr}=2,6\ {\text {кН}}\). Локальное и глобальное выпучивание на графиках интерпретируется как начало характерной нелинейности (рис. 11б).
Представленные результаты можно интерпретировать как вращение поперечного сечения балки вокруг продольной оси x. Балка С-образного сечения под действием приложенной нагрузки вращается даже при малых нагрузках. Причиной такой ситуации являются технологические и материальные несовершенства. Накладные ручки являются основой представленной ситуации. Экспериментальная методология также может быть причиной описанной проблемы. На основании экспериментальных характеристик рис. 10 можно найти критическую силу для локальной и общей потери устойчивости соответственно: \(F_{Lcr}=0,6\ {\text{кН}}\), \(F_{Gcr}=2,6\ {\text {кН}}\). Локальное и глобальное выпучивание на графиках интерпретируется как начало характерной нелинейности (рис. 11б).Рис. 10
С-образная форма без усиленного элемента.
Полноразмерное изображение
Рисунок 11
Точки смещения полотна. UG – смещение верхней точки стенки на неподвижной жесткой плите, UD – смещение нижней точки стенки на неподвижной жесткой плите, UGS – смещение верхней точки стенки на подвижной жесткой плите, UDS – смещение нижняя точка перемычки на подвижной жесткой стальной плите.
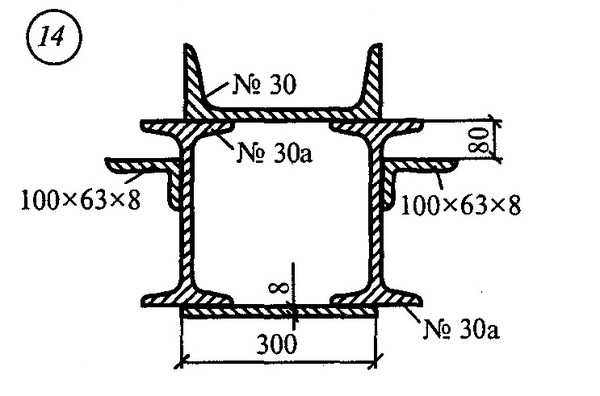
Изображение в полный размер
Точки смещения стенки для фланцев двойных коробок и деталей усиления также показывают относительное вращение поперечного сечения, но теперь вращение для всех точек измерения происходит в одном направлении (рис. 12). Даже если установочные точки и точки нагрузки применяются в центре сдвига, полностью уменьшить вращение невозможно. На наблюдаемые явления вращения поперечного сечения влияют граничные условия и применяемые специальные ручки. Найденные критические усилия для местного и глобального выпучивания полки двойного короба и арматуры соответственно равны: \(F_{Lcr}=13\ {\text{кН}}\), \(F_{Gcr}=16\ {\text {кН}}\).
Рисунок 12
Двойные фланцы коробки и усиливающий элемент.
Изображение полного размера
Результаты экспериментов, представленные на рис. 13, для однокорпусных фланцев без усиливающих деталей имеют более низкое значение критических усилий, чем для двухкорпусных фланцев и усиливающих элементов.
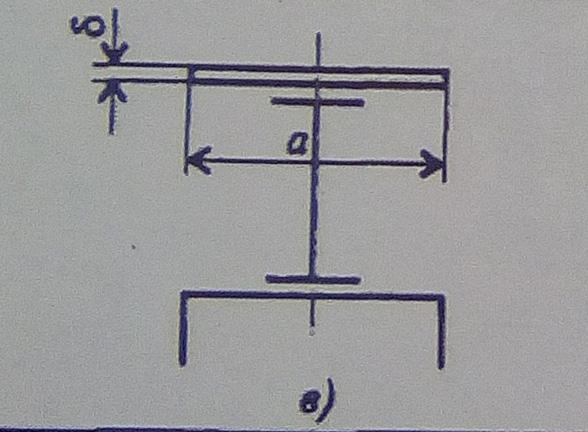 В этом случае критические силы для местного и глобального выпучивания составляют соответственно: \(F_{Lcr}=8\ {\text{кН}}\) и \(F_{Gcr}=9\ {\text{кН}}\ ). Результаты смещения на рис. 11c показывают, что вращение поперечного сечения зарегистрировано. Для всех испытанных балок можно наблюдать следующие режимы процесса потери устойчивости: локальное выпучивание, вызванное изгибающим моментом, деформационная фаза выпучивания под действием нагрузки изгибающего момента и общее выпучивание.
В этом случае критические силы для местного и глобального выпучивания составляют соответственно: \(F_{Lcr}=8\ {\text{кН}}\) и \(F_{Gcr}=9\ {\text{кН}}\ ). Результаты смещения на рис. 11c показывают, что вращение поперечного сечения зарегистрировано. Для всех испытанных балок можно наблюдать следующие режимы процесса потери устойчивости: локальное выпучивание, вызванное изгибающим моментом, деформационная фаза выпучивания под действием нагрузки изгибающего момента и общее выпучивание.Рисунок 13
Фланцы с одной коробкой без усиливающего элемента.
Изображение полного размера
Для балок с поперечным сечением, определяемым как двойные полки коробчатого сечения с усилением и одной полкой коробчатого сечения без усиления, проводят те же испытания, где набор и нагрузки находятся в центральной точке сдвига балок, но прикладывают дополнительно диафрагма, как показано на рис. 5b.
Экспериментальные результаты испытаний, в которых применялись диафрагмы в ручках, представлены на рис.
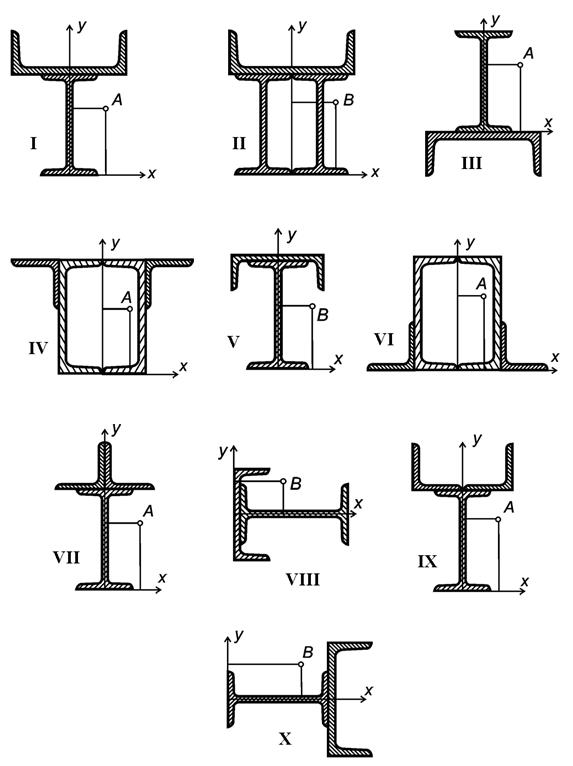 14. Диафрагмы представляли собой просто фанерные армирующие пластины, соответствующие форме поперечного сечения балки. Испытания с диафрагмами проводились для двух элементов: двойных коробчатых полок с усиливающей балкой, показанной на рис. 4b, и одной коробчатой полки без усиливающей балки, показанной на рис. 4c.
14. Диафрагмы представляли собой просто фанерные армирующие пластины, соответствующие форме поперечного сечения балки. Испытания с диафрагмами проводились для двух элементов: двойных коробчатых полок с усиливающей балкой, показанной на рис. 4b, и одной коробчатой полки без усиливающей балки, показанной на рис. 4c.Рисунок 14
Испытанные элементы с фанерными диафрагмами.
Изображение в натуральную величину
Применение диафрагм, как описано выше, привело к критическим силам для локальной и общей потери устойчивости соответственно: \(F_{Lcr}=15\ {\text{кН}}\), \(F_{Gcr }=19\ {\text{кН}}\) для двухкорпусных фланцев и деталей усиления с диафрагмами (рис. 15). Смещение (рис. 16), измеренное в верхнем и нижнем положении рукоятки, показывает небольшое вращение балки во время испытания, но характер вращения отличается от той же балки без диафрагм.
Однокорпусные полки без усиливающего элемента с примененными диафрагмами привели к возникновению критических усилий для местной и общей потери устойчивости соответственно: \(F_{Lcr}=4\ {\text{кН}}\), \(F_{Gcr}=11\ {\text{кН}}\) (рис.
 17). На рис. 17а четко виден пик графика вблизи \(F_{пик}=4\ {\text{кН}}\). Вероятно, это вызвано проскальзыванием рукоятки, системы настройки или стяжек. Выше \(F_{пик}=4\ {\text{кН}}\) кривая поднимается до \(F=16\ {\text{кН}}\), и эта сила может быть принята как глобальная максимальная сила потери устойчивости.
17). На рис. 17а четко виден пик графика вблизи \(F_{пик}=4\ {\text{кН}}\). Вероятно, это вызвано проскальзыванием рукоятки, системы настройки или стяжек. Выше \(F_{пик}=4\ {\text{кН}}\) кривая поднимается до \(F=16\ {\text{кН}}\), и эта сила может быть принята как глобальная максимальная сила потери устойчивости.Рисунок 15
Фланцы с двойной коробкой и усиливающие детали с диафрагмами.
Полноразмерное изображение
Рисунок 16
Точки смещения полотна. UG — смещение верхней точки стенки на неподвижной жесткой плите, UD — смещение нижней точки стенки на неподвижной жесткой плите, UGS — смещение верхней точки стенки на подвижной жесткой плите, UDS — смещение нижняя точка перемычки на подвижной жесткой стальной плите.
Полноразмерное изображение
Рисунок 17
Фланцы одной коробки без усиливающих деталей с диафрагмами.
Увеличенное изображение
Как видно на рис.
 18, при сравнении несущей способности исследуемых балок с применением диафрагм балки более устойчивы к выпучиванию. Конечно, диафрагмы находят практическое применение в качестве элементов повышения жесткости тонкостенных конструкций, но в представленном исследовательском случае в ходе экспериментальных испытаний пытались получить чистый изгиб. Полностью уменьшить повороты поперечного сечения балки не удалось, что было вызвано несовершенством граничных условий и процесса изготовления балок. Напрашивается и дополнительный практический вывод. Точность балок, условия сборки и эксплуатации имеют ключевое значение для работы тонкостенных систем.
18, при сравнении несущей способности исследуемых балок с применением диафрагм балки более устойчивы к выпучиванию. Конечно, диафрагмы находят практическое применение в качестве элементов повышения жесткости тонкостенных конструкций, но в представленном исследовательском случае в ходе экспериментальных испытаний пытались получить чистый изгиб. Полностью уменьшить повороты поперечного сечения балки не удалось, что было вызвано несовершенством граничных условий и процесса изготовления балок. Напрашивается и дополнительный практический вывод. Точность балок, условия сборки и эксплуатации имеют ключевое значение для работы тонкостенных систем.Рисунок 18
Кривая смещения: все балки.
Увеличенное изображение
Обсуждение
Экспериментальное исследование холодногнутых тонкостенных балок различной формы поперечного сечения, подвергнутых статическому четырехточечному изгибу, с приложением нагрузки и опорой в центре сдвига каждой балки, разрешено можно сделать следующие выводы:
Тонкостенные балки со сложными полками имеют более высокие критические усилия, чем тонкостенные балки с плоскими полками,
Локальная потеря устойчивости тонкостенных балок была четко видна при наблюдении за полками и стенками.
 Появились характерные полуволны.
Появились характерные полуволны.Измерения перемещений стенки (относительные смещения, оцененные на основе показаний датчиков перемещений) показали, что, несмотря на опору балок и воздействие в центре поперечных сил, каждая из балок вращалась вокруг продольной оси, проходящей через центр поперечных сил поперечного сечения испытываемой балки,
Причиной возникновения крутящего момента с вектором, направленным вдоль оси, проходящей через центр поперечных сил, при опирании балок в центре поперечных сил и нагрузке в центре поперечных сил явилась неточность изготовления испытуемых балок. Жесткость при кручении открытых тонкостенных профилей очень мала, что при неизбежных неточностях изготовления балок приводит к возникновению крутящего момента, несмотря на теоретическое действие чистого изгиба между центральными кронштейнами для четырехточечного изгиба.

Дополнительной трудностью, наблюдаемой при экспериментальных испытаниях, была сила тяжести, которая, несмотря на попытки уравновешивания, влияла на полученные результаты и действие крутящего момента относительно оси, проходящей через точки опоры и нагрузки,
Испытание тонкостенных профилей на сдвиг необходимо проводить с помощью диафрагм жесткости, что особенно важно при проведении динамических испытаний открытых тонкостенных балок. Отсутствие диафрагм приводит к локальному разрушению балок и распространению разрушения из-за локальной пластической деформации,
Тонкостенные открытые стальные профили широко применяются при строительстве объектов дорожной инфраструктуры, в т.ч. в качестве энергопоглощающих панелей для дорожных ограждений. Соответствующая форма поперечного сечения, выбор материала и точки опоры являются ключевыми принципами для достижения высокой степени поглощения энергии при разгоне автомобиля,
Для энергопоглощающих конструкций необходимы испытания на реальных объектах.
 Тонкостенные конструкции, например балки открытого сечения, характеризуются высокой податливостью к скручиванию, на что явно влияет точность тонкостенной конструкции, в том числе и системы крепления.
Тонкостенные конструкции, например балки открытого сечения, характеризуются высокой податливостью к скручиванию, на что явно влияет точность тонкостенной конструкции, в том числе и системы крепления.
Дальнейшая работа авторов исследования направлена на решение вопросов, связанных с энергоемкостью материалов и конструкций. Была разработана динамическая испытательная установка, и полученные результаты будут представлены далее.
Литература
Тимошенко С.П., Гир Дж.М. Теория упругой устойчивости. 2-е изд. (McGraw-Hill Book Company, Inc., Торонто, 1961).
Magnucka-Blandzi, E. & Zając, K. Устойчивость тонкостенных швеллерных балок с ортотропными полками. мех. мех. англ. 17 , 141–155 (2013).
Google ученый
Magnucki, K.
 & Stawecki, W. Stateczność Wybranych części Konstrukcji (Instytut Pojazdów Szynowych TABOR, 2016).
& Stawecki, W. Stateczność Wybranych części Konstrukcji (Instytut Pojazdów Szynowych TABOR, 2016).Google ученый
Анбарасу, М. Местно-деформационное выпучивание на швеллерах из холодногнутой стали с кромками. Тонкостенная конструкция. 98 , 351–359. https://doi.org/10.1016/j.tws.2015.10.003 (2016 г.).
Артикул
Google ученый
Анбарасу, М. Численное исследование локально-деформационно-поперечно-крутильного взаимодействия продольных балок из холодногнутой стали с кромками. Азиатский J. Гражданский инж. 18 , 643–656 (2016).
Google ученый
Анбарасу, М., Дар, М., Гоуси, А.Ф. и Дар, А. Поведение на изгиб составных балок из углеродного волокна с покрытием, состоящих из швеллеров с выступом: сравнение испытательной и расчетной прочности.
 Конструкции 30 , 294–304. https://doi.org/10.1016/j.istruc.2020.12.088 (2021 г.).
Конструкции 30 , 294–304. https://doi.org/10.1016/j.istruc.2020.12.088 (2021 г.).Артикул
Google ученый
Дар, М. и др. Эффективное профилирование поперечного сечения составных балок из CFS для улучшения характеристик на изгиб. Стальной композит. Структура 34 , 333–345. https://doi.org/10.12989/scs.2020.34.3.333 (2020 г.).
Артикул
Google ученый
Дар, М. и др. Прочность на изгиб сборных стальных холодногнутых балок с прямоугольными сжатыми полками. Стальной композит. Структура 34 , 171–188. https://doi.org/10.12989/scs.2020.34.2.171 (2020 г.).
Артикул
Google ученый
Дар, М. и др. Влияние угловых ребер жесткости на прочность на изгиб и жесткость балок из холодногнутой стали.
 Стальные композиты. Структура 33 , 225–243. https://doi.org/10.12989/scs.2019.33.2.225 (2019 г.).
Стальные композиты. Структура 33 , 225–243. https://doi.org/10.12989/scs.2019.33.2.225 (2019 г.).Артикул
Google ученый
Анбарасу, М. Моделирование поведения при изгибе и проектирование замкнутых сборных балок из холодногнутой стали, состоящих из двух сигма-сечений для локальной потери устойчивости. англ. Структура 191 , 594562. https://doi.org/10.1016/j.engstruct.2019.04.093 (2019).
Артикул
Google ученый
Баласубраманян К., Шива А., Беула Гнана Ананти Г. и Сараванакумар Р. Экспериментальное исследование несимметричного i-образного сечения. Междунар. Дж. Адв. Инф. науч. Технол. (IJAIST) 32 , 46–49 (2014).
Google ученый
Белингарди Г. и Скаттина А. Экспериментальное исследование поведения на изгиб гибридных и стальных тонкостенных коробчатых балок: роль клеевых соединений.
 Междунар. Дж. Адхес. Адгезив. 40 , 31–37. https://doi.org/10.1016/j.ijadhadh.2012.08.002 (2013 г.).
Междунар. Дж. Адхес. Адгезив. 40 , 31–37. https://doi.org/10.1016/j.ijadhadh.2012.08.002 (2013 г.).КАС
СтатьяGoogle ученый
Shokouhian, M., Shi, Y. & Head, M. Интерактивные режимы потери устойчивости изгибных элементов из гибридной стали. англ. Структура 125 , 153–166. https://doi.org/10.1016/j.engstruct.2016.07.001 (2016 г.).
Артикул
Google ученый
Ziółkowski, A. & Imełowski, S. Потеря устойчивости и после потери устойчивости призматических алюминиевых колонн, подвергающихся серии сжимающих нагрузок. Экспл. мех. 51 , 1335–1345. https://doi.org/10.1007/s11340-010-9455-y (2011 г.).
Артикул
Google ученый
Русинский Э., Копчинский А. и Чмоховски Дж. Испытания тонкостенных балок, соединенных точечной сваркой.
 Дж. Матер. Процесс. Технол. 157–158 , 405–409. https://doi.org/10.1016/j.jmatprotec.2004.09.063 (2004 г.).
Дж. Матер. Процесс. Технол. 157–158 , 405–409. https://doi.org/10.1016/j.jmatprotec.2004.09.063 (2004 г.).Артикул
Google ученый
Кальдерони, Б., Де Мартино, А., Формисано, А. и Фиорино, Л. Стальные балки холодного формования при монотонной и циклической нагрузке: экспериментальное исследование. Дж. Констр. Сталь рез. 65 , 219–227. https://doi.org/10.1016/j.jcsr.2008.07.014 (2009 г.).
Артикул
Google ученый
He, B., Zhang, Y., Ge, W., An, Y. & Liu, D. Анализ потери устойчивости тонкостенных элементов с разветвленным поперечным сечением с использованием полуаналитического метода матрицы переноса конечной полосы . Тонкостенная конструкция. 124 , 20–31. https://doi.org/10.1016/j.tws.2017.11.039 (2018 г.).
Артикул
Google ученый
«>
Унгуряну В. и Дубина Д. Чувствительность к дефектам перфорированных секций паллетных стеллажей. мех. мех. англ. 17 , 207–220 (2013).
Google ученый
Като, Х., Сасаки, К. и Мори, Т. Испытание эффекта Баушингера на изгиб в четырех точках в предварительно напряженном стальном тонком листе. Матер. науч. англ. 642 , 150–156. https://doi.org/10.1016/j.msea.2015.06.075 (2015 г.).
КАС
СтатьяGoogle ученый
Вигевич, Р. и др. Численное исследование влияния внутреннего гофрированного армирования на двухосный изгиб тонкостенных балок. Тонкостенная конструкция. 144 , 106277. https://doi.org/10.1016/j.tws.2019.106277 (2019).
Артикул
Google ученый
Обст, М., Курпиш, Д. и Пачос, П.
 Экспериментальные и аналитические исследования явления кручения тонкостенных холодногнутых швеллерных балок, подвергнутых четырехточечному изгибу. Тонкостенная конструкция. 106 , 179–186. https://doi.org/10.1016/j.tws.2016.05.002 (2016 г.).
Экспериментальные и аналитические исследования явления кручения тонкостенных холодногнутых швеллерных балок, подвергнутых четырехточечному изгибу. Тонкостенная конструкция. 106 , 179–186. https://doi.org/10.1016/j.tws.2016.05.002 (2016 г.).Артикул
Google ученый
Обст, М., Родак, М. и Пачос, П. Предельная нагрузка холодногнутых тонкостенных нестандартных швеллеров. Дж. Теор. заявл. мех. 54 , 1369–1377. https://doi.org/10.15632/jtam-pl.54.4.1369 (2016 г.).
Артикул
Google ученый
Эти авторы внесли равный вклад: Maciej Obst и Piotr Wasilewicz.
Кафедра прочности материалов и конструкций, Познаньский технологический университет, Познань, Польша
Maciej Obst и Piotr Wasilewicz Технологии, Познаньский институт машиностроения
Скачать ссылки
Информация об авторе
Примечания автора
Авторы и организации
7 z Польша
Jarosław Adamiec
- область в области. Полярный момент инерции против момента инерции
- Maciej Obst
Посмотреть публикации автора
Вы также можете искать этого автора в
PubMed Google Scholar - Piotr Wasilewicz
Посмотреть публикации автора
Вы также можете искать этого автора в
PubMed Google Scholar - Jarosław Adamiec
Посмотреть публикации автора
Вы также можете искать этого автора в
PubMed Google Академия
Авторы
Взносы
М. О. и П.В. задумал эксперимент(ы), М.О. и П.В. провел(а) эксперимент(ы), М.О. и Дж.А. проанализировал результаты. Все авторы рассмотрели рукопись.
О. и П.В. задумал эксперимент(ы), М.О. и П.В. провел(а) эксперимент(ы), М.О. и Дж.А. проанализировал результаты. Все авторы рассмотрели рукопись.
Автор, ответственный за переписку
Ярослав Адамец.
Заявление об этике
Конкурирующие интересы
Авторы не заявляют об отсутствии конкурирующих интересов.
Дополнительная информация
Примечание издателя
Springer Nature сохраняет нейтралитет в отношении юрисдикционных претензий в опубликованных картах и институциональной принадлежности.
Права и разрешения
Открытый доступ Эта статья находится под лицензией Creative Commons Attribution 4.0 International License, которая разрешает использование, совместное использование, адаптацию, распространение и воспроизведение на любом носителе или в любом формате при условии, что вы укажете соответствующую ссылку на оригинальный автор(ы) и источник, предоставьте ссылку на лицензию Creative Commons и укажите, были ли внесены изменения.