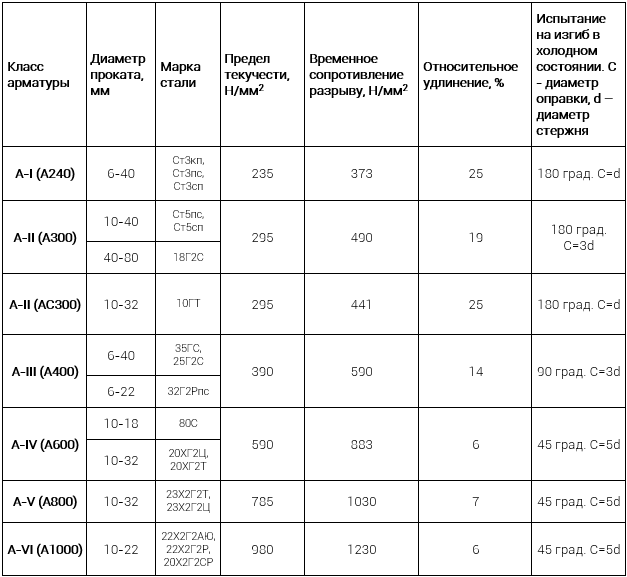
Классификация арматуры таблица по классам: Классы арматуры и марки стали

1.2.4. Классификация арматуры по основным характери­стикам. Сортамент арматуры

По
виду применяемой арматуры различают
железобетон с гибкой арматурой в виде
стальных стержней круглого или
периодическо­го профиля сравнительно
небольших диаметров (до 40 мм включи­тельно)
и конструкции с несущей или жёсткой
арматурой. К жёст­кой арматуре относится
профильная прокатная сталь (уголкового,
швеллерного и двутаврового сечения) и
горячекатаные стержни диа­метром
более 40 мм. Основным видом арматуры
является гибкая.

Вся
арматура, используемая в железобетоне,
по своим основным характеристикам
делится на ряд классов, причём в один
класс мо­жет входить арматура из
сталей нескольких марок.

Основным
нормируемым и контролируемым показателем
качества стальной арматуры является
класс арматуры по прочности на растяжение,
обозначаемый:

А
– для горячекатаной и термомеханически
упрочненной арматуры;

В
– для холоднодеформированной арматуры;

К
– для арматурных канатов.

Класс
арматуры соответствует гарантированному
значению предела текучести (физического
или условного) в МПа, устанавливаемому
в соответствии с требованиями стандартов
и технических условий, и принимается в
пределах от A 240 до A 1500, от B 500 до B 2000 и от
K 1400 до K 2500.

Классы
арматуры следует назначать в соответствии
с их параметрическими рядами, установленными
нормативными документами.

Кроме
требований по прочности на растяжение
к арматуре предъявляют требования по
дополнительным показателям, определяемым
по соответствующим стандартам:
свариваемость, выносливость, пластичность,
стойкость к коррозионному растрескиванию,
релаксационная стойкость, хладостойкость,
стойкость при высоких температурах,
относительное удлинение при разрыве и
др.

К неметаллической
арматуре (в том числе фибре) предъявляют
также требования по щелочестойкости и
адгезии к бетону.

Дадим краткие
характеристики арматуры перечисленных
клас­сов.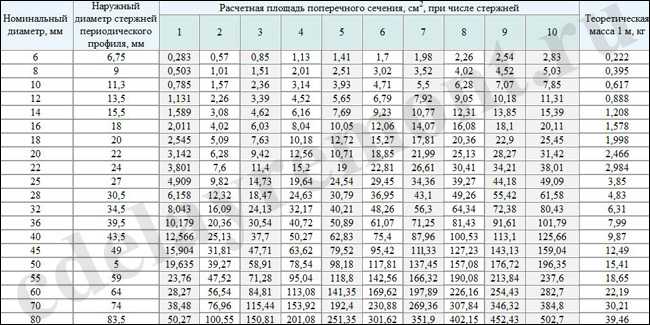

Арматуру
класса A240
изготовляют из стали марки Ст3. Она имеет
гладкую цилиндрическую поверхность и
применяется глав­ным образом в качестве
монтажной арматуры, хомутов, поперечных
стержней; из неё изготавливают монтажные
петли. Хорошо свари­вается. Прокатывается,
начиная с диаметра 6 мм (σ_v
= 230
МПа, σ_u
= 380
МПа и δ
≥ 25%).

Остальные
классы стержневой арматуры представляют
собой стальные стержни, поверхность
которых имеет периодический про­филь.
Выступы, имеющиеся на поверхности
стержней периодиче­ского профиля,
резко (в 2…3 раза) повышают сцепление
арматуры с бетоном и уменьшают ширину
раскрытия трещин в бетоне растя­нутой
зоны.

Например,
для арматуры класса А300 периодический
профиль имеет вид, показанный на рис.
19, а. Как видно из этого рисунка, арматура
класса А300 представляет собой круглые
стержни с часто расположенными выступами
и с двумя продольными рёбрами.

Арматура
класса А300 хорошо сваривается и
используется в каче­стве рабочей в
обычном железобетоне. Для её изготовления
исполь­зуются стали марок Ст5, 10ГТ,
18Г2С. Прокатывается, начиная с номинального
диаметра 10 мм. Основные её характеристики
σ_у
= 300
МПа, σ_и
= 500 МПа и δ
≥
19%.

Рис.
19. Арматура периодического профиля:

а,
б – стержневая; в – проволочная

Арматура
класса A400
имеет на своей поверхности выступы,
об­разующие «ёлочку» (рис. 19, 6). Эта
арматура является основной рабочей
арматурой в обычном железобетоне. Хорошо
сваривается. Выпускается диаметрами
6, 8, 10 мм в мотках массой до 1300 кг и
диаметрами 12…40 мм в прутках длиной до
13,2 м. Изготавливается из низколегированной
стали марок 18Г2С, 35ГС, 25Г2С по усмотре­нию
завода-изготовителя. Для неё σ_у
= 400
МПа, σ_и
= 600
МПа и δ≥
14%.

В
обозначениях марок стали отражается
содержание в них угле­рода и легирующих
добавок. Например, в марке стали 25Г2С
первые две цифры обозначают содержание
в стали углерода в сотых долях процента
(0,25%), буква Г – что сталь легирована
марганцем, цифра 2 – что его содержание
может достигать 2%, а буква С – наличие
в стали кремния. Буквой X
обозначается хром, Т – титан, Ц
– цирконий и т.д.

Обыкновенная
низкоуглеродистая проволока класса
В500 (ГОСТ 6727-80) выпускается диаметрами
3, 4, 5 мм. Изготовляют её во­лочением
катанки из низкоуглеродистой стали
группы Ст2 – Ст3 и используют преимущественно
в сварных изделиях – сетках и кар­касах;
σ_и
= 550…525
МПа в зависимости от диаметра, а σ_у
и
δ
не
нормируются.

Периодический
профиль проволоки класса В500 (рис. 19, в)
об­разуется расположенными на её
поверхности вмятинами (рифами).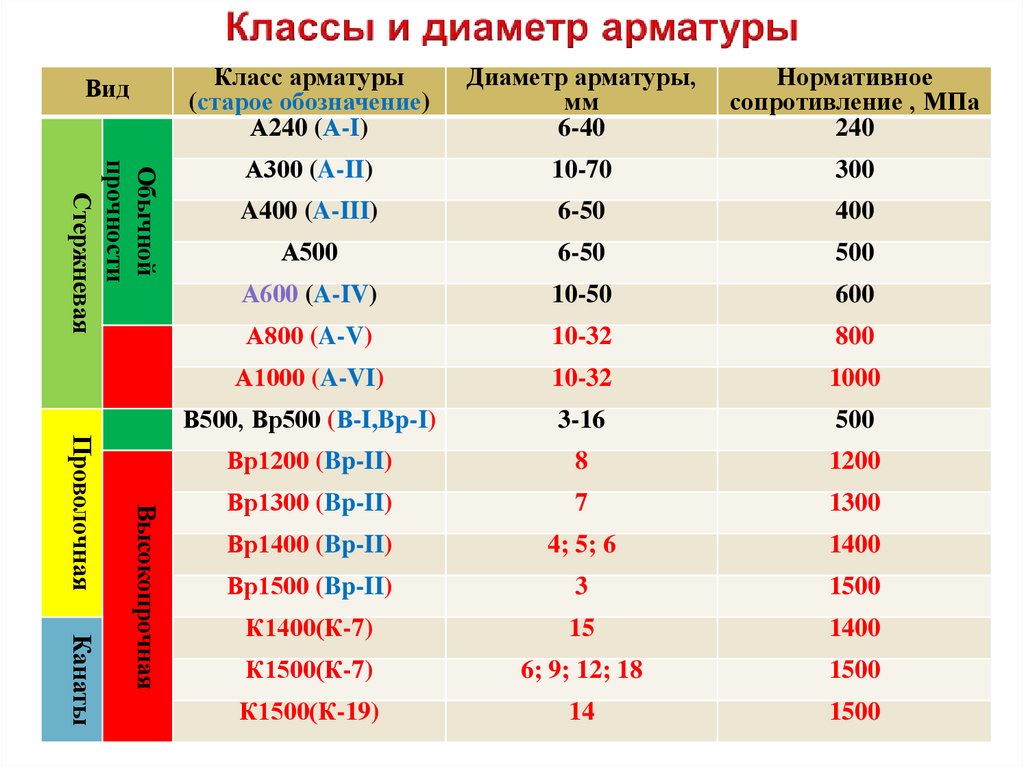 Размеры
вмятин зависят от диаметра проволоки.
Проволока хоро­шо сваривается, что
позволяет использовать её для изготовления
арматурных изделий.

Класс
арматурной стали при проектировании
выбирается в зависимости от типа
конструкции, условий ее возведения и
эксплуатации.

При
проектировании железобетонных конструкций
пользуются сортаментом арматуры.
Сортамент арматурной стали – это
перечень типоразмеров каждого вида
арматурных стержней, выпускае­мых в
настоящее время металлургической
промышленностью. В стране существует
единый сор­тамент для гладкой арматуры
и арматуры периодического профиля. Он
со­ставлен по номинальным диаметрам
стержней, выраженным в мм. Номинальный
диаметр гладкого стержня совпадает с
его фактиче­ским диаметром. Для
стержневой арматуры периодического
профи­ля номинальный диаметр (номер)
стержня, указанный в сортаменте,
соответствует диаметру гладкого круглого
стержня, равновеликого ему по площади
поперечного сечения. Например, арматурный
стер­жень, расчётный номинальный
диаметр которого равен 20 мм (см. рис. 19,
а, б), имеет наружный диаметр (по выступам)
22 мм и внут­ренний (по телу) – 19 мм, а
высота выступов на его поверхности
равна h
= 0,5(d₁–d)
= 0,5(22–19) = 15 мм.

3. Классификация арматуры

Стержневая горячекатаная арматура в
зависимости от ее основных механических
характеристик подразде­ляется на
шесть классов с условным обозначением:
A-I, А-Н, А-Ш,A-IV,A-V,A-VI(табл.
1.1). Термическому упрочнению подвергают
стержневую арматуру четы рех классов,
упрочнение в ее обозначении отмечается
до­полнительным индексом «т»: Ат-Ш,
Ат-IV,At-V,At-VI.
Дополнительной буквой С указывается
на возможность стыкования сваркой, К —
на повышенную коррозионную стойкость.

Каждому классу арматуры соответствуют
определенные марки арматурной стали
с одинаковыми механи­ческими
характеристиками, но различным химическим
составам. В обозначении марки стали
отражается содер­жание углерода и
легирующих добавок. Например, в марке
25Г2С первая цифра обозначает содержание
уг­лерода в сотых долях процента (0,25
%), буква Г —что сталь легирована
марганцем, цифра 2 — что его содер­жание
может достигать 2%, а буква С — наличие
в стали кремния (силиция).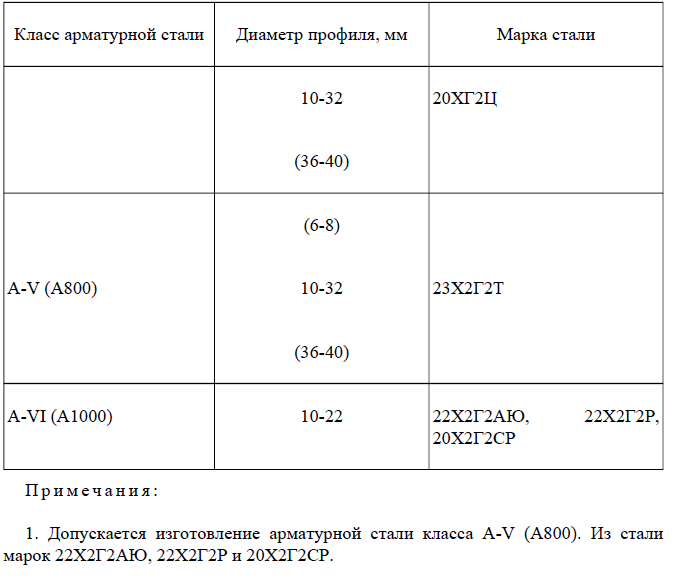 Наличие других
химических элементов, например в марках
20ХГ2Ц, 23Х2Г2Т, обоз­начается буквами:
X— хром, Т — титан, Ц —
цирконий. Периодический профиль имеет
стержневая армату­ра всех классов,
за исключением круглой (гладкой) ар­матуры
классаA-I.

Физический предел текучести ау = 23О…4ОО
МПа име­ет арматура классов A-I,
А-П,A-III,
условный предел текучести ао,2=600… 1000
МПа имеет высоколегирован­ная арматура
классовA-IV,A-V,A-VIи термически уп­рочненная арматура.

Относительное удлинение после разрыва
зависит от класса арматуры. Значительным
удлинением обладает арматура классов
А-Н, A-III(6=14…19*%), сравнитель­но небольшим
удлинением — арматура классовA-IV,A-V,A-VIи термически упрочненная всех классов
Модуль упругости стержневой арматурыEsс ростом ее прочности
несколько уменьшается и составляет:
2,1 • 105 МПа для арматуры классовA-I,
А-Н; 2-105 МПа для арматуры классовA-III,A-IVC; 1,9- Ю5
для арма­туры классаA-Vи термически упрочненной арматуры.

Арматурную проволоку диаметром 3—8 мм
подраз­деляют на два класса: Вр1
-обыкновенная арматурная проволока
(холоднотянутая, низкоуглеродистая),
пред­назначенная главным образом для
изготовления сварных сеток; B-II,
Вр-П — высокопрочная арматурная
прово­лока применя­емая в качестве
напрягаемой арматуры предварительно-напряженных
элементов. Периодический профиль
обоз­начается дополнительным индексом
«р»: Основная механическая характеристика
проволочной арматуры — ее временное
сопротивление сг«, которое возрастает
с уменьшением диаметра проволоки. Для
обыкновенной арматурной проволоки
аы=550 МПа, для высокопрочной проволоки
а«= 1300…1900 МПа. Относительное удлинение
после разрыва сравнительно невысо­кое
б=4…6 %. Разрыв высокопрочной проволоки
носит хрупкий характер. Модуль упругости
арматурной прово­локи классов В-И,
Вр-Н равен 2-Ю5 МПа; класса Вр-1 равен
1,7-105 МПа; арматурных канатов — 1,8-10* МПа.

Сортамент арматуры составлен по
номинальным диа­метрам, что соответствует
для стержневой арматуры пе­риодического
профиля диаметрам равновеликих по
площади поперечного сеченЕия круглых
гладких стерж­ней, для обыкновенной
и высокопрочной арматурной проволоки
периодического профиля — диаметру
прово­локи до профилирования (см.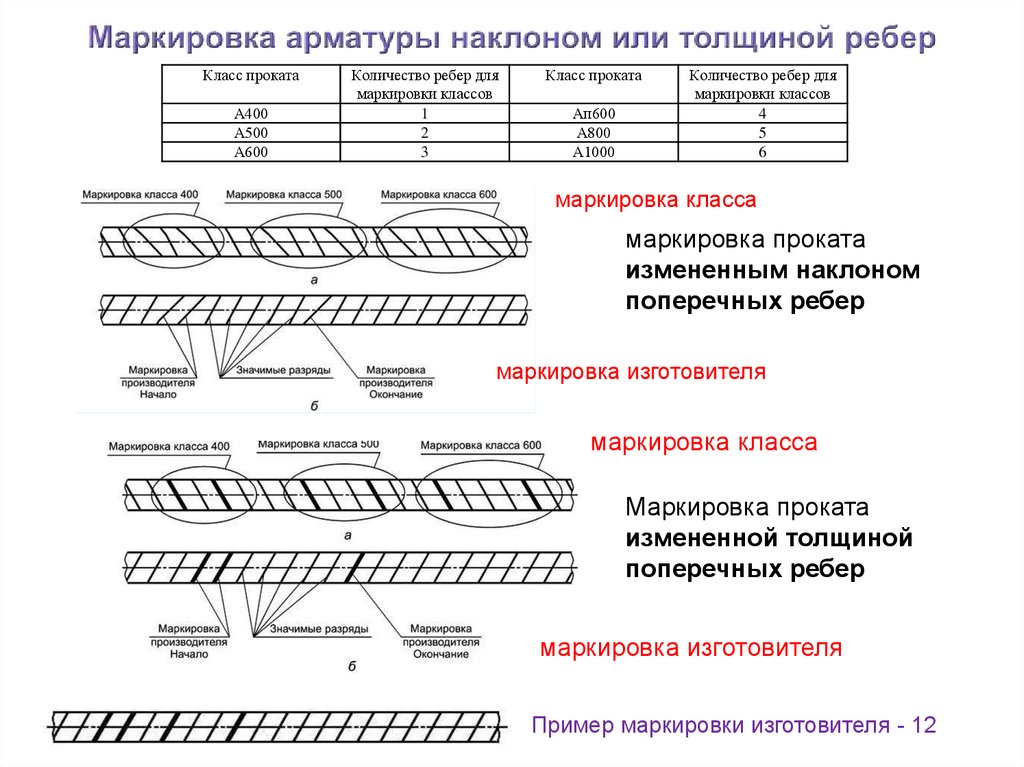
табл. 1.1 и прил. VI).

Таблица 1.1. Классификация и механические
характеристики арматуры

Четыре класса политики обучения с подкреплением | Автор Wouter van Heeswijk, PhD

Всесторонняя классификация стратегий решения для обучения с подкреплением

Изображение Ганса Браксмайера с сайта Pixabay

Политики обучения с подкреплением (RL) окутаны определенной мистикой. Проще говоря, политика π: s → a — это любая функция, которая возвращает допустимое действие для решения проблемы. Не меньше, не больше. Например, вы можете просто выполнить первое действие, которое придет вам в голову, выбрать действие наугад или запустить эвристику. Однако что делает RL особенным, так это то, что мы активно предвидим последствия решений и учимся на своих наблюдениях; поэтому мы ожидаем некоторого разума в нашей политике. В своей концепции последовательного принятия решений[1] Уоррен Пауэлл утверждает, что существует четыре класса политик для RL. Методы всех четырех классов широко используются в разных областях, но еще не получили всеобщего признания. В этой статье будет представлено краткое — и, несомненно, неполное — введение в эту классификацию стратегий решения.

Прежде чем перейти к обучению с подкреплением, давайте сначала немного освежим нашу память об аналитических решениях. Как правило, мы стремимся сформулировать задачу RL в виде модели марковского процесса принятия решений (MDP). Если мы останемся ближе к MDP, целью обучения с подкреплением будет решение соответствующей системы уравнений Беллмана и, таким образом, нахождение оптимальной политики π* :

уравнения Беллмана для MDP. Нахождение оптимальной политики π* дает функции оптимального значения В(с) 9π*(s’) , что мы делаем только в одном из четырех классов политик. Таким образом, мы можем сформулировать нашу цель следующим образом:

Функция вознаграждения на временном горизонте. Оптимальная политика π* максимизирует совокупное вознаграждение.

Для оптимизации модели MDP существует два основных подхода: (i) итерация политики и (ii) итерация значения. Итерация политики исправляет политику, вычисляет соответствующее значение политики и впоследствии обновляет политику, используя новое значение. Алгоритм выполняет итерацию между этими шагами до тех пор, пока политика не станет стабильной. Итерация значения на самом деле основана на очень похожих шагах (см. рисунок ниже), но направлена ​​на прямое максимизирование функций значения и только после этого обновляет политику. Обратите внимание, что поиск функций оптимального значения равен поиску оптимальной политики; либо достаточно для решения системы уравнений Беллмана.

Сравнение итерации политики (слева) и итерации значения (справа). Обратите внимание на итеративный характер итерации политики и оператор максимума в итерации значения. Адаптировано из Sutton & Barto [2]

Большинство — если не все — алгоритмы RL основаны либо на итерации политики, либо на итерации значения (или на их комбинации). Поскольку используемые методы моделирования обычно не гарантируют нахождение оптимальных политик, в RL мы говорим о политике , аппроксимации и значении , аппроксимации соответственно. Пауэлл утверждает, что обе стратегии можно разделить на два класса, что дает в общей сложности четыре класса, которые мы вскоре обсудим. Просто некоторые основные обозначения, и мы готовы к работе:

s : состояние (информация, необходимая для принятия решения)

a : действие (возможная операция над состоянием)

π : политика (сопоставление состояния с действием)

базис 8 0 : 90 функции из состояния)

θ : веса признаков (параметризация политики)

t : эпоха времени (дискретный момент времени)

R : функция вознаграждения (прямое вознаграждение за выполнение действий в состоянии)

0002 V : функция значения (вознаграждение нижестоящего уровня за определенное состояние)

В приближенных решениях политики мы напрямую изменяем саму политику. Такие стратегии решения, как правило, работают лучше всего, когда политика имеет четкую структуру. Мы можем выделить два класса: PFA и CFA.

Аппроксимация функции политики (PFA)

Аппроксимация функции политики (PFA) по существу представляет собой параметризованную функцию политики. Подключение состояния напрямую возвращает допустимое действие. Линейный PFA может выглядеть так:

Пример аппроксимации функций политики (PFA)

Основная задача здесь состоит в том, чтобы найти соответствующие базисные функции ϕ(s) , которые охватывают суть процесса принятия решений. Для этого необходимо хорошее понимание структуры проблемы. Усилия по проектированию можно облегчить, выбрав более общие представления функций, такие как нейронная сеть (сети акторов), используя состояние в качестве входных данных и выводя действие. Недостатком таких представлений PFA является то, что настройка параметров становится сложнее, а интерпретируемость страдает. Несмотря на это, необходимо четкое понимание структуры проблемы.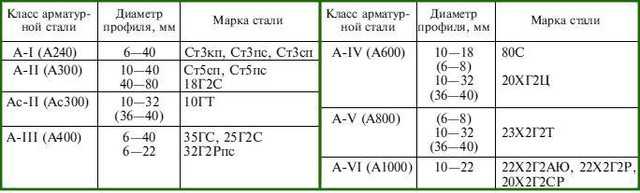 π ограничено политикой π и его параметризация θ , что обычно дает меньшее пространство действия, чем исходное. Обратите внимание, что простейшая форма CFA — это просто жадная эвристика, однако модифицированная функция вознаграждения может включать в себя элементы исследования. Вычислительные усилия на итерацию, вероятно, выше, чем для PFA (из-за шага максимизации), но требуется меньше усилий при проектировании.

Приблизительные значения явно учитывают последующее влияние текущих решений с учетом всего горизонта принятия решений. Напоминаем, что функции оптимальной стоимости приравниваются к оптимальной политике; они оба дают идентичные решения уравнений Беллмана. Аппроксимация стоимости может быть подходящей, когда структура политики не выдающаяся или мы не можем должным образом контролировать последующие эффекты текущих решений.

Аппроксимация функции ценности (VFA)

Аппроксимация функции ценности (VFA) представляет последующие значения как функцию. Одна из проблем с уравнением Беллмана заключается в том, что после совершения действия случайные события могут привести нас ко многим новым состояниям s’∈ S’ . Таким образом, для каждого действия мы должны учитывать значение всех достижимых состояний с’ и вероятность попадания в них. VFA обходят эту проблему, заменяя член стохастического ожидания детерминированной функцией аппроксимации В_т(с_т,а_т) . В канонической форме VFA выглядит следующим образом:

Пример аппроксимации функции ценности (VFA)

Простейшая VFA — это справочная таблица, в которой мы храним средние наблюдаемые значения для каждой пары состояние-действие. Достаточное количество итераций позволяет нам узнать точные значения для каждой пары, но это редко поддается вычислительной обработке. Поэтому мы обычно прибегаем к функциям, которые фиксируют суть состояния, которые мы могли бы спроектировать или извлечь вручную, например, с помощью автокодировщиков. Таким образом, мы фиксируем значения состояния-действия в компактных функциях (например, в сети критиков) и настраиваем веса признаков путем наблюдения.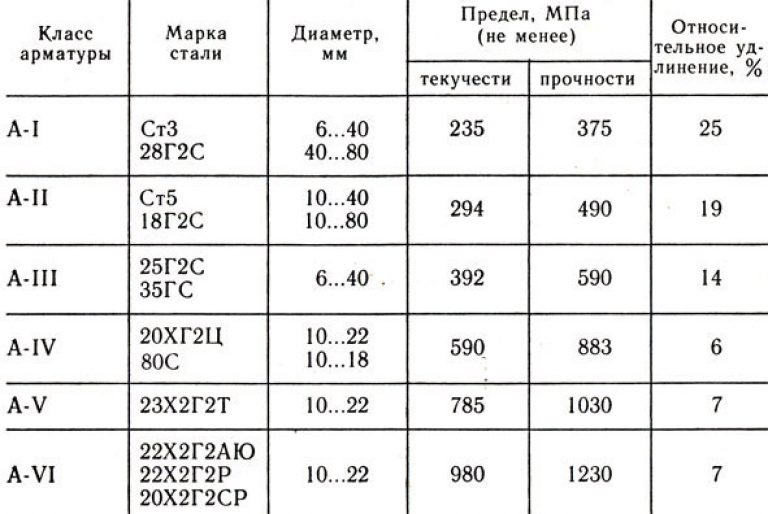

Прямая аппроксимация с опережением (DLA)

Разработка VFA обычно требует хорошего понимания структуры проблемы, хотя нейронные сети в некоторой степени решают эту проблему (за счет дополнительной настройки). Вместо того, чтобы выводить явную функцию, аппроксимация с прямым просмотром вперед (DLA) просто производит выборку нисходящих значений. DLA может быть представлен следующим образом:

Пример аппроксимации прямого просмотра (DLA)

Следует признать, что это уравнение выглядит довольно громоздким, но на самом деле может быть самым простым из всех. Условия ожидания подразумевают, что мы делаем выборку из будущего и применяем некоторую (субоптимальную) политику для оценки последующих значений. Принимая во внимание, что мы максимизируем все возможные действия в текущий момент времени t , для будущих временных эпох t’ мы обычно используем более легкую в вычислительном отношении политику (например, эвристику) и/или упрощенное представление проблемы (например, предполагая идеальное предвидение).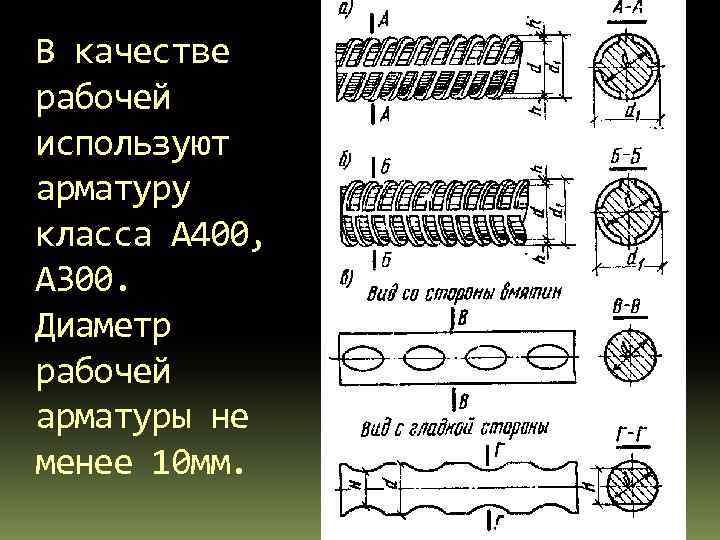 Стратегия DLA имеет свои собственные проблемы (выборка сценариев, методы агрегирования и т. д.), но, в отличие от трех других политик, она не требует оценки функции (поэтому нет, замена «функции» на «упреждающий просмотр» — это не просто семантика). Таким образом, он часто служит последним средством для решения сложных проблем, с которыми не срабатывают три другие стратегии.

Было бы упущением не упомянуть возможности объединения стратегий из нескольких классов. Например, классическая структура актер-критик содержит элементы как PFA (актер), так и VFA (критик). Однако существует гораздо больше комбинаций, таких как встраивание VFA в качестве нижестоящей политики в алгоритм прямого просмотра. Комбинированные стратегии могут сводить на нет недостатки друг друга, часто давая превосходные результаты по сравнению с одноклассовыми решениями.

Согласно Пауэллу, практически любую стратегию решения можно отнести к одному (или нескольким) из четырех классов политик. Кроме того, из классификации можно сделать несколько интересных выводов:

• Нет универсального решения. Несмотря на то, что существуют некоторые эмпирические правила, несколько стратегий могут дать хорошие решения. Наглядный пример этого утверждения можно найти у Пауэлла и Мейзеля [3], где демонстрируются реализации всех четырех стратегий решения одной и той же проблемы.
• Академикам нравится элегантность. PFA и VFA, по-видимому, наиболее популярны в академических кругах. В конце концов, есть определенная математическая красота в том, чтобы зафиксировать сложную политику принятия решений в одной функции.
• Промышленность любит результаты. Когда проблемы становятся слишком большими или сложными, CFA и DLA могут дать удивительно хорошие результаты. Несмотря на то, что мы больше полагаемся на грубую силу и перечисление, усилия по проектированию существенно меньше.
• Все имеет свою цену. Всегда есть компромиссы между удобством, трудоемкостью проектирования, вычислительной сложностью, интерпретируемостью и т. д. Природа проблемы определяет вес этих компромиссов.
• Классификация имеет ключевое значение. Существует много сообществ RL, много методов, много стилей обозначений, много алгоритмов. Чтобы оптимизировать домен и способствовать продвижению, необходима четкая всеобъемлющая структура.

[1] Пауэлл, Уоррен Б. «Единая структура стохастической оптимизации». Европейский журнал операционных исследований 275.3 (2019): 795–821.

[2] Саттон, Ричард С. и Эндрю Г. Барто. Обучение с подкреплением: введение . MIT Press, 2018.

[3] Пауэлл, Уоррен Б. и Стефан Мейзел. «Учебное пособие по стохастической оптимизации в энергетике — Часть II: Иллюстрация накопления энергии». IEEE Transactions on Power Systems 31.2 (2015): 1468–1475.

Алгоритмы обучения с подкреплением — интуитивно понятный обзор | by SmartLab AI

Автор: Роберт Мони

В этой статье делается попытка не исчерпывающим образом выделить основной тип алгоритмов, используемых для обучения с подкреплением (RL). Цель состоит в том, чтобы предоставить обзор существующих методов RL на интуитивном уровне, избегая глубокого погружения в модели или математику, стоящую за ними.

Когда дело доходит до объяснения машинного обучения тем, кто не связан с этой областью, обучение с подкреплением, вероятно, является самой простой частью этой задачи. RL это все равно, что учить собаку (или кошку, если вы живете сложной жизнью) выполнять трюки: вы даете лакомства в качестве награды, если ваш питомец выполняет трюк, который вы хотите, в противном случае вы наказываете его, не угощая его, или предоставление лимонов. Собаки действительно ненавидят лимоны.

Это только для обложки[Источник]

Помимо разногласий, RL является более сложным и трудным для реализации методом, но в основном он связан с обучением через взаимодействие и обратную связь, или, другими словами, обучением решению задачи путем проб и ошибок. ошибка, или иными-другими словами действие в среде и получение за это вознаграждения. По сути, строится агент (или несколько), способный воспринимать и интерпретировать среду, в которую он помещен, более того, он может совершать действия и взаимодействовать с ней.

Для начала давайте разберемся с терминологией, используемой в области RL.

Взаимодействие агента со средой [Источник]

1. Агент — обучающийся и принимающий решения.
2. Среда — где агент учится и решает, какие действия выполнять.
3. Действие — набор действий, которые может выполнять агент.
4. Состояние — состояние агента в среде.
5. Вознаграждение — за каждое выбранное агентом действие среда предоставляет вознаграждение. Обычно скалярное значение.
6. Политика — функция принятия решений (стратегии управления) агента, представляющая собой отображение ситуаций в действия.
7. Функция значения — преобразование состояний в действительные числа, где значение состояния представляет собой долгосрочное вознаграждение, достигаемое, начиная с этого состояния и выполняя определенную политику.
8. Аппроксиматор функций — относится к проблеме индуцирования функции из обучающих примеров. Стандартные аппроксиматоры включают деревья решений, нейронные сети и методы ближайших соседей
9. Марковский процесс принятия решений (MDP) — Вероятностная модель последовательной задачи принятия решений, в которой состояния могут быть восприняты точно, а текущее состояние и выбранное действие определяют распределение вероятностей будущих состояний. По сути, результат применения действия к состоянию зависит только от текущего действия и состояния (а не от предшествующих действий или состояний).
10. Динамическое программирование (ДП) — класс методов решения задач последовательного решения с композиционной структурой затрат. Ричард Беллман был одним из основных основоположников этого подхода.
11. Методы Монте-Карло — Класс методов изучения функций ценности, которые оценивают ценность состояния, выполняя множество испытаний, начиная с этого состояния, а затем усредняют общее вознаграждение, полученное в этих испытаниях.
12. Алгоритмы временной разности (TD) — Класс методов обучения, основанный на идее сравнения последовательных во времени предсказаний. Возможно, это самая фундаментальная идея во всем обучении с подкреплением.
13. Модель — Представление агента об окружающей среде, которое сопоставляет пары состояние-действие с распределением вероятностей по состояниям. Обратите внимание, что не каждый агент обучения с подкреплением использует модель своей среды

OpenAI — некоммерческая исследовательская компания в области искусственного интеллекта, миссия которой заключается в создании и совместном использовании безопасного искусственного общего интеллекта (AGI) — запустила программу для «раскрутки» глубокого RL . На веб-сайте представлено всестороннее введение в основные алгоритмы RL. Этот блог будет в основном следовать этому обзору с дополнительными пояснениями.

Таксономия обучения с подкреплением, как определено OpenAI [Источник]

RL на основе моделей использует опыт для построения внутренней модели переходов и немедленных результатов в среде. Затем путем поиска или планирования в этой модели мира выбираются соответствующие действия.

…

RL без моделей, с другой стороны, использует опыт для непосредственного изучения одной или обеих из двух более простых величин (значений состояния/действия или политик), которые могут обеспечить такое же оптимальное поведение, но без оценки или использования мира модель. При заданной политике состояние имеет значение, определяемое с точки зрения будущей полезности, которая, как ожидается, будет нарастать, начиная с этого состояния.

…

Методы без моделей статистически менее эффективны, чем методы на основе моделей, потому что информация из окружающей среды комбинируется с предыдущими и, возможно, ошибочными, оценками или убеждениями о значениях состояния, а не используется напрямую.

(Питер Даяна и Яэль Нив — Обучение с подкреплением: хорошее, плохое и злое, 2008 г.)

Ну, это должно было объяснить. Как правило: обучение на основе модели пытается смоделировать среду, а затем выбрать оптимальную политику на основе изученной модели; В Без модели Обучение агента основано на опыте проб и ошибок для настройки оптимальной политики.

Два основных подхода к представлению агентов с обучением с подкреплением без использования моделей — это оптимизация политик и Q-обучение.

I.1. Методы оптимизации политики или итерации политики

В методах оптимизации политики агент непосредственно изучает функцию политики, которая отображает состояние в действие. Политика определяется без использования функции значения.

Важно отметить, что существует два типа политики: детерминированная и стохастическая. Детерминированная политика отображает состояние в действие без неопределенности. Это происходит, когда у вас есть детерминированная среда, такая как шахматный стол. Стохастическая политика выводит распределение вероятностей по действиям в заданном состоянии. Этот процесс называется частично наблюдаемым марковским процессом принятия решений (POMDP).

I.1.1. Градиент политики (PG)

В этом методе у нас есть политика π с параметром θ. Это π выводит распределение вероятностей действий.

Вероятность совершения действия в заданном состоянии s с параметрами тета. [Источник]

Затем мы должны найти наилучшие параметры (θ), чтобы максимизировать (оптимизировать) функцию оценки J(θ), учитывая коэффициент дисконтирования γ и вознаграждение r.

Функция оценки политики [Источник]

Основные этапы:

• Измерение качества политики с помощью функции оценки политики.
• Используйте градиентное восхождение политики, чтобы найти лучший параметр, улучшающий политику.

Отличное и подробное объяснение со всей математикой, включенной в градиент политики, можно найти в блоге Джонатана Хуи или во вводном блоге Томаса Симонини к PG с примерами в Tensorflow.

I.1.2. Асинхронный Преимущество Актер-Критик (A3C)

Этот метод был опубликован группой Google DeepMind и охватывает следующую ключевую концепцию, заложенную в его названии: Модельная форма этих агентов собрана в главном агенте. Причина этой идеи в том, что опыт каждого агента не зависит от опыта других. Таким образом, общий опыт, доступный для обучения, становится более разнообразным.

Простое, но подробное объяснение кода, реализованного в Tensorflow, можно найти в блоге Артура Джулиани.

I.1.3. Оптимизация политики доверенного региона (TRPO)

Алгоритм политики, который можно использовать или среды с дискретными или непрерывными пространствами действий. TRPO обновляет политики, делая максимально возможный шаг для повышения производительности, соблюдая при этом специальное ограничение на то, насколько близкими могут быть новые и старые политики.

Подробное введение в TRPO представлено в этой и этой записи блога, а в большом репозитории представлены решения на основе Tensorflow и OpenAI Gym.

I.1.4. Проксимальная оптимизация политики (PPO)

Также алгоритм на основе политики, который, подобно TRPO, может выполняться в дискретных или непрерывных пространствах действий. PPO разделяет мотивацию с TRPO, отвечая на вопрос: как улучшить политику без риска падения производительности? Идея состоит в том, что PPO повышает стабильность обучения Актера, ограничивая обновление политики на каждом этапе обучения.

PPO стал популярным, когда OpenAI совершил прорыв в Deep RL, когда они выпустили алгоритм, обученный играть в Dota2, и они выиграли у некоторых из лучших игроков в мире. Смотрите описание на этой странице.

Для более подробного ознакомления с PPO посетите этот блог.

I.2. Q-обучение или методы итерации значения

Q-обучение изучает функцию действия-значения Q(s, a) : насколько хорошо выполнять действие в конкретном состоянии . В основном скалярное значение присваивается над действием в заданном состоянии s. Следующая диаграмма обеспечивает хорошее представление алгоритма.

Шаги Q-обучения [Источник]

I.2.1 Глубокая нейронная сеть Q (DQN)

DQN — это Q-обучение с нейронными сетями. Мотивация просто связана с большими средами пространства состояний, где определение Q-таблицы было бы очень сложной, сложной и трудоемкой задачей. Вместо Q-таблицы нейронные сети аппроксимируют Q-значения для каждого действия в зависимости от состояния.

Чтобы глубже погрузиться в DQN, посетите этот курс и тем временем поиграйте в Doom.

I.2.2 C51

C51 — допустимый алгоритм, предложенный Bellemare et al. для выполнения итеративной аппроксимации распределения значений Z с использованием уравнения распределенного Беллмана . Число 51 представляет использование 51 дискретного значения для параметризации распределения значений Z(s,a). См. исходную статью здесь, а для глубокого погружения следуйте этому ознакомительному руководству с реализацией в Keras.

I.2.3 Распределенное обучение с подкреплением с помощью квантильной регрессии (QR-DQN)

В QR-DQN для каждой пары состояние-действие вместо оценки одного значения используется распределение значений значений в изученном. Распределение значений, а не только среднее, может улучшить политику. Это означает, что квантили изучаются, какие пороговые значения связаны с определенными вероятностями в кумулятивной функции распределения. См. статью о методе здесь и простую реализацию с использованием Pytorch здесь.

I.2.4 Воспроизведение ретроспективного опыта (HER)

В методе воспроизведения ретроспективного опыта в основном DQN поставляется с состоянием и желаемым конечным состоянием, или, другими словами, целью. Это позволяет быстро узнать, когда награды редки. Другими словами, когда награды в большинстве случаев одинаковы, и только несколько редких наград действительно выделяются.

Для лучшего понимания, помимо статьи, ознакомьтесь с этим сообщением в блоге, fr кодирует этот репозиторий github

I.3 Гибрид

Как бы просто это ни звучало, эти методы сочетают в себе сильные стороны Q-обучения и градиентов политики, таким образом, функция политики, которая отображает состояние в действие, и функция действия-ценности, которая обеспечивает ценность для каждого действия. изучается.

Некоторые гибридные алгоритмы без моделей:

• Глубокие детерминированные градиенты политики (DDPG): бумага и код,
• Мягкий актер-критик (SAC): бумага и код.
• Глубокие детерминированные градиенты двойной задержки (TD3) бумага и код

RL на основе моделей оказывает сильное влияние на теорию управления, и цель состоит в том, чтобы планировать с помощью функции управления f(s,a) для выбора оптимальных действий. Дело в том, что это поле RL, где законы физики предусмотрены создателем. Недостатком методов, основанных на моделях, является то, что хотя они имеют больше предположений и приближений к данной задаче, но могут быть ограничены только этими конкретными типами задач. Существует два основных подхода: изучение модели или обучение на основе модели.

II.1. Изучите модель

Для изучения модели запускается базовая политика, такая как случайная или любая обученная политика, при этом наблюдается траектория. Модель подобрана с использованием выборочных данных. Ниже приведены шаги, описывающие процедуру:

Обучение с учителем используется для обучения модели для минимизации ошибки наименьших квадратов из выборочных данных для функции управления. Оптимальная траектория с использованием модели и функции стоимости используется на третьем этапе. Функция стоимости может измерять, насколько далеко мы находимся от целевого местоположения, и количество затраченных усилий. [источник]

• Модели мира: один из моих любимых подходов, в котором агент может учиться на своих собственных «мечтах» благодаря переменным автокодировщикам, см. документ и код.
• Агенты с расширенным воображением (I2A): учатся интерпретировать прогнозы из изученной модели среды для построения неявных планов произвольным образом, используя прогнозы в качестве дополнительного контекста в глубоких сетях политики. По сути, это гибридный метод обучения, потому что он сочетает в себе модельные и безмодельные методы. Бумага и реализация.
• Model-Based Priors для обучения с подкреплением без моделей (MBMF): направлен на преодоление разрыва между обучением с подкреплением без моделей и обучением с подкреплением на основе моделей. См. бумагу и код.
• Расширение значений на основе модели (MBVE): Авторы документа заявляют, что этот метод контролирует неопределенность в модели, позволяя воображению ограничиваться только фиксированной глубиной. Обеспечивая более широкое использование изученных динамических моделей в алгоритме обучения с подкреплением без моделей, мы улучшаем оценку ценности, что, в свою очередь, снижает сложность выборки обучения.