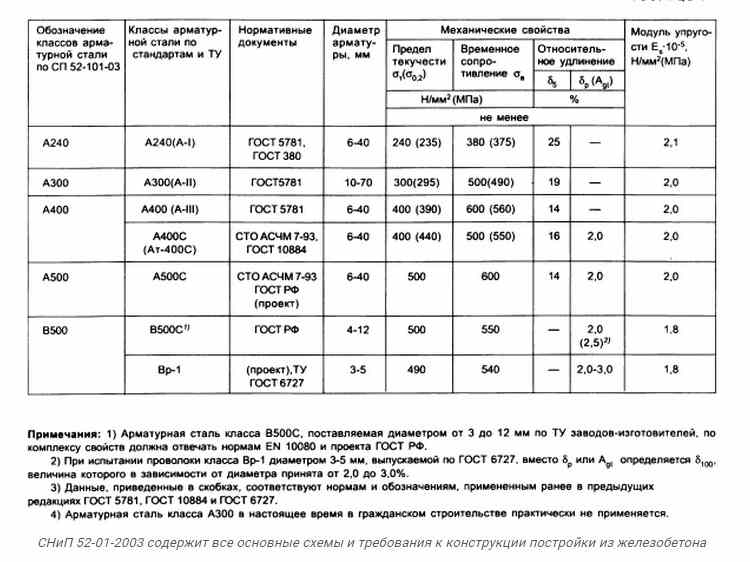
Классификация арматуры таблица по классам: Какая разница между классами арматуры

1.2.4. Классификация арматуры по основным характери­стикам. Сортамент арматуры

По
виду применяемой арматуры различают
железобетон с гибкой арматурой в виде
стальных стержней круглого или
периодическо­го профиля сравнительно
небольших диаметров (до 40 мм включи­тельно)
и конструкции с несущей или жёсткой
арматурой. К жёст­кой арматуре относится
профильная прокатная сталь (уголкового,
швеллерного и двутаврового сечения) и
горячекатаные стержни диа­метром
более 40 мм. Основным видом арматуры
является гибкая.

Вся
арматура, используемая в железобетоне,
по своим основным характеристикам
делится на ряд классов, причём в один
класс мо­жет входить арматура из
сталей нескольких марок.

Основным
нормируемым и контролируемым показателем
качества стальной арматуры является
класс арматуры по прочности на растяжение,
обозначаемый:

А
– для горячекатаной и термомеханически
упрочненной арматуры;

В
– для холоднодеформированной арматуры;

К
– для арматурных канатов.

Класс
арматуры соответствует гарантированному
значению предела текучести (физического
или условного) в МПа, устанавливаемому
в соответствии с требованиями стандартов
и технических условий, и принимается в
пределах от A 240 до A 1500, от B 500 до B 2000 и от
K 1400 до K 2500.

Классы
арматуры следует назначать в соответствии
с их параметрическими рядами, установленными
нормативными документами.

Кроме
требований по прочности на растяжение
к арматуре предъявляют требования по
дополнительным показателям, определяемым
по соответствующим стандартам:
свариваемость, выносливость, пластичность,
стойкость к коррозионному растрескиванию,
релаксационная стойкость, хладостойкость,
стойкость при высоких температурах,
относительное удлинение при разрыве и
др.

К неметаллической
арматуре (в том числе фибре) предъявляют
также требования по щелочестойкости и
адгезии к бетону.

Дадим краткие
характеристики арматуры перечисленных
клас­сов.

Арматуру
класса A240
изготовляют из стали марки Ст3. Она имеет
гладкую цилиндрическую поверхность и
применяется глав­ным образом в качестве
монтажной арматуры, хомутов, поперечных
стержней; из неё изготавливают монтажные
петли. Хорошо свари­вается. Прокатывается,
начиная с диаметра 6 мм (σ_v
= 230
МПа, σ_u
= 380
МПа и δ
≥ 25%).

Остальные
классы стержневой арматуры представляют
собой стальные стержни, поверхность
которых имеет периодический про­филь.
Выступы, имеющиеся на поверхности
стержней периодиче­ского профиля,
резко (в 2…3 раза) повышают сцепление
арматуры с бетоном и уменьшают ширину
раскрытия трещин в бетоне растя­нутой
зоны.

Например,
для арматуры класса А300 периодический
профиль имеет вид, показанный на рис.
19, а. Как видно из этого рисунка, арматура
класса А300 представляет собой круглые
стержни с часто расположенными выступами
и с двумя продольными рёбрами.

Арматура
класса А300 хорошо сваривается и
используется в каче­стве рабочей в
обычном железобетоне. Для её изготовления
исполь­зуются стали марок Ст5, 10ГТ,
18Г2С. Прокатывается, начиная с номинального
диаметра 10 мм. Основные её характеристики
σ_у
= 300
МПа, σ_и
= 500 МПа и δ
≥
19%.

Рис.
19. Арматура периодического профиля:

а,
б – стержневая; в – проволочная

Арматура
класса A400
имеет на своей поверхности выступы,
об­разующие «ёлочку» (рис. 19, 6). Эта
арматура является основной рабочей
арматурой в обычном железобетоне. Хорошо
сваривается. Выпускается диаметрами
6, 8, 10 мм в мотках массой до 1300 кг и
диаметрами 12…40 мм в прутках длиной до
13,2 м. Изготавливается из низколегированной
стали марок 18Г2С, 35ГС, 25Г2С по усмотре­нию
завода-изготовителя. Для неё σ_у
= 400
МПа, σ_и
= 600
МПа и δ≥
14%.

В
обозначениях марок стали отражается
содержание в них угле­рода и легирующих
добавок. Например, в марке стали 25Г2С
первые две цифры обозначают содержание
в стали углерода в сотых долях процента
(0,25%), буква Г – что сталь легирована
марганцем, цифра 2 – что его содержание
может достигать 2%, а буква С – наличие
в стали кремния. Буквой X
обозначается хром, Т – титан, Ц
– цирконий и т.д.

Обыкновенная
низкоуглеродистая проволока класса
В500 (ГОСТ 6727-80) выпускается диаметрами
3, 4, 5 мм. Изготовляют её во­лочением
катанки из низкоуглеродистой стали
группы Ст2 – Ст3 и используют преимущественно
в сварных изделиях – сетках и кар­касах;
σ_и
= 550…525
МПа в зависимости от диаметра, а σ_у
и
δ
не
нормируются.

Периодический
профиль проволоки класса В500 (рис. 19, в)
об­разуется расположенными на её
поверхности вмятинами (рифами). Размеры
вмятин зависят от диаметра проволоки.
Проволока хоро­шо сваривается, что
позволяет использовать её для изготовления
арматурных изделий.

Класс
арматурной стали при проектировании
выбирается в зависимости от типа
конструкции, условий ее возведения и
эксплуатации.

При
проектировании железобетонных конструкций
пользуются сортаментом арматуры.
Сортамент арматурной стали – это
перечень типоразмеров каждого вида
арматурных стержней, выпускае­мых в
настоящее время металлургической
промышленностью. В стране существует
единый сор­тамент для гладкой арматуры
и арматуры периодического профиля. Он
со­ставлен по номинальным диаметрам
стержней, выраженным в мм. Номинальный
диаметр гладкого стержня совпадает с
его фактиче­ским диаметром. Для
стержневой арматуры периодического
профи­ля номинальный диаметр (номер)
стержня, указанный в сортаменте,
соответствует диаметру гладкого круглого
стержня, равновеликого ему по площади
поперечного сечения. Например, арматурный
стер­жень, расчётный номинальный
диаметр которого равен 20 мм (см. рис. 19,
а, б), имеет наружный диаметр (по выступам)
22 мм и внут­ренний (по телу) – 19 мм, а
высота выступов на его поверхности
равна h
= 0,5(d₁–d)
= 0,5(22–19) = 15 мм.

таблица, классификация по ГОСТ и особенности изделий

Прокат арматурный – незаменимый элемент строительства жилых домов, общественных и промышленных зданий, масштабных сооружений. При разработке проекта для любого инженера или архитектора незаменимым инструментом становится таблица сечений арматуры по ГОСТ 5781-82.

Особенности и классификация

Общеизвестно, что для упрочнения бетонных, каменных, кирпичных и даже стеклянных конструкций применяется технология армирования. То есть внутри устройства формируется каркас, который частично либо полностью принимает на себя деформирующие нагрузки. В качестве основы используются металлические стержни круглого сечения или арматура. Производится из нескольких видов стали (в соответствии с ГОСТ 52544-2006, СТО АСЧМ 7-93, ТУ 14-1-5254-94 и другими) в диаметре от 4 до 80 мм с поверхностью гладкого или периодического профиля.

Изделия из стали классифицируются по двум основным параметрам – прочности и механическим свойствам. Исходя из этого выделяют следующие классы арматуры:

1. А1 (А240) – монтажная, чаще всего используется в железобетонных конструкциях в качестве распределительного и связующего элемента. Характерный признак – гладкая поверхность, применяется для железобетонных изделий.

2. А2 (А300) – рабочий арматурный прокат. Имеет рифленый профиль, относится к силовым элементам, которые несут основную нагрузку. Область использования – малоэтажное строительство, ремонт, монолитные сооружения.

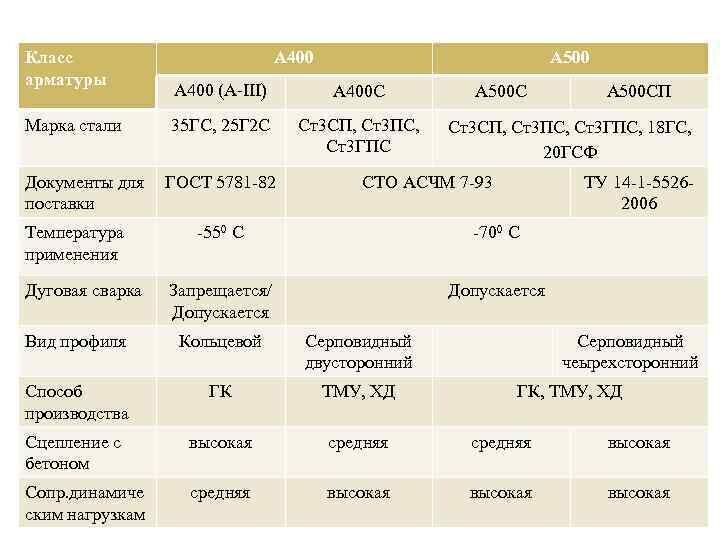
3. А3 (А400, А500) – горячекатаные пруты с периодической поверхностью. Это наиболее востребованная продукция, так как выпускается практически во всех диаметрах и применяется как в производстве ЖБИ, так и при возведении жилых, коммерческих и промышленных строений, обустройстве дорожного и тротуарного полотна.

4. А4 (А600) – вид рабочей арматуры, используемой в напряженных конструкциях. Из-за ограничений продукция из стали выпускается в диаметре 10-32 мм.

5. А5 (А800) – стержни повышенной прочности для тяжелых и крупногабаритных конструкций (причалы, метрополитен, ГЭС).

6. А6 (А1000) – арматура рабочего типа из термически упрочненной стали. Характеризуется высокой степенью сопротивляемости к деформациям, востребована в многоэтажном строительстве.

Помимо основной маркировки существует дополнительная, информирующая об особых механических свойствах стальных изделий. Так, литера «С» обозначает, что их можно соединять методом сварки. Добавленная к шифру буква «К» означает, что поверхность арматуры устойчива к коррозии.

На площадки прокат поставляется бухтами по 11,7 или прутами 6-12 м. Как правило, заводы и дилеры отпускают продукцию тоннами, а для пересчета в погонные метры продавцы используют сводные таблицы теоретического веса по ГОСТ Р-52544-2006.

Сортамент строительной арматуры

Как и любое другое производство, изготовление арматуры унифицировано. Поэтому разработанные государственные стандарты содержат единые нормативы по всем характеристикам, включая диаметр, вес, сечение стержней. Эти параметры объединяются достаточно емким термином – сортамент или сортимент. В переводе с французского assortir – подбирать, сортировать. То есть это состав продукции по размерам, профилю или другим характерным признакам.

Для изделий из металла в ГОСТ 5781-82 указана унифицированная таблица массогабаритных размеров, однако на практике у заводов не всегда получается соответствовать этим показателям. Вышеуказанным стандартом допускаются отклонения, но не более 9%.

Четыре класса политики обучения с подкреплением | Wouter van Heeswijk, PhD

Комплексная классификация стратегий решения для обучения с подкреплением

Wouter van Heeswijk, PhD

·

Follow

Published in

·

7 минут чтения

·

11 мая, 2021

Изображение Ханса Браксмайера с сайта Pixabay

Политики обучения с подкреплением (RL) окутаны определенной мистикой. Проще говоря, политика π: s → a — это любая функция, которая возвращает допустимое действие для решения задачи. Не меньше, не больше. Например, вы можете просто выполнить первое действие, которое придет вам в голову, выбрать действие наугад или запустить эвристику. Однако что делает RL особенным, так это то, что мы активно предвидим последствия решений и учимся на своих наблюдениях; поэтому мы ожидаем некоторого разума в нашей политике. В своей концепции последовательного принятия решений[1] Уоррен Пауэлл утверждает, что существует четыре класса политик для RL. Методы всех четырех классов широко используются в разных областях, но еще не получили всеобщего признания. В этой статье будет представлено краткое — и, несомненно, неполное — введение в эту классификацию стратегий решения.

Прежде чем перейти к обучению с подкреплением, давайте сначала немного освежим нашу память об аналитических решениях. Как правило, мы стремимся сформулировать задачу RL в виде модели марковского процесса принятия решений (MDP).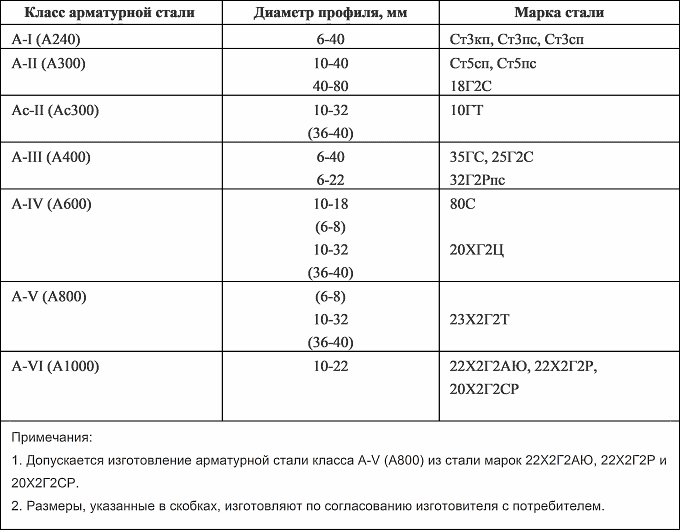 Если мы останемся ближе к MDP, целью обучения с подкреплением будет решение соответствующей системы уравнений Беллмана и, таким образом, нахождение оптимальной политики π* :

уравнения Беллмана для MDP. Поиск оптимальной политики π* дает функции оптимального значения В(с) 9π*(s’) , что мы делаем только в одном из четырех классов политик. Таким образом, мы можем сформулировать нашу цель следующим образом:

Функция вознаграждения на временном горизонте. Оптимальная политика π* максимизирует совокупное вознаграждение.

Для оптимизации модели MDP существует два основных подхода: (i) итерация политики и (ii) итерация значения. Итерация политики исправляет политику, вычисляет соответствующее значение политики и впоследствии обновляет политику, используя новое значение. Алгоритм выполняет итерацию между этими шагами до тех пор, пока политика не станет стабильной. Итерация значения на самом деле основана на очень похожих шагах (см. рисунок ниже), но направлена ​​на непосредственное максимизацию функций значения и только после этого обновляет политику. Обратите внимание, что поиск функций оптимального значения равен поиску оптимальной политики; либо достаточно для решения системы уравнений Беллмана.

Сравнение итерации политики (слева) и итерации значения (справа). Обратите внимание на итеративный характер итерации политики и оператор максимума в итерации значения. Адаптировано из Sutton & Barto [2]

Большинство — если не все — алгоритмы RL основаны либо на итерации политики, либо на итерации значения (или на их комбинации). Поскольку применяемые методы моделирования обычно не гарантируют нахождение оптимальных политик, в RL мы говорим о политике , аппроксимации и значении , аппроксимации соответственно. Пауэлл утверждает, что обе стратегии можно разделить на два класса, что дает в общей сложности четыре класса, которые мы вскоре обсудим. Просто некоторые основные обозначения, и мы готовы к работе:

s : состояние (информация, необходимая для принятия решения)

a : действие (возможная операция над состоянием)

π : политика (сопоставление состояния с действием)

ϕ : базовая функция (получает характеристики из состояния)

θ : веса признаков (параметризация политики)

t : эпоха времени (дискретный момент времени)

R : функция вознаграждения (прямое вознаграждение за выполнение действия в состоянии)

V : функция значения (вознаграждение нижестоящего уровня за определенное состояние)

В приближенных решениях политики мы напрямую изменяем саму политику. Такие стратегии решения, как правило, работают лучше всего, когда политика имеет четкую структуру. Мы можем выделить два класса: PFA и CFA.

Аппроксимация функции политики (PFA)

Аппроксимация функции политики (PFA) по существу представляет собой параметризованную функцию политики. Подключение состояния напрямую возвращает допустимое действие. Линейный PFA может выглядеть так:

Пример аппроксимации функций политики (PFA)

Основная задача здесь состоит в том, чтобы найти соответствующие базисные функции ϕ(s) , которые охватывают суть процесса принятия решений. Для этого необходимо хорошее понимание структуры проблемы. Усилия по проектированию можно облегчить, выбрав более общие представления функций, такие как нейронная сеть (сети акторов), используя состояние в качестве входных данных и выводя действие. Недостатком таких представлений PFA является то, что настройка параметров становится сложнее, а интерпретируемость страдает. Несмотря на это, необходимо четкое понимание структуры проблемы. π ограничено политикой π и его параметризация θ , что обычно дает меньшее пространство действия, чем исходное. Обратите внимание, что простейшая форма CFA — это просто жадная эвристика, однако модифицированная функция вознаграждения может включать в себя элементы исследования. Вычислительные усилия на итерацию, вероятно, выше, чем для PFA (из-за шага максимизации), но требуется меньше усилий при проектировании.

При приближении значений явно учитывается влияние текущих решений на последующие процессы с учетом всего горизонта принятия решений. Напоминаем, что функции оптимальной стоимости приравниваются к оптимальной политике; они оба дают идентичные решения уравнений Беллмана. Аппроксимация стоимости может быть подходящей, когда структура политики не выдающаяся или мы не можем должным образом контролировать последующие эффекты текущих решений.

Аппроксимация функции значения (VFA)

Аппроксимация функции значения (VFA) представляет последующие значения как функцию.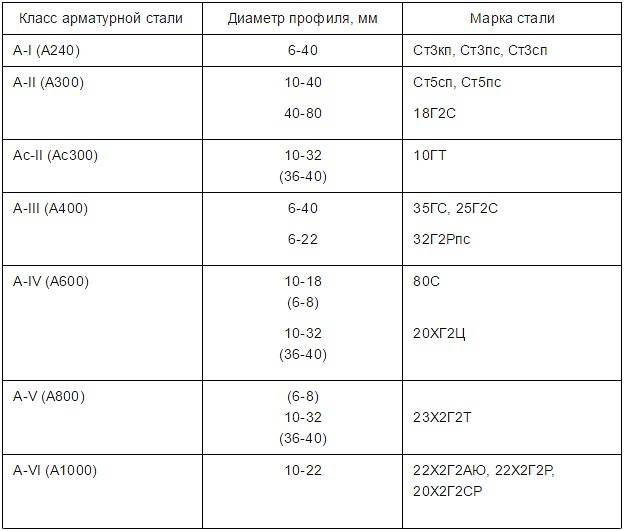 Одна из проблем с уравнением Беллмана заключается в том, что после совершения действия случайные события могут привести нас ко многим новым состояниям s’∈ S’ . Таким образом, для каждого действия мы должны учитывать значение всех достижимых состояний s’ и вероятность попадания в них. VFA обходят эту проблему, заменяя член стохастического ожидания детерминированной функцией аппроксимации В_т(с_т,а_т) . В канонической форме VFA выглядит следующим образом:

Пример аппроксимации функции ценности (VFA)

Простейший VFA — это справочная таблица, в которой мы храним средние наблюдаемые значения для каждой пары состояние-действие. Достаточное количество итераций позволяет нам узнать точные значения для каждой пары, но это редко поддается вычислительной обработке. Поэтому мы обычно прибегаем к функциям, которые фиксируют суть состояния, которые мы можем разработать или извлечь вручную, например, с помощью автокодировщиков. Таким образом, мы фиксируем значения состояния-действия в компактных функциях (например, в сети критиков) и настраиваем веса признаков путем наблюдения.

Прямая перспективная аппроксимация (DLA)

Разработка VFA обычно требует хорошего понимания структуры проблемы, хотя нейронные сети в некоторой степени решают эту проблему (за счет дополнительной настройки). Вместо того, чтобы выводить явную функцию, аппроксимация с прямым просмотром вперед (DLA) просто производит выборку нисходящих значений. DLA может быть представлено следующим образом:

Пример аппроксимации с прямым просмотром (DLA)

Следует признать, что это уравнение выглядит довольно громоздким, но на самом деле может быть самым простым из множества. Условия ожидания подразумевают, что мы делаем выборку из будущего и применяем некоторую (субоптимальную) политику для оценки последующих значений. Принимая во внимание, что мы максимизируем все возможные действия в текущий момент времени t , для будущих временных эпох t’ мы обычно используем более легкую в вычислительном отношении политику (например, эвристику) и/или упрощенное представление проблемы (например, предполагая идеальное предвидение). Стратегия DLA имеет свои собственные проблемы (выборка сценариев, методы агрегирования и т. д.), но, в отличие от трех других политик, она не требует оценки функции (поэтому нет, замена «функции» на «упреждающий просмотр» — это не просто семантика). Таким образом, он часто служит последним средством для решения сложных проблем, с которыми не срабатывают три другие стратегии.

Было бы упущением не упомянуть возможности объединения стратегий из нескольких классов. Например, классическая структура актер-критик содержит элементы как PFA (актер), так и VFA (критик). Однако существует гораздо больше комбинаций, таких как встраивание VFA в качестве нижестоящей политики в алгоритм прямого просмотра. Комбинированные стратегии могут свести на нет недостатки друг друга, часто давая превосходные результаты по сравнению с одноклассовыми решениями.

Согласно Пауэллу, практически любую стратегию решения можно отнести к одному (или нескольким) из четырех классов политик. Кроме того, из классификации можно сделать несколько интересных выводов:

• Нет универсального решения. Несмотря на некоторые эмпирические правила, несколько стратегий могут дать хорошие решения. Наглядный пример этого утверждения можно найти у Пауэлла и Мейзеля [3], где демонстрируются реализации всех четырех стратегий решения одной и той же проблемы.
• Академики любят элегантность. PFA и VFA, по-видимому, наиболее популярны в академических кругах. В конце концов, есть определенная математическая красота в том, чтобы зафиксировать сложную политику принятия решений в одной функции.
• Промышленность любит результаты. Когда задачи становятся слишком большими или сложными, CFA и DLA могут дать удивительно хорошие результаты. Несмотря на то, что мы больше полагаемся на грубую силу и перечисление, усилия по проектированию существенно меньше.
• Все имеет свою цену. Всегда есть компромиссы между удобством, трудоемкостью проектирования, вычислительной сложностью, интерпретируемостью и т. д. Природа проблемы определяет, насколько весомыми являются эти компромиссы.
• Классификация имеет ключевое значение. Существует много сообществ RL, много методов, много стилей обозначений, много алгоритмов. Чтобы оптимизировать домен и способствовать продвижению, необходима четкая всеобъемлющая структура.

[1] Пауэлл, Уоррен Б. «Единая структура стохастической оптимизации». Европейский журнал операционных исследований 275.3 (2019): 795–821.

[2] Саттон, Ричард С. и Эндрю Г. Барто. Обучение с подкреплением: введение . MIT Press, 2018.

[3] Пауэлл, Уоррен Б. и Стефан Мейзел. «Учебное пособие по стохастической оптимизации в энергетике — Часть II: Иллюстрация накопления энергии». IEEE Transactions on Power Systems 31.2 (2015): 1468–1475.

Простое обучение с подкреплением с использованием таблиц Q

Простое обучение с подкреплением с использованием таблиц Q | The Startup Опубликовано в

·

Чтение: 10 мин.

·

17 мая 2020 г.

Моя тестовая среда, вдохновленная OpenAI FrozenLake

исходное положение в ‘ G ‘(Цель), избегая всех отверстий (‘O’) на пути, она может легко увидеть всю игру и нарисовать линию, показывающую, как может двигаться ‘A’. Люди, больше полагающиеся на интуицию, находят эту задачу проще, чем машина. Конечно, мы можем написать программу с несколькими условиями if-else для навигации в этой среде. Но это не значит, что…

Автор Сатиш Кумар

9 подписчиков

·Писатель для

Еще от Сатиша Кумара и стартапа

Сатиш Кумар 9000 5

Социальная ответственность: одна простая вещь, которую вы можете сделать в период пандемии

Чтение через 4 минуты · 22 марта 2020 г.

Zulie Rane

в

Если вы хотите стать творцом, удалите все (кроме двух) платформы социальных сетей

2 октября 022, во время всего Илона Маска фиаско, я наконец-то удалил Твиттер со своего телефона. Примерно в то же время я также вышел из…

·8 min read·Apr 19

Nitin Sharma

in

т что 99% читателей не знакомы любым из этих инструментов.

·Чтение через 6 мин·5 апреля

Нитин Шарма

в

До свидания, ChatGPT: эти (новые) инструменты ИИ лишат вас дара речи

Бьюсь об заклад что 99% читателей не знакомы ни с одним этих инструментов.

·7 минут чтения·6 мая

Просмотреть все от Sathish Kumar

Рекомендовано Medium

Eligijus Bujokas

в

Первые шаги в мире армирования Обучение с использованием Python

Оригинальная реализация Python как найти лучшие места, чтобы оказаться в одном из фундаментальных миров обучения с подкреплением — сетка…

·15 минут чтения·13 января

Рену Ханделвал

Обучение с подкреплением: создание пользовательской среды

Создайте новую пользовательскую среду с помощью Open AI Gym

·6 мин чтения·21 декабря 2022 г.

Списки

Что такое ChatGPT?

9 историй·35 сохранений

Выбор персонала

307 историй·69 сохранений

Рену Ханделвал

Deep Q Learning: алгоритм глубокого обучения с подкреплением

9 0004

Простое для понимания объяснение Deep Q-Learning с реализацией кода PyTorch

·Чтение 11 мин·12 9 января0005

Wouter van Heeswijk, PhD

in

Объяснение проксимальной политики оптимизации (PPO)

Путь от REINFORCE к алгоритму перехода в непрерывном контроле

·Чтение через 13 минут·29 ноября 2022 г.