Крепость болтов и моменты разрывов: Крепость болтов и моменты разрывов. Механические характеристики винтов
Содержание
Характеристики и преимущества высокопрочного крепежа
Высокопрочные болты, винты и шпильки при небольших габаритах способны обеспечить разъемное соединение, не уступающее по прочности сварному и превосходящее заклепочное. Интенсивно эксплуатируемая техника или массивные строительные металлоконструкции требуют применения именно высокопрочного крепежа. Стремление снизить расходы и использовать в ответственных узлах крепления низкопрочные детали может привести к быстрому разрушению конструкций или выходу из строя механизмов.
Перед внедрением высокопрочного крепежа в той или иной проект проектировщики производят точный расчет болтовых соединений с учетом силовой нагрузки на метизы и их прочностных характеристик. К сожалению, в отечественной промышленности объем использования высокопрочных крепежных изделий меньше, чем в развитых зарубежных странах. Это связано с отсутствием достаточной информации о преимуществах и эффективности их применения, а также технической литературы и справочных данных для их практического использования.
Создание долговечной выносливой техники также невозможно без особо прочного крепежа. К сожалению, но факт, что наши автомобили часто не выдерживают даже гарантийного срока эксплуатации из-за крепежных деталей низкой прочности, чего не скажешь об автомобильном парке немецкого, японского, французского, американского производства. Но ситуация в нашей стране постепенно налаживается не только за счет импорта высокопрочного крепежа, но и из-за того, что многие отечественные метизные заводы налаживают его выпуск по российским и европейским стандартам.
В чем отличие высокопрочного крепежа от обычного?
Главное отличие от метизов общего назначения заключается в особых физико-механических свойствах высокопрочного крепежа, которые дают ему возможность воспринимать более тяжелую нагрузку. К примеру, болт высокого класса прочности 12.9 разорвется при нагрузке 1200 Н/мм², а аналогичный по диаметру низкого класса 4.8 – при 420 Н/мм², то есть при нагрузке в 2. 7 раза меньшей.
7 раза меньшей.
Высокопрочный винт ISO 7380-1 класса прочности 10.9
Помимо колоссальной стойкости к повышенным нагрузкам, крепеж высокого класса прочности дает еще целый ряд преимуществ:
-
Снижение металлоемкости изделий и конструкций, при одновременном сохранении надежности крепежных узлов. Это достигается путем использования меньших по размеру винтов, но рассчитанных на более высокие нагрузки. -
Использование шпилек меньшего диаметра влечет за собой уменьшение диаметра монтажных отверстий и, как следствие, повышение прочности металлоконструкций, фланцевых соединений. Кроме того, замена обычных метизов на более прочные позволяет сократить количество точек крепления, снизив тем самым затраты на крепеж. -
Возможность применения в различных климатических условиях. Высокопрочные болты северного исполнения могут эксплуатироваться в условиях сурового климата до -60°С (маркировка «ХЛ») или средних холодных температур до -40°С (маркировка «У»).
-
Способность воспринимать постоянные, переменные и особые нагрузки (подвижные, вибрационные, динамические, сейсмические). -
Возможность применения в конструкциях, эксплуатируемых в слабо-, средне-, сильноагрессивных средах с использованием защитных металлических или лакокрасочных покрытий. -
Создание сдвигоустойчивых соединений. В обычном болтовом соединении при нагрузке на сдвиг происходит смещение соединяемых элементов, равное величине зазора между шпилькой и стенкой отверстия. Высокопрочный болткомплект позволяет стянуть элементы с большим усилием, благодаря чему между ними возникает трение, исключающее сдвиг. Такое соединение называется фрикционным.
Преимущества перед сварочным соединением:
-
Соединения на болтах снижают трудоемкость монтажа, позволяют вести сборку силами рабочих невысокой квалификации, автоматизировать, механизировать сборочный процесс. -
Применение высокопрочных болтовых соединений при монтаже металлоконструкций позволяет использовать элементы из трудносвариваемых сталей повышенной прочности.
-
Возможность визуального контроля целостности монтажного соединения на болтах, тогда как в сварных швах могут быть скрытые дефекты.
Преимущества перед заклепочным соединением:
Сегодня при возведении металлоконструкций на смену заклепкам пришли высокопрочные болткомплекты, которые более выносливы переменным нагрузкам за счет равномерного распределения напряжения по сечению болтового соединения. К тому же в отличие от заклепок они могут быть легко заменены в случае износа, дают возможность сборки/разборки конструкции, могут использоваться многократно, что облегчают ремонт оборудования.
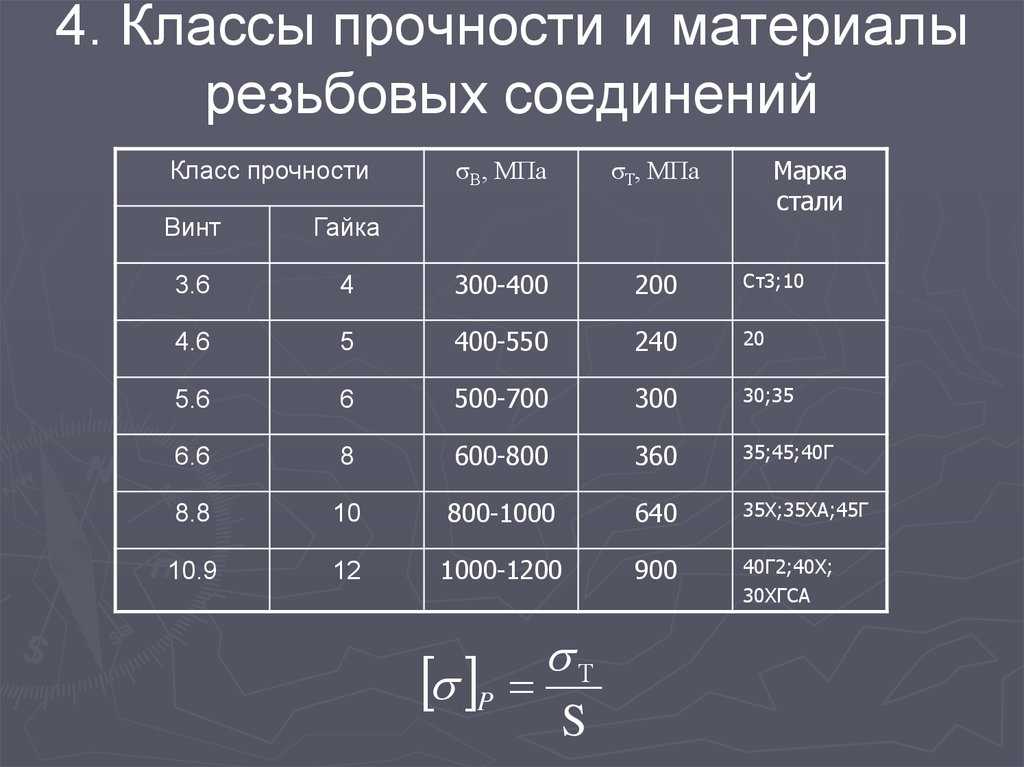
Высокие классы прочности и их расшифровка
Согласно международной классификации резьбовых метизов, к высокопрочным болтам, винтам, шпилькам относятся изделия, имеющие цифровую маркировку классов прочности 8.8, 9.8, 10.9, 12.9, а к сверхпрочным – 14.9. Это важнейшая из характеристик, которая обязательно учитывается в любом проекте. Чем выше эти значения, тем прочнее, выносливее, качественнее и соответственно дороже метиз.
Чем выше эти значения, тем прочнее, выносливее, качественнее и соответственно дороже метиз.
Первая цифра указывает на предельную нагрузку на растяжение, при которой крепеж разорвется. Эта величина называется пределом прочности на разрыв, определяется как одна сотая от номинального временного сопротивления, выражается в МПа или Н/мм².
Например, для болта 10.9 она равняется: 10 / 0,01 = 1000 МПа (Н/мм²).
Вторая цифра говорит нам о напряжении, при котором крепеж необратимо деформируется при изгибе, а называется этот параметр – предел текучести. Определяется умножением первой цифры на вторую и на 10.
Например, для того же болта 10.9 он равен: 10х9х10 = 900 МПа (Н/мм²).
При расчете соединения для заданной нагрузки значение предела текучести умножают на коэффициент 1/2 или 1/3 для обеспечения 2-х или 3-кратного прочностного запаса.
Марки сталей и особенности изготовления крепежа высокой прочности
Крепежные изделия классов от 8. 8 до 14.9, включая болты для автомобильной промышленности, производятся из конструкционных среднеуглеродистых сталей, легированных упрочняющими добавками. Эксплуатационные свойства крепежа определяются двумя факторами:
8 до 14.9, включая болты для автомобильной промышленности, производятся из конструкционных среднеуглеродистых сталей, легированных упрочняющими добавками. Эксплуатационные свойства крепежа определяются двумя факторами:
Самые популярные марки: 35, 40, 40Х Селект, 38ХА, 30ХГСА, 35ХГСА, 40ХН2МА, 38ХГНМ. Реже используют слаболегированные борсодержащие стали марок 12Г1Р, 20Г2Р, 30-35Г1Р. Стали, легированные бором, обладают благоприятным сочетанием прочностных и пластических свойств, но из-за некоторых технологических трудностей при их выплавке, их внедрение в метизное производство сдерживается.
Исходное сырье поступает на производство в виде стержней или проволоки. Болты формируют методом холодной штамповки под давлением на высадочных автоматах, затем на них наносят резьбу на накатных автоматах. Для придания готовым изделиям высоких прочностных характеристик, эксплуатационной надежности и устранения хрупкости их подвергают термическому упрочнению путем нагревания в закалочной печи и последующему отпуску (охлаждению).
Таблица 1. Марки сталей, рекомендованные для изготовления болтов, винтов, шпилек высоких классов прочности.
|
Класс прочности |
8.8 |
10.9 |
12.9 |
|
Марка стали |
Ст.35, Ст.35Х, Ст.38ХА, Ст.40Х, Ст.20Г2Р |
Ст.35Х, Ст.38ХА, Ст.45Г, Ст.40Г2, СТ.40Х, Ст.40Х Селект Ст.30ХГСА, Ст.35ХГСА |
Ст.30ХГСА, Ст.35ХГСА, Ст.40ХНМА |
|
Граница прочности, МПа |
800…830 |
1000…1040 |
1200…1220 |
|
Граница текучести, МПа |
640.  ..660 ..660
|
900…940 |
1080…1100 |
|
Твердость по Бринеллю, НВ |
242…318 |
304…361 |
366…414 |
Стандарты ГОСТ и DIN на высокопрочный крепеж
Сегодня “высокопрочка” поступает на рынок от отечественных, европейских и азиатских производителей. И если качество китайского крепежа вызывает недоверие у потребителей, то российский и европейский продукт пользуется большим спросом. Во многих зарубежных нормативах DIN, EN прописано использование болткомплектов (болт, гайка, шайба в сборе) от одного производителя. В наших документах нет таких правил. Нет в них и требований по виду защитного покрытия, тогда как европейские метизы оцинковываются, как правило, горячим методом.
Таблица 2. Стандарты на высокопрочный крепеж в России и Европе.
|
Национальные стандарты РФ |
Европейские стандарты |
|
ГОСТ Р 52643-2006 Общие технические условия |
DIN EN 14399-1:2006 Общие требования |
|
ГОСТ Р 52644-2006 (ИСО 7411:1987) Болты |
DIN EN 14399-2:2006 Проверка пригодности к предварительным натяжениям |
|
ГОСТ Р 52645-2006 (ИСО 4775:1984) Гайки |
DIN EN 14399-4:2006 Гарнитуры из болтов и гаек. Система HV |
|
ГОСТ Р 52646-2006 (ИСО 7415:1984) Шайбы |
DIN EN 14399-5:2006 Шайбы |
|
|
DIN EN 14399-6:2006 Шайбы с фаской |
Основные виды высокопрочных болтов, винтов и шпилек, используемые в России строительными компаниями и машиностроительными предприятиями:
-
ГОСТ 52644, ГОСТ 22353, DIN 6914, ISO 7412
Перечисленные стандарты распространяются на шестигранные болты высокой прочности (БВП), разработанные для использования при монтаже строительных металлоконструкций из стали, а также в мостостроении и тяжелом машиностроении для создания высоконагруженных соединений. Размерный ряд ограничен диаметрами М16 – М48. Выпускаются в климатическом исполнении «У» и «ХЛ»
Размерный ряд ограничен диаметрами М16 – М48. Выпускаются в климатическом исполнении «У» и «ХЛ»
-
ГОСТ 7798, ГОСТ 7805, DIN 933, DIN 931, ISO 4014, ISO 4017
Стандарты на БВП с нормальной шестигранной головкой, полной и неполной резьбой, используемые для скрепления деталей и элементов конструкций в автомобилестроении, других производственных и строительных областях. Имеют широкий диапазон диаметров от М3 до М64. Выпускаются без покрытия или оцинкованными разными способами (гальваническим, термодиффузионным, горячим). Аналоги с мелкой резьбой – DIN 960, DIN 961.
-
DIN 912, DIN 6912, ГОСТ 11738, ISO 4762
По данным стандартам изготавливаются винты с внутренним шестигранником и головкой в форме цилиндра, которые используются в самых разных отраслях промышленности. Винты DIN, ISO имеют более длинный перечень размеров, выпускаются только в высоких классах прочности 8. 8, 10.9, 12.9, тогда как ГОСТ допускает их изготовление и низких классов, но ограниченного диаметра от М3 до М36.
8, 10.9, 12.9, тогда как ГОСТ допускает их изготовление и низких классов, но ограниченного диаметра от М3 до М36.
-
DIN 444, ГОСТ 3033-79
Настоящие стандарты описывают требования к откидным винтам (болтам) с ушком и метрической резьбой диаметром от М5 до М36, которые применяются в станочных приспособлениях, в качестве детали соединения в машиностроении или совместно со строительными анкерами с внутренней резьбой.
-
DIN 975, DIN 976
Данные стандарты регламентируют размеры, длину, шаг и тип резьбы резьбовых шпилек (штанг). К высокопрочным относят шпильки с границей прочности 800…1200 Нм. Они имеют фиксированную длину 1000 или 2000 мм, диаметр от М4 до М48. Применяются в машиностроении, строительной отрасли, при монтаже кабельно-трубных эстакад.
Все вышеперечисленные метизы изготавливаются в черном исполнении (под покраску) и оцинкованном различными способами.
Усилие затяжки высокопрочных болтов
При установке БВП следует учитывать характер монтажного соединения: сдвигоустойчивое (фрикционное) или с несущими болтами. В первом случае соединение затягивается до требуемой (проектной) величины динамометрическими ключами для обеспечения сил трения между соединяемыми элементами. Момент затяжки – это усилие, приложенное к гайке или головке винта и создающее в теле метиза контролируемое усилие натяжения. Расчетные значения момента закручивания и усилия предварительной затяжки болтов сведены в специальные справочные таблицы.
Таблица 3. Нормы затяжки болтов (коэффициент трения 0,14)
|
Диаметр резьбы, мм |
Шаг резьбы, Р |
Площадь сечения As, мм |
Усилие предварительной затяжки Q, кН |
Крутящий момент Мкр, кН | ||||
|
8.  8 8
|
10.9 |
12.9 |
8.8 |
10.9 |
12.9 | |||
|
М4 |
0,7 |
8,78 |
4,3 |
6,3 |
7,4 |
3,3 |
4,8 |
5,6 |
|
М5 |
0,8 |
14,2 |
7 |
10,3 |
12 |
6,5 |
9,5 |
11,2 |
|
М6 |
1 |
20,1 |
9,9 |
14,5 |
17 |
11,3 |
16,5 |
19,3 |
|
М8 |
1,25 |
36,6 |
8,1 |
26,6 |
31,1 |
27,3 |
40,1 |
46,9 |
|
М10 |
1,5 |
58 |
28,8 |
42,2 |
49,4 |
54 |
79 |
93 |
|
М12 |
1,75 |
84,3 |
41,9 |
61,5 |
72 |
93 |
137 |
160 |
|
М14 |
2 |
115 |
57,5 |
84,4 |
98,8 |
148 |
218 |
155 |
|
М16 |
2 |
157 |
78,8 |
115,7 |
135,4 |
230 |
338 |
395 |
|
М18 |
2,5 |
193 |
99 |
141 |
165 |
329 |
469 |
549 |
|
М20 |
2,5 |
245 |
127 |
181 |
212 |
464 |
661 |
773 |
|
М22 |
2,5 |
303 |
158 |
225 |
264 |
634 |
904 |
1057 |
|
М24 |
3 |
353 |
183 |
260 |
305 |
798 |
1136 |
1329 |
|
М27 |
3 |
459 |
240 |
342 |
400 |
1176 |
1674 |
1959 |
|
М30 |
3,5 |
561 |
292 |
416 |
487 |
1597 |
2274 |
2662 |
|
М33 |
3,5 |
694 |
363 |
517 |
605 |
2161 |
3078 |
3601 |
|
М36 |
4 |
817 |
427 |
608 |
711 |
2778 |
3957 |
4631 |
|
М39 |
4 |
976 |
512 |
729 |
853 |
3597 |
5123 |
5994 |
Где и как маркируется прочность на изделии?
Маркировка высокопрочных болтов
Требования к обозначению прочности болтов, винтов, шпилек прописаны в ГОСТ 1759. 0-87 (для диаметров до 48 мм) и ГОСТ 18126-94 (для диаметров от 48 мм). Знаки маркировки хорошо читаются на метизах, поэтому потребитель может легко определить класс прочности крепежа, с которым имеет дело.
0-87 (для диаметров до 48 мм) и ГОСТ 18126-94 (для диаметров от 48 мм). Знаки маркировки хорошо читаются на метизах, поэтому потребитель может легко определить класс прочности крепежа, с которым имеет дело.
Болты с шестигранными головками, винты с цилиндрическими головками под внутренний шестигранник и резьбовые шпильки маркируются по прочности цифровым кодом 8.8, 10.9, 12.9, 14.9 (с разделительной точкой или без нее), а шестигранные гайки – 9, 10, 12, 14. Это нестираемые выпуклые или углубленные клейма, нанесенные на головку болтов сбоку или сверху.
Маркировка классов прочности на крепеже малых диаметров может выполняться по системе циферблата.
Таблица 4. Циферблатная маркировка прочности болтов
Классы прочности шпилек отображаются, как правило, на их торцевой поверхности. Если шпилька имеет неполную резьбу, то цифровой код может быть нанесен на ее гладкую часть. Для шпилек также может применяться маркировка цветом (желтый для класса 8. 8, белый для 10.9) или условными обозначением, нанесенным на торец:
8, белый для 10.9) или условными обозначением, нанесенным на торец:
Маркировка высокопрочных шпилек
Критерии выбора высокопрочного крепежа
-
Тип, размер и класс прочности крепежных изделий должен соответствовать проектной документации. -
Замену одних деталей крепления на другие вправе производить только специалист после проведения соответствующих нормативных расчетов. -
Крепежные изделия должны быть равны или превышать по прочности материал конструкции. -
Несущая способность БВП должна соответствовать поставленной задаче, а антикоррозийная защита соответствовать эксплуатационным условиям. -
Необходимо учитывать совместимость металла конструкции и метиза во избежание гальванической коррозии. -
Не стоит покупать высокопрочные метизы у поставщиков с сомнительной репутацией. -
Перед покупкой желательно провести визуальный контроль для выявления возможных дефектов.
Высокопрочные болты, винты и шпильки – это особый вид метизов, на которые возлагается большая ответственность за надежность и долговечность автомобилей, станков, грузоподъемной техники, мостов, эстакад, портовых сооружений, спортивных арен, других масштабных строительных объектов. Компания «Крепком» сотрудничает только с ответственными производителями, на предприятиях которых исследуется состав поступающего сырья, а каждая партия готового крепежа проходит испытания, установленные действующими стандартами. Кроме того, в собственной лаборатории «Крепком» осуществляется входной контроль поступающей продукции на соответствие стандартным прочностным показателям.
Высокопрочка
Обновлено: 29.09.2020 13:57:13
Поставить оценку
Успешно отправлено, Спасибо за оценку!
Нажмите, чтобы поставить оценку
Таблицы усилий затяжки болтов динамометрическим ключом.
 Таблицы для динамометрического ключа
Таблицы для динамометрического ключа
Момент затяжки – это усилие, которое прикладывается к резьбовому соединению при его завинчивании. Если закрутить крепеж с меньшим усилием, чем это необходимо, то, под воздействием вибраций, резьбовое соединение может раскрутиться, не обеспечивая нужную герметичность между скрепляемыми деталями, что может привести к тяжелым последствиям. Наоборот, если приложить к метизу большее усилие, чем требуется, произойдет разрушение резьбового соединения или скрепляемых деталей, например, может произойти срыв резьбы или появление трещин в деталях.
Для каждого размера и класса прочности резьбового соединения указаны определенные моменты затяжки. Все значения занесены в специальную таблицу усилий для затяжки динамометрическим ключом. Обычно, класс прочности болта указывается на его головке.
Классы прочности для метрических болтов
Класс прочности указывается цифрами на головке.
Классы прочности для дюймовых болтов
Информация о прочности выполнена в виде насечек на головке.
Резьбовые соединения затягивают стрелочным, предельным или цифровым динамометрическим ключом.
Таблица усилий затяжки метрических болтов
Усилие указано в Ньютон-метрах.
Таблица усилий затяжки дюймовых болтов
|
|
|
|
|
| ||||||||
|
|
|
|
|
| ||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для закручивания резьбовых соединений в соответствии с данными таблиц необходимо использовать специальный инструмент — динамометрический ключ.
Ниже представлены популярные модели ключей, диапазоны которых перекрывают большинство значений определенных моментов затяжки. Максимальную точность передачи крутящего момента обеспечивают электронные динамометрические ключи.
Максимальную точность передачи крутящего момента обеспечивают электронные динамометрические ключи.
Таблицы моментов затяжки колес
Примерные значения для легковых автомобилей
Для легковых автомобилей используют ключи с присоединительным квадратом 1/2. Самыми популярными ключами являются модели с затяжкой до 200-210 Нм, например, ключи с диапазоном 28-210 или 42-210. Ниже представлены варианты подобных ключей.
Примерные значения для грузовых автомобилей и автобусов
Для коммерческого транспорта используют ключи с присоединительным квадратом 1/2, 3/4 и даже 1 дюйм. Ниже представлены варианты ключей для автобусов, коммерческих и грузовых автомобилей.
Порядок затяжки
Компания AIST располагает широким ассортиментом профессиональных ключей для выполнения различных работ с резьбовыми соединениями. У нас всегда возможно подобрать необходимый динамометрический ключ для автомобиля, как для легкового, так и для грузового транспортного средства.
У нас всегда возможно подобрать необходимый динамометрический ключ для автомобиля, как для легкового, так и для грузового транспортного средства.
*Значения таблиц моментов затяжки носят информационный характер, без ссылки на какой-либо ГОСТ.
Полезные статьи:
- Виды динамометрических ключей
- Как пользоваться динамометрическим ключом
- Как выбрать динамометрический ключ
Распределение силы болтового соединения | МеханиКальк
Калькулятор
ИнструкцииСправочник по проверке
Калькулятор распределения силы
ПРИМЕЧАНИЕ. Эта страница использует JavaScript для форматирования уравнений для правильного отображения. Пожалуйста, включите JavaScript.
Массив болтов представляет собой расположение болтовых соединений, обычно четырех или более, которые соединяют два или более компонентов вместе. При проектировании массива болтов важно понимать нагрузки, которым эта схема должна противостоять в процессе эксплуатации, а также то, как эти приложенные нагрузки будут распределяться между отдельными болтовыми соединениями в этой схеме. После расчета осевых и сдвигающих нагрузок для отдельных болтовых соединений в схеме можно проанализировать отдельные соединения, как описано в нашем справочнике по анализу болтовых соединений.
При проектировании массива болтов важно понимать нагрузки, которым эта схема должна противостоять в процессе эксплуатации, а также то, как эти приложенные нагрузки будут распределяться между отдельными болтовыми соединениями в этой схеме. После расчета осевых и сдвигающих нагрузок для отдельных болтовых соединений в схеме можно проанализировать отдельные соединения, как описано в нашем справочнике по анализу болтовых соединений.
В следующих разделах подробно описывается методология преобразования сил и моментов, приложенных к массиву болтов, в осевые и сдвигающие нагрузки, действующие на отдельные болтовые соединения в массиве.
Содержимое
Обзор и обсуждение
Распределение сил и моментов по массиву болтов аналогично анализу балки или вала. Приложенные нагрузки переносятся в центр тяжести рисунка (аналогично нейтральной оси балки или вала). Затем силы и моменты в центре тяжести разлагаются на осевые и сдвигающие силы, действующие на отдельные болтовые соединения. Осевые силы распределяются по массиву болтов в зависимости от площади массива A и моментов инерции I c.x и I c.y . Точно так же поперечные силы распределяются на основе площади шаблона A и полярного момента инерции I cp .
Осевые силы распределяются по массиву болтов в зависимости от площади массива A и моментов инерции I c.x и I c.y . Точно так же поперечные силы распределяются на основе площади шаблона A и полярного момента инерции I cp .
Обратите внимание, что мы сохраняем различие в том, что силы распределяются на отдельные болтовые соединения , а не на отдельные болты . Причина этого в том, что не вся нагрузка, приложенная к болтовому соединению, фактически воспринимается болтом, как обсуждается здесь.
В следующих двух разделах обсуждаются два общих условия нагружения, за которыми следует обсуждение обобщенного подхода к распределению приложенных нагрузок по схеме болтов.
Внецентренная сдвигающая нагрузка в плоскости
На рисунке ниже показан шаблон с внецентренной сдвигающей нагрузкой, приложенной в плоскости шаблона. Нагрузка эксцентрична, потому что она не действует через центроид шаблона. Следовательно, он создает крутящий момент вокруг оси Z (перпендикулярной плоскости шаблона), который будет стремиться повернуть шаблон вокруг его центра тяжести. В этом случае болты нагружаются только сдвигом (без осевых нагрузок), а сдвигающие нагрузки обусловлены комбинацией прямой силы сдвига и индуцированного момента. Нагружение этого типа аналогично валу при комбинированной нагрузке сдвига и кручения.
В этом случае болты нагружаются только сдвигом (без осевых нагрузок), а сдвигающие нагрузки обусловлены комбинацией прямой силы сдвига и индуцированного момента. Нагружение этого типа аналогично валу при комбинированной нагрузке сдвига и кручения.
Внеплоскостная внецентренная сдвигающая нагрузка
На рисунке ниже показан шаблон с внецентренной поперечной нагрузкой, приложенной вне плоскости шаблона. В то время как эта приложенная нагрузка проходит над центроидом в плоскости X-Y, ее линия действия смещена от центроида в направлении Z. Следовательно, приложенная поперечная нагрузка создает изгибающий момент относительно оси X, что приводит к осевой нагрузке на болты.
Существует несколько стандартных подходов к распределению осевых нагрузок между болтами в подобном случае, каждый из которых включает расчет момента инерции шаблона относительно некоторой оси изгиба, а затем использование (Mr/I)·A для распределения нагрузок. (Следует отметить, что если все болты в схеме имеют одинаковый размер, то (Mr/I)·A упрощается до Mr/Σ r 2 ). Ключевое отличие стандартных подходов заключается в выборе точки, вокруг которой предполагается разворот паттерна:
Ключевое отличие стандартных подходов заключается в выборе точки, вокруг которой предполагается разворот паттерна:
- Один из подходов заключается в проверке геометрии компонента и предположении, что шаблон будет «наклоняться» относительно некоторой разумной точки, скажем, основания кронштейна на рисунке выше.
- Другой подход состоит в том, чтобы рассматривать эту проблему, как если бы шаблон был изгибающейся балкой, и вычислять соответствующее положение нейтральной оси.
- Методология, изложенная в «Руководстве по стальным конструкциям» AISC, признает, что на сжатой стороне балки сжатая площадь равна площади контакта компонентов ниже нейтральной оси. Со стороны натяжения балки натянуты только болты. Положение нейтральной оси находится с помощью итерационной процедуры, с помощью которой предполагаемое положение нейтральной оси изменяется до тех пор, пока момент инерции болтов, находящихся в напряжении над нейтральной осью, не станет равным моменту инерции сжатых пластин ниже нейтральная ось.

- В более простом подходе учитываются только площади болтов и предполагается, что нейтральная ось балки лежит в центре тяжести массива болтов.
- Методология, изложенная в «Руководстве по стальным конструкциям» AISC, признает, что на сжатой стороне балки сжатая площадь равна площади контакта компонентов ниже нейтральной оси. Со стороны натяжения балки натянуты только болты. Положение нейтральной оси находится с помощью итерационной процедуры, с помощью которой предполагаемое положение нейтральной оси изменяется до тех пор, пока момент инерции болтов, находящихся в напряжении над нейтральной осью, не станет равным моменту инерции сжатых пластин ниже нейтральная ось.
Важно понимать, что по мере того, как предполагаемое место поворота перемещается дальше от схемы, осевые нагрузки на болты уменьшаются. Этот факт справедлив для всех изложенных выше подходов, но его легче всего распознать при рассмотрении упрощенного случая, когда осевые нагрузки прямо пропорциональны Mr / Σ r 2 . Напомним, что r — это расстояние между точкой поворота и интересующим болтом. По мере увеличения r влияние члена r 2 в знаменателе опережает влияние члена r в числителе. Следовательно, наиболее консервативный подход состоит в том, чтобы считать, что паттерн вращается вокруг своего центроида.
Обобщенный подход
Если вы решите применить консервативный подход, переводя всю приложенную нагрузку в центр тяжести разболтовки, тогда будет легко обобщить анализ любой разболтовки с любой приложенной нагрузкой, как показано на рисунке ниже.
Шаги для распределения приложенных сил и моментов к отдельным болтовым соединениям в схеме:
- Расчет соответствующих свойств шаблона (площадь, центр тяжести, моменты инерции).
- Перенесите все приложенные силы и моменты в центр тяжести массива.
- Рассчитайте осевые и сдвигающие нагрузки, действующие на отдельные болтовые соединения в образце.
Подробная информация о выполнении каждого из этих шагов представлена в следующих разделах.
Свойства схемы расположения болтов
Те же свойства, которые требуются при анализе балки или вала, также требуются при распределении усилий по массиву болтов. Следует отметить, что уравнения, представленные в этом разделе для расчета свойств шаблона, не требуют, чтобы болты в шаблоне были одного размера.
Область расположения болтов
Общая площадь всех болтов в схеме должна быть рассчитана для распределения прямых сил между болтами:
где A i — площадь растягивающего напряжения отдельного болта.
Центроид схемы расположения болтов
Точно так же, как напряжения изгиба в балке и напряжения кручения в валу сосредоточены вокруг нейтральной оси, моменты на схеме болтов будут стремиться повернуть схему вокруг ее центра масс. Расположение центроида шаблона рассчитывается как:
где А i — это площадь болта, а x i и y i — расположение болтов по осям x и y соответственно.
Следует отметить, что этот расчет является прямым аналогом расчета центроида поперечного сечения.
Моменты инерции болтовой схемы
Моменты инерции массива болтов указывают на способность массива сопротивляться изгибающим моментам. Мы консервативно предполагаем, что моменты будут иметь тенденцию вызывать вращение паттерна вокруг его центра тяжести, поэтому интерес представляют моменты инерции относительно центроида паттерна. Центроидальные моменты инерции рассчитываются как:
| центральный момент инерции относительно оси X | |
| центральный момент инерции относительно оси Y |
где A i — площадь болта, а r c. x,i и r c.y,i — расстояния болта по осям x и y от центра масс шаблона соответственно.
x,i и r c.y,i — расстояния болта по осям x и y от центра масс шаблона соответственно.
Полярный момент инерции шаблона указывает на способность шаблона сопротивляться крутящим моментам (т. Е. Моментам относительно оси Z, перпендикулярной плоскости шаблона), и он рассчитывается как:
где r c.xy,i — кратчайшее расстояние между болтом и центром тяжести и рассчитывается как
.
Следует отметить, что эти расчеты прямо аналогичны расчету момента инерции поперечного сечения и полярного момента инерции поперечного сечения.
Силы и моменты в центроиде
Как обсуждалось ранее, все приложенные силы и моменты переносятся в центр тяжести массива болтов. Как показано на рисунке ниже, любое количество сил может быть приложено к массиву болтов в любом месте.
Силы в центре тяжести рассчитываются как сумма всех приложенных сил:
Моменты в центроиде рассчитываются как сумма всех приложенных моментов плюс сумма векторного произведения каждой приложенной силы с вектором от центроида к местоположению этой приложенной силы:
В приведенных выше уравнениях полосы над переменными указывают на то, что они являются векторами. Переменная F представляет собой вектор силы, состоящий из составляющих силы в каждом направлении: F x , F y и F z . Точно так же M представляет собой вектор момента, состоящий из моментов относительно каждой оси. R представляет собой вектор местоположения, определяющий местоположение приложенной силы относительно центра тяжести шаблона. Вектор местоположения R указывает от на центроид до на местоположение приложенной силы.
Переменная F представляет собой вектор силы, состоящий из составляющих силы в каждом направлении: F x , F y и F z . Точно так же M представляет собой вектор момента, состоящий из моментов относительно каждой оси. R представляет собой вектор местоположения, определяющий местоположение приложенной силы относительно центра тяжести шаблона. Вектор местоположения R указывает от на центроид до на местоположение приложенной силы.
Силы на отдельных болтовых соединениях
После того, как свойства шаблона известны и приложенные силы и моменты переведены в центр тяжести шаблона, можно рассчитать осевые и сдвигающие усилия на отдельных болтовых соединениях. На рисунке ниже показано отдельное болтовое соединение с приложенной осевой и поперечной нагрузкой:
Осевые силы
Осевые силы являются результатом действия прямой силы в направлении Z, F c.z , центрального момента относительно оси X, M c. x , и центрального момента относительно оси Y, M c.y . Эти силы и моменты показаны красными стрелками на рисунке ниже и действуют в центре массива болтов. Синие стрелки указывают осевые силы реакции на каждом болтовом соединении. Каждая синяя стрелка представляет собой составляющую осевой силы, обусловленную либо прямой силой по оси Z, либо центральным моментом относительно X, либо центральным моментом относительно Y. Расчет этих компонентов силы реакции является предметом данного раздела.
x , и центрального момента относительно оси Y, M c.y . Эти силы и моменты показаны красными стрелками на рисунке ниже и действуют в центре массива болтов. Синие стрелки указывают осевые силы реакции на каждом болтовом соединении. Каждая синяя стрелка представляет собой составляющую осевой силы, обусловленную либо прямой силой по оси Z, либо центральным моментом относительно X, либо центральным моментом относительно Y. Расчет этих компонентов силы реакции является предметом данного раздела.
Прямая сила в направлении Z, F c.z , распределяется между отдельными болтовыми соединениями в соответствии с жесткостью болтов. Поскольку предполагается, что все болты сделаны из одинакового материала и имеют одинаковую длину, жесткость зависит только от площади растягивающего напряжения болта. Осевая сила на болтовом соединении из-за прямой силы по оси Z рассчитывается как:
где А — площадь рассматриваемого болта. Если площади болтов одинаковые, приведенное выше уравнение упрощается до P z. FZ = F z.z /n, где n — количество болтов в схеме.
FZ = F z.z /n, где n — количество болтов в схеме.
Осевые силы на болте из-за моментов относительно осей X и Y рассчитываются как:
| осевое усилие на болт из-за MX вокруг центра тяжести | |
| осевое усилие на болт из-за MY относительно центроида |
где M c.x и M c.y — центральные моменты относительно осей X и Y, r c.x и r c.y — расстояния болтов от центра тяжести в направлениях X и Y, а I c.x и I c.y — моменты инерции шаблона относительно осей X и Y.
Если площади болтов одинаковы, приведенные выше уравнения упрощаются до:
Полная осевая сила, действующая на болт, представляет собой сумму составляющих осевой силы:
P осевой = P z.FZ + P z.MX + P z.MY
Силы сдвига
Силы сдвига являются результатом действия прямой силы в направлении X, F c. x , прямой силы в направлении Y, F c.y , и центроидального момента относительно оси Z, M c.z , как показано на рисунке ниже:
x , прямой силы в направлении Y, F c.y , и центроидального момента относительно оси Z, M c.z , как показано на рисунке ниже:
Прямые силы в направлениях X и Y, F c.x и F c.y , соответственно, делятся между болтами по жесткости болтов. Поскольку предполагается, что все болты сделаны из одинакового материала и имеют одинаковую длину, жесткость зависит только от площади. Реакции сдвига на болте из-за прямых сил в X- и Y- рассчитываются как:
| X-реакция на болт из-за прямого усилия в X | |
| Y-реакция на болт из-за прямого усилия в Y |
где А — площадь рассматриваемого болта. Если площади болтов одинаковые, приведенные выше уравнения упрощаются до P x.FX = F c.x /n и P y.FY = F c.y /n, где n — количество болтов в шаблон.
Реакция на сдвиг болта из-за момента относительно оси Z рассчитывается как:
где M c. z — центральный момент относительно оси Z, а I c.p — полярный момент инерции модели. Значение г c.xy — это кратчайшее расстояние между болтом и центром тяжести, которое рассчитывается как
z — центральный момент относительно оси Z, а I c.p — полярный момент инерции модели. Значение г c.xy — это кратчайшее расстояние между болтом и центром тяжести, которое рассчитывается как
.
Реакция сдвига P xy.MZ затем разлагается на компоненты X и Y в зависимости от угла θ (см. рисунок выше):
| P x.MZ = P xy.MZ · sinθ | Х-реакция на болте из-за MZ относительно центроида |
| P y.MZ = −P xy.MZ · cosθ | Y-реакция на болте из-за MZ относительно центроида |
Значение θ представляет собой угол между положением болта и положительной осью X и рассчитывается как θ = tan -1 (r c.y /r c.x ).
Полная реакция сдвига на болт рассчитывается как векторная сумма X-компонент плюс Y-компонент:
Что дальше?
Теперь, когда рассчитаны осевые и сдвигающие усилия на отдельных болтовых соединениях, можно проанализировать напряжения в болтовых соединениях, как описано здесь.
PDH Classroom предлагает курс повышения квалификации, основанный на этой странице со справочной информацией о разболтовке. Этот курс можно использовать для выполнения кредитных требований PDH для поддержания вашей лицензии PE.
Теперь, когда вы прочитали эту справочную страницу, заработайте за это признание!
Просмотреть курс сейчас:
Просмотреть курс
Каталожные номера
Барретт, Ричард Т., «Руководство по проектированию крепежа», справочная публикация НАСА 1228, 19.90.
Бикфорд, Джон, «Введение в конструкцию и поведение болтовых соединений», 4-е изд.
Брюн, Э.Ф., «Анализ и проектирование конструкций летательных аппаратов», июнь 1973 г.
Будинас-Нисбетт, «Машиностроение Шигли», 8-е изд.
Линдебург, Майкл Р., «Справочное руководство по машиностроению для экзамена PE», 13-е изд.
Ниу, Майкл С., «Анализ напряжений и размеры планера», октябрь 2011 г.

«Руководство по стальным конструкциям», Американский институт стальных конструкций (AISC), 14-е изд.
Расчет крутящего момента и силы для крепежа, болтов и винтов
Расчет крутящего момента и силы для конструкции крепежа, болтов и винтов — Engineers Edge
Технические данные по аппаратному обеспечению ISO
Технические данные по аппаратному обеспечению ANSI
Производитель поставщика оборудования
Сопротивление материалов
- Ниже приведены ссылки на технические ресурсы, инструменты, статьи и другие полезные данные.
- Если вы обнаружите какие-либо ошибки, упущения, неработающие ссылки, сообщите нам об этом — Обратная связь
- Вы хотите внести свой вклад в этот раздел? См. программу Premium Publisher
.
Следующие ресурсы по проектированию предназначены для проектирования винтов и болтов с надлежащим крутящим моментом, напряжением, деформацией, предварительным натягом и другими важными инженерными расчетными параметрами.
Калькулятор площади напряжения резьбы и формула
- Длина зацепления винтовой резьбы на. ИСО 965-1 Калькулятор, формула и таблица Длина зацепления сопрягаемой резьбы выбирается для использования полной прочности на растяжение болта до срезания и резьбы гайки.
- Обзор методов затяжки болтов
Формула и калькулятор момента трения головки болта или гайки пер. МИЛ-ХДБХ-60
Формулы и калькулятор напряжения при удлинении болта пер. MIL-HDBH-60 Микрометрический метод удлинения болта: Ниже пропорционального предела. удлинение болта прямо пропорционально осевому напряжению, т. е. удлинение увеличивается в той же пропорции, что и напряжение.
Болт Крепежная деталь Преднатяг Формулы и калькулятор напряжения при кручении пер. МИЛ-ХДБХ-60
- Формулы удлинения болта при повороте и калькулятор пер.
 МИЛ-ХДБХ-60
МИЛ-ХДБХ-60 Момент затяжки болтов в сборе для контактного напряжения прокладки пер. ASME PCC-1 Уравнения и калькулятор
- Таблица площади основания болта и напряжения при растяжении для метрической и дюймовой резьбы
- Формула удлинения болта и калькулятор пер. ASME PCC-1 Когда измерение удлинения болта (растяжение болта) выбрано в качестве используемого метода управления нагрузкой, требуемое удлинение болта рассчитывается в соответствии со следующим уравнением
- Резьба болтов, Марка, Прочность болтов, Калькулятор электронной таблицы Excel, Таблица рассчитана в соответствии с девятым изданием AISC
- Выдвижение группы схем расположения болтов Калькулятор электронных таблиц Excel, Калькулятор электронных таблиц Рассчитывается в соответствии с девятым изданием AISC
- Инженерные основы проектирования и анализа резьбовых крепежных изделий — требуется премиум-членство
- Расчет крутящего момента при сборке по ISO 68 и ISO 724
- Комбинированное удлинение резьбы и корпуса болта при предварительном натяге Формула и калькулятор Закручивая или поворачивая резьбу болта, мы пытаемся контролировать процесс затяжки посредством сил, приложенных к гайке, или движения гайки.

Зона напряжения винта 100 тысяч фунтов на квадратный дюйм и более
Зона напряжения болта менее 100 тысяч фунтов на квадратный дюйм
- Уравнение удлинения болта и калькулятор при осевом напряжении
Крепеж/резьба Площадь растяжения внешней резьбы Формула
Формула и расчет диаметра делительной окружности крепежа / резьбы
Формула и расчет площади сдвига крепежа/резьбы
- Руководство по проектированию крепежа — требуется премиум-членство
- Технический документ по проектированию и анализу резьбовых крепежных деталей (39 страниц, подробный инженерный анализ крутящего момента и усилий в крепежных элементах) Требуется бесплатное членство
- Соотношение между крутящим моментом, шагом резьбы и усилием зажима и калькулятором
- Соотношение между крутящим моментом болта и усилием зажима.
 Формула и калькулятор пер. ДЖИС Б 1083
Формула и калькулятор пер. ДЖИС Б 1083 - Зоны напряжения и сдвига метрической резьбы серии М
Минимальная формула зацепления резьбы и расчет ISO
- Сила, необходимая для зачистки резьбы болта Формула и калькулятор любой длины
- Сила, необходимая для зачистки болтовой резьбы Формула и калькулятор
- Уравнение площади напряжения ISO и калькулятор. Значения пробной нагрузки приведены в BS EN 20898-2:
- BS EN 20898-2 Значения пробной нагрузки — Грубая резьба
Минимальная длина резьбового зацепления Формула и расчеты в соответствии с FED-STD-h38/2B
- Влияние момента на круговое распределение болтов в соединении торцевой пластины
Площадь сдвига Внутренняя и внешняя резьба Формула и расчет в соответствии с FED-STD-h38/2B
- Расчет осевой силы винтовой передачи
- Сила, необходимая для зачистки болтовой резьбы Формула и калькулятор
- Обозначения резьбы и символы A-N
- Обозначения и символы резьбы N-Z
- Одноместный
Формула площади напряжения при растяжении резьбы и калькулятор Per. АСМЭ Б1.1
АСМЭ Б1.1 - Типовая диаграмма удлинения для обычных болтовых материалов Величина растяжения болта, которую вы хотите в своей конструкции конечного изделия, конечно же, будет определяться величиной предварительного натяга, который вы хотите получить в крепежном элементе.
- ANSI, ISO Обозначения резьбы и ссылки
- Характеристики прочности Стальные болты
- Система обозначения классов прочности стальных болтов и винтов
- ООН
Формулы и калькулятор для наружной резьбы - Винт
Формула резьбы и калькулятор для внутреннего унифицированного дюймового винта UN - Площадь сдвига резьбы для внешней и внутренней Формулы и калькулятор пер. АСМЭ Б1.1
.
Напряжение и сила отрыва резьбы
Напряжение вытягивания крепежного элемента с резьбовым отверстием
- Калькулятор вытягивания самонарезающего винта и крутящего момента
Таблицы стандартных размеров резьбы
Таблица моментов затяжки Стандартные размеры болтов SAE
Таблица моментов затяжки Стандартные размеры болтов Классы SAE 1–8
Таблица значений крутящего момента для болтов из нержавеющей стали
Калькулятор усилия зажима
Калькулятор усилия зажима
- Калькулятор предварительной нагрузки шпильки
- Уравнение предварительного натяжения болта и калькулятор
- Калькулятор усилия натяжения болта
- Таблица крутящего момента и натяжения болтов Болты SAE J429
- Изменение длины болта с несколькими диаметрами под действием осевой силы Формула и калькулятор
Преобразование крутящего момента
Преобразование крутящего момента
Руководство по расчету крутящего момента и рекомендации
- Руководство по расчету крутящего момента
- Типовая диаграмма удлинения для обычных болтовых материалов
Преобразование крутящего момента
Преобразование крутящего момента и эквиваленты
Расчет адаптера динамометрического ключа
Адаптер динамометрического ключа Расчет уменьшенной руки
Адаптер динамометрического ключа Расширенный расчет
Специальные приложения
Руководство по критериям проектирования болтовых и заклепочных соединений
Обзор применения гидравлических и пневматических динамометрических ключей
Тепловое расширение/сжатие крепежных изделий Приложение и уравнение
- Инженерные и расчетные уравнения с прессовой посадкой
- Расчеты с прессовой посадкой и уравнение
- Болт или штифт в уравнении одиночного сдвига и калькуляторе
- Болт или штифт в уравнении двойного сдвига и калькуляторе
- Формулы для расчетов напряжения и прочности и калькулятор для одиночных заклепок внахлестку
Формулы и калькулятор соединения внахлестку с двойной заклепкой для расчета напряжения и прочности
- Одинарное заклепочное соединение внахлестку с внутренней накладкой Формулы и калькулятор для расчета напряжения и прочности
- Соединение внахлестку с двойной заклепкой и внутренней накладкой Формулы и калькулятор для расчета напряжения и прочности.

- Грузоподъемность обычных болтов пер. BS449: Часть 2 Болт класса 4.6
- Грузоподъемность обычных болтов пер. BS449: Часть 2 Болт класса 6.8
- Грузоподъемность обычных болтов пер. BS449: Часть 2 Болт класса 8.8
Грузоподъемность обычных болтов на. BS449: Часть 2 Болт класса 10.9
Грузоподъемность обычных болтов на. BS449: Часть 2 Болт класса 12.9
- Калькулятор дизайна электронной таблицы Excel пер. BS: 449: для части 2 требуется активное членство Premium в Engineers Edge
- Резьбы с натягом Класс 5 Моменты затяжки, натяг и длина зацепления
- Резьба патрона лампы освещения Основание настольной лампы и резьба корпуса патрона. Резьба «Американский стандарт» для цоколя лампы и корпуса розетки спонсируется Американским обществом инженеров-механиков, Национальной ассоциацией производителей электрооборудования
- Таблица размеров резьбы свечей зажигания и резьбовых отверстий
Толстостенный цилиндр с прессовой или термоусадочной посадкой Уравнения натяга и давления и калькулятор Если два толстостенных цилиндра собираются методом горячей/холодной усадки или механической запрессовки, на границе раздела двух цилиндров возникает давление.

.



 6915
6915 5213
5213 4894
4894 8132
8132 3937
3937 0533
0533 4789
4789 5215
5215 1280
1280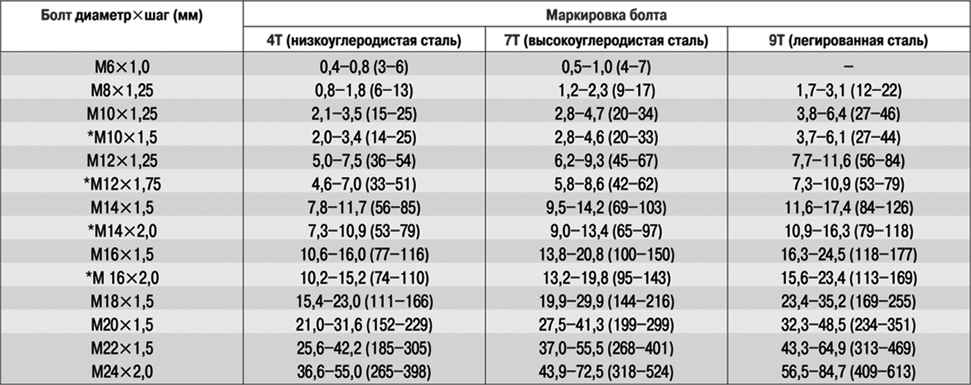 5005
5005

 МИЛ-ХДБХ-60
МИЛ-ХДБХ-60
 Формула и калькулятор пер. ДЖИС Б 1083
Формула и калькулятор пер. ДЖИС Б 1083 АСМЭ Б1.1
АСМЭ Б1.1
