Крепость болтов и моменты разрывов: Прочность болтов, расчет нагрузки | ГК ЕВРАЗИЯ

Моменты затяжки болтов — таблица

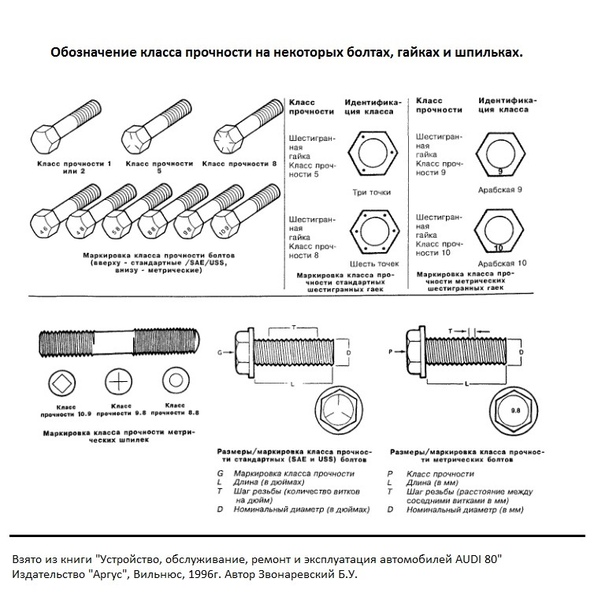
Болт или винт в сборе с гайкой соответствующего класса предназначены для создания соединений, которые можно затянуть до установленного значения пробной нагрузки болта без срыва резьбы.

Пробная нагрузка обычно составляет 85-95% от предела текучести и определяется как максимальное растягивающее усилие, которое можно приложить к болту и которое не приведет к его пластической деформации.





















Резьба/шаг мм.
Класс прочности болтов

4,6
5,8
8,8
10,9
12,9

Момент затяжки Н*м

5/0.8
2,1
3,5
5,5
7,8
9,3

6/1. 0
3,6
5,9
9,4
13,4
16,3

8/1.25
8,5
14,4
23,0
31,7
38,4

10/1.5
16,3
27,8
45,1
62,4
75,8

12/1.75
28,8
49,0
77,8
109,4
130,6

14/2.0
46,1
76,8
122,9
173,8
208,3

16/2. 0
71,0
118,1
189,1
265,9
319,7

18/2.5
98,9
165,1
264,0
370,6
444,5

20/2.5
138,2
230,4
369,6
519,4
623,0

22/2.5
186,2
311,0
497,3
698,9
839,0

24/3.0
239,0
399,4
638,4
897,6
1075,2

27/3. 0
345,6
576,0
922,6
1296,0
1555,2

30/3.5
472,3
786,2
1257,6
1766,4
2121,6

33/3.5
636,5
1056,0
1699,2
2380,8
2860,8

36/4.0
820,8
1363,2
2188,8
3081,6
3696,0

39/4.0
1056,0
1756,8
2820,2
3955,2
4742,4


Важное уточнение: любая таблица стандартизованных величин подходит только для новых болтов и гаек, которые ранее не были в использовании. Повторная эксплуатация резьбовых соединений приводит к увеличению трения в системе крепежа.

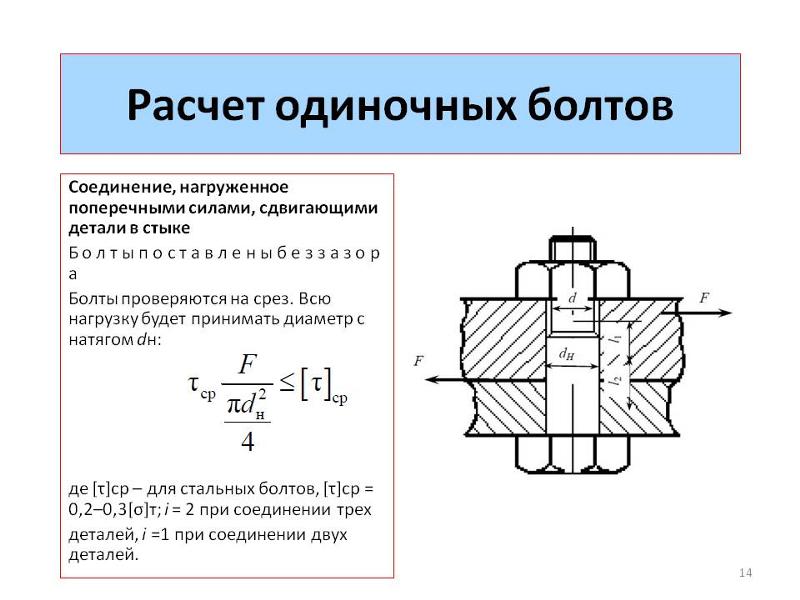
— Правильно затянутый болт немного растягивается, но не выходит за область своей упругой деформации. Находясь под постоянным напряжением, он сохраняет усилие затяжки и проявляет устойчивость к усталостному разрушению.

— Чрезмерно затянутый болт растягивается за границы упругого удлинения, что приводит к его необратимой пластической деформации и последующему разрушению.

— Недостаточно затянутый болт допускает незначительный зазор между соединяемыми заготовками, который будет увеличиваться после постоянной динамической нагрузки или других рабочих нагрузок. Зазор в соединении означает отсутствие предварительного натяжения, что неизбежно приведет к разрушению соединения.

Таблица 1. Моменты затяжки – винт (болт) без покрытия (черный), коэффициент трения 0,14.

Крупная резьба
























Диаметр резьбы
Класс прочности

5. 6
8.8
10.9
12.9

Nm
ft lb.
Nm
ft lb.
Nm
ft lb.
Nm
ft lb.

М3
0.6
0.44
1.37
1.01
1.92
1.42
2.3
1.7

М4
1.37
1.01
3.1
2.29
4.4
3. 05
5.25
3.87

М5
2.7
1.99
6.15
4.54
8.65
6.38
10.4
7.6

М6
4.6
3.3
10.5
7.7
15
11
18
13

М7
7.6
5.6
17.5
12.9
25
18.4
29
21. 3

М8
11
8.1
26
19
36
26
43
31

М10
22
16
51
37
72
53
87
64

М12
39
28
89
65
125
92
150
110

М14
62
45
141
103
198
146
240
117

М16
95
70
215
158
305
224
365
269

М18
130
95
295
217
420
309
500
368

М20
184
135
420
309
590
435
710
523

М22
250
184
570
420
800
590
960
708

М24
315
232
725
534
1020
752
1220
899

М27
470
346
1070
789
1510
1113
1810
1334

М30
635
468
1450
1069
2050
1511
2450
1806

М33
865
637
1970
1452
2770
2042
3330
2455

М36
1111
819
2530
1865
3560
2625
4280
3156

М39
1440
1062
3290
2426
4620
3407
5550
7093

Мелкая резьба














Диаметр резьбы
Класс прочности

8. 8
10.9
12.9

Nm
ft lb.
Nm
ft lb.
Nm
ft lb.

М8х1
27
19
38
28
45
33

М10х1,25
52
38
73
53
88
64

М12х1,25
95
70
135
99
160
118

М14х1,5
150
110
210
154
250
184

М16х1,5
225
165
315
232
380
280

М18х1,5
325
239
460
339
550
405

М20х1,5
460
339
640
472
770
567

М22х1,5
610
449
860
634
1050
774

М24х2
780
575
1100
811
1300
958

Таблица 2.

Моменты затяжки –  винт электролитически оцинкованный, коэффициент трения 0,125.

Крупная резьба
























Диаметр резьбы
Класс прочности

5.6
8.8
10.9
12.9

Nm
ft lb.
Nm
ft lb.
Nm
ft lb.
Nm
ft lb.

М3
0.56
0.41
1.28
0.94
1.8
1.33
2. 15
1.59

М4
1.28
0.94
2.9
2.14
4.1
3.02
4.95
3.65

М5
2.5
1.84
5.75
4.24
8.1
5.97
9.7
7.15

М6
4.3
3.1
9.9
7.3
14
10.3
16.5
12. 1

М7
7.7
5.2
16.5
12.1
23
16.9
27
19.9

М8
10.5
7.7
24
17.7
34
25
40
29

М10
21
15
48
35
67
49
81
59

М12
36
26
83
61
117
86. 2
140
103

М14
58
42
132
97
185
136
220
162

М16
88
64
200
147
285
210
340
250

М18
121
89
275
202
390
287
470
346

М20
171
126
390
287
550
405
660
486

М22
230
169
530
390
745
549
890
656

М24
295
217
675
497
960
708
1140
840

М27
435
320
995
733
1400
1032
1680
1239

М30
590
435
1350
995
1900
1401
2280
1681

М33
800
590
1830
1349
2580
1902
3090
2278

М36
1030
759
2360
1740
3310
2441
3980
2935

М39
1340
988
3050
2249
4290
3163
5150
3798

Мелкая резьба














Диаметр резьбы
Класс прочности

8. 8
10.9
12.9

Nm
ft lb.
Nm
ft lb.
Nm
ft lb.

М8х1
25
18
35
25
42
30

М10х1,25
49
36
68
50
82
60

М12х1,25
88
64
125
92
150
110

М14х1,5
140
103
195
143
235
173

М16х1,5
210
154
295
217
350
258

М18х1,5
305
224
425
313
510
376

М20х1,5
425
313
600
442
720
531

М22х1,5
570
420
800
590
960
708

М24х2
720
531
1000
737
1200
885

Возврат к списку

Распределение силы болтового соединения | МеханиКальк

Калькулятор

ИнструкцииСправочник по проверке

Калькулятор распределения силы

ПРИМЕЧАНИЕ. Эта страница использует JavaScript для форматирования уравнений для правильного отображения. Пожалуйста, включите JavaScript.

Массив болтов представляет собой расположение болтовых соединений, обычно четырех или более, которые соединяют два или более компонентов вместе. При проектировании массива болтов важно понимать нагрузки, которым эта схема должна противостоять в процессе эксплуатации, а также то, как эти приложенные нагрузки будут распределяться между отдельными болтовыми соединениями в этой схеме. После расчета осевых и сдвигающих нагрузок для отдельных болтовых соединений в схеме можно проанализировать отдельные соединения, как описано в нашем справочнике по анализу болтовых соединений.

В следующих разделах подробно описывается методология преобразования сил и моментов, приложенных к массиву болтов, в осевые и сдвигающие нагрузки, действующие на отдельные болтовые соединения в массиве.

Содержимое

Обзор и обсуждение

Распределение сил и моментов по массиву болтов аналогично анализу балки или вала. Приложенные нагрузки переносятся в центр тяжести рисунка (аналогично нейтральной оси балки или вала). Затем силы и моменты в центре тяжести разлагаются на осевые и сдвигающие силы, действующие на отдельные болтовые соединения. Осевые силы распределяются по массиву болтов в зависимости от площади массива A и моментов инерции I c.x и I c.y . Точно так же силы сдвига распределяются на основе площади шаблона A и полярного момента инерции I cp .

Обратите внимание, что мы сохраняем различие в том, что силы распределяются на отдельные болтовые соединения , а не на отдельные болты . Причина этого в том, что не вся нагрузка, приложенная к болтовому соединению, фактически воспринимается болтом, как обсуждается здесь.

В следующих двух разделах обсуждаются два общих условия нагружения, после чего следует обсуждение обобщенного подхода к распределению приложенных нагрузок по схеме болтов.

Внецентренная сдвигающая нагрузка в плоскости

На рисунке ниже показан шаблон с внецентренной сдвигающей нагрузкой, приложенной в плоскости шаблона. Нагрузка эксцентрична, потому что она не действует через центроид шаблона. Следовательно, он создает крутящий момент вокруг оси Z (перпендикулярной плоскости шаблона), который будет стремиться повернуть шаблон вокруг его центра тяжести. В этом случае болты нагружаются только сдвигом (без осевых нагрузок), а сдвигающие нагрузки обусловлены комбинацией прямой силы сдвига и индуцированного момента. Нагружение этого типа аналогично валу при комбинированной нагрузке сдвига и кручения.

Внеплоскостная внецентренная сдвигающая нагрузка

На рисунке ниже показан шаблон с внецентренной поперечной нагрузкой, приложенной вне плоскости шаблона. В то время как эта приложенная нагрузка проходит над центроидом в плоскости X-Y, ее линия действия смещена от центроида в направлении Z. Следовательно, приложенная поперечная нагрузка создает изгибающий момент относительно оси X, что приводит к осевой нагрузке на болты.

Существует несколько стандартных подходов к распределению осевых нагрузок между болтами в подобном случае, каждый из которых включает расчет момента инерции шаблона относительно некоторой оси изгиба, а затем использование (Mr/I)·A для распределения нагрузок. (Следует отметить, что если все болты в схеме имеют одинаковый размер, то (Mr/I)·A упрощается до Mr/Σ r 2  ). Ключевое отличие стандартных подходов заключается в выборе точки, вокруг которой предполагается разворот модели:

  • Один из подходов заключается в проверке геометрии компонента и предположении, что шаблон будет «наклоняться» относительно некоторой разумной точки, скажем, основания кронштейна на рисунке выше.
  • Другой подход состоит в том, чтобы рассматривать эту проблему, как если бы шаблон был изгибающейся балкой, и вычислять соответствующее положение нейтральной оси.

    • Методология, изложенная в «Руководстве по стальным конструкциям» AISC, признает, что на сжатой стороне балки сжатая площадь равна площади контакта компонентов ниже нейтральной оси. Со стороны натяжения балки натянуты только болты. Положение нейтральной оси находится с помощью итерационной процедуры, с помощью которой предполагаемое положение нейтральной оси изменяется до тех пор, пока момент инерции растянутых болтов над нейтральной осью не станет равным моменту инерции сжатых пластин ниже нейтральная ось.
    • В более простом подходе учитываются только площади болтов и предполагается, что нейтральная ось балки лежит в центре тяжести массива болтов.

Важно понимать, что по мере того, как предполагаемое место поворота перемещается дальше от схемы, осевые нагрузки на болты уменьшаются. Этот факт справедлив для всех изложенных выше подходов, но его легче всего распознать при рассмотрении упрощенного случая, когда осевые нагрузки прямо пропорциональны Mr / Σ r 2 . Напомним, что r — это расстояние между точкой поворота и интересующим болтом. По мере увеличения r влияние члена r 2 в знаменателе опережает влияние члена r в числителе. Следовательно, наиболее консервативный подход состоит в том, чтобы считать, что паттерн вращается вокруг своего центроида.

Обобщенный подход

Если вы решите применить консервативный подход к переводу всей приложенной нагрузки в центр тяжести раскладки болтов, тогда будет легко обобщить анализ любой расстановки болтов с любой приложенной нагрузкой, как показано на рисунке ниже.

Шаги для распределения приложенных сил и моментов к отдельным болтовым соединениям в схеме:

  1. Расчет соответствующих свойств шаблона (площадь, центр тяжести, моменты инерции).
  2. Перенесите все приложенные силы и моменты в центр тяжести массива.
  3. Рассчитайте осевые и сдвигающие нагрузки, действующие на отдельные болтовые соединения в образце.

Подробная информация о выполнении каждого из этих шагов представлена ​​в следующих разделах.

Свойства схемы расположения болтов

Те же свойства, которые требуются при анализе балки или вала, также требуются при распределении усилий по массиву болтов. Следует отметить, что уравнения, представленные в этом разделе для расчета свойств шаблона, не требуют, чтобы болты в шаблоне были одного размера.

Область расположения болтов

Общая площадь всех болтов в схеме должна быть рассчитана для распределения прямых сил между болтами:

где A i — площадь растягивающего напряжения отдельного болта.

Центроид схемы расположения болтов

Точно так же, как напряжения изгиба в балке и напряжения кручения в валу сосредоточены вокруг нейтральной оси, моменты на схеме болтов будут стремиться повернуть схему вокруг ее центра тяжести. Расположение центроида шаблона рассчитывается как:

где А i — это площадь болта, а x i и y i — расположение болтов по осям x и y соответственно.

Следует отметить, что этот расчет является прямым аналогом расчета центроида поперечного сечения.

Моменты инерции болтовой схемы

Моменты инерции массива болтов указывают на способность массива сопротивляться изгибающим моментам. Мы консервативно предполагаем, что моменты будут иметь тенденцию вызывать вращение паттерна вокруг его центра тяжести, поэтому интерес представляют моменты инерции относительно центроида паттерна. Центроидальные моменты инерции рассчитываются как:

центральный момент инерции относительно оси X
центральный момент инерции относительно оси Y

где A i — площадь болта, а r c. x,i и r c.y,i — расстояния болта по осям x и y от центра масс шаблона соответственно.

Полярный момент инерции шаблона указывает на способность шаблона сопротивляться крутящим моментам (т. Е. Моментам относительно оси Z, перпендикулярной плоскости шаблона), и он рассчитывается как:

где r c.xy,i — кратчайшее расстояние между болтом и центром тяжести и рассчитывается как

.

Следует отметить, что эти расчеты прямо аналогичны расчету момента инерции поперечного сечения и полярного момента инерции поперечного сечения.

Силы и моменты в центроиде

Как обсуждалось ранее, все приложенные силы и моменты переносятся в центроид массива болтов. Как показано на рисунке ниже, любое количество сил может быть приложено к массиву болтов в любом месте.

Силы в центре тяжести рассчитываются как сумма всех приложенных сил:

Моменты в центре тяжести рассчитываются как сумма всех приложенных моментов плюс сумма векторного произведения каждой приложенной силы с вектором от центра тяжести к местоположению этой приложенной силы:

В приведенных выше уравнениях полосы над переменными указывают на то, что они являются векторами. Переменная F представляет собой вектор силы, состоящий из составляющих силы в каждом направлении: F x , F y и F z . Точно так же M представляет собой вектор момента, состоящий из моментов относительно каждой оси. R представляет собой вектор местоположения, определяющий местоположение приложенной силы относительно центра тяжести шаблона. Вектор местоположения R указывает от на центроид до на местоположение приложенной силы.

Силы на отдельных болтовых соединениях

После того, как свойства шаблона известны и приложенные силы и моменты переведены в центр тяжести шаблона, можно рассчитать осевые и сдвигающие усилия на отдельных болтовых соединениях. На рисунке ниже показано отдельное болтовое соединение с приложенной осевой и поперечной нагрузкой:

Осевые силы

Осевые силы являются результатом действия прямой силы в направлении Z, F c.z , центрального момента относительно оси X, M c. x , и центрального момента относительно оси Y, M c.y . Эти силы и моменты показаны красными стрелками на рисунке ниже и действуют в центре массива болтов. Синие стрелки указывают осевые силы реакции на каждом болтовом соединении. Каждая синяя стрелка представляет собой составляющую осевой силы, обусловленную либо прямой силой по оси Z, либо центральным моментом относительно X, либо центральным моментом относительно Y. Расчет этих компонентов силы реакции является предметом данного раздела.

Прямая сила в направлении Z, F c.z , распределяется между отдельными болтовыми соединениями в соответствии с жесткостью болтов. Поскольку предполагается, что все болты сделаны из одинакового материала и имеют одинаковую длину, жесткость зависит только от площади растягивающего напряжения болта. Осевая сила на болтовом соединении из-за прямой силы по оси Z рассчитывается как:

где А — площадь рассматриваемого болта. Если площади болтов одинаковые, приведенное выше уравнение упрощается до P z. FZ = F z.z /n, где n — количество болтов в схеме.

Осевые силы на болте из-за моментов относительно осей X и Y рассчитываются как:

осевое усилие на болт из-за MX вокруг центра тяжести
осевое усилие на болт из-за MY относительно центроида

где M c.x и M c.y — центральные моменты относительно осей X и Y, r c.x и r c.y — расстояния болтов от центра тяжести в направлениях X и Y, а I c.x и I c.y — моменты инерции шаблона относительно осей X и Y.

Если площади болтов одинаковы, приведенные выше уравнения упрощаются до:

Полная осевая сила, действующая на болт, представляет собой сумму составляющих осевой силы:

P осевой = P z.FZ + P z.MX + P z.MY

Силы сдвига

Силы сдвига являются результатом действия прямой силы в направлении X, F c. x , прямой силы в направлении Y, F c.y , и центроидального момента относительно оси Z, M c.z , как показано на рисунке ниже:

Прямые силы в направлениях X и Y, F c.x и F c.y , соответственно, делятся между болтами по жесткости болтов. Поскольку предполагается, что все болты сделаны из одинакового материала и имеют одинаковую длину, жесткость зависит только от площади. Реакции сдвига на болте из-за прямых сил в X- и Y- рассчитываются как:

X-реакция на болт из-за прямого усилия в X
Y-реакция на болт из-за прямого усилия в Y

где А — площадь рассматриваемого болта. Если площади болтов одинаковые, приведенные выше уравнения упрощаются до P x.FX = F c.x /n и P y.FY = F c.y /n, где n — количество болтов в шаблон.

Реакция на сдвиг болта из-за момента относительно оси Z рассчитывается как:

где M c.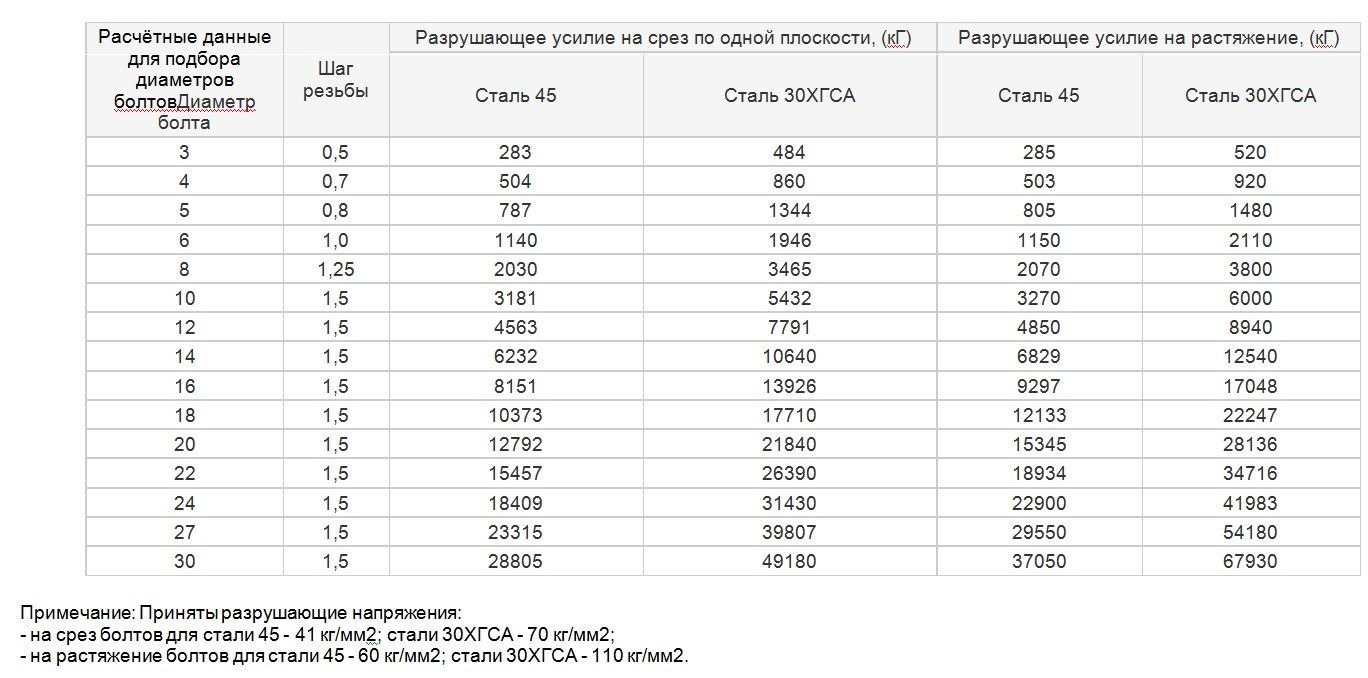 z — центральный момент относительно оси Z, а I c.p — полярный момент инерции модели. Значение г c.xy — это кратчайшее расстояние между болтом и центром тяжести, которое рассчитывается как

.

Реакция сдвига P xy.MZ затем разлагается на компоненты X и Y в зависимости от угла θ (см. рисунок выше):

P x.MZ = P xy.MZ · sinθ Х-реакция на болте из-за MZ относительно центроида
P y.MZ = −P xy.MZ · cosθ Y-реакция на болте из-за MZ относительно центроида

Значение θ представляет собой угол между положением болта и положительной осью X и рассчитывается как θ = tan -1 (r c.y /r c.x ).

Полная реакция сдвига на болт рассчитывается как векторная сумма X-компонент плюс Y-компонент:

Что дальше?

Теперь, когда рассчитаны осевые и сдвигающие усилия на отдельных болтовых соединениях, можно проанализировать напряжения в болтовых соединениях, как описано здесь.

PDH Classroom предлагает курс повышения квалификации, основанный на этой странице со справочной информацией о разболтовке. Этот курс можно использовать для выполнения кредитных требований PDH для поддержания вашей лицензии PE.

Теперь, когда вы прочитали эту справочную страницу, заработайте за это признание!

Просмотреть курс сейчас:

Просмотреть курс

Каталожные номера

  1. Барретт, Ричард Т., «Руководство по проектированию крепежа», справочная публикация НАСА 1228, 19.90.

  2. Бикфорд, Джон, «Введение в конструкцию и поведение болтовых соединений», 4-е изд.

  3. Брюн, Э.Ф., «Анализ и проектирование конструкций летательных аппаратов», июнь 1973 г.

  4. Будинас-Нисбетт, «Машиностроение Шигли», 8-е изд.

  5. Линдебург, Майкл Р., «Справочное руководство по машиностроению для экзамена PE», 13-е изд.

  6. Ниу, Майкл С., «Анализ напряжений и размеры планера», октябрь 2011 г.

  7. «Руководство по стальным конструкциям», Американский институт стальных конструкций (AISC), 14-е изд.

    8. (Технический отчет) ) | ОСТИ.GOV

    перейти к основному содержанию

    • Полная запись
    • Другое связанное исследование

    Представлены аналитические методы и данные испытаний, использованные при расчете болтовых соединений активной зоны LWBR. Эффекты внешних рабочих нагрузок, теплового расширения и релаксации напряжения в материале учитываются в формуле, разработанной для анализа характеристик соединения. Расширения этих методов также предусмотрены для болтовых соединений, обладающих как осевой гибкостью, так и гибкостью при изгибе, а также для влияния пластической деформации на внутренние усилия, возникающие в болтовом соединении. Дизайн приложений иллюстрируется примерами.

    Авторов:

    Крешиманно, П.Дж.;

    Келлер, К.Л.

    Дата публикации:
    Исследовательская организация:
    Лаборатория атомной энергии Беттис. (BAPL), Уэст-Миффлин, Пенсильвания (США)
    Идентификатор ОСТИ:
    6551356
    Номер(а) отчета:
    WAPD-TM-1349
    РНН: 81-009216
    Номер контракта Министерства энергетики США:  
    АК11-76ПН00014
    Тип ресурса:
    Технический отчет
    Страна публикации:
    США
    Язык:
    Английский
    Тема:
    21 СПЕЦИАЛЬНЫЕ ЯДЕРНЫЕ РЕАКТОРЫ И СОПУТСТВУЮЩИЕ УСТАНОВКИ; КРЕПЕЖ; ТЕСТИРОВАНИЕ ПРОИЗВОДИТЕЛЬНОСТИ; АНАЛИЗ СТРЕССА; РЕАКТОРЫ ТИПА LWBR; РЕАКТОРНЫЕ АКТЕРЫ; БОЛТОВЫЕ СОЕДИНЕНИЯ; КРЕПЛЕНИЕ; НАПРЯЖЕНИЯ; РЕАКТОРЫ-БРИДЕРЫ; ИЗГОТОВЛЕНИЕ; ПРИСОЕДИНЕНИЕ; СУСТАВЫ; КОМПОНЕНТЫ РЕАКТОРА; РЕАКТОРЫ; ТЕСТИРОВАНИЕ; ТЕПЛОВЫЕ РЕАКТОРЫ; ВОДЯНЫЕ РЕАКТОРЫ; ВОДЯНЫЕ РЕАКТОРЫ; 210500* — Энергетические реакторы, разведение

    Форматы цитирования

    • MLA
    • АПА
    • Чикаго
    • БибТекс


    Crescimanno, P. J., and Keller, K.L. Силы в болтовых соединениях: методы анализа и результаты испытаний, используемые для ядерных приложений (Программа развития LWBR) . США: Н. П., 1981.
    Веб. дои: 10.2172/6551356.

    Копировать в буфер обмена


    Crescimanno, P.J., & Keller, K.L. Силы в болтовых соединениях: методы анализа и результаты испытаний, использованные для ядерных приложений (Программа развития LWBR) . Соединенные Штаты. https://doi.org/10.2172/6551356

    Копировать в буфер обмена


    Крешиманно, П.Дж., и Келлер, К.Л., 1981.
    «Силы в болтовых соединениях: методы анализа и результаты испытаний, используемые для ядерных приложений (Программа развития LWBR)». Соединенные Штаты. https://doi.org/10.2172/6551356. https://www.osti.gov/servlets/purl/6551356.

    Копировать в буфер обмена

    @статья{osti_6551356,
    title = {Силы в болтовых соединениях: методы анализа и результаты испытаний, использованные для ядерных реакторов (Программа разработки LWBR)},
    автор = {Крешиманно, П. Дж. и Келлер, К.Л.},
    abstractNote = {Представлены аналитические методы и данные испытаний, использованные при расчете болтовых соединений сердечника LWBR. Эффекты внешних рабочих нагрузок, теплового расширения и релаксации напряжения в материале учитываются в формуле, разработанной для анализа характеристик соединения. Расширения этих методов также предусмотрены для болтовых соединений, обладающих как осевой гибкостью, так и гибкостью при изгибе, а также для влияния пластической деформации на внутренние усилия, возникающие в болтовом соединении. Дизайн приложений проиллюстрирован примерами.},
    дои = {10,2172/6551356},
    URL-адрес = {https://www.osti.gov/biblio/6551356},
    журнал = {},
    номер =,
    объем = ,
    место = {США},
    год = {1981},
    месяц = ​​{3}
    }

    Копировать в буфер обмена

    Посмотреть технический отчет (12,19 МБ)

    https://doi.

Published by admin