Лепестковые круги маркировка: Применение лепестковых торцевых кругов — Зернистость и виды
Содержание
Лепестковые тарельчатые круги: применение, виды, производители
Содержание
- Что такое тарельчатый лепестковый круг
- Применение тарельчатых абразивных кругов
- Какие бывают тарельчатые круги для шлифовки
- — Типы дисков по назначению
- — Зернистость
- — Виды абразивного покрытия
- — Размеры и форма
- — Состав
- Преимущества тарельчатых лепестковых кругов
- Рекомендации по использованию
- Лучшие производители
- Где купить продукцию: цены в Москве
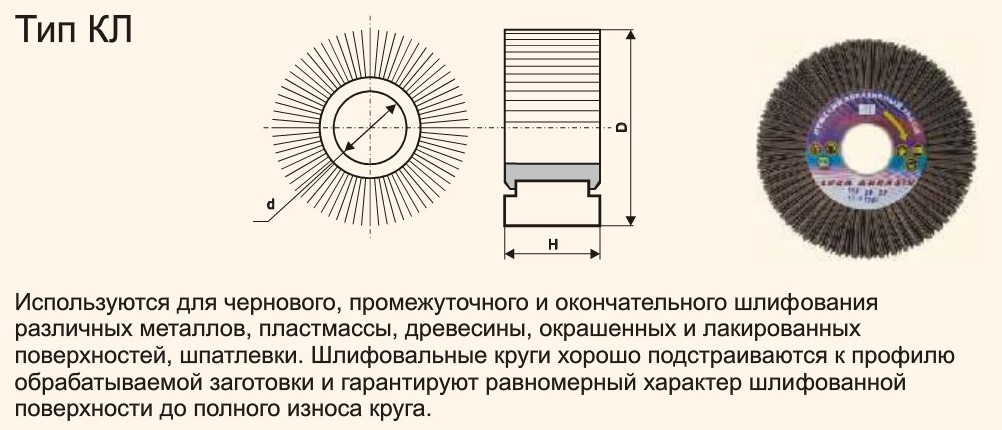
Тарельчатые лепестковые круги
Тарельчатые лепестковые круги (или КЛТ) — это специальная насадка в форме диска на шлифовальную машинку, болгарку, стационарные станки и другое электрооборудование. Изделия применяют в строительстве, ремонте, производстве, автомобильной сфере для полировки, зачистки, финишной шлифовки различных поверхностей. Название «лепестковый круг» получено из-за того, что кусочки подложки с абразивным материалом наложены друг на друга и напоминают лепестки цветов.
Название «лепестковый круг» получено из-за того, что кусочки подложки с абразивным материалом наложены друг на друга и напоминают лепестки цветов.
Где применяют тарельчатые абразивные круги
КЛТ, как и стандартные шлифкруги, предназначены для обработки поверхностей из разных материалов:
- металла;
- цветных сплавов;
- дерева;
- стекла;
- полимеров;
- гипсокартона;
- лакированного пола;
- камня.
Обработка поверхностей абразивами предполагает такие работы:
- зачистка сварочного шва;
- обточка изделия;
- удаление металлических заусениц;
- сглаживание острых кромок;
- круглая шлифовка;
- плоская шлифовка;
- финишная полировка;
- сухая и мокрая обработка.
Применение тарельчатого абразивного круга
Проведение полировальных работ необходимо не только для того, чтобы обеспечить презентабельный внешний вид изделия. Отполированный материал прочнее сцепляется с покрытием (краска, лак, антисептик), дольше сохраняет свои эффективные технические характеристики.
Отполированный материал прочнее сцепляется с покрытием (краска, лак, антисептик), дольше сохраняет свои эффективные технические характеристики.
- Детали, которые находятся в движении, нуждаются в полировке, чтобы при трении с другими элементами механизма не возникало торможения.
- Металлические изделия шлифуют, избавляя от скопившейся ржавчины, что увеличивает срок эксплуатации металла.
- Бетонные стены полируют до гладкого состояния, чтобы покрытие (обои, краска, штукатурка) прочно держалось длительное время.
- Ювелирные мастера используют шлифовальный тарельчатый круг для огранки минералов и камней и придания им естественного блеска.
- В сантехнических работах КЛТ позволяют удалить следы коррозии с труб и застарелую эмаль.
Какие бывают тарельчатые круги для шлифовки
тарельчатые абразивные круги
Разновидностей тарельчатых дисков для шлифовки много — они разделяются на несколько групп:
- По инструменту.
 Круги могут быть использованы на электродрели, болгарке, угловой шлифмашине, производственном станке.
Круги могут быть использованы на электродрели, болгарке, угловой шлифмашине, производственном станке. - По назначению. Могут быть с вентиляцией, оправкой, пакетными, торцевыми, радиальными, складчатыми, комбинированными.
- По зернистости. Размер зерна зависит от типа обработки. Чем крупнее кристаллы абразива, тем меньше числовое обозначение.
- По размерам. Форма бывает прямой, выпуклой или конусной. Диаметр зависит от того, для какого инструмента предназначен диск, обычно он составляет 115-180 мм.
- По составу. Отличаются по материалу эластичного основания, клеевой связки и абразиву зерна.
- По абразивному покрытию. В качестве покрытия наждачки используют алюминий, керамику, цирконий, кремний, электрокорунд, алмаз и другие материалы.
Типы дисков по назначению
Лепестковый круг
- Торцевой (КЛТ). Лепестковый круг применяют для плоской обработки полос, кромки, бордюров, окаймления и труднодоступных областей изделия.

- Радиальный (КЛР). Имеет прямую объёмную форму, необходим для обработки профильных и деревянных материалов.
- Пакетный (КЛП). Предназначен для крупных изделий, оснащён большим количеством лепестков.
- Складчатый (КЛС). Нужен для выполнения пазов, углублений, затирки швов, имеет небольшую рабочую ширину.
- С простой ступицей (КЛ). Обычный тип диска с отверстием для крепления и фланцами.
- С оправкой (КЛО). Используют для устранения окалин, коррозии, остатков материала на труднодоступных поверхностях.
- С вентиляцией (КЛВ). Отличается высокой скоростью работы и способностью удалять самые мелкие заусеницы, окалины, стружку.
Какая бывает зернистость
зернистость абразивного круга
Зернистость — это размер абразивных микрокристаллов и частота их выкладки на наждачке. Стандартное обозначение противоположно размеру, например, при Р120 зерно мельче, чем при Р40. Российские производители указывают наоборот — чем выше значение, тем крупнее кристаллы.
Размер зерна зависит от назначения работы. Мелкая зернистость необходима для деликатной обработки — стекла, фарфора, пластика, мягких сплавов, кожи, полудрагоценных камней и металлов. Крупное зерно подходит для грубой полировки изделий больших размеров из металла, дерева, стали, камня. Самые востребованные тарельчатые круги для шлифовки имеют зернистость от 24 до 150.
Виды абразивного покрытия
В качестве абразива для наждачки применяют натуральные и синтетические материалы. Они отличаются не только составом, но и внешними признаками.
Обычно абразивы бывают такими:
абразивное покрытие
- Электрокорунд. Может быть чистым, а также циркониевым или керамическим. Обладает высокой прочностью и твёрдостью, сохраняет свойства при повышенных температурах.
- Алюминий. Применяют цирконат или оксид алюминия. Абразивы подходят для всех типов поверхности — от грубых до деликатных.
- Цирконий. Обладает вязкостью, что благоприятно сказывается на полировке нержавеющей стали.
 Имеет повышенную плотность и способность самозатачиваться.
Имеет повышенную плотность и способность самозатачиваться. - Карбид кремния. Имеет устойчивость к температурным перепадам и деформации при высоких температурах, позволяет обрабатывать или править поверхности после термообработки.
- Нитрид бора (эльбор). Отличается отменными техническими характеристиками, подобными алмазу, при этом устойчив к термическому воздействию.
- Алмаз. Обладает хорошей прочностью и твёрдостью, используется для полировки, а также для выполнения выемок, надрезов и пазов.
- Неорганическое сырьё. Обычно это глина, кварц, песок, корунд, пемза. Применяют обычно в финишной обработке мягких или хрупких поверхностей.
Также возможно разное цветовое оформление. Красный цвет говорит о максимальной стойкости, зелёный и синий — о прочности и твёрдости, коричневый — о наличии в составе оксида алюминия.
Размеры и форма
Размеры и форма абразивных кругов
Тарельчатые лепестковые диски всегда круглые, но могут быть плоскими, выпуклыми или конусообразными. Прямые предназначены для полировки плоских ровных изделий, подходят для деталей и предметов больших размеров. Выпуклые необходимы для изделий с углублениями, пазами, выемками, а также для оформления кромок, швов, следов сварки.
Прямые предназначены для полировки плоских ровных изделий, подходят для деталей и предметов больших размеров. Выпуклые необходимы для изделий с углублениями, пазами, выемками, а также для оформления кромок, швов, следов сварки.
Размер диаметра зависит от инструмента и площади обработки:
- 115 мм — небольшие диски на болгарку для работы маленького объёма.
- 125 мм — стандартный диаметр, подходящий к дрели, болгарке, угловой шлифмашине.
- 150 мм — специфический размер для ограниченного количества электроприборов.
- 180 мм — отличаются высокой мощностью и производительностью, подходят для станков и большинства шлифовальных машин.
Из чего состоит тарельчатый круг для шлифовки
лепестковый круг
Стандартный лепестковый круг состоит из трёх слоёв:
- Основание. Основа может быть выполнена из стекловолокна, ткани, бумаги, плёнки, фибры или комбинации нескольких материалов. Имеет форму тарелки.

- Связка. Клеевая связка необходима для скрепления основы и абразивного зерна. Обычно используют смолу, бакелит, керамику, вулканит, силикат, металл.
- Абразив. Рабочее зерно, выполняющее роль наждачки. Может быть алюминиевым, электрокорундовым, кремниевым, циркониевым, алмазным и другими.
В чём преимущества тарельчатых лепестковых кругов
Лепестковый диск
Лепестковый диск обладает мощными техническими характеристиками, которые ускоряют и оптимизируют работу электрооборудования:
- слабый уровень вибрации;
- высокая производительность;
- низкий уровень шума;
- равномерная обработка;
- многофункциональное применение;
- гибкость и эластичность;
- высокая скорость оборотов;
- устойчивость к нагреванию;
- способность к самозатачиванию;
- упругость лепестков;
- долговечность наждачки.
Рекомендации по использованию
Работа с абразивным кругом
Чтобы повысить эффективность использования абразивных кругов, следует придерживаться несложных правил эксплуатации:
- Перед эксплуатацией проверьте диск на отсутствие сколов, трещин и других дефектов.

- Проверьте работоспособность инструмента на холостом ходу, после чего можно установить круг.
- Начинайте полировать или зачищать поверхность, когда наберётся нужная скорость оборотов.
- Поддерживайте мягкий и плавный ход шлифмашины без резких толчков.
- Старайтесь держать электроприбор под углом 15-20 градусов по отношению к изделию.
Применение смазочно-охлаждающий жидкости
Для того чтобы снизить силу трения и уровень нагревания инструмента, можно применять смазочно-охлаждающие жидкости. Они бывают в виде эмульсии или масла. На каждые 20 мм диаметра диска понадобится 10-15 мл эмульсии. Жидкость охлаждает поверхность работающего КЛТ, быстро устраняет стружку и пыль, оптимизирует качество обработки.
Лучшие производители абразивных тарельчатых кругов
Klingspor
Немецкая корпорация имеет официальные филиалы в Польше, России, Украине, Казахстане. Абразивное производство Klingspor развито на европейском уровне и отвечает всем нормам отечественного ГОСТа. Изготовление инструментов и комплектующих осуществляется на собственном оборудовании в цехах с инновационной оснасткой. КЛТ Klingspor востребованы в строительстве, ремонте, автомобильном и мебельном производстве, ювелирной и текстильной сфере.
Абразивное производство Klingspor развито на европейском уровне и отвечает всем нормам отечественного ГОСТа. Изготовление инструментов и комплектующих осуществляется на собственном оборудовании в цехах с инновационной оснасткой. КЛТ Klingspor востребованы в строительстве, ремонте, автомобильном и мебельном производстве, ювелирной и текстильной сфере.
Orientcraft
Лепестковые диски компании Orientcraft производят в Китае, а также в России в официальных филиалах. Каждая партия инструментов проходит несколько проверок и полностью соответствует заявленным характеристикам. Круги можно использовать для электродрелей, угловых, прямых и щёточных шлифовальных приборов, болгарки.
Matrix
Компания немецко-российского происхождения специализируется на выпуске электрооборудования, абразивных инструментов, комплектующих. КЛТ этого производителя выдерживают высокие нагрузки, перепады температур. Минус — лепестковые круги Matrix подходят только на инструменты этой же фирмы, поэтому бывает затруднительно подобрать подходящий диск.
Минус — лепестковые круги Matrix подходят только на инструменты этой же фирмы, поэтому бывает затруднительно подобрать подходящий диск.
Bosch
Тарельчатые лепестковые круги немецкого производства отличаются отменным качеством изделий, долговечностью эксплуатации и применением прочного Х-волокна для изготовления опорных тарелок. Единственный минус таких дисков — завышенная стоимость, обусловленная именем бренда.
Гибкие абразивы
Где купить шлифовальный тарельчатый круг: цены в Москве
шлифовальный тарельчатый круг
Выгодные покупки абразивных кругов возможны с интернет-магазином «Е-Абразив». Мы предлагаем самый большой выбор КЛТ в Москве — более 320 видов дисков, отличающихся назначением, зернистостью, диаметром. В каталоге представлены изделия по работе с деревом, металлом, стеклом, краской и лаком, пластиком, камнем и другими материалами. У нас можно купить тарельчатые лепестковые круги по цене, которая вас устроит. Если найдёте дешевле, мы сделаем скидку.
В каталоге представлены изделия по работе с деревом, металлом, стеклом, краской и лаком, пластиком, камнем и другими материалами. У нас можно купить тарельчатые лепестковые круги по цене, которая вас устроит. Если найдёте дешевле, мы сделаем скидку.
Преимущества покупок в нашем магазине:
- Вся продукция поставляется от компаний-производителей, что убережёт вас от подделок.
- Покупки станут максимально выгодными — мы делаем хорошие скидки постоянным клиентам.
- Вы сможете самостоятельно забрать заказ со склада в Москве или оформить доставку в любую точку России.
- Наш менеджер всегда проконсультирует по вопросам подбора необходимых инструментов индивидуально под ваш профиль работы.
Звоните нам по телефону 8 (800) 301-9121.
Круги лепестковые: виды и применение
Круги лепестковые шлифовальные
С помощью лепестковых кругов выполняется шлифование и полировка различных поверхностей, как на производствах, так и в бытовых условиях. Сегменты с абразивом расположены на основе по кругу в форме веера и имеют сходство с лепестками, оттого и получили свое название.
Сегменты с абразивом расположены на основе по кругу в форме веера и имеют сходство с лепестками, оттого и получили свое название.
Разновидности лепестковых кругов
Существуют разные параметры отличия лепестковых кругов, такие как назначение и тип обработки.
По назначению лепестковые круги делятся на инструменты для работы на угловых шлифовальных машинках (УШМ), для электродрелей или для выполнения работ на производственных станках.
В зависимости от типа обработки определяется размер и зернистость материала абразива.
В таблице приведены маркировки абразивных кругов.
Существуют также нестандартные и комбинированные шлифовальные лепестковые круги, работают они по тому же принципу что и все остальные.
Особенности применения лепестковых дисков
Лепестковые круги наиболее популярный инструмент в строительной и производственной сферах. По своей структуре такой инструмент схож со шлифовальными дискам, однако он имеет некоторые конструктивные отличия, что позволяет использовать лепестковые круги для обработки не только плоских, но и вогнутых поверхностей заготовок самой различной конфигурации.
Лепестковые круги могут применяться для обработки металла, пластмассы, дерева и других материалов.
Абразивный слой расположенный на лепестках круга позволяет использовать подобные инструменты для подготовки поверхностей к нанесению различных покрытий (например лака), лепестки эффективно очищают поверхность от ржавчины, удаляют заусенцы, кромку со швов и окалины.
Продолжительность использования и равномерность износа лепесткового круга обусловлена тем, что при стирании абразива с одного из сегментов, за ним следует другой – с меньшим износом.
В зависимости от вида выполняемых работ подбираются разные виды лепестковых кругов. При обработке плоских поверхностей используется клт-1, а вот для заготовок со сложной конфигурацией подойдет клт-2. Существуют лепестковые круги модификации клт-3, которые имеют дополнительные лепестки, что позволяет увеличить производительность выполняемых работ, как и круги клт-1 они подходят для обработки плоских поверхностей. Для обработки сильно изогнутых заготовок используют гибкие диски – клт-4, а клт-5 применяю как для чистовой, так и для грубой обработки.
Вне зависимости от вида выполняемых работ и обрабатываемого материала, самое главное – это правильно подобрать инструмент и соблюдать технику безопасности при работе с ним.
Основные преимущества
Лепестковые круги используются практически во всех сферах промышленности, их использование для обработки поверхностей имеет ряд преимуществ:
- стабильная скорость вращения круга;
- достаточно низкий уровень шума и вибрации;
- возможность обработки заготовок сложной конфигурации;
- высокое качество обработанных поверхностей;
- значительный срок эксплуатации инструмента.
Зернистость лепестковых кругов
В зависимости от назначения круга выбирается размер абразивного зерна. Более крупные зерна предназначены для грубой обработки. Зернистость абразива обозначается буквой Р и числом. Чем более большое значение имеет число рядом с обозначение зернистости, тем для более тонкой работы используется абразивный круг. Самые популярные круги имеют зернистость от 40 до 120. Для их изготовления используется оксид алюминия, который отлично подходит для грубой шлифовки, но не эффективен для выполнения зачистных и полировальных работ.
Самые популярные круги имеют зернистость от 40 до 120. Для их изготовления используется оксид алюминия, который отлично подходит для грубой шлифовки, но не эффективен для выполнения зачистных и полировальных работ.
Размеры и конфигурация
Шлифовальные диски бывают плоской и конической формы. Плоские круги используют для обработки гладких деталей большого размера. Конусные более универсальны, с их помощью можно обрабатывать заготовки сложной конфигурации, зачищать швы и устранять дефекты.
Наиболее распространены следующие размеры лепестковых кругов: 115 мм – подходят для работы на угловых шлифовальных машинках в условиях ограниченного пространства; 125 мм – также используются на УШМ, но имеют значительно более высокую мощность имея при этом компактный габаритный размер, шлифовальные круги диаметром 150 мм и 180 мм считаются высокомощными и производительными, однако для их использования сложнее подобрать подходящую по характеристикам угловую шлифовальную машинку. Указанные диаметры лепестковых кругов применяются, как правило, для обработки металла, при работой с деревянными поверхностями чаще всего использую круги диаметром от 150 мдо 300 мм.
Указанные диаметры лепестковых кругов применяются, как правило, для обработки металла, при работой с деревянными поверхностями чаще всего использую круги диаметром от 150 мдо 300 мм.
Торцевой лепестковый круг
Как и любой другой шлифовальный круг, диск торцевой лепестковый состоит из трех основных элементов: абразив, клеевая связка и основа. В качестве материала основы используется: бумага, ткань, фибра или смесь этих материалов.
Режущая часть состоит из абразива, который может быть как натуральным, так и искусственным. Лепестковые торцевые диски могут иметь абразив из карбида кремния(SiC), окиси алюминия(AiO), циркониевое корунда(Zn), керамического корунда(Cer).
Самые дешевые из представленных абразивов – оксид алюминия T29 (диски имеют коричневый цвет) и цирконий Deerfos KZ563 (синие и зеленые диски), в то же самое время, диски с абразивом из керамического корунда Deerfos PS994 считаются очень агрессивными и производительными.
Цена лепесткового круга напрямую зависит от материала, из которого он изготовлен.
Торцевые диски бывают плоской и конусной формы. Конусные используют для зачистки швов от сварки и обработки поверхности со сложной конфигурацией, а плоские диски отлично справляются с обработкой плоских деталей. Мы рекомендуем выбирать лепестковые круги конической формы КЛТ2.
При выборе лепестковых кругов важно учитывать не только материал, который будет обрабатываться, но и инструмент, на который устанавливается шлифовальный диск. Для тяжёлых операций по съему металла зернистостью Р40 и грубее, необходима УШМ мощностью от 1000 Вт и более. При выборе зернистости круга следует ориентироваться на исходное качество обрабатываемой поверхности, и желаемый результат.
Как равномерно расположить лепестки цветов (или другие предметы) по кругу
Если вы много занимаетесь рукоделием, возможно, вы ищете простой способ равномерно распределить лепестки цветов (или другие предметы) по кругу для ручной вышивки, рисования, аппликации, черчения и т. д. Вы, вероятно, уже знаете, что можно взять круг бумаги и сложить его, а затем открыть его и использовать линии сгиба в качестве направляющих для размещения объектов. Это легко сделать, если у вас есть четыре или восемь элементов, но что, если вы хотите равномерно распределить семь элементов? Или пять?
Это легко сделать, если у вас есть четыре или восемь элементов, но что, если вы хотите равномерно распределить семь элементов? Или пять?
Я знаю, это ВЫГЛЯДИТ как математика, но это очень просто. Вам понадобится транспортир. Они очень недорогие, и, возможно, у вас уже есть один. Тот, что у меня есть, представляет собой полукруг, как этот, но они также бывают и полными кругами. Любой из них будет работать нормально. Я положил глаз на этот транспортир, который также является инструментом, который вы можете использовать для рисования кругов разных размеров.
Я демонстрирую использование обертки от шоколада из фольги и спама. (Заметка для себя: мне нужно купить больше шоколада.)
Допустим, вы хотите сделать аппликацию из шести лепестков. Круг имеет 360 градусов, поэтому разделите 360 на количество лепестков цветка. 360 разделить на 6 = 60, поэтому каждый лепесток должен располагаться под углом 60 градусов к следующему.
Все, что вам нужно сделать, это отметить центральную точку вашего цветка и положить первый лепесток. Теперь поместите центральную отметку транспортира в центральную точку цветка и выровняйте каждый лепесток так, чтобы его кончик находился на расстоянии 60 градусов от кончика последнего лепестка. Повторите для всех 6 лепестков. Я нарисовал здесь линии маркером, чтобы вы могли видеть, что я делаю: обратите внимание, что две линии идут от центральной точки под углами 60 и 120 градусов. Следующие лепестки находятся под углами 0 и 180 градусов. (Вы также можете расположить лепестки под углом 20, 80 и 140 градусов и т. д. Точное число не имеет значения, главное, чтобы каждое число отличалось от предыдущего на 60.)
Теперь поместите центральную отметку транспортира в центральную точку цветка и выровняйте каждый лепесток так, чтобы его кончик находился на расстоянии 60 градусов от кончика последнего лепестка. Повторите для всех 6 лепестков. Я нарисовал здесь линии маркером, чтобы вы могли видеть, что я делаю: обратите внимание, что две линии идут от центральной точки под углами 60 и 120 градусов. Следующие лепестки находятся под углами 0 и 180 градусов. (Вы также можете расположить лепестки под углом 20, 80 и 140 градусов и т. д. Точное число не имеет значения, главное, чтобы каждое число отличалось от предыдущего на 60.)
Если у вас есть полукруг-транспортир, вам нужно будет повернуть его, чтобы разместить все элементы. Вы также можете нарисовать точки, отстоящие друг от друга на 60 градусов, если вам так проще, и поместить середину каждого лепестка на точку.
Если вы размещаете 5 элементов, просто рассчитайте 360, деленное на 5 (что равно 72), и поместите каждый элемент на 72 градуса от последнего. Каждый из восьми предметов будет находиться под углом 45 градусов друг к другу и так далее.
Каждый из восьми предметов будет находиться под углом 45 градусов друг к другу и так далее.
Конечно, вам НЕ ОБЯЗАТЕЛЬНО быть настолько точным. Настоящие цветы часто немного неуклюжи, и чаще всего я просто смотрю на расположение природных объектов, как я делал, когда рисовал цветы, чтобы скрыть пятна на одежде, используя маркеры для ткани. Возможно, вы даже захотите сделать свои цветы немного нестандартными, чтобы они выглядели немного более причудливо и причудливо. Я вышел во двор, чтобы сделать несколько снимков цветов, которые расцвели, и вы можете видеть на каждом снимке, насколько они неточны на самом деле.
У этого космоса погнуты некоторые лепестки. Был ли это ветер? Или он только готовится бросить свои лепестки? Я не знаю, но я думаю, что это красиво.
Взгляните на этот лилейник. Каждый лепесток совершенно точно НЕ находится на расстоянии 60 градусов друг от друга, и это совершенно нормально.
У дикой маргаритки несколько лепестков не на месте или отсутствуют, и все равно она прекрасна.
У этого цветка зверобоя скрученные лепестки, поэтому он похож на вертушку. Интересно, к чему этот баг?
А вот и моя кошечка Патч, пытается выглядеть небрежно, но я думаю, что она намеренно ведет себя мило, так что я перестану фотографировать цветы и сфотографирую ее. Я должен признать, что это сработало, поэтому я не могу спорить с ее методом.
Надеюсь, вы воспользуетесь этим приемом в следующий раз, когда захотите равномерно распределить предметы по кругу для своих художественных или поделок! И если вы хотите равномерно расположить предметы вдоль прямой линии, перейдите по ссылке, чтобы узнать об удивительном трюке, который я впервые узнал из просмотра 9.0029 Этот старый дом.
Приятного творчества!
Лепестки, цветы и круглые упаковки
Обратите внимание, что эта экспозиция предназначена для того, чтобы передать общую картину, поэтому мы намеренно сделаем несколько сокращений и пропустим некоторые детали и технические детали, которые можно найти в ссылках. ..
..
Дэвид Остин
Государственный университет Гранд-Вэлли
Электронная почта Дэвида Остина
Введение
Скромный круг может показаться не самым захватывающим кандидатом для дальнейшего математического исследования. Однако в этой колонке мы увидим, как упаковки кругов объединяют некоторые важные идеи геометрии, топологии и анализа и образуют мост между дискретным и непрерывным мирами.
Чтобы ввести упаковки кругов, мы начнем с двумерной ориентированной поверхности $S$. В примере слева внизу поверхность топологически эквивалентна замкнутому диску. Затем мы рассматриваем триангуляцию $T$ поверхности, разложение поверхностей на треугольники, которые подходят друг к другу край к краю.
Вот упаковка кругов, связанная с этой триангуляцией:
Вообще говоря, упаковка кругов связана с триангуляцией $T$, когда
1. Окружность связана с каждой вершиной триангуляции. Окружность связана с каждой вершиной триангуляции. | ||
| 2. Ребро подразумевает касание двух окружностей, связанных с его конечными точками. | ||
| 3. Грань подразумевает тройку касаний. |
Чтобы увидеть, что приведенная выше упаковка кругов связана с триангуляцией $T$, мы нарисуем нерв упаковки, добавив вершину в центре каждой окружности и ребра для касательных окружностей.
Если мы добавим к нерву треугольные грани, то найдем носитель упаковки круга, который является триангуляцией $T’$ новой поверхности $S’$. Заметим, что $S’$ топологически эквивалентна (гомеоморфна) исходной поверхности $S$, а $T’$ комбинаторно эквивалентна исходной триангуляции $T$. Таким образом, носитель обеспечивает геометрическую реализацию триангуляции $T$.
| $T’$ триангулирует $S’$ | $T$ триангулирует $S$ |
В более общем плане нет причин ограничиваться упаковками окружностей в евклидовой плоскости ${\Bbb C}$; мы также можем искать упаковки в гиперболической плоскости ${\Bbb D}$ и сфере Римана ${\Bbb P}$. Вот, например, упаковка того же комплекса в гиперболической плоскости.
Вот, например, упаковка того же комплекса в гиперболической плоскости.
Кроме того, мы можем начать с триангуляции любой двумерной ориентированной поверхности с границей или без нее; однако для простоты мы будем рассматривать здесь только односвязные поверхности. (Помните, что поверхность называется односвязной, если любую петлю на поверхности можно непрерывно стянуть в точку.)
Обратите внимание, что это изложение предназначено для того, чтобы передать общую картину, поэтому мы намеренно сделаем несколько сокращений и пропустим некоторые детали и технические детали, которые можно найти в ссылках. Имея это в виду, давайте научимся создавать упаковки кругов.
Как сконструировать круглые насадки
Первые вопросы, которые мы должны задать, — когда существуют упаковки кругов и как мы можем их построить. Но прежде чем мы начнем думать над этими вопросами, давайте рассмотрим более простую задачу с аналогичным решением.
Метод релаксации: Предположим, мы хотим найти линейную функцию $f(x)$ на интервале $[a,b]$ с заданными значениями в точках $a$ и $b$.
Конечно, мы знаем, что существует единственная линейная функция, удовлетворяющая этому условию. Метод, известный как релаксация , предоставляет алгоритм для его нахождения.
Обратите внимание, что линейные функции характеризуются локальным условием; а именно, значение функции в точке $c$ есть среднее значение $f$ в двух точках, равноотстоящих от $c$. То есть
$$f(c)=\frac{f(c-h)+f(c+h)}{2}.$$
| Чтобы начать наш алгоритм, мы строим равноотстоящую сетку точек $x_0, x_1, \ldots, x_n$, где $x_0 = a$ и $x_n = b$, и случайным образом присваиваем значения внутренним точкам. | |
Начиная с самой левой точки $x_1$, мы заменяем значение в $x_1$ средним значением соседних точек. | |
| Затем мы делаем то же самое для $x_2$. | |
| Перебирая все внутренние точки, получаем новые значения: | |
| Повторение снова дает: |
После 10 и 25 итераций имеем
Обратите внимание, что каждый шаг алгоритма нарушает локальное условие, которое мы установили на предыдущем шаге. Тем не менее значения во внутренних точках сходятся к значениям искомой линейной функции.
В более общем смысле этот метод релаксации применяется в более высоких измерениях к проблеме нахождения гармонических функций с заданными граничными значениями.
Используя ту же идею, мы найдем упаковку кругов для треугольной двумерной ориентированной поверхности с краем. Рассмотрим показанную здесь триангуляцию замкнутого диска
и предположим, что мы задаем радиусы окружностей, связанных с граничными вершинами.
Нахождение радиусов: Мы определим радиусы окружностей, связанных с внутренними вершинами, для создания упаковки окружностей
| Как и в методе релаксации, который мы использовали для нахождения линейной функции, нам нужно соответствующее локальное условие, определяемое упаковкой кругов. Поэтому мы рассматриваем одну внутреннюю вершину $v$, связанную с ней окружность и ее соседей по упаковке. Соседние круги называются лепестков , которые вместе с кругом, связанным с $v$, образуют цветок . Обратите внимание, что сумма мер углов, пересекающихся в этой вершине, равна $2\pi$. Обозначим через $\theta_v$ сумму углов в точке $v$, сумму мер углов всех граней, сходящихся в точке $v$. Как мы только что видели, $\theta_v = 2\pi$ для внутренней вершины в упаковке кругов. | |
92}{2(х+у)(х+г)}. $ $ | |
| Теперь мы начинаем наш алгоритм со случайного назначения радиусов внутренним кругам. | |
| Скорее всего, у нас нет упаковки кругов, поэтому нам нужно настроить радиусы внутренних кругов. Например, радиус синего круга слишком велик, что наш алгоритм обнаруживает, вычисляя, что $\theta_v < 2\pi$. | |
| Затем мы вычисляем требуемый радиус этой внутренней окружности, чтобы $\theta_v=2\pi$, и обновляем радиус внутренней окружности до этого нового значения. |
Действуя как в нашем алгоритме нахождения линейной функции, применим этот шаг к каждой из внутренних вершин по очереди. Конечно, обновление радиуса одной окружности может нарушить сумму углов, которую мы ранее скорректировали. Следовательно, после одного прохода по всем внутренним точкам у нас, скорее всего, не будет упаковки кругов; однако можно доказать, что общая ошибка сумм углов уменьшилась. Поэтому мы продолжаем проходить через внутренние вершины, обновляя их радиусы, пока все суммы углов не окажутся в пределах желаемого допуска $2\pi$.
Поэтому мы продолжаем проходить через внутренние вершины, обновляя их радиусы, пока все суммы углов не окажутся в пределах желаемого допуска $2\pi$.
Нахождение центров: Теперь, когда у нас есть радиусы внутренних окружностей, нам еще нужно определить центры окружностей. Выберем окружность $C_0$ радиуса $r_0$ и один из ее лепестков $C_1$ радиуса $r_1$. Как только мы выбираем центр для $C_0$, центр $C_1$ должен находиться на расстоянии $r_0+r_1$.
Затем мы раскладываем лепестки $C_0$ по одному, начиная с $C_2$, которая касается $C_0$ и $C_1$.
Продолжая таким же образом, мы размещаем все лепестки $C_0$.
Мы продолжаем этот процесс, размещая лепестки $C_1$ и так далее, пока не будут выложены все круги.
Оказывается, найденная нами упаковка кругов единственна с точностью до изометрии. Это станет ясно, если мы заметим, что радиусы внутренних окружностей определяются однозначно, а все центры определяются, когда мы выбираем центры $C_0$ и $C_1$.
В предыдущем примере получившиеся окружности имеют непересекающиеся внутренности, и в этом случае мы называем упаковку одновалентной. Однако можно выбрать граничные радиусы, которые приводят к упаковкам, которые не являются однолистными; ниже показаны две упаковки одной и той же триангуляции, причем одна слева одновалентна, а другая справа нет. Эту возможность необходимо учитывать, но в этой статье мы всегда будем встречать одновалентные упаковки кругов.
В нашем обсуждении мы построили упаковку кругов, потребовав $\theta_v = 2\pi$ в каждой из внутренних вершин. Интересные примеры и явления можно найти, потребовав, чтобы $\theta_v = 2\pi n$ для некоторого $n>1$ в некоторых внутренних вершинах. Две приведенные ниже упаковки имеют одинаковые граничные радиусы; однако мы требуем, чтобы вершина, связанная с заштрихованным кругом, удовлетворяла $\theta_v=2\pi$ слева и $\theta_v=4\pi$ справа. Это приводит к тому, что лепесток в этом цветке обвивается вокруг центрального круга более одного раза, что приводит к явлению ветвления, которое мы не будем здесь исследовать.
В более общем смысле мы также можем создавать упаковки кругов в гиперболической плоскости, где граничные круги имеют бесконечный радиус; мы называем это максимальной упаковкой триангуляции $T$ и обозначаем ${\cal P}_T$. Например, вот такая упаковка триангуляции, с которой мы только что работали. Это в некотором смысле каноническая упаковка поверхности.
Комментарии ?
Теорема дискретной униформизации
Теперь, когда мы можем построить упаковки окружностей поверхностей с краем, давайте обратимся к триангуляциям топологического открытого диска. Мы увидим, что есть два возможных поведения.
Параболический случай: Рассмотрим триангуляцию $T$ плоскости ${\Bbb C}$, в которой каждая вершина имеет шесть соседей.
В этом случае мы будем рассматривать набор вложенных подтриангуляций $T_k$, каждая из которых триангулирует поверхность с краем и объединением которых является поверхность $S$.
Например, вот такой набор для триангуляции выше:
| $T_1$ | $T_2$ | |
| $T_3$ | $T_4$ |
Поскольку эти поверхности имеют границы, к ним применимо наше предыдущее обсуждение. Выбрав вершину $v_0$ в $T_1$ и соседа $v_1$, найдите максимальную окружность, упаковывающую $P_k$ в гиперболической плоскости для каждого $T_k$. Расположите окружности так, чтобы $C_0$, окружность, связанная с $v_0$, находилась в центре начала координат, а $C_1$, окружность, связанная с $v_1$, была ориентирована, скажем, вдоль горизонтальной оси. На рисунках ниже мы выделили кружок $C_0$.
| $P_1$ | $P_2$ | |
| $P_3$ | $P_4$ |
Обратите внимание, что радиус $C_0$ приближается к нулю, когда $k$ стремится к бесконечности. На самом деле оказывается, что радиусы всех окружностей стремятся к нулю.
На самом деле оказывается, что радиусы всех окружностей стремятся к нулю.
Равномерно масштабируем круги в каждой упаковке так, чтобы радиус $C_0$ был одинаковым в каждой упаковке. Наложение этих уплотнений друг на друга,
мы видим, что упаковки будут сходиться к обычной гексагональной пенни-упаковке на плоскости. Это максимальная упаковка ${\cal P}_T$ гексагональной триангуляции в плоскости ${\Bbb C}$.
Этот пример иллюстрирует общее явление: всякий раз, когда радиус $C_0$ стремится к нулю при стремлении $k$ к бесконечности, мы можем таким образом создать упаковку ${\cal P}_T$, которая заполняет всю плоскость ${\Bbb C}$. В этом случае мы говорим, что $T$ является -параболической -триангуляцией.
Гиперболический случай: Для сравнения рассмотрим открытый диск, триангулированный так, что каждая вершина имеет семь соседей:
Выбираем вложенный набор триангуляций
| $T_1$ | $T_2$ | |
| $T_3$ | $T_4$ |
и найти их упаковки кругов в гиперболической плоскости.
| $P_1$ | $P_2$ | |
| $P_3$ | $P_4$ |
В этом случае мы находим, что радиусы окружностей $C_0$ как бы сходятся к положительному значению, и упаковки действительно сходятся к упаковке ${\cal P}_T$, которую мы называем максимальной.
Это иллюстрирует явление, дополнительное к параболическому случаю. Всякий раз, когда радиусы окружностей $C_0$ сходятся к положительному значению, упаковки окружностей сходятся к максимальной упаковке в гиперболической плоскости ${\Bbb D}$. Назовем такую триангуляцию гиперболический.
Теорема о дискретной униформизации: Эти примеры иллюстрируют тот факт, что мы можем классифицировать триангуляцию открытого диска либо как параболическую, когда ее максимальная упаковка заполняет евклидову плоскость ${\Bbb C}$, либо как гиперболическую, когда ее максимальная упаковка заполняет гиперболическую плоскость ${\Bbb D}$.
Мы не обсуждали упаковки, возникающие из триангуляций двумерной сферы. Однако относительно легко увидеть, что такая триангуляция дает упаковку ${\cal P}_T$, которая заполняет сферу Римана ${\Bbb P}$. Это приводит к
Теорема о дискретной униформизации: Триангуляция $T$ односвязной поверхности без края допускает упаковку ${\cal P}_T$ поверхности $T$, которая заполняет либо евклидову плоскость ${\Bbb C}$, либо гиперболическую плоскость ${\Bbb D}$, либо риманову сферу ${\Bbb P}$.
Эта теорема об упаковке кругов является аналогом теоремы об униформизации для римановых поверхностей:
Теорема об униформизации: Односвязная риманова поверхность конформно эквивалентна либо евклидовой плоскости $\Bbb C$, либо гиперболической плоскости $\Bbb D$, либо римановой сфере $\Bbb D$.
Комментарии ?
Дискретные аналитические функции
Если комплексная функция $f$ аналитична в точке $z_0$, то $f$ приблизительно линейна вблизи точки $z_0$:
$$f(z_0+z) \ приблизительно f(z_0) + f'(z_0)(z-z_0)$$
или
$$ \Дельта f \приблизительно f'(z_0)\Дельта z. $$
$$
Для комплексного числа $m$ умножение $z$ на $m$ имеет простую геометрическую интерпретацию: $mz$ получается растяжением $z$ по модулю в множитель $|m|$ и поворотом $z$ на аргумент $m$. Это означает, что функция $z\mapsto mz$ растягивает и поворачивает комплексную плоскость.
Аналитические функции локально представляются умножением на производную $f'(z_0)$; в малом масштабе вблизи $z_0$, поэтому функция $f$ растягивает и поворачивает плоскость. 92$-самолет. В этом масштабе сетка изогнута и скручена.
Однако, если мы посмотрим в небольшом масштабе вблизи точки, мы увидим, что $f$ просто растягивает и вращает сетку. В частности, это означает, что аналитическая функция переводит маленькие круги в маленькие круги.
Давайте теперь вернемся к триангуляции, которую мы рассмотрели ранее
и две различные упаковки кругов, заданные двумя наборами граничных радиусов.
Поскольку оба являются упаковками одной и той же триангуляции, существует взаимно однозначное соответствие между кругами в одной упаковке и кругами в другой, на что указывает цвет. Это устанавливает функцию между упаковками кругов, которая может быть распространена на лежащие в их основе носители.
Поскольку эта функция переводит круги в круги, мы можем считать ее дискретным аналогом аналитической функции. На самом деле такие функции называются дискретных аналитических функций, , и их поведение удивительно похоже на аналитические функции.
Чтобы проиллюстрировать, мы можем использовать такие функции для построения аналитических карт. Например, теорема об отображении Римана утверждает, что
Если $S$ — односвязное открытое собственное подмножество плоскости, то существует обратимая аналитическая функция $f:S\to {\Bbb D}$, обратная которой также является аналитической.
Это замечательная теорема, служащая воротами к глубокому пониманию двумерных римановых поверхностей. Однако, проще говоря, из него следует нетривиальный факт, что любые два таких подмножества плоскости гомеоморфны.
Однако, проще говоря, из него следует нетривиальный факт, что любые два таких подмножества плоскости гомеоморфны.
Упаковки кругов и дискретные аналитические функции позволяют построить функцию $f$.
Для начала рассмотрим ограниченную односвязную открытую область $S$, как показано ниже. Выберем число $r>0$ и построим в плоскости шестиугольную пенни-упаковку, в которой каждая окружность имеет радиус $r$.
Теперь удалите окружности, центры которых лежат вне $S$, чтобы получить окружность, упаковывающую $P_r$.
Носителем $P_r$ является триангуляция $T_r$ поверхности с краем. Обозначим одну из окружностей в $P_r$ через $C_0$ и выберем точку $p$ внутри $C_0$. Пусть $C_1$ — лепесток, скажем, справа от $C_0$ в $P_r$. Будем называть $Q_r$ максимальной упаковкой $T_r$ в круг ${\Bbb D}$, где центр окружности, соответствующей $C_0$, находится в начале координат, а центр $C_1$ проходит вдоль горизонтальной оси.
Это определяет дискретную аналитическую функцию $f_r:P_r\to Q_r$. Мы можем повторить этот процесс с последовательностью $r_n$, где $r_n\to 0$.
| $r = 0,2$ | ||
| $\stackrel{f_{0.2}}{\longrightarrow}$ | ||
| $r = 0,1$ | ||
| $\stackrel{f_{0.1}}{\longrightarrow}$ | ||
| $r = 0,05$ | ||
| $\stackrel{f_{0.05}}{\longrightarrow}$ | ||
| $r = 0,025$ | ||
| $\stackrel{f_{0,025}}{\longrightarrow}$ |
Руководствуясь наблюдениями, что дискретные аналитические функции переводят окружности в окружности и что окружности в $P_r$ и $Q_r$ становятся все меньше, разумно ожидать, что дискретные аналитические функции $f_r:P_r\to Q_r$ аппроксимируют аналитическую функцию $f:S\to {\Bbb D}$, описанную теоремой об отображении Римана. Фактически, это содержание теоремы Родена-Салливана, первоначально выдвинутой Тёрстоном:0003
Фактически, это содержание теоремы Родена-Салливана, первоначально выдвинутой Тёрстоном:0003
При $r\to0$ функции $f_r$ сходятся к отображению Римана $f$ равномерно на компактных подмножествах.
Резюме
Мы только что прикоснулись к красоте дискретных аналитических функций; дальнейшее исследование обнаруживает много аналогий с классическими аналитическими функциями.
Например, мы видели ранее, что параболическая триангуляция не может быть упакована в круг ${\Bbb D}$. Это может напомнить вам о классическом Теорема Лиувилля . Если вспомнить, что целая функция является аналитической функцией, определенной на всей комплексной плоскости, теорема Лиувилля утверждает
Теорема Лиувилля: Не существует целых ограниченных функций, которые не были бы постоянными.
По аналогии рассмотрим параболическую триангуляцию $T$ с максимальной упаковкой ${\cal P}_T$. Мы говорим, что дискретная аналитическая функция $f:{\cal P}_T\to P$ является целой, если $P$ является упаковкой в ${\Bbb C}$, евклидовой плоскости. Дискретная теорема Лиувилля утверждает
Мы говорим, что дискретная аналитическая функция $f:{\cal P}_T\to P$ является целой, если $P$ является упаковкой в ${\Bbb C}$, евклидовой плоскости. Дискретная теорема Лиувилля утверждает
Дискретная Теорема Лиувилля: Не существует ограниченных дискретных целых функций.
Классическая теорема Литтла Пикара расширяет теорему Лиувилля немного дальше:
Теорема Литтла Пикара: Образ целой функции $f:{\Bbb C}\to{\Bbb C}$ не совпадает не более чем с одной точкой плоскости ${\Bbb C}$.
Существует также дискретный аналог, который остается в силе, если мы предположим, по крайней мере пока, что параболическая триангуляция $T$ является шестиугольной триангуляцией $H$ плоскости.
Дискретная теорема Пикара: Целая дискретная функция $f:{\cal P}_H\to P$ не попадает не более чем в одну точку плоскости ${\Bbb C}$.
Существование упаковок кругов на сфере было впервые доказано Кёбе в 1936 г. , а затем независимо Андреевым и Терстоном. Фактически, использование Терстоном упаковок кругов в его работе над геометрическими 3-многообразиями является причиной того серьезного внимания, которое в последнее время уделяется упаковкам кругов.
, а затем независимо Андреевым и Терстоном. Фактически, использование Терстоном упаковок кругов в его работе над геометрическими 3-многообразиями является причиной того серьезного внимания, которое в последнее время уделяется упаковкам кругов.
Помимо присущего им математического интереса, упаковки кругов нашли практическое применение в самых разных приложениях, включая «уплощение мозга» — процесс создания плоских карт сильно запутанной поверхности трехмерного мозга.
Результаты, описанные в этой статье, являются лишь верхушкой айсберга. Несмотря на то, что существуют связи между упаковками кругов и богатой математической мыслью, одним из настоящих удовольствий для меня было реализовать алгоритм для построения упаковок кругов и прогнать с его помощью множество примеров. Такого рода эксперименты создают почти тактильное понимание упаковок, что, в свою очередь, ведет к более глубокому пониманию классических аналитических функций.
Комментарии ?
Каталожные номера
- Кеннет Стефенсон.
 Введение в круговую упаковку. Издательство Кембриджского университета. 2005.
Введение в круговую упаковку. Издательство Кембриджского университета. 2005.Как следует из названия, эта книга — хорошее место для начала изучения упаковок кругов и включает в себя обширную библиографию.
- Кеннет Стефенсон. Circle Pack, бесплатное программное обеспечение для упаковки кругов.
Я написал свои собственные программы для создания изображений, описанных в этой статье, но CirclePack намного мощнее и стабильнее. Я модифицировал один из комплексов, включенных в CirclePack, и использовал его для создания некоторых изображений.
- Уильям Терстон. Геометрия и топология трехмерных многообразий. Доступно по адресу http://library.msri.org/books/gt3m/.
Основополагающие заметки Терстона, в которых излагается, среди прочего, его гипотеза геометризации для трехмерных многообразий. Эти заметки впервые появились в мимеографической форме, распространяемой Принстонским университетом. Первые несколько глав были отредактированы Сильвио Леви и впоследствии появились в виде книги, доступной в Princeton University Press по ссылке выше.

