Масса круга: Калькулятор веса стального круга
Содержание
Теоретическая масса круга. Расчёт удельного веса. Рассчитать удельный вес. Узнать какой удельный вес круга
Теоретическая масса 1 метра круга Мкр определяется по формуле: Мкр = L • ρу
L — длина круга;
ρу — теоретическая масса 1 м круга, вычисленная по его номинальным размерам:
При плотности стали ρ = 7850 кг/м3: ρу = 0,0061654 • d2, (кг/м)
d — диаметр круга в мм
| Диаметр круга, мм | Вес метра, кг | Метров в тонне |
| Круг 5 | 0.154 | 6493.51 |
| Круг 5.5 | 0. 187 187 | 5347.59 |
| Круг 6.0 | 0.222 | 4504.5 |
| Круг 6.3 | 0.245 | 4081.63 |
| Круг 6.5 | 0.261 | 3831.42 |
| Круг 7 | 0.302 | 3311.26 |
| Круг 8 | 0.395 | 2531.65 |
| Круг 9 | 0.499 | 2004.01 |
| Круг 10 | 0.617 | 1620.75 |
| Круг 11 | 0.746 | 1340.48 |
| Круг 12 | 0.888 | 1126.13 |
| Круг 13 | 1.042 | 959.69 |
| Круг 14 | 1.208 | 827.81 |
| Круг 15 | 1.387 | 720.98 |
| Круг 16 | 1. 578 578 | 633.71 |
| Круг 17 | 1.782 | 561.17 |
| Круг 18 | 1.998 | 500.5 |
| Круг 19 | 2.226 | 449.24 |
| Круг 20 | 2.466 | 405.52 |
| Круг 21 | 2.719 | 367.78 |
| Круг 22 | 2.984 | 335.12 |
| Круг 23 | 3.262 | 306.56 |
| Круг 24 | 3.551 | 281.61 |
| Круг 25 | 3.853 | 259.54 |
| Круг 26 | 4.168 | 239.92 |
| Круг 27 | 4.495 | 222.47 |
| Круг 28 | 4.834 | 206.87 |
| Круг 29 | 5. 185 185 | 192.86 |
| Круг 30 | 5.549 | 180.21 |
| Круг 31 | 5.925 | 168.78 |
| Круг 32 | 6.313 | 158.4 |
| Круг 33 | 6.714 | 148.94 |
| Круг 34 | 7.127 | 140.31 |
| Круг 35 | 7.553 | 132.4 |
| Круг 36 | 7.990 | 125.16 |
| Круг 37 | 8.440 | 118.48 |
| Круг 38 | 8.903 | 112.32 |
| Круг 39 | 9.378 | 106.63 |
| Круг 40 | 9.865 | 101.37 |
| Круг 41 | 10.364 | 96.49 |
| Круг 42 | 10. 876 876 | 91.95 |
| Круг 43 | 11.400 | 87.72 |
| Круг 44 | 11.936 | 83.78 |
| Круг 45 | 12.485 | 80.1 |
| Круг 46 | 13.046 | 76.65 |
| Круг 47 | 13.619 | 73.43 |
| Круг 48 | 14.205 | 70.4 |
| Круг 50 | 15.413 | 64.88 |
| Диаметр круга, мм | Вес метра, кг | Метров в тонне |
| Круг 52 | 16.671 | 59.98 |
| Круг 53 | 17.319 | 57.74 |
| Круг 54 | 17.978 | 55.62 |
| Круг 55 | 18. 650 650 | 53.62 |
| Круг 56 | 19.335 | 51.72 |
| Круг 58 | 20.740 | 48.22 |
| Круг 60 | 22.195 | 45.06 |
| Круг 62 | 23.700 | 42.19 |
| Круг 63 | 24.470 | 40.87 |
| Круг 65 | 26.049 | 38.39 |
| Круг 67 | 27.676 | 36.13 |
| Круг 68 | 28.509 | 35.08 |
| Круг 70 | 30.210 | 33.1 |
| Круг 72 | 31.961 | 31.29 |
| Круг 73 | 32.855 | 30.44 |
| Круг 75 | 34.680 | 28.84 |
| Круг 78 | 37. 510 510 | 26.66 |
| Круг 80 | 39.458 | 25.34 |
| Круг 82 | 41.456 | 24.12 |
| Круг 85 | 44.545 | 22.45 |
| Круг 87 | 46.666 | 21.43 |
| Круг 90 | 49.940 | 20.02 |
| Круг 92 | 52.184 | 19.16 |
| Круг 95 | 55.643 | 17.97 |
| Круг 97 | 58.010 | 17.24 |
| Круг 100 | 61.654 | 16.22 |
| Диаметр круга, мм | Вес метра, кг | Метров в тонне |
| Круг 105 | 67.973 | 14.71 |
| Круг 110 | 74.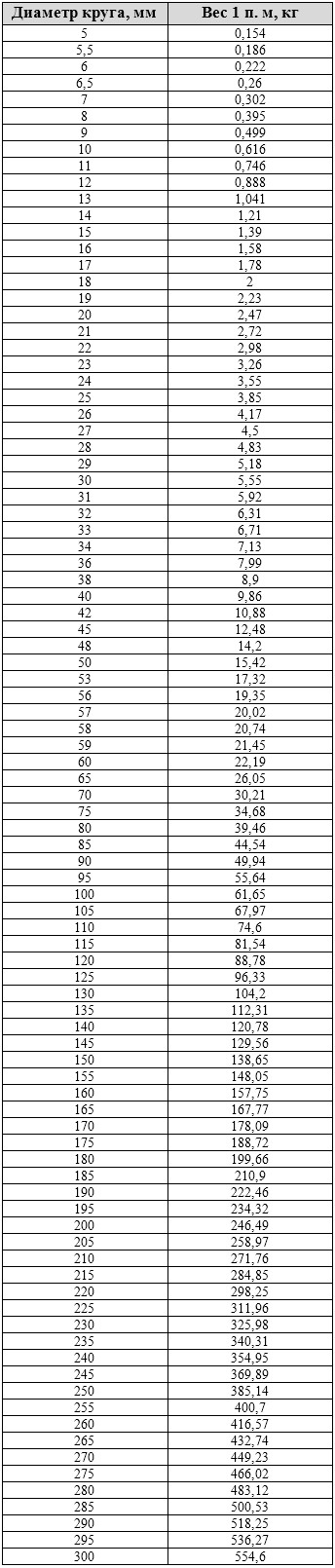 601 601 | 13.4 |
| Круг 115 | 81.537 | 12.26 |
| Круг 120 | 88.781 | 11.26 |
| Круг 125 | 96.334 | 10.38 |
| Круг 130 | 104.195 | 9.6 |
| Круг 135 | 112.364 | 8.9 |
| Круг 140 | 120.841 | 8.28 |
| Круг 145 | 129.627 | 7.71 |
| Круг 150 | 138.721 | 7.21 |
| Круг 155 | 148.123 | 6.75 |
| Круг 160 | 157.834 | 6.34 |
| Круг 165 | 167.852 | 5.96 |
| Круг 170 | 178.179 | 5.61 |
| Круг 175 | 188.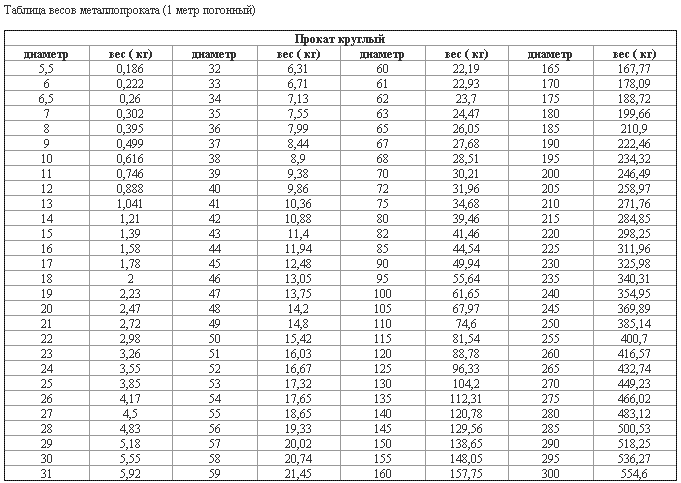 815 815 | 5.3 |
| Круг 180 | 199.758 | 5.01 |
| Круг 185 | 211.010 | 4.74 |
| Круг 190 | 222.570 | 4.49 |
| Круг 195 | 234.438 | 4.27 |
| Круг 200 | 246.615 | 4.05 |
| Круг 210 | 271.893 | 3.68 |
| Круг 220 | 298.404 | 3.35 |
| Круг 230 | 326.148 | 3.07 |
| Круг 240 | 355.126 | 2.82 |
| Круг 250 | 385.336 | 2.6 |
| Круг 260 | 416.779 | 2.4 |
| Круг 270 | 449.456 | 2.22 |
таблица для расчета массы круга
Стальной круг – вид проката, изготавливаемый способом горячей прокатки.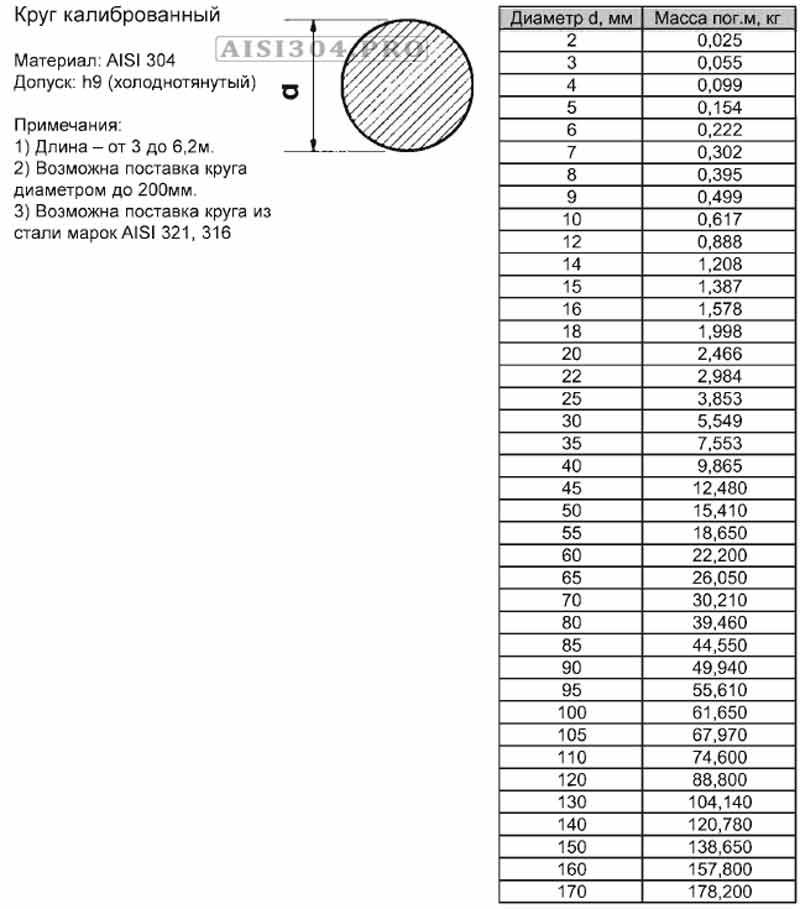 Горячекатаные изделия обладают хорошими прочностными характеристиками, но имеют невысокую точность размеров и качество поверхности. Для улучшения эстетических и размерных параметров используют калибрование или другие способы холодного деформирования. Горячекатаная продукция используется как в качестве подката при производстве холоднодеформированной продукции, так и при изготовлении крепежа, изделий для строительства, для устройства ограждений. Калиброванный круг – металлоизделия, применяемые в автомобиле- и машиностроении, для создания функционально-декоративных конструкций в строительстве и архитектуре.
Горячекатаные изделия обладают хорошими прочностными характеристиками, но имеют невысокую точность размеров и качество поверхности. Для улучшения эстетических и размерных параметров используют калибрование или другие способы холодного деформирования. Горячекатаная продукция используется как в качестве подката при производстве холоднодеформированной продукции, так и при изготовлении крепежа, изделий для строительства, для устройства ограждений. Калиброванный круг – металлоизделия, применяемые в автомобиле- и машиностроении, для создания функционально-декоративных конструкций в строительстве и архитектуре.
Основные характеристики стального круга
Стальной прокат с круглым поперечным сечением изготавливают из «черных» нелегированный сталей, низколегированных, коррозионностойких, жаростойких и жаропрочных. Их плотность зависит от конкретной марки и находится в диапазоне 7700-7900 кг/м3.
В нормативной документации и справочниках для вычисления массы 1 м погонного стального круга используют среднюю плотность стали – 7,85 кг/дм3. Более точные вычисления проводят с помощью онлайн-калькуляторов, в которых для расчетов используются точные значения плотностей основных марок стали.
Более точные вычисления проводят с помощью онлайн-калькуляторов, в которых для расчетов используются точные значения плотностей основных марок стали.
Сортамент горячекатаного круга определяется ГОСТом 2590-2006. В соответствии с этим нормативом горячекатаный прокат круглого сечения выпускается в диапазоне диаметров – 5-270 мм. Круги диаметрами – 270-300 мм изготавливаются только по индивидуальным заказам. Холоднокатаная продукция производится в соответствии с ГОСТом 7417-77, диапазон диаметров – 3-100 мм.
Определение веса 1 м металлического круга с помощью формулы
Для расчета массы 1 погонного метра стального проката с круглым сечением используют формулу M = 7,85*π*(d2/4000), в которой:
- 7,85 – среднее значение плотности стали, кг/дм3;
- π – 3,14;
- d – наружный диаметр проката с круглым поперечным сечением, мм.
Результат по этой формуле – в килограммах.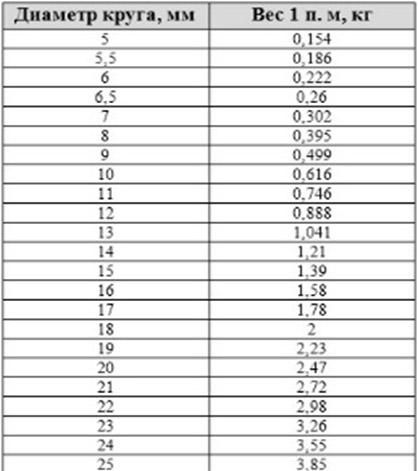 По этой же формуле можно подсчитать массу погонного метра и для других металлов и сплавов, подставив вместо значения 7,85 кг/дм3 плотность конкретного материала.
По этой же формуле можно подсчитать массу погонного метра и для других металлов и сплавов, подставив вместо значения 7,85 кг/дм3 плотность конкретного материала.
- алюминий – 2,7 кг/дм3;
- титан – 4,5 кг/дм3;
- цинк – 7,14 кг/дм3;
- олово – 7,29 кг/дм3;
- медь – 8,94 кг/дм3;
- свинец – 11,34 кг/дм3.
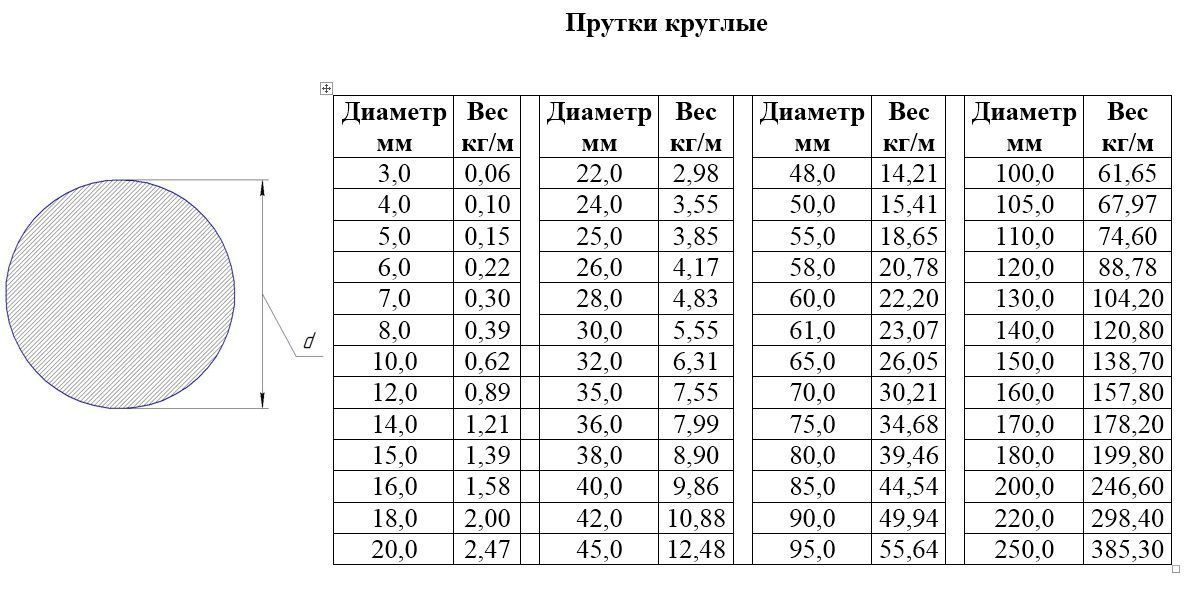
Для определения массы стального круга можно воспользоваться таблицей.
Таблица веса 1 м стального круга
| Диаметр, мм | Масса 1 м, кг | Диаметр, мм | Масса 1 м, кг | Диаметр, мм | Масса 1 м, кг |
| 5 | 0,154 | 34 | 7,13 | 110 | 74,6 |
| 6 | 0,222 | 36 | 7,99 | 120 | 88,78 |
| 7 | 0,302 | 38 | 8,9 | 130 | 104,2 |
| 8 | 0,395 | 40 | 9,86 | 140 | 120,84 |
| 9 | 0,499 | 42 | 10,88 | 150 | 138,72 |
| 10 | 0,616 | 45 | 12,48 | 160 | 157,83 |
| 11 | 0,746 | 48 | 14,2 | 170 | 178,18 |
| 12 | 0,888 | 50 | 15,42 | 180 | 199,76 |
| 13 | 1,041 | 53 | 17,32 | 190 | 222,57 |
| 14 | 1,21 | 56 | 19,32 | 200 | 246,62 |
| 16 | 1,58 | 58 | 20,74 | 210 | 271,89 |
| 18 | 2,0 | 60 | 22,19 | 220 | 298,4 |
| 20 | 2,47 | 65 | 26,05 | 230 | 326,15 |
| 22 | 2,98 | 70 | 30,25 | 240 | 355,13 |
| 24 | 3,55 | 75 | 34,68 | 250 | 385,34 |
| 26 | 4,17 | 80 | 39,46 | 260 | 416,57 |
| 28 | 4,83 | 85 | 44,54 | 270 | 449,22 |
| 30 | 5,55 | 90 | 49,94 | 280 | 483,12 |
| 32 | 6,31 | 100 | 61,65 | 554,6 |
Определение массы партии стального проката круглого сечения
Нормативная длина хлыстов проката круглого сечения зависит от марки стали, использованной для изготовления продукции.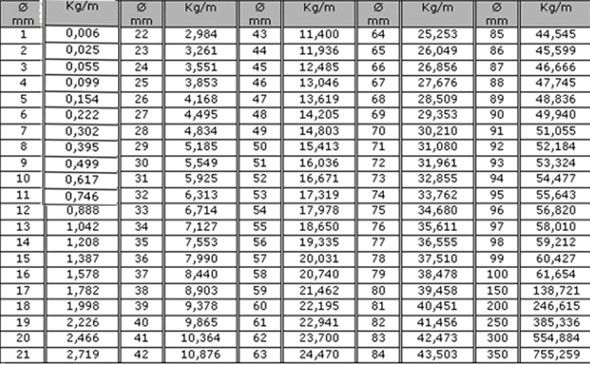 Для горячекатаной металлопродукции установлены следующие нормы:
Для горячекатаной металлопродукции установлены следующие нормы:
- прокат из «черных» нелегированных марок обыкновенного качества и низкоуглеродистой стали – 2-12 м;
- металлоизделия из углеродистой качественной стали и легированных марок – 2-6 м;
- продукция из высоколегированной стали – 1-6 м.
Для холоднокатаного проката:
- из «черной», низколегированной, автоматной, низколегированной, легированной стали – 2-6,5 м;
- из высоколегированных марок – 1,5-6,5 м.
Для определения массы партии проката круглого сечения длину отрезков умножают на их количество, а затем – на массу 1 м погонного.
исчисление — Центр масс окружности
Задавать вопрос
спросил
Изменено
10 лет, 2 месяца назад
Просмотрено
17 тысяч раз
$\begingroup$
9{?}_{?} \ро ? dA$$
«?» значит не знаю что туда поставить. 2)) * dr. Удивительно, но этот интеграл оценивается в начале координат!
2)) * dr. Удивительно, но этот интеграл оценивается в начале координат!
$\endgroup$
3
$\begingroup$
Ваш первый интеграл верен. Однако для нахождения центра масс сферы требуется три интеграла, по одному на каждую координату. Каждый из этих интегралов будет похож на тот, который вы записали.
$$
\bar x = \frac{1}{M}\int_{S} \rho xdA
$$
$$
\bar y = \frac{1}{M}\int_{S} \rho ydA
$$
$$
\bar z = \frac{1}{M}\int_{S} \rho zdA
$$ 92}} \rho (x,y) ydx dy$, где $r$ — радиус
$\endgroup$
7
Математика кругового движения
Существуют три математические величины, которые представляют для нас наибольший интерес при анализе движения объектов по окружности. Этими тремя величинами являются скорость, ускорение и сила. Скорость объекта, движущегося по окружности, определяется следующим уравнением.
Ускорение объекта, движущегося по кругу, можно определить с помощью любого из двух следующих уравнений.
Уравнение справа (выше) получено из уравнения слева заменой выражения для скорости.
Суммарная сила ( F сеть ), действующая на объект, движущийся по кругу, направлена внутрь. Хотя на объект может действовать более одной силы, векторная сумма всех их должна составлять результирующую силу. В общем, внутренняя сила больше, чем внешняя сила (если она есть), так что внешняя сила уравновешивается, а неуравновешенная сила направлена в центр круга. Суммарная сила связана с ускорением объекта (как всегда) и, таким образом, определяется следующими тремя уравнениями:0003
Уравнения в середине (вверху) и справа (вверху) получаются из уравнения слева заменой выражений для ускорения.
Этот набор уравнений кругового движения можно использовать двумя способами:
- как «рецепт» для решения алгебраических задач для решения неизвестной величины.
- как руководство к размышлению о том, как изменение одной величины повлияет на другую величину.
Эти два способа показаны ниже.
Уравнения как руководство к мышлению
Уравнение выражает математическую связь между величинами, присутствующими в этом уравнении. Например, уравнение для второго закона Ньютона определяет, как ускорение связано с результирующей силой и массой объекта.
Связь, выраженная уравнением, заключается в том, что ускорение объекта прямо пропорционально действующей на него чистой силе. Другими словами, чем больше значение чистой силы, тем больше будет значение ускорения. По мере увеличения чистой силы ускорение увеличивается. На самом деле, если бы результирующая сила увеличилась в 2 раза, уравнение предсказало бы, что ускорение увеличилось бы в 2 раза. Точно так же, если бы результирующая сила уменьшилась в 2 раза, уравнение предсказало бы, что ускорение уменьшилось бы в 2,9 раза.0003
Уравнение второго закона Ньютона также раскрывает связь между ускорением и массой. Согласно уравнению, ускорение объекта обратно пропорционально массе объекта. Другими словами, чем больше значение массы, тем меньше значение ускорения. С увеличением массы ускорение уменьшается. На самом деле, если бы масса увеличилась в 2 раза, уравнение предсказало бы, что ускорение уменьшится в 2 раза. Точно так же, если бы масса уменьшилась в 2 раза, уравнение предсказало бы, что ускорение уменьшится. увеличить в 2,9 раза0003
Согласно уравнению, ускорение объекта обратно пропорционально массе объекта. Другими словами, чем больше значение массы, тем меньше значение ускорения. С увеличением массы ускорение уменьшается. На самом деле, если бы масса увеличилась в 2 раза, уравнение предсказало бы, что ускорение уменьшится в 2 раза. Точно так же, если бы масса уменьшилась в 2 раза, уравнение предсказало бы, что ускорение уменьшится. увеличить в 2,9 раза0003
Как упоминалось ранее, уравнения позволяют делать прогнозы о влиянии изменения одной величины на другую величину. Поскольку уравнение второго закона Ньютона показывает три величины, каждая из которых возведена в первую степень, предсказательная способность уравнения довольно проста. Предсказательная способность уравнения усложняется, когда одна из величин, входящих в уравнение, возводится в степень. Например, рассмотрим следующее уравнение, связывающее результирующую силу ( F net ) к скорости ( v ) объекта, движущегося в равномерном круговом движении.
Это уравнение показывает, что результирующая сила, необходимая для движения объекта по кругу, прямо пропорциональна квадрату скорости объекта. Для постоянной массы и радиуса F сеть пропорциональна скорости 2 .
Коэффициент изменения чистой силы равен квадрату коэффициента изменения скорости. Следовательно, если скорость объекта удваивается, чистая сила, необходимая для кругового движения этого объекта, увеличивается в четыре раза. А если скорость объекта уменьшится вдвое (уменьшится в 2 раза), необходимая результирующая сила уменьшится в 4 раза.0003
Уравнения как средство решения задач
Приведенные выше математические уравнения для движения объектов по окружности можно использовать для решения задач о движении по окружности, в которых необходимо определить неизвестную величину. Процесс решения задачи о круговом движении очень похож на любую другую задачу на уроках физики. Этот процесс включает в себя внимательное прочтение задачи, идентификацию известной и требуемой информации в переменной форме, выбор соответствующих уравнений, подстановку известных значений в уравнение и, наконец, алгебраические манипуляции с уравнением для определения отвечать. Рассмотрим применение этого процесса к следующим двум задачам о круговом движении.
Этот процесс включает в себя внимательное прочтение задачи, идентификацию известной и требуемой информации в переменной форме, выбор соответствующих уравнений, подстановку известных значений в уравнение и, наконец, алгебраические манипуляции с уравнением для определения отвечать. Рассмотрим применение этого процесса к следующим двум задачам о круговом движении.
Автомобиль массой 900 кг, движущийся со скоростью 10 м/с, совершает поворот по окружности радиусом 25,0 м. Определить ускорение и результирующую силу, действующую на автомобиль. |
Решение этой задачи начинается с идентификации известной и запрашиваемой информации.
Известная информация:
| Запрашиваемая информация:
|
Чтобы определить ускорение автомобиля, используйте уравнение a = v 2 / R. Решение выглядит следующим образом:
Решение выглядит следующим образом:
а = (10,0 м/с) 2 / (25,0 м)
а = (100 м 2 /с 2 ) / (25,0 м)
а = 4 м/с 2
Чтобы определить результирующую силу, действующую на автомобиль, используйте уравнение F net = m•a. Решение заключается в следующем.
F нетто = (900 кг) • (4 м/с 2 )
F нетто = 3600 Н
Полузащитник весом 95 кг делает разворот на футбольном поле. Полузащитник прокладывает путь, который представляет собой часть круга радиусом 12 метров. Полузащитник делает четверть оборота по кругу за 2,1 секунды. |
Решение этой задачи начинается с идентификации известной и запрашиваемой информации.
Известная информация:
| Запрашиваемая информация:
|
Чтобы определить скорость полузащитника, используйте уравнение v = d / t, где d — одна четвертая длины окружности, а время — 2,1 с. Решение выглядит следующим образом:
v = (0,25 • 2 • пи • R) / t
v = (0,25 • 2 • 3,14 • 12,0 м) / (2,1 с)
v = 8,97 м/с
Для определения ускорения полузащитника воспользуемся уравнением a = v 2 /R. Решение будет следующим:
Решение будет следующим:
а = (8,97 м/с) 2 / (12,0 м)
а = (80,5 м 2 /с 2 ) / (12,0 м)
а = 6,71 м/с 2
Чтобы определить результирующую силу, действующую на полузащитника, используйте уравнение F нетто = м•а. Решение заключается в следующем.
F нетто = (95,0 кг)*(6,71 м/с 2 )
F нетто = 637 Н
В уроке 2 этого модуля принципы кругового движения и приведенные выше математические уравнения будут объединены для объяснения и анализа различных реальных сценариев движения, включая аттракционы в парке развлечений и круговые движения в легкой атлетике.
Мы хотели бы предложить…
Иногда недостаточно просто прочитать об этом. Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием либо нашего интерактивного равномерного кругового движения, либо нашего моделирования горизонтального круга. Вы можете найти их в разделе Physics Interactives на нашем сайте. Интерактивное приложение «Равномерное круговое движение» позволяет учащимся в интерактивном режиме исследовать взаимосвязь между скоростью, ускорением и силой для объекта, движущегося по кругу. Наше моделирование горизонтального круга моделирует движение трех разных объектов, движущихся по горизонтальному кругу, при этом анализируя влияние, которое изменения переменной могут оказать на движение.
Мы хотели бы предложить вам совместить чтение этой страницы с использованием либо нашего интерактивного равномерного кругового движения, либо нашего моделирования горизонтального круга. Вы можете найти их в разделе Physics Interactives на нашем сайте. Интерактивное приложение «Равномерное круговое движение» позволяет учащимся в интерактивном режиме исследовать взаимосвязь между скоростью, ускорением и силой для объекта, движущегося по кругу. Наше моделирование горизонтального круга моделирует движение трех разных объектов, движущихся по горизонтальному кругу, при этом анализируя влияние, которое изменения переменной могут оказать на движение.
Посетите: Интерактивное равномерное круговое движение || Моделирование горизонтального круга
Проверьте свое понимание
1. Анна Литикал тренируется дома с демонстрацией центростремительной силы. Она наполняет ведро водой, привязывает его к прочной веревке и раскручивает по кругу.

 Определить скорость, ускорение и чистую силу, действующую на полузащитника.
Определить скорость, ускорение и чистую силу, действующую на полузащитника.