Расчет двутавровой балки на прочность: Расчёт металлической балки онлайн (калькулятор)
Содержание
Расчет прочности и жесткости сварной балки двутаврового сечения
а – схема изменения сечения по длине балки; б – сечение балки и эпюры напряжений.
Цель: Проверка режима расчета сопротивления сечений в постпроцессоре «Сталь» вычислительного комплекса SCAD
Задача: Проверить расчетное сечение сварного двутаврового профиля для главных балок пролетом 18 м в балочной клетке нормального типа. Верхний пояс главных балок раскреплен балками настила, расположенными с шагом 1,125 м.
Источник: Металлические конструкции : учебник для студ. Учреждений высш. проф. Образования / [Ю. И. Кудишин, Е. И. Беленя, В. С. Игнатьева и др.] ; под. Ред. Ю. И. Кудишина. — 13-е изд., испр. — М. : Издательский центр «Академия», 2011. С 195.
Соответствие нормативным документам: СНиП II-23-81*, СП 16.13330, ДБН В.2.6-163:2010.
Имя файла с исходными данными:
4. 1 SectionResistance_Example_4.1.spr;
1 SectionResistance_Example_4.1.spr;
отчет — 4.1 SectionResistance_Example_4.1.doc
Исходные данные:
Параметры SCAD Постпроцессор СТАЛЬ:
[Элемент № 1] Усилия
N Макс. 0 Т Макс. 0 Т | My Макс. 0 Т*м Макс. 353,65 Т*м | Mz Макс. 0 Т*м Макс. 0 Т*м |
Mk Макс. 0 Т*м Макс. 0 Т*м | Qz Макс. 94,31 Т
| Qy Макс. 0 Т Макс. |
Длина стержня 3,75 м |
Расчет выполнен по СНиП II-23-81*
Конструктивный элемент Section
Сталь: C255
Длина элемента 3,75 м
Предельная гибкость для сжатых элементов: 220
Предельная гибкость для растянутых элементов: 300
Коэффициент условий работы 1
Коэффициент надежности по ответственности 1
Расчетная длина в плоскости XoY 1,125 м
Расчетная длина в плоскости XoZ 18 м
Расстояние между точками раскрепления на плоскости 1,125 м
Сечение
Результаты расчета | Проверка | Коэффициент использования |
|---|---|---|
п.5.12 | Прочность при действии изгибающего момента My | 0,99 |
пп. | Прочность при действии поперечной силы Qz | 0,41 |
пп.5.24,5.25 | Прочность при совместном действии продольной силы и изгибающих моментов без учета пластики | 0,99 |
п. 5.14* | Прочность по приведенным напряжениям при одновременном действии изгибающего момента и поперечной силы | 0,86 |
п.5.15 | Устойчивость плоской формы изгиба | 0,99 |
пп.6.15,6.16 | Предельная гибкость в плоскости XoY | 0,09 |
пп.6.15,6.16 | Предельная гибкость в плоскости XoZ | 0,09 |
Коэффициент использования 0,99 — Прочность при действии изгибающего момента My
Ручной расчет (СНиП II-23-81*)
1. {2} \]
{2} \]
4. Гибкость элемента в плоскости действия момента:
\[ \lambda_{y} =\frac{\mu l}{i_{y} }=\frac{18\cdot 100}{63,715}=28,2508. \]
5. Гибкость элемента из плоскости действия момента:
\[ \lambda_{y} =\frac{\mu l}{i_{y} }=\frac{1,125\cdot 100}{4,265}=26,3775. \]
Сравнение решений
Фактор | Источник | Ручной счет | SCAD | Отклонение от ручного счета, % |
|---|---|---|---|---|
Прочность при действии изгибающего момента Му | 0,99 | 15083,826/15187,794 = 0,993 | 0,993 | 0,0 |
Прочность при действии поперечной силы Qz | – | 5,4388/13,3 = 0,4089 | 0,408 | 0,0 |
Прочность по приведенным напряжениям | – | 22,7715/1,15/23 = 0,861 | 0,861 | 0,0 |
Прочность при совместном действии продольной силы и изгибающих моментов без учета пластики | – | 15083,826/15187,794 = 0,993 | 0,993 | 0,0 |
Устойчивость плоской формы изгиба | – | 15083,826/1/15187,794 = 0,993 | 0,993 | 0,0 |
Предельная гибкость в плоскости XoY | – | 26,3775/300 = 0,088 | 0,088 | 0,0 |
Предельная гибкость в плоскости XoZ | – | 28,2508/300 = 0,094 | 0,094 | 0,0 |
Калькулятор расчета металлической двутавровой балки на прогиб, прочность
A1 6 ммА1 8 ммA1 10 ммА1 12 ммА1 14 ммА1 16 ммА1 18 ммА1 20 ммА3 35ГС 6 ммА3 35ГС 8 ммА3 35ГС 10 ммА3 35ГС 12 ммА3 35ГС 14 ммА3 35ГС 16 ммА3 35ГС 18 ммА3 35ГС 20 ммА3 35ГС 22 ммА3 35ГС 25 ммА3 35ГС 28 ммА3 35ГС 32 ммА3 35ГС 36 ммА3 25Г2С 8 ммА3 25Г2С 10 ммА3 25Г2С 12 ммА3 25Г2С 14 ммА3 25Г2С 16 ммА3 25Г2С 18 ммА3 25Г2С 20 ммА3 25Г2С 22 ммА3 25Г2С 25 ммА3 25Г2С 28 ммА3 25Г2С 32 ммА3 25Г2С 36 ммA500С 8 ммA500С 10 ммA500С 12 ммA500С 14 ммA500С 16 ммA500С 18 ммA500С 20 ммA500С 22 ммA500С 25 ммА500С 28 ммA500С 32 ммA500С 36 ммA500С 40 ммA400С 8 ммA400С 10 ммA400С 12 ммАт800 12 ммАт800 14 мм10, г/к12, г/к14, г/к16, г/к18, г/к20, г/к30, г/к36, г/к45, г/к24М30М36М45М10Б112Б114Б116Б120Б125Б130Б135Б140Б145Б150Б155Б160Б125Б230Б235Б240Б245Б255Б260Б220Ш125Ш130Ш135Ш140Ш145Ш150Ш130Ш235Ш240Ш250Ш220К125К130К135К140К120К225К230К235К240К220Б1 (09Г2С)25Б1 (09Г2С)30Б1 (09Г2С)35Б1 (09Г2С)40Б1 (09Г2С)45Б1 (09Г2С)50Б1 (09Г2С)55Б1 (09Г2С)60Б1 (09Г2С)25Б2 (09Г2С)30Б2 (09Г2С)35Б2 (09Г2С)40Б2 (09Г2С)45Б2 (09Г2С)55Б2 (09Г2С)20К1 (09Г2С)25К1 (09Г2С)30К1 (09Г2С)35К1 (09Г2С)25К2 (09Г2С)30К2 (09Г2С)35К2 (09Г2С)20Ш1 (09Г2С)25Ш1 (09Г2С)30Ш1 (09Г2С)35Ш1 (09Г2С)45Ш1 (09Г2С)30Ш2 (09Г2С)35Ш2 (09Г2С)50Ш2 (09Г2С)1,5х1250 г/к2,0х1250 г/к2,5х1250 г/к3,0х1250 г/к4,0х1500 г/к5,0х1500 г/к6,0х1500 г/к8,0х1500 г/к10,0х1500 г/к12,0х1500 г/к14,0х1500 г/к16,0х1500 г/к18,0х1500 г/к20,0х1500 г/к25,0х1500 г/к30,0х1500 г/к36,0х1500 г/к40,0х1500 г/к50,0х1500 г/к60,0х1500 г/к80,0х1500 г/к100,0х1500 г/к4,0х1500 г/к (09Г2С)5,0х1500 г/к (09Г2С)6,0х1500 г/к (09Г2С)8,0х1500 г/к (09Г2С)10,0х1500 г/к (09Г2С)12,0х1500 г/к (09Г2С)14,0х1500 г/к (09Г2С)16,0х1500 г/к (09Г2С)18,0х1500 г/к (09Г2С)20,0х1500 г/к (09Г2С)25,0х1500 г/к (09Г2С)30,0х1500 г/к (09Г2С)36,0х1500 г/к (09Г2С)50,0х1500 г/к (09Г2С)0,50х1250 х/к0,60х1250 х/к0,70х1250 х/к0,80х1250 х/к0,90х1250 х/к1,0х1250 х/к1,2х1250 х/к1,4х1250 х/к1,5х1250 х/к1,8х1250 х/к2,0х1250 х/к2,5х1250 х/к3,0х1250 х/к0,50х1250 х/к оц. 0,55х1250 х/к оц.0,70х1250 х/к оц.0,80х1250 х/к оц.1,0х1250 х/к оц.1,2х1250 х/к оц.1,5х1250 х/к оц.2,0х1250 х/к оц.3,0 мм (чечевица)4,0 мм (чечевица)5,0 мм (чечевица)6,0 мм (чечевица)8,0 мм (чечевица)ПВЛ-406ПВЛ-408ПВЛ-410ПВЛ-506ПВЛ-508ПВЛ-51025х25х4,032х32х4,035х35х4,040х40х4,045х45х4,045х45х5,050х50х5,063х63х5,063х63х6,070х70х6,075х75х5,075х75х6,075х75х8,080х80х6,080х80х8,090х90х7,090х90х8,0100х100х7,0100х100х8,0100х100х10,0110х110х8,0125х125х8,0125х125х9,0125х125х10,0125х125х12,0140х140х9,0140х140х10,0160х160х10,0160х160х12,0180х180х12,0200х200х12,0200х200х16,063х40х6,075х50х5,075х50х6,0100х63х6,0100х63х8,05П6,5П8П10П12П14П16П18П20П22П24П27П30П40П5У6,5У8У10У12У14У16У18У20У22У24У27У30У40У80х60х4,0100х50х4,0100х50х5,0120х50х3,0120х60х4,0120х60х5,0160х80х4,0180х80х5,0250х125х6,015х2,515×2,820х2,825х3,232х3,240х3,040х3,550х3,050х3,515×2,820х2,825х3,232х3,240х3,550х3,557х3,057х3,576х3,076х3,589х3,089х3,589х4,0102х3,0102х3,5102х4,0108х3,5108х4,0114х4,0114х4,5127х4,5133х4,0133х4,5159х4,0159х4,5159х5,0159х6,0219х4,5219х5,0219х6,0219х8,0273х5,0273х6,0273х7,0273х8,0325х6,0325х7,0325х8,0426х6,0426х7,0426х8,0426х9,0530х7,0530х8,0530х10,057х3,576х3,589х3,5108х3,5530х7,0530х8,0530х9,0530х10,0530х12,0630х8,0630х9,0630х10,0630х12,0720х8,0720х9,0720х10,0720х11,0720х12,0820х8,0820х9,0820х10,0820х11,0820х12,0530х7,0530х8,0530х9,0530х10,0530х12,0720х8,0720х9,0720х10,0720х11,0720х12,0820х9,0820х10,01020х10,01020х12,01020х14,01220х11,01220х12,01220х14,01420х14,057х3,557х4,057х5,057х6,076х3,576х4,076х5,076х6,083х4,089х3,589х4,089х5,089х6,0102х4,0102х5,0102х6,0108х4,0108х5,0108х6,0114х5,0114х6,0121х6,0127х5,0133х4,0133х4,5133х5,0133х6,0133х8,0146х5,0146х6,0159х5,0159х6,0159х7,0159х8,0168х6,0168х7,0168х8,0219х6,0219х7,0219х8,0219х10,0273х7,0273х8,0273х10,0325х8,0325х10,0377х9,0426х9,0426х10,010х2,014х2,016х2,016х3,018х2,018х3,020х2,022х2,022х2,522х3,025х2,025х3,027х3,028х3,028х4,028х7,032х3,034х3,538х3,038х4,040х3,040х3,542х3,042х5,045х3,045х6,048х3,051х2,551х3,057х3,060х3,063х4,015х1,520х1,520х2,025х1,525х2,030х1,530х2,040х1,540х2,040х2,540х3,050х2,050х3,050х4,060х2,060х3,060х4,080х3,080х4,080х5,0100×4,0100×5,0100×6,0120х4,0120х5,0120х8,0140х5,0140х6,0160х4,0160х5,0160х6,0180х8,0100х4,0100х5,0120х4,0120х5,0140х5,0140х6,0160х5,0160х6,0160х8,020х2,025х2,030х2,040х2,040х3,050х2,050х2,550х3,050х4,060х2,060х3,080х5,080х6,0100х5,0140х5,0140х6,028х25х1,530х20х1,540х20х1,540х20х2,040х25х1,540х25х2,050х25х1,550х25х2,050х25х2,550х30х2,060х30х2,060х30х2,560х30х3,060х40х2,060х40х2,560х40х3,080х40х2,080х40х3,080х40х4,080х60х4,0100х50х3,0100х50х4,0100х60х4,0120х60х4,0120x80x4,0120х80х6,0140x60x4,0150х100х6,0160х80х5,0160х120х4,028х25х2,040х20х2,040х25х2,050х25х2,050х25х2,560х30х2,060х30х2,560х40х2,060х40х2,580х40х2,080х60х4,0120х80х4,0150х100х6,0160х120х4,0Ø 6,5 мм (в бухтах)Ø 8 мм (в бухтах)Ø 10 мм (в бухтах)Ø 12 ммØ 14 ммØ 16 ммØ 18 ммØ 20 ммØ 22 ммØ 25 ммØ 28 ммØ 30 ммØ 32 ммØ 34 ммØ 36 ммØ 40 ммØ 42 ммØ 45 ммØ 50 ммØ 52 ммØ 56 ммØ 60 ммØ 70 ммØ 80 ммØ 90 ммØ 100 ммØ 110 мм10 мм12 мм14 мм16 мм18 мм20 мм25 мм20х4,025х4,025х5,030х4,030х5,040х4,040х5,040х6,050х5,060х5,060х6,080х6,0100х8,0
0,55х1250 х/к оц.0,70х1250 х/к оц.0,80х1250 х/к оц.1,0х1250 х/к оц.1,2х1250 х/к оц.1,5х1250 х/к оц.2,0х1250 х/к оц.3,0 мм (чечевица)4,0 мм (чечевица)5,0 мм (чечевица)6,0 мм (чечевица)8,0 мм (чечевица)ПВЛ-406ПВЛ-408ПВЛ-410ПВЛ-506ПВЛ-508ПВЛ-51025х25х4,032х32х4,035х35х4,040х40х4,045х45х4,045х45х5,050х50х5,063х63х5,063х63х6,070х70х6,075х75х5,075х75х6,075х75х8,080х80х6,080х80х8,090х90х7,090х90х8,0100х100х7,0100х100х8,0100х100х10,0110х110х8,0125х125х8,0125х125х9,0125х125х10,0125х125х12,0140х140х9,0140х140х10,0160х160х10,0160х160х12,0180х180х12,0200х200х12,0200х200х16,063х40х6,075х50х5,075х50х6,0100х63х6,0100х63х8,05П6,5П8П10П12П14П16П18П20П22П24П27П30П40П5У6,5У8У10У12У14У16У18У20У22У24У27У30У40У80х60х4,0100х50х4,0100х50х5,0120х50х3,0120х60х4,0120х60х5,0160х80х4,0180х80х5,0250х125х6,015х2,515×2,820х2,825х3,232х3,240х3,040х3,550х3,050х3,515×2,820х2,825х3,232х3,240х3,550х3,557х3,057х3,576х3,076х3,589х3,089х3,589х4,0102х3,0102х3,5102х4,0108х3,5108х4,0114х4,0114х4,5127х4,5133х4,0133х4,5159х4,0159х4,5159х5,0159х6,0219х4,5219х5,0219х6,0219х8,0273х5,0273х6,0273х7,0273х8,0325х6,0325х7,0325х8,0426х6,0426х7,0426х8,0426х9,0530х7,0530х8,0530х10,057х3,576х3,589х3,5108х3,5530х7,0530х8,0530х9,0530х10,0530х12,0630х8,0630х9,0630х10,0630х12,0720х8,0720х9,0720х10,0720х11,0720х12,0820х8,0820х9,0820х10,0820х11,0820х12,0530х7,0530х8,0530х9,0530х10,0530х12,0720х8,0720х9,0720х10,0720х11,0720х12,0820х9,0820х10,01020х10,01020х12,01020х14,01220х11,01220х12,01220х14,01420х14,057х3,557х4,057х5,057х6,076х3,576х4,076х5,076х6,083х4,089х3,589х4,089х5,089х6,0102х4,0102х5,0102х6,0108х4,0108х5,0108х6,0114х5,0114х6,0121х6,0127х5,0133х4,0133х4,5133х5,0133х6,0133х8,0146х5,0146х6,0159х5,0159х6,0159х7,0159х8,0168х6,0168х7,0168х8,0219х6,0219х7,0219х8,0219х10,0273х7,0273х8,0273х10,0325х8,0325х10,0377х9,0426х9,0426х10,010х2,014х2,016х2,016х3,018х2,018х3,020х2,022х2,022х2,522х3,025х2,025х3,027х3,028х3,028х4,028х7,032х3,034х3,538х3,038х4,040х3,040х3,542х3,042х5,045х3,045х6,048х3,051х2,551х3,057х3,060х3,063х4,015х1,520х1,520х2,025х1,525х2,030х1,530х2,040х1,540х2,040х2,540х3,050х2,050х3,050х4,060х2,060х3,060х4,080х3,080х4,080х5,0100×4,0100×5,0100×6,0120х4,0120х5,0120х8,0140х5,0140х6,0160х4,0160х5,0160х6,0180х8,0100х4,0100х5,0120х4,0120х5,0140х5,0140х6,0160х5,0160х6,0160х8,020х2,025х2,030х2,040х2,040х3,050х2,050х2,550х3,050х4,060х2,060х3,080х5,080х6,0100х5,0140х5,0140х6,028х25х1,530х20х1,540х20х1,540х20х2,040х25х1,540х25х2,050х25х1,550х25х2,050х25х2,550х30х2,060х30х2,060х30х2,560х30х3,060х40х2,060х40х2,560х40х3,080х40х2,080х40х3,080х40х4,080х60х4,0100х50х3,0100х50х4,0100х60х4,0120х60х4,0120x80x4,0120х80х6,0140x60x4,0150х100х6,0160х80х5,0160х120х4,028х25х2,040х20х2,040х25х2,050х25х2,050х25х2,560х30х2,060х30х2,560х40х2,060х40х2,580х40х2,080х60х4,0120х80х4,0150х100х6,0160х120х4,0Ø 6,5 мм (в бухтах)Ø 8 мм (в бухтах)Ø 10 мм (в бухтах)Ø 12 ммØ 14 ммØ 16 ммØ 18 ммØ 20 ммØ 22 ммØ 25 ммØ 28 ммØ 30 ммØ 32 ммØ 34 ммØ 36 ммØ 40 ммØ 42 ммØ 45 ммØ 50 ммØ 52 ммØ 56 ммØ 60 ммØ 70 ммØ 80 ммØ 90 ммØ 100 ммØ 110 мм10 мм12 мм14 мм16 мм18 мм20 мм25 мм20х4,025х4,025х5,030х4,030х5,040х4,040х5,040х6,050х5,060х5,060х6,080х6,0100х8,0
Расчет
Расчет балок на изгиб и прогиб, крутящие моменты и выбор двутавра для монтажа
Главная / Статьи / Расчет балок
Расчет нагрузки двутавровой балки – определяем нагрузку на изгиб
Расчет нагрузки двутавровой балки осуществляется с целью вычисления номера из реестра металлопроката при составлении проекта основных конструкций и сооружений, а так же производства по ГОСТ или СТО АСЧМ. Он выполняется точно по формулам и таблицам, а вычисленные значения оказывают влияние на проектировку и ход строительных работ, также на рабочую функциональность и технические характеристики при эксплуатации.
Он выполняется точно по формулам и таблицам, а вычисленные значения оказывают влияние на проектировку и ход строительных работ, также на рабочую функциональность и технические характеристики при эксплуатации.
Сфера применения и параметры металлических двутавров
Главное предназначение двутавра во время проектировки любого типа сооружения заключается в изготовлении безопасной и крепкой несущей конструкции. В отличие от железобетонных опорных оснований, применение двутавровой балки дает возможность наиболее увеличить площадь пролетов частных либо коммерческих строений и снизить предельный вес важных опорных элементов. Благодаря этому, значительно увеличивается прибыльность строительства и решается ряд важных инженерных задач.
Двутавровая балка подбирается из расчета длины и массы. Балочная продукция бывает обычного горячего проката либо специализированного, и иметь параллельные и с наклоном полочные грани. Они производятся из углеродистой или из низколегированной стали и применяются во всех строительных отраслях.
Согласно требованиям стандартизации 8239-89, размер металлического двутавра варьируется от трех до двенадцати метров. По способу применения данные элементы являются балочными, колонными, широко — полочными либо монорельсными, использующиеся при возведении подвесных элементов подкрановых путей и мостов. Определяется категория балки по специальному маркированию в таблице металлопроката, а точнее в ГОСТе и СТО АСЧМ, а правила применения и монтажа регламентированы документацией СНиП (Строительных норм и правил).
Масса двутавра определяется по утвержденному графику, в котором четко указан определенный числовой символ и обозначение балки, а еще немало важные параметры (ширина, высота, объемность полок и оптимальная толщина граней). Таким образом, для вычисления массы, по реестру требуется учесть установленный нетто погонного метра. К примеру, изделие под номером 46, при массе 65,5 кг, обладает длинной 15,5 метров.
Кроме расчетов массы, которые выполняются при помощи обычного калькулятора, во время проектирования важно вычислить наибольшую и наименьшую совокупность сил на предмет повреждения.
Расчеты основываются на следующих характеристиках металлопрофиля:
- Минимальная и максимальная дистанция между полками, беря во внимание их размеры.
- Наибольшая нагрузочная величина на проектируемое сооружение.
- Тип и геометрические формы изделий, способ фиксирования.
- Плоскость поперечного диаметра.
- Возникают ситуации, когда для вычислений требуется укладочный шаг (промежуток укладывания балок относительно друг друга).
Расчет двутавровой балки зачастую производится по критериям безопасности и просчета изгиба. Для достижения наиболее высокоточных значений в таблице металлопроката и основных требованиях указываются все дополнительные значения (момент сопротивления, делящийся на осевой и статический). Кроме этого нужно учитывать нагрузку на двутавр, зависящую от разновидностей металла, из которого изготавливается двутавр, и метод производства (сварка либо прокат). При сварном производстве во время расчетов добавляется около 30% к опорной нагрузке металлопрофиля.
Выбор металлической балки по номеру и примеры расчета
В реестре металлопроката все номера двутавровых швеллеров указаны по всем требованиям ГОСТ стандарта. Таким образом, подбор номера обязан производиться, учитывая рабочую нагрузку, расстояние пролетов и вес продукции. К примеру, если наибольшая нагрузка на двутавр равняется 300 кг/м.п, из таблицы берется двутавровая балка под цифрой 16, при этом промежуточная дистанция равняется шести метрам при укладочном шаге от 1 до 1,2 метров. При подборе 20 металлопрофиля нагрузка на двутавр сильнее – до 500 кг/ м.п, а шаг соответственно до 1,5 метра. Изделие с порядковой нумерацией 10 либо 12 обозначает предельно установленную нагрузку до 300 кг/м.п и уменьшение пролета.
Таким образом, расчетные действия, какую нагрузку может выдержать металлическое изделие, осуществляются так:
- Высчитывается единица нагрузки на двутавр, давящая на опорное основание с учетом массы металлопрофиля, которая рассматривается на один погонный метр изделия.

- Полученная величина, согласно нормативным документам, перемножается на коэффициент прочности стали, указанным в ГОСТ.
- Пользуясь данными расчетных величин, требуется вычислить значение сопротивляющегося момента.
- Далее из полученного результата, выбираем нужный элемент из реестра металлопроката.
- Делая расчеты опорной физической нагрузки при определении профиля, советуем подбирать числа на пару строк больше имеющегося значения. Несущая особенность металлопрофиля определяется при вычислении двутавра на сгибание.
Как марки стали воздействуют на предстоящее проектирование?
При вычислении прочности опорной балки следует учитывать марку металла, использующегося в технологическом процессе, и категорию металлопроката. Для сложнейших металлоконструкций и строений, перекрытий многоэтажных коттеджей, индустриальных комплексах, требуется подбирать элементы из наиболее крепкого металла высшего качества. Продукция с наивысшей прочностью отличается небольшими габаритами, но при этом могут выдерживать существенные нагрузки. Поэтому вычисления на прочность рекомендуется выполнять несколькими методами, а информацию всегда требуется сравнивать для получения наиболее правильных математических расчетов. При определении пределов надежности и безопасности требуется учитывать существующие величины давления и не забывать немаловажные факторы, такие как, поперечные и продольные силы, крутящий момент. Можно применять разные способы калькуляции, при помощи которой можно определить разрешенные пределы надежности.
Поэтому вычисления на прочность рекомендуется выполнять несколькими методами, а информацию всегда требуется сравнивать для получения наиболее правильных математических расчетов. При определении пределов надежности и безопасности требуется учитывать существующие величины давления и не забывать немаловажные факторы, такие как, поперечные и продольные силы, крутящий момент. Можно применять разные способы калькуляции, при помощи которой можно определить разрешенные пределы надежности.
Как подсчитать предстоящую нагрузку?
С целью определения нагрузочных параметров на деформирование требуется четко придерживаться нижеперечисленных моментов:
- Прогнозируемая и существующая нагрузка.
- Размеры и масса предполагаемой конструкции.
- Нормативная сопротивляемость.
Для многих видов балок нет возможности произвести определение нагрузки на сгибание, ввиду их конфигурации и разновидности установки при возведении сооружений. Деформирование балки (прогиб) образуется в поворотных углах. Поэтому оно очень зависит от общих параметров сооружения, ее предназначения, марки стали и иных функциональных факторов.
Поэтому оно очень зависит от общих параметров сооружения, ее предназначения, марки стали и иных функциональных факторов.
Существуют различные варианты уравнений и способов для расчета балки на прогиб, их использование характеризуется расчетом деформирования обоих оснований. Наиболее чаще для проведения любых вычислений максимального нагрузочного давления на прогиб, профессионалы применяют специальную математическую формулу. Величину нагрузки проектируемой опоры следует перемножить на промежуток пролета в кубе. Итоговый результат делится на общую сумму модуля гибкости и величины момента инерции.
Модуль гибкости можно вычислить по марке стали, момент инерции обозначен в правилах стандартизации по цифровому коду исходного материала. Исходные цифры требуется удвоить на коэффициент, который равен 0,013. Если уже имеющийся относительный коэффициент деформирование выше либо ниже, чем обозначено в существующих правилах, то в будущей конструкции следует брать изделия большего либо меньшего диаметра.
Требуется понимание того, что двутавровая балка, из — за своей конфигурации и массы, не очень часто находит применение при строительстве частных одноэтажных сооружений. Зачастую вместо них применяются облегченные швеллеры либо металлические углы. Но если вы все же планируете приобретение балок для постройки маленького домика, то не нужно решать сложнейшие математические задачи по всем критериям деформационных нагрузок. Хватит и элементарных расчетов допустимых пределов.
- Двутавровая балка
- Балка Б1
- Балка Б2
- Балка К1
- Балка К2
- Балка Ш1
- Балка Ш2
- Балка М
- Балка 09г2с
Задание 3 расчет балки на прочность и жесткость
Целью задания
является расчет балки на прочность при
плоском изгибе и исследование влияния
формы поперечного сечения на ее
металлоемкость.
Для заданной балки
(рис. 18):
1) определить
реакции опор;
2) записать уравнения
поперечной силы и изгибающего момента
для всех участков и построить эпюры
поперечной силы и изгибающего момента;
3) подобрать балку
двутаврового поперечного сечения из
условия прочности по нормальным
напряжениям и проверить балку на
прочность по касательным напряжениям;
4) произвести анализ
изменения веса балки в зависимости от
формы ее поперечного сечения (рис. 17),
17),
приняв за единицу вес двутавровой балки;
5) построить эпюры
распределения нормальных и касательных
напряжений по высоте двутавровой балки
в произвольном ее сечении, в котором ни
поперечная сила, ни изгибающий момент
не равны нулю;
6) записать уравнения
углов поворота и прогибов сечений балки
для всех участков и построить эпюры
углов поворота и прогибов;
7) графическая
часть задания должна содержать чертеж
балки в стандартном масштабе с указанием
размеров балки и нагрузки (под чертежом
балки расположить эпюры поперечных
сил, изгибающих моментов, углов поворота
и прогибов сечений балки), эпюры
распределения нормальных и касательных
напряжений по высоте сечения балки.
Материал балки –
сталь Ст.3. При расчетах принять:
допускаемые напряжения adm
= 160 МПа, adm
= 100 МПа, модуль упругости Е
= = 2105
МПа.
Для построения
эпюр углов поворота и прогибов сечений
балки необходимо подсчитать соответствующие
величины в 4-6 сечениях на каждом участке.
Разрешается
ординаты эпюр углов поворота и прогибов
сечений балки увеличить в EI
раз.
Исходные данные
взять из табл. 3.
Таблица 3
Номер | l, | l1, | l2, | F, | M, | q, |
а | б | в | г | а | б | |
1 | 2,0 | 4,0 | 3,0 | 50 | 10 | 40 |
2 | 2,5 | 5,0 | 3,5 | 45 | 20 | 30 |
3 | 3,0 | 6,0 | 4,5 | 40 | 30 | 20 |
4 | 3,5 | 7,0 | 1,5 | 35 | 40 | 10 |
5 | 4,0 | 6,0 | 2,0 | 30 | 50 | 15 |
6 | 1,5 | 5,0 | 2,5 | 25 | 15 | 25 |
7 | 2,0 | 4,0 | 3,0 | 20 | 25 | 35 |
8 | 3,0 | 3,0 | 3,5 | 15 | 35 | 45 |
9 | 4,0 | 2,0 | 4,0 | 10 | 45 | 20 |
0 | 2,5 | 7,0 | 2,0 | 60 | 55 | 30 |
Рассчитать балку
(рис. 19) постоянного поперечного сечения
19) постоянного поперечного сечения
на прочность при плоском поперечном
изгибе и исследовать влияние формы
поперечного сечения на ее весовые
характеристики.
Исходные данные:
l
= 2 м, l1
= 5 м, l2
= 2 м, F
= 30 кН, М
= 30 кНм,
q
= 20 кН/м, adm
= 160 МПа; adm
= 100 МПа.
Решение
1. Определим опорные
реакции из условия равновесия балки:
,
НА
=0;
,
;
=
= -57,14
кН.
,
;
== 27,14 кН.
Проверка правильности
определения реакций опор:
,
;
27,14 — 57,14 — 20·2 + 30 +
202
= 0;
0 = 0.
2.
Запишем выражения поперечной силы Q
и изгибающего момента Mz
по участкам, используя
метод сечений. Определим значения
Определим значения
поперечных
сил Q
и изгибающих моментов Мz
в характерных точках по длине балки
и построим эпюры Q
и Mz.
1-й
участок: 0 ≤х1≤
2 м (рис. 20)
;
=
= 10.
При х1
= 0 Q
= 0, Mz
= 0; при х1
= 3 м Q
= -40 кН,
-40 кНм.
2-й участок: 2 м ≤
х2
≤ 7 м
=
27,14 — 202
= -12,86 кН;
.
При х2
= 2 м
-10 кНм,
при х2
= 7 м
-74,3 кНм.
3-й участок: 7 м ≤
х3
≤ 9 м
При х3
= 7 мQy
= 17,14 кН,
= -74,3 кНм,
при х3
= 13 м 0,
Qy
=57,14 кН.
По результатам
расчета построим эпюры поперечных сил
Q
и изгибающих моментов Mz
(рис. 19).
3. Определим опасное
сечение: из эпюр поперечных сил и
изгибающих моментов
=
57,14 кН,74,3
кНм.
4. Подбираем
двутавровую балку из условия прочности
по нормальным напряжениям
,
Откуда
см3.
По величине осевого
момента сопротивления выбираем двутавр
№30 по ГОСТ 8239-72, у которого Wzтабл
= 472 см3.
Вычисляем фактическое максимальное
напряжение
фmax
=
==
157,4 МПа.
Вычисляем
недонапряжение по нормальным напряжениям
=100%=100 = 1,6 % < 5 %.
При расчетах
допускается недонапряжение и
перенапряжение до 5 %.
Выбранный двутавр № 40 удовлетворяет
условию прочности по нормальным
напряжениям. Из таблицы балок двутавровых
Из таблицы балок двутавровых
выписываем геометрические характеристики:
Wz
= 472 см3,
h
= 30 см, b
= 13,5 см, А1
= =46,5 см2;
7080
см4,
=
268 см3,
s
= 0,65 см, t
=1,02 см.
Проверяем балку
на прочность по касательным напряжениям
max
=
=
МПа
аdm
= 100 МПа.
Таким образом,
выбранная двутавровая балка удовлетворяет
условию прочности по касательным
напряжениям.
5. Определим размеры
поперечных сечений балки различной
формы:
а) коробчатое
сечение (рис. 23)
;
= 10,6 см,
0,7210,62
= 80,9 см2;
б) прямоугольное
сечение (рис. 24)
=
464,4,
= 8,9 см,
28,92
= 158,4 см2;
в) квадратное
сечение (рис. 25)
25)
464,4,
а
=
= 14,1 см,198,8
см2;
г) круглое сечение
(рис. 26)
=
464,4,
см,
= 221,6 см2;
д) трубчатое
сечение (рис. 27)
,
;
ymax
= d/2,
=464,4,см,
=
113 см2;
е) квадратное
сечение с углами по осям координат (рис.
28)
,
0,707
a,
(для квадратного сечения моменты инерции
относительно любых центральных осей
одинаковы),
464,4,
а
=
= 15,8 см,
= 249,6 см2.
6. Производим анализ
изменения веса балки в зависимости от
формы ее сечения, приняв за единицу вес
двутавровой балки. Вес балки определим
по формуле
.
Обозначим
отношение веса балки различной формы
сечения к весу двутавровой балки:
Таким образом,
сечения балки в порядке возрастания ее
веса выстроятся в ряд: двутавр, коробчатое
сечение, трубчатое сечение, прямоугольное
сечение, квадратное сечение, круглое
сечение, квадратное сечение с углами
по осям координат.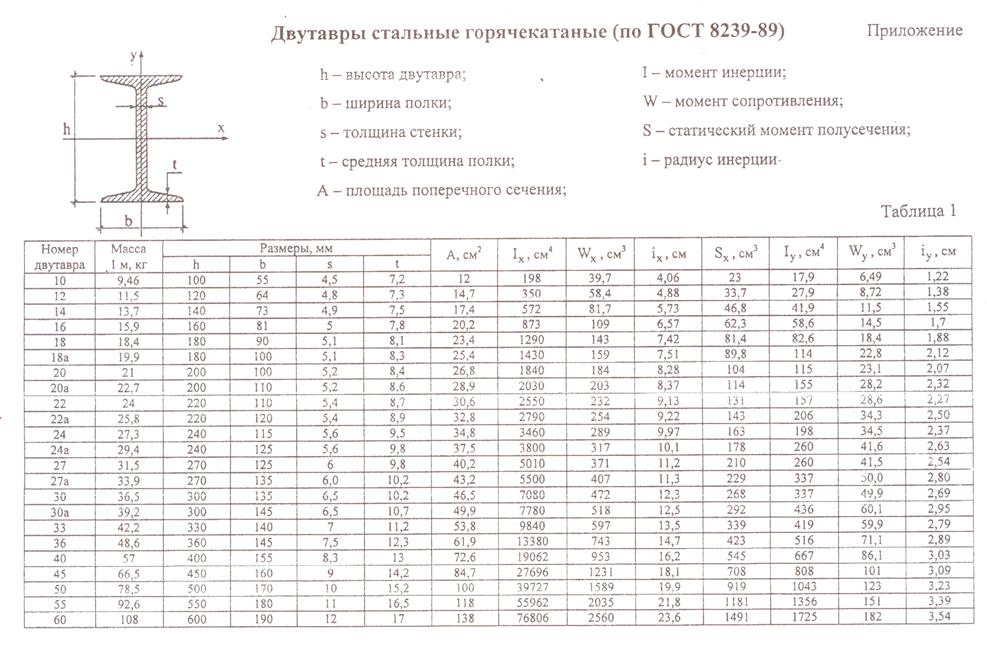
7. Строим эпюры
распределения нормальных и касательных
напряжений по высоте двутавровой
балки для сечения, где приложена сила
F.
В этом сечении Q
= 17,14 кН, Мz
= 74,3 кНм.
Нормальные
напряжения определяются по формуле
=
.
Подсчитаем
нормальные напряжения в характерных
точках сечения:
y1
= h
/ 2, 1
=
= 157,4 МПа;
y4
= 0, 4
= 0.
Эпюра нормальных
напряжений показана на рис. 29.
Касательные
напряжения определяются по формуле
Журавского
=
.
У двутаврового
сечения ширина b
сечения и
статический момент
отсеченной части сечения меняются по
высоте, поэтому вычисляем касательные
напряжения в характерных точках сечения:
Точка 1:
;.
Точка 2:
199,5
см3.
В точке 2 ширина
волокон равна ширине полки b,
поэтому
0,35
МПа.
Точка 3:
= 199,5 см3,
ширина волокон
равна толщине стенки s,
поэтому
7,4
МПа.
Точка 4:
268
см3,
ширина волокон
равна толщине стенки s,
поэтому
10 МПа.
Эпюра касательных
напряжений показана на рис. 29.
8. Определим углы
поворота и прогибы сечений балки методом
начальных параметров. Уравнения углов
поворота и
прогибов сечений
пометоду
начальных параметровимеют
вид:
;
,
где
,- угол поворота и прогиб сечения балки
в начале координат (на левом конце
балки).
Запишем уравнения
углов поворота и прогибов сечений балки
для различных участков:
1-й участок: 0 ≤ х1
≤ 2 м
,
.
2-й участок:
2 м ≤
х2
≤
7 м
,
.
3-й участок: 7 м ≤
х3
≤ 9 м
Постоянные
интегрирования C
и D
определяем из граничных условий — прогибы
на опорах равны нулю:
при
x
= l
= 2 м yA= y1
= y2
= 0;
при x2
= l
+ l1
+ l2
= L
= 9 м yB
= y3
= 0.
Получаем систему
уравнений
или
Решая систему
уравнений, получаем С
= 159,1 кНм2,
D
= -304,8 кНм3.
Вычислим значения
углов поворота и прогибов сечений балки
в 3-4 точках на каждом участке. Результаты
расчета приведены в табл. 4.
Таблица 4
№ участка, | 1 | 2 | ||||
xi, | 0 | 1 | 2 | 2 | 3 | 5 |
, | 159,1 | 155,8 | 132,4 | 132,4 | 101,0 | 44,6 |
EIzyi, | -304,8 | -146,5 | 0 | 0 | 125,4 | 294,5 |
Продолжение
табл. 4
4
№ участка, | 2 | 3 | |||
xi, | 6 | 7 | 7 | 8 | 9 |
,кНм2 | -10,4 | -78,3 | -78,3 | -140,7 | -166,0 |
EIzyi, | 312,6 | 269,3 | 269,3 | 157,5 | 0 |
Определим
экстремальное (максимальное) значение
прогиба на 2-м участке:
Решая уравнение
методом последовательных приближений,
получим х2
= 5,827 м,
313,5 кН· м3.
На основе полученных
результатов строим эпюры углов поворота
и прогибов сечений балки (рис. 21).
Расчёт балок на прочность при изгибе
Задача 1
В некотором сечении балки прямоугольного сечения 20×30см М=28 кНм, Q=19 кН.
Требуется:
а) определить нормальное и касательное напряжения в заданной точке К, отстоящей от нейтральной оси на расстоянии 11 см,
б) проверить прочность деревянной балки, если [σ]=10 МПа, [τ]=3 МПа.
Решение
а) Для определения σ(К), τ(К) и maxσ,maxτ потребуется знать величины осевого момента инерции всего сечения IН.О., осевого момента сопротивления WН.О., статического момента отсечённой части и статического момента половины сечения Smax:
Тогда:
б) Проверка прочности:
— по условию прочности нормальных напряжений:
— по условию прочности касательных напряжений:
Задача 2
В некотором сечении балки М=10кНм, Q=40кН. Поперечное сечение – треугольное. Найти нормальное и касательное напряжения в точке, отстоящей от нейтральной оси на расстоянии 15 см.
Поперечное сечение – треугольное. Найти нормальное и касательное напряжения в точке, отстоящей от нейтральной оси на расстоянии 15 см.
где
Тогда
где:
Тогда
Задача 3
Подобрать сечение деревянной балки в двух вариантах: круглое и прямоугольное (при h/b=2), если [σ]=10 МПа, [τ]=3 МПа, и сравнить их по расходу материала.
Задаёмся направлениями опорных реакций А и В и составляем уравнения статики:
(1) ∑М(В) = F·8 – М – А·6 + (q·6)·3 =0,
откуда
(2) ∑М(А) = F·2 – М + В·6 — (q·6)·3 =0,
откуда
Iучасток
∑М(С) = М(z1) +F·z1=0,
ММ(z1) = —F·z1= — 30 ·z1 —
– уравнение прямой.
При z1 = 0: М = 0,
z1 = 2: М =- 60 кНм.
∑у= — F — Q(z1) = 0,
Q(z1) = — F = -30 кН – постоянная функция.
II участок
откуда
— уравнение параболы.
При z2=0: М = 0,
z2=3м: М = 30 · 3 – 5 · 32 = 90 — 45 = 45кНм,
z2=6м: М = 30 · 6 – 5 · 62 = 180 — 180 = 0.
∑у= Q(z2) — q·z2 + B= 0,
Q(z2) = q·z2 — B= 10·z2 – 30 – уравнение прямой,
при z2 = 0: Q = -30,
z2 = 6м: Q = 10·6 – 30 = 30.
Определение аналитического максимума изгибающего момента второго участка:
из условиянаходим :
И тогда
Заметим, что скачок в эп.М расположен там, где приложен сосредоточенный момент М = 60кНм и равен этому моменту, а скачок в эп.Q – под сосредоточенной силой А = 60 кН.
Подбор сечения балок производится из условия прочности по нормальным напряжениям, куда следует подставлять наибольший по абсолютной величине изгибающий момент из эпюры М.
В данном случае максимальный момент по модулю М = 60кНм
откуда: :
а) сечение круглой формы d=?
б) сечение прямоугольной формы при h/b = 2:
тогда
Размеры сечения, определенные из условия прочности по нормальным напряжениям, должны удовлетворять также условию прочности по касательным напряжениям:
Для простых форм сечений известны компактные выражения наибольшего касательного напряжения:
— для круглого сечения
— для прямоугольного сечения
Воспользуемся этими формулами. Тогда
Тогда
— для балки круглого сечения при :
— для балки прямоугольного сечения
Чтобы выяснить, какое сечение требует меньшего расхода материала, достаточно сравнить величины площадей поперечных сечений:
Апрямоугольного = 865,3см2 < Акруглого = 1218,6см2, следовательно, балка прямоугольного сечения в этом смысле выгоднее, чем круглого.
Задача 4
Подобрать двутавровое сечение стальной балки, если [σ]=160МПа, [τ]=80МПа.
Задаёмся направлениями опорных реакций А и В и составляем два уравнения статики для их определения:
(1) ∑М(А) = – М1– F ·2 — (q·8)·4 + М2 + В·6 =0,
откуда
(2) ∑М(В) = – М1– А · 6 + F · 4 + (q·8)·2 + М2 =0,
откуда
Проверка:
∑у = А – F – q · 8 + В = 104 – 80 – 20 · 8 +136 = 240 – 240 ≡ 0.
∑М(С) = М(z1) — М1=0,
М(z1) = М1= 40 кНм – постоянная функция.
∑у= — Q(z1) = 0,
Q(z1) = 0.
II участок
— парабола.
Приz2=0: М = 40 кНм,
z2=1м: М = 40 + 104 – 10=134кНм,
z2=2м: М = 40+ 104 · 2 – 10 · 22 = 208 кНм.
∑у=А — q·z2 — Q(z2) = 0,
Q(z2) =А— q·z2 = 104 – 20·z2 – уравнение прямой,
при z2 = 0: Q = 104кН,
z2 = 6м: Q = 104 – 40 = 64кН.
III участок
— парабола.
Приz3=0: М = 24+40=-16 кНм,
z3=2м: М = 24 + 136·2 — 10 (2+2)2 = 24 + 272 – 160 = 136кНм,
z3=4м: М = 24 + 136·4 – 10 (2+4)2 = 24 + 544 – 360 = 208 кНм.
∑у=В — q(2+z3 ) + Q(z3) = 0,
Q(z3) =- В + q(2+z3 ) = -136 + 20 (2+z3 ) – уравнение прямой,
при z3 = 0: Q = -136 + 40 = — 94кН,
z3 = 4м: Q = — 136 + 20 (2+4) = — 136 + 120 = — 16кН.
IV участок
— парабола.
z4=0: М = 0кНм,
z4=1м: М = – 10кНм,
z4=2м: М = — 40кНм.
∑у=- q·z4 + Q(z4) = 0,
Q(z4) =q·z4 = 20·z4 – уравнение прямой.
Приz4 = 0: Q = 0,
z4 = 2м: Q = 40кН.
Проверяем скачки в эпюрах:
а) В эпюре М скачок на правой опоре величиной 24кНм (от 16 до 40) равен сосредоточенному моменту М2=24, приложенному в этом месте.
б) В эпюре Q три скачка:
первый из них на левой опоре соответствует сосредоточенной реакции А=104кН,
второй – под силой F=80кН и равен ей (64+16=80кН),
третий – на правой опоре и соответствует правой опорной реакции 136кН (94+40=136 кН)
Наконец, проектируем двутавровое сечение.
Подбор его размеров производится из условия прочности по нормальным напряжениям :
В сортаменте двутавровых профилей профиля с точно таким моментом сопротивления Wх нет. Есть № 40а с Wх=1190 см3 и № 45а с Wх=1430 см3
Есть № 40а с Wх=1190 см3 и № 45а с Wх=1430 см3
Попробуем меньший из них. Если принять двутавр № 40а, у которого Wх=1190 см3 , то наибольшее напряжение в опасном сечении будет:
и перенапряжение составитчто превышает рекомендуемую величину отклонения, равную 5%.
Поэтому приходится принимать ближайший больший размер двутавра, а именно №45а, у которого Wх=1430 см3. В этом случае балка будет работать с недонапряжением:
что меньше [σ]=160МПа на
Итак, принимается двутавр №45а, у которого: Wх=1430 см3, Iх=32240см4, Iх: Sх=38,6см, d=11,5мм.
Далее необходима проверка прочности по касательным напряжениям с помощью условия прочности :
Это условие прочности выполняется, даже с избыточным запасом.
Задача 5
Подобрать сечение балки, рассмотрев шесть вариантов форм и три вида материалов (древесина, чугун, сталь).
Решение
1.Определение опорных реакций
∑М(А) = F · 2 + М1 — М2— q·6·7 + В · 8 =0,∑М(В) = F · 10 + М1— М2 – А · 8 + q·6·1 =0,Проверка:
∑у = – 20 – 40 ·6 +50+210 = — 260 + 260 ≡ 0.
2.Построение эпюр изгибающих моментов и поперечных сил.
I участок
∑М(С) = М(z1) + F·z1=0,
М(z1) = — F·z1= -20·z1.
При z1=0: М = 0,
z1=2м: М = – 40кНм,
∑у= — F— Q(z1) = 0,
Q(z1) = — 20кН.
II участок
z2=0: М = — 20 – 40 = -60 кНм,
z2=4м: М = 200 — 20 – 120 = 200 — 140 = 60кНм.
∑у=- F + А — Q(z2) = 0,
Q =- F + А= -20+50=30кН.
III участок
— парабола.
Приz3=0: М = — 20·4= — 80 кНм,
z3=2м: М = 210·2 — 20·(2+2)2 = 420 – 320 = 100кНм,
z3=4м: М = 210·4 – 20 · (2+4)2 = 840 – 720 = 120кНм.
∑у= Q(z3) + В — q·(2+z3) = 0,
Q(z3) = — В + q·(2+z3) = — 210 + 40·(2+z3) – уравнение прямой.
Приz3 = 0: Q = -130кН,
z3 = 4м: Q = 30кН.
Q(z0) = — 210 + 40·(2+z0) = 0,
— 210 + 80 + 40·z0 = 0,
40·z0 = 130,
z0 =3,25м,
IV участок
парабола.
Приz4=0: М = 0 кНм,
z4=1м: М = – 20кНм,
z4=2м: М = — 80кНм.
∑у=- q·z4 + Q(z4) = 0,
Q(z4) =q·z4 = 40·z4 – уравнение прямой,
z4 = 0: Q = 0,
z4 = 2м: Q = 80кН.
3. Подбор сечений (опасное сечение по σ: |maxМ|=131,25кНм,
опасное сечение по τ: |maxQ|=130кН).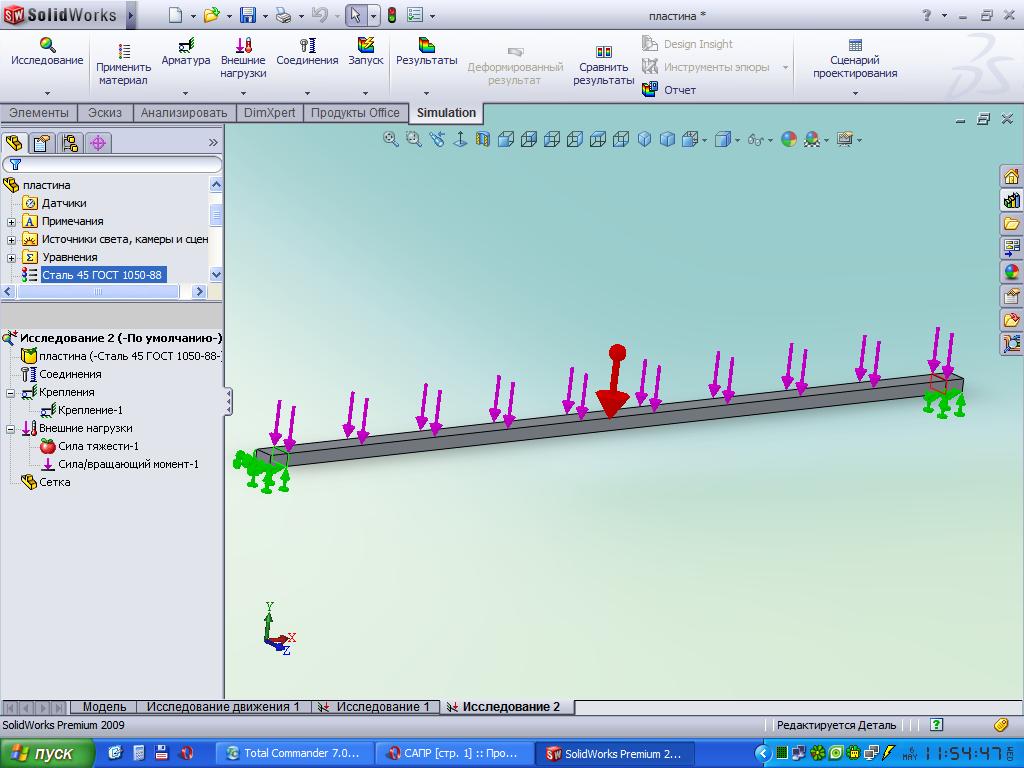
Вариант 1. Деревянное прямоугольное ([σ]=15МПа, [τ]=3МПа)
Принимаем: В=0,24м,
Н=0,48м.
Проверяем по τ:
Вариант 2. Деревянное круглое
Принимаем d=0,45м,
Проверяем по τ:
Вариант 3. Чугун : ([σР]=30МПа, [σс]=120МПа, [τ]=15МПа)
Принимаем b=0,19м, тогда h=0,38м, d=0,076м.
Проверка по τ:
b(у)= b — d= 0,19 — 0,076 = 0,114м
Вариант 4. Сталь, двутавр : ([σ]=160МПа, [τ]=80МПа).
по сортаменту Wх=953см3. Это №40: Ix=19062см4, Sх=545см3, d=0,83см.
Проверка по τ:
Вариант 5. Сталь, круглая труба
Сталь, круглая труба
Принимаем D=0,22м → d = 0,6·D =0,132м.
Проверка по τ:
Вариант 6. Сталь, прямоугольная труба
b1= b — 2t = b — 2·0,1b = 0,8b,
h1= h — 2t = 0,8h,
Принимаем b=0,13м, h=0,26м.
Проверка по τ:
Кстати: какое из сечений стальной балки выгодней по расходу материала?
Двутавр — А = 72,6см2 = 72,6·10-4 = 0,00726м2,
круглая труба –
прямоугольная труба —
Самый лёгкий: двутавр → самый выгодный с точки зрения изгиба.
Расчет балки прокатного профиля и выбор ее номера по сортаменту.
Примеры решения задач по сопротивлению материалов
На этой странице приведен пример решения задачи по Сопромату, в которой необходимо произвести расчет горизонтальной балки, нагруженной поперечными силовыми факторами.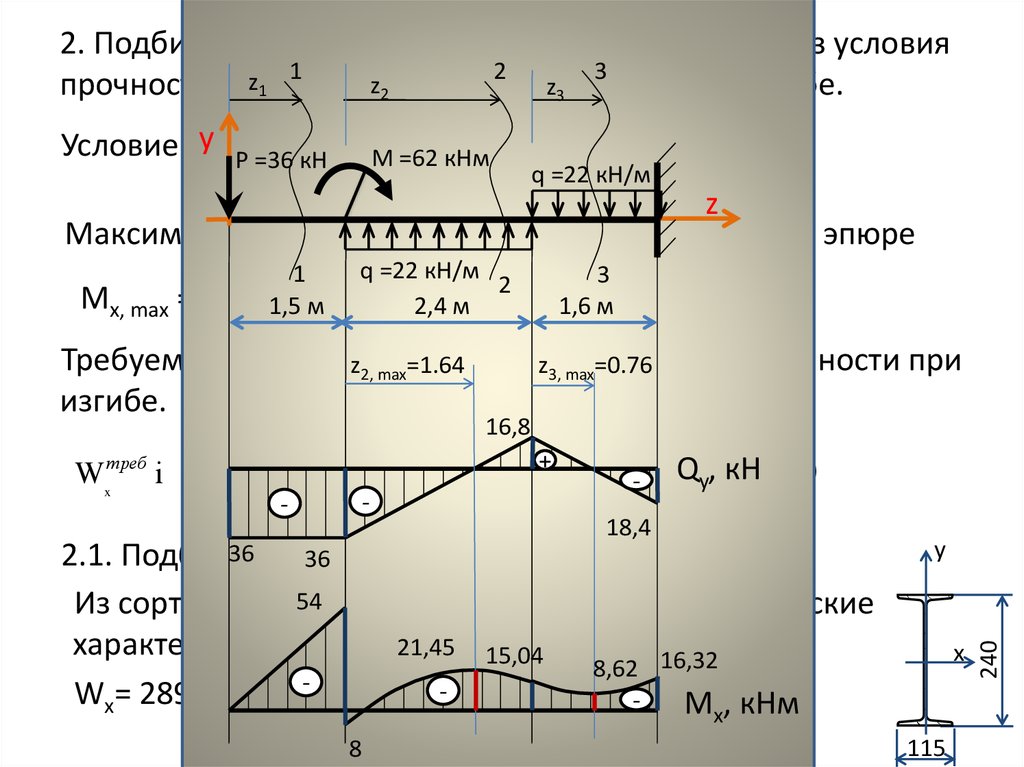 По результатам расчетов внутренних силовых факторов осуществлен подбор размеров сечения балки из расчета на прочность.
По результатам расчетов внутренних силовых факторов осуществлен подбор размеров сечения балки из расчета на прочность.
Результаты расчетов балки оформлены эпюрами изгибающих моментов и поперечных сил.
Здесь можно скачать готовые варианты контрольных работ по сопромату (прикладной механике) для учащихся Алтайского Государственного технического университета.
Варианты контрольных работ можно скачать в формате Word для ознакомления с порядком решения заданий, или для распечатывания и защиты (при совпадении вариантов).
***
Условие задачи:
На горизонтально расположенную балку, закрепленную на двух шарнирных опорах, действуют активные нагрузки: изгибающий момент М, сосредоточенная сила F и распределенная нагрузка q (см. рис. 3).
Материал стержня – сталь Ст.3.
Требуется:
Построить эпюры поперечных сил QY и изгибающих моментов МX и подобрать сечение балки из расчета на прочность.
Исходные данные:
Нагрузки:
- М = 6 кН×м;
- F = -7 кН;
- q = -8 кН/м;
- a = 2 м;
- Сечение балки: двутавр.
Координаты приложения нагрузок:
- ZM = 3а — координата приложения изгибающего момента;
- ZF = а — координата приложения сосредоточенной силы;
- начало распределенной нагрузки: Zq = 2а;
- конец распределенной нагрузки: Zq = 3а;
- ZB = 3а — координата опоры В.
Указания:
Шарнирно-неподвижную опору А располагать на левом конце балки, этот же конец балки принимаем за начало координат.
Шарнирно-неподвижную опору В и внешние нагрузки располагать на соответствующих участках, в соответствии с которыми разбиваем балку на силовые участки.
Силовым участком считать ту часть балки, в пределах которой законы измерения QY и MX остаются постоянными.
Решение:
1. Из условия равновесия балки определим неизвестные опорные реакции RА и RВ (см. рис. 3). Для этого составляем уравнения равновесия для изгибающих моментов сначала относительно опоры А, затем относительно опоры В.
При этом изгибающие моменты, направленные по часовой стрелке относительно опоры считаем отрицательными, против часовой стрелки – положительными.
∑МА = М — q×a×2,5а — F×а + RВ×3а = 0,
откуда находим реакцию RВ:
RВ = (qa×2,5а + F×а – М)/3а = (8×2×2,5×2 + 7×2 – 6)/3×2 =14,67 кН.
∑МВ = М + q×a×0,5а + F×2а – RА×3а = 0,
откуда находим реакцию RА:
RА = (М + qa×0,5а + F×2а)/3а = (6 + 8×2×0,5×2 + 7×2×2)/3×2 = 8,33 кН.
Произведем проверку правильности найденных значений опорных реакций, используя уравнение равновесия действующих на балку сил с учетом их направления:
∑FY = RА – F – q×a + RВ = 8,33 – 7 – 8×2 + 14,67 = 0.
Опорные реакции найдены правильно.
2. Составим уравнения внутренних усилий QY и MX для каждого силового участка балки.
2.1. Участок I: 0 ≤ Z1 ≤ 2 м.
- QY1 = RA ;
- MX1 = — RA×ZY.
На протяжении всего участка I внутренняя сила равна RA = 8,33 кН.
Изгибающий момент на этом силовом участке изменяется линейно, поэтому для построения эпюры достаточно рассчитать его значение в двух крайних сечениях участка:
- МX1=0 = 0;
- МX1=2 = -8,33×2 = -16,66 кН×м.
2. 2. Участок II: 2 м ≤ Z2 ≤ 4 м.
2. Участок II: 2 м ≤ Z2 ≤ 4 м.
- QY2 = RА – F = 8,33 – 7 = 1,33 кН;
- MX2 = — RА×(2м + Z2) + F×Z2.
Изгибающий момент на этом силовом участке тоже изменяется линейно:
- МX2=2 = -16,66 кН×м;
- МX2=4 = -8,33×(2+2) + 7×2 = -19,32 кН×м.
2.3. Участок III: 4 м ≤ Z3< 6 м (кроме крайней точки В, где приложен момент М).
QY3 = RА – F — q×Z3;
MX3 = — RА×(4м + Z3) + F×(2м + Z3) + q×Z3×Z3/2).
В крайней точке В (Z3 = 2 м) алгебраическая сумма всех изгибающих моментов должна быть равна нулю:
MX3=6м = — RА×(4 м + Z3=2м) + F×(2м + Z3=2м) + q×Z3=2м × Z3=2м /2) + М =
= -8,33×6 +7×4 + 8×2×1 + 6 = 0.
Сила QY3 на силовом участке III изменяется линейно, поэтому для построения эпюры находим ее значение в крайних сечениях участка:
- QY Z3=0 = RА – F — q×Z3=0 = 8,33 — 7 = 1,33 кН;
- QY Z3=2 = RА + q×Z3=2 = 8,33 — 7 — 8×2 = -14,67 кН,
т. е. сила в крайней точке равна реакции опоры B, но направлена в противоположную сторону, что свидетельствует о правильности произведенных расчетов.
Поскольку сила на силовом участке III поменяла знак, то изгибающий момент МX при QY= 0 имеет экстремальное значение. Найдем координату экстремальной точки Z3экст и величину экстремального изгибающего момента MXэкст.
QY = RА – F — q× Z3экст = 0 , откуда: Z3экст = (RА – F) / q = (8,33 – 7)/8 = 0,166 м.
Подставив полученное значение в уравнение изгибающего момента, получим:
MXэкст = — RА×(4м + Z3экст) + F×(2м + Z3экст) + q×Z3экст×Z3экст/2) =
= -8,33×4,166+7×2,166 + 8×0,1662/2 = -19,43 кН×м.
Изгибающий момент на силовом участке III изменяется по квадратичной зависимости, поэтому его эпюра имеет криволинейный вид. Для того, чтобы построить эпюру изгибающих моментов на этом участке необходимо вычислить значение моментов в нескольких промежуточных точках.
- MX3=0 = -8,33×4 +7×2 = -19,32 кН×м;
- MXэкст = -19,43 кН×м;
- MX3=0,5м = -8,33×4,5 +7×2,5 + 8×0,52/2 = -18,985 кН×м;
- MX3=1м = -8,33×5 +7×3 + 8×12/2 = -16,65 кН×м;
- MX3=1,5м = -8,33×5,5 +7×3,5 + 8×1,52/2 = 15,255 кН×м;
- MX3=2м = -6,0 кН×м.

3. По результатам расчетов строим эпюры поперечных сил и изгибающих моментов (рис. 4 внизу страницы).
4. По эпюре МX определяем опасное сечение балки, где изгибающий момент имеет максимальное значение (по абсолютной величине):
MXmax = 19,43 кН×м.
Размер сечения (по условию варианта задания — № двутавра) вычисляем из условия прочности при изгибе по осевому моменту сопротивления сечения:
WX = MXmax/[σ] = 19,43×103/160×106 = 0,000121 м3 = 121 см3.
По таблице сортаментов выбираем двутавр №18, у которого момент сопротивления
WX = 143 см3 (ближайший по сортаменту двутавр №16 имеет момент сопротивления сечения равный 109 см3, что недостаточно для выполнения условия прочности).
***
Расчет статически неопределимой балки
Сопротивление материалов
Главная страница
- Страничка абитуриента
Дистанционное образование
- Группа ТО-81
- Группа М-81
- Группа ТО-71
Специальности
- Ветеринария
- Механизация сельского хозяйства
- Коммерция
- Техническое обслуживание и ремонт автотранспорта
Учебные дисциплины
- Инженерная графика
- МДК.
 01.01. «Устройство автомобилей»
01.01. «Устройство автомобилей» - Карта раздела
- Общее устройство автомобиля
- Автомобильный двигатель
- Трансмиссия автомобиля
- Рулевое управление
- Тормозная система
- Подвеска
- Колеса
- Кузов
- Электрооборудование автомобиля
- Основы теории автомобиля
- Основы технической диагностики
- Основы гидравлики и теплотехники
- Метрология и стандартизация
- Сельскохозяйственные машины
- Основы агрономии
- Перевозка опасных грузов
- Материаловедение
- Менеджмент
- Техническая механика
- Советы дипломнику
Олимпиады и тесты
- «Инженерная графика»
- «Техническая механика»
- «Двигатель и его системы»
- «Шасси автомобиля»
- «Электрооборудование автомобиля»
Расчет прочности на напряжение двутавровой балки
Калькулятор расчета прочности двутавровой балки для расчета
нормальное напряжение, напряжение сдвига и напряжение фон Мизеса в критических точках заданного
поперечное сечение двутавровой балки.
Поперечная нагрузка на двутавровую балку может привести к нормальным и касательным напряжениям.
одновременно на любом поперечном сечении двутавра. Нормальное напряжение в данном поперечном сечении изменяется по отношению к
расстояние y от нейтральной оси, и оно наибольшее в самой дальней точке от
нервная ось. Нормальное напряжение также зависит от изгибающего момента в
сечение и максимальное значение нормальных напряжений в двутавре возникает там, где
изгибающий момент наибольший. Максимальное касательное напряжение возникает на нейтральной оси
двутавровой балки, где поперечная сила максимальна.
Примечание. Для получения дополнительной информации о
тему см. в разделах «Касательные напряжения в тонкостенных элементах» и «Расчетные
балок и валов на прочность» главы механики материалов
.
| ВХОДНЫЕ ПАРАМЕТРЫ | ||
| Параметр | Значение | |
| Высота несущей балки [2c] | ||
| Ширина структурной балки [w] | ||
| I Толщина полки балки [t 1 ] | ||
| Толщина стенки двутавровой балки [т 2 ] | ||
| Сила сдвига [В] | кН фунт-сила | |
| Изгибающий момент [М] | Н*мкН*млфунт-сила*дюймфунт-сила*фут | |
Примечание. V и M — поперечная сила и изгибающий момент в сечении, как показано на рис.
V и M — поперечная сила и изгибающий момент в сечении, как показано на рис.
рисунок.Посетить »
Калькуляторы прогиба и напряжения конструкционной балки». Для расчета поперечной силы и изгибающего момента.
Примечание. Предполагается, что конструкционная балка подвергается действию вертикальной поперечной силы в вертикальной плоскости симметрии.
| РЕЗУЛЬТАТЫ | ||
| Параметр | Значение | |
| Площадь поперечного сечения [A] | ||
| Первый момент площади для сечения B [Q B ] | — | |
| Первый момент площади сечения D [Q D ] | — | |
| Расчет напряжения на участке A | МПапсикси | |
| Нормальное напряжение [σ x_A ] | — | |
| Напряжение сдвига [τ ху_А ] | — | |
| Напряжение фон Мизеса при A [σ v_A ] | — | |
| Расчет напряжения на участке B | ||
| Нормальное напряжение в B [σ х_В ] | — | |
| Напряжение сдвига в B [τ xy_B ] | — | |
| Напряжение фон Мизеса в B [σ v_B ] | — | |
| Расчет напряжения на участке D | ||
| Нормальное напряжение при D [σ x_D ] | — | |
| Напряжение сдвига при D [τ xy_D ] | — | |
| Напряжение фон Мизеса при D [σ v_D ] | — | |
Примечание.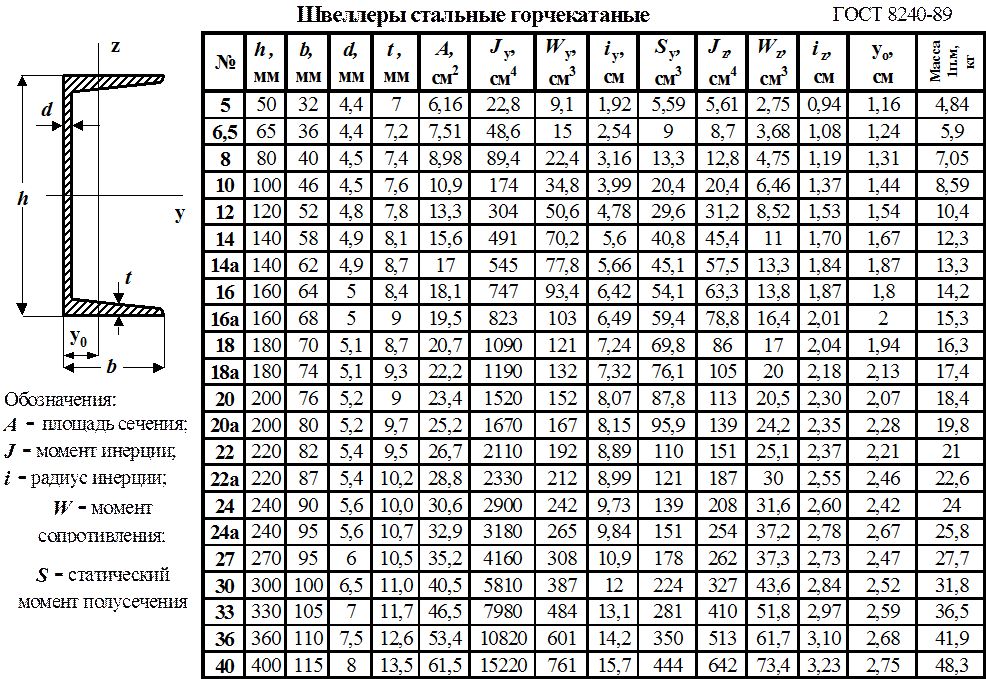 Используйте точку «.» как десятичный разделитель.
Используйте точку «.» как десятичный разделитель.
Примечание. Напряжения — это положительные числа, и это величины напряжений в
луч. Он не различает растяжение или сжатие конструкции.
луч.
Примечание: Влияние концентрации напряжений не учитывается в расчетах.
Двутавровая балка: Двутавровая балка — это тип балки
часто используется в фермах в зданиях. Двутавровая балка обычно изготавливается из
конструкционные стали методами горячей и холодной прокатки или сварки. Верхняя и нижняя пластины двутавровой балки называются полками, а вертикальная пластина, соединяющая полки, называется стенкой.
Напряжение сдвига: Форма напряжения, действующая параллельно поверхности (поперечному сечению), имеет режущий характер.
Напряжение и прогиб балки | MechaniCalc
Калькулятор
ПРИМЕЧАНИЕ. Эта страница использует JavaScript для форматирования уравнений для правильного отображения. Пожалуйста, включите JavaScript.
Эта страница использует JavaScript для форматирования уравнений для правильного отображения. Пожалуйста, включите JavaScript.
Многие конструкции можно аппроксимировать прямой балкой или набором прямых балок. По этой причине анализ напряжений и прогибов в балке является важной и полезной темой.
В этом разделе рассматриваются поперечная сила и изгибающий момент в балках, диаграммы сдвига и момента, напряжения в балках, а также таблица общих формул прогиба балки.
Содержимое
Ограничения и граничные условия
Чтобы балка оставалась в статическом равновесии, когда к ней приложены внешние нагрузки, балка должна быть закреплена. Ограничения определяются в отдельных точках вдоль балки, и граничное условие в этой точке определяет характер ограничения. Граничное условие указывает, является ли луч фиксированным (ограниченным от движения) или свободным для перемещения в каждом направлении. Для двумерного луча интересующими направлениями являются направление x (осевое направление), направление y (поперечное направление) и вращение. Чтобы ограничение существовало в точке, граничное условие должно указывать, что хотя бы одно направление зафиксировано в этой точке.
Чтобы ограничение существовало в точке, граничное условие должно указывать, что хотя бы одно направление зафиксировано в этой точке.
Общие граничные условия показаны в таблице ниже. Для каждого граничного условия в таблице указано, является ли луч фиксированным или свободным в каждом направлении в точке, где определено граничное условие.
| Граничное условие | Направление | |||
|---|---|---|---|---|
| Осевое (X) | Поперечное (Y) | Вращение | ||
| Свободно | Свободно | Свободно | Свободно | |
| Fixed | Fixed | Fixed | Fixed | |
| Pinned | Fixed | Fixed | Free | |
| Guided along X | Free | Fixed | Fixed | |
| Guided along Y | Фиксированный | Свободный | Фиксированный | |
| Ролик по оси X | Свободно | Фиксированный | Свободно | |
| Ролик по Y | 0013 | Фиксированный | Свободный | Свободный |
Если граничное условие указывает, что луч зафиксирован в определенном направлении, то в месте расположения граничного условия может существовать внешняя реакция в этом направлении. Например, если балка закреплена в направлении y в определенной точке, то в этой точке может возникнуть поперечная (y) внешняя сила реакции. Точно так же, если балку зафиксировать от вращения в определенной точке, то в этой точке может возникнуть внешний реактивный момент.
Например, если балка закреплена в направлении y в определенной точке, то в этой точке может возникнуть поперечная (y) внешняя сила реакции. Точно так же, если балку зафиксировать от вращения в определенной точке, то в этой точке может возникнуть внешний реактивный момент.
Основываясь на приведенном выше обсуждении, мы можем видеть, что фиксированное граничное условие может развивать осевые и поперечные силы реакции, а также момент. Точно так же мы видим, что закрепленное граничное условие может развивать осевые и поперечные силы реакции, но не может создавать реактивный момент.
Обратите внимание на условие свободной границы в таблице выше. Это граничное условие указывает, что луч может свободно двигаться в любом направлении в этой точке (т. е. он не зафиксирован и не ограничен ни в каком направлении). Следовательно, на данный момент ограничения не существует. Это подчеркивает тонкую разницу между ограничением и граничным условием. Граничное условие указывает фиксированное/свободное условие в каждом направлении в определенной точке, а ограничение — это граничное условие, в котором зафиксировано хотя бы одно направление.
Сила сдвига и изгибающий момент
Чтобы найти поперечную силу и изгибающий момент по длине балки, сначала решите внешние реакции при каждом ограничении. Например, консольная балка ниже имеет приложенную силу, показанную красной стрелкой, а реакции показаны синими стрелками при фиксированном граничном условии.
Внешние реакции должны уравновешивать приложенные нагрузки таким образом, чтобы балка находилась в статическом равновесии. После того, как внешние реакции определены, сделайте разрезы по длине балки и определите внутренние реакции в каждом разрезе сечения. (Силы реакции и моменты в разрезах сечения называются внутренними реакциями, поскольку они являются внутренними по отношению к балке.) Пример сечения показан на рисунке ниже:
Когда балка разрезается в сечении, при расчете внутренних реакций можно учитывать любую сторону балки. Выбранная сторона не влияет на результаты, поэтому выбирайте ту сторону, которая проще всего. На рисунке выше выбрана сторона балки справа от разреза сечения.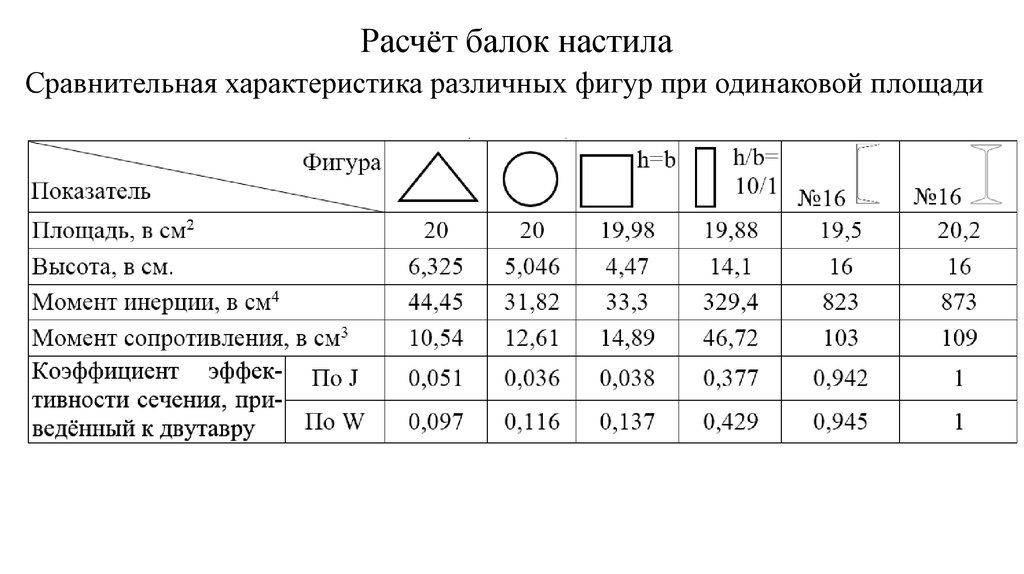 Выбранная сторона отображается в виде синего участка луча, а участок, показанный серым цветом, игнорируется. Внутренние реакции на разрезе показаны синими стрелками. Реакции рассчитываются таким образом, чтобы рассматриваемое сечение балки находилось в статическом равновесии.
Выбранная сторона отображается в виде синего участка луча, а участок, показанный серым цветом, игнорируется. Внутренние реакции на разрезе показаны синими стрелками. Реакции рассчитываются таким образом, чтобы рассматриваемое сечение балки находилось в статическом равновесии.
Соглашение о знаках
Важны знаки сдвига и момента. Знак определяется после разреза сечения и решения реакций для части балки по одну сторону от разреза. Перерезывающая сила в срезе сечения считается положительной, если она вызывает вращение выбранного сечения балки по часовой стрелке, и считается отрицательной, если вызывает вращение против часовой стрелки. Изгибающий момент в разрезе сечения считается положительным, если он сжимает верхнюю часть балки и удлиняет нижнюю часть балки (т. е. заставляет балку «улыбаться»).
На основании этого соглашения о знаках поперечная сила в разрезе сечения консольной балки в качестве примера на рисунке выше положительна, поскольку она вызывает вращение выбранного сечения по часовой стрелке. Момент отрицательный, так как он сжимает нижнюю часть балки и удлиняет верхнюю (т. е. заставляет балку «нахмуриться»).
Момент отрицательный, так как он сжимает нижнюю часть балки и удлиняет верхнюю (т. е. заставляет балку «нахмуриться»).
На рисунке ниже показаны стандартные знаки для поперечной силы и изгибающего момента. Силы и моменты слева положительны, а справа отрицательны.
Ознакомьтесь с нашим калькулятором луча, основанным на методологии, описанной здесь.
- Расчет напряжений и прогибов в прямых балках
- Построение диаграмм сдвига и моментов
- Можно указать любую конфигурацию ограничений, сосредоточенных сил и распределенных сил
Диаграммы сдвига и момента
Перерезывающая сила и изгибающий момент в балке обычно изображаются на диаграммах. Диаграмма сдвига показывает поперечную силу по длине балки, а диаграмма моментов показывает изгибающий момент по длине балки. Эти диаграммы обычно располагаются друг над другом, и комбинация этих двух диаграмм представляет собой диаграмму момента сдвига. Диаграммы поперечного момента для некоторых распространенных конечных условий и конфигураций нагрузки показаны в таблицах прогиба балки в конце этой страницы. Пример диаграммы поперечного момента показан на следующем рисунке:
Пример диаграммы поперечного момента показан на следующем рисунке:
Общие правила построения диаграмм поперечных моментов приведены в таблице ниже. Все правила этой таблицы показаны на рисунке выше.
| Диаграмма сдвига | Диаграмма моментов |
|---|---|
|
|
Изгибающие напряжения в балках
Изгибающий момент М по длине балки можно определить по диаграмме моментов. Затем изгибающий момент в любом месте балки можно использовать для расчета изгибающего напряжения в поперечном сечении балки в этом месте. Изгибающий момент изменяется по высоте поперечного сечения в соответствии с формула изгиба ниже:
где M — изгибающий момент в интересующем месте по длине балки, I c — центральный момент инерции поперечного сечения балки, а y — расстояние от нейтральной оси балки до интересующей точки по высоте. сечения. Отрицательный знак указывает на то, что положительный момент приведет к сжимающему напряжению над нейтральной осью.
Напряжение изгиба равно нулю на нейтральной оси балки, которая совпадает с центром тяжести поперечного сечения балки. Напряжение изгиба увеличивается линейно по направлению от нейтральной оси до максимальных значений на крайних волокнах вверху и внизу балки.
Напряжение изгиба увеличивается линейно по направлению от нейтральной оси до максимальных значений на крайних волокнах вверху и внизу балки.
Максимальное изгибающее напряжение возникает на крайних волокнах балки и рассчитывается как:
где c — центроидальное расстояние поперечного сечения (расстояние от центроида до крайнего волокна).
Если балка асимметрична относительно нейтральной оси, так что расстояния от нейтральной оси до верха и до низа балки не равны, максимальное напряжение возникнет в самом удаленном месте от нейтральной оси. На рисунке ниже растягивающее напряжение в верхней части балки больше, чем сжимающее напряжение в нижней части.
Модуль поперечного сечения объединяет центральный момент инерции I c и центральное расстояние с:
Преимущество модуля сечения заключается в том, что он характеризует сопротивление поперечного сечения изгибу в одном выражении. Модуль сечения можно подставить в формулу изгиба для расчета максимального напряжения изгиба в поперечном сечении:
Ознакомьтесь с нашим калькулятором луча, основанным на методологии, описанной здесь.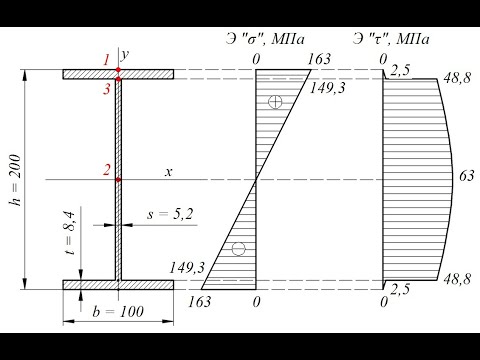
- Расчет напряжений и прогибов в прямых балках
- Построение диаграмм сдвига и моментов
- Можно указать любую конфигурацию ограничений, сосредоточенных сил и распределенных сил
Касательные напряжения в балках
Сила сдвига V по длине балки может быть определена по диаграмме сдвига. Сила сдвига в любом месте балки затем может быть использована для расчета напряжения сдвига по поперечному сечению балки в этом месте. Среднее касательное напряжение по поперечному сечению определяется выражением:
Напряжение сдвига изменяется по высоте поперечного сечения, как показано на рисунке ниже:
Напряжение сдвига равно нулю на свободных поверхностях (вверху и внизу балки) и максимально в центре тяжести. Уравнение для напряжения сдвига в любой точке, расположенной на расстоянии y 1 от центра тяжести поперечного сечения, имеет вид:
где V — поперечная сила, действующая в месте поперечного сечения, I c — центральный момент инерции поперечного сечения, а b — ширина поперечного сечения. Все эти термины являются константами. Член Q — это первый момент площади, ограниченной точкой интереса и крайним слоем поперечного сечения:
Все эти термины являются константами. Член Q — это первый момент площади, ограниченной точкой интереса и крайним слоем поперечного сечения:
Напряжения сдвига для нескольких распространенных поперечных сечений обсуждаются в разделах ниже.
Касательные напряжения в прямоугольных сечениях
Распределение касательного напряжения по высоте прямоугольного сечения показано на рисунке ниже:
Первый момент площади в любой заданной точке y 1 по высоте поперечного сечения рассчитывается по формуле:
Максимальное значение Q приходится на нейтральную ось пучка (где y 1 = 0):
Напряжение сдвига в любой заданной точке y 1 по высоте поперечного сечения рассчитывается по формуле:
где I c = b·h 3 /12 – центральный момент инерции поперечного сечения. Максимальное напряжение сдвига возникает на нейтральной оси балки и рассчитывается по формуле:
где A = b·h – площадь поперечного сечения.
Из предыдущего уравнения видно, что максимальное касательное напряжение в поперечном сечении на 50% выше, чем среднее напряжение V/A.
Касательные напряжения в круглых сечениях
Круглое сечение показано на рисунке ниже:
Уравнения для касательного напряжения в балке были выведены с использованием предположения, что касательное напряжение по ширине балки постоянно. Это предположение справедливо в центре тяжести круглого поперечного сечения, хотя нигде больше оно недействительно. Следовательно, хотя распределение напряжения сдвига по высоте поперечного сечения не может быть легко определено, максимальное напряжение сдвига в сечении (возникающее в центре тяжести) все же можно рассчитать. Максимальное значение первого момента Q, возникающее в центре тяжести, определяется выражением:
Затем максимальное напряжение сдвига рассчитывается по формуле:
где b = 2r — диаметр (ширина) поперечного сечения, I c = πr 4 /4 — центроидальный момент инерции, A = πr 2 — площадь поперечного сечения.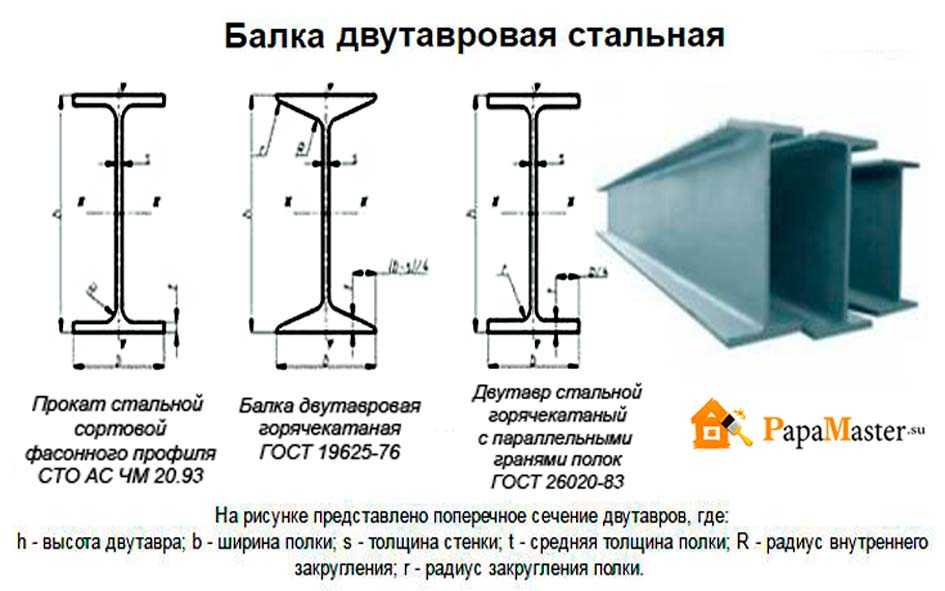
Касательные напряжения в сечениях круглых труб
Поперечное сечение круглой трубы показано на рисунке ниже:
Максимальное значение первого момента Q, возникающее в центре тяжести, определяется выражением:
Затем максимальное напряжение сдвига рассчитывается по формуле:
где b = 2 (r o − r i ) – эффективная ширина поперечного сечения, центроидальный момент инерции, а A = π (r o 2 − r i 2 ) площадь поперечного сечения.
Касательные напряжения в двутавровых балках
Распределение напряжения сдвига вдоль стенки двутавровой балки показано на рисунке ниже:
Уравнения для касательного напряжения в балке были выведены с использованием предположения, что касательное напряжение по ширине балки постоянно. Это предположение справедливо для стенки двутавровой балки, но неверно для полки (особенно там, где стенка пересекает полки). Тем не менее, стенка двутавровой балки принимает на себя подавляющую часть силы сдвига (примерно 90–98%, по Гиру), и поэтому можно консервативно предположить, что стенка несет всю силу сдвига.
Первый момент площади стенки двутавровой балки определяется по формуле:
Напряжение сдвига вдоль стенки двутавровой балки определяется по формуле:
где t w — толщина стенки, а I c — центральный момент инерции двутавровой балки:
Максимальное значение напряжения сдвига возникает на нейтральной оси ( y 1 = 0 ), а минимальное значение напряжения сдвига в стенке возникает на внешних волокнах стенки, где она пересекает полки y 1 = ±h w /2 ):
PDH Classroom предлагает курс повышения квалификации на основе этой справочной страницы по анализу луча. Этот курс можно использовать для выполнения кредитных требований PDH для поддержания вашей лицензии PE.
Теперь, когда вы прочитали эту справочную страницу, заработайте за это признание!
Просмотреть курс сейчас:
Просмотреть курс
Таблицы прогиба балки
В таблицах ниже приведены уравнения для прогиба, наклона, сдвига и момента вдоль прямых балок для различных условий на концах и нагрузок. Вы можете найти исчерпывающие таблицы в таких справочниках, как Gere, Lindeburg и Shigley. Однако приведенные ниже таблицы охватывают большинство распространенных случаев.
Вы можете найти исчерпывающие таблицы в таких справочниках, как Gere, Lindeburg и Shigley. Однако приведенные ниже таблицы охватывают большинство распространенных случаев.
Консольные балки
| Консоль, торцевая нагрузка |
| |||||||||||||||||||
| Консоль, промежуточная нагрузка |
| |||||||||||||||||||
| Консоль, равномерно распределенная нагрузка |
| |||||||||||||||||||
| Консоль, треугольная распределенная нагрузка |
| |||||||||||||||||||
| Консоль, Конечный момент |
|
Просто поддерживаемые балки
| Простая опора, промежуточная нагрузка |
Для a ≥ b:
| |||||||||||||||||||||
| Простая опора, центральная нагрузка |
| |||||||||||||||||||||
| Просто поддерживаемый, 2 нагрузки на равном расстоянии от опор |
| |||||||||||||||||||||
| Простая опора, равномерная распределенная нагрузка |
| |||||||||||||||||||||
| Простая опора, момент на каждой опоре |
| |||||||||||||||||||||
| Простая поддержка, Момент в одну опору |
| |||||||||||||||||||||
| Простая опора, центральный момент |
|
Фиксированные-фиксированные балки
| Фиксированный-Фиксированный, центральная нагрузка |
| |||||||||||||||
| Фиксированная-фиксированная, равномерная распределенная нагрузка |
|
Подпишитесь, чтобы время от времени получать обновления о последних улучшениях:
Ссылки
Будинас-Нисбетт, «Машиностроение Шигли», 8-е изд.
Гир, Джеймс М., «Механика материалов», 6-е изд.
Линдебург, Майкл Р., «Справочное руководство по машиностроению для экзамена PE», 13-е изд.
«Руководство по анализу напряжений», Лаборатория динамики полета ВВС, октябрь 1986 г.
Калькулятор прочности и прогиба балки
Балка или стержень – это любой конструктивный элемент, длина которого значительно превышает его ширину или глубину. Однако термин «значительно» означает разные вещи для разных людей. Некоторым достаточно вдвое большей длины, другие сочтут пятикратную длину слишком короткой и поэтому сочтут такой элемент пластиной, рамой или конструкцией. Процедуры расчета балок не налагают таких ограничений или различий.
Балки обычно используются для несущей нагрузки, при этом они охватывают опоры, расположенные на значительном расстоянии друг от друга, например пол (см. калькулятор CalQlata Floors). При указании балки необходимо определить ее максимальную грузоподъемность (т. е. ее прочность) и ее максимально допустимый прогиб.
е. ее прочность) и ее максимально допустимый прогиб.
Прочность и жесткость балки
Прочность балки зависит от предела текучести материала, из которого изготовлена балка, тем самым определяя максимальную нагрузку, которая может быть приложена до того, как она окончательно деформируется (или сломается, если ее из хрупкого материала), а
его жесткость зависит от второго момента площади поперечного сечения балки (например, швеллера, двутавровой балки, двутавровой балки, угла и т. д.) вместе с модулем Юнга ее материал, тем самым определяя ожидаемый прогиб балки для любой заданной нагрузки
Обе вышеуказанные характеристики определяют поведение балки под нагрузкой.
Проектирование балки
Предположим, у вас есть равномерно распределенная нагрузка в 4000 Н по балке длиной 4 м (1 Н/мм) и максимально допустимый прогиб, скажем, 1/200 длины балки (20 мм).
Используя Балки, вы вводите известную информацию и изменяете второй момент площади (I), пока не получите желаемое отклонение (20 мм в середине балки, где ее отклонение будет наибольшим), что в данном случае дает вам значение для I около 800000 мм⁴.
Предполагая, что вы планируете использовать секцию швеллера, отсортировав швеллеры в базе данных стальных секций CalQlata, вы обнаружите, что размер вашей балки должен быть секции «3×6», которая является наименьшей секцией балки со значением I выше 800000 мм⁴, и найдите значение для y (расстояние от нейтральной оси луча до внешней стороны его сечения), которое в данном случае составляет 38,1 мм.
Вернитесь к Балкам, введите правильное значение для I (863 264 мм⁴), а также введите значение 38,1 мм для d, чтобы установить максимальное напряжение в материале балки, которое в данном случае составляет 88 Н/мм².
Если это значение находится в пределах ваших требований к безопасности, то ваш луч приемлем. Если нет, но приходится работать с данным материалом, то следует изменить (увеличить) сечение балки, тем самым уменьшая допустимый прогиб до тех пор, пока напряжение не станет приемлемым.
Калькулятор прогиба балки — Техническая помощь
Рис. 1. Схема нагружения балки
1. Схема нагружения балки
Предполагается, что любая нагрузка в калькуляторе прочности балок действует одинаково через плоскость или сечение балки во всех направлениях, перпендикулярных (другими словами, @ 90° до) его продольной оси.
Если нагрузка локализована в поперечном сечении балки (т. е. распределена по ней неравномерно), могут потребоваться дополнительные расчеты для выявления местных (сосредоточенных) реакций и напряжений (см. калькуляторы плит и листов CalQlata).
Напряжение изгиба
Изгибающие напряжения в балках применяются к балке на заданном расстоянии (d) от ее нейтральной оси. Эта входная переменная (‘d’) используется только в расчетах напряжения (σx) и деформации (ex). Если вы оставите это поле пустым или установите его равным нулю, Beams не будет рассчитывать напряжение или деформацию в указанном вами месте вдоль балки (рис. 1 «x»). Никакие другие результаты не будут затронуты.
Условия многократной/одновременной нагрузки
Если у вас есть балка с более чем одной приложенной нагрузкой, вы просто суммируете результаты в указанном месте.
Пример расчета прочности балки (рис. 2):
Детали балки:
Д = 2000 мм
I = 1,2E+08 мм⁴
E = 2,07E+05 Н/мм²
у = 200 мм
Состояние загрузки 1:
wA и wB = 450 Н/мм
л = 0
Состояние загрузки 2:
F = 150000 Н
l = 700 мм
Расстояние вдоль луча до выхода:
х = 1000
Шаг 1:
Введите данные для балки и условия нагрузки 1 (простая фиксированная/распределенная нагрузка), установив wA (/L) и wB (/L) на 450 футов, скопируйте список данных и вставьте в электронную таблицу.
Шаг 2:
Введите условие нагрузки 2 (простая фиксированная / точечная нагрузка), установив F на 150000, скопируйте список данных и вставьте в ту же электронную таблицу.
Шаг 3:
Добавьте результаты обоих калькуляторов, и вы получите условия в нужном месте.
Рис. 2. Процедура расчета составной нагрузки
Ограничения
Эти расчеты действительны только в том случае, если материал по всей длине и толщине сечения подчиняется закону Гука.
Результаты остаются действительными для этого калькулятора, если прогиб таков, что на длину балки условия нагрузки не оказывают существенного влияния.
Калькулятор больших прогибных балок CalQlata (Flexible Beams) следует использовать, если длина балки изменяется более чем на 5% в результате приложенной нагрузки.
Единицы
Вы можете использовать любые единицы измерения, которые вам нравятся, но вы должны быть последовательны.
Дополнительная литература
Дополнительную информацию по этому вопросу вы найдете в справочных публикациях (2, 3 и 4)
Бесплатный калькулятор луча | ClearCalcs
Калькулятор балки ClearCalcs позволяет пользователю ввести геометрию и нагрузку балки для анализа за несколько простых шагов. Затем он определяет изгибающий момент, диаграммы сдвига и прогиба, а также максимальные требования, используя мощный механизм анализа методом конечных элементов.
Затем он определяет изгибающий момент, диаграммы сдвига и прогиба, а также максимальные требования, используя мощный механизм анализа методом конечных элементов.
Регистрация учетной записи ClearCalcs откроет доступ к дополнительным расширенным функциям для проектирования и расчета балок и множества других структурных элементов. ClearCalcs позволяет выполнять проектирование из стали, бетона и дерева в соответствии со стандартами Австралии, США и ЕС.
Лист разделен на три основных раздела:
- «Основные свойства», где пользователь вводит геометрию выбранного сечения и опор балки.
- «Нагрузки», где можно вводить распределенные, точечные и приложенные моментные нагрузки,
- «Сводка», в которой отображаются основные результаты и диаграммы.
Также имеется раздел «Комментарии», в котором пользователь может оставить любые примечания к дизайну. Щелчок по любой из меток ввода/свойства дает описательное справочное объяснение.
1.
 Свойства ключа ввода
Свойства ключа ввода
Свойства балки и сечения задаются путем ввода непосредственно в поля ввода.
Длина балки – общая, включая все пролеты балки, в мм или футах.
Для модуля Юнга установлено значение по умолчанию 200 000 МПа или 29 000 тысяч фунтов на квадратный дюйм для конструкционной стали, но пользователь может изменить его.
Площадь поперечного сечения зависит от выбранного сечения балки и по умолчанию соответствует значениям для обычной стальной балки.
Второй момент площади (или момент инерции) также относится к выбранному сечению балки и снова по умолчанию соответствует свойствам обычной стальной балки.
Свойства E, A и Ix для других сечений балки можно получить из библиотеки свойств сечений ClearCalcs. Кроме того, вы можете создать свой собственный раздел, используя наш бесплатный калькулятор момента инерции.
Положение опор слева позволяет пользователю ввести любое количество опор и указать их положение по длине балки.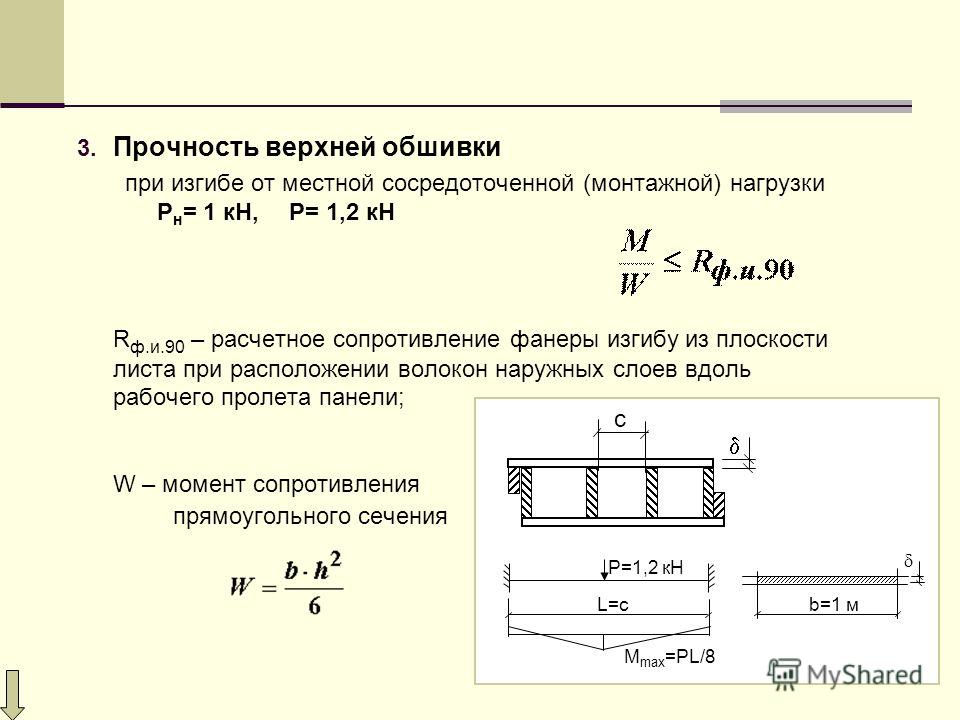 Тип опоры может быть фиксированным (фиксированным при перемещении, свободным при вращении) или фиксированным (фиксированным как при перемещении, так и при вращении) и выбирается из раскрывающегося меню. Требуется как минимум одна фиксированная опора или две опоры на штифтах.
Тип опоры может быть фиксированным (фиксированным при перемещении, свободным при вращении) или фиксированным (фиксированным как при перемещении, так и при вращении) и выбирается из раскрывающегося меню. Требуется как минимум одна фиксированная опора или две опоры на штифтах.
Калькулятор балки также позволяет использовать консольные пролеты на каждом конце, так как положение первой опоры не обязательно должно быть равно 0 мм, а положение последней опоры не должно быть равно длине балки.
Реакции на каждой из опор автоматически обновляются при добавлении, изменении или удалении опор в зависимости от заданной нагрузки.
2. Входные нагрузки
Калькулятор поддерживает различные типы нагрузок, которые можно применять в комбинации. Каждая загрузка может быть названа пользователем.
Для нагрузки используются следующие знаки (показаны положительные значения):
Распределенные нагрузки указаны в единицах силы на единицу длины, кН/м или pf, вдоль балки и могут быть приложены между любыми двумя точками.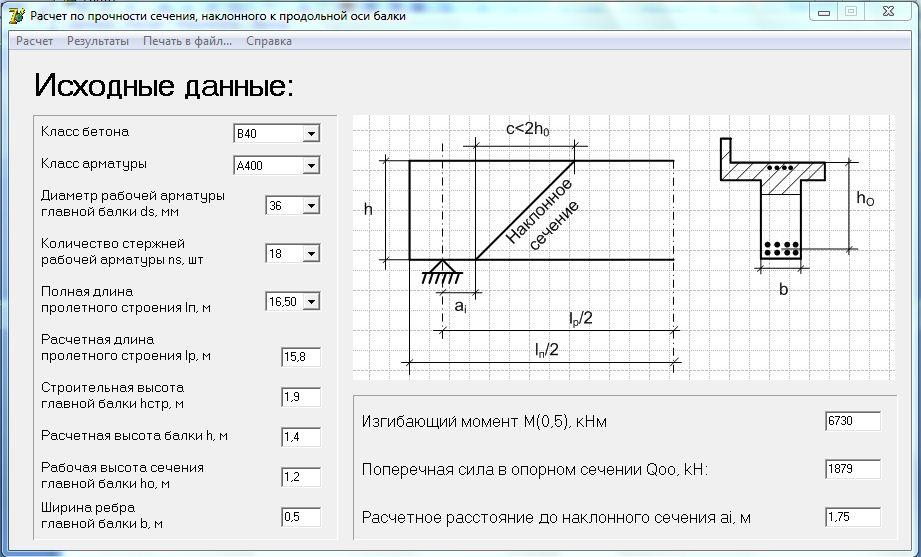 В калькуляторе можно применять два разных типа:
В калькуляторе можно применять два разных типа:
Равномерные нагрузки имеют постоянную величину по длине приложения. Следовательно, начальная и конечная величины, указанные пользователем, должны совпадать.
Линейные нагрузки имеют различную величину по длине приложения. Различные начальные и конечные величины должны быть указаны пользователем, и их можно использовать для представления треугольных или трапециевидных нагрузок.
Точечные нагрузки указаны в единицах силы, кН или тысяч фунтов, и площади, приложенной в дискретных точках вдоль балки. Например, они могут представлять реакции других элементов, соединяющихся с балкой. Пользователь вводит имя, величину и местоположение слева от луча.
На диаграмме ниже в качестве примера из сводного раздела показана двухпролетная неразрезная балка с линейной распределенной патч-нагрузкой и точечной нагрузкой.
3. Итоговые результаты расчетов
После задания нагрузки и геометрии калькулятор автоматически использует механизм анализа методом конечных элементов ClearCalcs для определения моментов, поперечных сил и прогибов. Максимальные значения каждого из них выводятся как «Запрос на момент» , «Запрос на сдвиг» и 9.1680 «Прогиб» вместе с диаграммами по длине балки.
Максимальные значения каждого из них выводятся как «Запрос на момент» , «Запрос на сдвиг» и 9.1680 «Прогиб» вместе с диаграммами по длине балки.
Положительные значения означают отклонение вниз, а отрицательные значения — отклонение вверх. На диаграммах поперечной силы и изгибающего момента используются следующие знаки (показаны положительные значения):
Если навести курсор на любую точку на диаграмме изгибающего момента, поперечной силы или прогиба, можно получить конкретные значения в этом месте вдоль балки. В приведенном ниже примере показаны выходные данные для двухпролетной неразрезной балки с линейной распределенной патч-нагрузкой и точечной нагрузкой.
Калькулятор напряжения сдвига (анализ балки)
Создано Луисом Хойосом
Рассмотрено Стивеном Вудингом
Последнее обновление: 24 мая 2022 г. по крутящему моменту
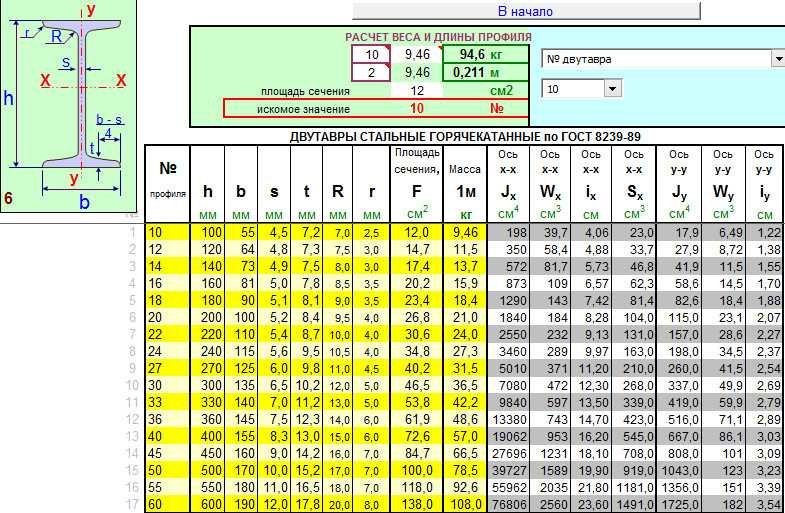
Этот калькулятор напряжения сдвига рассчитывает горизонтальное напряжение сдвига из-за поперечных нагрузок и напряжения сдвига из-за кручения, приложенного к круглому валу.
Напряжение сдвига, вызванное поперечными силами, имеет решающее значение при расчете тонкостенных элементов. Для элементов без оловянных стенок, таких как круглый вал, наиболее важным, вероятно, будет осевое напряжение, вызванное изгибающим моментом, и вам, вероятно, потребуется использовать наш калькулятор модуля упругости. Наш калькулятор напряжения также может быть полезен, если вы имеете дело с осевым напряжением. Если это не так, используйте этот калькулятор!
Используемое уравнение напряжения сдвига будет зависеть от того, прикладываем ли мы поперечную нагрузку к балке или торсионную пару к круглому валу. В следующем разделе вы можете посмотреть формулы для напряжения сдвига при этих двух условиях.
В следующем разделе вы можете посмотреть формулы для напряжения сдвига при этих двух условиях.
Напряжение сдвига присутствует не только в твердых телах; это также необходимая величина при изучении жидкостей и газов. По этой причине мы создали раздел часто задаваемых вопросов, посвященный таким вопросам, как расчет напряжения сдвига жидкости или расчет ее вязкости по напряжению сдвига и скорости сдвига.
Формула напряжения сдвига для поперечного сдвига
Напряжение определяется как силы на единицу площади . В сечении балки, на которое действует сила сдвига, среднее касательное напряжение в этом сечении составляет:
τavg=VA\tau_{\text{avg}} = \frac{V}{A}τavg=AV всего в среднем , так как напряжение сдвига поперек балки, подвергаемой поперечному сдвигу, сильно различается.
Вы можете найти точное напряжение сдвига на любом расстоянии от центральной оси с помощью следующего уравнения:
τ=VQIt\tau = \frac{VQ}{It}τ=ItVQ
где:
- τ\tauτ – касательное напряжение на определенном расстоянии от нейтральной оси;
- VVV – внутренняя поперечная сила в интересующем сечении балки;
- QQQ – Первый момент относительно нейтральной оси площади поперечного сечения, лежащей выше точки, где мы будем вычислять напряжение;
- ttt – ширина сечения в точке, где мы будем рассчитывать касательное напряжение; и
- III – Второй момент площади всего поперечного сечения балки относительно нейтральной оси (можно найти с помощью нашего калькулятора момента инерции).

Предыдущее уравнение также дает нам среднее значение напряжения, поскольку оно зависит не только от вертикального расстояния от нейтральной оси, но и от ширины балки. К счастью, эта вариация обычно незначительна, и ею можно пренебречь.
Как рассчитать касательное напряжение по крутящему моменту
Чтобы рассчитать касательное напряжение по крутящему моменту, приложенному к круглому валу, используйте формулу напряжения сдвига при кручении:
τ=TρJ\tau = \frac{T \rho}{ J}τ=JTρ 94)/2J=π(c24−c14)/2.
Как рассчитать максимальное напряжение сдвига по крутящему моменту
Максимальное напряжение сдвига при скручивающих нагрузках возникает на внешней поверхности круглого вала, где ρ=c\rho = cρ=c или ρ=c2\rho = c_2ρ=c2 . Другими словами, максимальное касательное напряжение определяется как:
τmax=TcJ\tau_{max} = \frac{Tc}{J}τmax=JTc
, где:
- τmax\tau_{max}τmax — максимальное касательное напряжение; и
- ccc — Радиус вала.

Вы также должны учитывать это при использовании следующих формул:
- Единицами напряжения сдвига являются фунты на квадратный дюйм или паскали.
- Эта формула применима только к однородным материалам с линейной упругостью.
Формулы для расчета максимального касательного напряжения при поперечной сдвигающей нагрузке.
Как упоминалось ранее, максимальное напряжение сдвига круглой балки при кручении — это напряжение сдвига в ее самой внешней части. Но если вас интересует, как рассчитать максимальное касательное напряжение для балки при поперечном сдвиге ВВВ, это не так просто.
К счастью, наш калькулятор может сделать это за вас, используя следующие формулы для различных балок при поперечном сдвиге ВВВ:
Форма | Максимальное напряжение сдвига | |
|---|---|---|
Прямоугольник | τmax=3V2A\tau_{max} = \frac{3V}{2A}τmax=2A3V | |
А=дБА = дБА=дБ | ||
В двутавровой (широкополочной) балке значение τmin\tau_{min}τmin (значение напряжения в стыке между полкой и стенкой) является критической величиной, так как иногда стык в этой зоне создается с помощью сварки или клея, и нам нужно рассчитать, какое напряжение выдержат эти элементы.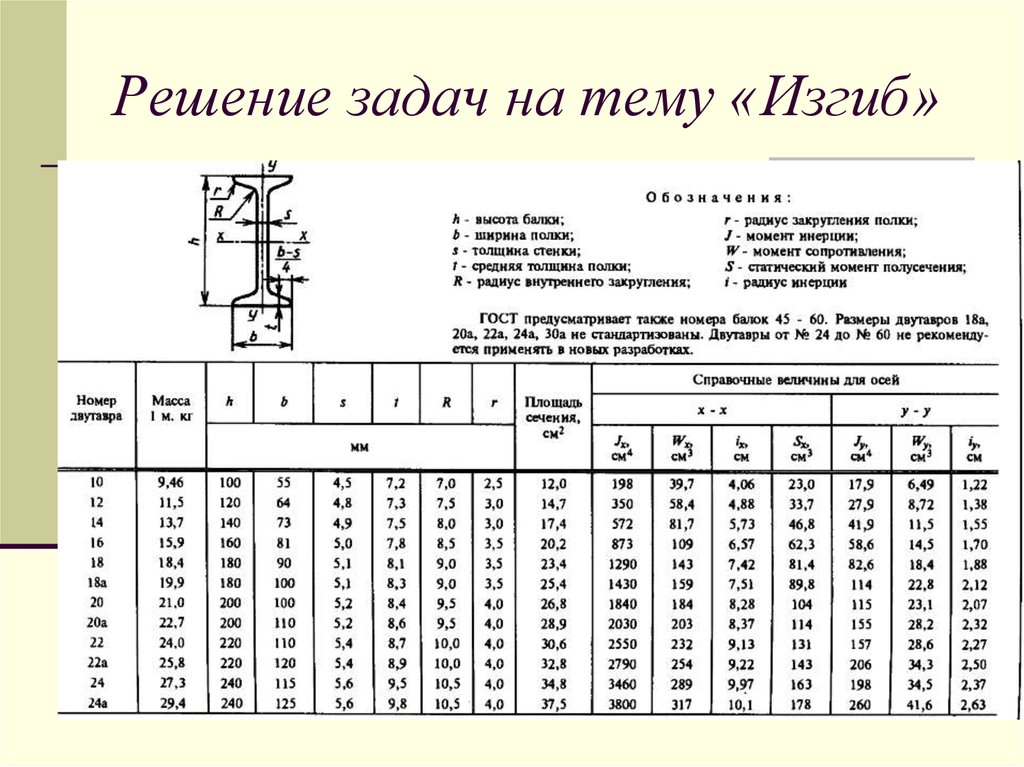
Важные соображения при использовании этих уравнений напряжения сдвига и калькулятора
Помните об этом:
- Когда мы прикладываем поперечную нагрузку к балке, возникают поперечные и продольные касательные напряжения. Благодаря дополнительному свойству сдвига эти продольные и поперечные напряжения имеют одинаковую величину. Следовательно, для расчета напряжения горизонтального сдвига требуется знать только значение напряжения поперечного сдвига, так как они оба одинаковы.
Балка прямоугольная на поперечный сдвиг ВВВ. τmax\tau_{max}τmax происходит на горизонтальной центральной оси, где QQQ максимально.
- QQQ — хитрая величина. Математически это площадь над интересующей точкой, умноженная на расстояние между центром тяжести этой области и нейтральной осью. Например, для поперечного сечения с кулачковой геометрией, если вы хотите рассчитать напряжение сдвига на расстоянии y′y’y′ от нейтральной оси, соответствующее QQQ будет Q=yˉ′AˉQ = \bar y’ \ бар AQ=yˉ′Aˉ.

- Из предыдущего изображения мы также можем заметить, что означает термин ttt.
Каковы единицы измерения напряжения сдвига?
Единицами напряжения сдвига являются паскаль (Па) в Международной системе единиц и фунта на квадратный дюйм (psi) в системе единиц, принятых в США. Мы также можем описать это количество в бар единиц.
Часто задаваемые вопросы
Каков полярный момент инерции круга радиусом 10 см?
Полярный момент инерции круга радиусом 10 см равен 15708 см 4 . В системе обычных единиц США ее полярный момент инерции равен 9.0003 377,4 в 4 .
Как рассчитать напряжение сдвига жидкости?
Для расчета напряжения сдвига 𝜏ᵧₓ жидкости:
- Определите, является ли жидкость ньютоновской или неньютоновской.
- Для ньютоновской жидкости умножить на вязкость
μна скорость сдвигаdu/dy:𝜏ᵧₓ = μ(du/dy).
- Если он неньютоновский, умножьте на кажущуюся вязкость
ηпо скорости сдвигадн/дн:
𝜏ᵧₓ = η(дн/дн).
η и μ являются аналогами, с той разницей, что η меняется с du/dy .
Как рассчитать вязкость по напряжению сдвига и скорости сдвига?
Чтобы рассчитать вязкость μ из напряжения сдвига 𝜏ᵧₓ и скорости сдвига du/dy , разделите напряжение сдвига на деформацию сдвига:
μ = 𝜏ᵧₓ/(du/dy)
Как рассчитать напряжение сдвига по расходу?
Чтобы вычислить напряжение сдвига по расходу в трубе, используйте формулу 𝜏ᵣₓ = -(4µrQ)/(πR⁴) , где: точка интереса;
μ – Абсолютная (или динамическая) вязкость жидкости; r – Радиальное расстояние от центра трубы до интересующей точки; Q – Расход; и R – Радиус трубы.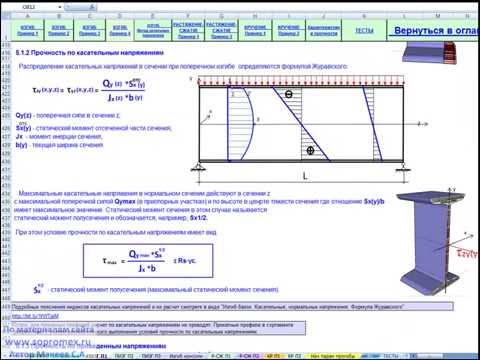
Вот как можно рассчитать напряжение сдвига по скорости потока! Учтите, что эта формула применима к ньютоновским жидкостям при полностью развитом ламинарном течении.
Как рассчитать напряжение сдвига в болтах?
Максимальное напряжение сдвига тела шнека, подвергнутого скручиванию, может быть выражено как:
𝜏ₘₐₓ = 16T / (πdᵣ³)
где:
- ☓ 𝜏ₘₐₓ0004 – максимальное номинальное касательное напряжение;
- T – Крутящий момент приложен к винту; и
- dᵣ – Внутренний диаметр винта.
Luis Hoyos
Входные данные
Выберите форму
Рассчитайте напряжение сдвига в произвольной балке, на которую действует поперечная сила V, используя формулу сдвига 𝜏 = VQ/It.
Кроме того, вы можете использовать калькулятор модуля сечения, чтобы найти центр тяжести и момент инерции площади многих структурных форм, что поможет вам найти Q, I и t.
Величина поперечной силы (В)
Ширина (т)
Первый момент площади (Q = ȳ’A’)
Момент инерции (I)
Ответ
Величина касательного напряжения (𝜏) Проверить
5
5
из 82 похожих калькуляторов классической механики ⚙️
AccelerationBank angleBelt length… Еще 79
Beam Deflection Calculator
Создано Николасом Суонсоном и Кеннетом Аламбра
Отзыв от Bogna Szyk
0005 Содержание:
- Что такое прогиб и изгиб балки
- Как рассчитать максимальный прогиб балки
- Метод суперпозиции
- Жесткость балки
- Понимание формул прогиба балки
- Пример расчета прогиба балки 90 375 90 375 90 Калькулятор прогиба балки поможет вам определить максимальный прогиб свободно опертой балки и консольной балки, несущей простых конфигурации нагрузки . Вы можете выбрать один из нескольких типов нагрузки, которые могут воздействовать на балку любой длины. Величина и расположение этих нагрузок влияют на то, насколько сильно изгибается балка.
 В этом калькуляторе прогиба балки вы узнаете о различных формулах прогиба балки , используемых для расчета прогибов свободно опертой балки и прогибов консольной балки. Вы также узнаете, как модуль упругости балки и ее момент инерции поперечного сечения влияют на рассчитанный максимальный прогиб балки.
В этом калькуляторе прогиба балки вы узнаете о различных формулах прогиба балки , используемых для расчета прогибов свободно опертой балки и прогибов консольной балки. Вы также узнаете, как модуль упругости балки и ее момент инерции поперечного сечения влияют на рассчитанный максимальный прогиб балки.Прогиб балки является важной частью анализа балки, но другой важной частью является анализ напряжения. Мощным инструментом для изучения напряжений изгиба балки является модуль сопротивления, который можно рассчитать с помощью нашего калькулятора модуля сечения.
Что такое прогиб и изгиб балки
В строительстве мы обычно используем каркасные конструкции , которые удерживаются фундаментом в земле. Эти каркасные конструкции подобны каркасам зданий, домов и даже мостов. В кадре мы называем вертикальное кадрирование колонны , а горизонтальные балки . Балки — это длинные элементы конструкции, которые несут нагрузки, создаваемые горизонтальными плитами конструкций, такими как сплошные бетонные полы, деревянные балочные системы полов и крыши.

Когда балки несут слишком тяжелые для них нагрузки, они начинают прогибаться. Мы называем величину изгиба балки прогибом балки . Прогиб балки — это вертикальное смещение точки вдоль центра тяжести балки. Мы также можем рассматривать поверхность балки в качестве нашей точки отсчета, если во время изгиба нет изменений высоты или глубины балки.
Как рассчитать максимальное отклонение балки
Мы оснастили наш калькулятор прогиба балки формулами, которые инженеры и студенты-инженеры используют для быстрого определения максимального прогиба конкретной балки из-за нагрузки, которую она несет. Однако эти формулы могут решать только простые нагрузки и их комбинации. Мы свели для вас эти формулы в таблицу, как показано ниже:
Формулы прогиба свободно опертой балки
Формулы прогиба консольной балки
Метод суперпозиции
Для расчета максимального прогиба балки при сочетании нагрузок можно использовать метод суперпозиции .
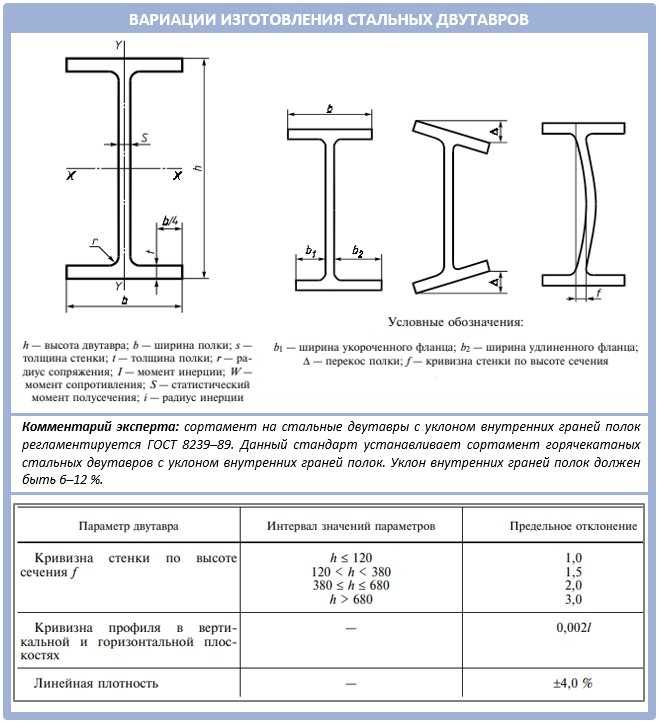 Метод суперпозиции утверждает, что мы можем аппроксимировать полное отклонение балки, суммируя все отклонения, вызванные каждой конфигурацией нагрузки. Однако этот метод дает нам только приблизительное значение фактического максимального отклонения. Расчет сложных нагрузок потребовал бы от нас использования так называемого метод двойного интегрирования .
Метод суперпозиции утверждает, что мы можем аппроксимировать полное отклонение балки, суммируя все отклонения, вызванные каждой конфигурацией нагрузки. Однако этот метод дает нам только приблизительное значение фактического максимального отклонения. Расчет сложных нагрузок потребовал бы от нас использования так называемого метод двойного интегрирования .Жесткость балки
Для расчета прогиба балки необходимо знать жесткость балки и величину силы или нагрузки, которые могут повлиять на изгиб балки. Мы можем определить жесткость балки, умножив модуль упругости балки, E , на ее момент инерции, I . Модуль упругости зависит от материала балки. Чем выше модуль упругости материала, тем больше прогиб может выдержать огромные нагрузки, прежде чем он достигнет предела прочности. Модуль упругости бетона составляет от 15 до 50 ГПа (гигапаскалей), в то время как у стали около 200 ГПа и выше. Эта разница в значениях модуля упругости показывает, что бетон может выдерживать только небольшое отклонение и растрескивается раньше, чем сталь.

Вы можете узнать больше о модуле упругости, воспользовавшись нашим калькулятором напряжений. С другой стороны, чтобы определить момент инерции для определенного поперечного сечения балки, вы можете посетить наш калькулятор момента инерции. Момент инерции представляет собой величину сопротивления материала вращательному движению. Момент инерции зависит от размеров поперечного сечения материала.
Момент инерции также меняется в зависимости от того, вдоль какой оси вращается материал. Чтобы лучше понять эту концепцию, давайте рассмотрим поперечное сечение прямоугольного бруса шириной 20 см и высотой 30 см. Используя формулы, которые вы также можете увидеть в нашем калькуляторе момента инерции, мы можем рассчитать значения момента инерции поперечного сечения этой балки следующим образом:
Iₓ = ширина × высота Quest³ / 12
= 20 × (30³) / 12
= 45 000 смIᵧ = Высота × ширина / 12
= 30 × (20 минут) (20 минут) (20 минут).
= 20 000 см⁴Обратите внимание на два значения момента инерции. Это потому, что мы можем считать, что балка изгибается вертикально вдоль пролета балки (или испытывает изгибающий момент вокруг оси x) и в поперечном направлении вдоль пролета балки (или согнуть вокруг оси Y). Поскольку мы рассматриваем отклонение луча, когда он изгибается по вертикали или вокруг оси x, мы должны использовать Iₓ для наших вычислений. Полученные нами значения момента инерции говорят нам о том, что балка труднее изгибается при вертикальной нагрузке и легче изгибается при горизонтальной поперечной нагрузке. Эта разница в значениях моментов инерции является причиной того, что мы видим балки в такой конфигурации, где их высота больше, чем их ширина.
Понимание формул прогиба балки
Теперь, когда мы знаем понятия модуля упругости и момента инерции, мы теперь можем понять, почему эти переменные являются знаменателями в наших формулах прогиба балки.
 Из формул видно, что чем жестче балка, тем меньше будет ее прогиб. Однако, изучив наши формулы, мы также можем сказать, что длина балки также напрямую влияет на отклонение балки. Чем длиннее становится балка, тем больше она может изгибаться и тем больше может быть отклонение.
Из формул видно, что чем жестче балка, тем меньше будет ее прогиб. Однако, изучив наши формулы, мы также можем сказать, что длина балки также напрямую влияет на отклонение балки. Чем длиннее становится балка, тем больше она может изгибаться и тем больше может быть отклонение.Нагрузки, с другой стороны, влияют на прогиб балки двумя способами: направление прогиба и величина прогиба. Нагрузки, направленные вниз, имеют тенденцию отклонять балку вниз. Нагрузки могут быть в виде одноточечной нагрузки, линейного давления или мгновенной нагрузки. Формулы в этом калькуляторе ориентированы только на направление вниз или вверх для точечной нагрузки и распределенной нагрузки. Распределенные нагрузки аналогичны давлению, но учитывают только длину балки, а не ширину балки. Формулы в этом калькуляторе также учитывают момент или крутящий момент нагрузки по часовой стрелке или против часовой стрелки. Просто сверьтесь с направлениями стрелок на соответствующем изображении формулы, чтобы выяснить, какие направления имеют положительное значение нагрузки.

Пример расчета прогиба балки
Для примера расчета прогиба балки рассмотрим простую деревянную скамью с ножками, расположенными на расстоянии 1,5 м друг от друга в их центрах. Допустим, у нас есть доска из восточной белой сосны толщиной 4 см и шириной 30 см, которая служит сиденьем для этой скамьи. Мы можем рассматривать это сиденье как балку, которая будет отклоняться всякий раз, когда кто-то садится на скамейку. Зная размеры этого сиденья, мы можем рассчитать его момент инерции, как в нашем примере выше. Поскольку нам нужно рассчитать Iₓ, его момент инерции будет:
Iₓ = ширина * Высота сегодня / 12
= 30 * (4³) / 12
= 160,0 см или 1,6x10⁻⁶ M⁴Восточная белая сосна имеет модуль эластичности
6,8001 (6.8 (6.8 (6.8.8002 (6.8 (6.8.8002 (6.8 (6.8.8002 (6.8.8002 (6.8. x10⁹ Па), что является значением, полученным из Справочника по дереву. Вы также можете легко получить значение модуля упругости для других материалов, таких как сталь и бетон, в Интернете или в местной библиотеке.

 0 Т
0 Т 5.12,5.18
5.12,5.18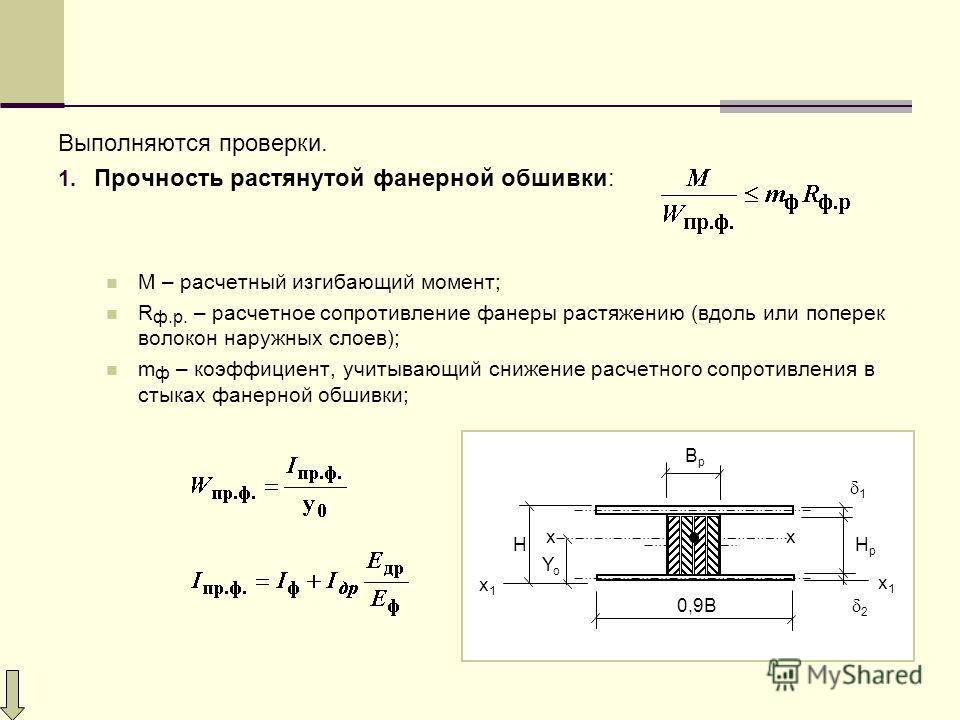
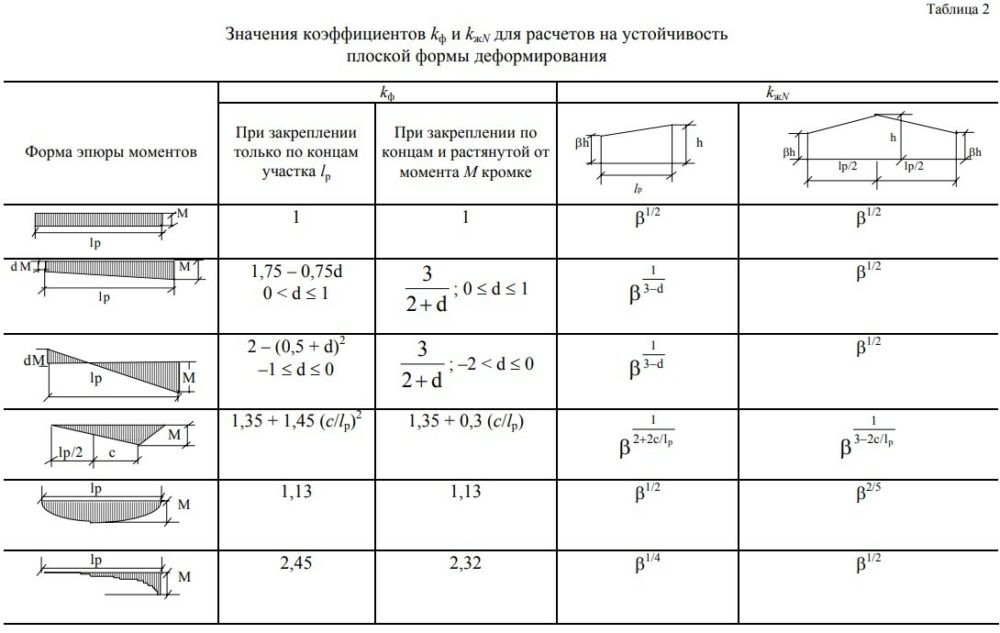 = +wL
= +wL = +Fab / L
= +Fab / L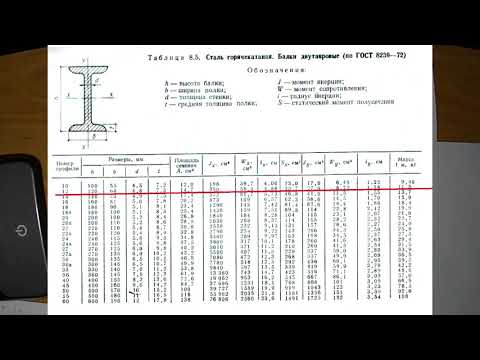 = Fa
= Fa = М 0
= М 0