Схемы фрезерования: ОСНОВНЫЕ ВИДЫ И СХЕМЫ ФРЕЗЕРОВАНИЯ. КЛАССИФИКАЦИЯ И КОНСТРУКЦИЯ ФРЕЗ
Содержание
Схемы фрезерования
При
фрезеровании движение резания сообщается
фрезе, а движение подачи – заготовке.
При этом при одном и том же прямолинейном
перемещении заготовки, направление
движения инструмента может с движением
подачи, может быть направлено встречно.
Попутное
фрезерование
– это вид фрезерования, при котором
направления движения резания и движения
подачи совпадают. К недостаткам этой
схемы относится то, что при касании зуба
фрезы о заготовку при максимальном
значении толщины стружки amax
происходит удар. Условия фрезерования
могут усложняться, если заготовка имеет
литейную корку. К достоинствам попутного
фрезерования относится тот факт, что
результирующая усилия резания Р прижимает
заготовку к приспособлению, что не
требует дополнительных усилий на её
закрепление. Изменение толщины стружки
от максимального значения до нуля
обеспечивает высокое качество
обрабатываемой поверхности, то есть
низкую шероховатость.
При
встречном
фрезеровании
толщина срезаемого слоя меняется от
нуля до amax,
поэтому в начальный момент резания
фреза может проскальзывать относительно
обрабатываемой поверхности, что не
позволяет обеспечить высокое качество
последней. К тому же результирующая
К тому же результирующая
усилия резания Р стремится оторвать
заготовку от приспособления, что требует
дополнительных усилий для закрепления
заготовки. Достоинством метода является
возможность работы из-под корки.
Фрезерование
проводится на горизонтальных или
вертикальных фрезерных станках.
Износ фрез и скорость фрезерования
Основной
износ зуба фрезы происходит по задней
поверхности, на которой образуется
площадочка с задним углом =0.
Допустимый
износ f
зуба фрезы при черновой обработке f=0,6
мм, при чистовой f=0,25
мм.
Экономическая
скорость резания рассчитывается по
формуле.
Данная
формула позволяет определять экономическую
скорость резания с учётом заданной
стойкости фрезы.
ω
– угол наклона винтовых канавок
В
– ширина
z
– количество зубьев
Анализ
этой формулы показывает, что увеличение
диаметра благоприятно сказывается на
условиях работы, то есть при том же
количестве зубьев, каждый из них большее
время охлаждается за один оборот фрезы,
что позволяет увеличить скорость резания
при прочих неизменных условиях.
Обработка абразивным инструментом
Все
методы обработки абразивным (abrasio
– соскабливание) инструментом основаны
на соскабливании материала заготовки
абразивными зёрнами, входящими в состав
инструмента. Каждое воздействие такого
зерна приводит к удалению микрообъёма
материала заготовки, то есть происходит
процесс микрорезания.
В общем случае,
абразивный диск (инструмент) можно
представить в виде фрезы, на цилиндрической
наружной поверхности которой расположены
микрозубья различной геометрии.
Обрабатываемая
поверхностьОбработанная
поверхностьП
оверхность
резанияУсловная
наружная поверхность инструментаУ
словная
поверхность связки
Г
еометрия
каждого зерна характеризуется
отрицательными передними углами.
Разнообразие величин углов, определяемое
формой каждого абразивного зерна,
приводит к тому, что при сильном увеличении
обработанная поверхность не будет
казаться гладкой, но, учитывая поперечные
размеры зерна, не превышающие 0,5 мм и
глубины резания (десятые доли мм), можно
предположить, что каждое отдельное
зерно (зуб фрезы) удаляет микрочастицу
материала.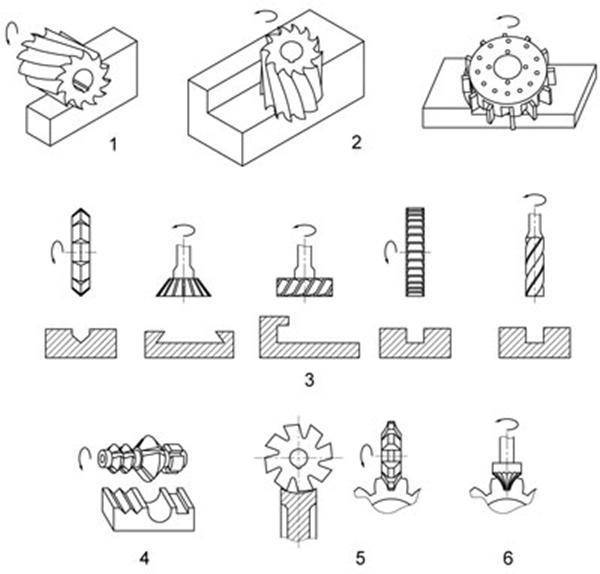 При этом образующаяся
При этом образующаяся
шероховатость будет измеряться
микровеличинами, то есть минимальными
размерами впадин и выступов.
Н
еодинаковость
размеров зёрен приводит к тому, что в
контакт с материалом заготовки вступают
наиболее выступающие зёрна. Учитывая
отрицательные значения передних углов,
а также износ в процессе соскабливания
(что увеличивает силы резания) можно
предположить, что в определённый момент
времени силы резания будут превышать
силы, с которыми связка удерживает
абразивное зерно. Оно выкрашивается. В
этот момент в контакт с материалом
заготовки вступает следующее, наиболее
выступающее абразивное зерно. Этот
процесс называется самозатачиванием,
то есть происходит обновление режущих
зубьев.
═══════════════════════════════════
4. Схемы фрезерования поверхностей на горизонтально- и вертикально-фрезерных станках.
Движения,
участвующие в формообразовании
поверхностей в процессе резания, в
схемах указаны стрелками.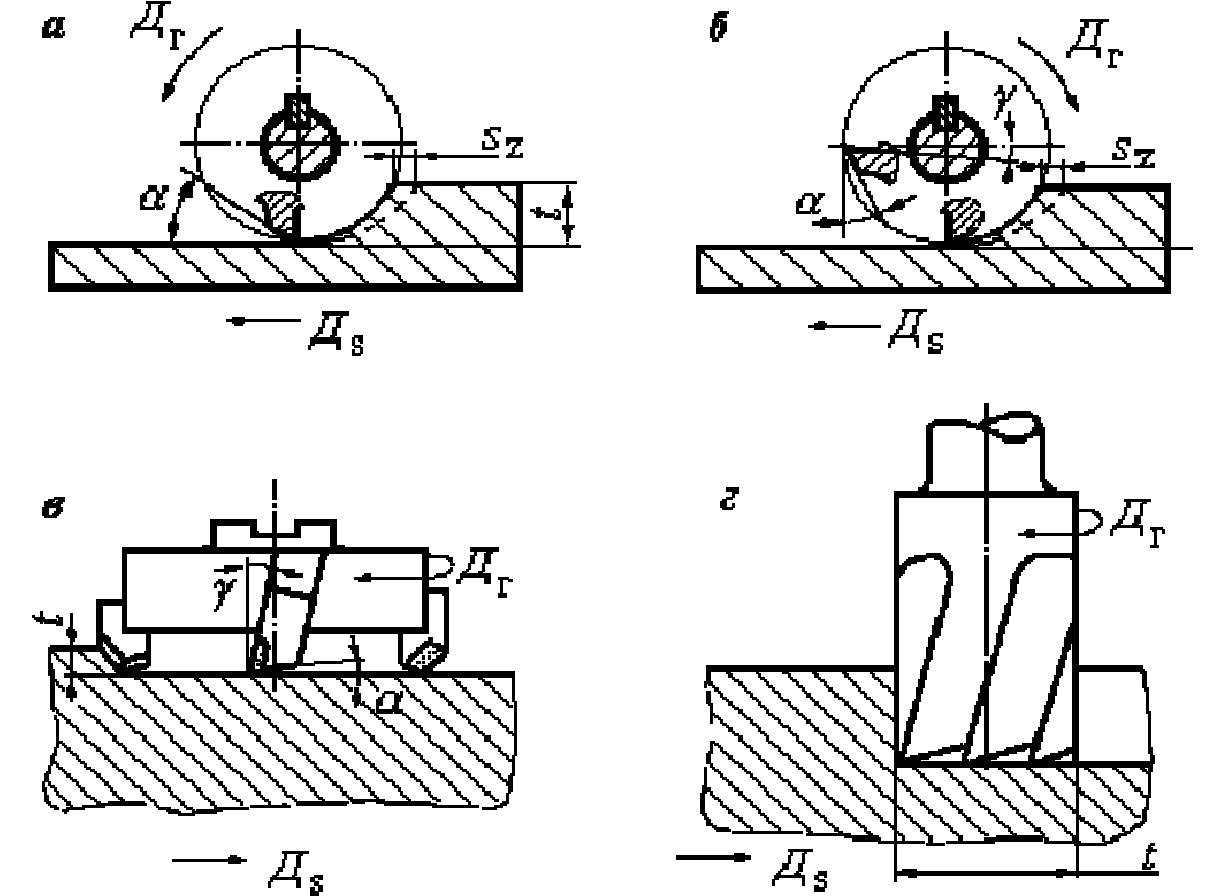
Горизонтальные
плоскости
фрезеруют на горизонтально-фрезерных
станках цилиндрическими фрезами
(рис.7,а) и на вертикально-фрезерных
осанках — торцовыми
фрезами (рис.8,а), цилиндрическими фрезами
целесообразно обрабатывать горизонтальные
плоскости шириной до 120
мм,
при этом длина фрезы должна быть немного
больше ширины обрабатываемой заготовки.
В большинстве случаев плоскости удобнее
обрабатывать торцовыми
фрезами вследствие большей жесткости
их крепления в шпинделе и более плавной
работы, так как число одновременно
работающих зубьев торцовой фрезы больше
числа зубьев цилиндрической фрезы.
Рис.7
Схемы фрезерования плоскостей на ГФС
Вертикальные
плоскости
фрезеруют на горизонтально-фрезерных
станках торцовыми
фрезами (рис.7,б) и торцовыми
фрезерными головками, а на
вертикально-фрезерных станках — концевыми
фрезами (рис.8,б).
Наклонные
плоскости и скосы
фрезеруют торцовыми (рис. 8,в) концевыми
8,в) концевыми
(рис.8,г) фрезами на вертикально-фрезерных
станках, у которых фрезерная головка
со шпинделем поворачивается в вертикальной
плоскости. Скосы фрезеруют на
горизонтально-фрезерном станке
одноугловой фрезой (рис.7,в).
Рис.8
Схемы фрезерования плоскостей на ВФС
Комбинированные
поверхности
фрезеруют набором фрез (рис.7,г) на
горизонтально-фрезерных станках.
Точность взаиморасположения обработанных
поверхностей зависит от жесткости
крепления фрез по длине оправки. С этой
целью применяют дополнительные опоры
(подвески), избегают использования
несоразмерных по диаметру фрез
(рекомендуемое отношение диаметров
фрез не более 1,5).
Уступы
и прямоугольные пазы
фрезеруют дисковыми (рис.7,д) и концевыми
(рис.8,д) фрезами на горизонтально- и
вертикально- фрезерных станках.
Уступы
и пазы целесообразнее фрезеровать
дисковыми фрезами, так как они имеют
большее число зубьев и допускают работу
с большими скоростями резания.
Угловые
пазы
фрезеруют
одноугловой и двухугловой (рис.7,е)
фрезами на горизонтально -фрезерных
станках.
Паз
типа «ласточкин хвост»
фрезеруют на вертикально-фрезерном
станке за
два прохода:
прямоугольный паз — концевой фрезой,
затем скосы паза концевой одноугловой
фрезой (рис.8,е).
Т-образные
пазы
(рис.8,ж), которые широко применяют в
машиностроении как станочные пазы,
например, на столах фрезерных станков,
фрезеруют обычно за два прохода: вначале
паз прямоугольного профиля концевой,
реже дисковой фрезой, затем нижнюю часть
паза — фрезой для Т-образных пазов.
Закрытые
шпоночные пазы
фрезеруют концевыми фрезами (рис.8,з), а
открытые — концевыми фрезами или
шпоночными на вертикально-фрезерных
станках. Точность получения шпоночного
паза является важным условием при
фрезеровании, т.к. от нее зависит характер
посадки на шпонку сопрягаемых с валом
деталей. Фрезерование шпоночной фрезой
Фрезерование шпоночной фрезой
обеспечивает получение более точного
паза; при переточке по торцовым
зубьям диаметр шпоночной фрезы практически
не изменяется.
Анализ схем профильного фрезерования длинномерных и нетехнологичных заготовок
Открытый доступ
| Проблема | Веб-конференция MATEC. Том 224, 2018 Международная конференция «Современные тенденции в производственных технологиях и оборудовании» (ICMTMTE 2018) | |
|---|---|---|
| Номер статьи | 01016 | |
| Количество страниц) | 7 | |
| Секция | Производственные технологии, инструменты и оборудование | |
| ДОИ | https://doi.org/10.1051/matecconf/201822401016 | |
| Опубликовано онлайн | 30 октября 2018 г. | |
MATEC Web of Conferences 224 , 01016 (2018)
Гусев Владимир Григорьевич 1 , Фомин Анатолий Александрович 1 * и Салдаев Владимир Анатольевич 2 9000 3
1
Институт машиностроения и автомобильного транспорта Владимирского государственного университета, ул.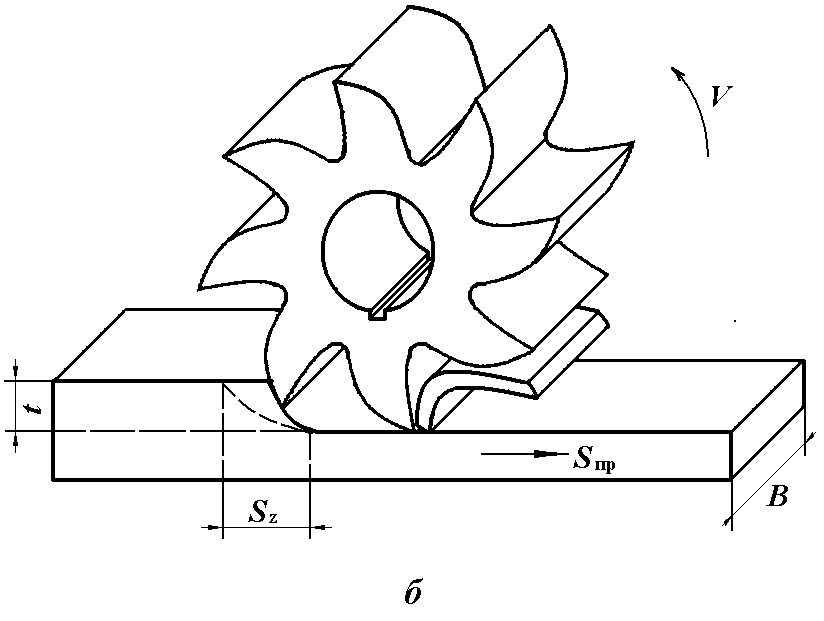 Горького, 87, г. Владимир, 600000, Российская Федерация
Горького, 87, г. Владимир, 600000, Российская Федерация
2
Научный центр перспективных энергетических технологий Казанского государственного энергетического университета, ул. Красносельская, 51, г. Казань, 420066, Российская Федерация,
* Автор, ответственный за переписку: [email protected]
Реферат
В статье рассмотрены альтернативные схемы профильного фрезерования длинномерных нетехнологичных заготовок – периферийных сегментов, образующихся при продольном раскрое бревен. Периферийные сегменты являются крупным отходом производства и содержат древесные волокна с высокими физико-механическими и эксплуатационными свойствами. Поэтому изготовление качественных изделий из древесины из периферийных сегментов является особенно актуальной задачей. Однако названные заготовки характеризуются низкой технологичностью, поэтому необходимы разработка и анализ схем механической обработки, исключающих резонанс в технологической системе. Безрезонансная схема обработки использована в конструкции фрезерного станка ПФП-100 для профильного фрезерования крупных древесных отходов.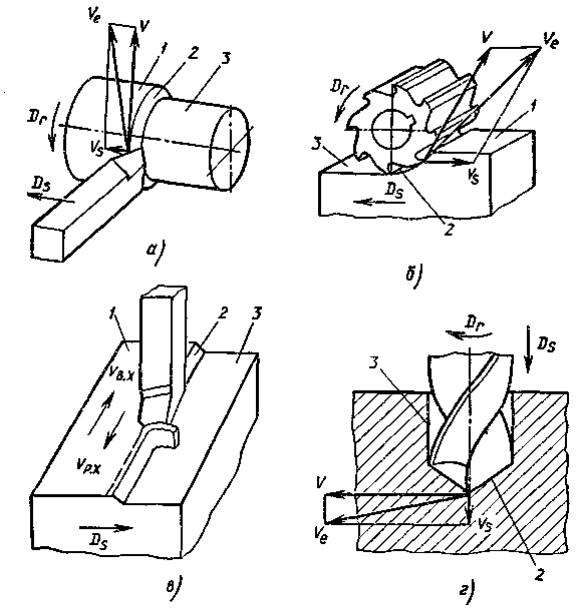
© The Authors, опубликовано EDP Sciences, 2018 г. разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии надлежащего цитирования оригинальной работы.
Показатели текущего использования показывают совокупное количество просмотров статей (просмотры полнотекстовых статей, включая просмотры HTML, загрузки PDF и ePub, согласно имеющимся данным) и просмотров рефератов на платформе Vision4Press.
Данные соответствуют использованию на платформе после 2015 года. Текущие показатели использования доступны через 48-96 часов после онлайн-публикации и обновляются ежедневно в рабочие дни.
Методы полудискретизации на основе численных схем интегрирования для прогнозирования устойчивости при фрезеровании
Мерритт Х.Е. (1965) Теория самовозбуждающейся вибрации станка: вклад в исследование вибрации станка—1. J Eng Ind 87 (4): 447–454. https://doi.org/10.1115/1.3670861
Статья
Google Scholar
Altintas Y (2000) Автоматизация производства: механика резки металла, вибрации станков и проектирование ЧПУ. Издательство Кембриджского университета, Кембридж
Google Scholar
Zhang XJ, Xiong CH, Ding Y, Xiong YL (2012) Анализ стабильности фрезерования с одновременным учетом эффекта связи структурных мод и регенеративного эффекта. Int J Mach Tools Manuf 53 (1): 127–140. https://doi.org/10.1016/j.ijmachtools.2011.10.004
Артикул
Google Scholar
Wiercigroch M (1781) Budak E (2001) Источники нелинейности, генерация вибрации и ее подавление при резании металлов. Philos Trans R Soc AMath Phys Eng Sci 359: 663–693. https://doi.org/10.1098/rsta.2000.0750
Статья
МАТЕМАТИКА
Google Scholar
Верцигрох М. (1781) Кривцов А.М. (2001) Фрикционная вибрация при ортогональном резании металлов. Philos Trans R Soc A Math Phys Eng Sci 359: 713–738. https://doi.org/10.1098/rsta.2000.0752
Philos Trans R Soc A Math Phys Eng Sci 359: 713–738. https://doi.org/10.1098/rsta.2000.0752
Статья
Google Scholar
Altintas Y, Budak E (1995) Аналитический прогноз выступов устойчивости при фрезеровании. CIRP Ann-Manuf Techn 44(1):357–362. https://doi.org/10.1016/S0007-8506(07)62342-7
Статья
Google Scholar
Мердол С.Д., Алтинтас Ю. (2004) Многочастотное решение для снижения вибрации при фрезеровании с низким погружением. J Manuf Sci Eng 126 (3): 459–466. https://doi.org/10.1115/1.1765139
Статья
Google Scholar
Инспергер Т., Степан Г. (2002) Метод полудискретизации для систем с задержкой. междунар. J Numer Methods Engrg 55 (5): 503–518. https://doi.org/10.1002/nme.505
Статья
MathSciNet
МАТЕМАТИКА
Google Scholar
Инспергер Т., Степан Г. (2004) Обновленный метод полудискретизации для периодических дифференциальных уравнений с запаздыванием с дискретным запаздыванием. Int J Numer Methods Eng 61 (1): 117–141. https://doi.org/10.1002/nme.1061
Артикул
MathSciNet
МАТЕМАТИКА
Google Scholar
Инспергер Т., Степан Г., Тури Дж. (2008) О полудискретизации высшего порядка для периодических систем с запаздыванием. J Sound Vib 313 (1-2): 334–341. https://doi.org/10.1016/j.jsv.2007.11.040
Статья
Google Scholar
Jiang S, Sun Y, Yuan X, Liu W (2017) Метод полудискретизации второго порядка для эффективного и точного прогнозирования стабильности процесса фрезерования. Int J Adv Manuf Technol 92 (1-4): 583–595. https://doi.org/10.1007/s00170-017-0171-y
Статья
Google Scholar
Дин Ю., Чжу Л.М., Чжан С.Дж., Дин Х. (2010) Метод полной дискретизации для прогнозирования стабильности фрезерования. Int J Mach Tools Manuf 50 (5): 502–509. https://doi.org/10.1016/j.ijmachtools.2010.01.003
Статья
Google Scholar
Дин Ю., Чжу Л.М., Чжан С.Дж., Дин Х. (2010) Метод полной дискретизации второго порядка для прогнозирования стабильности фрезерования. Int J Mach Tools Manuf 50 (10): 926–932. https://doi.org/10.1016/j.ijmachtools.2010.05.005
Статья
Google Scholar
Guo Q, Sun YW, Jiang Y (2012) О точном расчете пределов устойчивости при фрезеровании с использованием метода полной дискретизации третьего порядка. Int J Mach Tools Manuf 62: 61–66. https://doi.org/10.1016/j.ijmachtools.2012.07.008
Статья
Google Scholar
Zhang XJ, Xiong CH, Ding Y (2010) Усовершенствованный метод полной дискретизации для прогнозирования стабильности вибрации при фрезеровании с несколькими задержками. В: Международная конференция по интеллектуальной робототехнике и приложениям. ICIRA 2010. Конспект лекций по информатике, том 6425. Springer, Берлин, Гейдельберг. https://doi.org/10.1007/978-3-642-16587-0_50
Глава
Google Scholar
Лю Ю.Л., Чжан Д.Х., Ву Б.Х. (2012) Эффективный метод полной дискретизации для прогнозирования стабильности фрезерования. Int J Mach Tools Manuf 63:44–48. https://doi.org/10.1016/j.ijmachtools.2012.07.008
Статья
Google Scholar
Jin G, Qi HJ, Cai YJ, Zhang QC (2015) Прогнозирование стабильности процесса фрезерования с несколькими задержками с использованием усовершенствованного метода полудискретизации. Математический метод Appl Sci 39(4): 949–958. https://doi.org/10.1002/mma.3543
https://doi.org/10.1002/mma.3543
Статья
MathSciNet
МАТЕМАТИКА
Google Scholar
Ozoegwu CG (2014) Метод наименьших квадратов аппроксимировал границы устойчивости процесса измельчения. Int J Mach Tools Manuf 79: 24–30. https://doi.org/10.1016/j.ijmachtools.2014.02.001
Статья
Google Scholar
Озоэгву К.Г., Омени С.Н., Офочебе С.М. (2015) Методы полной дискретизации гипертретьего порядка в прогнозировании стабильности фрезерования. Int J Mach Tools Manuf 92:1–9. https://doi.org/10.1016/j.ijmachtools.2015.02.007
Статья
Google Scholar
Tang X, Peng F, Yan R, Gong Y, Li Y, Jiang L (2016) Точное и эффективное прогнозирование стабильности фрезерования с помощью обновленного метода полной дискретизации. Int J Adv Manuf Technol 88 (9-12): 2357–2368. https://doi.org/10.1007/s00170-016-8923-7
https://doi.org/10.1007/s00170-016-8923-7
Статья
Google Scholar
Yan ZH, Wang XB, Liu ZB, Wang DQ, Jiao L, Ji YJ (2017) Обновленный метод полной дискретизации третьего порядка для прогнозирования устойчивости фрезерования. Int J Adv Manuf Technol 92(5-8):2299–2309. https://doi.org/10.1007/s00170-017-0243-z
Статья
Google Scholar
Чжоу К., Фэн П., Сюй С., Чжан Дж., У З. (2017) Методы полной дискретизации высокого порядка для прогнозирования устойчивости фрезерования путем интерполяции члена задержки дифференциальных уравнений с запаздыванием. Int J Adv Manuf Technol 93 (5-8): 2201–2214. https://doi.org/10.1007/s00170-017-0692-4
Статья
Google Scholar
Dai YB, Li H, Hao B (2018) Усовершенствованный метод полной дискретизации для прогнозирования стабильности вибрации.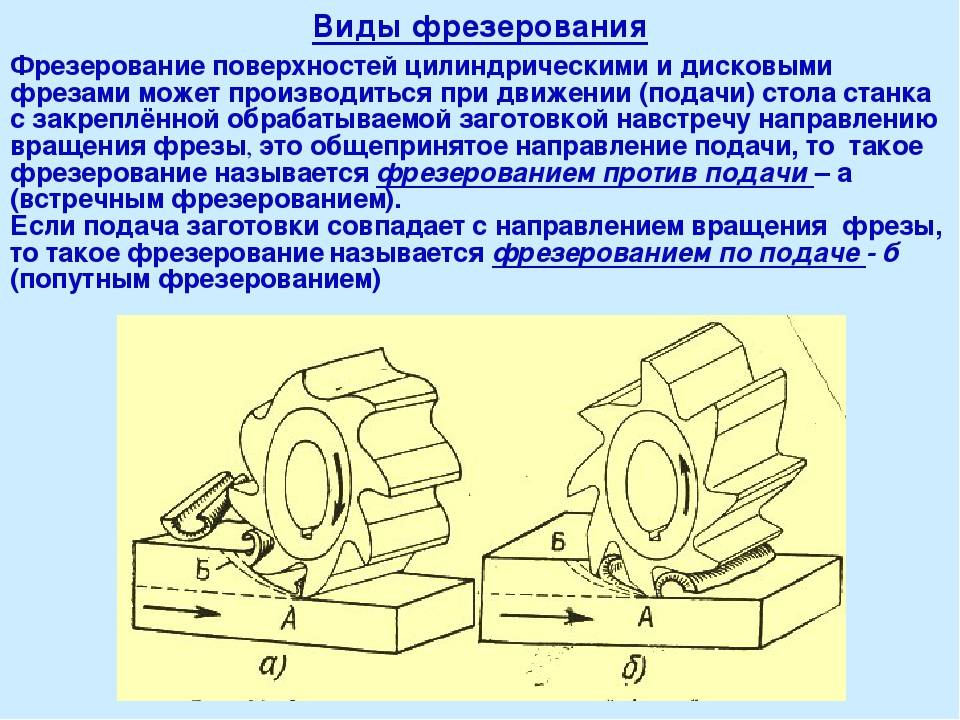 Int J Adv Manuf Technol 96 (9-12): 3503–3510. https://doi.org/10.1007/s00170-018-1767-6
Int J Adv Manuf Technol 96 (9-12): 3503–3510. https://doi.org/10.1007/s00170-018-1767-6
Статья
Google Scholar
Dai YB, Li HK, Xing XY, Hao BT (2018) Прогнозирование стабильности вибрации для процесса фрезерования с использованием метода точного интегрирования. Precis Eng 52: 152–157. https://doi.org/10.1016/j.precisioneng.2017.12.003
Артикул
Google Scholar
Li H, Dai Y, Fan Z (2019) Усовершенствованный метод точного интегрирования для прогнозирования устойчивости к вибрации фрезерной системы с двумя степенями свободы. Int J Adv Manuf Technol 101 (5-8): 1235–1246. https://doi.org/10.1007/s00170-018-2981-y
Статья
Google Scholar
Цинь С., Тао Дж., Лю С. (2019) Новый метод прогнозирования устойчивости для операций фрезерования с использованием схемы целостной интерполяции. PI Mech Eng CJ Mec 233 (13): 4463–4475. https://doi.org/10.1177/0954406218815716
PI Mech Eng CJ Mec 233 (13): 4463–4475. https://doi.org/10.1177/0954406218815716
Артикул
Google Scholar
Qin C, Tao J, Liu C (2018) Метод целостной дискретизации на основе предиктора-корректора для точного и эффективного анализа стабильности фрезерования. Int J Adv Manuf Technol 96: 2043–2054. https://doi.org/10.1007/s00170-018-1727-1
Статья
Google Scholar
Yang WA, Huang C, Cai X, You Y (2020) Эффективное и быстрое прогнозирование стабильности фрезерования с использованием точного метода полной дискретизации третьего порядка на основе интегрирования. Int J Adv Manuf Technol 106 (9): 4477–4498. https://doi.org/10.1007/s00170-019-04790-z
Статья
Google Scholar
Wu Y, You YP, Jiang JJ (2020) Новые методы предиктора-корректора, основанные на кусочно-полиномиальной интерполяции для прогнозирования устойчивости фрезерования. Mach Sci Technol 24 (5): 688–718. https://doi.org/10.1080/10910344.2020.1752235
Mach Sci Technol 24 (5): 688–718. https://doi.org/10.1080/10910344.2020.1752235
Статья
Google Scholar
Озоэгву К.Г., Эберхард П. (2019 г.) Автоматическое вычисление произвольного порядка на основе тензора метода полной дискретизации для анализа устойчивости фрезерования. В: Альтенбах Х., Ирщик Х., Матвеенко В. (ред.) Вклад в продвинутую динамику и механику сплошной среды. Усовершенствованные структурированные материалы, том 114. Спрингер, Чам, стр. 179–205. https://doi.org/10.1007/978-3-030-21251-3_11
Глава
Google Scholar
Дин Ю., Чжу Л.М., Чжан XJ, Дин Х. (2011) Метод численного интегрирования для прогнозирования стабильности фрезерования. J Manuf Sci Eng 133 (3): 031005. https://doi.org/10.1115/1.4004136
Артикул
Google Scholar
Zhang XJ, Xiong CH, Ding Y, Xiong YL (2011) Метод интегрирования с переменным шагом для прогнозирования стабильности вибрации при фрезеровании с несколькими задержками. Sci China Technol Sc 54 (12): 3137–3154. https://doi.org/10.1007/s11431-011-4599-2
Статья
МАТЕМАТИКА
Google Scholar
Ozoegwu CG (2016) Схемы векторного численного интегрирования высокого порядка, применяемые в анализе устойчивости фрезерования в пространстве состояний. Appl Math Comput 273: 1025–1040. https://doi.org/10.1016/j.amc.2015.10.069
Артикул
MathSciNet
МАТЕМАТИКА
Google Scholar
Dong X, Qiu Z (2020) Анализ стабильности в процессе фрезерования на основе обновленного метода численного интегрирования. Сигнал механической системы Pr 137:106435. https://doi.org/10.1016/j.ymssp.2019.106435
Статья
Google Scholar
Li WT, Wang LP, Yu G (2020) Точный и быстрый подход к прогнозированию стабильности фрезерования на основе правил Ньютона-Котеса. Int J Mech Sci Volume 177: 105469. https://doi.org/10.1016/j.ijmecsci.2020.105469
Статья
Google Scholar
Niu JB, Ding Y, Zhu LM, Ding H (2014) Методы Рунге-Кутта для полуаналитического прогнозирования устойчивости при измельчении. Нелинейный Динамик 76 (1): 289–304. https://doi.org/10.1007/s11071-013-1127-x
Статья
MathSciNet
МАТЕМАТИКА
Google Scholar
Zhang Z, Li HG, Meng G, Liu C (2015) Новый подход к прогнозированию стабильности фрезерования на основе метода Симпсона. Int J Mach Tools Manuf 99:43–47. https://doi.org/10.1016/j.ijmachtools.2015.09.002
Статья
Google Scholar
Qin CJ, Tao JF, Li L, Liu CL (2017) Метод Адамса-Моултона для прогнозирования стабильности процессов измельчения.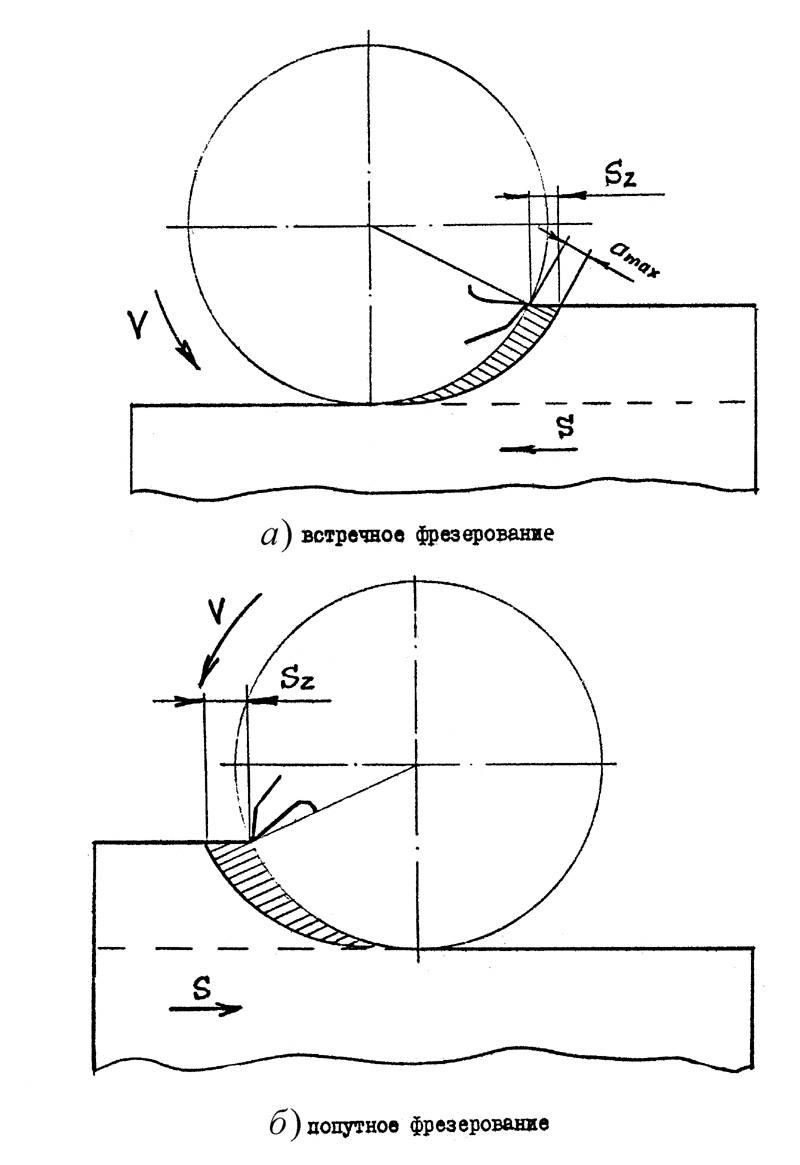 Int J Adv Manuf Technol 89 (9-12): 3049–3058. https://doi.org/10.1007/s00170-016-9293-x
Int J Adv Manuf Technol 89 (9-12): 3049–3058. https://doi.org/10.1007/s00170-016-9293-x
Статья
Google Scholar
Qin CJ, Tao JF, Liu CL (2017) Анализ стабильности операций фрезерования с использованием метода Адамса-Симпсона. Int J Adv Manuf Technol 92: 969–979. https://doi.org/10.1007/s00170-017-0186-4
Статья
Google Scholar
Mei YG, Mo R, Sun HB (2019) Прогнозирование стабильности при фрезеровании на основе линейного многошагового метода. Int J Adv Manuf Technol 105: 2677–2688. https://doi.org/10.1007/s00170-019-04379-6
Статья
Google Scholar
Бутчер Э.А., Бобренков О.А., Бюлер Э., Ниндуярла П. (2009) Анализ устойчивости измельчения методом коллокации Чебышева: алгоритм и оптимальные уровни стабильного погружения. J Вычислительная нелинейная динамика 4 (3): 031003.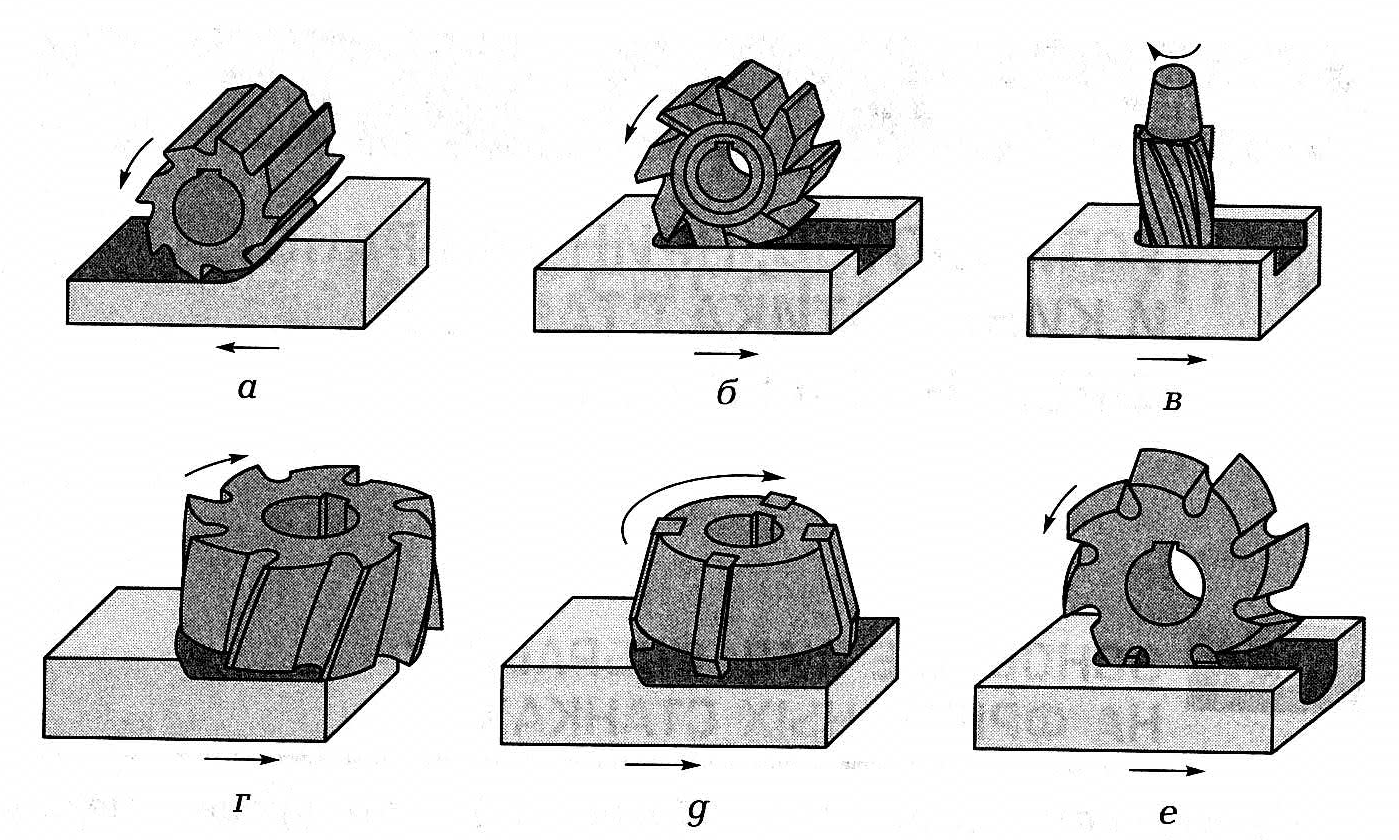 https://doi.org/10.1115/1.3124088
https://doi.org/10.1115/1.3124088
Артикул
Google Scholar
Дин Ю., Чжу Л.М., Чжан XJ, Дин Х. (2013) Анализ устойчивости фрезерования методом дифференциальных квадратур. J Manuf Sci E-T ASME 135(4):044502. https://doi.org/10.1115/1.4024539
Статья
Google Scholar
Дин Ю., Чжу Л.М., Дин Х. (2015) Основанный на вейвлетах подход к анализу устойчивости периодических дифференциально-дифференциальных систем с дискретной задержкой. Нелинейный Динамик 79(2): 1049–1059. https://doi.org/10.1007/s11071-014-1722-5
Статья
MathSciNet
Google Scholar
Li MZ, Zhang G, Huang Y (2013) Полная схема дискретизации для прогнозирования стабильности фрезерования. Нелинейный Динамик 71: 187–199. https://doi.org/10.1007/s11071-012-0651-4
Статья
MathSciNet
Google Scholar
