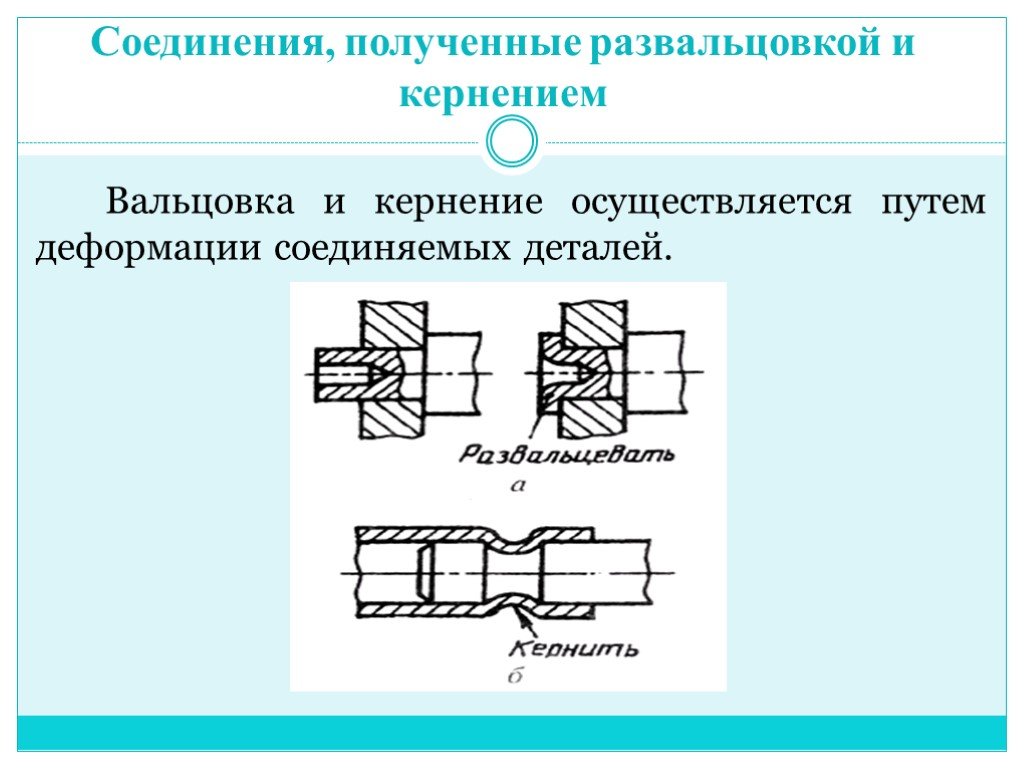
Вальцовка это что: Процесс вальцовки металла: назначение и применение

Вальцовка листового металла — услуги по вальцовке листового металла в Екатеринубрге.

Услуги по вальцовке листового металла

Производственное объединение «СанТермо» предоставляет широкий спектр услуг по обработке металлов, среди которых вальцовка листового металла занимает особое место. Заказ любой степени сложности выполняется с идеальным качеством, быстро и по доступной цене. Установленное на предприятии оборудование, позволяет производить вальцовку листов стали (в том числе – нержавейки), алюминия, других видов цветных металлов, с учетом следующих параметров:

  • Ширина заготовки – до 1 м 20 см.

  • Толщина листов-заготовок – не более 4-х мм.

  • Радиус заготовки: минимальный 30 см, максимальный – 1 м 20 см.

Вальцовка листового металла является одним из наиболее востребованных видов работ. Различные металлические материалы, детали и конструкции, широко распространены в следующих отраслях народного хозяйства:

  • строительство;

  • энергетика;

  • сельскохозяйственное производство;

  • добывающий, перерабатывающий сектора промышленности;

  • машиностроении, ВПК.

Существует множество видов и способов металлообработки – от гибки и сварки, до сверления, лазерной, плазменной резки и т.п. Широким спросом у самых разных категорий заказчиков, пользуются услуги по вальцовке листового металла.

Выгодное предложение от профессионалов

ООО «Производственное объединение «СанТермо»» наряду с другими видами работ по изготовлению металлопродукции и металлообработке выполняет работы по вальцовке листового металла. В компании созданы все необходимые условия для того чтобы выполнять работу на высоком профессиональном уровне, качественно и недорого:

  • Организовано современное высокотехнологичное производство.

  • Приобретено, установлено и введено в эксплуатацию новейшее оборудование.

  • Подобран и обучен персонал компании. Все работники – мастера высокой квалификации с большим стажем практической деятельности.

  • Строго соблюдается технологический процесс металлообработки, вальцовка листового металла осуществляется при постоянном, строгом контроле качества.

Принятые меры обеспечивают возможность выполнения вальцовки быстро и качественно по доступной цене.

Сущность технологического процесса

Вальцовка листового металла – это один из видов металлообработки, принцип действия заключается в последовательном механическом воздействии на заготовку методом давления и последующего деформирования. В вальцовочное оборудование устанавливается специальная объемная заготовка (штамповка). Вращающиеся в противоположные стороны вальцы захватывают лист металла и деформируют ее в соответствии с заданными параметрами и конфигурацией.

В ООО «СанТермо» можно заказать и на выгодных условиях приобрести следующие виды продукции, изготовленной методом гибки листового металла:

— различные детали и элементы строительных конструкций;

— изделия, позволяющие выполнять те или иные архитектурные решения

— элементы транспортеров, другого сельскохозяйственного и промышленного оборудования;

— детали вентиляционных систем, кондиционирования, дымоотведения;

— лопатки для компрессоров и турбин;

— другие предметы народного потребления.

Преимущества использования 

вальцовки

Вальцовка листового металла, выполненная на лучшем оборудовании профессионалами компании, обеспечивает:

  1. Существенное повышение прочность заготовки.

  2. Сокращение количества сварных швов на конечной детали.

  3. Повышение эксплуатационного ресурса изделия.

  4. Стойкость к коррозии.

  5. Минимизацию отходов при производстве. Как результат – снижение себестоимости производства, повышение рентабельности и увеличение прибыли.

  6. В процессе вальцовки сталь, алюминий (другие листовые изделия) не подвергается воздействию высоких температур, способных изменить структуру и существенно ухудшить физико-механические характеристики.

Любое изделие в указанных габаритных размерах, мастера ООО «СанТермо» изготовят с идеальным качеством. Обращайтесь!

Вальцовка листа цена в Новосибирске


Вальцовка листа — поставки напрямую с завода в любом
количестве в Новосибирске
Для заказа звоните:

+7 (383) 312-37-02  
Пишите: nsk@uralocm. ru

3.00 руб ₽ ./м

1

Более 10 лет работы

2

Филиал в Новосибирске

3

Оперативные поставки
по всей России

4

Любые объемы,
высокое качество

Описание

Вальцовка листа – это способ формообразования металла путём использования специального вращающегося вала. В основном металлы подвергаются холодной обработке, но некоторые – горячей, требующей предварительный подогрев. Горячая вальцовка проводится с металлами сложного сплава или имеющими большую толщину с целью избежать повреждений при больших нагрузках.

Процедура обработки проводится при помощи вальца путём пропуска листа через валки, в ходе которого он приобретает форму цилиндра, овала или конуса. Вальцовке могут подвергаться листы длиной до 12 м толщиной до 0,06 м (зависящей от ширины вальцуемой заготовки), что делает этот способ крайне универсальным в работе. Верхние валки в вальцовочном станке служат для обкатки заготовки, а боковые – для регулировки диаметра получающегося цилиндрического или конического элемента – обечайки. Станки бывают двух-, трех- и четырёхвалковые, но чаще используются последние два, так как они позволяют вальцевать габаритные листы и обеспечивают надёжность обработки.

Одной из главных особенностей гибки листового металла вальцеванием является то, что деформация листа происходит равномерно по всей площади. Другим важным преимуществом служит то, что в процессе вальцевания возможно изменение скорости деформирования металла без потери качества. При вальцовке лист металла сохраняет все свои свойства и не получает никаких дефектов.

Вальцовка может осуществляться способом продольной и поперечной подачи заготовки для получения незамкнутых длинных и коротких труб соответственно. Способ спиральной подачи служит для свёртывания труб без применения дальнейшей герметизации стыка.

На нашем сайте вы можете заказать услугу вальцовки металла в соответствии с ГОСТами и другими нормативными документами. Наша компания предлагает доступную цену листовой вальцовки даже для самых нестандартных случаев. Мы гарантируем качественное и быстрое выполнение работы!

 

Есть вопросы?

Звоните
+7 (383) 312-37-02
или отправьте запрос на почтовый адрес
[email protected]

Rolling — Гиперучебник по физике

[закрыть]

Качение без проскальзывания представляет собой комбинацию поступательного движения и вращения, при которой точка контакта мгновенно находится в состоянии покоя.

Когда объект испытывает чисто поступательное движение , все его точки движутся с той же скоростью, что и центр масс; то есть в том же направлении и с той же скоростью

v ( r ) =  v центр масс

Объект также будет двигаться по прямой линии в отсутствие результирующей внешней силы.

Увеличить

Когда объект совершает чистое вращательное движение вокруг своего центра масс, все его точки движутся под прямым углом к ​​радиусу в плоскости, перпендикулярной оси вращения, со скоростью, пропорциональной расстоянию от оси вращения…

v ( r ) =  рω

Таким образом точки по разные стороны от оси движутся в противоположных направлениях, точки по оси вообще не двигаются, так как r  = 0 там…

v центр масс  =  0

и точки на внешнем ребре двигаются с максимальной скоростью…

v внешний край  =  Rω

./rolling/wheel-rotation.svg»> Увеличить

Когда объект испытывает катящееся движение , точка объекта, соприкасающаяся с поверхностью, мгновенно становится неподвижной…

v точка контакта  =  0

и является мгновенной осью вращения. Таким образом, центр масс объекта движется со скоростью…

v центр масс  =  Rω

и точка, удаленная от точки касания, движется с удвоенной скоростью

v напротив точки контакта  =  2 v см  = 2 Rω

Увеличить

трискелион

Колесо является продолжением стопы.

./rolling/triskelion-greece.svg»> Увеличить

рулетки

  • циклоиды
    • циклоида
    • вытянутая циклоида
    • циклоид куртате
  • эпициклоиды
    • эпициклоида
    • кардиоидная
    • нефроид
    • ранункулоид
  • гипоциклоиды
    • гипоциклоида
    • астроид
    • дельтовидная

сопротивление качению

сопротивление качению

Коэффициент сопротивления качению для выбранных интерфейсов Источник: Analytic Cycling
интерфейс коэффициент
велосипедная шина на… деревянная дорожка 0,001
гладкий бетон 0,002
асфальтированная дорога 0,004
неровная, но асфальтированная дорога 0,008

11.

2: Катящееся движение — Физика LibreTexts

  1. Последнее обновление
  2. Сохранить как PDF
  • Идентификатор страницы
    4034
    • OpenStax
    • OpenStax
    Цели обучения
    • Описать физику качения без проскальзывания
    • Объясните, как линейные переменные связаны с угловыми переменными для случая качения без проскальзывания
    • Найти линейное и угловое ускорения при качении с проскальзыванием и без него
    • Рассчитать силу трения покоя, связанную с качением без проскальзывания
    • Использование энергосбережения для анализа качения

    Вращательное движение — это обычное сочетание вращательного и поступательного движения, которое мы видим повсюду, каждый день. Подумайте о различных ситуациях, когда колеса движутся по шоссе, или колеса самолета приземляются на взлетно-посадочную полосу, или колеса робота-исследователя на другой планете. Понимание сил и крутящих моментов, возникающих при качении , является решающим фактором во многих различных ситуациях.

    Для анализа качения в этой главе обратитесь к рисунку 10.5.4 в разделе «Вращение с фиксированной осью», чтобы найти моменты инерции некоторых общих геометрических объектов. Вы также можете найти его полезным в других расчетах, связанных с вращением.

    Перекатывание без проскальзывания

    Люди наблюдали перекатывание без проскальзывания с момента изобретения колеса. Например, мы можем посмотреть на взаимодействие шин автомобиля и поверхности дороги. Если водитель нажимает педаль акселератора в пол так, что шины крутятся, а автомобиль не движется вперед, между колесами и поверхностью дороги должно быть кинетическое трение. Если водитель медленно нажимает на педаль акселератора, заставляя автомобиль двигаться вперед, то шины катятся без проскальзывания. Для большинства людей удивительно, что на самом деле нижняя часть колеса находится в покое по отношению к земле, что указывает на наличие статического трения между шинами и поверхностью дороги. На рисунке \(\PageIndex{1}\) велосипед движется, а всадник остается в вертикальном положении. Шины соприкасаются с дорожным покрытием, и, несмотря на то, что они катятся, нижняя часть шин слегка деформируется, не скользит и находится в состоянии покоя относительно дорожного покрытия в течение измеримого промежутка времени. Для этого между шиной и поверхностью дороги должно быть статическое трение.

    Рисунок \(\PageIndex{1}\): (a) Велосипед движется вперед, и его шины не скользят. Нижняя часть слегка деформированной шины находится в покое относительно поверхности дороги в течение измеримого периода времени. (b) На этом изображении видно, что верхняя часть катящегося колеса кажется размытой из-за его движения, но нижняя часть колеса мгновенно остается в покое. (кредит a: модификация работы Нельсона Лоуренсо; кредит b: модификация работы Колина Роуза)

    Чтобы проанализировать качение без проскальзывания, мы сначала выводим линейные переменные скорости и ускорения центра масс колеса в терминах угловые переменные, описывающие движение колеса. Ситуация показана на рисунке \(\PageIndex{2}\).

    Рисунок \(\PageIndex{2}\): (a) Колесо тянется по горизонтальной поверхности под действием силы \(\vec{F}\). Сила трения покоя \(\vec{f}_{s}\), \(|\vec{f}_{s}|\) ≤ \(\mu_{s}\)N достаточно велика, чтобы это от скольжения. (b) Векторы линейной скорости и ускорения центра масс и соответствующие выражения для \(\omega\) и \(\alpha\). Точка P покоится относительно поверхности. (c) Относительно системы центра масс (ЦМ) точка P имеет линейную скорость −R\(\omega \hat{i}\).

    На рисунке \(\PageIndex{2}\)(a) мы видим векторы сил, участвующих в предотвращении проскальзывания колеса. В (b) точка P, которая касается поверхности, покоится относительно поверхности. Относительно центра масс точка P имеет скорость −R\(\omega\hat{i}\), где R – радиус колеса, а \(\omega\) – угловая скорость колеса относительно своей оси. Поскольку колесо катится, скорость P относительно поверхности равна его скорости относительно центра масс плюс скорость центра масс относительно поверхности:

    \[\vec{v}_{P} = -R \omega \hat{i} + v_{CM} \hat{i} \ldotp\]

    Так как скорость P относительно поверхности равна нулю , v P = 0, это говорит о том, что

    \[v_{CM} = R \omega \ldotp \label{11. 1}\]

    Таким образом, скорость центра масс колеса равна его радиусу, умноженному на угловой скорость относительно своей оси. Покажем соответствие линейной переменной в левой части уравнения угловой переменной в правой части уравнения. Это сделано ниже для линейного ускорения.

    Если продифференцировать уравнение \ref{11.1} в левой части уравнения, мы получим выражение для линейного ускорения центра масс. В правой части уравнения R является константой, и поскольку \(\alpha = \frac{d \omega}{dt}\), мы имеем

    \[a_{CM} = R \alpha \ldotp \label {11.2}\]

    Кроме того, мы можем найти расстояние, пройденное колесом, в терминах угловых переменных, обратившись к рисунку \(\PageIndex{3}\). Когда колесо катится из точки А в точку В, его внешняя поверхность совпадает с землей ровно на пройденное расстояние, равное d СМ .

    Из рисунка \(\PageIndex{3}\) видно, что длина внешней поверхности, которая отображается на землю, равна длине дуги R\(\theta\). Приравнивая два расстояния, получаем

    \[d_{CM} = R \theta \ldotp \label{11. 3}\]

    Рисунок \(\PageIndex{3}\): Когда колесо катится по поверхности, дуга длина R\(\theta\) от A до B отображается на поверхность, соответствующую расстоянию d CM , на которое переместился центр масс.

    Пример \(\PageIndex{1}\): скатывание по наклонной плоскости

    Сплошной цилиндр катится по наклонной плоскости без проскальзывания, начиная с состояния покоя. Он имеет массу m и радиус r. а) Чему равно его ускорение? б) Какому условию должен удовлетворять коэффициент трения покоя \(\mu_{S}\), чтобы цилиндр не скользил?

    Стратегия

    Нарисуйте эскиз и диаграмму свободного тела и выберите систему координат. Положим x в направлении вниз по плоскости, а y вверх перпендикулярно плоскости. Определить задействованные силы. Это нормальная сила, сила тяжести и сила трения. Запишите законы Ньютона в направлениях x и y и закон Ньютона для вращения, а затем определите ускорение и силу трения.

    Решение
    1. Диаграмма свободного тела и эскиз показаны на рисунке \(\PageIndex{4}\), включая нормальную силу, компоненты веса и силу трения покоя. Трения едва хватает, чтобы цилиндр вращался без проскальзывания. Поскольку скольжения нет, величина силы трения меньше или равна \(\mu_{S}\)N. Записав законы Ньютона в направлениях x и y, мы получим

    \[\sum F_{x} = ma_{x};\; \сумма F_{y} = ma_{y} \ldotp\]

    Рисунок \(\PageIndex{4}\): Твердый цилиндр катится по наклонной плоскости, не соскальзывая с места. Система координат имеет x в направлении вниз по наклонной плоскости и y перпендикулярно плоскости. Диаграмма свободного тела показана с нормальной силой, силой трения покоя и компонентами веса m\(\vec{g}\). Трение заставляет цилиндр катиться по плоскости, а не скользить.

    Подстановка из диаграммы свободного тела

    \[\begin{split} mg \sin \theta — f_{s} & = m(a_{CM}) x, \\ N — mg \cos \theta & = 0 \end{split}\]

    мы можем найти линейное ускорение центра масс из этих уравнений:

    \[a_{CM} = g\sin \theta — \frac{f_s}{m} \ldotp\]

    полезно выразить линейное ускорение через момент инерции. Для этого запишем второй закон Ньютона для вращения:

    \[\sum \tau_{CM} = I_{CM} \alpha \ldotp\]

    Моменты вычисляются относительно оси, проходящей через центр масс цилиндр. Единственный ненулевой крутящий момент обеспечивается силой трения. У нас есть

    \[f_{s} r = I_{CM} \alpha \ldotp\]

    Наконец, линейное ускорение связано с угловым ускорением соотношением

    \[(a_{CM})_{x} = r \alpha \ldotp\]

    Эти уравнения можно использовать для решения для CM , \(\alpha\) и f S с точки зрения момента инерции, где мы опустили индекс x. Запишем CM через вертикальную составляющую силы тяжести и силы трения и сделаем следующие замены.

    9{2}}\right)} = \frac{1}{3} \tan \theta \ldotp$$

    Значение

    1. Линейное ускорение линейно пропорционально греху \(\тета\). Таким образом, чем больше угол наклона, тем больше линейное ускорение, как и следовало ожидать. Однако угловое ускорение линейно пропорционально sin \(\theta\) и обратно пропорционально радиусу цилиндра. Таким образом, чем больше радиус, тем меньше угловое ускорение.
    2. Чтобы не происходило скольжения, коэффициент трения покоя должен быть больше или равен \(\frac{1}{3}\)tan \(\theta\). Таким образом, чем больше угол наклона, тем больше должен быть коэффициент трения покоя, чтобы цилиндр не проскальзывал.
    Упражнение \(\PageIndex{2}\)

    Полый цилиндр находится под наклоном под углом 60°. Коэффициент трения покоя о поверхность \(\mu_{s}\) = 0,6. а) Катится ли цилиндр без проскальзывания? б) Будет ли сплошной цилиндр катиться без проскальзывания? 9{2}}\right)} \ldotp \label{11.4}\]

    Это очень полезное уравнение для решения задач, связанных с качением без проскальзывания. Обратите внимание, что ускорение меньше, чем у объекта, скользящего по плоскости без трения без вращения. Ускорение также будет разным для двух вращающихся цилиндров с разной инерцией вращения.

    Качение с проскальзыванием

    В случае качения с проскальзыванием мы должны использовать коэффициент кинетического трения, который приводит к кинетической силе трения, поскольку статического трения нет. Ситуация показана на рисунке \(\PageIndex{5}\). В случае проскальзывания v CM − R\(\omega\) ≠ 0, так как точка P на колесе не покоится на поверхности, и v P ≠ 0. Таким образом, \(\omega\) ≠ \(\frac{ v_{CM}}{R}\), \(\alpha \neq \frac{a_{CM}}{R}\).

    Рисунок \(\PageIndex{5}\): (a) Между колесом и поверхностью возникает кинетическое трение, потому что колесо проскальзывает. (b) Простые отношения между линейными и угловыми переменными больше не действуют.

    Пример \(\PageIndex{2}\): скатывание по наклонной плоскости с проскальзыванием

    Твердый цилиндр скатывается с наклонной плоскости из состояния покоя и испытывает проскальзывание (рис. \(\PageIndex{6}\)). Он имеет массу m и радиус r. а) Чему равно его линейное ускорение? б) Чему равно его угловое ускорение относительно оси, проходящей через центр масс?

    Стратегия

    Нарисуйте эскиз и диаграмму свободного тела, показывающую действующие силы. Диаграмма свободного тела аналогична случаю отсутствия проскальзывания, за исключением того, что сила трения является кинетической, а не статической. Используйте второй закон Ньютона, чтобы найти ускорение в направлении x. Используйте второй закон вращения Ньютона, чтобы найти угловое ускорение.

    Решение

    Рис. \(\PageIndex{6}\): Твердый цилиндр скатывается из состояния покоя по наклонной плоскости и скользит. Система координат имеет x в направлении вниз по наклонной плоскости и y вверх перпендикулярно плоскости. Диаграмма свободного тела показывает нормальную силу, кинетическую силу трения и компоненты веса m\(\vec{g}\).

    Сумма сил в направлении y равна нулю, поэтому сила трения теперь равна f k = \(\mu_{k}\)N = \(\mu_{k}\)mg cos \(\ тета\). Второй закон Ньютона в направлении x принимает вид

    \[\sum F_{x} = ma_{x}, \nonumber\]

    \[mg \sin \theta — \mu_{k} mg \cos \theta = m(a_{CM})_{x}, \nonumber\]

    или

    \[(a_{CM})_{x} = g(\sin \theta — \mu_{k} \cos \theta ) \ldotp \nonumber\]

    Сила трения обеспечивает единственный крутящий момент относительно оси, проходящей через центр масс, поэтому второй закон вращения Ньютона принимает вид 9{2} \alpha \ldotp \nonumber\]

    Решая для \(\alpha\), получаем

    \[\alpha = \frac{2f_{k}}{mr} = \frac{2 \mu_{ k} g \cos \theta}{r} \ldotp \nonumber\]

    Значение

    Линейное и угловое ускорения запишем через коэффициент кинетического трения. Линейное ускорение такое же, как у тела, скользящего по наклонной плоскости с кинетическим трением. Угловое ускорение относительно оси вращения линейно пропорционально нормальной силе, зависящей от косинуса угла наклона. Как \(\тета\) → 9{2} + mgh \ldotp\]

    При отсутствии каких-либо неконсервативных сил, отнимающих энергию из системы в виде тепла, полная энергия катящегося тела без проскальзывания сохраняется и постоянна на протяжении всего движения. Примерами, когда энергия не сохраняется, являются катящийся объект, который скользит, выделение тепла в результате кинетического трения и катящийся объект, встречающий сопротивление воздуха.

    Вы можете спросить, почему катящийся объект, который не скользит, сохраняет энергию, ведь сила трения покоя не является консервативной. Ответ можно найти, вернувшись к рисунку \(\PageIndex{2}\). Точка P, соприкасающаяся с поверхностью, покоится относительно поверхности. Следовательно, его бесконечно малое перемещение d\(\vec{r}\) относительно поверхности равно нулю, и равна нулю дополнительная работа силы трения покоя. Мы можем применить закон сохранения энергии к нашему изучению качения, чтобы получить некоторые интересные результаты.

    Пример \(\PageIndex{3}\): Марсоход Curiosity

    Марсоход Curiosity , показанный на рисунке \(\PageIndex{7}\), был отправлен на Марс 6 августа 2012 года. Ровер имеет радиус 25 см. Предположим, астронавты прибывают на Марс в 2050 году и обнаруживают ныне неработающий Curiosity на краю бассейна. Пока разбирают марсоход, космонавт случайно теряет сцепление с одним из колес, которое катится, не соскальзывая, на дно котловины на 25 метров ниже. Если колесо имеет массу 5 кг, какова его скорость на дне чаши?

    Рисунок \(\PageIndex{7}\): Марсоход Curiosity из научной лаборатории НАСА во время испытаний 3 июня 2011 года. Место находится внутри цеха сборки космических кораблей в Лаборатории реактивного движения НАСА в Пасадене, Калифорния. (кредит: NASA/JPL-Caltech)

    Стратегия

    Мы используем сохранение механической энергии для анализа проблемы. На вершине холма колесо покоится и обладает только потенциальной энергией. На дне бассейна колесо имеет вращательную и поступательную кинетическую энергию, которая должна быть равна начальной потенциальной энергии по закону сохранения энергии. Поскольку колесо катится без проскальзывания, воспользуемся соотношением v 9{2})(25,0\; м)} = 9,63\; м/с \ldotp \nonumber\]

    Значимость

    Это довольно точный результат, учитывая, что на Марсе очень мало атмосферы, и потери энергии из-за сопротивления воздуха минимальны. Результат также предполагает, что местность гладкая, так что колесо не будет натыкаться на камни и неровности на своем пути.

    Кроме того, в этом примере кинетическая энергия или энергия движения поровну распределяется между линейным и вращательным движением. Если мы посмотрим на моменты инерции на рис. 10.5.4, то увидим, что полый цилиндр имеет наибольший момент инерции для данного радиуса и массы. Если бы колеса вездехода были твердыми и аппроксимировались твердыми цилиндрами, например, кинетическая энергия была бы больше при прямолинейном движении, чем при вращательном.

    Published by admin