Как усилить двутавровую балку от прогиба: Усиление металлических балок, ферм и прогонов — ТехЛиб СПБ УВТ
Содержание
Как усилить швеллер от прогиба
Внимание! Вы находитесь в архиве сайта StroimDom.com.ua, рекомендуем Вам перейти на более удобную, полную версию сайта.
Форум Строим Дом > Строительство дома > Стены, перекрытия, фасады > Каким образом можно усилить балку перекрытия?
PDA
Просмотр полной версии : Каким образом можно усилить балку перекрытия?
Каким образом можно усилить балку перекрытия (швеллер №10) без ввода дополнительной опоры на проеме 4500 мм?
Описание: размеры по стенам 4700*6500мм, пояс опирания балок — монолитный бетон (армопояс H=300мм, B=200мм) с закладными уголками в месте опирания балки (балка приваривается к закладным), шаг установки балок 1000 мм.
Наличие: 3 балки — швеллер № 10, 2 балки — двутавр №10.
Ау, спецы есть тут? Мне хочеться узнать где у балки наибольшие напряжения возникают, чтоб усилить именно те участки
Ау, спецы есть тут? Мне хочеться узнать где у балки наибольшие напряжения возникают, чтоб усилить именно те участки
Сопромат давно не вспоминал, но думаю похоже на то что на рисунке. Для расчетов лучше обращаться к конструктору.
Для расчетов лучше обращаться к конструктору.
Вот обсуждение похожей темы http://forum.dwg.ru/showthread.php?t=23324
На такой пролёт при шаге 1м, нужен 16й двутавр или 18й швеллер +-:rolleyes:
Исходя из чего такие утверждения 16-й двутавр…?
vadim.bild
24.11.2010, 16:16
Исходя из чего такие утверждения 16-й двутавр…?
Если это балки перекрытия, то для жилья только полезных нагрузок 150х1.2=180 кг/м2, добавте сюда собственный вес перекрытия, потолков, и полов, вот и получится около 400 — 500 кг/м2. При пролете 4,7м и шаге балок 1м, изгибающий момент в элементе 1.1т*м, при расчетном сопротивлении стали 2450 кг/см2, получаем момент сопротивления 45см3, а это уже 12 двутавр, это только по прочности, а метал надо подбирать по прогибам, вот и выходит 16 как минимум, если не хотите чтоб высота помещения в центре комнаты была на 5-10 см меньше чем у стены, хотя и в этом есть свои плюсы, воду разлитую на втором этаже можно кружкой будет собрать на полу
mans_2008
24. 11.2010, 16:37
11.2010, 16:37
На такой пролёт при шаге 1м, нужен 16й двутавр или 18й швеллер +-:rolleyes:
Вы знаете сколько может нести 18-й швеллер при жесткой заделке?
Или Вам абы ляпнуть что-нибудь?
Перекрытие собственно деревянное толщ. 50 мм (оно же и потолок), более никакой дополнительной нагрузки кроме жилой в 180 кг небудет.
Возникла идея балки соеденить между собой по бокам чтоб нагрузка от одной передавалась частично на другую — поможет?
mans_2008
24.11.2010, 16:45
Если это балки перекрытия, то для жилья только полезных нагрузок 150х1.2=180 кг/м2, добавте сюда собственный вес перекрытия, потолков, и полов, вот и получится около 400 — 500 кг/м2. При пролете 4,7м и шаге балок 1м, изгибающий момент в элементе 1.1т*м, при расчетном сопротивлении стали 2450 кг/см2, получаем момент сопротивления 45см3, а это уже 12 двутавр, это только по прочности, а метал надо подбирать по прогибам, вот и выходит 16 как минимум, если не хотите чтоб высота помещения в центре комнаты была на 5-10 см меньше чем у стены, хотя и в этом есть свои плюсы, воду разлитую на втором этаже можно кружкой будет собрать на полу
При жесткой заделке с обоих сторон, 10 швеллер/двутавр несет 350 кг на м. п. Если на эти перекрытия уложен пол из досок то вполне нормально!
п. Если на эти перекрытия уложен пол из досок то вполне нормально!
16-й швеллер несет тонну на м.п.
Вы знаете сколько может нести 18-й швеллер при жесткой заделке?
Или Вам абы ляпнуть что-нибудь?
А Вы уверены, что у автора топика будет жёсткая заделка?;)
Перекрытие собственно деревянное толщ. 50 мм (оно же и потолок), более никакой дополнительной нагрузки кроме жилой в 180 кг небудет.
Возникла идея балки соеденить между собой по бокам чтоб нагрузка от одной передавалась частично на другую — поможет?
Фото или рисунки, где и как и из чего закладные сделаны?
Набросано от руки, но думаю понятно будет.
*Alexey*
24.11.2010, 19:25
При жесткой заделке с обоих сторон, 10 швеллер/двутавр несет 350 кг на м.п. Если на эти перекрытия уложен пол из досок то вполне нормально!…
Так швеллер или балка?? Нормы трошки отличаются…
Незабудьте пожалуйста о коефициенте перегрузки (хотя бы 1,5).
…..16-й швеллер несет тонну на м. п.
п.
Теоретическая жесткая заделка не предполагает «жесткого задела» металла на поясе 200Х200 мм. При Вашей нагрузке на пролет 4,5 метра ляжет 4,5 ТОННЫ, пусть даже распределенной нагрузки. Я ОЧЧЧень хочу посмотреть на эти останки (в случае испытаний отдельной балки). А не дай боже сосредоточенной??- ваще полная ж.па. Конечно в каркасе с шагом в 1м теоретически все должно работать в норме. Но с точки зрения практики (я не спец, но от него не далек), запас прочности на перегруз — маловат. Нормативная нагрузка на 1 квм в таких случаях берется 250 кг/квм+вес самого перекрытия в 10м сечении метала с конструктивом пола и шумейкой составит ок 30-40кг/квм=280,,290 кг/квм. Т.е. если брать минимальный запас по прочности с МАХ доспустимой нагрузкой в 290*1,5=435 кг, попадаем в 14 (балка)…16 (швел) сечение
Это ж перекрытие дома а не времянки/сарая
Кроме того 10е сечение не даст нормальной шумоизоляции.
ИМХО Больше не меньше, я за 14ю балку.
А если от опоры сбоку к швеллеру доварить еще отрезок швеллера около 500 мм с обеих коцов, чтобы уменьшить пролет тонкого сечения, тогда опасный пролет станет уже 3500 мм?????
mans_2008
25. 11.2010, 06:44
11.2010, 06:44
Так швеллер или балка?? Нормы трошки отличаются…
Практически одинаково. Ну до 10% максимум различия.
Использование швеллера экономически целесообразней чем двутавра (если переводить нагрузки на единицу веса балки).
Незабудьте пожалуйста о коефициенте перегрузки (хотя бы 1,5).
Вы имели в виду коэф. надежности?
Тут согласен с Вами, хотя везде принимают 1,2.
mans_2008
25.11.2010, 06:59
Теоретическая жесткая заделка не предполагает «жесткого задела» металла на поясе 200Х200 мм.
Изначально не было ясно что да как.
Для меня жесткая заделка — если к примеру, сверху на балках будет стоять стена второго этажа.
При Вашей нагрузке на пролет 4,5 метра ляжет 4,5 ТОННЫ, пусть даже распределенной нагрузки. Я ОЧЧЧень хочу посмотреть на эти останки (в случае испытаний отдельной балки). А не дай боже сосредоточенной??- ваще полная ж.па.
Такие цифры подтверждаются расчетами для жесткой заделки, при этом учтен Кнадежноси=1,2. Законы писали/доказывали не я и не Вы, но ими пользуются уже не один десяток лет.
Законы писали/доказывали не я и не Вы, но ими пользуются уже не один десяток лет.
Т.е. если брать минимальный запас по прочности с МАХ доспустимой нагрузкой в 290*1,5=435 кг
Еще раз скажу что при расчетах к=1.2.
Кроме того 10е сечение не даст нормальной шумоизоляции.
Думаю 10 см. мин ваты вполне достаточно для шумки.
mans_2008
25.11.2010, 07:01
А если от опоры сбоку к швеллеру доварить еще отрезок швеллера около 500 мм с обеих коцов, чтобы уменьшить пролет тонкого сечения, тогда опасный пролет станет уже 3500 мм?????
Поставьте лучше с шагом, например, не 1 м, а 0,7-0,8 метра.
*Alexey*
25.11.2010, 08:07
Вы имели в виду коэф. надежности?
Тут согласен с Вами, хотя везде принимают 1,2.
Не спорю. Есть одно НО: чем меньше сечение несущего элемента, тем больше тот самый К… На 20 балке К можно применять и 1,12. На 24 — К=1,1, А на 10м номере К=1,5 (не могу найти йенту умную книгу, так бы дал автора)
Поставьте лучше с шагом, например, не 1 м, а 0,7-0,8 метра.
+1 или вдвойне делать.
Я наверное так бы и сделал, шаг уменьшил, но вот уже закладные расставленые на шаг 1м и бетоном залиты. Швеллера предварительно кинул, пробовал становиться прогибаються, думаю всетаки обварить их между собой уголком или проф. трубой — понимаю что колхоз, но нет возможности купить хорошие балки. Так все-таки кто может эпюры привести для таких конструкций.
mans_2008
25.11.2010, 15:46
Я наверное так бы и сделал, шаг уменьшил, но вот уже закладные расставленые на шаг 1м и бетоном залиты. Швеллера предварительно кинул, пробовал становиться прогибаються, думаю всетаки обварить их между собой уголком или проф. трубой — понимаю что колхоз, но нет возможности купить хорошие балки. Так все-таки кто может эпюры привести для таких конструкций.
Вставляйте две балки друг в друга или ставьте двутавром.
*Alexey*
25.11.2010, 16:02
…Так все-таки кто может эпюры привести для таких конструкций.
Есть программулина, БАЛКА называется. Пошукайте в ИНете. Классная фишка, выдает эпюры на прогиб, момент иннерции, крутящий и т.д. Неплохой выбор по конструкциям опор.
Пошукайте в ИНете. Классная фишка, выдает эпюры на прогиб, момент иннерции, крутящий и т.д. Неплохой выбор по конструкциям опор.
К стати, можете поиграться и с нагрузками в различных вариантах. Сама проверяет удовлетворение сечения заданным нагрузкам в металле, дереве.
Удачи :beer:
Ксати именно этой прогой и пользовался она у меня давно есть, просто засомневался она пропустила 10-й швеллер, но хотелось еще и мнение людей выслушать
vadim.bild
25.11.2010, 18:40
16-й швеллер несет тонну на м.п.
На каком пролете?
От куда такие суждения, вы не правильно ставите задачу, есть исходные данные: пролет, назначение помещений, конструкция пола, перекрытия и потолков.
Дальше все просто:
1)собираем нагрузки,
2) определяем усилия,
3) принимаем сечения.
А бросаться голыми цифрами каждый может, благо ответственности нико за эти тоны не несет.
Я наверное так бы и сделал, шаг уменьшил, но вот уже закладные расставленые на шаг 1м и бетоном залиты. Швеллера предварительно кинул, пробовал становиться прогибаються, думаю всетаки обварить их между собой уголком или проф. трубой — понимаю что колхоз, но нет возможности купить хорошие балки. Так все-таки кто может эпюры привести для таких конструкций.
Швеллера предварительно кинул, пробовал становиться прогибаються, думаю всетаки обварить их между собой уголком или проф. трубой — понимаю что колхоз, но нет возможности купить хорошие балки. Так все-таки кто может эпюры привести для таких конструкций.
Можно уменьшить шаг, не обязательно привязыватся к закладным, закрепите доп. балки анкерами. Но, главная проблема в металлоконструкциях- прогибы, по ним надо подбирать сечения, развязав их между собой полностью проблему не решить, прогибы в пролетных конструкциях убираются жесткостью сечения (определяющим фактором является его высота) может решить проблему поставив балку на балку с верху, что это даст кроме перерасхода материала- не скажу надо считать, проще купить нужные сечения и не выдумывать велосипед, а 10й швеллер еще пригодятся.
Эпюры усилий- это прочностная характеристика.
Не спорю. Есть одно НО: чем меньше сечение несущего элемента, тем больше тот самый К… На 20 балке К можно применять и 1,12. На 24 — К=1,1, А на 10м номере К=1,5 (не могу найти йенту умную книгу, так бы дал автора)
Не вводите людей в заблуждения, чем меньше сечение — тем меньше его жесткость, причем зависимость тут не прямая, и коэффициенты надежности по нагрузкам тут не причем, они зависят от используемых материалов, условий монтажа, класса ответственности здания, у вас алгоритм подбора не верный в корне, описал выше.
Для меня жесткая заделка — если к примеру, сверху на балках будет стоять стена второго этажа.
Думаю 10 см. мин ваты вполне достаточно для шумки.
Жесткая заделка на опорах не определяется нагрузкой в месте опирания- это условие передачи нагрузки, чтоб на опоре была жесткая заделка надо создать хотя-бы две точки передачи нагрузки, причем на дальней от пролета опоре будет усилие от балки направленное в верх, а в самой балке у стены будет присутствовать крутящий момент.
Еще есть такое явление как зыбкость (раскачивание конструкции или в народе называемое «резонанс»), очень характерно для маленьких сечений с малыми нагрузками.
Касаемо шумоизоляции лучше всего использовать в данном случае песок, или хотя-бы керамзит, звуковая волна убирается массой, утеплитель ее только ломает, + это поможет избежать раскачивания конструкции (ее зыбкости).
А если от опоры сбоку к швеллеру доварить еще отрезок швеллера около 500 мм с обеих коцов, чтобы уменьшить пролет тонкого сечения, тогда опасный пролет станет уже 3500 мм?????
расчетный пролет можно уменьшить поставив доп. подпорки с низу под углом 45градусов, тогда опирание можно условно считать как жестко защемленное на опорах.
подпорки с низу под углом 45градусов, тогда опирание можно условно считать как жестко защемленное на опорах.
Есть программулина, БАЛКА называется.
Желательно еще много техничной литературы почитать чтоб корректно ей пользоваться. Можно легко напутать с размерностью величин, необходимыми требованиями к прогибам на разных пролетах, условиями опирания, шагом раскрепления элементов.
Хотя для общего развития ознакомится полезно будет, удачи)
Про зыбкость можно подробнее, это что то вроде вибрации при ударе по балкам или как?
mans_2008
25.11.2010, 19:43
Есть программулина, БАЛКА называется.
Еще есть Beam, таже БАЛКА, только функций больше!
mans_2008
25.11.2010, 19:44
На каком пролете?
От куда такие суждения, вы не правильно ставите задачу, есть исходные данные: пролет, назначение помещений, конструкция пола, перекрытия и потолков.
Вы сначала читаете или так ляпнуть?
vadim.bild
25.11.2010, 19:45
Про зыбкость можно подробнее, это что то вроде вибрации при ударе по балкам или как?
Иногда можно наблюдать такое явление, когда шагаешь по лестнице с длинными маршами, опущение такое что марш уходит из под ног, так как раскачивается в такт ходьбе, как при шагании в ногу по мостам, устраняется в основном добавлением массы конструкции, явление в нашем случае не опасное но весьма не приятное в процессе эксплуатации, не стоит упускать из виду в конструкциях с малой жесткостью элементов.
mans_2008
25.11.2010, 19:48
чем меньше сечение — тем меньше его жесткость,
Прям Америку открыли. Я то думал наоборот!
vadim.bild
25.11.2010, 19:58
При жесткой заделке с обоих сторон, 10 швеллер/двутавр несет 350 кг на м.п. 16-й швеллер несет тонну на м.п.
КГ/на М.П.- это равномерно распределенная НАГРУЗКА, а нести он может и больше чем 1т/м.п. в зависимости от пролета и условий опирания, для этого и существует много методов расчета. Вы каким пользуетесь? Методом сил, перемещений, или конечных элементов?
Вы сначала читаете или так ляпнуть?
Или я не понимаю о чем пишу?
Еще есть Beam, таже БАЛКА, только функций больше!
Еще есть Лира, Мономах, СКАД, и куча самописных програм. Дело то не в программах а в корректном их использовании, одна из самых распространенных ошибок- неправильный переводом единиц измерения, надо быть внимательным чтоб не получалось 10й швеллер на 10ит метровых пролетах перекрытия, видал и такое…
*Alexey*
25. 11.2010, 20:46
11.2010, 20:46
Или я не понимаю о чем пишу?
..
Да нет. Похоже, что пишите то Вы верно… Только грубо как то.
Типа бестолочи тут все, без понятия, так вот нате вам расчеты/консультации.
Грубиян и редиска…:(
Ведь появяться еще у Вас вопросики и темки для дискуссий. Ведь не можете Вы все знать!!
И ведь у нас же ОСОБО КРУГЛЫХ БАОБАБОВ спрашивать будете.
«Не плюй в колодец …..» (концевочку я думаю знаете)
mans_2008
27.11.2010, 09:13
Вы каким пользуетесь? Методом сил, перемещений, или конечных элементов?
Это у разработчиков программ нужно спросить, но думаю что там разые алгоритмы заложены.
Или я не понимаю о чем пишу?
Вначале указывался пролет!
Еще есть Лира, Мономах, СКАД, и куча самописных програм. Дело то не в программах а в корректном их использовании, одна из самых распространенных ошибок- неправильный переводом единиц измерения, надо быть внимательным чтоб не получалось 10й швеллер на 10ит метровых пролетах перекрытия, видал и такое…
Ну программа то правильно считает, а единицы измерения можно не те подставлять и при ручном расчете!
vadim. bild
bild
29.11.2010, 12:15
Ну программа то правильно считает, а единицы измерения можно не те подставлять и при ручном расчете!
Проектирует не программа а человек, программа- всего лишь инструмент, желательно хоть какое представление иметь о том чем занимаешься, разработчики программы никакой ответственности нести не будут, в случае если вы получили 10 швеллер, потратились на отделку и вся горе- конструкция у вас не дай Бог завалится, правильность принятых решений все-равно остается за «оператором». Это все равно, что если я буду бухгалтерию вести в 1С, я то и дебит от кредита не отличу, что тогда я буду объяснять налоговому инспектору, извините я не знал?
Не в обиду будет сказано, но если Вы советуете что-либо, так постарайтесь это делать так, чтоб потом на вас не обижались в случае каких-либо казусов, к вам то человек обращается в надежде услышать квалифицированный ответ, ведь с Вас то ответственности никакой, в данном случае, а человек может понести материальные затраты.
И не воспринимайте мои посты так враждебно, я ничем не хвалюсь и не пытаюсь никого унизить, просто иногда для вас здесь просто голые буквы и цифры, мотивированные опытом какого-то дяди Пети, который давно так делал и все стояло, а для некоторых тысячи гривен, кровно заработанные.
Удачи.
*Alexey*
29.11.2010, 12:50
И не воспринимайте мои посты так враждебно, я ничем не хвалюсь и не пытаюсь никого унизить….
Удачи.
Удачи, это конечно хорошо, но все же….
Кроме обьемных по писанине и критике постов, полезной инфы не поступило. Ждем обоснованных советов специалистов. Без обид. Действительно ждем:rolleyes:
по прочности 10 балка проходит, по прогибам нет. лучше брать 14 балку, это я прикинул для нагрузки 250 кг/м2 и шага 1 метр.
усилить можно, сварив два швеллера в коробочку:) но один 14 все равно лучше.
*Alexey*
29.11.2010, 17:07
…это я прикинул для нагрузки 250 кг/м2 и шага 1 метр…
Я конечно извеняюсь, а сосредоточенные нагрузки ( к примеру 4-5 чел по центру пролета с мартини + пригруженный жрачкой стол) на пргиб?? Вопрос без подковырки. Мне кажется, что 14го все же маловато (если взять вышеизложенные перегрузы). Или я ошибаюсь??:sorry:
Мне кажется, что 14го все же маловато (если взять вышеизложенные перегрузы). Или я ошибаюсь??:sorry:
mans_2008
29.11.2010, 19:33
Проектирует не программа а человек, программа- всего лишь инструмент, желательно хоть какое представление иметь о том чем занимаешься
Че там проектировать то? Задаешь исходные данные и прога выдаст сечение нужного сортамента.
А хоть какое предствление сопромата имеется, только вручную это считать нет смысла т.к. за тебя это сделает комп. (его для этих целей и придумали).
Я конечно извеняюсь, а сосредоточенные нагрузки ( к примеру 4-5 чел по центру пролета с мартини + пригруженный жрачкой стол) на пргиб?? Вопрос без подковырки. Мне кажется, что 14го все же маловато (если взять вышеизложенные перегрузы). Или я ошибаюсь??:sorry:
расчетная нагрузка от веса людей, мебели и т.д. для перекрытий жилых зданий принимается 150 кг/м2 умноженная на коефициент надежности 1.3, т.е. около 200 кг/м2. этого вполне достаточно в большинстве случаев.
стол и люди будут весить, пускай, 500 кг, и давить как минимум на две балки (это не сосредоточенная нагрузка). то есть еще останется запас на шкаф с посудой.
вот если возникнет желание устроить камин, кирпичную перегородку или джакузи объемом в пару кубов, тогда, конечно, нужно пересчитывать.
зы: забыл сказать, 14 швеллер проходит, если надежно связан с доской пола, т.е. раскреплен из плоскости, иначе может произоити потеря устойчивости.
Спасибо всем за советы, очень внимательно слежу за развитием дискуссии.
Доски планирую крепить болтами м5-м6 по потай — нарезать резьбу в теле швеллера, или можно попроще? И еще, на много-ли отличаеться несущая способность двутавра от швеллера, скажем если заменить 10-й шв. 10-м двутавром?
*Alexey*
30.11.2010, 10:12
Спасибо всем за советы, очень внимательно слежу за развитием дискуссии.
Доски планирую крепить болтами м5-м6 по потай — нарезать резьбу в теле швеллера, или можно попроще? И еще, на много-ли отличаеться несущая способность двутавра от швеллера, скажем если заменить 10-й шв. 10-м двутавром?
10-м двутавром?
где то на 8…10% в пользу балки
*Alexey*
30.11.2010, 10:16
…..на много-ли отличаеться несущая способность двутавра от швеллера, скажем если заменить 10-й шв. 10-м двутавром?
От Ulan: по прочности 10 балка проходит, по прогибам нет. лучше брать 14 балку,…. Я бы прислушался :rolleyes:
несущая способность 10 двутавра выше на 13%. чего увы, недостаточно.
резьбу нарезать геморойно будет, проще гайку с шайбой. можно саморезами, только нужно покупать с длинным сверлом, рассчитаным на металл до 8 — 10 мм.
Саморезами тоже геморно крепить, про гайку с шайбой не совсем понял, у двутавра ведь стенки с уклоном.
В результате мозгового штурма возникла идейка: если в промежутки между балками поставить брус 100*50 мм на ребро — сразу отпадает проблема с закреплением пола + повышается несущая способность перекрытия, брусья ведь тоже дадут жесткость. Но все же остается такой момент как зыбкость пока ничего не могу придумать — ведь если ставить доп. брусья не удасться разварить балки между собой.
брусья не удасться разварить балки между собой.
Вот схемку набросал.
ау отзовитесь товарищи, или сказать нечего?
vBulletin® v3.8.11, Copyright ©2000-2019, vBulletin Solutions, Inc. Перевод: zCarot
Источник
Источник2
При расширении существующих или устройстве новых проемов в несущих стенах, проект перепланировки квартиры может содержать различные способы металлоусиления. Здесь мы рассмотрим такой распространенный вариант, как усиление швеллером.
Швеллерное усиление в форме П-образной рамы или горизонтальной перемычки подходит для бетонных и кирпичных несущих стен.
Рама или перемычка из металлических профилей принимает на себя нагрузку, которая до этого приходилась на демонтированный участок стены, что позволяет сохранить несущую способность стены, не снижая ее. Таким образом, усиление дверного проема швеллером позволяет предотвратить растрескивание или даже обрушение стены.
Таким образом, усиление дверного проема швеллером позволяет предотвратить растрескивание или даже обрушение стены.
Примеры усиления проемов в бетонных стенах
Пример усиления проемов в кирпичных стенах
Технология усиления швеллером
Для демонтажа проемов лучше применять метод алмазной резки, поскольку он проще и быстрее, а главное не повреждает стену, т.е. не приводит к образованию трещин, чего нельзя сказать об обычном перфораторе или болгарке. Ровные края проема после алмазной резки существенно ускоряют и упрощают работы по монтажу элементов усиления. Перед началом вырезания проема, необходимо подстраховаться и установить временные подпорки, которые разгрузят перекрытия. Также не следует забывать об обесточивании электросетей и переносе при необходимости электропроводки.
Самый простой и распространенный способ укрепления проемов в нашем случае — это П-образная швеллерная рама, которая монтируется по краям вырезанного проема и состоит из горизонтальной перемычки и вертикальных подпорок.
Вся конструкция крепится к стене при помощи химических анкерных болтов или ребристых кусков арматуры, а на полу она приваривается к опорным пяткам из толстых металлических пластин. Для установки такой конструкции могут использоваться два типа швеллеров и разные способы их монтажа на стену (об этом читайте ниже).
Поскольку зачеканивать раму из швеллеров после ее установки крайне затруднительно из за специфической конфигурации профиля, то она как правило монтируется на предварительно нанесенный слой цементного раствора. Для лучшей связки раствора со стеной на последней можно сделать насечки.
Любопытна технология крепежа швеллерного усиления с помощью химических анкеров. Для этого в просверленное отверстие вставляется касула с химическим клеевым составом, а затем устанавливается анкерный болт, который разбивает капсулу. Происходит реакция, и через 20 минут соединение затвердевает и болт затягивают гайкой. Такое соединение способно выдерживать огромные нагрузки, а главное, обеспечивает совместную работу материала стены и металла швеллера.
Если же в качестве анкерных стержней используется обычная арматура, то ее вставляют в заранее просверленные отверстия, заполненные цементно-полимерцементным раствором.
Шаг и взаимное расположение крепежных отверстий в стене определяются инженерными расчетами по проекту перепланировки и техническому заключению.
Читайте также:Подробнее о техническом заключении ОАО МНИИТЭП
В углах металлоконструкции выполняется сварка ее вертикальных и горизонтальных элементов. Затем она покрывается специальной грунтовкой для защиты от коррозии.
Для усиления дверных проемов в кирпичных стенах может применяться т.н. комбинированное усиление, поскольку такие стены бывают намного толще бетонных. Как выглядит такое усиление? Как правило, это два швеллера, которые устанавливаются параллельно в качестве верхней перемычки и связываются стяжками через стену. Боковое обрамление такого проема выполняется из уголков. Все параллельные элементы такой рамы дополнительно стягивают поперечно приваренными пластинами.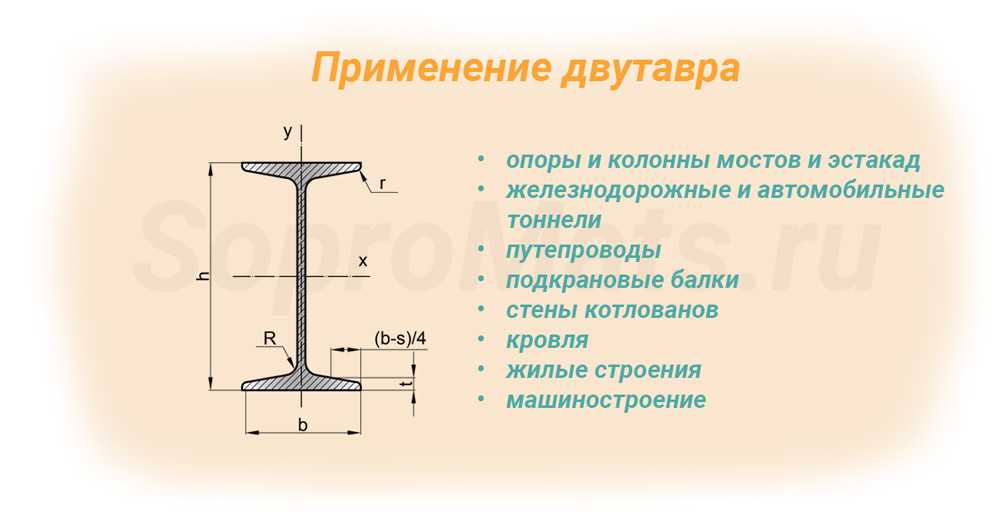
При усилении проемов в кирпичной стене верхняя швеллерная перемычка устанавливается до начала резки проема, для чего стена штробится в нужных местах. При этом соответствующие пазы делаются несколько шире проема.
Вид стены, подготовленной к установке швеллера:
А вот швеллерная перемычка уже смонтирована (на картинке видно, что усиление комбинированное — сверху швеллер, а по бокам уголки, стянутые хомутами):
Еще примеры комбинированного усиления проемов (в кирпичной и бетонной стене):
Верхняя швеллерная перемычка без вертикальных подпорок часто применяется для усиления оконных проемов. Таким способом также укрепляют проемы на верхних этажах многоэтажек или в коттеджах – то есть там, где нет большой нагрузки. Длина профиля в этом случае подбирается так, чтобы он был шире проема и опирался на стену, будучи уложенным в пазы. Впрочем, иногда оконный проем усиливают и по контуру.
Виды швеллеров
Швеллер – это разновидность металлического профиля П-образного сечения (высотой 50—400 мм, с толщиной стенки 4—15 мм и шириной полок от 32 до 115 мм ). Стальные швеллера получают главным образом горячей прокаткой заготовки на сортовых станах, а также холодной или горячей прокаткой рулонной стали на профилегибочных станах. Швеллер предназначен для придания жесткости и устойчивости конструкции, в которой он применяется. Он хорошо работает на изгиб и воспринимает осевые нагрузки.
Швеллеры (ГОСТ 8240-89) делятся на:
- швеллер с уклоном внутренних граней полок (ставится буква У).
- швеллер с параллельными гранями полок (ставится буква П).
Способы монтажа швеллеров на стену
1. Накладка У-образного швеллера внахлест. Это самый простой и способ. Его недостаток состоит в том, что полки У-образного профиля скруглены и скошены, и при установке профиля, между швеллером и поверхностью стены образуется пустое пространство. Чтобы добиться как можно более плотного прилегания конструкции, зазор зачеканивается инъектированием, либо швеллер устанавливается на заранее нанесенный раствор.
Чтобы добиться как можно более плотного прилегания конструкции, зазор зачеканивается инъектированием, либо швеллер устанавливается на заранее нанесенный раствор.
2. Накладка У-образного швеллера заподлицо. Это более аккуратный способ монтажа швеллеров подобной формы, поскольку оштукатуривать стену после усиления проема будет проще: нет выступающих деталей. В этом случае перфоратором немного скашивают края стены, чтобы добиться более плотного соединения металла и бетона. Это весьма трудоемкая и не слишком распространенная процедура, поэтому чаще крепят, как в первом случае. К тому же, перфоратор — не слишком «филигранный» инструмент, и подобрать нужный угол наклона очень непросто.
3. Накладка П-образного швеллера на стену внахлест. Как и в первом случае, это очень простой способ, но требующий идеально ровной поверхности стены. При этом швеллер П-образной формы образует меньшие зазоры, чем У-образный.
4. Установка П-образного швеллера заподлицо.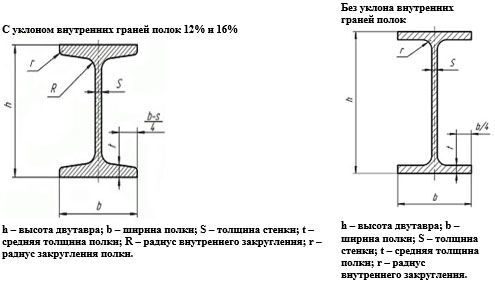 Также позволяет (аналогично п.2) легко оштукатурить стену после окончания работ по монтажу усиления проема. Боковые пазы для полок швеллера вырезаются алмазной пилой для получения ровной поверхности. Дорого, но красиво.
Также позволяет (аналогично п.2) легко оштукатурить стену после окончания работ по монтажу усиления проема. Боковые пазы для полок швеллера вырезаются алмазной пилой для получения ровной поверхности. Дорого, но красиво.
5. Как чаще всего укладывают швеллер на практике. Как мы уже отмечали, перфоратор не отличается ювелирной точностью, поэтому торец стены часто «подгогяется» под установку швеллера «на глаз». При этом рабочие часто халтурят и срубают края очень грубо — принцип показан на картинке. Промежуток между стеной и швеллером заполняется строительным мусором. При этом ни о каком заполнении полости раствором речь, конечно же, не идет.
Примечание: при установке швеллера внахлест он подбирается на размер-два больше стены, а при монтаже заподлицо — по размеру стены.
Дополнительно: усиление проема уголком
А также: алмазная резка проемов
Источник
youtube.com/embed/az6yVSrowk4″ frameborder=»0″ allowfullscreen=»allowfullscreen»>
Источник3
Как усилить деревянную балку перекрытия своими руками: материалы и инструменты, технология укрепления, усиление металлом — советы, пошаговые инструкции, фото, схемы
В случае неправильного подбора строительных материалов или ошибок в конструкции может возникнуть необходимость в усилении потолочных балок и защите их от провисания и прогибов. Я хотел бы поделиться опытом того, как подобная проблема возникла у меня, а главное, каким способом удалось ее ликвидировать.
При строительстве собственного дома в одной из комнат возникла необходимость в потолочных креплениях длиной 5 м. Для их возведения я воспользовался балками большей длины (7 м), так как из них одновременно можно будет сделать выпуск для крыши, защищающий стены и фундамент дома от подмывания снегом и дождем.
В этой статье я расскажу, как укрепить балки перекрытия металлическим уголком.
Усиление деревянных балок перекрытия: материалы и инструменты
- Уголок металлический 75?75 мм
- Металлическая полоса толщиной 5мм и шириной 75мм
- Болты и гайки Ф12мм
- Дрель, сверло Д12, гаечные ключи
Усиление деревянных балок перекрытия металлическим уголком. Процесс работы
Процесс работы
В центре комнаты установил два швеллера высотой в 14 см, прикреплённых друг к другу плоской частью в виде двутавра. Далее купил 4 м балки сечением 70?100 мм (в чём и была моя ошибка, так как удобней было бы использовать балки с сечением 100?150 мм) и закрепил их в швеллере и на несущей стене.
После монтажа крыши (использовал подпорки для стропил, которые опирались на эти балки), появился небольшой прогиб балок. Чтобы избежать дельнейшей деформации, решил усилить их уголком размерами 75?75 мм с одной стороны балки, а с другой, закрепить металлическую полосу толщиной 5 мм и шириной 75 мм.
Для стягивания уголка и полосы к балке использовал болты Ф12 длиной 100 мм, которые крепил на расстоянии 400 мм друг от друга
Вот таким образом усилил балки.
Если есть необходимость дополнительно укрепить балки с сечением 50?200 мм при ширине пролета 5 м, могу порекомендовать для усиления конструкции закрепить металлическую полосу толщиной 5 мм и шириной 75-80 мм по диагонали к центру с обеих сторон балки.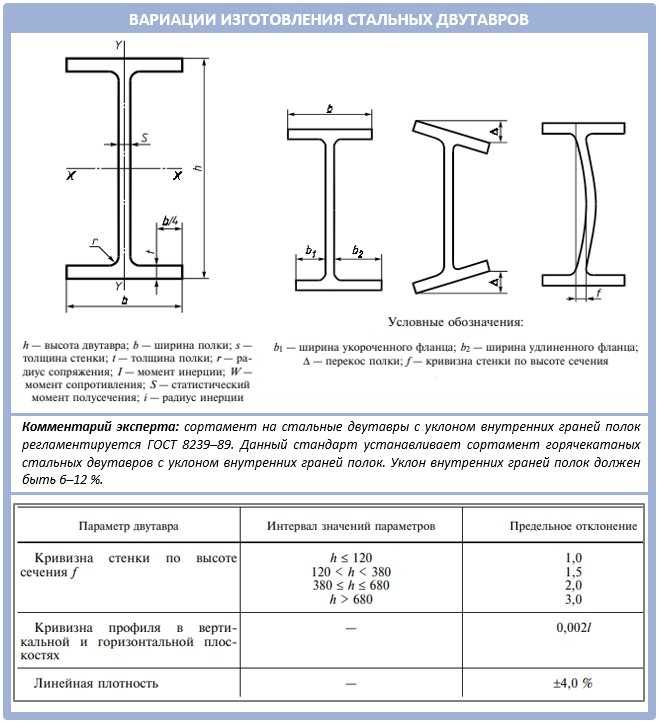
При этом сначала вдоль всей длины балки надо закрепить шнурок, и при помощи домкрата, посередине приподнять балку выше уровня шнурка и после крепить металлическую полосу.
Если в продаже не оказалось металлической полосы с нужными размерами, можно нарезать на гильотине полосы длиной 1,5 м, и сварить их между собой, получив необходимую длину.
В случае, если необходимо добавить дополнительные балки для усиления потолка в случаях его провисания и прогиба. Для этого необходимо подобрать балку соответствующего сечения, стянуть её уголком и прикрепим торцевой частью к стене.
Также возможно при помощи тарлена устранить провисание и прогиб балок, закрепив его на коньковой части крыши и самой балке. При таком креплении тарлена нагрузка будет перераспределяться на стропильную часть крыши. Однако этот метод применяется только в крайних случаях, если нет возможности добавить дополнительные балки.
Источник
youtube.com/embed/gcWKMxC8zA0″ frameborder=»0″ allowfullscreen=»allowfullscreen»>
Усиление деревянных балок перекрытия — как укрепить межэтажные, чердачные и подвальные лаги по полу и потолку
Основным элементом чердачных и межэтажных перекрытий во многих частных домах является деревянная балка. Срок службы перекрытий из дерева ограничен ввиду свойств древесины,
особенно, если она была плохо обработана или подвергалась нагрузке и воздействию влаги.
В следствие таких факторов балка перестает справляться с возложенной на нее функцией (возможно провисание, прогиб, искривление) и потребуется усиление деревянных балок перекрытия.
Помимо повреждений и утраты несущей способности балок пола и потолка (лаг, прогонов), укрепление может быть продиктовано увеличением нагрузки на перекрытие.
Когда нужно усиливать деревянные балки перекрытия
- плохое состояние балочной конструкции. Является следствием
повреждение древесины. Повышенная влажность, перепады температуры, деятельность
различных вредителей (жуков короедов), растрескивание – все это приводит к
деформированию балки перекрытия;
- снижение несущей способности.
 Под собственным весом,
Под собственным весом,
постоянной и переменной нагрузкой балки перекрытия могут прогибаться. Согласно
нормативам, если прогиб находится в пределах 1:300, то беспокоится не о чем.
Например, если балка длиной 2500 мм. прогнулась на 10 мм. это соответствует
нормальному значению прогиба. Если показатель прогиба больше – ее следует
усилить;
- необходимость увеличения несущей способности балки.
Связанная, например, с перестройкой чердака под мансарду или жилое помещение.
Такая перестройка приведет к увеличению постоянных и переменных нагрузок на
перекрытия второго этажа, что автоматически требует изменения сечения установленных
деревянных балок.
В пределах статьи будут приведены несколько распространенных способов усиления перекрытия (ремонт, реконструкция). Но, точно ответить на вопрос, как усилить деревянные балки перекрытия может только профессионал и только после анализа состояния конструкции. Ведь в каждом случае решение будет индивидуально.
Воспользовавшись таблицей можно получить представление о
том, какое сечение должно быть у балки при определенной нагрузке.
Допустимое сечение балок при нагрузке
Материал подготовлен для сайта moydomik.net
Способы усиления деревянных балок перекрытия
Основные типы и методы усиления деревянных перекрытий приведены в порядке увеличения трудозатрат и длительности на выполнение работ.
Тип усиления без изменения условий работы
Усиление деревянными накладками
Способ применяется в том случае, когда дерево повреждено.
Накладки устанавливаются с двух сторон от балки из бруса (по бокам или сверху и
снизу), максимально плотно к ней и скрепляются (затягиваются) насквозь болтом.
При этом важно обработать поврежденный участок и накладки противогрибковым
раствором. В критическом случае, если участок поврежден сильно – его лучше
удалить. Чтобы усилить балку нужно крепить накладку по всей ее длине.
Усиление пролетов металлическими накладками (пластинами) или прутковыми протезами
Стальные пластины используются вместо деревянных, описанных
выше. Металл также нужно обработать антикоррозионным раствором. Схема
Схема
устройства показана на рисунке.
Усиление пролетов балок металлическими накладками и прутковыми протезами
Усиление перекрытия углеволокном (углепластиком)
Современная технология усиления (армирование углеродным волокном). Углеволокно (ленты, листы, пластины, нити, ткань) наклеивается в
несколько слоев, пока не будут достигнуты требуемые показатели жесткости балки.
Удобство работы и легкость материала приводят к тому, что углепластик
приобретает популярность как эффективное средство для восстановления балок и строительных конструкций.
Ниже приведена схема армирования (усиления) балок перекрытия углеволокном.
Усиление балок углеволокномУсиление балок углеволокном — схемаУсиленные балки углеродным волокном
Усиление на торцах деревянными или металлическими протезами
Технология позволяет усилить балку в местах стыка с несущей
стеной. Это именно то место, где, за счет перепадов температур повреждение
древесины происходит быстрее.
На схеме ниже показана технология усиление протезами из швеллера, прокатного профиля
Усиление протезами из швеллера, прокатного профиляУсиление протезами из швеллера, прокатного профиля — 2
Монтаж пруткового протеза
Прутковый протез системы Дайдбекова выполняется из двух спаренных ферм, которые изготавливаются из обрезков арматурной стали сечением (диаметром) 10-25 мм. Длина протеза должна быть на 10% больше двойной длины сгнившего конца балки, но не более 1,2 м.
Длина протеза должна быть на 10% больше двойной длины сгнившего конца балки, но не более 1,2 м.
Устройство пруткового протеза
- Установить временные опоры под перекрытие на расстоянии 1-1,5 м от несущей стены,
состоящие из стоек и прогона. - Разобрать перекрытие снизу на ширину 75 см и сверху – 1,5 м от стены.
- Отрезать поврежденный участок балки (0,5м)
- Завести заготовку протеза вертикально в междуэтажное перекрытие и повернуть в горизонтальное положение, сначала надвигая на балку, затем, в обратную сторону задвигая в нишу стены.
- Сместить и прибить гвоздями сдвижную планку.
Установка пруткового протеза
Усиление балок шпренгельными затяжками
Усиление перекрытий — установка шпренгелей
Тип усиления с изменением условий работы
Усиление деревянных перекрытий такими способами предусматривает
существенную перестройку несущей конструкции балочных пролетов.
Изменение условий работы конструкций
Изменение схемы работы
Нестандартные решения
Если нет возможности усилить деревянные балки перекрытия,
можно попытаться их разгрузить, т. е., распределить нагрузку с существующих
е., распределить нагрузку с существующих
балок на дополнительно установленные элементы.
Усиление перекрытий путем установки опор под несущие балки
Опоры, подпирающие балки снизу, являются хорошим способом
перераспределить нагрузку с балки на опору.
Усиление перекрытий — установка опор
Усиление перекрытий путем установки дополнительных балок
Если существующие лаги находятся в целости и сохранности,
увеличить их несущую способность можно посредством увеличения их количества.
Установка дополнительных деревянных балок позволит увеличить нагрузку на
конструкцию. Устанавливая новые лаги нужно обязательно защитить их торцы
рубероидом, чтобы избежать повреждения.
Усиление перекрытий — установка дополнительных балок
Надеемся, что из приведенных способов усиления деревянных
балок перекрытия вы подберете именно тот, который решит вашу проблему наилучшим
образом и с минимальными затратами.
Как усилить деревянные балки перекрытия от прогиба
Усиление деревянного перекрытия – способы укрепить потолочные и балки второго этажа
Основным элементом чердачных и межэтажных перекрытий во многих частных домах является деревянная балка. Срок службы перекрытий из дерева ограничен ввиду свойств древесины, особенно, если она была плохо обработана или подвергалась нагрузке и воздействию влаги.
Срок службы перекрытий из дерева ограничен ввиду свойств древесины, особенно, если она была плохо обработана или подвергалась нагрузке и воздействию влаги.
В следствие таких факторов балка перестает справляться с возложенной на нее функцией (возможно провисание, прогиб, искривление) и потребуется усиление деревянных балок перекрытия.
Помимо повреждений и утраты несущей способности балок пола и потолка (лаг, прогонов), укрепление может быть продиктовано увеличением нагрузки на перекрытие.
Спаренные балки из доски. Типы и виды деревянных перекрытий
По предназначению деревянные балки перекрытия разделяются на такие виды:
- подвальное;
- чердачное;
- междуэтажное.
С каждым из подвидов следует ознакомиться более детально.
Подвальное
Конструкция должна обладать высокими показателями прочности, выдерживать значительные усилия, ведь балки будут служить основой для устройства пола. Если в проекте жилого дома предусмотрен подвал или гараж для автомобиля, то деревянные бруски заменяют металлическими несущими конструкциями. Это связано с быстрым разрушением дерева от воздействия высокой влажности. Альтернативным вариантом считается уменьшение расстояния между балками перекрытия и обработка деревянных элементов антисептиком.
Это связано с быстрым разрушением дерева от воздействия высокой влажности. Альтернативным вариантом считается уменьшение расстояния между балками перекрытия и обработка деревянных элементов антисептиком.
Чердачное
Перекрытие устанавливается независимо или является продолжением кровельной стропильной системы. Лучшие технические характеристики у первого варианта. Устраивать независимое перекрытие более рационально, такая конструкция улучшает звукоизоляционные показатели всего дома, считается ремонтопригодной.
Междуэтажное
Конструкция балок перекрытия в каркасном доме имеет свои особенности. Одна сторона деревянного бруса используется в качестве опорных элементов для крепления потолка, вторая (верхняя часть) применяется в качестве лаг для монтажа напольного покрытия. Пространство между балками межэтажного перекрытия заполняют минеральной ватой или другим теплоизоляционным материалом, пароизоляционная мембрана применяется в обязательном порядке. В нижней части пирога закрепляют гипсокартонные листы, сверху застилают дощатый деревянный пол.
Когда нужно усиливать деревянные балки перекрытия
- плохое состояние балочной конструкции
. Является следствием повреждение древесины. Повышенная влажность, перепады температуры, деятельность различных вредителей (жуков короедов), растрескивание – все это приводит к деформированию балки перекрытия;
- снижение несущей способности
. Под собственным весом, постоянной и переменной нагрузкой балки перекрытия могут прогибаться. Согласно нормативам, если прогиб находится в пределах 1:300, то беспокоится не о чем. Например, если балка длиной 2500 мм. прогнулась на 10 мм. это соответствует нормальному значению прогиба. Если показатель прогиба больше – ее следует усилить;
- необходимость увеличения несущей способности балки
. Связанная, например, с перестройкой чердака под мансарду или жилое помещение. Такая перестройка приведет к увеличению постоянных и переменных нагрузок на перекрытия второго этажа, что автоматически требует изменения сечения установленных деревянных балок.
В пределах статьи будут приведены несколько распространенных способов усиления перекрытия (ремонт, реконструкция). Но, точно ответить на вопрос, как усилить деревянные балки перекрытия может только профессионал и только после анализа состояния конструкции. Ведь в каждом случае решение будет индивидуально.
Воспользовавшись таблицей можно получить представление о том, какое сечение должно быть у балки при определенной нагрузке.
Допустимое сечение балок при нагрузке
Материал подготовлен для сайта moydomik.net
Преимущества использования настила на лагах
- При одной и той же высоте подъёма полы, организованные с помощью лаг, имеют намного меньший вес конструкции, например, по сравнению с железобетонными.
- Пол, организованный таким образом, хорошо проветривается.
- Между брусьями настила можно установить скрытые коммуникации.
- Пол, имеющий свободное пространство под настилом, можно дополнительно утеплить и сделать шумоизоляцию.

- Такие полы можно выровнять даже в том случае, если они имеют большой перепад по высоте.
- Пол, который имеет такую конструкцию, может быть легко демонтирован для реставрации.
Чтобы перекрытия были надёжными и долго служили, сечение балок должно быть правильно рассчитано. Для этого можно воспользоваться специальными таблицами.
Таблица расчёта сечения балки
Однако возникают такие ситуации, когда полы необходимо усиливать. Это происходит в следующих случаях:
- увеличивается нагрузка на пол, например, вследствие переоборудования чердака в мансарду;
- поражение несущих деревянных элементов, из которых выполнялся пол, грибковыми заболеваниями иди вследствие повреждения грызунами;
- превышение несущей способности, на которую первоначально рассчитывался пол;
- первоначальный неправильный расчёт сечения деревянных элементов и т. д.
Внимание! Допускается, чтобы пол имел прогиб 1:300. То есть, если балка имеет длину 3 метра и при этом прогиб составляет 10 мм, то это допустимая величина, и усиления не требуется.
Существует несколько способов усиления лаг. Рассмотрим некоторые из них.
Расчет двутавра на прогиб и изгиб
Калькулятор
| Пример расчета |
Калькуляторы по теме:
- Сбор нагрузок на балки перекрытия онлайн
- Расчет прямоугольной трубы
- Расчет квадратной трубы
- Расчет швеллера
- Расчет уголка
- Расчет деревянной балки
- Расчет двутавра на устойчивость.
Разновидности
Металлические конструкции отличаются по многим признакам. Это рекомендуется учитывать при выборе изделия.
По назначению
С помощью металлических балок можно создать качественное прочное перекрытие, выбрав один из вариантов.
Монолитное. В опалубку заливается бетон, производится усиление решеткой из арматуры. Поверхность получается бесшовной, отличается высокой прочностью.
- Монолитно-сборное. В этом случае помимо металлических балок используются бетонные блоки, которые укладываются на стальной профиль.
 Участки стыков заливаются бетоном.
Участки стыков заливаются бетоном. - Составное. Используется комбинация материалов, то есть на несущие металлические изделия укладываются плиты, доски, панели. Этот вариант предполагает создание дополнительного утепления и звукоизоляции поверхности.
По материалу: стальные и алюминиевые
Металлические конструкции могут изготовляться из разных материалов. Самыми популярными являются стальные и алюминиевые балки для перекрытий.
- Стальные изделия изготавливаются из сплава стали способом холодного или горячего катания. Стальные конструкции бывают нескольких видов: уголок, швеллер, двутавр. Из преимуществ стальных балок можно выделить огнеустойчивость, устойчивость к гниению и внешним факторам, высокую прочность.
Основными недостатками являются: высокая стоимость, низкие показатели тепло и звукоизоляции, риск образования коррозии. Монтаж стальных конструкций невозможно осуществлять без привлечения специальной техники. - Алюминиевые балки.
 При их изготовлении используется не просто алюминий, а его сплавы. В строительстве такие изделия применяются реже, чем стальные аналоги, так как они уступают по показателям устойчивости при сильных нагрузках. Чаще всего алюминиевые балки применяют при строительстве малогабаритных зданий. При возведении промышленных объектов изделия из данного металла применяются только в комбинации со стальными конструкциями.
При их изготовлении используется не просто алюминий, а его сплавы. В строительстве такие изделия применяются реже, чем стальные аналоги, так как они уступают по показателям устойчивости при сильных нагрузках. Чаще всего алюминиевые балки применяют при строительстве малогабаритных зданий. При возведении промышленных объектов изделия из данного металла применяются только в комбинации со стальными конструкциями.
По конструкции
В современном строительстве применяют несколько разновидностей металлических балок, различных по конструкции.
Тавровые. Основное сечение представляет собой стенку и полку в виде буквы «Т».
- Двутавровые. Сечение металлопроката выглядит как буква «Н». Изделие отличается большей жесткостью, чем тавровое, за счет того, что с противоположной стороны имеет дополнительную полку.
Двутавровые элементы подразделяются на несколько видов, каждый из которых имеет маркировку: - У – узкополочные конструкции.

- Д – среднеполочные изделия.
- К – колонные балки. Ширина полки такого элемента может равняться высоте изделия.
- Швеллер. Сечение элемента представляет собой букву «П». Эти балки считаются универсальными, применяются во всех сферах промышленности.
Существуют двутавры не с параллельными, а с наклонными полками. Их классифицируют на специальные и обычные. Их характеристики регламентирует ГОСТ 19425-74.
Инструкция к калькулятору
Обращаю ваше внимание, что в нецелых числах необходимо ставить точку, а не запятую, то есть, например, 5.7 м, а не 5,7. Также двутавр необходимо проверять на устойчивость (на заваливание от момента). Это можно сделать с помощью калькулятора, ссылка на который расположена выше (в списке «Калькуляторы по теме»). Если что-то не понятно, задавайте свои вопросы через форму комментариев, расположенную в самом низу.
Исходные данные
Расчетная схема:
Длина пролета (L) — минимальное расстояние между двумя крайними опорами или длина консоли.
Расстояния (A и B) — расстояния от опор до мест приложения нагрузок. Для 3 схемы А равна длине консоли балки, опирающейся на 2 опоры.
Нормативная и расчетная нагрузки — нагрузки, на которые рассчитывается квадратная труба. Рассчитать их можно с помощью следующих материалов:
- калькулятор по сбору нагрузок на балку перекрытия;
- пример сбора нагрузок на балку перекрытия.
Fmax — максимально возможный прогиб согласно таблицы E.1 СНиПа «Нагрузки и воздействия». Некоторые из них выписаны в таблицу 1.
Количество двутавров — этот показатель введен на случай, если балку перекрытия придется усилить еще такой же, положив ее рядом. То есть, если у вас одна балка, то указывается «один», если две рядом, то необходимо выбрать «две».
Расчетное сопротивление Ry— для каждой марки стали он свой. Наиболее распространенные значения приведены в таблице 2.
Размер двутавра — здесь следует выбрать профиль двутавра по тому или иному ГОСТу.
Что это такое и каких размеров бывают?
Балка является одним из основных элементов любой конструкции, ее функции – повысить устойчивость конструкции и укрепить ее. Балка (или ригель) состоит из полок и стенок различного размера, соединенных стыковыми швами с использованием сварки. Изготавливаются элементы на оборудованных предприятиях с использованием специальных станков.
Процедура изготовления осуществляется в несколько этапов, после чего готовое изделие проверяется на соответствие ГОСТам.
Металлические конструкции различаются по размерам, для удобства они имеют номера, с помощью которых можно подобрать необходимый материал для строительства.
Сфера применения
Металлические балки для перекрытий нашли свое применение в различных областях. Могут использоваться для:
- Укрепления кровли в жилом и промышленном строительстве.
- Создания межэтажных перекрытий.
- Устройства опор и различных колонн в промышленных сооружениях и архитектурных зданиях.

- Монтажа ангарных каркасов.
- Шахтовых стволов.
- Создания разнообразных железнодорожных вагонов.
- Строительства мостов, эстакад.
- Возведения металлических ферм.
На заметку: балки перекрытий из металла также можно использовать при строительстве малоэтажных частных домов.
Особенности процесса монтажа
Процедура устройства перекрытий с использованием металлических балок имеет определенные особенности, которые необходимо знать и четко соблюдать.
Обязательно наличие четкой схемы постройки с произведенными расчетами на прочность и изгиб изделий.
- К боковым граням балок крепятся бруски сечением 60х60, после чего размещается накат из досок.
- Накат накрывается слоем утеплителя, выполняющего функции звуко и теплоизоляции.
- Шаг между стальными балками не должен превышать 150 см, оптимальное расстояние – 100 см.
- Глубина опирания концов металлических конструкций на стены – максимум 25 см.

- Чтобы добиться большей звукоизоляции можно использовать не обычные, а пружинные скобы.
Характеристики
Балки перекрытий, в зависимости от технологии производства, имеют различные характеристики.
Двутавры с наклонными полками. Угол уклона 6-12 градусов. Основные параметры:
- длина – 10-60 см;
- ширина – 5,5-19 см;
- толщина полки – 7,2 мм-1,8 см;
- толщина стенки – 4,5мм-1,2 см.
- Двутавры с параллельными гранями (ГОСТ 26020, СТО АСЧМ 20-93) имеют иные характеристики:
- длина — Б-1 – 100 Б-4;
- толщина полок – 5,7 мм-3,3 см;
- ширина профиля – 55 мм-32 см;
- толщина стенки – 4,1 мм-1,95 см.
- Широкополочные металлические конструкции имеют следующие характеристики:
- длина — 20Ш1- 70Ш5;
- ширина профиля – 15-32 см;
- толщина стенки – 6,0 мм- 2,3 см;
- толщина полок – от 9 мм -3,65 см.
- Колонные балки имеют следующие показатели:
- длина – 20 К1-40 К5;
- ширина профиля – от 20 до 40 см;
- толщина стенки – от 6,5 до 2,3 см;
- толщина полок – 1-3,55 см.

Построение эпюр изгибающего момента и поперечной силы при изгибе
Полученные значения изгибающего момента и поперечной силы в двух сечениях (при положении x=0 и x=l) откладываем соответствующие ординаты, т.е. буквально строим графики обеих функций.
Что мы видим из построенных эпюр, какие выводы мы можем сделать:
- из эпюры поперечной силы видно, что она не меняется по всей длине и равна внешней силе F
- так как в начале координат x (т.е. справа) мы видим на эпюре «скачок» на величину этой силы, то в конце, в заделке скачок говорит о том, что реакция в заделке равна силе F
- на эпюре моментов график выходит из нуля координаты x (справа на балке) и момент тоже равен нулю
- по мере удаления сечения от силы влево момент растет и достигает своей наибольшей величины в заделке, где наблюдается такой же скачок как и на эпюре поперечной силы и равен (- F x). Это говорит о том, что момент в заделке равен именно этому значению
Что такое «скачок» на эпюре
Когда график начинается не из нуля или не из значения полученного на предыдущем участке, а имеет в одном и том же сечении x два разных значения — такой разрыв функции называется скачок.
Т.е. если рассматривать график бесконечно близко слева и бесконечно близко справа мы получаем два разных значения как поперечной силы, так и момента. И этот скачок для поперечной силы должен равняться приложенной сосредоточенной силе, а для момента приложенному сосредоточенному моменту.
Вот и все секреты построения эпюр для моментов и поперечных сил. Конечно дальше немного усложняется сам процесс, но принцип остается тот же.
Дальше в видео представлены примеры построения эпюр для распределенной нагрузки изгибающего момента. Чтобы было проще показать разницу все собрано в одном видео:
Рубрики
Изгиб, Сопромат онлайн
Метки
внутренние усилия, внутренние усилия при изгибе, задачи курса сопротивление материалов, изгиб, изгиб балки, изгибающий момент, Как построить эпюры изгибающих моментов и поперечных сил, краткий курс сопротивления материалов, поперечная сила, построение эпюр изгибающего момента, построение эпюр поперечной силы, правило знаков, правило знаков при изгибе, расчет балки, расчет балки на изгиб, Сопромат для чайников, Сопротивление материалов, сопротивление материалов краткий курс, сопротивление материалов примеры решения задач
- Сопротивление материалов
- Что такое сопромат
- Диаграмма растяжения стали на разрыв
- Как построить эпюры при растяжении-сжатии
- Эпюры моментов M(x) поперечных сил Q(x)
- Момент инерции сечения
- Сложное сопротивление
- Отзывы про репетитора по сопромату и строймеху
- Строительная механика
- Помочь проекту
- Курсы для инженеров
Цены на все виды
В строительстве чаще всего используются двутавровые металлические балки. Средняя стоимость продукции представлена в таблице.
Средняя стоимость продукции представлена в таблице.
| Наименование балки | Длина | Стоимость |
| двутавровая № 10 | 12 м | 880 |
| двутавровая № 10 Б-1 | 12 м | 780 |
| двутавровая № 12 | 12 м | 900 |
| двутавровая № 12 Б-1 | 12 м | 660 |
| двутавровая № 14 | 12 м | 1050 |
| двутавровая № 14 Б-1 | 12 м | 740 |
| двутавровая № 16 | 12 м | 1300 |
| двутавровая № 16 Б-1 | 12 м | 980 |
| двутавровая № 18 | 12 м | 1280 |
| двутавровая № 18 Б-1 | 12 м | 1150 |
| двутавровая № 20 | 12 м | 1560 |
| двутавровая № 25 Б-1 | 12 м | 2150 |
| двутавровая № 25 Ш-1 | 12 м | 3500 |
| двутавровая № 30 | 12 м | 2600 |
| двутавровая № 35 | 12 м | 3300 |
| двутавровая № 40 | 12 м | 3500 |
| двутавровая № 45 Б-1 | 12 м | 5200 |
Выбор размера швеллера на примере
Пусть имеется швеллер, длина которой составляет 6 метров и он имеет шарнирное закрепление. На него действует распределенная нагрузка, величина которой составляет 250 кг/м. Расчет ведется в следующей последовательности:
На него действует распределенная нагрузка, величина которой составляет 250 кг/м. Расчет ведется в следующей последовательности:
- Максимальное значение момента в профиле швеллера М = 9,81 х 250 х 6²/ 8 / 1000 = 11,04 кН∙м.
- Необходимое значение момента сопротивления сечения швеллера, Wн = 11,04 х 1000 / 240 = 46,0 см3 (согласно СНиП 2-23-81 для стали С245 Ry = 240 МПа).
- Подбираем по таблице ГОСТ размер швеллера с моментом сопротивления не ниже вычисленного значения 46,0 см3.
Это будет швеллер 12П (У) ГОСТ 8240-97 — значение момента сопротивления 50,8 см3 или швеллер гнутый 140х60х5 ГОСТ 8278-83 — значение момента сопротивления 47,8 см3.
Плюсы и минусы применения в зданиях
Конструкции из металла обладают рядом преимуществ, благодаря которым материал широко используется:
- повышенной прочностью;
- огнестойкостью;
- устойчивостью к внешним факторам;
- повышенной надежностью;
- большим периодом эксплуатации;
- возможностью усилить уже построенное здание;
- увеличенной несущей способностью.

Однако такие балки имеют и свои недостатки, которые также следует учитывать:
- сложность проведения строительных работ;
- необходимость задействовать тяжелую технику;
- металл может подвергаться коррозии;
- требуется производить сложные подсчеты, с чем у новичка могут возникнуть серьезные сложности.
Способы выполнить расчет и проверку на прогиб
Причина, по которой СНиПы устанавливают столь драконовские ограничения, проста и очевидна. Чем меньше деформация, тем больше запас прочности и гибкости конструкции. Для прогиба менее 0,5% несущий элемент, балка или плита все еще сохраняет упругие свойства, что гарантирует нормальное перераспределение усилий и сохранение целостности всей конструкции. С увеличением прогиба каркас здания прогибается, сопротивляется, но стоит, с выходом за пределы допустимой величины происходит разрыв связей, и конструкция лавинообразно теряет жесткость и несущую способность.
Просчитать прогиб конструкции можно несколькими способами:
- Воспользоваться программным онлайн-калькулятором, в котором «зашиты» стандартные условия, и не более того;
- Использовать готовые справочные данные для различных типов и видов балок, для различных опор схем нагрузок.
 Нужно только правильно идентифицировать тип и размер балки и определить искомый прогиб;
Нужно только правильно идентифицировать тип и размер балки и определить искомый прогиб; - Посчитать допустимый прогиб руками и своей головой, большинство проектировщиков так и делают, в то время как контролирующие архитектурные и строительные инспекции предпочитают второй способ расчета.
К сведению! Чтобы реально представлять, почему так важно знать величину отклонения от первоначального положения, стоить понимать, что измерение величины прогиба является единственным доступным и достоверным способом определить состояние балки на практике.
Измерив, насколько просела балка потолочного перекрытия, можно с 99% уверенностью определить, находится ли конструкция в аварийном состоянии или нет.
Требования
Все требования, предъявляемые к балкам из металла, четко обозначены в ГОСТах и СНиПах. Основными требованиями являются:
- Прочность. В зависимости от типа материала, используемого при изготовлении изделия, показатели прочности могут отличаться, но они должны соответствовать значениям, указанным в нормативных документах.

- Период эксплуатации. Металлические конструкции, согласно ГОСТ, должны прослужить минимум 80 лет.
- Устойчивость к коррозии. Готовые элементы должны быть дополнительно обработаны составами, предотвращающими образование коррозии.
Деревянные балки перекрытия – как правильно использовать, усиление для балок
В современном строительстве деревянные балки перекрытия используются наравне с железобетонными или металлическими деталями. Независимо от разновидности они должны соответствовать своему назначению, надежно распределять нагрузку от крыши, стен, расположенных выше предметов мебели, коммуникаций.
Из чего делают деревянные балки перекрытия?
Для данной цели преимущественно применяют древесину хвойной породы. Лучше всего подходит лиственница, сосна или ель. Оптимальная величина влажности материала – до 14%. Пиломатериалы с большим количеством сучков выбраковывают. Балки перекрытия из дерева распространенных лиственных пород обладают меньшей прочностью и долговечностью. Волокна древесины должны располагаться вдоль длины. Перед монтажом обязательно деревянные элементы обрабатывают огнестойкими составами и антисептиками.
Волокна древесины должны располагаться вдоль длины. Перед монтажом обязательно деревянные элементы обрабатывают огнестойкими составами и антисептиками.
Характеристики деревянных балок перекрытия
При неправильном выборе деревянные балки для перекрытия могут прогибаться или разрушиться в точках заделки. Хорошо высушенная древесина хвойных пород обладает приемлемыми характеристиками для использования в качестве элементов перекрытия:
- При нормальных режимах эксплуатации плотность древесины составляет 500 кг/м³, для улицы и влажных помещений – 600 кг/м³.
- Предел прочности хвойных пород на изгиб – около 75 МПа.
- Деревянные балки просты в использовании.
- Благодаря небольшому весу конструкции из древесины оказывают меньшую нагрузку на основание дома.
- Возможность самостоятельной установки без применения дополнительных дорогих материалов.
- Мелкий ремонт можно производить в процессе эксплуатации.
- Меньшая стоимость в сравнении с железобетонными плитами.

- Хорошая ремонтопригодность.
- Отлично подходят для возведения частных коттеджей с небольшой величиной пролета.
- Дерево – экологически чистый материал.
Минусы деревянных балок перекрытия:
- Нужна обязательная обработка антисептиками против воздействия грибков и плесени.
- Дерево – горючий материал, поэтому требует обязательной пропитки огнеупорными составами.
- Не подходят для зданий с большими пролетами.
- Уступают по допустимой нагрузке железобетонным конструкциям.
- Лиственные породы плохо подходят для использования в качестве балок перекрытия.
- Перепады температуры могут приводить к деформации деревянных элементов.
- При влажности более 14% повышается риск критического прогиба.
Размеры деревянных балок перекрытия
Выбор сечения зависит непосредственно от шага установки и длины пролета. Если планируете производить перекрытие по балкам из древесины, то минимальные размеры можно выбирать из таблицы в зависимости от расчетной нагрузки. Размеры прямоугольных брусьев по ширине – 4-20 см, по высоте – 10-30 см. Диаметр оцилиндрованного бревна выбирают в пределах от 11 до 30 см.
Размеры прямоугольных брусьев по ширине – 4-20 см, по высоте – 10-30 см. Диаметр оцилиндрованного бревна выбирают в пределах от 11 до 30 см.
Размеры допустимой нагрузки на перекрытия:
- Для не нагруженного чердачного помещения – 130-150 кг/м².
- Используемое чердачное помещение – до 250 кг/м².
- Межэтажные перекрытия – 350-400 кг/м².
Размеры деревянных двутавровых балок:
- Поперечные габариты – от 65х200 мм до 85х280 мм.
- Высота балок ДДБ – от 200 до 320 мм.
- Сечение бруса – 42х85 мм.
- Длина – до 6 м.
Виды деревянных балок перекрытия
В общей смете на строительство стоимость данных работ доходит до 15-20%. Чердачное перекрытие по деревянным балкам разрешает сократить расходы, уменьшить трудозатраты, отказаться от использования аренды грузоподъемных механизмов. Для монтажа быстровозводимых зданий в частном секторе отлично подходят брусья и бревна из хвойных пород. Можно использовать их современные аналоги из клееного материала и OSB-плит, прочных и долговечных металлодеревянных изделий.
Доска для перекрытия
Размеры и характеристики используемого материала следует подбирать, исходя из длины пролета и расчетной нагрузки. Возводя перекрытие первого этажа по деревянным балкам, нужно помнить, что на прочностные характеристики и жесткость большее влияние оказывает высота сечения, а не его ширина. При длине до 4 м разрешается применение толстой качественной доски ходовых размеров – 50х200 мм, 50х100 мм. При длине пролетов от 6 м лучше приобретать более подходящие конструкции из железобетона.
Двутавровая балка перекрытия
Двутавры производятся из клееного сухого бруса (влажность до 8%) и OSB-плит. Материалы сращиваются под прессом при помощи клея (D4 или аналогов). Далее конструкция для крепости усиливается метизами, обрабатывается огнезащитными составами и антисептиками. Балки на перекрытия данного типа стоят дороже природного обработанного бруса, но обладают следующими плюсами:
- Сравнительно легкий вес.
- Двутавровые деревянные балки перекрытия имеют высокую прочность и надежность.

- Отличная точность размеров.
- Низкая теплопроводность.
- Деревянные балки из OSB-плит имеют огнебиозащитное покрытие первой степени.
- Экологичность в пределах нормы.
LVL-брус
Этот материал получают путем склеивания нескольких подготовленных листов древесины. Технология разрешает получать изделия большой длины, что помогает возводить перекрытие второго этажа по деревянным балкам с меньшим количеством опор. При этом в финале конструкция будет обладать значительно меньшим весов в сравнении со стропильной системой из природной доски или бруса.
Плюсы LVL-бруса:
- Балочные перекрытия из LVL-бруса обладают повышенной прочностью.
- Небольшая масса
- Однородность структуры.
- Влагостойкость.
- Большой спектр размеров (толщина 21-75 мм, ширина 40-1000 мм, длина до 12 м и больше).
- Возможность получения бруса разной оригинальной формы.
- Удобство в работе.
Минусы LVL-бруса:
- Деревянные LVL-балки перекрытия из клееной доски менее экологичны.

- При использовании некачественного LVL-бруса существует риск расслаивания материала.
Комбинированная балка
Тандем стальных деталей и древесины существенно расширяет спектр использования материалов в строительстве. Стандартное перекрытие по деревянным балкам в газобетонном доме не всегда может удовлетворить заказчика. Металлодеревянные комплектующие являются более универсальными деталями, они обеспечивают легкость и повышенную надежность системы, риск усыхания при этом снижается. Современная МД-балка представляет собой сборную конструкцию из деревянной рамы, скрепленную вместе зубчатыми металлическими пластинами и кронштейнами.
Плюсы МК-балок:
- Комбинированные деревянные балки перекрытия разрешают возводить пролеты до 10 м без дополнительных перегородок.
- Исключено провисание.
- Облегчается скрытый монтаж коммуникаций, процесс утепления и звукоизоляции.
- Уменьшение количества крепежа.
- Высокая точность при сборке.

Четырехкантовый брус
Используемые в строительстве несущие балки в зависимости от числа продольных обработанных сторон делятся на двухкантные, трехкантные и четырехкантные брусья. Четырехугольная форма является более универсальной. Обработанные со всех сторон калиброванные заготовки можно использовать в открытых местах, где внешний дизайн играет роль. По ширине и толщине прямоугольного сечения размеры четырехкантного бруса лежат в пределах 100-250 мм. Помимо квадратной формы нередко используются балки 125х150 мм, 150х200мм или другие вариации.
Лафет для крыши
Данный материал представляет собой двухкантный опиленный с двух сторон брус, который укладывается при строительстве в горизонтальной плоскости. Две остальные его стороны имеют округлую форму. Лафет – традиционный элемент несущих конструкций для срубов в скандинавских странах, делают его преимущественно из сосны и лиственницы. Двухкантные брусья являются, по сути, промежуточными звеньями между профилированными заготовками и оцилиндрованным бревном.
Оцилиндрованное бревно
Перед тем как попасть на строительство такие балки перекрытия проходят несколько стадий обработки. Вначале торцуют края, затем в станках при помощи фрезеровочной каретки снимается лишняя древесина для придания заготовке максимально цилиндрической формы. В финале происходит вырезание пазов, облегчающих стыковку деталей, и подгонка детали до требуемой длины. Благодаря правильной геометрической форме и удобным технологическим вырезам оцилиндрованное бревно по свойствам приближается к профилированному брусу.
Устройство перекрытия по деревянным балкам
По прочности и другим показателям опоры из древесины уступают железобетонным конструкциям, но они вполне успешно исполняют свою функцию при соблюдении технологии в зданиях до 4-х этажей. Несущие балки перекрытия делают длиной до 5-6,5 м. Для удобства их укладку осуществляют в каменных домах с шагом, кратным размеру строительного блока. Глубина размера гнезда под опору – 0,6-0,8h (где h является высотой балки).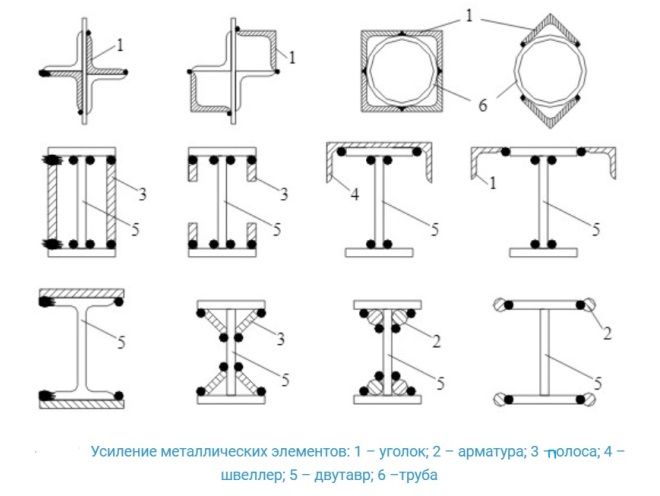 Стандартное значение 180-200 мм, минимальное – 150 мм. Зазор от торца балки до поверхности стены – 3-6 мм.
Стандартное значение 180-200 мм, минимальное – 150 мм. Зазор от торца балки до поверхности стены – 3-6 мм.
Существуют следующие виды заделки деревянных балок перекрытия:
- глухая;
- открытая;
- соединения встык;
- соединение вразбежку.
Усиление деревянных балок перекрытия от прогиба
Дополнительные работы по упрочнению несущих конструкций производятся при ухудшении состояния древесины, появлении прогиба с показателями более 1:300, при перестройке чердаков под мансарду. Перекрытие чердака по деревянным балкам можно усилить следующими способами:
- Установка деревянных накладок с обеих сторон бруса в поврежденных местах при помощи сквозного крепления болтами.
- Установка металлических пластин или прутковых протезов, обработанных антикоррозийными растворами.
- Армирование углеволокном – наклеивание ленты из углепластика в несколько слоев для увеличения жесткости балок.

- Усиление торцов балки протезами из дерева или древесины в местах стыка. Используются швеллеры, арматура, стальная полоса, прутья.
- Установка шпренгельных затяжек – использование стержневой конструкции для создания искусственного растягивающего усилия.
- Установка под проблемные деревянные балки дополнительных опор.
- Использование дополнительных балок.
- Уменьшение нагрузки на перекрытие за счет внесения изменений в конструкцию кровли.
виды, метод расчёта на прогиб
Важный этап строительства любого здания – установка межэтажных перекрытий. Они распределяют вес находящихся выше элементов строения, таких как крыша и стены, а также коммуникаций и деталей интерьера верхних этажей. Чтобы выдержать немалую нагрузку, нужны прочные перекрытия. В статье расскажем, какие виды балок применяют для разных частей здания, и рассмотрим, как правильно рассчитывать нагрузку и длину балочных перекрытий.
Межэтажное перекрытие деревянными балками
Содержание статьи
- 1 Виды перекрытий
- 2 Типы деревянных балок
- 2.
 1 Цельные балки
1 Цельные балки - 2.2 Клеёный брус
- 2.3 Двутавровые балки
- 2.
- 3 Сечение балочных перекрытий
- 4 Расчёт нагрузки и размеров деревянных балок
- 5 Монтаж перекрытия
- 6 Достоинства и недостатки балок из дерева
Виды перекрытий
Перекрытие – это горизонтальная несущая конструкция из балок, разделяющая здание по высоте на функциональные зоны или этажи и поддерживающая прочность всего строения. При строительстве дома применяют следующие виды перекрытий:
- цокольное или подвальное перекрытие;
- межэтажное перекрытие;
- чердачное перекрытие.
Чердачное перекрытие
Естественно, самые прочные – металлические балки в виде швеллера, уголка или двутавра, изготовленные из высокопрочной стали. Их лучше всего использовать для цокольного перекрытия, так как оно несёт наибольшую нагрузку. Из стальных балок можно устраивать длинные пролёты с большим расстоянием между балками. Они устойчивы к механическим повреждениям и гниению. Однако из-за большого веса с ними тяжело работать, а высокая цена металла увеличивает расходы на строительство.
Однако из-за большого веса с ними тяжело работать, а высокая цена металла увеличивает расходы на строительство.
Железобетонные балки перекрытия выдерживают большие нагрузки и подходят для строительства многоэтажных домов. Но для их монтажа понадобится специальная техника.
В основном при строительстве частных домов для перекрытий используют деревянные балки. Дерево – надёжный и экологически безопасный материал, который не навредит жильцам дома. Балки из дерева относительно недорого стоят и имеют небольшой, по сравнению с предыдущими видами вес, поэтому их легко устанавливать. Однако дерево огнеопасно, подвержено гниению и поражению короедом, поэтому требует предварительной обработки.
Типы деревянных балок
Деревянные балочные перекрытия различаются размерами, сечением, способом производства и породой дерева, из которого они сделаны. От выбора деревянных балок зависит надёжность и прочность строения. В зависимости от расстояния между стенами и предполагаемой нагрузки для перекрытий, используют доску или брус из цельного массива дерева, или клеёные изделия.
Разновидности деревянных балок
Цельные балки
Балки сделанные из цельного массива дерева, менее прочные, чем клеёные или двутавровые. Поэтому их длина не должна превышать 6 метров. Часто для увеличения прочности, строители на объекте спаривают доски. Стягивают их болтами и гайками с резиновыми или пластиковыми прокладками, предотвращающими попадание влаги и образованию ржавчины на крепеже.
Клеёный брус
Клеёный брус изготавливают методом склеивания нескольких частей между собой. Балки из этого материала способны выдерживать высокие нагрузки, поэтому их можно использовать в конструкции перекрытий длиной до 14 метров. Из такого бруса можно изготовить гнутые перекрытия для арок.
Имеются у таких изделий и недостатки. При изготовлении могут использовать некачественные пиломатериалы, поэтому со временем возможна усадка балочного перекрытия. К тому же клеёные балки значительно дороже цельных. Чтобы рациональнее использовать средства отведённые на строительство, нужно правильно рассчитать нагрузку и длину балок.
Клееный брус при аналогичном сечении с обычным имеет большую прочность
Балки перекрытия изготавливают из хвойных пород дерева, но также часто используют древесину дуба, акации, клёна и других деревьев. Главное условие необходимое для прочности конструкции – влажность не более 12–14%. Виды некоторых изделий приведены в таблице ниже.
Двутавровые балки
Достоинства двутавровых деревянных балок – универсальность применения, простота установки и высокая прочность. Они сохраняют свои параметры при больших нагрузках без вспомогательных конструкций для усиления.
Устройство двутавровой балки
Двутавр делают с использованием хорошо просушенного строганного или клеёного бруса, прочной проклеенной водостойкой фанеры или OSB-плит, на основе огнеупорного и влагостойкого клея. Поэтому двутавровая деревянная балка не требует пропитки специальными составами и легко поддаётся распиловке. Однако из-за сложной технологии изготовления их редко применяют для устройства перекрытий.
Двутавровые балки из OSB (ОСП)Соединение двутавровых балок между собой
Для всех видов выпускаемой продукции есть свой сортамент. Сортамент — это подбор различных изделий готовой продукции по маркам, профилям или размерам. Часто в таблице указаны дополнительные сведения о прочности, весе и т. д.
Сортамент — это подбор различных изделий готовой продукции по маркам, профилям или размерам. Часто в таблице указаны дополнительные сведения о прочности, весе и т. д.
Сечение балочных перекрытий
На прочность перекрытия также влияет сечение балки. По типу сечения включают следующие виды пиломатериалов:
- прямоугольные;
- квадратные;
- круглые;
- овальные;
- двутавровые.
Самые распространённые – балочные перекрытия прямоугольного сечения. Их легко устанавливать и такие балки будут служить лагами для обустройства полов. При монтаже прямоугольных балок их устанавливают вертикально широкой частью, так как с увеличением высоты повышается прочность конструкции.
Для чердачных перекрытий часто используют круглые балки или оцилиндрованные брёвна. Такие балки имеют хорошую прочность и устойчивость на прогиб.
Наиболее крепкие и функциональные – двутавровые балки перекрытия.
Расчёт нагрузки и размеров деревянных балок
Перед возведением здания необходимо рассчитать нагрузку и длину балочных перекрытий. Для лучшей прочности перекрытия при строительстве нужно использовать деревянные балки с немного большим, чем расчётный, запасом прочности.
Для лучшей прочности перекрытия при строительстве нужно использовать деревянные балки с немного большим, чем расчётный, запасом прочности.
Выбор ширины или толщины балки в зависимости от длины
Чтобы правильно произвести расчёт нагрузки на балку перекрытия, нужно:
- Знать расстояние между стенами и шаг между балками.
- Вычислить постоянную нагрузку, складывающуюся из массы балок, утеплителя и материалов, из которых изготовлен пол и потолок.
Для вычисления необходимо сложить удельный вес на кв. метр всех стройматериалов
- Временную нагрузку. К ней относятся масса мебели и находящихся в здании людей. Как правило, её считают равной 150 кг/м2.
- Высчитать предполагаемую нагрузку на 1 м2 перекрытия (сумма временных и постоянных показателей).
Так как для расчёта требуется знать нагрузку на погонный метр, нужно предполагаемую нагрузку на 1 м2 умножить на расстояние между балками. Далее, полученную цифру умножают на квадрат расстояния между несущими стенами и делят на 8. Так проводят расчёт нагрузки балочного перекрытия.
Так проводят расчёт нагрузки балочного перекрытия.
Mmax = (q*L2)/8
Где:
- q — полная нагрузка на кв. м;
- L2 — квадрат расстояния между стенами.
При проектировании каркаса перекрытия нужно уделить внимание пространственной жёсткости, которая во многом зависит от показателей прогиба балочного перекрытия.
Расчёт деревянной балки на прогиб проводят по формуле: W = Mmax / R, где M – максимальная нагрузка, а R – сопротивление древесины из СП 64.13330.2017 от 2017 г. (актуальная редакция СНиП II-25-80). Для древесины 2 сорта её принято считать равной 130 кг/см2.
Из формулы W = b*h2/6, зная показатель W, вычисляем сечение перекрытия. Достаточно задать одну геометрическую характеристику b (ширину сечения) или h (его высоту).
Прогиб деревянного перекрытия при вычисленной нагрузке не должен быть больше соотношения к длине балки 1:350 для подвальных и межэтажных перекрытий, а для чердачных и мансардных – 1:250.
Размер балок зависит от расстояния между несущими стенами. Для определения необходимой длины балки к этой величине прибавляют 40 см, примерно по 15–20 см с каждой стороны. Профессиональные строители рекомендуют для устройства перекрытия использовать балки с сечением равным 4–5% длины пролёта.
Монтаж перекрытия
Чтобы здание долго прослужило, балочные перекрытия должны соответствовать высокому уровню прочности. Иметь хорошую звуковую и теплоизоляцию, а также хорошо вентилироваться.
При установке деревянных балок чаще всего используют маячный способ монтажа. Вначале монтируют крайние балки, а затем промежуточные. Чтобы не допускать ошибок во время работы, используют уровень. В случае перепадов высоты, балки можно выровнять подложив под торцевые концы пропитанные битумным праймером обрезки.
В случае перепадов высоты, балки можно выровнять подложив под торцевые концы пропитанные битумным праймером обрезки.
Перед началом установки проводят сращивание или обрезку балок до нужных размеров. Сращивание балок из бруса по длине обычно проводят способом «замочный паз». Для этого концы брусьев спиливают на 1\2 толщины и заглубляют один торец в толщу другого. Затем места соединений фиксируют.
Сращивание двух балок
Расстояние между деревянными балками не должно быть меньше 60 см и превышать 1 метр. В конструкции из брёвен или клеёного бруса шаг делают больше, чем в дощатых перекрытиях. При монтаже чердачного перекрытия расстояние между дымоходом и балками должно быть не менее 40 сантиметров.
Для прочности каркаса торцы балок заглубляют в несущую стену минимум на 15 см. У двутавровых балок это значение разрешено уменьшить до 7 см. Заделывают углубления раствором или монтажной пеной. Возможно закрепление концов на стенах с помощью стальных связей. В местах опор на балках делается гидроизоляция.
Гидроизоляция балок в местах опор обязательна
Достоинства и недостатки балок из дерева
Использование в строительстве зданий деревянных балок в отличие от других видов характеризуется следующими достоинствами:
- доступная цена;
- простота доставки на строительную площадку;
- возможность установки без применения спецтехники;
- экологическая безопасность;
- ремонтопригодность.
Однако, несмотря на многие достоинства, такие перекрытия менее прочны, чем металлические и железобетонные. Требуют обработки антипиренами, а также средствами против гнили и плесени. Монтаж деревянных балок возможен только после тщательных расчётов.
В заключение статьи нужно добавить, что применение дерева в строительстве значительно сокращает расходы. Чтобы не нарушить конструкцию всего здания и установить прочные перекрытия, их проектирование и монтаж лучше доверить профессиональным строителям.
Эффект уменьшения прогиба стальных двутавровых балок, усиленных при нагрузке – IJERT
КОНЕЧНО-ЭЛЕМЕНТНОЕ МОДЕЛИРОВАНИЕ
Описание модели
Все образцы дискретизированы с использованием коммерческого программного обеспечения ANSYSTM.
 Полки балки, стенка, ребра жесткости, накладка и сварные швы моделируются с использованием четырехузлового элемента 181 конструктивной оболочки. SHELL181 подходит для анализа оболочечных конструкций от тонких до умеренно толстых[2]. Четыре ребра жесткости полностью соединены в точках нагрузки. Контактный элемент 174 и мишень 170 используются для моделирования поверхности между накладкой и фланцем образца. Все узлы усиленного фланца и накладки сцеплены на расстоянии, равном средней их толщине. Толщина сварных элементов варьируется, чтобы обеспечить поперечное сечение, равное сечению углового шва толщиной 6 мм.
Полки балки, стенка, ребра жесткости, накладка и сварные швы моделируются с использованием четырехузлового элемента 181 конструктивной оболочки. SHELL181 подходит для анализа оболочечных конструкций от тонких до умеренно толстых[2]. Четыре ребра жесткости полностью соединены в точках нагрузки. Контактный элемент 174 и мишень 170 используются для моделирования поверхности между накладкой и фланцем образца. Все узлы усиленного фланца и накладки сцеплены на расстоянии, равном средней их толщине. Толщина сварных элементов варьируется, чтобы обеспечить поперечное сечение, равное сечению углового шва толщиной 6 мм.Настройка модели
Разрешены повороты на одной опоре, а повороты и осевое смещение разрешены на другой опоре. Реализовано начальное несовершенство с максимальным прогибом L/500 на середине длины. Это максимальное несовершенство превышает L/1000 (максимально допустимое отклонение от прямолинейности). Несовершенство заключается в косвенном учете остаточных напряжений, которые не учитываются при моделировании.
 На рис. 1 показан пример предлагаемой модели с наложенными граничными условиями.
На рис. 1 показан пример предлагаемой модели с наложенными граничными условиями.Нагрузка с регулируемым смещением используется для определения несущей способности усиленных балок; нагрузка, регулируемая смещением, прикладывается со скоростью 0,5 мм/час, 0,167 мм/час в вертикальном и поперечном направлениях соответственно. Скорость загрузки выбирается путем проб и ошибок в качестве компромисса для сокращения времени выполнения вычислений при минимизации разницы между экспериментальным анализом и анализом конечных элементов.
Сварка
Накладка
Сечение
шарнирная опора (допускаются повороты)
Элементы жесткости
Чувствительность сетки
Сначала проводится исследование чувствительности сетки, чтобы убедиться, что используемая сетка дает разумные результаты. Сетка, использованная Lui et al. (2009b), Lui использовал максимальную ширину элемента 20 мм. Окончательная сетка, показанная на рис. 1, выбрана потому, что при дальнейшем измельчении сетки в результатах наблюдаются незначительные изменения.
 Здесь используются элементы с максимальной шириной 50 мм и соотношением сторон 0,5.
Здесь используются элементы с максимальной шириной 50 мм и соотношением сторон 0,5.Проверка модели
Роликовая опора (допускаются вращение и осевое смещение)
Модель конечных элементов проверяется с использованием результатов экспериментальных испытаний, описанных в части I. Экспериментальные предельные нагрузки образцов (Pexp) сравниваются с соответствующими предельными нагрузками модели конечных элементов (PF.E.), как показано в таблице 1. Сравнение показывает, что разница между экспериментальными и ЭЭ результатами находится в разумных пределах
Рис. 1 Конечно-элементная модель усиливающей балки
Нагрузка с регулируемым перемещением прикладывается к точке нагружения до отказа. Для балки, усиленной под нагрузкой, показанной на рис. 2, процесс нагружения требует пяти шагов: 1) создается моделирование сечения балки, накладки и сварных швов, а первоначальный дефект включается в модель. 2) Все элементы накладки и сварные швы деактивируются с помощью функции рождения и смерти элемента, затем 3) в модели выполняется нелинейный анализ с использованием нагрузки, контролируемой перемещением, до уровня предварительного нагружения. 4) На предварительно нагруженном уровне контролируется прогиб узлов нижней полки (на средней панели). 5) Затем все деактивируемые элементы снова активируются, и процесс загрузки возобновляется до отказа.
4) На предварительно нагруженном уровне контролируется прогиб узлов нижней полки (на средней панели). 5) Затем все деактивируемые элементы снова активируются, и процесс загрузки возобновляется до отказа.
, разница между предельными нагрузками не превышает 2,3%. Деформации экспериментальных образцов вместе с результатами конечных элементов показаны на рис. 3 – 4 для БЛ-90-50 и БЛ-65 соответственно. Экспериментальные и численные кривые совпадают, а деформации, представленные численной моделью, являются разумной аппроксимацией результатов испытаний, как показано на рис. 5. Сравнение экспериментальных и численных результатов подчеркивает хорошую точность модели.
ТАБЛИЦА 1 СРАВНЕНИЕ ЭКСПЕРИМЕНТАЛЬНЫХ И Ф.Э. РЕЗУЛЬТАТОВ
Испытанные балки | Экспериментальная предельная нагрузка Pexp (кН) | FE предельная нагрузка PF.E. (кН) | Pexp/ PF.E. | Процент увеличения грузоподъемности *% |
г. г. до н.э. | 218,15 | 215,15 | 1.01 | 1,3 |
БЛ-65 | 220,62 | 219,54 | 1,00 | 0,5 |
БЛ-90 | 229,17 | 231.06 | 0,99 | -0,8 |
СИНИЙ-45 | 226.02 | 222,68 | 1.01 | 1,5 |
БЛ-90-25 | 235,76 | 232,23 | 1,02 | 1,5 |
БЛ-90-50 | 242,34 | 236,78 | 1,02 | 2,3 |
Испытательный образец перед нагрузкой
Деформированная форма при степени предварительного натяга
Шаг 1: коэффициент загрузки до предварительной нагрузки
Испытательный образец перед нагрузкой
с
Деформированная форма при степени предварительного натяга
Шаг 2: уменьшение прогиба во время сварки
Деформированная форма при степени предварительного натяга
Сварочная пластина
Шаг 3: сварная пластина
Рис. 2 Техника усиления при нагружении
2 Техника усиления при нагружении
*Процент увеличения предельной грузоподъемности равен .. %
ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ
A. Влияние длины и площади накладки
Экспериментальные результаты с данными Liu et al. [2, 3] показали, что: 1) Увеличение длины приварной накладки приводит к увеличению предельной емкости Pu, для анализируемой балки BL с длиной балки 180 см предельная емкость увеличивается в 1,1
%, 5 % и 23 % при увеличении длины плиты с 60 см, 90 см и 170 см соответственно. 2) Влияние длины накладки уменьшается, когда площадь накладки меньше площади фланца. Эти моменты предполагают, что для
Изучение таблицы 5 показывает, что изменение коэффициента предварительного нагружения оказывает незначительное влияние на прирост предельной нагрузки (величина прироста предельной грузоподъемности в процентах варьируется от -1,96 % до 0,79 %). Даже в этом случае увеличение коэффициента предварительного нагружения вблизи конца зоны упругости снижает приращение предельной нагрузки для схемы упрочнения А.
ТАБЛИЦА 3 СХЕМЫ УСИЛЕНИЯ
Шаблоны* | А | Б | С | Д | |
Сечение | |||||
Рассчитано момент инерции относительно большой оси | 2665,5 см4 | 2836,2 см4 | 2433,06 см4 | 3467,32 см4 | |
Описание/Имя | Усиление нижнего фланца / BL | Усиление нижнего и верхний фланец / BLU | Усиление верхнего фланца /БУ | Усиление нижнего фланца по вертикали /BLV | |
* Для всех моделей усиления: площадь накладки = площадь полки, длина накладки = пролет балки
160
следующая анализируемая балка, длина и площадь сварной накладки адаптированы в этой работе, чтобы быть равными усиленному пролету балки
140
Нагрузка (кН)
120
Образец B Образец D
и площадь фланца соответственно.
Эффект схемы упрочнения с различным коэффициентом предварительного натяга
Двутавровая балка может быть усилена стальной пластиной, приваренной к верхнему или нижнему фланцу с различной ориентацией. Таблица
100
80
60
40
20
0
Образец А
Управление
Образец С
3 указывает схемы усиления, предложенные в этом исследовании. Предлагаемые схемы основаны на использовании одной и той же области накладной пластины с разными ориентациями для улучшения поведения балки.
На рис. 6 представлены кривые прогиба под нагрузкой для различных моделей усиливающих балок с двумя соотношениями пролет/глубина. Усиление стальных балок под нагрузкой увеличивает мощность контрольной балки для всех схем усиления. Можно отметить, что схема B является наиболее эффективной, хотя схема B менее инерционна, чем схема D. Усиление верхней и нижней полки для схемы B улучшает поведение балки, кроме того, схема D имеет трудности с техникой сварки, т.
 к. первоначальный прогиб накладки вокруг своей большой оси (для принятия под нагрузкой изогнутой формы усиливающей балки) вызывает в плите дополнительные напряжения.
к. первоначальный прогиб накладки вокруг своей большой оси (для принятия под нагрузкой изогнутой формы усиливающей балки) вызывает в плите дополнительные напряжения.Еще один важный эффект схемы упрочнения связан с отклонением предела текучести wy. Прогиб середины пролета при пределе текучести для двух разных пролетов указан в таблице 4. При определенном коэффициенте предварительного натяга схемы усиления A и D уменьшают предельный прогиб контрольной балки, незначительное уменьшение прогиба почти на 3% и 8 % для моделей A и D соответственно. Напротив, наблюдалось увеличение отклонения урожайности примерно на 5% и 15% для моделей С и В соответственно.
0 20 40 60
Прогиб
Рис. 6 Влияние схемы усиления на предельную прочность усиленной балки (L = 3600 мм, Lpl = 3500 мм и
коэффициент предварительной нагрузки = 0,60)
ТАБЛИЦА 4 ВЛИЯНИЕ СХЕМЫ УСИЛЕНИЯ НА ПРОКЛОН УСИЛИТЕЛЬНОЙ БАЛКИ
Рисунок для усиления
Длина пролета = 360 см
Длина пролета = 270 см
wy выход прогиб (мм)
Инкрементальный*
%
wy доходность отклонение
(мм)
Инкрементальный*
%
Контроль (БК)
12,6
–
22
–
А
12,2
-3,2
21,2
-3,6
Б
14,5
15,1
24,86
13,0
С
12
4,8
20.
 19
198.2
Д
11,7
-7,1
20.22
-8.1
*Приращение предельного отклонения предела текучести в средней точке = ( )
Отношение пролет/глубина
Коэффициент предварительной нагрузки
Узор
Приращение предельной нагрузки
%
Узор
Приращение предельной нагрузки
%
Узор
Приращение предельной нагрузки
%
Узор
Приращение предельной нагрузки
%
9
0
23.12
46.13
39.11
36,30
13,5
22,25
47,28
38,55
38,61
18
22.
 32
3249.09
36,85
36,71
9
0,41:
0,42
23,34
46,38
39,59
36,19
13,5
А
23.21
Б
47,93
С
38,95
Д
37,66
18
21,79
48,67
37,15
35.01
9
0,73:
0,76
23.02
46,70
40.
 41
4136.10
13,5
21,77
48.06
39,39
36,35
18
21,95
49.13
39.05
32,34
( )
различных коэффициентов предварительного натяга, как показано на рис. 7. Особенно для модели B, при более высоком коэффициенте предварительного натяга (Pstr/Punstr = 0,87), общая тенденция предельной грузоподъемности в зависимости от величины уменьшенного прогиба остается прежней. Для шаблона D результаты конечных элементов показывают, что уменьшенный прогиб не является желательным методом для усиления этого типа балки. Так как при увеличении прогиба пластину трудно приварить к нижней полке, тем более принять прогнутую форму балки.
ТАБЛИЦА 6 ПРЕДЕЛЬНАЯ НАГРУЗКА НА БАЛКИ С РАЗЛИЧНЫМ ОТНОШЕНИЕМ ПРОЛЕТА/ГЛУБИНЫ
100%
ТАБЛИЦА 5 ПРЕДЕЛЬНЫЕ НАГРУЗКИ ДЛЯ БАЛКИ С РАЗЛИЧНЫМ СООТНОШЕНИЕМ ПРЕДВАРИТЕЛЬНОГО НАГРУЗКИ И ЧЕТЫРЬМЯ СХЕМАМИ
л
(луч
пролет в мм)
Коэффициент предварительной нагрузки
Укрепить
образец А
Укрепить
узор В
Укрепить
узор С
Укрепить
модель D
Пу (кН)
Инкр.
 (2)%
(2)%Пу (кН)
Инкр.(2)%
Пу (кН)
Инкр.
(2)%
Пу (кН)
Инкр
.(2)%
2700(1)
0,00
162,41
0,00
195,66
0
184,07
0
183,75
0
0,26
163,60
0,73
196,50
0,43
184,47
0,22
183,14
-0,33
0,42
163,69
0,79
196,53
0,44
184,60
0,29
182,48
-0,69
0,59
162,46
0,03
196,60
0,48
184,98
0,49
181,58
-1,18
0,76
161,77
-0,39
196,70
0,53
185,18
0,60
180,74
-1,64
0,85
161,41
-0,62
196,81
0,59
185,43
0,74
180,20
-1,93
(1) Предельная нагрузка на неусиленную балку ВС-260 = 132,85 кН (2) Приращение предельной нагрузки (=0) 100%
(=0)
Влияние отношения пролета к глубине
Для изучения влияния отношения пролета к глубине стальных балок, усиленных под нагрузкой, были проанализированы короткие, промежуточные и длинные балки. Исследовано отношение пролета к глубине 9, 13,5 и 18 усиливающих балок. Была проведена серия прогонов для трех разных передаточных чисел с разным рисунком и передаточным отношением, результаты приведены в таблице 6.
Исследовано отношение пролета к глубине 9, 13,5 и 18 усиливающих балок. Была проведена серия прогонов для трех разных передаточных чисел с разным рисунком и передаточным отношением, результаты приведены в таблице 6.
Общеизвестно, что отношение пролета/высоты влияет на вид разрушения исследуемых балок, что приводит к различной предельной несущей способности. Таблица 6 показывает, что влияние соотношения пролет/глубина незначительно. Изменение приращения предельной нагрузки составляет примерно от 1% до 3% при изменении отношения пролет/глубина. Это можно объяснить, так как поперечное смещение составляет
120
Нагрузка (кН)
118
116
114
112
110
145
143
Загрузить
141
139
Коэффициент предварительной нагрузки = 0,26 Коэффициент предварительной нагрузки = 0,60 Коэффициент предварительной нагрузки = 0,87
0 5 10 15
Уменьшенный прогиб (мм)
Образец А
Коэффициент предварительной нагрузки = 0,26 Коэффициент предварительной нагрузки = 0,60
, и сбой произошел из-за чрезмерной производительности в
.
середина балки, соотношение между прогибом и боковым
137
135
Коэффициент предварительной нагрузки = 0,87
перемещение в точках нагрузки w/v = 3.
D. Влияние уменьшенного прогиба w
Эффект уменьшенного прогиба w (приложенного к исследуемым балкам перед приваркой накладки) изучен для 60 анализируемых балок. Все изученные балки имеют отношение пролет/высота, равное 18, с тремя коэффициентами предварительного нагружения 0,26, 0,60 и 0,87, как указано в таблице 2.
Результаты, представленные на рис. 7, показывают, что увеличение величины уменьшенного прогиба увеличивает предельную мощность усиливающей балки. Для схемы А предельная нагрузка балки БЛ-350-87 увеличивается с 112,23 кН (w = 0) до
117,12 кН (ш = 12,58 мм) с передаточным отношением, равным
4,3 %. Для шаблонов B и C уменьшенный прогиб оказывает незначительное влияние на предельную нагрузку усиленной балки при
.
140
138
Загрузить
136
134
132
130
0 5 10 15 20
Уменьшенный прогиб (мм)
Шаблон В
Коэффициент предварительной нагрузки = 0,26 Коэффициент предварительной нагрузки = 0,60 Коэффициент предварительной нагрузки = 0,87
0 5 10 15 20
Уменьшенный прогиб (мм)
Образец С
130
Нагрузка (кН)
128
126
124
122
120
Коэффициент предварительной нагрузки = 0,26 Коэффициент предварительной нагрузки = 0,60 Коэффициент предварительной нагрузки = 0,87
0 1 2 3 4
Уменьшенный прогиб (мм)
Образец D
Результаты конечных элементов для балки БУ-350-60 с различными боковыми ограничениями в точках нагрузки представлены на рис. 8 – 9. Результаты показывают, что частичное боковое закрепление, налагаемое в точках нагрузки, вызывает более высокое боковое смещение в начале нагрузки по сравнению со свободным боковым закреплением. В частности, наблюдается высокий прирост бокового смещения на этапе уменьшения прогиба, в то время как боковое смещение все еще находится под контролем даже в случае отказа. Более того, боковое смещение, инкрементное для незакрепленной балки, не контролируется в пределах предела текучести сжимающей полки, что приводит к значительному увеличению бокового смещения и разрушению.
8 – 9. Результаты показывают, что частичное боковое закрепление, налагаемое в точках нагрузки, вызывает более высокое боковое смещение в начале нагрузки по сравнению со свободным боковым закреплением. В частности, наблюдается высокий прирост бокового смещения на этапе уменьшения прогиба, в то время как боковое смещение все еще находится под контролем даже в случае отказа. Более того, боковое смещение, инкрементное для незакрепленной балки, не контролируется в пределах предела текучести сжимающей полки, что приводит к значительному увеличению бокового смещения и разрушению.
Рис. 7 Зависимость предельной нагрузки от количества
восстановленный прогиб при различном коэффициенте предварительной нагрузки
Влияние бокового ограничения и начального бокового смещения
Реакция исследуемой балки на боковое выпучивание представляет интерес для определения ее предела прочности, на боковое выпучивание влияет поперечное защемление балки сжатой полки. Чтобы изучить влияние бокового ограничения, были рассмотрены три случая бокового ограничения для полки сжатия: 1) частичное ограничение с соотношением (w/v = 3), 2) полное боковое ограничение и 3) отсутствие бокового ограничения.

Из экспериментального исследования, представленного автором в сопроводительном документе, эффект механизма загрузки может быть смоделирован путем введения контролируемого вертикального смещения w и горизонтального смещения v, которые имитируют частичное ограничение в точках нагрузки сжимающей полки.
В случае свободного поперечного ограничения начальное боковое смещение должно быть введено в идеальную геометрию для анализа поведения после потери устойчивости, где начальное боковое смещение (vi) представляет собой поперечное смещение на середине длины. Таблица 7 показывает, что начальное боковое смещение оказывает значительное влияние на предельную мощность свободных боковых удерживающих балок, поскольку начальное боковое смещение на 1 мм, 3 мм, 5 мм и 8 мм, приложенное к средней длине, вызывает уменьшение примерно на 3,85, 5,53, 6,74 и 8,31. % предельной грузоподъемности свободной поперечной ограничивающей балки с идеальной геометрией (без начальной деформации) соответственно.

В случаях частичного и полного защемления, показанных в таблице 7, начальное боковое смещение оказывает незначительное влияние на предельную несущую способность исследуемых балок, так как максимальное снижение предельной нагрузки балки при частичном защемлении составило 0,9 % за счет начального поперечного смещение (vi) равно 8 мм.
ТАБЛИЦА 7 ПРЕДЕЛЬНЫЕ НАГРУЗКИ БУ-350-0,6 ПРИ РАЗЛИЧНЫХ НАЧАЛЬНЫХ
БОКОВОЕ ПЕРЕМЕЩЕНИЕ
Д (мм)
Предварительная загрузка
отношение
* (vi) в мм
Без бокового ограничения
С частичной боковой частью
ограничитель w/v = 3
С боковым
ограничение
Пу (кН)
Сокращение
**
Пу (кН)
Сокращение*
*
Пу (кН)
Сокращение*
*
3600
0,6
0
137,60
–
131,54
–
137,62
–
1
132,50
3,71%
131,45
0,07%
137,59
0,02%
3
129,99
5,53%
131,15
0,30%
137,49
0,09%
5
128,33
6,74%
130,86
0,52%
137,36
0,19%
8
126,16
8,31%
130,36
0,90%
137,30
0,23%
*Максимальное вынужденное боковое смещение посередине длины перед нагрузкой
**Уменьшение предельной нагрузки (=0) 100%
(=0)
Боковое ограничение в точках нагрузки
План верхнего фланца
Балка с боковым ограничением
Частичное ограничение
(вес/объем = 3)
План верхнего фланца
Балка с частичным закреплением
Рис.
 9 Зависимость между нагрузкой и боковым смещением () в средней точке верхней полки для балок с разным боковым защемлением (схема C, L
9 Зависимость между нагрузкой и боковым смещением () в средней точке верхней полки для балок с разным боковым защемлением (схема C, L= 3600 мм, Pstr./ Punstr = 0,60 и vi = 5 мм)
Влияние стали марки
Для старых конструкций балки могут быть из стали с низким номинальным пределом текучести по сравнению с современными конструкциями, которые будут использоваться для усиления пластин. Поэтому усиливающие балки могут состоять из двух разных марок. Были исследованы балки с двумя различными сочетаниями марок стали: 1) балки, усиленные одной маркой стали для толстого листа и прокатного профиля (fy = 235 МПа или fy = 275 МПа), 2) балки усиленные с fy = 235 МПа для сечения и fy = 275 МПа для пластин, как показано в таблице 2
Табл. 8 и рис. 10 показывают, что при повышении класса прочности стального листа с fy = 235 МПа до fy = 275 МПа марки стали существенно не влияют на прочность усиленной балки, максимальное увеличение составило около 5,05 % от предела прочности. предельная грузоподъемность для БУЛ-350-60 при длине пролета 360, ни уменьшить прогиб, как показано на рис. 10.
предельная грузоподъемность для БУЛ-350-60 при длине пролета 360, ни уменьшить прогиб, как показано на рис. 10.
ТАБЛИЦА 8 ПРЕДЕЛЬНЫЕ НАГРУЗКИ ДЛЯ БАЛКИ ИЗ РАЗЛИЧНОЙ МАРКИ СТАЛИ И ЧЕТЫРЕХ СХЕМ
л (мм) | fy для балки (МПа) | fy для Pl (МПа) | Укрепить образец А | Укрепить узор В | Укрепить узор С | Укрепить модель D | ||||
Пу (кН) | Инкр.% | Пу (кН) | Инкр.% | Пу (кН) | Инкр.% | Пу (кН) | Инкр.% | |||
3600 | 235 | 235 | 100,92 | 0,5 | 123,73 | 5,05 | 115,75 | 2,68 | 112. | 1,97 |
235 | 275 | 101,43 | 129,99 | 118,85 | 114,22 | |||||
140
120
Нагрузка (кН)
100
80
60
40 fy (плита) = 275 кН
20 fy (плита) = 235 кН 0
0 10 20 30 40 50
Прогиб (мм)
Рис. 10 Зависимость нагрузка-прогиб для БЛУ-350-60 при изменении марки стали накладки (схема Б, L=3600 мм, Pстр./Пунстр.=0,60 и vi=
5 мм (fy) для сечения балки = 235 кН)
Лучшее руководство по минимизации прогиба балки – инженер-наставник
Как инженер, во многих случаях проектирование балки только по напряжению недостаточно. Проходы и настилы рассчитаны на отклонение, потому что человеческий разум чувствует движение, и если движение чрезмерное и слишком сильное, он делает вывод, что конструкция небезопасна.
Еще одним примером конструкции с учетом отклонения является крыло самолета. У коммерческих самолетов крылья очень жесткие по сравнению с крыльями грузовых военных самолетов. Никто не хочет смотреть в окно и видеть, как крыло подпрыгивает на 10-15 футов вверх и вниз во время грозы. Вы бы пришли к выводу, что в любой момент крылья могут оторваться.
Для уменьшения прогиба балки вы можете: уменьшить нагрузку, момент или длину балки; изменить типы поддержки или местоположение; добавить больше опор; увеличьте момент инерции модуля упругости или добавьте другие балки, чтобы разделить нагрузку.
Расчет на прогиб, а не на напряжение, иногда совершенно необходимое. Эмпирические правила при проектировании балки на прогиб:
- Прогиб динамической и статической нагрузки не может превышать L / 240 и
- Прогиб динамической нагрузки не может превышать L / 360
Вы можете использовать мой окончательный калькулятор балки, чтобы помочь . Давайте рассмотрим, как каждый из них изменит отклонение луча.
Давайте рассмотрим, как каждый из них изменит отклонение луча.
Уменьшить нагрузку/момент
Очевидно, что это самый простой способ уменьшить прогиб, но, скорее всего, маловероятный. Если я проектирую дорожку для одного человека, я не могу легко снизить свой вес (хотя мне нужно сбросить несколько фунтов). Кроме того, существует множество стандартов, которые диктуют требуемые постоянные и постоянные нагрузки. Скорее всего, это нестартер.
https://mentoredengineer.com/the-best-guide-to-solving-statically-indeterminate-beams/
Уменьшить длину луча
Этот вариант также вполне очевиден, но часто невозможен. Вероятно, вы уже оптимизировали это в своем дизайне. Если вы строите мост, вы хотите, чтобы сваи стояли на твердом грунте, но если это невозможно, вы хотите, чтобы они были на мелководье.
Если вы можете перемещать опоры балки, подумайте о том, чтобы один или оба конца были консольными. Подробнее об этом чуть позже.
Возможно, сближение опор возможно
Замена концевых опор
Замена концевых опор позволит увеличить жесткость балки без изменения сечения балки. Вот иерархия опор с их относительной жесткостью по отношению к консольной балке.
Вот иерархия опор с их относительной жесткостью по отношению к консольной балке.
- Фиксированные на каждом конце (48x)
- Фиксированные на одном конце, с опорой на другом (23x)
- С опорой на обоих концах (9,6x)
- Фиксированные на одном конце, направляемые на другом (3x)
- Консольные на одном конец (1x)
В каждом случае вы можете видеть, что преимущество подъема на одну ступень иерархии опор делает одну и ту же балку почти в три раза более жесткой. Если у вас есть консольная балка, добавление опоры под свободный конец изменит жесткость на фиксированную и поддерживаемую балку, увеличив жесткость в 23 раза!
Наиболее распространенная балочная опора, поддерживаемая с обеих сторон, также известная как простая опора. Эта балка уже достаточно жесткая и простая в изготовлении. Однако, если мы сделаем один пролет балки тремя опорами, мы фактически изменим центральную часть на почти фиксированную опору. Я говорю «почти исправлено», потому что опора все еще может вращаться в центральном положении. Однако эта опора все еще прикреплена к другим концам, поэтому на центральной опоре должен пройти некоторый момент. Если эта максимальная нагрузка на балку симметрична относительно центральной опоры, мы можем предположить, что соединение зафиксировано в центре. Это сделает нашу ту же балку в 2,4 раза жестче, чем она была раньше. Это небольшое изменение может похвастаться отличными результатами.
Однако эта опора все еще прикреплена к другим концам, поэтому на центральной опоре должен пройти некоторый момент. Если эта максимальная нагрузка на балку симметрична относительно центральной опоры, мы можем предположить, что соединение зафиксировано в центре. Это сделает нашу ту же балку в 2,4 раза жестче, чем она была раньше. Это небольшое изменение может похвастаться отличными результатами.
Балка с тремя опорами
Добавление консольной секции на концах
Это способ сохранить ту же общую длину балки при уменьшении расстояния между опорами. Из приведенной выше иерархии можно сказать, что свободно опертая балка в 9,6 раза более жесткая, чем консольная балка. Это означает, что я мог бы фактически консольно выдвинуть балку с одного конца на 10,4% (1 / 9,6)
Добавление консоли к одному концу балки
Например, если бы у меня была свободно поддерживаемая балка длиной 100 дюймов, я мог бы сдвинуть опору на одном конце примерно на 10% от общей длины. Это не только уменьшает прогиб на 31% (результаты зависят от используемых материалов и поперечного сечения), но и при использовании в настиле дает ощущение, что настил растягивается там, где должен. Отличное чувство для владельца колоды.
Отличное чувство для владельца колоды.
При необходимости вы можете сделать это на обоих концах балки.
https://mentoredengineer.com/determining-deflection-in-variable-cross-section-beams/
Увеличение момента инерции площади то же самое, только момент инерции площади. I и модуль упругости E можно изменить, чтобы уменьшить прогиб v. В этом разделе мы обсудим момент инерции площади.
Общая форма уравнения балки
Момент инерции площади полностью основан на форме поперечного сечения. По мере увеличения поперечного сечения увеличивается и момент инерции. Фактически, для прямоугольника, если вы удвоите высоту, вы увеличите момент инерции в четыре раза. Однако, если вы удвоите ширину, вы только удвоите момент инерции.
Вот что нужно сделать со следующими структурными формами
Круглая труба или труба
В случае круглых труб или труб простым решением является утолщение стенки. Например, труба толщиной 1/4 дюйма становится толщиной 3/8 дюйма или сортамент 40 меняется на трубу сортамента 80. Вы увидите лишь умеренное увеличение жесткости по мере утолщения стенки. Этого может быть достаточно, но ваш раздел становится тяжелее. В какой-то момент дополнительный вес может увеличить прогиб.
Вы увидите лишь умеренное увеличение жесткости по мере утолщения стенки. Этого может быть достаточно, но ваш раздел становится тяжелее. В какой-то момент дополнительный вес может увеличить прогиб.
Наилучшее решение — увеличить наружный диаметр трубы или трубы, сохранив первоначальную толщину стенки. Если это невозможно, подумайте о переходе на квадратную трубу.
Квадратная трубка
Квадратная трубка очень похожа на круглую трубку, но имеет то преимущество, что весь материал находится на внешней кромке и отлично подходит для изгиба как в горизонтальном, так и в вертикальном направлениях (при условии горизонтальной балки). Имея это в виду, убедитесь, что плоская поверхность на трубе ориентирована с наибольшим моментом на трубе . Трубка не такая прочная, когда нагружена как алмаз.
Квадратная труба без поворота и с поворотом
Углы
Углы просто не дают хороших лучей. Если у вас возникли проблемы со слишком большим отклонением угла, рассмотрите возможность изменения его формы. Любая форма лучше. Просто сделай это. Вы будете благодарить меня.
Любая форма лучше. Просто сделай это. Вы будете благодарить меня.
Балки с широкими полками
Балки с широкими полками предлагают широкий спектр решений для вашего дизайна. Есть так много разделов на выбор, и часто вам не нужно увеличивать свой рост, чтобы резко изменить силу. 94)
to W16 x 31
Из приведенной выше таблицы видно, что переход от W16 x 31 к W16 x 45 удваивает жесткость при увеличении веса только на 45%. Переход на W16 x 67 удваивает вес и утраивает жесткость.
Переход на W16 x 67 удваивает вес и утраивает жесткость.
Если ваша балка с широкими полками воспринимает нагрузки на слабую ось, подумайте о том, чтобы зафиксировать боковые стороны. Вообще говоря, пластины не должны быть очень тонкими, чтобы оказывать большое влияние.
Увеличить модуль упругости
Увеличить модуль упругости в большинстве случаев сложно. Практически единственный способ увеличить это — изменить материал. Если вы уже используете сталь, вы находитесь на вершине пищевой цепи; нет больше возможностей для улучшения.
В области пластмасс и неметаллических материалов гораздо больше возможностей. Часто переход от стандартного пластика к армированному волокном пластику, стекловолокну или углеродному волокну является хорошим шагом.
Ниже приведен список обычных предметов и их модуль упругости, отсортированный от самого высокого к самому низкому. Если вам нужно свести к минимуму прогиб, рассмотрите материал выше в этом списке.
| Material | Modulus of Elasticity (ksi) | Material | Modulus of Elasticity (ksi) |
| Tungsten | 59465 | Zinc | 12000 |
| Monel | 48000 | Gold | 10733 |
| Inconel | 31000 | Aluminum | 10008 |
| Steel | 29000 | Glass | 7252 – 13053 |
| Nickel Steel | 29000 | Олово | 6817 |
| Никель | 25000 | Хром | 5221 | 21756 | Beryllium Copper | 2611 |
| Gray Cast Iron | 18855 | Wood (Douglas Fir) | 1885 |
| Silicone | 18855 – 26832 | Wood (Oak) | 1595 |
| Nickel Silver | 18500 | Средняя плотность. 0057 0057 | |
| Copper | 16969 | Polycarbonate | 377 |
| Phosphor Bronze | 16824 | PVC | 348 – 595 |
| Titanium Alloy | 16000 | Nylon 6-6 | 290 – 580 |
| Brass | 14794 – 18130 | HDPE | 116 |
| Bronze | 14504 | LDPE | 16 – 65 |
https://mentoredengineer.com/what-to-do-when-your-beam-load-case-isnt-in-a-table/
Добавление других балок для распределения нагрузки
Добавление дополнительных балок к перенос груза может быть эффективным способом минимизации прогиба. Если у нас будет одна балка и мы добавим вторую, наш прогиб сократится вдвое. Превосходно!
Если у нас будет одна балка и мы добавим вторую, наш прогиб сократится вдвое. Превосходно!
Однако, если у нас будет 2 балки и мы перейдем к трем, мы можем получить такое же отклонение, если вы неправильно спланируете расположение балок. Предполагая распределенную нагрузку по ширине балок, центральная балка может принять на себя 1/2 нагрузки, а внешние балки — только по 1/4 нагрузки каждая. Рисунок ниже иллюстрирует этот момент, а уравнения дают нагрузку на каждую балку. 92 или psf), W — ширина конструкции, n — количество балок.
Центральная балка отвечает за 18″ ширины груза, а на концы приходится только 9″ нагрузки. Вот почему добавление еще одного луча таким образом контрпродуктивно.
Теперь, чтобы каждая балка несла равную часть нагрузки, нам нужно сдвинуть внешние балки так, чтобы расстояние от центра внешних балок до конца равнялось половине расстояния между балками. На рисунке ниже показано правильное соотношение.
Равнонагруженные балки
Это работает, потому что каждая секция балки отвечает за 6 дюймов нагрузки с каждой стороны.
В следующий раз, когда будете проезжать под бетонным мостом, посмотрите, как расположены балки.
Подробнее
Лучшее руководство по определению прогиба в балках переменного сечения
Лучшее руководство по решению статически неопределимых балок
Как рассчитать данные балки, если ваш случай не указан в таблице
Резюме
Существует множество способов минимизировать прогиб балки. Глядя на нагрузки, опоры, свойства сечения и материал, вы сможете увидеть, какие варианты доступны для придания жесткости вашей балке.
Как контролировать прогиб балки и плиты
Прогиб балки и плиты необходимо контролировать в соответствии с требованиями эксплуатационной пригодности. В противном случае плиты и балки треснут из-за чрезмерных прогибов.
Кроме того, увеличение прогиба балок и плит может привести к повреждению ненесущих элементов, таких как перегородки, обшивка, соединенная с конструкцией, потолки и т. д.
Поэтому при проектировании требуется контролировать прогиб плит.
Существует несколько методов, которые можно использовать для уменьшения прогиба плиты и балки.
- Увеличьте глубину балок и плиты
- Использование альтернативной нагрузки
- Увеличьте усиление натяжения
- Увеличение Увеличение сжатия
- Увеличение Увеличение сжатия.1766
- Уменьшение пролетов
- Использование предварительного напряжения
Давайте обсудим каждый метод по отдельности.
Увеличение толщины балок и перекрытий
Жесткость конструктивного элемента является ключевым фактором, влияющим на прогиб элемента, поскольку мы не можем контролировать прилагаемые к элементу нагрузки, которые следует учитывать при проектировании.
Нет никакой возможности уменьшить нагрузку на конструкцию, кроме рассмотрения возможности изменения веса ненесущих элементов.
Жесткость элемента конструкции можно увеличить, увеличив глубину элемента.
Жесткость балки Элементы, соответствующие EI/L
Здесь «I» — второй момент площади балки.
I = bh 3 /12
Где «h» — высота секции.
Следовательно, с увеличением высоты сечения увеличивается жесткость и, как следствие, уменьшается прогиб.
Аналогичная концепция типа применяется и для плит.
Использование альтернативной нагрузки
Применяется к элементам конструкции, влияет на прогиб плиты или балки.
Уменьшение динамической нагрузки невозможно ни по какой причине. Необходимо спроектировать конструкцию с учетом нагрузок, возникающих при ее использовании.
Однако мы можем уменьшить собственный вес конструкции.
Альтернативные материалы уменьшают вес конструкции. Например, использование легкого материала вместо тяжелого уменьшит вес конструкции.
Мы можем заменить внутренние перегородки, которые планируется построить из кирпича или блоков, на сухие перегородки.
Кроме того, если нам нужна сплошная перегородка, мы можем использовать пустотелые блоки. Это значительно уменьшит вес конструкции.
Уменьшение ширины сплошных стен также оказывает значительное влияние на прогиб плиты.
Точно так же мы можем изменить собственный вес конструкции.
Увеличить усилие натяжения
На основе приложенных нагрузок мы рассчитали силы изгиба и сдвига элемента конструкции.
Соответственно находим потребность в армировании. Затем проверяем элемент на прогиб.
Если мы увеличим армирование, необходимое для изгиба и сдвига, жесткость балки увеличится.
Как обсуждалось выше, увеличение жесткости уменьшает прогиб плиты и балок.
Увеличенная компрессионная арматура
Когда мы используем компрессионную арматуру там, где она не требуется, это увеличивает жесткость балки.
Кроме того, даже когда мы предоставляем сжатую арматуру в виде минимум стали , это также увеличивает жесткость балки или плиты.
Увеличение ширины балки
Существуют ограничения на увеличение глубины балки для управления отклонением.
Если мы не сможем увеличить глубину, прогиб будет больше. В таких ситуациях нам нужно обеспечить больше армирования, чтобы контролировать прогиб, а также расчетный момент и поперечные силы.
Чтобы получить больше подкреплений, нам нужно достаточно места. Это может быть достигнуто за счет расширения луча. Так что больше арматуры можно разместить.
Уменьшить диапазон
Это довольно интересная тема для обсуждения.
Нам действительно нужно уменьшить пролет, чтобы контролировать отклонение?
Это должно решаться исходя из планировки этажа и других аспектов.
Уменьшение пролета уменьшит усиление балки и прогибы.
Уменьшение диапазона не применимо в большинстве случаев.
Использование Предварительное напряжение
Увеличение пролета балки или плиты приводит к увеличению высоты элементов. За пределами определенного уровня увеличивать толщину плиты экономически нецелесообразно.
Пролет плиты более 6-7 м не может быть более экономичным, если мы строим ее как обычную железобетонную плиту.
Поэтому в конструкции плит используются такие опции, как методы пост-натяжения.
При использовании методов предварительного напряжения прогиб значительно уменьшается.
Изгиб усиленных поврежденных стальных балок с использованием полимерных листов, армированных углеродным волокном. Замена изношенных конструкций часто невозможна, а их ремонт с использованием обычных материалов неэффективен с точки зрения затрат, социальных и экологических последствий и долговечности. Некоторые конструкции всегда эксплуатируются в условиях перегрузок, при которых эксплуатационная нагрузка превышает 70 % предельной нагрузки конструкции. В последние годы новым методом ремонта поврежденных стальных конструкций стало использование листов из полимера, армированного углеродным волокном (CFRP). Листы из углепластика обладают уникальными свойствами материала и механическими свойствами, такими как низкий собственный вес, высокая прочность и жесткость, а также хорошая долговечность.
 Листы углепластика могут быть приклеены эпоксидной смолой к натянутой поверхности поврежденных элементов для восстановления или повышения предельной несущей способности стальных элементов. В последние годы было проведено множество исследований по ремонту и модернизации стальных элементов с использованием материалов из армированного волокном полимера (FRP) на эпоксидной основе. Коломби и Поджи 1 исследовал экспериментальную и численную программу, чтобы охарактеризовать статическое поведение армирования стальной балки пултрузионными полосами углепластика. Основной целью экспериментальной программы была оценка механизма передачи усилия, увеличение несущей способности и жесткости на изгиб. Использование пултрузионных полос углепластика также позволило нам проверить различные аналитические и численные модели для статического анализа армированных балок. Bocciarelli 2 представил простой подход к оценке реакции статически определяемых стальных балок, армированных полимерными пластинами, армированными углеродным волокном, в упруго-пластическом режиме.
Листы углепластика могут быть приклеены эпоксидной смолой к натянутой поверхности поврежденных элементов для восстановления или повышения предельной несущей способности стальных элементов. В последние годы было проведено множество исследований по ремонту и модернизации стальных элементов с использованием материалов из армированного волокном полимера (FRP) на эпоксидной основе. Коломби и Поджи 1 исследовал экспериментальную и численную программу, чтобы охарактеризовать статическое поведение армирования стальной балки пултрузионными полосами углепластика. Основной целью экспериментальной программы была оценка механизма передачи усилия, увеличение несущей способности и жесткости на изгиб. Использование пултрузионных полос углепластика также позволило нам проверить различные аналитические и численные модели для статического анализа армированных балок. Bocciarelli 2 представил простой подход к оценке реакции статически определяемых стальных балок, армированных полимерными пластинами, армированными углеродным волокном, в упруго-пластическом режиме. Предложенное решение было действительным только на определенном расстоянии от концов арматуры, где на реакцию конструкции не влияли локальные эффекты из-за резкого прекращения арматуры. Сугиура и др. 3 представил применимость адгезии углепластика для ремонта элементов из коррозионной стали. Поведение углепластика при отслаивании было исследовано экспериментально при испытаниях на растяжение и изгиб стальных элементов с приклеенным углепластиком. На основании результатов эксперимента была дана расчетная методика определения необходимого объема и длины склеивания углепластика и проверки отслаивания углепластика от стали. Ву и др. 4 исследовали усталостные характеристики стальных балок с искусственными надрезами, усиленных четырьмя различными типами материалов, испытанных при эквивалентной жесткости на растяжение. Результаты испытаний показали, что применение композитной пластины, армированной волокном, может не только задержать зарождение трещины, уменьшить скорость роста трещины и продлить усталостную долговечность, но также уменьшить спад жесткости и остаточный прогиб.
Предложенное решение было действительным только на определенном расстоянии от концов арматуры, где на реакцию конструкции не влияли локальные эффекты из-за резкого прекращения арматуры. Сугиура и др. 3 представил применимость адгезии углепластика для ремонта элементов из коррозионной стали. Поведение углепластика при отслаивании было исследовано экспериментально при испытаниях на растяжение и изгиб стальных элементов с приклеенным углепластиком. На основании результатов эксперимента была дана расчетная методика определения необходимого объема и длины склеивания углепластика и проверки отслаивания углепластика от стали. Ву и др. 4 исследовали усталостные характеристики стальных балок с искусственными надрезами, усиленных четырьмя различными типами материалов, испытанных при эквивалентной жесткости на растяжение. Результаты испытаний показали, что применение композитной пластины, армированной волокном, может не только задержать зарождение трещины, уменьшить скорость роста трещины и продлить усталостную долговечность, но также уменьшить спад жесткости и остаточный прогиб. Ю и др. 5 исследовали эффективность пластин из углепластика в продлении срока службы стальных конструкций. Экспериментальные результаты показали, что заплатки из углепластика могут эффективно замедлять рост трещин, продлевая усталостную долговечность, а позднее упрочнение при более высоком уровне повреждения, как правило, приводит к более значительному увеличению оставшейся усталостной долговечности. Bocciarelli и Colombi 6 представили простой подход к расчету упругопластического отклика стальной балки, армированной пластиной углепластика. Основной вывод заключался в том, что усиленный профиль должен был достичь большой кривизны, чтобы развить сопротивление предельному изгибающему моменту, и по этой причине необходимо было использовать ребра жесткости, чтобы избежать проблем с локальной нестабильностью как в стенке, так и в полках. Хмидан и др. 7 сообщили о поведении вершин трещины широкополочных стальных балок W4 × 13, усиленных листами из углепластика.
Ю и др. 5 исследовали эффективность пластин из углепластика в продлении срока службы стальных конструкций. Экспериментальные результаты показали, что заплатки из углепластика могут эффективно замедлять рост трещин, продлевая усталостную долговечность, а позднее упрочнение при более высоком уровне повреждения, как правило, приводит к более значительному увеличению оставшейся усталостной долговечности. Bocciarelli и Colombi 6 представили простой подход к расчету упругопластического отклика стальной балки, армированной пластиной углепластика. Основной вывод заключался в том, что усиленный профиль должен был достичь большой кривизны, чтобы развить сопротивление предельному изгибающему моменту, и по этой причине необходимо было использовать ребра жесткости, чтобы избежать проблем с локальной нестабильностью как в стенке, так и в полках. Хмидан и др. 7 сообщили о поведении вершин трещины широкополочных стальных балок W4 × 13, усиленных листами из углепластика. Результаты показали, что свойства углепластика, такие как количество слоев и модуль, повлияли на пластичность вершины трещины усиленных балок. Коломби и др. 8 проведены испытания на усталость стальных пластин с трещинами (образцы с одной кромкой), армированные полосами, приклеенными к одной стороне. Результаты показали, что материалы из углепластика, связанные вокруг области наконечника, увеличили усталостную долговечность поврежденных стальных элементов примерно в 3 раза. Гафури и Мотавалли 9 экспериментально и численно исследовал потерю устойчивости при поперечном кручении (LTB) стальных балок, усиленных нормальным модулем (NM) ламинатов углепластика. Было показано, что увеличение предварительного напряжения в ламинате углепластика не всегда увеличивает прочность на изгиб модернизированных тонких стальных балок. Ван и др. 10 использовали листы углепластика и предварительно напряженные листы углепластика для ремонта сталежелезобетонных композитных балок.
Результаты показали, что свойства углепластика, такие как количество слоев и модуль, повлияли на пластичность вершины трещины усиленных балок. Коломби и др. 8 проведены испытания на усталость стальных пластин с трещинами (образцы с одной кромкой), армированные полосами, приклеенными к одной стороне. Результаты показали, что материалы из углепластика, связанные вокруг области наконечника, увеличили усталостную долговечность поврежденных стальных элементов примерно в 3 раза. Гафури и Мотавалли 9 экспериментально и численно исследовал потерю устойчивости при поперечном кручении (LTB) стальных балок, усиленных нормальным модулем (NM) ламинатов углепластика. Было показано, что увеличение предварительного напряжения в ламинате углепластика не всегда увеличивает прочность на изгиб модернизированных тонких стальных балок. Ван и др. 10 использовали листы углепластика и предварительно напряженные листы углепластика для ремонта сталежелезобетонных композитных балок. Результаты показали, что листы углепластика не оказали существенного влияния на предел текучести усиленных композитных балок, но оказали значительное влияние на предельные нагрузки. Коломби и Фава 11 исследовал девять стальных балок с трещинами, усиленных углепластиком, под действием усталостной нагрузки. Экспериментальные результаты показали наличие зоны отслоения между арматурой и стальной подложкой в месте расположения трещины. Дебондинг явно отрицательно сказался на эффективности армирования. Голами и др. 12 оценили характеристики стальных балок двутаврового сечения, усиленных пултрузионными пластинами из углепластика на нижней полке, после воздействия различных условий, включая естественный тропический климат, циклы влажный/сухой, обычную воду, соленую воду и кислый раствор. Исследование показало, что клеевой слой является критически важной частью, а производительность системы напрямую связана с поведением и пластичностью всех усиленных балок, которые увеличиваются после воздействия.
Результаты показали, что листы углепластика не оказали существенного влияния на предел текучести усиленных композитных балок, но оказали значительное влияние на предельные нагрузки. Коломби и Фава 11 исследовал девять стальных балок с трещинами, усиленных углепластиком, под действием усталостной нагрузки. Экспериментальные результаты показали наличие зоны отслоения между арматурой и стальной подложкой в месте расположения трещины. Дебондинг явно отрицательно сказался на эффективности армирования. Голами и др. 12 оценили характеристики стальных балок двутаврового сечения, усиленных пултрузионными пластинами из углепластика на нижней полке, после воздействия различных условий, включая естественный тропический климат, циклы влажный/сухой, обычную воду, соленую воду и кислый раствор. Исследование показало, что клеевой слой является критически важной частью, а производительность системы напрямую связана с поведением и пластичностью всех усиленных балок, которые увеличиваются после воздействия. Альджабар и др. 13 расширил современные знания об упрочнении углепластиком стальных элементов при усталостной нагрузке растяжением на случай смешанной нагрузки растяжения и сдвига. Явление сдвига было выявлено для описания влияния смешанного режима с точки зрения распространения трещины. Коэффициент модификации смешанного режима был разработан для оценки усталостной долговечности стальных пластин, упрочненных углепластиком, с наклонными начальными трещинами. Ху и др. 14 предлагаемые руководства и программы расчета на усталость для стальных конструкций, усиленных углепластиком. Было показано, что углепластик эффективен для укрепления стальных конструкций при усталости. Углепластик может продлить усталостную долговечность при определенных условиях нагрузки или увеличить допустимый диапазон напряжений, когда требуется определенная усталостная долговечность. Юсефи и др. 15 представлены результаты экспериментальных и численных исследований по анализу разрушения и структурного поведения стальных двутавровых балок с надрезом, армированных склеенными пластинами из углепластика, под действием статической нагрузки.
Альджабар и др. 13 расширил современные знания об упрочнении углепластиком стальных элементов при усталостной нагрузке растяжением на случай смешанной нагрузки растяжения и сдвига. Явление сдвига было выявлено для описания влияния смешанного режима с точки зрения распространения трещины. Коэффициент модификации смешанного режима был разработан для оценки усталостной долговечности стальных пластин, упрочненных углепластиком, с наклонными начальными трещинами. Ху и др. 14 предлагаемые руководства и программы расчета на усталость для стальных конструкций, усиленных углепластиком. Было показано, что углепластик эффективен для укрепления стальных конструкций при усталости. Углепластик может продлить усталостную долговечность при определенных условиях нагрузки или увеличить допустимый диапазон напряжений, когда требуется определенная усталостная долговечность. Юсефи и др. 15 представлены результаты экспериментальных и численных исследований по анализу разрушения и структурного поведения стальных двутавровых балок с надрезом, армированных склеенными пластинами из углепластика, под действием статической нагрузки. Результаты показали, что режимы отказа углепластика при укреплении дефектных стальных двутавровых балок включали отслоение концов, отслоение при нагрузке ниже точки, расщепление и расслоение. Боччарелли и др. 16 предложены аналитические и численные модели упругохрупких клеев для оценки распределения напряжений и деформаций в арматуре при заданной длине трещины. Экспериментальные результаты рассматривались как подтверждение предложенных численных и аналитических методов. Результаты расчетов хорошо согласуются с экспериментальными результатами. Мартинелли и др. 17 изучали характеристики сцепления композитов из армированного волокном полимера (FRP), приклеенных к стальным подложкам, с помощью экспериментального и численного моделирования. Результаты показали, что включенная связь связь-скольжение в предложенной численной модели оказала значительное влияние на численные результаты. Поэтому было важно определить реалистичные отношения адгезии к скольжению с различными типами клея и условиями отверждения (путем проведения экспериментальных испытаний).
Результаты показали, что режимы отказа углепластика при укреплении дефектных стальных двутавровых балок включали отслоение концов, отслоение при нагрузке ниже точки, расщепление и расслоение. Боччарелли и др. 16 предложены аналитические и численные модели упругохрупких клеев для оценки распределения напряжений и деформаций в арматуре при заданной длине трещины. Экспериментальные результаты рассматривались как подтверждение предложенных численных и аналитических методов. Результаты расчетов хорошо согласуются с экспериментальными результатами. Мартинелли и др. 17 изучали характеристики сцепления композитов из армированного волокном полимера (FRP), приклеенных к стальным подложкам, с помощью экспериментального и численного моделирования. Результаты показали, что включенная связь связь-скольжение в предложенной численной модели оказала значительное влияние на численные результаты. Поэтому было важно определить реалистичные отношения адгезии к скольжению с различными типами клея и условиями отверждения (путем проведения экспериментальных испытаний). Чжан и др. 18 исследовал поведение на изгиб корродированных стальных балок, усиленных пластинами из углепластика. Было исследовано влияние уровней коррозии и предварительного напряжения на изгибную способность, режимы разрушения и межфазное напряжение. Результаты показали, что режим разрушения корродированных балок был перелом углепластиковой плиты после разрушения при сдвиге интерфейса на середине пролета, а место перелома углепластиковой плиты было в основном в точке нагрузки. Шероховатая поверхность корродированной стали может повысить эффективность передачи напряжения на границе раздела, тем самым увеличивая эффективную длину связи на границе раздела. Касательное напряжение было сосредоточено в основном на конце пластины из углепластика, и пиковое значение появилось в точке нагрузки. По сравнению с эталонной балкой предел прочности на изгиб корродированной балки, усиленной пластиной из углепластика с уровнем предварительного напряжения 15%, увеличился на 21%, а коэффициент использования пластин из углепластика составил до 71,59.
Чжан и др. 18 исследовал поведение на изгиб корродированных стальных балок, усиленных пластинами из углепластика. Было исследовано влияние уровней коррозии и предварительного напряжения на изгибную способность, режимы разрушения и межфазное напряжение. Результаты показали, что режим разрушения корродированных балок был перелом углепластиковой плиты после разрушения при сдвиге интерфейса на середине пролета, а место перелома углепластиковой плиты было в основном в точке нагрузки. Шероховатая поверхность корродированной стали может повысить эффективность передачи напряжения на границе раздела, тем самым увеличивая эффективную длину связи на границе раздела. Касательное напряжение было сосредоточено в основном на конце пластины из углепластика, и пиковое значение появилось в точке нагрузки. По сравнению с эталонной балкой предел прочности на изгиб корродированной балки, усиленной пластиной из углепластика с уровнем предварительного напряжения 15%, увеличился на 21%, а коэффициент использования пластин из углепластика составил до 71,59. %. Ху и Фэн 19 представили метод проектирования поврежденных стальных конструкций, армированных углепластиком, и разработали программу проектирования. Результаты показали, что армирование углепластиком может улучшить срок службы при определенном диапазоне напряжений и допустимом диапазоне напряжений при условии достижения целевого срока службы. Денг и др. 20 изучали усталостные характеристики при изгибе поврежденных стальных балок, усиленных пластинами брэгговской решетки из армированного углеродным волокном пластика и оптического волокна (CFRP-OFBG). Результаты испытаний показали, что армирование пластин CFRP-OFBG эффективно снижает скорость роста усталостных трещин поврежденных стальных балок и увеличивает усталостную долговечность поврежденных стальных балок на 22,46%. Анализ и результаты испытаний показали, что минимальная ошибка между расчетным значением модели прогнозирования жизни и тестовым значением составила - 24,13%, а максимальная ошибка составила - 5,61%.
%. Ху и Фэн 19 представили метод проектирования поврежденных стальных конструкций, армированных углепластиком, и разработали программу проектирования. Результаты показали, что армирование углепластиком может улучшить срок службы при определенном диапазоне напряжений и допустимом диапазоне напряжений при условии достижения целевого срока службы. Денг и др. 20 изучали усталостные характеристики при изгибе поврежденных стальных балок, усиленных пластинами брэгговской решетки из армированного углеродным волокном пластика и оптического волокна (CFRP-OFBG). Результаты испытаний показали, что армирование пластин CFRP-OFBG эффективно снижает скорость роста усталостных трещин поврежденных стальных балок и увеличивает усталостную долговечность поврежденных стальных балок на 22,46%. Анализ и результаты испытаний показали, что минимальная ошибка между расчетным значением модели прогнозирования жизни и тестовым значением составила - 24,13%, а максимальная ошибка составила - 5,61%.
Однако в нескольких исследованиях обсуждалось использование склеенных эпоксидной смолой пластин или листов для усиления стальных балок, имеющих растянутую полку или дефект стенки, такой как выемка, особенно при перегрузке этих стальных балок. В этой статье растяжения фланца или стены частично наблюдалось в середине пролета стальных балок. Листы углепластика были приклеены к нижней стороне полки стальных балок для восстановления несущей способности и упругой жесткости, а затем к этим стальным балкам была применена статическая нагрузка или перегрузка. Было исследовано влияние слоев листа углепластика, уровень повреждения стальной балки и число перегрузок.
Экспериментальная программа
Всего было изготовлено семь стальных балок с искусственными повреждениями. Стальные балки были изготовлены из стали стандарта Китая I20A, глубина которой составляла 200 мм, ширина полки 100 мм, толщина полки и стенки 11,4 мм и 7 мм соответственно, а площадь сечение было 3550 мм 2 . Стальные профили были разрезаны на балки длиной 1,9 м, и в середине пролета стальных балок были разрезаны четыре различных уровня повреждения: 100% потеря растянутой полки и 15%, 28%, 40% потеря натянутой стенки, как показано на Рис. 1а. Было проведено испытание на растяжение двутавровой стали. Предел текучести и предел прочности при растяжении двутавровой стали составили 265 МПа и 442 МПа соответственно. В качестве внешних систем укрепления, выбранных для этого испытания, использовались высокопрочные листы углепластика. Толщина листов углепластика составляла 0,167 мм, ширина — 60 мм, а длина — 1500 мм. Испытание на растяжение листов углепластика было проведено, как описано в ссылке 9.2179 21 , а средний предел прочности при растяжении составил 3456 МПа; модуль упругости 258 ГПа. Клей на основе смолы, используемый для приклеивания листа углепластика, был подобран к листу углепластика, и его прочность на сдвиг составляла 19,4. Лист углепластика был приклеен таким же образом, как описано в ссылке 21 .
Стальные профили были разрезаны на балки длиной 1,9 м, и в середине пролета стальных балок были разрезаны четыре различных уровня повреждения: 100% потеря растянутой полки и 15%, 28%, 40% потеря натянутой стенки, как показано на Рис. 1а. Было проведено испытание на растяжение двутавровой стали. Предел текучести и предел прочности при растяжении двутавровой стали составили 265 МПа и 442 МПа соответственно. В качестве внешних систем укрепления, выбранных для этого испытания, использовались высокопрочные листы углепластика. Толщина листов углепластика составляла 0,167 мм, ширина — 60 мм, а длина — 1500 мм. Испытание на растяжение листов углепластика было проведено, как описано в ссылке 9.2179 21 , а средний предел прочности при растяжении составил 3456 МПа; модуль упругости 258 ГПа. Клей на основе смолы, используемый для приклеивания листа углепластика, был подобран к листу углепластика, и его прочность на сдвиг составляла 19,4. Лист углепластика был приклеен таким же образом, как описано в ссылке 21 . Листы углепластика были приклеены к нижней части натяжной полки, а затем на концах листов углепластика были приклеены U-образные обручи, чтобы обеспечить возможность крепления листов углепластика к стальным балкам, как показано на рис. 1b. Подробные параметры стальных балок приведены в таблице 1.
Листы углепластика были приклеены к нижней части натяжной полки, а затем на концах листов углепластика были приклеены U-образные обручи, чтобы обеспечить возможность крепления листов углепластика к стальным балкам, как показано на рис. 1b. Подробные параметры стальных балок приведены в таблице 1.
Рисунок 1
Подготовка образцов.
Изображение в полный размер
Таблица 1 Тестовая матрица и результаты.
Полноразмерный стол
Экспериментальная установка
Стальные балки были нагружены на четырехточечный изгиб с расстоянием 500 мм между двумя сосредоточенными точечными нагрузками и с двумя равными пролетами сдвига по 650 мм, как показано на рис. 2. Резиновые опоры использовались на опорах. Нагрузка была приложена по всей ширине верхней полки стальной балки с помощью траверсы, которая была помещена между резиновыми опорами на верхней части стальной балки. Испытания на четырехточечный изгиб проводились с использованием гидравлических домкратов, как показано на рис. 2а. Процесс перегрузки, необходимый для установки минимальной нагрузки (стр. мин ), максимальная нагрузка (P макс ) и количество перегрузок. Затем стальные балки будут вращаться в этом диапазоне. Продолжительность одного цикла составляла примерно 6 мин, как показано на рис. 3. После перегрузки стальные балки подвергались нагружению до разрушения. Чтобы наблюдать за поведением исследуемых стальных балок, в нужных местах измерялись деформации, нагрузки и прогибы. Деформации измерялись тензодатчиками электрического сопротивления, которые размещались на верхней части верхней полки, нижней полке или стенке рядом с надрезом и в середине пролета листов углепластика, как показано на рис. 2b. Пять измерителей перемещения были установлены на конце и в середине пролета балок, и эти измерители использовались для измерения вертикального отклонения, как показано на рис. 2а.
2а. Процесс перегрузки, необходимый для установки минимальной нагрузки (стр. мин ), максимальная нагрузка (P макс ) и количество перегрузок. Затем стальные балки будут вращаться в этом диапазоне. Продолжительность одного цикла составляла примерно 6 мин, как показано на рис. 3. После перегрузки стальные балки подвергались нагружению до разрушения. Чтобы наблюдать за поведением исследуемых стальных балок, в нужных местах измерялись деформации, нагрузки и прогибы. Деформации измерялись тензодатчиками электрического сопротивления, которые размещались на верхней части верхней полки, нижней полке или стенке рядом с надрезом и в середине пролета листов углепластика, как показано на рис. 2b. Пять измерителей перемещения были установлены на конце и в середине пролета балок, и эти измерители использовались для измерения вертикального отклонения, как показано на рис. 2а.
Рисунок 2
Схема расположения измерителей перемещения и тензодатчиков на балке.
Полноразмерное изображение
Рисунок 3
Процесс перегрузки.
Изображение в натуральную величину
Результаты испытаний и обсуждение
Виды разрушения
Как указывалось ранее, стальные балки, усиленные приклеенными листами углепластика, могут демонстрировать четыре различных режима разрушения: деформация нижней полки; Разрыв углепластикового листа с повреждением полотна; Отклеивание листа углепластика с повреждением полотна; и разрыв листа углепластика с повреждением нижнего фланца.
Разрыв углепластика с повреждением стенки был доминирующим видом разрушения стальных балок без перегрузки. Разрыв листов углепластика был внезапным, и не было никаких признаков нарушения связи между листом углепластика и стальным фланцем в образцах FSB1 и FSB4. Поскольку степень повреждения образца ФСБ4 была небольшой, повреждена была только нижняя полка. Вид отказа SB0 заключался в том, что нижний фланец был поврежден, потому что лист углепластика не был приклеен.
Виды отказа стальных балок при перегрузке: разрыв листа углепластика с деформацией стенки и отслоение листа углепластика с деформацией стенки. На образцах ФСБ2 и ФСБ3 появилось отслоение углепластика. Разрыв углепластика появился в образцах ФСБ5 и ФСБ6. Все стенки стальных балок были повреждены при отслоении или разрыве листов углепластика.
Результаты экспериментов показали, что окончательное разрушение обычно сопровождалось большим прогибом и деформацией стенки или нижней полки. Как стенка, так и полки стальных балок поддались, как показано на рис. 4.
Рисунок 4
Режимы разрушения испытательных образцов
Изображение полного размера
Кривые нагрузка-прогиб на циклической стадии
На рис. 5 показаны кривые нагрузка-прогиб на циклической стадии. В процессе разгрузки ФСБ2, ФСБ3, ФСБ5 и ФСБ6 после 100 циклов кривые не снижались прямо в соответствии с исходными кривыми. Это условие показало, что амплитуда перегрузки превысила критическое значение упругой стадии стальной балки, и все стальные балки находились в упругопластической стадии. Кривые нагрузка-прогиб FSB2 и FSB3 были более гладкими, чем кривые нагрузка-прогиб FSB5 и FSB6 из-за больших надрезов FSB5 и FSB6. Способность восстановления FSB5 и FSB6 была снижена, что привело к неровной кривой.
Кривые нагрузка-прогиб FSB2 и FSB3 были более гладкими, чем кривые нагрузка-прогиб FSB5 и FSB6 из-за больших надрезов FSB5 и FSB6. Способность восстановления FSB5 и FSB6 была снижена, что привело к неровной кривой.
Рисунок 5
Зависимость нагрузки от деформации образцов после 100 циклов.
Изображение с полным размером
Влияние листа углепластика
На рис. 6а показана кривая нагрузка-прогиб стальных балок со 100% повреждением полки. SB0 представлял собой неармированную стальную балку, а FSB4 представлял собой стальную балку, усиленную одним слоем листа углепластика. Оба образца подвергались только статической нагрузке. Предел текучести FSB4 составил 137 кН, что на 10 % больше, чем предел текучести SB0, а упругая жесткость на 14,5 % больше, чем упругая жесткость SB0. Предельная нагрузка ФСБ4 составила 195,46 кН, что на 10,3 % превышает предельную нагрузку SB0. Результаты показывают, что лист углепластика с эпоксидной связкой значительно увеличил предел текучести, предельную несущую способность и упругую жесткость стальной балки.
Рисунок 6
Кривые нагрузка-прогиб усиленных стальных балок.
Изображение в полный размер
Влияние степени повреждения
На рисунке 6b показана кривая нагрузка-прогиб стальных балок с различными уровнями повреждения, обе из которых были усилены одним слоем углепластикового листа. Уровни повреждения 100% потери напряженной полки и 28% потери стенки были сокращены в середине пролета стальных балок в FSB4 и FSB1, соответственно. Оба образца подвергались только статической нагрузке. Когда нагрузка не достигла 65% Pu, упругая жесткость двух стальных балок была одинаковой. Нагрузка текучести и предельная нагрузка FSB4 были на 68,3% и 73,8% больше, чем нагрузка текучести и предельная нагрузка FSB1, а упругая жесткость была на 13,5% больше, чем упругая жесткость FSB1. Нагрузка текучести и предельная нагрузка, очевидно, изменились в результате уровня повреждения. По сравнению с нагрузкой текучести и предельной нагрузкой уровень повреждения не оказал существенного влияния на упругую жесткость.
Влияние перегрузки номер
На рисунке 6c показана кривая нагрузка-прогиб стальных балок со 100% повреждением полки после перегрузки. FSB4 представлял собой стальную балку только со статической нагрузкой. FSB2 представлял собой стальную балку с 100-кратной перегрузкой по 0,7 Pu и полностью статической нагрузкой. Когда нагрузка не достигала 60 кН, упругая жесткость двух стальных балок была одинаковой. Предел текучести FSB2 составил 148,9 кН, что на 8,7 % больше, чем предел текучести FSB4, а упругая жесткость на 24,5 % больше, чем упругая жесткость FSB4. Предельная нагрузка FSB2 составила 185,08 кН, что на 5,3 % меньше предельной нагрузки FSB4. Результаты показывают, что перегрузка может повлиять на предел текучести и упругую жесткость. Предел текучести и упругая жесткость увеличивались с увеличением числа перегрузок из-за наклепа стали, но предельная нагрузка уменьшалась.
Влияние уровня повреждения после перегрузки
На рисунке 6d показана кривая нагрузка-прогиб стальных балок с различными уровнями повреждения после перегрузки. Уровни повреждения 100% потери натяжной полки и 15% потери стенки были сокращены в середине пролета стальных балок в FSB2 и FSB3, соответственно. Стальные балки подвергались 100-кратной перегрузке 0,7 Pu и полностью статической нагрузке. Когда нагрузка не достигла 75% Pu, упругая жесткость двух стальных балок была одинаковой. Предел текучести FSB2 был на 24,1% больше, чем предел текучести FSB3. Предельная нагрузка FSB2 была на 32% больше, чем предельная нагрузка FSB3. Было показано, что предел текучести и предельная несущая способность усиленных стальных балок изменяются в результате уровней повреждений после перегрузки.
Уровни повреждения 100% потери натяжной полки и 15% потери стенки были сокращены в середине пролета стальных балок в FSB2 и FSB3, соответственно. Стальные балки подвергались 100-кратной перегрузке 0,7 Pu и полностью статической нагрузке. Когда нагрузка не достигла 75% Pu, упругая жесткость двух стальных балок была одинаковой. Предел текучести FSB2 был на 24,1% больше, чем предел текучести FSB3. Предельная нагрузка FSB2 была на 32% больше, чем предельная нагрузка FSB3. Было показано, что предел текучести и предельная несущая способность усиленных стальных балок изменяются в результате уровней повреждений после перегрузки.
Влияние количества слоев углепластикового листа после перегрузки
На рисунке 6e показана кривая нагрузка-прогиб стальных балок с 40%-ным повреждением стенки, усиленных различным количеством слоев углепластиковых листов после перегрузки. FSB5 был отремонтирован с одним слоем листа углепластика, а FSB6 был отремонтирован с двумя слоями листов углепластика. Стальные балки подвергались 100-кратной перегрузке 0,7 Pu и полностью статической нагрузке. Предел текучести FSB6 составил 78,6 кН, что на 38,4 % больше, чем предел текучести FSB5, а упругая жесткость составила 36,9 кН.% больше упругой жесткости FSB5. Предельная нагрузка FSB6 составила 94,32 кН, что на 24,9 % больше предельной нагрузки FSB5. Результаты показывают, что увеличение слоев листа углепластика может улучшить предел текучести, упругую жесткость и предельную несущую способность стальных балок после перегрузки.
Стальные балки подвергались 100-кратной перегрузке 0,7 Pu и полностью статической нагрузке. Предел текучести FSB6 составил 78,6 кН, что на 38,4 % больше, чем предел текучести FSB5, а упругая жесткость составила 36,9 кН.% больше упругой жесткости FSB5. Предельная нагрузка FSB6 составила 94,32 кН, что на 24,9 % больше предельной нагрузки FSB5. Результаты показывают, что увеличение слоев листа углепластика может улучшить предел текучести, упругую жесткость и предельную несущую способность стальных балок после перегрузки.
Кривые нагрузка-прогиб до и после перегрузки
На рисунке 7 показаны кривые нагрузка-прогиб при первом и последнем нагружении FSB2, FSB3, FSB5 и FSB6. После перегрузки упругая жесткость всех стальных балок увеличилась. Упругая жесткость FSB2, FSB3, FSB5 и FSB6 последней нагрузки была на 31,1%, 23,2%, 14% и 15% больше, чем упругая жесткость первой нагрузки, соответственно. Упругая жесткость стальных балок с большими уровнями повреждений увеличилась меньше, чем упругая жесткость стальных балок с малыми уровнями повреждений. Показано, что упругая жесткость стальных балок может увеличиваться после перегрузок за счет наклепа стали. Однако влияние холодного упрочнения на стальную балку уменьшалось с увеличением уровня повреждения стальной балки.
Показано, что упругая жесткость стальных балок может увеличиваться после перегрузок за счет наклепа стали. Однако влияние холодного упрочнения на стальную балку уменьшалось с увеличением уровня повреждения стальной балки.
Рисунок 7
Кривая нагрузка-прогиб усиленных стальных балок под нагрузкой.
Изображение полного размера
Кривые деформации
В начале испытаний кривые деформации усиленной стальной балки были линейными, как показано на рис. 8. Линии представляют деформации в области растяжения стальные балки, область сжатия стальных балок и листов углепластика. Растяжимая область стальных балок начала уступать примерно от 30 до 35% от предельной нагрузки. Однако из-за эффекта наклепа образец ФСБ2 выдержал 58 % предельной нагрузки. После текучести эффективность листов углепластика была намного выше. Деформации в области растяжения усиленных стальных балок значительно уменьшились. При том же уровне нагрузки деформации стальной балки с большим уровнем повреждения были больше, чем деформации других стальных балок. Когда нагрузка достигла примерно 70-85% предельной нагрузки, область сжатия стальных балок начала поддаваться. Затем сжимающие деформации в области сжатия стальных балок стали нелинейными. Деформации листов углепластика составляли примерно 10 000 мкЕ после статической нагрузки и примерно 7500 мкЕ после перегрузки. Результаты показывают, что уровни повреждения стальных балок могут повлиять на деформации усиленных стальных балок. После перегрузки предел текучести стальной балки увеличился, но перегрузка не оказала существенного влияния на стальные балки с большими уровнями повреждений. Количество слоев листового углепластика может влиять на предельную нагрузку и предельную несущую способность. Деформации листов углепластика будут уменьшаться из-за перегрузки.
Когда нагрузка достигла примерно 70-85% предельной нагрузки, область сжатия стальных балок начала поддаваться. Затем сжимающие деформации в области сжатия стальных балок стали нелинейными. Деформации листов углепластика составляли примерно 10 000 мкЕ после статической нагрузки и примерно 7500 мкЕ после перегрузки. Результаты показывают, что уровни повреждения стальных балок могут повлиять на деформации усиленных стальных балок. После перегрузки предел текучести стальной балки увеличился, но перегрузка не оказала существенного влияния на стальные балки с большими уровнями повреждений. Количество слоев листового углепластика может влиять на предельную нагрузку и предельную несущую способность. Деформации листов углепластика будут уменьшаться из-за перегрузки.
Рисунок 8
Кривые нагрузки-деформации усиленных стальных балок.
Полноразмерное изображение
Численный анализ
Разработка модели
КЭ анализ был выполнен с помощью ABAQUS. Все стальные балки были смоделированы. Геометрия и расположение нагрузки модели были приняты в соответствии с испытанными балками. Торцевая опора была смоделирована с помощью роликовой опоры, сдерживающей вертикальное перемещение балки. Допускался продольный перенос балки. Галстук ограничение было использовано для связей между стальной балкой и листом углепластика, потому что скольжение интерфейса не учитывалось в этой модели.
Все стальные балки были смоделированы. Геометрия и расположение нагрузки модели были приняты в соответствии с испытанными балками. Торцевая опора была смоделирована с помощью роликовой опоры, сдерживающей вертикальное перемещение балки. Допускался продольный перенос балки. Галстук ограничение было использовано для связей между стальной балкой и листом углепластика, потому что скольжение интерфейса не учитывалось в этой модели.
Стальная балка была смоделирована как конечный элемент C3D8R (восьмиузловые твердотельные конечные элементы с уменьшенной интеграцией). Лист углепластика был смоделирован как конечный элемент SR4 (четырехузловые конечные элементы оболочки с уменьшенной интеграцией). Размеры элементов были приняты на основе исследования дискретизации сетки. Сетка конечных элементов, использованная для анализа, показана на рис. 9. В анализе методом конечных элементов использовалось 4 модели повреждений, как показано на рис. 10.
Рисунок 9
Генерация сетки. {{\text{2}}} + B\varepsilon _{{\text{t}}} + C} \hfill & {(\varepsilon _{{{\text{te}}}} < \varepsilon _{t} \le \varepsilon _{{{\text{te1}}}} )} \hfill \\ {f_{{{ \text{ty}}}} } \hfill & {(\varepsilon _{{{\text{te1}}}} < \varepsilon _{t} \le \varepsilon _{{{\text{te2}}} } )} \hfill \\ {f_{{{\text{ty}}}} \left[ {{\text{1}} + {\text{0}}{\text{.6}}\frac{ {\varepsilon _{{\text{t}}} - \varepsilon _{{{\text{e2}}}} }}{{\varepsilon _{{{\text{e3}}}} - \varepsilon _ {{{\text{e2}}}} }}} \right]} \hfill & {(\varepsilon _{{{\text{te2}}}}} < \varepsilon _{{\text{t}}} \le \varepsilon _{{{\text{te3}}}} )} \hfill \\ {{\text{1}}{\text{.6}}f_{{{\text{ty}}}} } \hfill & {(\varepsilon _ {{\text{t}}} > \varepsilon _{{{\text{te3}}}} )} \hfill \\ \end{массив} } \right. $$ 9{{2}} — B\varepsilon_{{{\text{te}}}}\, \(\varepsilon_{{{\text{te}}}} = 0,8f_{{{\text{ty}} }} /E_{{\text{t}}}\),\(\varepsilon_{{{\text{te1}}}} = {1}.{5}\varepsilon_{{{\text{te}} }}\), \(\varepsilon_{{{\text{te2}}}} = {10}\varepsilon_{{{\text{te}}}}\), \(\varepsilon_{{{\text{ te3}}}} = {100}\varepsilon_{{{\text{te}}}}\, \(E_{{\text{t}}}\) — модуль упругости стали, \(f_{ {{\text{ty}}}}\) — предел текучести стали, а \(f_{{{\text{tu}}}}\) — предел прочности стали.
{{\text{2}}} + B\varepsilon _{{\text{t}}} + C} \hfill & {(\varepsilon _{{{\text{te}}}} < \varepsilon _{t} \le \varepsilon _{{{\text{te1}}}} )} \hfill \\ {f_{{{ \text{ty}}}} } \hfill & {(\varepsilon _{{{\text{te1}}}} < \varepsilon _{t} \le \varepsilon _{{{\text{te2}}} } )} \hfill \\ {f_{{{\text{ty}}}} \left[ {{\text{1}} + {\text{0}}{\text{.6}}\frac{ {\varepsilon _{{\text{t}}} - \varepsilon _{{{\text{e2}}}} }}{{\varepsilon _{{{\text{e3}}}} - \varepsilon _ {{{\text{e2}}}} }}} \right]} \hfill & {(\varepsilon _{{{\text{te2}}}}} < \varepsilon _{{\text{t}}} \le \varepsilon _{{{\text{te3}}}} )} \hfill \\ {{\text{1}}{\text{.6}}f_{{{\text{ty}}}} } \hfill & {(\varepsilon _ {{\text{t}}} > \varepsilon _{{{\text{te3}}}} )} \hfill \\ \end{массив} } \right. $$ 9{{2}} — B\varepsilon_{{{\text{te}}}}\, \(\varepsilon_{{{\text{te}}}} = 0,8f_{{{\text{ty}} }} /E_{{\text{t}}}\),\(\varepsilon_{{{\text{te1}}}} = {1}.{5}\varepsilon_{{{\text{te}} }}\), \(\varepsilon_{{{\text{te2}}}} = {10}\varepsilon_{{{\text{te}}}}\), \(\varepsilon_{{{\text{ te3}}}} = {100}\varepsilon_{{{\text{te}}}}\, \(E_{{\text{t}}}\) — модуль упругости стали, \(f_{ {{\text{ty}}}}\) — предел текучести стали, а \(f_{{{\text{tu}}}}\) — предел прочности стали.
Рисунок 11
Зависимость напряжения от деформации.
Изображение полного размера
Таблица 2 Свойства материалов.
Полноразмерный стол
Лист углепластика
Углепластик был смоделирован как линейный упругий ортотропный материал, как показано на рис. 11b, и соотношение напряжения и деформации было следующим:
$$ \left\{ {\begin{ array}{*{20}l} {\sigma_{cf} = E_{cf} \varepsilon_{cf} \begin{array}{*{20}c} {} & {0 \le} \\ \end{ массив} \varepsilon_{cf} \le \varepsilon_{cfu} } \\ {\sigma_{cf} = 0\begin{array}{*{20}c} {} & {} & {\varepsilon_{cfu} \ le } \\ \end{массив} \varepsilon_{cf} } \\ \end{массив} } \right. $$
(2)
где \(\varepsilon_{cf}\) — напряжение листа углепластика, \(\sigma_{cf}\) — напряжение листа углепластика, \(\varepsilon_{cfu}\ ) — допустимая предельная деформация листа углепластика, а \(E_{cf}\) — модуль упругости листа углепластика.
Результаты и обсуждение
Анализ напряжений
Изображения напряжения стальной балки и листа углепластика показаны на рис. 12, 13 и 14. После перегрузки концентрация напряжения появилась на надрезе стальной балки и в середине пролета листа углепластика. По сравнению со стальной балкой без перегрузки деформации стальной балки и листа углепластика были меньше. Показано, что перегрузка может повлиять на окончательную деформацию стальной балки, а перегрузка уменьшит использование листа углепластика.
12, 13 и 14. После перегрузки концентрация напряжения появилась на надрезе стальной балки и в середине пролета листа углепластика. По сравнению со стальной балкой без перегрузки деформации стальной балки и листа углепластика были меньше. Показано, что перегрузка может повлиять на окончательную деформацию стальной балки, а перегрузка уменьшит использование листа углепластика.
Рисунок 12
Изображения стресса после перегрузки.
Изображение полного размера
Рис. 13
Сравнение напряжений стальной балки с перегрузкой и без нее.
Изображение в полный размер
Рис. 14
Сравнение напряжений листа углепластика с перегрузкой или без нее.
Изображение полного размера
Прогиб
На рисунках 15 и 16 показаны изображения прогиба стальной балки с перегрузкой и без нее. После перегрузки в стальной балке произошел остаточный прогиб. Величина остаточного прогиба была связана с числом перегрузок и амплитудой перегрузок. Прогиб стальной балки после перегрузки был меньше, чем прогиб стальной балки после статической нагрузки.
Величина остаточного прогиба была связана с числом перегрузок и амплитудой перегрузок. Прогиб стальной балки после перегрузки был меньше, чем прогиб стальной балки после статической нагрузки.
Рисунок 15
Остаточный прогиб после перегрузки.
Изображение полного размера
Рис. 16
Сравнение прогиба стальной балки с перегрузкой и без нее.
Полноразмерное изображение
Сравнение результатов испытаний и результатов расчета методом конечных элементов
На рисунках 17 и 18 показано сравнение результатов испытаний и результатов расчета методом конечных элементов. Результаты расчета методом конечных элементов хорошо согласуются с результатами испытаний, что свидетельствует о том, что расчетная модель поврежденных стальных балок, усиленных листами углепластика, была правильной.
Рис. 17
Сравнение тестов и расчетов методом конечных элементов кривых нагрузка-прогиб.
Изображение полного размера
Рис. 18
Сравнение тестов и расчета методом конечных элементов кривых нагрузка-деформация (деформация сжатия).
Изображение в полный размер
Анализ параметров
Влияние числа перегрузок
На рисунке 19 показаны кривые нагрузка-прогиб стальных балок со 100% повреждением полки при различных числах перегрузок. Упругая жесткость стальных балок при 100–1000 циклах перегрузок была намного больше, чем упругая жесткость стальных балок только при статических циклах нагружения. Однако среди них было мало изменений. Пределы текучести стальных балок при 100–1000 циклах перегрузок составили 13,5 %, 12,6 %, 11,2 %, 10,1 %, 9%, 7,9%, 7% и 6% больше, чем предел текучести стальных балок только при статической нагрузке. Предельные нагрузки стальных балок при 100–1000 перегрузках были меньше, чем предельные нагрузки стальных балок только при статической нагрузке. Предел текучести и упругая жесткость увеличивались с увеличением числа перегрузок из-за наклепа стали. Однако улучшение уменьшается по мере увеличения числа перегрузок. Предельная нагрузка будет снижена из-за холодной закалки стали. Число перегрузок повлияло на предельную нагрузку перегрузочных балок.
Однако улучшение уменьшается по мере увеличения числа перегрузок. Предельная нагрузка будет снижена из-за холодной закалки стали. Число перегрузок повлияло на предельную нагрузку перегрузочных балок.
Рисунок 19
Эффект перегрузки номера.
Изображение полного размера
Влияние амплитуды перегрузки
На рисунке 20 показана кривая нагрузка-прогиб стальных балок со 100% повреждением полки при различных амплитудах перегрузки. Упругая жесткость стальных балок с амплитудой перегрузки 0,6 Pu-0,76 Pu соответственно на 6,2 %, 6,5 %, 8,6 %, 11,2 %, 14,1 %, 15,8 %, 16,5 %, 18,4 %, 19,8 % превышала упругую жесткость стали. балка только со статической нагрузкой, а предел текучести составил соответственно 15,8%, 17,9%, 21,1%, 22,8%, 25%, 26,8%, 27%, 28,9%, 30,5% больше, чем предел текучести стальной балки только при статической нагрузке. Предельные нагрузки были на 1,9%, 2,3%, 2,9%, 3,2%, 4%, 4,7%, 5,7%, 6,8% и 7,7% меньше, чем предельные нагрузки стальной балки только при статической нагрузке. Амплитуда перегрузки увеличилась на 0,02 Pu, а предельная нагрузка увеличилась примерно на 2 кН, но предельная нагрузка уменьшилась примерно на 1 кН. Когда амплитуда перегрузки достигла 0,77 Pu, на стадии перегрузки была разрушена усиленная стальная балка.
Амплитуда перегрузки увеличилась на 0,02 Pu, а предельная нагрузка увеличилась примерно на 2 кН, но предельная нагрузка уменьшилась примерно на 1 кН. Когда амплитуда перегрузки достигла 0,77 Pu, на стадии перегрузки была разрушена усиленная стальная балка.
Рисунок 20
Влияние амплитуды перегрузки.
Изображение в полный размер
Выводы
Результаты этого исследования показали, что склеенные листы углепластика можно эффективно использовать для усиления поврежденных стальных балок и что перегрузка может повлиять на предел текучести и упругую жесткость стальных балок. Были сделаны следующие выводы.
Все стальные балки после перегрузки могут увеличить предел текучести и упругую жесткость из-за закалки стали после перегрузки. Однако чем выше уровень повреждения стальной балки, тем меньше будет приращение предела текучести и упругой жесткости. Предел текучести и упругая жесткость стальной балки после перегрузки были на 8,7% и 24,5% больше, чем предел текучести и упругая жесткость стальной балки без перегрузки.
 Предельная нагрузка стальной балки после перегрузки была на 5,3% меньше, чем предельная нагрузка стальной балки без перегрузки.
Предельная нагрузка стальной балки после перегрузки была на 5,3% меньше, чем предельная нагрузка стальной балки без перегрузки.Предел текучести, предельная нагрузка и упругая жесткость стальных балок со 100%-ной потерей растянутой полки были на 68,3%, 73,8% и 13,5% выше, чем у стальной балки с 28%-й потерей стенки после статической нагрузки. Предельная нагрузка и предельная нагрузка стальной балки со 100%-ной потерей растянутой полки были на 24,1% и 32% больше, чем у стальной балки с 15%-ной потерей стенки после перегрузки. Независимо от статической нагрузки или перегрузки уровень повреждения оказал существенное влияние на предельную нагрузку и предельную несущую способность стальных балок.
Стальная балка, усиленная листами углепластика, может увеличить предел текучести, предельную нагрузку и упругую жесткость на 10%, 10,3% и 14,5% соответственно по сравнению со стальной балкой без усиления после статической нагрузки.
 Стальная балка, усиленная двумя слоями углепластиковых листов, увеличила нагрузку текучести, предельную нагрузку и упругую жесткость на 38,4%, 24,9% и 36,9% соответственно по сравнению со стальной балкой, усиленной одним слоем углепластикового листа после перегрузки. Было показано, что поврежденная стальная балка может быть усилена листами углепластика, а увеличенные слои листов углепластика показали, что они могут улучшить предел текучести, предельную несущую способность и упругую жесткость стальных балок.
Стальная балка, усиленная двумя слоями углепластиковых листов, увеличила нагрузку текучести, предельную нагрузку и упругую жесткость на 38,4%, 24,9% и 36,9% соответственно по сравнению со стальной балкой, усиленной одним слоем углепластикового листа после перегрузки. Было показано, что поврежденная стальная балка может быть усилена листами углепластика, а увеличенные слои листов углепластика показали, что они могут улучшить предел текучести, предельную несущую способность и упругую жесткость стальных балок.Углепластиковые деформации стальных балок, усиленных листами углепластика, составили примерно 10 000 мкЕ после статической нагрузки и примерно 7500 мкЕ после перегрузки. Было показано, что деформации листов углепластика уменьшаются из-за перегрузки.
По сравнению с усиленной стальной балкой без перегрузки прогиб и деформации усиленной стальной балки с перегрузкой были намного меньше.
 Из-за холодной закалки стали предел текучести и упругая жесткость увеличиваются с увеличением амплитуды перегрузки, а увеличение числа перегрузок может уменьшить предел текучести и упругую жесткость, но предельная нагрузка будет уменьшена.
Из-за холодной закалки стали предел текучести и упругая жесткость увеличиваются с увеличением амплитуды перегрузки, а увеличение числа перегрузок может уменьшить предел текучести и упругую жесткость, но предельная нагрузка будет уменьшена.
Ссылки
Коломби П. и Поджи К. Экспериментальное, аналитическое и численное исследование статического поведения стальных балок, армированных пултрузионными полосами из углепластика. Композ. Часть B 37 (1), 64–73 (2006).
Артикул
Google ученый
Боччарелли, М. Реакция статически определяемых стальных балок, армированных пластинами из углепластика, в упруго-пластическом режиме. англ. Структура 31 , 956–967 (2009).
Артикул
Google ученый
«>Ву, Г. и др. Экспериментальное исследование усталостных характеристик стальных балок, усиленных различными композитными пластинами, армированными волокном. Дж. Компос. Констр. 16 (2), 127–137 (2012).
КАС
СтатьяGoogle ученый
Ю, К. К., Чен, Т., Гу, С. Л., Чжао, С. Л. и Сяо, З. Г. Усталостное поведение стальных пластин, упрочненных углепластиком, с различной степенью повреждения. Тонкостенная конструкция. 69 , 10–17 (2013).
Артикул
Google ученый
Боччарелли, М.
 и Коломби, П. Об упруго-пластическом поведении неразрезных стальных балок, армированных склеенным углепластиковым листом. англ. Структура 49 , 756–766 (2013).
и Коломби, П. Об упруго-пластическом поведении неразрезных стальных балок, армированных склеенным углепластиковым листом. англ. Структура 49 , 756–766 (2013).Артикул
Google ученый
Хмидан, А., Ким, Ю. Дж. и Яздани, С. Поправочные коэффициенты для интенсивности напряжений широкополочных стальных балок, усиленных углепластиком, с различными конфигурациями трещин. Констр. Строить. Матер. 70 , 522–530 (2014).
Артикул
Google ученый
Коломби, П., Фава, Г., Поджи, К. и Сонзогни, Л. Усталостное армирование стальных элементов материалами из углепластика: экспериментальные данные, аналитическая модель и численное моделирование. Проц. англ. 74 , 384–387 (2014).
КАС
СтатьяGoogle ученый
«>Wang, L., Hou, W., Han, H. & Huo, J. Ремонт стальных композитных балок с повреждением полки с использованием листов CFRP. Стр. англ. мех. 55 (3), 511–523 (2015).
Артикул
Google ученый
Коломби, П. и Фава, Г. Экспериментальное исследование усталостных характеристик стальных балок с трещинами, отремонтированных с помощью пластин из углепластика. англ. Фракт. мех. 145 , 128–142 (2015).
Артикул
Google ученый
«>Альджабар, Нью-Джерси, Чжао, С.Л., Аль-Махайди, Р., Гафури, Э. и Мотавалли, М. Пауэрс. Влияние ориентации трещин на усталостные характеристики стальных пластин, упрочненных углепластиком. Композ. Структура 152 , 295–305 (2016).
Артикул
Google ученый
Ху Л., Фэн П. и Чжао С.-Л. Усталостный расчет стальных элементов, усиленных углепластиком. Тонкостенная конструкция. 119 , 482–498 (2017).
Артикул
Google ученый
Юсефи О.
 , Нармашири К. и Гаемдуст М. Р. Поведение стальных балок с надрезами, усиленных полосами углепластика. Стальной композит. Структура 25 (1), 35–43 (2017).
, Нармашири К. и Гаемдуст М. Р. Поведение стальных балок с надрезами, усиленных полосами углепластика. Стальной композит. Структура 25 (1), 35–43 (2017).Google ученый
Боччарелли, М., Коломби, П., Д’Антино, Т. и Фава, Г. Расклейка стальных балок, армированных пластинами из углепластика, вызванная промежуточными трещинами, под усталостной нагрузкой. англ. Структура 171 , 883–893 (2018).
Артикул
Google ученый
Мартинелли Э., Хоссейни А., Гафури Э. и Мотавалли М. Поведение предварительно напряженных углепластиковых пластин, приклеенных к стальной основе: численное моделирование и экспериментальная проверка. Композ. Структура 207 , 974–984 (2019).
Артикул
Google ученый
Zhang, Z.
 , Xu, S., Mu, L. & Peng, S. Экспериментальное и теоретическое исследование изгибных свойств корродированных стальных балок, усиленных пластинами из углепластика. Структура. англ. 24 (7), 2160–2172 (2020).
, Xu, S., Mu, L. & Peng, S. Экспериментальное и теоретическое исследование изгибных свойств корродированных стальных балок, усиленных пластинами из углепластика. Структура. англ. 24 (7), 2160–2172 (2020).Google ученый
Ху, Л. и Фэн, П. Метод расчета усталостного поведения и программа для усиленных поврежденных стальных конструкций из углепластика. Сталь Констр. 33 , 1491–1502 (2021).
Google ученый
Дэн, Л. и др. Исследование характеристик усталостной прочности при изгибе поврежденных стальных балок, армированных CFRP-OFBG. Структура. англ. 25 (12), 4686–4697 (2021).
Google ученый
Хоу, В., Ван, Ф. и Ван, Л. Испытание и численный анализ поврежденной стальной балки, усиленной предварительно напряженным листом из углепластика.
 Доп. Гражданский англ. 2021 , 1–19 (2021).
Доп. Гражданский англ. 2021 , 1–19 (2021).Google ученый
Сугиура, Х., Инаба, Н., Кобаяши, А., Огаки, К. и Нагаи, М. Экспериментальное исследование отслаивания листов из углеродного волокна при ремонте стальных элементов. Сталь Констр. англ. 16 (63), 87–98 (2009).
Google ученый
Гафури, Э. и Мотавалли, М. Потеря устойчивости при кручении стальных двутавровых балок, модернизированных склеенными и несвязанными ламинатами из углепластика с различными уровнями предварительного напряжения: экспериментальное и численное исследование. Констр. Строить. Матер. 76 , 194–206 (2015).
Артикул
Google ученый
Голами, М., Мохд Сэм, А.Р., Марсоно, А.К., Тахир, М.М. и Фаридмер, И. Характеристики стальных балок, усиленных пултрузионной плитой из углепластика, при различных воздействиях. Стальной композит. Структура 20 (5), 999–1022 (2016).
Артикул
Google ученый
Ссылки на скачивание
Структурные напряжения луча и отклонение для не инженеров
Связанные ресурсы: изгиб луча
Структурное напряжение луча и отклонения для нежелателей
Пресс. Расчет напряжения и прогиба балки для не инженеров
Ниже приведена процедура определения критических элементов конструкции простой конфигурации конструкции, находящейся под нагрузкой. Имейте в виду, что выполнение этой процедуры не дает вам квалификацию инженера-строителя или любого другого инженера. Мы в Engineers Edge не несем никакой ответственности за какие-либо проектные сбои, которые могут возникнуть. Если вы проектируете что-то, что в случае неудачи может привести к травме, смерти или серьезным финансовым потерям, наймите лицензированного инженера-строителя, который сделает для вас проект. Будьте осторожны, идите медленно, помните о безопасности выше денег и думайте. Кроме того… если у вас есть вопрос, разместите его на инженерных форумах, пожалуйста, не пишите по электронной почте, не пишите отзывы, а звоните нам.
Будьте осторожны, идите медленно, помните о безопасности выше денег и думайте. Кроме того… если у вас есть вопрос, разместите его на инженерных форумах, пожалуйста, не пишите по электронной почте, не пишите отзывы, а звоните нам.
Первый . Посетите нашу веб-страницу, посвященную деформированию и напряжению балки, и узнайте, есть ли у нас расчет конфигурации загрузки и калькулятор, которые лучше всего подходят для вашего приложения. Если мы это сделаем, классная закладка, помните или что-то в этом роде.
Если вы хорошо разбираетесь в математике, сделайте расчеты вручную, если нет и/или вам нужна двойная проверка, используйте автоматические калькуляторы. Возможно, вам придется стать Премиум-членом, чтобы использовать калькулятор (это поможет нам оплачивать веб-сайт и сделает вашу работу НАМНОГО проще).
Секунда , определите максимальную приложенную нагрузку в фунтах (фунтах) или в ньютонах (Н).
Третий , какова максимальная длина вашего нагруженного элемента конструкции? дюймы, футы или миллиметры (мм)
Далее , решите, какой материал вы хотели бы использовать в своей конструкции — дерево, алюминий, сталь и т. д. Это всего лишь исходное предположение о материальной части. На самом деле вам может понадобиться использовать более прочную, дорогую руду, другую геометрию в вашем окончательном дизайне, так что это всего лишь предположение, с которого вы начали. Инженерное проектирование обычно представляет собой итеративный процесс, а это означает, что вы будете пробовать несколько конфигураций, пока не получите хорошие результаты.
д. Это всего лишь исходное предположение о материальной части. На самом деле вам может понадобиться использовать более прочную, дорогую руду, другую геометрию в вашем окончательном дизайне, так что это всего лишь предположение, с которого вы начали. Инженерное проектирование обычно представляет собой итеративный процесс, а это означает, что вы будете пробовать несколько конфигураций, пока не получите хорошие результаты.
Как только вы узнаете, какой материал вы хотите использовать, получите и запишите для этого материала следующее:
- Модуль упругости или модуль Юнга
- Предел текучести
Модуль упругости или модуль Юнга – это константа (число), характеризующая склонность материалов к прогибу или деформации под нагрузкой. Иногда его называют модулем упругости. указывается в фунтах на квадратный дюйм или Н/мм. 2
Предел текучести — это просто напряжение, при котором элемент конструкции начинает постоянно растягиваться или деформироваться при приложении нагрузки. Вы захотите спроектировать элемент конструкции таким образом, чтобы максимальное напряжение в процессе эксплуатации было значительно ниже предела текучести, поскольку это число, и, в этом отношении, предел пропорциональности — не самое удачное место. Нам не нужны сбои, изгибы и поломки!
Вы захотите спроектировать элемент конструкции таким образом, чтобы максимальное напряжение в процессе эксплуатации было значительно ниже предела текучести, поскольку это число, и, в этом отношении, предел пропорциональности — не самое удачное место. Нам не нужны сбои, изгибы и поломки!
Вот задача с модулем упругости и пределом текучести. Вы будете искать какой-то материал и получите общее типичное значение, а не сертифицированное или гарантированное значение. Если вы не покупаете прослеживаемость вашего материала, вы не знаете, что у вас есть. Вот почему всегда лучше перепроектировать структуру, а затем испытать нагрузку (пробная нагрузка) вашего готового устройства.
Пятый , решите, какую геометрию или структурную форму вы хотите использовать. Опять же, это исходная догадка по геометрии. Вы можете попасть в яблочко с первой попытки или вам нужно разработать дизайн для большей или другой формы. Как только вы узнаете, какая геометрия, по вашему мнению, будет работать, получите момент инерции площади для этой геометрии. Вот несколько ссылок:
Вот несколько ссылок:
- Площадь Момент инерции для обычных форм
- Средство просмотра профилей из конструкционной стали AISC
Момент инерции площади, который вам нужен, это когда нагрузка перпендикулярна линии сечения следующим образом:
Нагрузка «p» в приложенном перпендикуляре | Нагрузка «p» в приложенном перпендикуляре |
Итак, теперь у вас должна быть вся основная информация о конструкции, необходимая для начала, давайте рассмотрим:
- Максимальная прилагаемая нагрузка (расчетная или реальная) равна максимальной поднимаемой нагрузке.
- Загрузка конфигурации — знание уравнений и/или использование калькулятора.
- Длина,
- Материал,
- Модуль упругости (модуль Юнга)
- Предел текучести
- Площадь Момент инерции для загружаемой геометрии.

- Расстояние до нейтральной оси
Пример конструкции :
Давайте создадим простую структурную конструкцию, которая поднимет двигатель и поместит его в нашу дорогую проектную машину в нашем гараже.
Вес двигателя по данным производителя = 300 фунтов.
Блок и такелаж на балке правильно , который мы собираемся использовать для подъема двигателя (намного выше 300 фунтов) весит 40 фунтов.
Цепь прикреплена к двигателю спереди и сзади для равномерного подъема (10 фунтов).
Разное оборудование (5 фунтов).
Таким образом, мы собираемся поднять максимум: 300 + 40 + 10 + 5 = 355 фунтов
Я предлагаю блок и снасти, рассчитанные не менее чем на 1,5 х максимальный груз, который вы поднимаете.
План представляет собой простую балку, расположенную поверх очень прочной стены из бетонных блоков поперек гаража. Мы планируем закатать кузов автомобиля под двигатель для установки. Поэтому конфигурация загрузки такая:
Поэтому конфигурация загрузки такая:
Давайте воспользуемся этим калькулятором:
Напряженная и прогибаемая балка, поддерживаемая обоими концами. Нагрузка в центре. Уравнение и/или калькулятор
Балка, которую мы хотим использовать, будет сделана из дерева, возможно, из обработанной под давлением сосны из местного оборудования. хранить. Таким образом:
Модуль упругости для древесины = 0,99 x 10 6 ( 990 000) фунтов на квадратный дюйм (фунтов на квадратный дюйм)
Предел текучести. Это сложный вопрос для древесины, поскольку, как правило, не существует спецификации предела текучести. Мы будем использовать данные для спецификации «Модуль разрыва», который для сосны восточной равен примерно 4,9.00 фунтов/кв.
Итак, давайте попробуем стандартную деревянную балку 4 x 4, которая на самом деле имеет размеры 3,5 x 3,5 дюйма. Балка должна быть шире автомобиля, поэтому давайте сделаем 7 футов или 84 дюйма от опоры до опоры.
Расстояние до нейтральной оси (крайняя точка) составляет половину толщины, перпендикулярной нагрузке моего поперечного сечения, или 3,5 дюйма / 2 = 1,75 дюйма
Итак, вот мои расчеты:
Расчетное приложенное напряжение равно -1043,7 фунта на квадратный дюйм, а мой прогиб равен 3,54225 дюйма . Следовательно, у меня есть коэффициент запаса прочности = разрушающая нагрузка / приложенная нагрузка = 4,395.
Теоретически это должно работать, хотя я бы предположил, что из-за отклонения в 3,54 дюйма более высокий коэффициент безопасности был бы лучше, поскольку чем меньше отклонение балки, тем лучше, так как большие отклонения могут привести ко всем видам особых проблем, которые я м не буду включать сюда.
Если поставить две стандартные доски размером 4 x 4 дюйма друг на друга, вы получите расчетный момент инерции площади = 100
Пересчет напряжения и прогиба. Я получаю:
Приложенное напряжение = 260,925 фунтов на квадратный дюйм и отклонение 0,44278 дюймов. Низкий прогиб и напряжение, и все, что мне было нужно, это еще один 4 x 4.
Низкий прогиб и напряжение, и все, что мне было нужно, это еще один 4 x 4.
Это должно работать хорошо, а риск отказа сведен к минимуму — ДЕЙСТВУЙТЕ!
В заключение:
Поскольку вы приложили все усилия , я рекомендую вам собрать свой аппарат и испытать его. Осторожно приложите 355 фунтов в центре и измерьте фактическое отклонение. Проверьте фактические размеры ваших 4 x 4. Затем сравните фактический прогиб и размеры с расчетным прогибом и размерами луча, которые вы использовали. Скорее всего, разница будет надеюсь, не слишком большая. Если вам интересно, вернитесь к калькулятору прогиба балки и напряжения и изменяйте модуль упругости, пока не получите такой же прогиб путем расчета. Это даст вам представление о том, каковы на самом деле инженерные свойства древесины. Древесина варьируется от партии к партии.
Это очень простой подход к определению теоретического напряжения и прогиба конкретной конфигурации нагрузки. Знайте, что инженерные материалы никогда не бывают тем, за что себя выдают, и что гораздо проще и разумнее перепроектировать, чем спроектировать «в самый раз».
Материалы | Бесплатный полнотекстовый | Прогнозирование прогиба железобетонных балок, усиленных полимером, армированным волокном
1. Введение
Одним из самых больших преимуществ, которое может обеспечить усиление полимером, армированным углеродным волокном (CFRP), является увеличение гибкости балки. Разрушение железобетонной балки связано с деформацией стали, разрушением бетона или разрушением при сдвиге. Краткосрочные и долгосрочные эксперименты показали, что усиление ж/б балок углепластиком может замедлить текучесть стали [1,2,3,4,5,6]. Равномерно, если достигнута текучесть стали или сталь заржавела, усиленные балки могут служить до тех пор, пока не будет достигнут разрыв, отслоение слоя углепластика, усталостное разрушение стали или разрушение бетона [7,8,9].,10,11]. Благодаря высокой прочности и высокой эластичности натянутый слой углепластика может воспринимать растягивающие усилия (напряжения) при достижении предела текучести арматуры. Поэтому может развиться прогиб балки, что приведет к податливости арматуры на более позднем этапе. Однако существует опасность преждевременного отслоения слоя углепластика. Чтобы предотвратить это, правильная дополнительная фиксация может отсрочить это явление [12]. Кроме того, углепластик, монтируемый вблизи поверхности, из-за большего отношения периметра к площади сечения может обеспечить лучшую производительность склеивания [13].
Поэтому может развиться прогиб балки, что приведет к податливости арматуры на более позднем этапе. Однако существует опасность преждевременного отслоения слоя углепластика. Чтобы предотвратить это, правильная дополнительная фиксация может отсрочить это явление [12]. Кроме того, углепластик, монтируемый вблизи поверхности, из-за большего отношения периметра к площади сечения может обеспечить лучшую производительность склеивания [13].
Различные исследования показывают, что развитие прогиба и достигнутая текучесть зависят от соотношения армирования (стали) [14,15]. Это может быть связано с эксплуатацией сжатого бетона. Если коэффициент армирования низкий, эксплуатация сжатого бетона также значительно снижается до тех пор, пока не будет достигнута текучесть армирования. Поэтому прогиб (при достижении податливости арматуры) укрепленных балок с низким коэффициентом армирования наибольший. Это связано с неиспользованной деформируемостью сжатого бетона.
Существующие методы расчета прогиба могут выполнять оценку до тех пор, пока не будет достигнут предел текучести арматуры. Наиболее распространенные и простые методы основаны на рекомендациях по проектированию ACI318 [16] и Еврокоде 2 [17]. Кроме того, многослойный метод можно использовать для расчета прогиба усиленных балок; однако этот метод не так удобен для инженеров, поэтому в этой статье мы его рассматривать не будем. Метод расчета, основанный на ACI318 [16], оценивает эффективный момент инерции, а метод, основанный на Еврокоде 2 [17], обычно оценивает среднюю кривизну изгибаемого элемента. Оба метода оценивают момент инерции полного поперечного сечения и момент инерции поперечного сечения, где трещина раскрыта. Однако эти методы оценивают напряженно-деформированное состояние в поперечном сечении до достижения предела текучести в арматуре. Существует несколько методов [18,19,20,21], которые позволяют оценить напряженно-деформированное состояние в сечении после достижения пределов текучести, но эти методы трудно применимы проектировщиком. Доступно несколько вкладов, основанных на моделировании момент-кривизна [22,23].
Наиболее распространенные и простые методы основаны на рекомендациях по проектированию ACI318 [16] и Еврокоде 2 [17]. Кроме того, многослойный метод можно использовать для расчета прогиба усиленных балок; однако этот метод не так удобен для инженеров, поэтому в этой статье мы его рассматривать не будем. Метод расчета, основанный на ACI318 [16], оценивает эффективный момент инерции, а метод, основанный на Еврокоде 2 [17], обычно оценивает среднюю кривизну изгибаемого элемента. Оба метода оценивают момент инерции полного поперечного сечения и момент инерции поперечного сечения, где трещина раскрыта. Однако эти методы оценивают напряженно-деформированное состояние в поперечном сечении до достижения предела текучести в арматуре. Существует несколько методов [18,19,20,21], которые позволяют оценить напряженно-деформированное состояние в сечении после достижения пределов текучести, но эти методы трудно применимы проектировщиком. Доступно несколько вкладов, основанных на моделировании момент-кривизна [22,23]. Точность предложенной модели [22,23] впечатляет, однако некоторые параметры, такие как момент инерции, глубина нейтральной оси, остаются неизвестными.
Точность предложенной модели [22,23] впечатляет, однако некоторые параметры, такие как момент инерции, глубина нейтральной оси, остаются неизвестными.
Грузоподъемность усиленных балок может быть значительно увеличена, так что повышенная эксплуатационная нагрузка может располагаться в диапазоне кривой нагрузки-прогиба, где достигается предел текучести стали. Основная цель этой статьи состоит в том, чтобы рассчитать прогиб усиленной балки, когда достигается текучесть стали и когда только слой углепластика перехватывает растягивающие усилия.
2. Анализируемые балки
ЖБ-балки с различными коэффициентами армирования были выбраны для выполнения расчета прогиба. Данные о пучках были собраны из различных исследований. Ссылки и названия анализируемых балок с кратким описанием представлены в таблице 1. Выбранные балки подходят для анализа прогиба, потому что прогиб развивается, когда достигается текучесть арматуры. Как упоминалось выше, более низкий коэффициент армирования позволяет увеличить приращение прогиба, когда достигается предел текучести армирования.
Механические параметры материала, такие как модуль упругости и прочность на растяжение, необходимы для расчета прогиба балки. Этот и другие механические параметры представлены в таблице 2.
3. Расчет прогиба
Развитие прогиба усиленной и неусиленной балки делится на этапы. На первом этапе прогиб развивается до раскрытия вертикальных трещин в растянутой части сечения. На втором этапе прогиб развивается при раскрытии вертикальной трещины до достижения предела текучести растянутой арматуры. На третьем этапе прогиб развивается при достижении предела текучести арматуры и только слой углепластика воспринимает растягивающую силу. Таким образом, существует две стадии развития прогиба для неусиленных балок и три стадии для усиленных (рис. 1). Изгибающие моменты М I и M I.S показаны на (рис. 1), что представляет собой момент растрескивания неусиленной и усиленной балки соответственно. Из-за слоя углепластика вклад момента растрескивания усиленной балки немного больше, чем у неусиленной балки (M I. S > MI). Изгибающие моменты (М I.S и М I ) соответствуют концу первой стадии. Максимальный несущий изгибающий момент неусиленной балки (M R = M II ) меньше изгибающего момента усиленной балки (M II.S ) при достижении текучести арматуры. Эти изгибающие моменты соответствуют концу второй стадии. Максимальный несущий изгибающий момент усиленной балки обозначен как M R.S = M III и соответствует концу третьего этапа.
S > MI). Изгибающие моменты (М I.S и М I ) соответствуют концу первой стадии. Максимальный несущий изгибающий момент неусиленной балки (M R = M II ) меньше изгибающего момента усиленной балки (M II.S ) при достижении текучести арматуры. Эти изгибающие моменты соответствуют концу второй стадии. Максимальный несущий изгибающий момент усиленной балки обозначен как M R.S = M III и соответствует концу третьего этапа.
На прогиб балок на определенном этапе влияет разная жесткость на изгиб. Как правило, на изгибную жесткость E·I (произведение модуля упругости и момента инерции) влияет момент инерции. Современные методы расчета прогиба обычно оценивают модуль упругости, как и для эластичного материала. Затем развитие прогиба проходит все стадии, развиваются трещины в растянутой части сечения, поэтому момент инерции непостоянен. Таким образом, на определенном этапе глубина нейтральной оси и момент инерции различны. Изменение глубины нейтральной оси усиленной и неусиленной балок представлено на рис. 2 и рис. 3. Таким образом, имеются участки поперечного сечения, содержащие и не имеющие трещин. Поэтому необходимо оценить эффективный момент инерции. Прогноз глубины нейтральной оси на каждом этапе подтверждает линейность распределения деформаций. Напряжения в сжатой части сечения находятся в области упругости. Кроме того, справедлива гипотеза о плоском сечении. Деформация внутренней и внешней арматуры равна деформациям окружающего бетона (скольжение сцепления не оценивается).
Изменение глубины нейтральной оси усиленной и неусиленной балок представлено на рис. 2 и рис. 3. Таким образом, имеются участки поперечного сечения, содержащие и не имеющие трещин. Поэтому необходимо оценить эффективный момент инерции. Прогноз глубины нейтральной оси на каждом этапе подтверждает линейность распределения деформаций. Напряжения в сжатой части сечения находятся в области упругости. Кроме того, справедлива гипотеза о плоском сечении. Деформация внутренней и внешней арматуры равна деформациям окружающего бетона (скольжение сцепления не оценивается).
Прогиб усиленной балки на этапе 1 вплоть до растрескивания растянутой части поперечного сечения можно предсказать по уравнению:
где l — длина пролета балки, a — расстояние от опоры до положения внешней нагрузки, M I — действующий момент, E см — модуль упругости бетона, I I.red — приведенный момент инерции всего поперечного сечения относительно нейтральной оси поперечного сечения.
На этапе 1 расчетный действующий момент равен 0 < M I ≤ M I.S , а предельный изгибающий момент 1-й ступени – момент разрушения:
где f ct — предел прочности бетона при растяжении, y c.I — центр тяжести поперечного сечения на стадии 1. Центр тяжести можно рассчитать по следующим уравнениям:
где А красный — приведенное сечение усиленной балки, А ф — сечение углепластика, А с 1 , А с 2 — сечение стального стержня, S красный — статический момент приведенного сечения усиленной балки, α ф , α с 1 , α с 4 2 — коэффициенты приведения, Е ф — модуль упругости волокон, Е с 1 , Е с 2 — модуль упругости стальных стержней.
Приведенный момент инерции поперечного сечения можно рассчитать по следующему уравнению:
Прогиб усиленной балки на стадии 2, когда растянутая часть поперечного сечения трескается и не достигается податливость растянутой арматуры, можно рассчитать по уравнению:
Действующий изгибающий момент на стадии 2 есть M II и момент M I.S < M II ≤ M II.S . Момент достижения текучести арматуры М II.S . Эффективный момент инерции оценивается по уравнению Брэнсона [45] для параметра I II :
Если оценивается изменение нейтральной оси, то уравнение (11) изменяется следующим образом:
где I II.red — приведенный момент инерции поперечного сечения раскрытия вертикальной трещины. Этот момент инерции можно предсказать с помощью уравнения:
Коэффициенты γ 1. c и γ 1.t оценивают изменение нейтральной оси и могут быть предсказаны с помощью уравнений:
c и γ 1.t оценивают изменение нейтральной оси и могут быть предсказаны с помощью уравнений:
Глубина нейтральной оси при стадия 1 предсказывается уравнением:
Прогноз глубины нейтральной оси в сечении с открытой трещиной основан на ранее упомянутых предположениях. Гипотеза плоских сечений верна. Распределение деформации по высоте сечения носит линейный характер (рис. 4б). Тогда по подобию треугольников можно выразить деформации в каждом слое пропорционально деформации сжатого слоя бетона, а глубину нейтральной оси выразить квадратным уравнением. Глубину нейтральной оси на этапе 2 можно предсказать по уравнению:
где коэффициенты А, В и С:
Прогиб усиленной балки на стадии 3 при достижении предела текучести растянутой арматуры можно рассчитать по уравнению:
Действующий изгибающий момент на стадии 3 М III и момент M II. u < M III ≤ M III.u . Предельный изгибающий момент на 3 стадии М III.у . Новый эффективный момент инерции оценивается в уравнении для параметра I III :
u < M III ≤ M III.u . Предельный изгибающий момент на 3 стадии М III.у . Новый эффективный момент инерции оценивается в уравнении для параметра I III :
Если оценивается изменение нейтральной оси, то уравнение (22) изменяется следующим образом:
где I III.red — приведенный момент инерции поперечного сечения раскрытия вертикальной трещины. Этот момент инерции можно предсказать по уравнению:
Коэффициенты γ 2.c и γ 2.t :
Глубина нейтральной оси на этапе 3 также прогнозируется из подобия треугольников (рис. 5б). ).
Глубина нейтральной оси на этапе 3 прогнозируется по уравнению:
Были коэффициенты A, B и C:
Прогиб неусиленной балки можно предсказать по тем же уравнениям (1) и (10). Однако параметры слоя FRP в других уравнениях следует игнорировать. Если балки усилены предварительно напряженным стеклопластиком, то в этом случае необходимо рассчитывать дополнительную кривизну и прогиб от силы предварительного напряжения. Полный прогиб получается суммированием всех прогибов.
Если балки усилены предварительно напряженным стеклопластиком, то в этом случае необходимо рассчитывать дополнительную кривизну и прогиб от силы предварительного напряжения. Полный прогиб получается суммированием всех прогибов.
4. Результаты
Сравнение прогибов (рис. 6, рис. 7, рис. 8 и рис. 9)) показывает, что метод уравнений подходит для железобетонных балок с различными коэффициентами армирования. Расчетные прогибы всех указанных балок представлены в приложении А. На этих рисунках обозначение «Расч. I» относится к уравнениям (11) и (22). Обозначение «Расч. II», связанный с уравнениями (12) и (23). Ясно, что метод теоретического уравнения дает точки торможения, такие как момент образования трещины и момент текучести стали на кривой отклонения нагрузки. Разница между расчетным и экспериментальным прогибом увеличивается с увеличением уровня нагрузки. Это может произойти из-за того, что теоретический метод оценивает упругую работу бетона и постоянную глубину нейтральной оси. Таким образом, кривизна кривой прогиба зависит именно от соотношения изгибающих моментов. Для повышения точности теоретического метода необходимо оценить нелинейное распределение напряжения-деформации по высоте поперечного сечения. Предлагаемый метод оценивает линейное распределение напряжения-деформации. Оценка нелинейного распределения напряжения-деформации может быть сложной для проектировщиков, поэтому треугольное распределение легче оценить. Кроме того, сравнение положения центра параболической и треугольной формы дает мало различий. На разницу результатов также влияет точность эксперимента. В некоторых опытах прогиб в момент взлома может быть большим. Основным недостатком предлагаемого метода является прогнозирование изгибающего момента при достижении текучести стали. Трудно предсказать момент включения слоя FRP, потому что напряжения в сжатом бетоне и натянутом слое углепластика неизвестны. В таком случае задача должна решаться итерационным подходом до достижения баланса внутренних сил.
Таким образом, кривизна кривой прогиба зависит именно от соотношения изгибающих моментов. Для повышения точности теоретического метода необходимо оценить нелинейное распределение напряжения-деформации по высоте поперечного сечения. Предлагаемый метод оценивает линейное распределение напряжения-деформации. Оценка нелинейного распределения напряжения-деформации может быть сложной для проектировщиков, поэтому треугольное распределение легче оценить. Кроме того, сравнение положения центра параболической и треугольной формы дает мало различий. На разницу результатов также влияет точность эксперимента. В некоторых опытах прогиб в момент взлома может быть большим. Основным недостатком предлагаемого метода является прогнозирование изгибающего момента при достижении текучести стали. Трудно предсказать момент включения слоя FRP, потому что напряжения в сжатом бетоне и натянутом слое углепластика неизвестны. В таком случае задача должна решаться итерационным подходом до достижения баланса внутренних сил. Это также сложная задача для дизайнеров. Для этого исследования значения растрескивания, текучести и предельного момента были предсказаны по графикам эволюции прогиба.
Это также сложная задача для дизайнеров. Для этого исследования значения растрескивания, текучести и предельного момента были предсказаны по графикам эволюции прогиба.
Эксперименты, в которых измерялся прогиб от рамы, установленной на балке, дают более точный результат. Расчетный прогиб (Расч. I) с использованием уравнения эффективного момента инерции без каких-либо коэффициентов подходит для этой системы измерения. Уравнение эффективного момента инерции должно быть без коэффициентов — оно связано с нейтральной осью. Обратите внимание, что второй этап не имеет горизонтальной прямой линии. Другие экспериментальные результаты «отклонения», более близкие к «расч. II” можно связать с измеренным смещением.
5. Выводы
Согласно предложенной методике расчета прогиба усиленной железобетонной балки можно прогнозировать прогиб при достижении предела текучести стали. Когда прогиб рассчитывается с использованием обычного выражения эффективного момента инерции (уравнения (11) и (22)), в некоторых случаях получаются меньшие прогибы. Это несоответствие может быть связано с неправильно определенным экспериментальным прогибом, так как в некоторых экспериментах неясно, определяется ли прогиб компенсацией подъемной силы нейтральной оси на опорах. В большинстве случаев наиболее точен расчет с использованием нормального выражения эффективного момента инерции (уравнения (11) и (22)). Оценка изменения нейтральной оси (уравнения (12) и (23)) приводит к большим отклонениям, но более точна, когда отклонения меньше при нормальном выражении (уравнения (11) и (22)). Другим важным критерием, связанным с точностью прогибов, является коэффициент оценки характера внешней нагрузки, так как после упрочнения меняется развитие трещин, меняется и развитие кривизны. Для проверки точности экспериментальных и расчетных результатов требуется дальнейший анализ методом конечных элементов.
Это несоответствие может быть связано с неправильно определенным экспериментальным прогибом, так как в некоторых экспериментах неясно, определяется ли прогиб компенсацией подъемной силы нейтральной оси на опорах. В большинстве случаев наиболее точен расчет с использованием нормального выражения эффективного момента инерции (уравнения (11) и (22)). Оценка изменения нейтральной оси (уравнения (12) и (23)) приводит к большим отклонениям, но более точна, когда отклонения меньше при нормальном выражении (уравнения (11) и (22)). Другим важным критерием, связанным с точностью прогибов, является коэффициент оценки характера внешней нагрузки, так как после упрочнения меняется развитие трещин, меняется и развитие кривизны. Для проверки точности экспериментальных и расчетных результатов требуется дальнейший анализ методом конечных элементов.
Вклад авторов
Концептуализация, доктор медицины; Исследование, доктор медицины; Ресурсы, Т.С.; Supervision, J.V.
Финансирование
Это исследование не получало внешнего финансирования.
Благодарности
Спасибо всем исследователям, которые публикуют подробную теоретическую и экспериментальную информацию.
Конфликт интересов
Авторы заявляют об отсутствии конфликта интересов.
Обозначение
| А, В, С | обозначение уравнения глубины нейтральной оси; |
| А с | поперечное сечение слоя сжатого бетона; |
| A f | площадь поперечного сечения углеродного волокна; |
| А красный | преобразованное сечение балки; |
| А с 1 и А с 2 | площадь поперечного сечения растянутой и сжатой арматуры; |
| E см | модуль упругости бетона; |
| E f | модуль упругости углеродного волокна; |
| E s 1 , E s 2 | модуль упругости стальных стержней; |
| I II , I III | эффективный момент инерции на 2 и 3 ступенях; |
I I. red , I II.red , I III.red red , I II.red , I III.red | момент инерции преобразованного сечения на 1, 2 и 3 стадиях; |
| M I и M I.S | момент растрескивания неусиленной балки и усиленной балки соответственно; |
| M II.S | изгибающий момент усиленной балки при достижении текучести арматуры; |
| М R , M II | максимальный несущий изгибающий момент неусиленной балки; |
| M R.S , M II I | максимальный несущий изгибающий момент усиленной балки; |
| S красный | статический момент преобразованного сечения; |
| a | расстояние от опоры до нагрузки; |
| б | ширина балки; |
| d 1 и d 2 | расстояние от края балки до центра растянутой и сжатой арматуры; |
| f c | прочность на сжатие бетонных цилиндров; |
| f ct | прочность бетона на растяжение; |
| h | высота балки; |
| к 1 | коэффициент, оценивающий форму распределения напряжений; |
| l | длина пролета балки; |
| т ф | толщина слоя углеродного волокна; |
| х I , х II и х III | глубина нейтральной оси на этапах 1, 2 и 3; |
y c. I , y c.II , y c.III , I , y c.II , y c.III , | центр тяжести поперечного сечения балки на 1, 2 и 3 этапах; |
| α f , α s 1 , α s 2 | относительные коэффициенты; |
| γ 1.c , γ 1.t | относительные коэффициенты, оценивающие изменение глубины нейтральной оси на этапе 2; |
| γ 2.c , γ 2.t | относительные коэффициенты, оценивающие изменение глубины нейтральной оси на этапе 3; |
| е с | деформации сжатого бетона; |
| ε c 1 | деформации при достижении максимальной прочности бетонного материала; |
| ε f | деформация слоя углеродного волокна; |
| ε s | деформация растянутой арматуры; |
| ε s 2 | деформация сжатой арматуры; |
| σ c | напряжения в слое сжатого бетона; |
| σ f | напряжения в слое углеродного волокна; |
| σ s | напряжения в растянутой арматуре; |
| σ s 2 | напряжения в сжатой арматуре; |
| ω I , ω II | отклонение управляющей балки до конца I и II этапов. |
| ω I.S , ω II.S , ω III.S | прогиб усиленной балки до конца этапов I, II и III |
Приложение A
Рисунок A1.
Barros et al., 2005 [24] исследование смещения балки по сравнению с рассчитанным прогибом, ( a ) балка V1; ( б ) балка В1Р1; ( c ) балка V2; ( d ) балка V2R2; ( и ) балка V3; ( ф ) балка V3R2; ( г ) балка V4; ( х ) балка V4R3; ( i ) Разброс результатов при 60% и 80% предельной нагрузки.
Рисунок A1.
Barros et al., 2005 [24] исследование смещения балки по сравнению с рассчитанным прогибом, ( a ) балка V1; ( б ) балка В1Р1; ( c ) балка V2; ( d ) балка V2R2; ( и ) балка V3; ( f ) балка V3R2; ( г ) балка V4; ( х ) балка V4R3; ( и ) разброс результатов при 60% и 80% предельной нагрузки.
Рисунок A2.
Bilotta et al., 2015 [25] исследование отклонения балки по сравнению с расчетной, ( a ) балка Ref_c_no_1; ( b ) балка Ref_d_no_1; ( c ) балка EBR_c_1.4 × 40_1; ( d ) балка EBR_c_1,4 × 40_2; ( и ) балка EBR_d_1,4 × 40_1; ( ф ) балка ЭБР_d_1,4×40_2; ( г ) балка NSM_c_2 × 1,4 × 10_1; ( ч ) луч NSM_d_2 × 1,4 × 10_1; ( и ) луч NSM_c_3 × 1,4 × 10_1; ( j ) балка NSM_d_3 × 1,4 × 10_1; ( k ) разброс результатов при 60% и 80% предельной нагрузки.
Рисунок A2.
Bilotta et al., 2015 [25] исследование отклонения балки по сравнению с расчетной, ( a ) балка Ref_c_no_1; ( b ) балка Ref_d_no_1; ( c ) балка EBR_c_1.4 × 40_1; ( d ) балка EBR_c_1,4 × 40_2; ( и ) балка EBR_d_1,4 × 40_1; ( ф ) балка ЭБР_d_1,4×40_2; ( г ) пучок NSM_c_2×1,4×10_1; ( ч ) луч NSM_d_2 × 1,4 × 10_1; ( i ) луч NSM_c_3 × 1,4 × 10_1; ( j ) балка NSM_d_3 × 1,4 × 10_1; ( k ) разброс результатов при 60% и 80% предельной нагрузки.
Рисунок A3.
David et al., 2003 [26] исследование отклонения балки по сравнению с расчетным, ( a ) балка P1; ( б ) балка Р2; ( c ) балка P5; ( d ) Разброс результатов при 60% и 80% предельной нагрузки.
Рисунок A3.
David et al., 2003 [26] исследование отклонения балки по сравнению с расчетным, ( a ) балка P1; ( б ) балка Р2; ( c ) балка P5; ( d ) Разброс результатов при 60% и 80% предельной нагрузки.
Рисунок A4.
El-Gamal et al., 2016 [27] исследование отклонения балки по сравнению с расчетным ( a ) балкой REF; ( b ) балка CN1; ( c ) балка CN2; ( d ) балка ГН1; ( е ) балка ГН2; ( ф ) балка ЧЫБ; ( г ) балка GHYB; ( h ) балка REF-II; ( и ) балка CN1-II; ( j ) балка CN2-II; ( k ) разброс результатов при 60% и 80% предельной нагрузки.
Рисунок A4.
El-Gamal et al. , 2016 [27] исследование отклонения балки по сравнению с расчетным ( a ) балкой REF; ( b ) балка CN1; ( c ) балка CN2; ( d ) балка ГН1; ( и ) балка GN2; ( ф ) балка ЧЫБ; ( г ) балка GHYB; ( h ) балка REF-II; ( и ) балка CN1-II; ( j ) балка CN2-II; ( k ) разброс результатов при 60% и 80% предельной нагрузки.
, 2016 [27] исследование отклонения балки по сравнению с расчетным ( a ) балкой REF; ( b ) балка CN1; ( c ) балка CN2; ( d ) балка ГН1; ( и ) балка GN2; ( ф ) балка ЧЫБ; ( г ) балка GHYB; ( h ) балка REF-II; ( и ) балка CN1-II; ( j ) балка CN2-II; ( k ) разброс результатов при 60% и 80% предельной нагрузки.
Рисунок A5.
Ferrier et al., 2003 [28] исследование отклонения балки по сравнению с расчетным, ( a ) балка A2; ( b ) балка A0; ( c ) Разброс результатов при 60% и 80% предельной нагрузки.
Рисунок A5.
Ferrier et al., 2003 [28] исследование отклонения балки по сравнению с расчетным, ( a ) балка A2; ( b ) балка A0; ( c ) Разброс результатов при 60% и 80% предельной нагрузки.
Рисунок A6.
Gao et al., 2004 [29] исследование отклонения балки по сравнению с расчетным, ( a ) балка CON1; ( b ) балка A0; ( c ) балка A10; ( d ) балка А20; ( e ) балка B0; ( f ) балка B10; ( г ) балка В20; ( ч ) разброс результатов при 60% и 80% предельной нагрузки.
Рисунок A6.
Gao et al., 2004 [29] исследование отклонения балки по сравнению с расчетным, ( a ) балка CON1; ( b ) балка A0; ( c ) балка A10; ( d ) балка А20; ( e ) балка B0; ( f ) балка B10; ( г ) балка В20; ( ч ) разброс результатов при 60% и 80% предельной нагрузки.
Рисунок A7.
Gao et al., 2006 [30] исследование смещения балки по сравнению с рассчитанным отклонением, ( a ) балка 2O; ( б ) балка 2Н4; ( c ) балка 2Н6; ( д ) балка 2Т450-1; ( и ) балка 2Т625-1; ( ф ) балка 2Т650-1; ( г ) балка 2Т675-1; ( ч ) балка 2Т4100-1; ( i ) Разброс результатов при 60 % и 80 % предельной нагрузки.
Рисунок A7.
Gao et al., 2006 [30] исследование смещения балки по сравнению с рассчитанным прогибом, ( а ) балка 2О; ( б ) балка 2Н4; ( c ) балка 2Н6; ( д ) балка 2Т450-1; ( и ) балка 2Т625-1; ( ф ) балка 2Т650-1; ( г ) балка 2Т675-1; ( ч ) балка 2Т4100-1; ( i ) Разброс результатов при 60 % и 80 % предельной нагрузки.
Рисунок A8.
Heffernan 1997 [31] исследование смещения балки по сравнению с рассчитанным отклонением, ( a ) балка Обычная; ( b ) Усиленная балка из углепластика; ( c ) разброс результатов при 60% и 80% предельной нагрузки.
Рисунок A8.
Heffernan 1997 [31] исследование смещения балки по сравнению с рассчитанным отклонением, ( a ) балка Обычная; ( b ) Усиленная балка из углепластика; ( c ) Разброс результатов при 60% и 80% предельной нагрузки.
Рисунок A9.
Heffernan and Erki 2004 [32] исследование смещения балки по сравнению с рассчитанным отклонением, ( a ) балка CFRP усиленная; ( b ) балка Обычная; ( c ) Разброс результатов при 60% и 80% предельной нагрузки.
Рисунок A9.
Heffernan and Erki 2004 [32] исследование смещения балки по сравнению с рассчитанным отклонением, ( a ) балка CFRP усиленная; ( b ) балка Обычная; ( c ) Разброс результатов при 60% и 80% предельной нагрузки.
Рисунок A10.
Hosseini et al., 2014 [33] исследование отклонения балки по сравнению с расчетным, ( а ) балка SREF; ( б ) балка С2Л-0; ( c ) балка С2Л-20; ( д ) балка С2Л-40; ( e ) Разброс результатов при 60% и 80% предельной нагрузки.
Рисунок A10.
Hosseini et al., 2014 [33] исследование отклонения балки по сравнению с расчетным ( a ) балкой SREF; ( б ) балка С2Л-0; ( c ) балка С2Л-20; ( д ) балка С2Л-40; ( e ) Разброс результатов при 60% и 80% предельной нагрузки.
Рисунок A11.
Khalifa et al., 2016 [34] исследование отклонения балки по сравнению с расчетным, ( a ) балка B-C; ( б ) балка Б-С-2; ( c ) балка Б-С-4; ( д ) балка Б-Н-1-2; ( и ) балка Б-Н-2-2; ( ф ) балка Б-Н-2-4; ( г ) Разброс результатов при 60% и 80% предельной нагрузки.
Рисунок A11.
Khalifa et al., 2016 [34] исследование отклонения балки по сравнению с расчетным, ( a ) балка В-С; ( б ) балка Б-С-2; ( c ) балка Б-С-4; ( д ) балка Б-Н-1-2; ( и ) балка Б-Н-2-2; ( ф ) балка Б-Н-2-4; ( г ) Разброс результатов при 60% и 80% предельной нагрузки.
Рисунок A12.
Kotynia et al., 2008 [35] исследование прогиба балки по сравнению с расчетной, ( a ) балка Б-08С; ( б ) балка Б-083м; ( c ) Разброс результатов при 60% и 80% предельной нагрузки.
Рисунок A12.
Kotynia et al., 2008 [35] исследование прогиба балки по сравнению с расчетной, ( a ) балка Б-08С; ( б ) балка Б-083м; ( c ) Разброс результатов при 60% и 80% предельной нагрузки.
Рисунок A13.
Kotynia et al., 2011 [36] исследование прогиба балки по сравнению с расчетной, ( a ) балка G1; ( b ) балка G2; ( c ) балка G3; ( d ) балка G4; ( e ) Разброс результатов при 60% и 80% предельной нагрузки.
Рисунок A13.
Kotynia et al., 2011 [36] исследование прогиба балки по сравнению с расчетной, ( a ) балка G1; ( b ) балка G2; ( c ) балка G3; ( d ) балка G4; ( e ) Разброс результатов при 60% и 80% предельной нагрузки.
Рисунок A14.
Kotynia et al., 2014 [37] исследование прогиба балки по сравнению с расчетной, ( a ) балка B12; ( б ) балка б12-а; ( c ) балка Б12-аспид; ( д ) балка В12-асп-э; ( и ) балка B16; ( ф ) балка Б16-осевая; ( г ) балка B16-asp-e; ( ч ) разброс результатов при 60% и 80% предельной нагрузки.
Рисунок A14.
Kotynia et al., 2014 [37] исследование прогиба балки по сравнению с расчетной, ( a ) балка B12; ( б ) балка б12-а; ( c ) балка Б12-аспид; ( d ) балка B12-asp-e; ( и ) балка B16; ( ф ) балка Б16-осевая; ( г ) балка Б16-асп-э; ( ч ) разброс результатов при 60% и 80% предельной нагрузки.
Рисунок A15.
Omran et al., 2012 [38] исследование отклонения балки по сравнению с расчетным, ( a ) балка B0; ( б ) балка Б1-НП; ( c ) балка B1-P1; ( д ) балка Б1-П2; ( и ) балка Б1-П3; ( f ) Разброс результатов при 60% и 80% предельной нагрузки.
Рисунок A15.
Omran et al., 2012 [38] исследование отклонения балки по сравнению с расчетным, ( а ) балка В0; ( б ) балка Б1-НП; ( c ) балка B1-P1; ( д ) балка Б1-П2; ( и ) балка Б1-П3; ( f ) Разброс результатов при 60% и 80% предельной нагрузки.
Рисунок A16.
Rezazadeh et al., 2014 [39] исследование отклонения балки по сравнению с расчетным, ( a ) контроль балки; ( b ) балка Ненапряженная; ( c ) балка предварительно напряжена на 20%; ( d ) балка предварительно напряженная на 30%; ( е ) балка предварительно напряженная на 40 %; ( f ) Разброс результатов при 60% и 80% предельной нагрузки.
Рисунок A16.
Rezazadeh et al., 2014 [39] исследование отклонения балки по сравнению с расчетным, ( a ) контроль балки; ( b ) балка Ненапряженная; ( c ) балка предварительно напряжена на 20%; ( d ) балка предварительно напряженная на 30%; ( e ) балка предварительно напряженная на 40%; ( f ) Разброс результатов при 60% и 80% предельной нагрузки.
Рисунок A17.
Sharaky et al., 2014 [40] исследование прогиба балки по сравнению с расчетной, ( a ) балкой CB; ( b ) балка LB1C1; ( c ) балка LB1G1; ( d ) балка LB2C1; ( и ) балка LB2G1; ( f ) балка LA2C1; ( г ) балка ЛА2Г1; ( х ) балка LB1G2; ( i ) Разброс результатов при 60% и 80% предельной нагрузки.
Рисунок A17.
Sharaky et al., 2014 [40] исследование прогиба балки по сравнению с расчетным, ( а ) балка СВ; ( b ) балка LB1C1; ( c ) балка LB1G1; ( d ) балка LB2C1; ( и ) балка LB2G1; ( f ) балка LA2C1; ( г ) балка ЛА2Г1; ( х ) балка LB1G2; ( i ) Разброс результатов при 60% и 80% предельной нагрузки.
Рисунок A18.
Soudki et al., 2007 [41] исследование прогиба балки по сравнению с расчетной, ( a ) балка Т-0; ( б ) балка С-0; ( c ) балка С-0; ( d ) разброс результатов при 60% и 80% предельной нагрузки.
Рисунок A18.
Soudki et al., 2007 [41] исследование прогиба балки по сравнению с расчетной, ( a ) балка Т-0; ( б ) балка С-0; ( c ) балка С-0; ( d ) Разброс результатов при 60% и 80% предельной нагрузки.
Рисунок A19.
Teng et al., 2006 [42] исследование отклонения балки по сравнению с расчетным, ( a ) балка B0; ( б ) балка В500; ( c ) балка B1200; ( d ) балка B1800; ( и ) балка B2900; ( f ) Разброс результатов при 60% и 80% предельной нагрузки.
Рисунок A19.
Teng et al., 2006 [42] исследование отклонения балки по сравнению с расчетным, ( a ) балка B0; ( б ) балка В500; ( c ) балка B1200; ( d ) балка B1800; ( и ) балка B2900; ( f ) Разброс результатов при 60% и 80% предельной нагрузки.
Рисунок A20.
Valivonis et al., 2010 [14] исследование отклонения балки по сравнению с расчетным, ( a ) балка B6. 5; ( b ) балка B6.1C; ( c ) балка B6.2C; ( d ) балка В8.3; ( и ) балка B8.1C; ( f ) балка B8.2C; ( г ) балка В12,5; ( ч ) балка В12.6; ( и ) балка B12.1C; ( j ) балка B12.2C; ( k ) разброс результатов при 60% и 80% предельной нагрузки.
5; ( b ) балка B6.1C; ( c ) балка B6.2C; ( d ) балка В8.3; ( и ) балка B8.1C; ( f ) балка B8.2C; ( г ) балка В12,5; ( ч ) балка В12.6; ( и ) балка B12.1C; ( j ) балка B12.2C; ( k ) разброс результатов при 60% и 80% предельной нагрузки.
Рисунок A20.
Valivonis et al., 2010 [14] исследование отклонения балки по сравнению с расчетным, ( a ) балка B6.5; ( b ) балка B6.1C; ( c ) балка B6.2C; ( d ) балка В8.3; ( и ) балка B8.1C; ( f ) балка B8.2C; ( г ) балка В12,5; ( ч ) балка В12.6; ( и ) балка B12.1C; ( j ) балка B12.2C; ( k ) разброс результатов при 60% и 80% предельной нагрузки.
Рисунок A21.
Wu et al., 2014 [43] исследование отклонения балки по сравнению с расчетным, ( a ) управление балкой; ( б ) балка В11; ( c ) балка B21; ( d ) балка В22; ( и ) балка ВР11; ( f ) бам BP12; ( г ) балка ВР13; ( х ) балка ВР14; ( i ) Разброс результатов при 60% и 80% предельной нагрузки.
Рисунок A21.
Wu et al., 2014 [43] исследование отклонения балки по сравнению с расчетным, ( а ) Управление лучом; ( б ) балка В11; ( c ) балка B21; ( d ) балка В22; ( и ) балка ВР11; ( f ) бам BP12; ( г ) балка ВР13; ( х ) балка ВР14; ( i ) Разброс результатов при 60% и 80% предельной нагрузки.
Рисунок A22.
Xiong et al., 2007 [44] исследование отклонения балки по сравнению с расчетным, ( a ) луч Па; ( b ) балка Pb; ( c ) балка 2С; ( d ) разброс результатов при 60% и 80% предельной нагрузки.
Рисунок A22.
Xiong et al., 2007 [44] исследование отклонения балки по сравнению с расчетным, ( a ) луч Па; ( b ) балка Pb; ( c ) балка 2С; ( d ) Разброс результатов при 60% и 80% предельной нагрузки.
Ссылки
- Скутурна Т.; Валивонис, Дж.; Вайнюнас, П.; Марчукайтис, Г.
 ; Даугявичюс, М. Анализ прогибов мостовых балок, усиленных армированием из углеродного волокна. Балт. Дж. Роуд-Бридж, инженер. 2008 , 3, 145–151. [Google Scholar] [CrossRef]
; Даугявичюс, М. Анализ прогибов мостовых балок, усиленных армированием из углеродного волокна. Балт. Дж. Роуд-Бридж, инженер. 2008 , 3, 145–151. [Google Scholar] [CrossRef] - Даугявичюс М.; Валивонис, Дж.; Марчукайтис, Г. Анализ прогиба железобетонных балок, армированных полимером, армированным углеродным волокном, при длительном воздействии нагрузки. J. Zhejiang Univ.-Sci. A (Appl. Phys. Eng.) 2012 , 13, 571–583. [Google Scholar]
- Скутурна Т.; Валивонис, Дж. Статистическая оценка методов расчета несущей способности изгибаемых железобетонных элементов, усиленных стеклопластиком. Арка Гражданский мех. англ. 2015 , 15, 214–222. [Google Scholar] [CrossRef]
- Скутурна Т.; Валивонис, Дж. Экспериментальное исследование влияния систем анкеровки на железобетонные балки, усиленные с использованием FRP. Композиции Часть B 2016 , 91, 283–290. [Google Scholar] [CrossRef] «> Скутурна Т.; Валивонис, Дж. Оценка методов расчета, используемых для оценки сопротивления предельному моменту мостовых настилов, армированных стержнями из стеклопластика. Балт. Дж. Роуд-Бридж, инженер. 2016 , 11, 22–34. [Академия Google] [CrossRef]
- Эслами А.; Ронах, HR; Мостофинежад, Д. Аналитическая оценка железобетонных зданий, модернизированных из углепластика, подверженных колебаниям грунта, близким к разлому. Дж. Выполнить. Констр. Фасил. 2016 . [Google Scholar] [CrossRef]
- Аль-Русан, Р.; Исса, М. Усталостные характеристики железобетонных балок, усиленных листами углепластика. Констр. Строить. Матер. 2011 , 25, 3520–3529. [Google Scholar] [CrossRef]
- Аттари, Н.; Амзиан, С .; Чемрук, М. Усиление бетонных балок на изгиб с использованием листов из углепластика, стеклопластика и гибридных листов из стеклопластика. Констр. Строить. Матер. 2012 , 37, 746–757. [Google Scholar] [CrossRef] «> Li, X.; Гу, Х .; Песня, X .; Оуян, Ю.; Фэн, З. Вклад U-образных полос в изгибную способность низкопрочных железобетонных балок, усиленных композитными листами из углеродного волокна. Композиции Часть B 2013 , 45, 117–126. [Google Scholar] [CrossRef]
- Charalambidi, B.G.; Русакис, Т.С.; Карабинис, А.И. Анализ усталостных характеристик железобетонных балок, усиленных на изгиб армированными волокном полимерными ламинатами. Композиции Часть Б 2016 , 96, 69–78. [Google Scholar] [CrossRef]
- Triantafyllou, GG; Русакис, Т.С.; Карабинис, А.И. Поврежденные ж/б балки отремонтированы и усилены на изгиб полимерными ламинатами, армированными волокном. Композиции Часть B 2017 , 112, 125–136. [Google Scholar] [CrossRef]
- Charalambidi, B.G.; Русакис, Т.С.; Карабинис, А.И. Усталостные характеристики крупногабаритных железобетонных балок, усиленных на изгиб армированными волокном полимерными ламинатами.
 Дж. Компос. Констр. 2016 , 20. [Google Scholar] [CrossRef]
Дж. Компос. Констр. 2016 , 20. [Google Scholar] [CrossRef] - Чжан, С.С.; Ю, Т .; Чен, Г.М. Железобетонные балки, усиленные при изгибе с помощью приповерхностных (NSM) углепластиковых полос: текущее состояние и потребности в исследованиях. Композиции Часть B 2017 , 131, 30–42. [Google Scholar] [CrossRef]
- Valivonis, J.; Скутурна, Т .; Даугявичюс, М. Несущая способность железобетонных балок, усиленных углеродным волокнистым композитом, в растянутой зоне при временной или длительной нагрузке. В материалах 10-й Международной конференции по современным строительным материалам. Конструкции и техника, Вильнюс, Литва, 19–21 мая 2010 г.; стр. 818–825. [Google Scholar]
- Hawileh, R.A. Нелинейное конечно-элементное моделирование железобетонных балок, усиленных стержнями NSM FRP. Констр. Строить. Матер. 2012 , 27, 461–471. [Google Scholar] [CrossRef]
- Комитет ACI 318.
 Требования строительных норм и правил к конструкционному бетону; Американский институт бетона: Фармингтон-Хиллз, Мичиган, США, 2002 г. [Google Scholar]
Требования строительных норм и правил к конструкционному бетону; Американский институт бетона: Фармингтон-Хиллз, Мичиган, США, 2002 г. [Google Scholar] - Еврокод 2. Проектирование бетонных конструкций. Часть 1. Общие нормы и правила для зданий; Европейский комитет по стандартизации: Брюссель, Бельгия, 2004 г.
- Паттини, М.М.; Бургойн, А .; Бургойн, К. Момент-кривизна и энергия деформации балок с внешним армированием полимером, армированным волокном. Структура АКИ. Дж. 2009 , 106, 20–29. [Google Scholar]
- Yinghao, L.; Йонг, Ю. Расположение гибридных стержней на изгибе балок HSC. Композиции Часть B 2013 , 45, 22–31. [Google Scholar] [CrossRef]
- Guan, G.X.; Бургойн, С. Дж. Сравнение моделей момент-кривизна для исследований разрушения концов пластин из армированного волокном полимера с использованием подхода глобального энергетического баланса. Структура АКИ. Дж.
 2014 , 111, 27–36. [Google Scholar]
2014 , 111, 27–36. [Google Scholar] - Резазаде М.; Баррос, Дж.; Коста, Л. Аналитический подход к анализу на изгиб железобетонных балок, усиленных предварительно напряженным углепластиком. Композиции Часть B 2015 , 73, 16–34. [Google Scholar] [CrossRef]
- Smith, ST; Ким, С.Дж. Расчет прогиба изгибаемых элементов из железобетона, армированного армированным волокном. Ауст. Дж. Структура. англ. 2010 , 11, 75–86. [Google Scholar] [CrossRef]
- Smith, ST; Рашид, HA; Ким, С.Дж. Момент-кривизна, основанная на моделировании усиленных FRP элементов RC, закрепленных с помощью анкеров FRP. В материалах APFIS, Сингапур, 19– 21 июля 2017 г. [Google Scholar]
- Barros, J.A.O.; Фортес, А.С. Усиление бетонных балок на изгиб ламинатом из углепластика, вклеенным в прорези. Цем. Конкр. Композиции 2005 , 27, 471–480. [Google Scholar] [CrossRef] «> Билотта, А.; Черони, Ф .; Нигро, Э.; Печче, М. Эффективность полос NSM из углепластика и плит EBR для усиления изгиба железобетонных балок и влияния схемы нагрузки. Композиции Структура 2015 , 124, 163–175. [Google Scholar] [CrossRef]
- Дэвид Э.; Рагно, Э .; Бойл-Боден, Э. Экспериментальный анализ поведения на изгиб железобетонных конструкций из углепластика, скрепленных снаружи. Матер. Структура 2003 , 36, 238–241. [Google Scholar] [CrossRef]
- El-Gamal, SE; Аль-Нуайми, А. Эффективность метода поверхностного монтажа с использованием полимеров, армированных волокном, для усиления изгиба железобетонных балок. Констр. Строить. Матер. 2016 , 118, 52–62. [Google Scholar] [CrossRef]
- Ferrier, E.; Аврил, А .; Гамелин, П.; Вотрен, А. Механическое поведение железобетонных балок, армированных листами углепластика, скрепленными снаружи. Матер. Структура 2003 , 36, 522–529. [Академия Google] [CrossRef] «> Гао, Б.; Ким, Дж. К.; Люн, C.K.Y. Экспериментальное исследование железобетонных балок с полосами FRP, склеенными смолами, модифицированными каучуком. Композиции науч. Технол. 2004 , 64, 2557–2564. [Google Scholar] [CrossRef]
- Гао, Б.; Ким, Дж. К.; Люн, C.K.Y. Повышение эффективности полос FRP с коническими концами, приклеенных к железобетонным балкам. Композиции науч. Технол. 2006 , 66, 2257–2264. [Google Scholar] [CrossRef]
- Хеффернан, П. Дж. Усталостное поведение железобетонных балок, усиленных ламинатом из углепластика. Кандидат наук. Диссертация кафедры гражданского строительства Королевского военного колледжа Канады, Кингстон, Онтарио, Канада, 19 мая.97. [Google Scholar]
- Heffernan, P.J.; Эрки, М.А. Усталостное поведение железобетонных балок, усиленных пластиковыми ламинатами, армированными углеродным волокном. Дж. Компос. Констр. 2004 , 8, 132–140. [Google Scholar] [CrossRef] «> Hosseini, MRM; Диас, SJE; Баррос, Ж.А.О. Эффективность предварительно напряженных ламинатов NSM CFRP для укрепления на изгиб железобетонных плит. Композиции Структура 2014 , 111, 249–258. [Google Scholar] [CrossRef]
- Халифа, А.М. Прочность железобетонных балок на изгиб. Усилено полосами углепластика, установленными вблизи поверхности. Алекс. англ. Дж. 2016 , 55, 1497–1505. [Google Scholar] [CrossRef]
- Котыня Р.; Бакы, HA; Нил, KW; Эбеад, Ю.А. Усиление изгиба железобетонных балок с системами углепластика с внешним соединением: результаты испытаний и трехмерный нелинейный анализ конечного элемента. Дж. Компос. Констр. 2008 , 12, 190–201. [Google Scholar] [CrossRef]
- Котыня Р.; Валензиак, Р.; Стоклин, И.; Мейер, У. Железобетонные плиты, усиленные предварительно напряженными и постепенно закрепляемыми полосами из углепластика при монотонной и циклической нагрузке. Дж. Компос.
 Констр. 2011 , 15, 168–180. [Google Scholar] [CrossRef]
Констр. 2011 , 15, 168–180. [Google Scholar] [CrossRef] - Котыня Р.; Ласек, К.; Стаскевич, М. Поведение предварительно нагруженных железобетонных плит, усиленных предварительно напряженными ламинатами из углепластика, при изгибе. Дж. Компос. Констр. 2014 , 18, А4013004. [Google Scholar] [CrossRef]
- Omran, HY; Эль-Хача, Р. Нелинейное трехмерное моделирование методом конечных элементов железобетонных балок, усиленных предварительно напряженными полосами NSM-CFRP. Констр. Строить. Матер. 2012 , 31, 74–85. [Академия Google] [CrossRef]
- Резазаде, М.; Коста, И.; Баррос, Дж. Влияние уровня предварительного напряжения на ламинаты NSM CFRP для усиления изгиба железобетонных балок. Композиции Структура 2014 , 116, 489–500. [Google Scholar] [CrossRef]
- Шаракий И.А.; Торрес, Л.; Комас, Дж.; Баррис, К. Реакция на изгиб железобетонных (ЖБ) балок, усиленных стержнями из полимера, армированного волокном (FRP) с поверхностным монтажом (NSM).
 Композиции Структура 2014 , 109, 8–22. [Google Scholar] [CrossRef]
Композиции Структура 2014 , 109, 8–22. [Google Scholar] [CrossRef] - Судки, К.; Эль-Салакави, Э.; Крейг, Б. Поведение балок из армированного армированного бетона, усиленного углепластиком, в коррозионной среде. Дж. Компос. Констр. 2007 , 11, 291–298. [Google Scholar] [CrossRef]
- Teng, J.G.; Де Лоренцис, Л.; Ван, Б.; Ли, Р .; Вонг, Т. Н.; Лам, Л. Неисправности при разрушении железобетонных балок, усиленных полосами углепластика, установленными вблизи поверхности. Дж. Компос. Констр. 2006 , 10, 92–105. [Google Scholar] [CrossRef]
- Ву, Г.; Донг, ZQ; Ву, З.С.; Чжан, Л.В. Производительность и параметрический анализ усиления на изгиб железобетонных балок с стержнями NSM-CFRP. Дж. Компос. Констр. 2014 . [Академия Google] [CrossRef]
- Сюн, Г.Дж.; Цзян, X .; Лю, JW; Чен, Л. Способ предотвращения расслоения бетонного покрытия в середине пролета усиленных FRP балок.
 Констр. Строить. Матер. 2007 , 21, 402–408. [Google Scholar] [CrossRef]
Констр. Строить. Матер. 2007 , 21, 402–408. [Google Scholar] [CrossRef] - Branson, D.E. деформация бетонных конструкций; McGraw-Hill: New York, NY, USA, 1977. [Google Scholar]
Рис. 1.
Развитие прогиба усиленной и неусиленной балки.
Рис. 1.
Развитие прогиба усиленной и неусиленной балки.
Рисунок 2.
Изменение глубины нейтральной оси железобетонной усиленной балки: ( a ) Поперечное сечение усиленной балки; ( b ) глубина нейтральной оси перед открытием вертикальных трещин; ( c ) глубина нейтральной оси при вскрытии вертикальных трещин; ( d ) глубина нейтральной оси при достижении текучести стали.
Рис. 2.
Изменение глубины нейтральной оси железобетонной усиленной балки: ( a ) Поперечное сечение усиленной балки; ( b ) глубина нейтральной оси перед открытием вертикальных трещин; ( c ) глубина нейтральной оси при вскрытии вертикальных трещин; ( d ) глубина нейтральной оси при достижении текучести стали.
Рисунок 3.
Изменение глубины нейтральной оси ж/б балки: ( a ) Сечение балки ( b ) глубина нейтральной оси до раскрытия вертикальных трещин; ( c ) глубина нейтральной оси при раскрытии вертикальных трещин.
Рис. 3.
Изменение глубины нейтральной оси ж/б балки: ( a ) Поперечное сечение балки ( b ) глубина нейтральной оси перед раскрытием вертикальных трещин; ( c ) глубина нейтральной оси при раскрытии вертикальных трещин.
Рисунок 4.
Напряженно-деформированное состояние в усиленной ЖБ балке до достижения предела текучести арматуры: ( a ) Глубина нейтральной оси; ( b ) распространение штаммов; ( c ) распределение напряжений; ( d ) внутренние силы.
Рис. 4.
Напряженно-деформированное состояние в усиленной ЖБ балке до достижения текучести арматуры: ( a ) Глубина нейтральной оси; ( b ) распространение штаммов; ( c ) распределение напряжений; ( d ) внутренние силы.
Рисунок 5.
Напряженно-деформированное состояние в усиленной ЖБ балке при достижении податливости арматуры: ( a ) Глубина нейтральной оси; ( b ) распространение штаммов; ( c ) распределение напряжений; ( d ) внутренние силы.
Рис. 5.
Напряженно-деформированное состояние в усиленной ЖБ балке при достижении текучести арматуры: ( a ) Глубина нейтральной оси; ( b ) распространение штаммов; ( c ) распределение напряжений; ( d ) внутренние силы.
Рисунок 6.
Кривые изгибающий момент–прогиб, ( а ) балка В1Р1; ( б ) луч NSM_c_2 × 1,4 × 10_1; ( c ) балка P1; ( d ) балка CN1.
Рис. 6.
Кривые изгибающий момент-прогиб, ( a ) балка V1R1; ( б ) луч NSM_c_2 × 1,4 × 10_1; ( c ) балка P1; ( d ) балка CN1.
Рис. 7.
Кривые изгибающий момент-прогиб, ( a ) балка A2; ( b ) балка A0; ( c ) балка 2Н4; ( d ) Усиленная балка из углепластика; ( e ) балка усиленная углепластиком; ( ф ) балка С2Л-0; ( г ) балка Б-Н-1-2; ( ч ) Балка Б-08С.
Рис. 7.
Кривые изгибающий момент-прогиб, ( a ) балка A2; ( b ) балка A0; ( c ) балка 2Н4; ( d ) Усиленная балка из углепластика; ( e ) усиленная балка из углепластика; ( ф ) балка С2Л-0; ( г ) балка Б-Н-1-2; ( ч ) Балка Б-08С.
Рис. 8.
Кривые изгибающий момент–прогиб, ( а ) балка Г2; ( б ) балка В12-а; ( c ) балка Б1-НП; ( d ) балка ненапряженная, ( e ) балка LB1C1; ( ф ) балка Т-0; ( г ) B500; ( ч ) B6.1C.
Рис. 8.
Кривые изгибающий момент-прогиб, ( a ) балка G2; ( б ) балка В12-а; ( c ) балка Б1-НП; ( d ) балка ненапряженная, ( e ) балка LB1C1; ( ф ) балка Т-0; ( г ) B500; ( ч ) B6.1C.
Рис. 9.
Кривые зависимости изгибающего момента от прогиба, ( a ) балка B11; ( б ) балка 2С.
Рис. 9.
9.
Кривые зависимости изгибающего момента от прогиба, ( a ) балка B11; ( б ) балка 2С.
Таблица 1.
Характеристики исследуемых экспериментальных пучков.
Таблица 1.
Характеристики исследуемых экспериментальных пучков.
| Автор | Beam Name | l, m | Load Positions, m | b, m | h, m | A s1 | A s2 | d 1 , m | d 2 , m | A f | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Barros et al. , 2005 [24] , 2005 [24] | V1 | 1.5 | 0.5 + 0.5 + 0.5 | 0.1 | 0.178 | 2Ø6 | 2Ø8 | 0,024 | 0,025 | – | |||||||
| V1R1 | 0.17 | 2Ø6 | 1 × 1.45 × 9.59 | ||||||||||||||
| V2 | 0.173 | 3Ø6 | – | ||||||||||||||
| V2R2 | 0. 177 177 | 3Ø6 | 2 × 1.45 × 9.59 | ||||||||||||||
| V3 | 0.175 | 2Ø6 | – | ||||||||||||||
| V3R2 | 0.175 | 2Ø6 + Ø8 | 2 × 1.45 × 9.59 | ||||||||||||||
| V4 | 0.175 | 3Ø8 | 0.025 | – | |||||||||||||
| V4R3 | 0.18 | 3Ø8 | 3 × 1.45 × 9. 59 59 | ||||||||||||||
| Bilotta et al., 2015 [25] | Ref_c_no_1 | 2.1 | 0.925 + 0.25 + 0.925 | 0.12 | 0.16 | 2Ø10 | 2Ø10 | 0.05 | 0.035 | – | |||||||
| Ref_d_no_1 | Distributed load | – | |||||||||||||||
| EBR_c_1.4 × 40_1 | 0.925 + 0.25 + 0. 925 925 | 56 mm 2 | |||||||||||||||
| EBR_c_1.4 × 40_2 | 56 mm 2 | ||||||||||||||||
| EBR_d_1.4 × 40_1 | Distributed load | 56 mm 2 | |||||||||||||||
| EBR_d_1.4 × 40_2 | 56 mm 2 | ||||||||||||||||
| NSM_c_2_1.4 × 10_1 | 0.925 + 0.25 + 0.925 | 28 mm 2 | |||||||||||||||
| NSM_d_2_1.4 × 10_1 | Distributed load | 28 mm 2 | |||||||||||||||
NSM_c_3_1. 4 × 10_1 4 × 10_1 | 0.925 + 0.25 + 0.925 | 42 mm 2 | |||||||||||||||
| NSM_d_3_1.4 × 10_1 | Distributed load | 42 mm 2 | |||||||||||||||
| David et al., 2003 [26] | P1 | 2.8 | 0.9 + 1.0 + 0.9 | 0.15 | 0.3 | 2Ø14 | 2Ø8 | 0,027 | 0,024 | — | |||||||
| P2 | 1,2 (CM 2 ) | ||||||||||||||||
| P5 | |||||||||||||||||
| P5 | |||||||||||||||||
| P5 | |||||||||||||||||
| P5 | |||||||||||||||||
| P5 | |||||||||||||||||
. ] ] | REF | 2.36 | 0.93 + 0.5 + 0.93 | 0.2 | 0.3 | 2Ø12 | 2Ø8 | 0.04 | 0.032 | – | |||||||
| CN1 | 71.26 (mm 2 ) | ||||||||||||||||
| CN2 | 2 × 71.26 (mm 2 ) | ||||||||||||||||
| GN1 | 71.3 (mm 2 ) | ||||||||||||||||
| GN2 | 2 × 71. 3 (mm 2 ) 3 (mm 2 ) | ||||||||||||||||
| CHYB | 71.26 + 25.8 (mm 2 ) | ||||||||||||||||
| GHYB | 71.3 + 25.8 (mm 2 ) | ||||||||||||||||
| REF-II | 4Ø12 | – | |||||||||||||||
| CN1-II | 71.26 ( мм 2 ) | ||||||||||||||||
| CN2-II | 2 × 71,26 (мм 2 ) | ||||||||||||||||
| Ferrier et al., 2003 [28] | A1 | 3 2,057 | A1 | 3 2,057 | 333333355 A1 | 3 2,057 | 33333355 A1 | 3 2,057 | A1 | 3 2,057 | A1 | 2,057 | 2Ø14 | 2Ø8 | 0.025 | 0.025 | – |
| A2 | 120 (mm 2 ) | ||||||||||||||||
| Gao et al., 2004 [29] | CON1 | 1.5 | 0.5 | 0,15 | 0.2 | 2Ø10 | 2Ø8 | 0.038 | 0. 027 027 | – | |||||||
| A0 | 0.22 × 75 | ||||||||||||||||
| A10 | 0.22 × 75 | ||||||||||||||||
| A20 | 0.22 × 75 | ||||||||||||||||
| B0 | 0,44 × 75 | ||||||||||||||||
| B10 | 0,44 × 75 | ||||||||||||||||
| B20 | 0,44 × 75 | ||||||||||||||||
| 0,44 × 75 | |||||||||||||||||
| .0057 | 0.5 | 0.15 | 0. 2 2 | 2Ø10 | 2Ø8 | 0.038 | 0.027 | – | |||||||||
| 2N6 | 6 × 0.11 × 150 | ||||||||||||||||
| 2T625-1 | |||||||||||||||||
| 2T650-1 | |||||||||||||||||
| 2T675-1 | |||||||||||||||||
| 2N4 | 4 × 0.11 × 150 | ||||||||||||||||
| 2T450-1 | |||||||||||||||||
| 2T4100-1 | |||||||||||||||||
| Heffernan 1997 [31] | Conventional | 4. 8 8 | 1.6 + 1.6 + 1.6 | 0.3 | 0.5739 | 2Ø25 + Ø20 | 2Ø10 | 0.074 | 0.067 | – | |||||||
| CFRP strengthened | 65.5 (mm 2 ) | ||||||||||||||||
| Heffernan and Erki 2004 [32] | Conventional | 2.85 | 1.1 + 0.65 + 1.1 | 0.15 | 0. 3 3 | 2Ø20 + Ø10 | 2Ø10 | 0.041 | 0.037 | – | |||||||
| CFRP strengthened | 89.4 (mm 2 ) | ||||||||||||||||
| Hosseini et al., 2014 [33] | SREF | 2.4 | 0.9 + 0.6 + 0.9 | 0.6 | 0.12 | 4Ø8 | 3Ø6 | 0. 024 024 | 0.023 | – | |||||||
| S2L-0 | 2 × 1.4 × 20 | ||||||||||||||||
| S2L-20 | |||||||||||||||||
| S2L-40 | |||||||||||||||||
| Khalifa et al ., 2016 [34] | B-C | 2.2 | 0.95 + 0.3 + 0.95 | 0.15 | 0.26 | 2Ø12 | 2Ø12 | 0.041 | 0.031 | – | |||||||
| B-S-2 | 60 (mm 2 ) | ||||||||||||||||
| B-S-4 | 120 (mm 2 ) | ||||||||||||||||
| B-N-1-2 | 60 (mm 2 ) | ||||||||||||||||
| B-N-2-2 | 60 (mm 2 ) | ||||||||||||||||
| Б-Н-2-4 | 120 (mm 2 ) | ||||||||||||||||
Kotynia et al. , 2008 [35] , 2008 [35] | B-08S | 4.2 | 1.4 + 1.4 + 1.4 | 0.15 | 0.3 | 3Ø12 | 2Ø10 | 0,03 * | 0,03 ** | 60 (мм 2 ) | |||||||
| B-083M | 58,5 (мм 2 ) | 58,5 (мм 2 ) | 58,5 (мм 2 ) | 58,5 (мм 2 ) | 6,0 | 1,2 + 1,2 + 1,2 + 1,2 + 1,2 | 1. 0 0 | 0.22 | 7Ø12 | 7Ø8 | 0.03143 * | 0.024 ** | – | ||||
| G2 | 120 (mm 2 ) | ||||||||||||||||
| G3 | 120 (mm 2 ) | ||||||||||||||||
| G4 | 120 (mm 2 ) | ||||||||||||||||
| Kotynia et al., 2014 [37] | B12-a | 6.0 | 1.2 + 1. 2 + 1.2 + 1.2 + 1.2 2 + 1.2 + 1.2 + 1.2 | 0,5 | 0,22 | 4Ø12 | 4Ø8 | 0.031 | 0.029 | 1.2 × 100 | |||||||
| B12-asp | 1.2 × 100 | ||||||||||||||||
| B16-asp | 1.2 × 100 | ||||||||||||||||
| Omran et al., 2012 [38] | B0 | 5.0 | 2 + 1 + 2 | 0.2 | 0. 4 4 | 3Ø15 | 2Ø10 | 0.057 | 0.036 | – | |||||||
| B1-NP | 2 × 2 × 16 | ||||||||||||||||
| B1-P1 | |||||||||||||||||
| B1-P2 | |||||||||||||||||
| B1-P3 | |||||||||||||||||
| . 0.3 | 2Ø10 | 2Ø10 | 0.035 | 0.025 | – | ||||||||||||
| Non prestressed | 1. 4 × 20 4 × 20 | ||||||||||||||||
| 20% prestressed | |||||||||||||||||
| 30% prestressed | |||||||||||||||||
| 40% prestressed | |||||||||||||||||
| Sharaky et al., 2014 [40] | CB | 2.4 | 0.8 + 0.8 + 0.8 | 0.16 | 0.28 | 2Ø12 | 2Ø8 | 0.036 | 0.034 | – | |||||||
| LB1C1 | 1Ø8 | ||||||||||||||||
| LB1G1 | 1Ø8 | ||||||||||||||||
| LB2C1 | 2Ø8 | ||||||||||||||||
| LB2G1 | 2Ø8 | ||||||||||||||||
| LA2C1 | 2Ø8 | ||||||||||||||||
| LA2G1 | 2Ø8 | ||||||||||||||||
| LB1G2 | 1Ø12 | ||||||||||||||||
Soudki et al. , 2007 [41] , 2007 [41] | C-0 | 2.25 | 0.75 | 0.15 | 0.25 | 2ø10 | 2ø6 | 0,025 | 0,023 | — | |||||||
| T-0 | 4 × 0,11 | ||||||||||||||||
| B0 | 3.0 | 1.2 + 0.6 + 1. 2 2 | 0.15 | 0.3 | 2Ø12 | 2Ø8 | 0.036 | 0.034 | – | ||||||||
| B500 | 2 × 16 | ||||||||||||||||
| B1200 | |||||||||||||||||
| B1800 | |||||||||||||||||
| B2900 | |||||||||||||||||
| Valivonis et al., 2010 [14] | B6.1C | 1.2 | 0.4 + 0.4 + 0.4 | 100 | 200 | 2Ø6 | 2Ø6 | 0. 025 025 | 0.025 | 0.167 (cm 2 ) | |||||||
| B6.2C | |||||||||||||||||
| B6.5 | – | ||||||||||||||||
| B8.1C | 2Ø8 | 0.167 (cm 2 ) | |||||||||||||||
| B8.2C | |||||||||||||||||
| B8.3 | – | ||||||||||||||||
| B12.1C | 203 | 2Ø12 | 2Ø8 | 0.167 (cm 2 ) | |||||||||||||
B12 . 2С 2С | 200 | ||||||||||||||||
| B12.5 | 104 | 198 | — | ||||||||||||||
| B12.6 | 105 | 201 9007 | |||||||||||||||
| 575757757757757757757757757757775777777777 | 57. | 0.6 + 0.6 + 0.6 | 0.15 | 0.3 | 3Ø14 | 2Ø6 | 0.037 | 0. 033 033 | – | ||||||||
| B11 | Ø7.9 | ||||||||||||||||
| B21 | 2Ø7.9 | ||||||||||||||||
| B22 | |||||||||||||||||
| BP11 | Ø7.9 | ||||||||||||||||
| BP12 | |||||||||||||||||
| BP13 | |||||||||||||||||
| BP14 | |||||||||||||||||
| Xiong et al., 2007 [44] | Pa | 2.1 | 0.7 | 0.125 | 0. 2 2 | 2 × 10 | 2×8 | 0.03 | 0.024 | – | |||||||
| 2C | 0.22 × 100 | ||||||||||||||||
| Pb | 2 × 12 | 0,031 | – |
* a s = h-A s1 /ń s1 ·b; ** оценивается индивидуально; l – длина пролета; б — общая ширина балки; h – высота балки; А с1 — поперечное сечение растянутых стальных стержней; А с2 — поперечное сечение сжатого стального стержня; д 1 —положение растянутых стальных стержней; d 2 —положение сжатых стальных стержней; A f — поперечное сечение натянутых волокон или FRP; ńs1 – коэффициент усиления на А с1 .
Таблица 2.
Механические характеристики материалов исследуемых экспериментальных балок.
Таблица 2.
Механические характеристики материалов исследуемых экспериментальных балок.
| Author | Beam Name | f c , MPa | f ct , MPa | E c , GPa | f y1 , MPa | f y2 , MPa | Е с1 , GPA | E 3 S2 , GPA | F F, FE , MPA | E F, FE , GPA | 33 F, FE , GPA | 3. | 46.1 | 3.37 | 33.35 | 730 | 554.32 | 200 | 200 | – | – |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| V1R1 | 2740 | 158.8 | ||||||||||
| V2 | 46.1 | 3.58 | 36.5 | 730 | – | – | ||||||
| V2R2 | 2740 | 158. 8 8 | ||||||||||
| V3 | 46.1 | 3.21 | 34.89 | 730 | – | – | ||||||
| V3R2 | 730; 554.32 | 2740 | 158.8 | |||||||||
| V4 | 46.1 | 3.43 | 35.86 | 554.32 | – | – | ||||||
| V4R3 | 2740 | 158. 8 8 | ||||||||||
| Bilotta et al., 2015 [25] | Ref_c_no_1 | 17.4 | 1.34 | 25.98 | 540 | 540 | 200 | 200 | – | – | ||
| Ref_d_no_1 | – | – | ||||||||||
| EBR_c_1.4 × 40_1 | 2052 | 171 | ||||||||||
EBR_c_1. 4 × 40_2 4 × 40_2 | ||||||||||||
| EBR_d_1.4 × 40_1 | ||||||||||||
| EBR_d_1.4 × 40_2 | ||||||||||||
| NSM_c_2_1.4 × 10_1 | ||||||||||||
| NSM_d_2_1.4 × 10_1 | ||||||||||||
| NSM_c_3_1.4 × 10_1 | ||||||||||||
| NSM_d_3_1.4 × 10_1 | ||||||||||||
| David et al., 2003 [26] | P1 | 38.7 | 2.94 1 | 33.02 2 | 500 | 500 | 205 3 | 205 3 | – | – | ||
| P2 | 39. 2 2 | 2.97 1 | 33.14 2 | 2400 | 150 | |||||||
| P5 | 40.1 | 3.03 1 | 33.37 2 | |||||||||
| EL-Gamal et al., 2016 [27] | REF | 49.62 | 2.99 | 35.57 2 | 480 | 455 | 205 3 | 205 3 | – | – | ||
| CN1 | 1588 | 119. 4 4 | ||||||||||
| CN2 | ||||||||||||
| GN1 | 1185 | 52.34 | ||||||||||
| GN2 | ||||||||||||
| CHYB | 2096 * | 147.47 * | ||||||||||
| GHYB | 1800 * | 98.22 * | ||||||||||
| REF-II | – | – | ||||||||||
| CN1-II | 1588 | 119.4 | ||||||||||
| CN2-II | ||||||||||||
Ferrier et al. , 2003 [28] , 2003 [28] | A1 | 39 | 2.96 1 | 31 | 550 | 550 3 | 210 | 210 3 | – | – | ||
| A2 | 650 | 80 | ||||||||||
| Gao et al., 2004 [29] | CON1 | 35.7 | 2. 75 1 75 1 | 25 | 531 | 400 | 200 | 200 | – | – | ||
| A0 | 4200 | 235 | ||||||||||
| A10 | ||||||||||||
| A20 | ||||||||||||
| B0 | ||||||||||||
| B10 | ||||||||||||
| B20 | ||||||||||||
| Gao et al., 2006 [30] | 2O | 62. 1 1 | 4.29 1 | 37.1 | 460 | 460 | 200 | 205 | – | – | ||
| 2N6 | 4200 | 235 | ||||||||||
| 2T625-1 | ||||||||||||
| 2T650-1 | ||||||||||||
| 2T675-1 | ||||||||||||
| 2N4 | ||||||||||||
| 2T450-1 | ||||||||||||
| 2T4100-1 | ||||||||||||
| HEFFERNAN 1997 [31] | . 0057 0057 | — | 200 | 200 | – | – | ||||||
| CFRP strengthened | 325 | |||||||||||
| Heffernan and Erki 2004 [32] | Conventional | 37 | 2.83 1 | 32.57 2 | 511 и 411 | 411 | 210 | 210 | — | — | ||
5. 0057 0057 | SREF | 46.7 | 3.43 1 | 29.7 | 486 | 464 | 200 | 200 | – | – | ||
| S2L-0 | 2483.9 | 153.2 | ||||||||||
| S2L-20 | ||||||||||||
| S2L-40 | ||||||||||||
| Khalifa et al., 2016 [34] | B-C | 35 | 2. 7 1 7 1 | 28 | 400 | 400 | 200 | 200 | 2800 | 165 | ||
| B-S-2 | ||||||||||||
| B-S-4 | ||||||||||||
| B-N-110057 | ||||||||||||
| . -4 | ||||||||||||
| Kotynia et al., 2008 [35] | B-08S | 32. 3 3 | 2.52 1 | 31.27 2 | 490 | 524 | 195 | 209 | 2915 | 172 | ||
| B-083m | 34.4 | 2.66 1 | 31.87 2 | 436 | 524 | 220 | 209 | 3500 | 230 | |||
Kotynia et al. , 2011 [ 36] , 2011 [ 36] | G1 | 45 | 3.33 1 | 34.55 2 | 554 | 561 | 200 | 200 | – | – | ||
| G2 | 46.2 | 3.4 1 | 34.82 2 | 2800 | 165 | |||||||
| G3 | 45. 9 9 | 3.39 1 | 34.75 2 | |||||||||
| G4 | 45.6 | 3.37 1 | 34.68 2 | 2235 | 149 | |||||||
| Kotynia et al., 2014 [37] | B12-a | 45.3 | 3.35 | 24.3 | 539.6 | 416.2 | 191.3 | 186.1 | 2800 | 173. 3 3 | ||
| B12-asp | 32.2 | 2.51 | 23.7 | 511.4 | 583.2 | 191.4 | 200.7 | |||||
| B16-ASP | 49 | 3,57 | 25,4 | 595 | 555,8 | 198 | 196,4 | |||||
| 40 | 3.02 1 | 27. 84 84 | 478 | 500 | 200 | 200 | – | – | ||||
| B1-NP | 2610 | 130.5 | ||||||||||
| B1-P1 | ||||||||||||
| B1-P2 | ||||||||||||
| B1-P3 | ||||||||||||
| Rezazadeh et al., 2014 [39] | Control | 32.2 | 2.51 1 | 27. 4 4 | 585 | 585 | 208 | 208 | – | – | ||
| Non prestressed | 1922 | 164 | ||||||||||
| 20% prestressed | ||||||||||||
| 30% prestressed | ||||||||||||
| 40% prestressed | ||||||||||||
| Sharaky et al., 2014 [40] | CB | 32.4 | 2.8 | 31. 7 7 | 545 | 545 | 205 | 205 | – | – | ||
| LB1C1 | 2350 | 170 | ||||||||||
| LB1G1 | 1350 | 64 | ||||||||||
| LB2C1 | 2350 | 170 | ||||||||||
| LB2G1 | 1350 | 64 | ||||||||||
| LA2C1 | 2350 | 170 | ||||||||||
| LA2G1 | 1350 | 64 | ||||||||||
| LB1G2 | 1350 | 64 9007 9007 9007 9007 9007 9007 9007 9007 9007 9007 9007. 0057 0057 | C-0 | 35 | 2.7 | 32.04 | 460 | 460 | 205 | 205 | – | – |
| T-0 | 3480 | 230 | ||||||||||
| S -0 | 2800 | 165 | ||||||||||
| Teng et al., 2006 [42] | B0 | 44 | 3. 27 1 27 1 | 34.31 2 | – | – | 210 | 210 | – | – | ||
| B500 | 2068 | 131 | ||||||||||
| B1200 | ||||||||||||
| B1800 | ||||||||||||
| B2900 | ||||||||||||
| Valivonis et al., 2010 [14] | B6 .1C | 34.4 | 2. 93 93 | 32.45 | 358 | 358 | 205 | 205 | 4800 | 231 | ||
| B6.2C | ||||||||||||
| B6.5 | – | – | ||||||||||
| B8.1C | 29.7 | 2.63 | 30.91 | 557 | 358 | 195 | 205 | 4800 | 231 | |||
B8. 2C 2C | ||||||||||||
| B8.3 | – | – | ||||||||||
| B12.1C | 30.4 | 2.67 | 31.14 | 318 | 420 | 204.9 | 204.1 | 4800 | 231 | |||
| B12.2C | ||||||||||||
| B12.5 | 28.7 | 2.56 | 30. 55 55 | – | – | |||||||
| B12.6 | – | – | ||||||||||
| Wu et al., 2014 [43] | Control | 34.4 | 2.66 1 | 31.87 2 | 340 | 240 | 200 | 200 | – | – | ||
| B11 | 2629 | 170 | ||||||||||
| B21 | ||||||||||||
| B22 | ||||||||||||
| BP11 | ||||||||||||
| BP12 | ||||||||||||
| BP13 | ||||||||||||
| BP14 | ||||||||||||
Xiong et al. , 2007 [44] , 2007 [44] | Pa | 30.71 | 2.41 1 | 30.8 2 | 411 | 233 | 200 | 210 | – | – | ||
| 2C | 3652 | 252 | ||||||||||
| Pb | 606 | 210 | – | – |
1 f ctm = 0.

 Под собственным весом,
Под собственным весом,


 Участки стыков заливаются бетоном.
Участки стыков заливаются бетоном. При их изготовлении используется не просто алюминий, а его сплавы. В строительстве такие изделия применяются реже, чем стальные аналоги, так как они уступают по показателям устойчивости при сильных нагрузках. Чаще всего алюминиевые балки применяют при строительстве малогабаритных зданий. При возведении промышленных объектов изделия из данного металла применяются только в комбинации со стальными конструкциями.
При их изготовлении используется не просто алюминий, а его сплавы. В строительстве такие изделия применяются реже, чем стальные аналоги, так как они уступают по показателям устойчивости при сильных нагрузках. Чаще всего алюминиевые балки применяют при строительстве малогабаритных зданий. При возведении промышленных объектов изделия из данного металла применяются только в комбинации со стальными конструкциями.

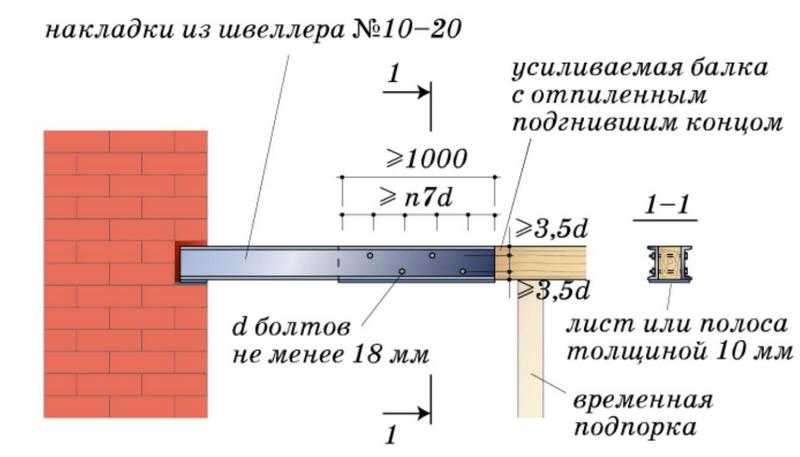

 Т.е. если рассматривать график бесконечно близко слева и бесконечно близко справа мы получаем два разных значения как поперечной силы, так и момента. И этот скачок для поперечной силы должен равняться приложенной сосредоточенной силе, а для момента приложенному сосредоточенному моменту.
Т.е. если рассматривать график бесконечно близко слева и бесконечно близко справа мы получаем два разных значения как поперечной силы, так и момента. И этот скачок для поперечной силы должен равняться приложенной сосредоточенной силе, а для момента приложенному сосредоточенному моменту.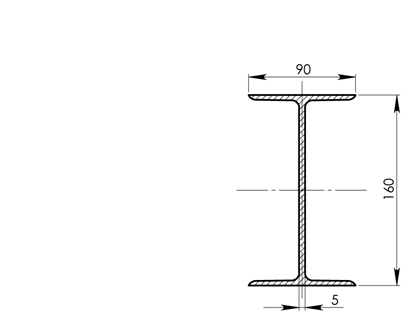
 Нужно только правильно идентифицировать тип и размер балки и определить искомый прогиб;
Нужно только правильно идентифицировать тип и размер балки и определить искомый прогиб;





 1 Цельные балки
1 Цельные балки Полки балки, стенка, ребра жесткости, накладка и сварные швы моделируются с использованием четырехузлового элемента 181 конструктивной оболочки. SHELL181 подходит для анализа оболочечных конструкций от тонких до умеренно толстых[2]. Четыре ребра жесткости полностью соединены в точках нагрузки. Контактный элемент 174 и мишень 170 используются для моделирования поверхности между накладкой и фланцем образца. Все узлы усиленного фланца и накладки сцеплены на расстоянии, равном средней их толщине. Толщина сварных элементов варьируется, чтобы обеспечить поперечное сечение, равное сечению углового шва толщиной 6 мм.
Полки балки, стенка, ребра жесткости, накладка и сварные швы моделируются с использованием четырехузлового элемента 181 конструктивной оболочки. SHELL181 подходит для анализа оболочечных конструкций от тонких до умеренно толстых[2]. Четыре ребра жесткости полностью соединены в точках нагрузки. Контактный элемент 174 и мишень 170 используются для моделирования поверхности между накладкой и фланцем образца. Все узлы усиленного фланца и накладки сцеплены на расстоянии, равном средней их толщине. Толщина сварных элементов варьируется, чтобы обеспечить поперечное сечение, равное сечению углового шва толщиной 6 мм.