Расчет балки двутавра на изгиб: Расчёт металлической балки онлайн (калькулятор)

Содержание

Напряжение балки из-за изгибающих моментов – Приложение по сопротивлению материалов для энергетики

Перейти к содержимому

Основной корпус

Напряжение при изгибе

Цели обучения

После изучения этой главы вы должны уметь:

Использовать формулу изгиба для расчета максимального напряжения изгиба
Конструктивные балки, способные безопасно нести груз
Определить требуемый модуль упругости балки
Выберите стандартные конструктивные формы для использования в заданной задаче балки

Рассмотрим свободно опертую балку, на которую действуют внешние направленные вниз нагрузки. Балка будет деформироваться (прогибаться) таким образом, что верхняя поверхность поперечного сечения балки будет сжиматься, а нижняя — растягиваться. В некотором месте вдоль вертикальной оси балки напряжение будет равно нулю; это место является центром тяжести поперечного сечения, также называемым нейтральной осью.

Формула изгиба

Для определения максимального напряжения из-за изгиба используется формула изгиба :

где:

σ _max — максимальное напряжение на самой дальней поверхности от нейтральной оси (может быть сверху или снизу)
М — изгибающий момент по длине балки, при котором рассчитывается напряжение.
- если требуется максимальное напряжение изгиба, то М — максимальный изгибающий момент, действующий на балку
I _x — момент инерции относительно центральной оси x (горизонтальной)
c — максимальное расстояние от центральной оси до крайнего волокна (опять же, это может быть верх или низ фигуры)
Z _x называется модуль секции и является термином, который сочетает в себе момент инерции и расстояние до экстремального волокна ( Z _x = I _x / c )

= I _x / c )

Формула изгиба действительна, если выполняются следующие критерии:

балка прямая, относительно длинная и узкая, одинакового поперечного сечения
все нагрузки действуют перпендикулярно продольной оси балки
результирующее напряжение ниже предела пропорциональности материала
материал балки однороден и имеет одинаковую прочность на растяжение и сжатие
- если материал имеет разную прочность на растяжение и сжатие (например, чугун или другие анизотропные материалы), то для поверхностей растяжения и сжатия требуются отдельные расчеты
не происходит скручивания, коробления или деформации

Дизайнерские кейсы

Проблемы проектирования могут возникать по разным сценариям:

рассчитайте размеры поперечного сечения балки (найдите минимальный модуль сечения Z и выберите стандартную форму большей жесткости), учитывая геометрию балки, нагрузку и материал.
выберите материал балки (найдите максимальное рабочее напряжение и выберите материал большей прочности), учитывая размеры балки, нагрузку и размеры/форму.
определить, безопасна ли балка (найти фактическое рабочее напряжение и сравнить с расчетным напряжением), учитывая размеры балки, нагрузку и материал.

Задача 1: Свободно опертая балка длиной 9,9 м нагружена сосредоточенными нагрузками следующим образом:

40 кН на расстоянии 1,2 м от левого конца
10 кН на расстоянии 3,7 м от левого конца
10 кН на расстоянии 6,2 м от левого конца
10 кН на расстоянии 8,7 м от левого конца

Балка изготовлена из двутаврового профиля W200×100 из холоднокатаного материала AISI-1020. AISC рекомендует, чтобы максимальное напряжение изгиба для строительных конструкций под действием статических нагрузок не превышало 0,66×S _y . Соответствует ли эта конструкция проектным требованиям?

Задача 2: Трубопровод просто поддерживается над землей на горизонтальных балках длиной 4,5 м.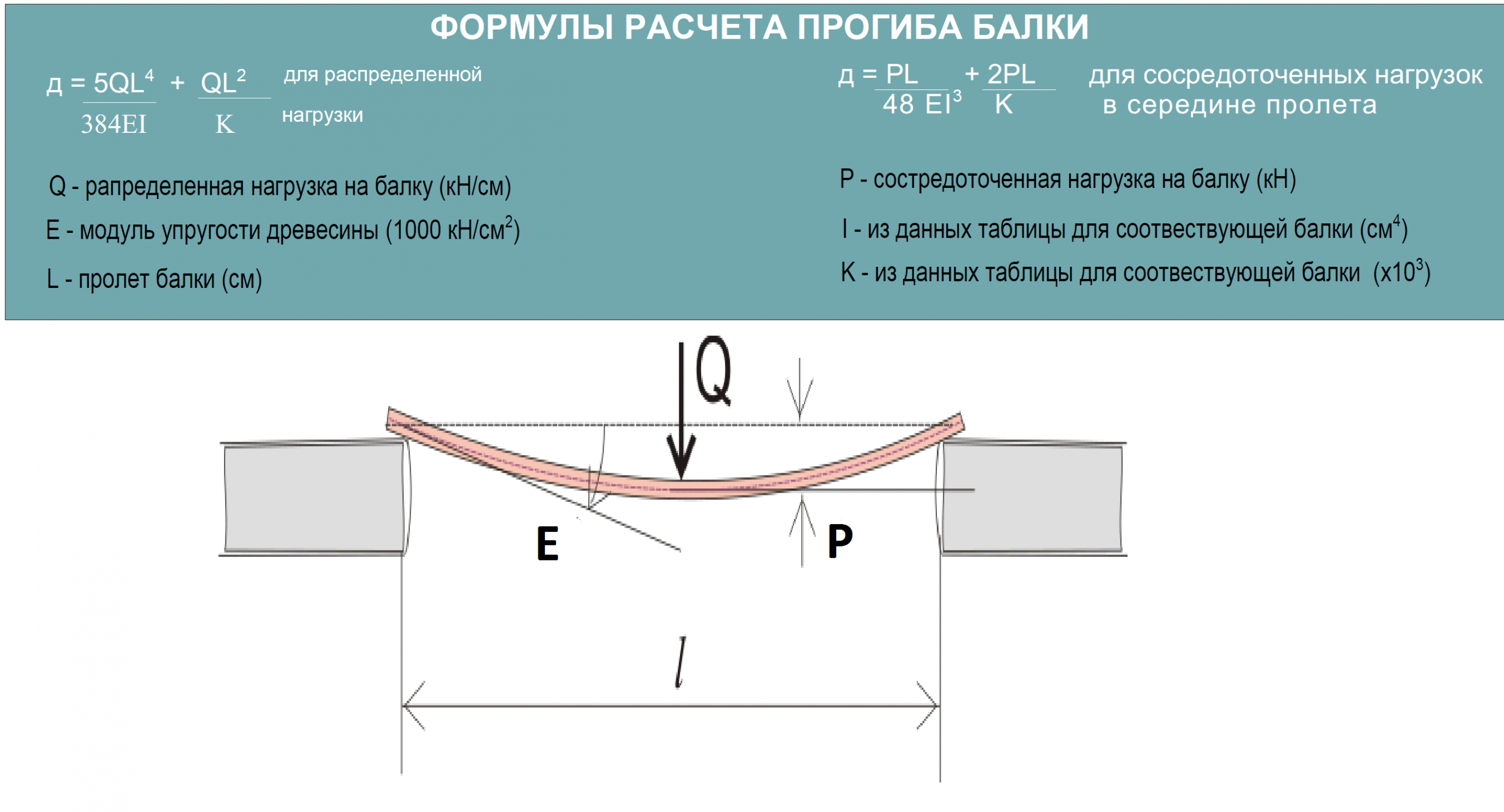 Каждая балка несет вес 20 м трубы Щ 40 DN-600 (см. PanGlobal Academic Extract), заполненной маслом 0,9 SG . Предполагая, что нагрузка действует в центре балки, рассчитайте требуемый модуль сопротивления балки, чтобы ограничить изгибающее напряжение до 140 МПа; затем выберите самую легкую W-образную балку SI, которая удовлетворяет критериям.

Задача 3: На рисунке показано поперечное сечение балки из алюминия 6061-Т6. Балка используется как консоль длиной 45 дюймов. Рассчитайте максимально допустимую равномерно распределенную нагрузку, которую он может нести, ограничивая напряжение из-за изгиба до одной пятой предела прочности.

Проблема 4: Спроектируйте дорожку для перекрытия только что проложенного трубопровода на вашем предприятии. Жесткие опоры доступны с каждой стороны трубопровода на расстоянии 14 футов друг от друга. Проход должен быть шириной 3,5 фута и выдерживать равномерно распределенную нагрузку 60 фунтов/фут9. 0141 2 по всей поверхности. Спроектируйте только доски настила и боковые балки. Используйте любые размеры пиломатериалов и сорта материалов из учебника Приложение Е или другие, разработанные вами.

Задача 5: Предложите одну задачу проектирования балки, которую вы считаете актуальной и полезной для инженеров-энергетиков.

Момент инерции двутавровой балки: пример расчета

Вы инженер, студент или человек, который хочет лучше понять, как рассчитывается момент инерции двутавровой балки? 🙋‍♂️🙋‍♂️

Момент инерции является важным параметром при расчете изгибающих напряжений для проверки структурных объектов, таких как балки, колонны и плиты.

Поняв расчет момента инерции, вы на один шаг приблизитесь к проектированию двутавровой или двутавровой балки. 🔥🔥

В этом руководстве для начинающих мы шаг за шагом проведем вас через процесс определения момента инерции двутаврового сечения.

Итак, приступим. 🚀🚀 93}{12}$$

Симметричное двутавровое сечение с размерами.

Вы можете ознакомиться с другими формулами момента инерции в этом сообщении блога. 👈👈

Но если вы хотите знать, как складывается эта формула или как рассчитать момент инерции несимметричного i-го сечения, тогда оставайтесь с нами. 👍👍

По сути, формула вычисляет момент инерции прямоугольного сечения с размерами w x h, а затем вычитает 2 «отверстия» слева и справа от стенки.

Хорошо, это может показаться запутанным, так что давайте посмотрим на картинку. 🖼️🖼️ 94$$

Хорошо, это была самая простая часть – симметричные i-лучи. Теперь мы собираемся вычислить момент инерции для несимметричного i-го сечения. 👇👇

И кстати, если вам нужно, чтобы мы также включили расчет момента инерции слабой оси, сообщите нам об этом в комментариях ниже. 📝📝

Момент инерции несимметричного I сечения

Момент инерции несимметричного I сечения не так однозначен, как для симметричного профиля.

Но мы объясним это как можно более практично на примере ниже. ⬇️⬇️ 92$$
С,
n = количество «частей», на которые делится сечение (n=2 на рисунке ниже)
$I_{0.n}$ = момент инерции части n сечения поперечное сечение относительно центральной оси
$A_n$ = площадь детали
x = расстояние от центра детали n до центральной оси

Теперь есть простая пошаговая процедура, которую мы можем следуйте, чтобы вычислить момент инерции балки i с помощью теоремы о параллельных осях . 👍👍

Процедура:

Разделить (крест-) сечение на части (см. рисунок выше – части 1, 2, 3).
Найдите центр тяжести каждой части (см. рисунок ниже).
Вычислите площадь каждой части.
Рассчитайте момент инерции каждой детали.
Используйте теорему о параллельных осях для расчета момента инерции i-го сечения.

Теперь давайте пошагово выполним эту процедуру.

Шаг #1

Раздел разделен на 3 части, как вы можете видеть на картинке выше.

Шаг #2

Теперь необходимо найти центр тяжести каждого из них. Во-первых, давайте нарисуем их в разделе.

Красные точки визуализируют центроиды 3-х частей сечения i.

Подробнее о расчете центроида можно прочитать здесь.

Центроид части 1

$$z_{c.1} = \frac{t_{f.t}}{2} = \frac{10mm}{2} = 5mm$$

Центроид части 2

$$z_{c.2} = t_{f.t} + \frac{h-t_{f.t}-t_{t.b}}{2} = 10 мм + \frac{200 мм – 10мм – 15мм}{2} = 97,5мм$$

Центроид части 3

$$z_{c.3} = h – t_{f.b} + \frac{t_{t.b}}{ 2} = 200 мм – 15 мм + \frac{15 мм}{2} = 192,5 мм$$

Шаг №3

Теперь вычислим площадь каждой части. 2$$ 94$$

💡💡 Бонусный совет: если вам нужно рассчитать момент инерции сложного двутаврового сечения или любого сечения в целом, то вы можете использовать такой инструмент, как Rhino, где вы рисуете сечение. Выполнив несколько простых шагов, вы сможете определить его центроидные размеры. 💡💡

Вот руководство по использованию Rhino для автоматического расчета момента инерции.

Дайте нам знать в комментариях ниже, если вы хотите, чтобы мы добавили расчет момента инерции для слабой оси тоже. ✍️✍️

Что такое момент инерции?

Момент инерции является ключевым параметром, используемым при конструктивном расчете балок и других конструктивных элементов, подверженных изгибу. Используется для расчета напряжения изгиба, которое элемент конструкции будет испытывать при воздействии нагрузки.

Проще говоря, это мера того, как материал структурного элемента распределяется относительно оси вращения, как, например, осевая линия балки.