Расчет двутавровой балки: Расчёт металлической балки онлайн (калькулятор)
Содержание
Вес двутавровой балки – Калькулятор и таблицы
Двутавровая балка – один из видов металлического профиля, как правило, изготавливаемый из углеродистой и низколегированной стали. Находит широкое применение в строительстве, так как обладает высочайшими показателями жесткости и прочности.
Калькулятор веса двутавровой балки от сервиса KALK.PRO позволяет рассчитать массу металлопроката на основании известных параметров сортамента и его длины. Алгоритм программы основан на табличных значениях ГОСТ 8239-89 «Двутавры стальные горячекатаные», ГОСТ 26020-83 «Двутавры стальные горячекатаные с параллельными гранями полок».
В расчетах используются все возможные серии двутавровых балок, такие как 12, 14, 16, 18, 20, 30, 25б1, 30б1 и т.д. При необходимости, вы сразу же можете воспользоваться марочником металлов или заглянуть в ГОСТы, в соответствующих вкладках инструмента.
По умолчанию считается вес 1 метра двутавровой балки.
Рассчитать вес двутавра
- Выберите тип металла (по умолчанию Сталь).

- Подтвердите тип сортамента – Балка / Двутавр.
- Выберите способ расчета – Расчет веса.
- Выберите тип балки – Двутавр нормальный / С уклоном полок / Широкополочный / Колонный / Сварной / Дополнительной серии.
- Укажите серию балки.
- Введите длину металлопроката L, м.
Перевод балки из тонн в метры
- Выберите тип металла (по умолчанию Сталь).
- Подтвердите тип сортамента – Балка / Двутавр.
- Выберите способ расчета – Расчет длины.
- Выберите тип балки – Двутавр нормальный / С уклоном полок / Широкополочный / Колонный / Сварной / Дополнительной серии.
- Укажите серию балки.
- Введите вес металлопроката W, кг.
Формула расчета веса двутавра
Вес двутавровой балки, также можно рассчитать классическим способом вручную – для это необходимо подставить значения из таблиц ГОСТ в простую математическую формулу:
Формула расчета веса двутавра: m = ρ × (2 × b × t + (h — 2 × t) × s) × L
- h – высота балки;
- t – толщина полки;
- b – ширина полки;
- s – толщина стенки;
- ρ – плотность металла;
- L – длина проката.
Балка двутавровая – Размеры и вес (таблица)
Для определения размера и веса двутавра используют таблицы из государственных стандартов и стандарта ассоциации предприятий продукции черной металлургии. Для обозначения типов стальных балок с уклоном внутренних граней используют ГОСТ 8239-89 «Двутавры стальные горячекатаные», для двутавров с параллельными гранями – ГОСТ 26020-83 «Двутавры стальные горячекатаные с параллельными гранями полок». В последнем нормативном документе, также используются обозначения:
- Ш – широкополочный;
- К – колонный;
- Б – нормальный;
- Д – дополнительной серии.
Балка двутавровая с уклоном внутренних граней
| Номер двутавра | Размеры, мм | Вес метра, кг | Метров в тонне | |||
| h | b | s | t | |||
| 10 | 100 | 55 | 4,5 | 7,2 | 9,46 | 105,71 |
| 12 | 120 | 64 | 4,8 | 7,3 | 11,5 | 86,96 |
| 14 | 140 | 73 | 4,9 | 7,5 | 13,7 | 72,99 |
| 16 | 160 | 81 | 5 | 7,8 | 15,9 | 62,89 |
| 18 | 180 | 90 | 5,1 | 8,1 | 18,4 | 54,35 |
| 20 | 200 | 100 | 5,2 | 8,4 | 21 | 47,62 |
| 22 | 220 | 110 | 5,4 | 8,7 | 24 | 41,67 |
| 24 | 240 | 115 | 5,6 | 9,5 | 27,3 | 36,63 |
| 27 | 270 | 125 | 6 | 9,8 | 31,5 | 31,75 |
| 30 | 300 | 135 | 6,5 | 10,2 | 36,5 | 27,4 |
| 33 | 330 | 140 | 7 | 11,2 | 42,2 | 23,7 |
| 36 | 360 | 145 | 7,5 | 12,3 | 48,6 | 20,58 |
| 40 | 400 | 155 | 8,3 | 13 | 57 | 17,54 |
| 45 | 450 | 160 | 9 | 14,2 | 66,5 | 15,04 |
| 50 | 500 | 170 | 10 | 15,2 | 78,5 | 12,74 |
| 55 | 550 | 180 | 11 | 16,5 | 92,6 | 10,8 |
| 60 | 600 | 190 | 12 | 17,8 | 108 | 9,26 |
Балка двутавровая широкополочная
| Номер двутавра | Размеры, мм | Вес метра, кг | Метров в тонне | |||
| h | b | s | t | |||
| 20Ш1 | 193 | 150 | 6 | 9 | 30,6 | 32,7 |
| 23Ш1 | 226 | 155 | 6,5 | 10 | 36,2 | 27,6 |
| 26Ш1 | 251 | 180 | 7 | 10 | 42,7 | 23,4 |
| 26Ш2 | 255 | 180 | 7,5 | 12 | 49,2 | 20,3 |
| 30Ш1 | 291 | 200 | 8 | 11 | 53,6 | 18,7 |
| 30Ш2 | 295 | 200 | 8,5 | 13 | 61 | 16,4 |
| 30Ш3 | 299 | 200 | 9 | 15 | 68,3 | 14,6 |
| 35Ш1 | 338 | 250 | 9,5 | 12,5 | 75,1 | 13,3 |
| 35Ш2 | 341 | 250 | 10 | 14 | 82,2 | 12,2 |
| 35Ш3 | 345 | 250 | 10,5 | 16 | 91,3 | 11 |
| 40Ш1 | 388 | 300 | 9,5 | 14 | 96,1 | 10,4 |
| 40Ш2 | 392 | 300 | 11,5 | 16 | 111,1 | 9 |
| 40Ш3 | 396 | 300 | 12,5 | 18 | 123,4 | 8,1 |
| 50Ш1 | 484 | 300 | 11 | 15 | 114,4 | 8,7 |
| 50Ш2 | 489 | 300 | 14,5 | 17,5 | 138,7 | 7,2 |
| 50Ш3 | 495 | 300 | 15,5 | 20,5 | 156,4 | 6,4 |
| 50Ш4 | 501 | 300 | 16,5 | 23,5 | 174,1 | 5,7 |
| 60Ш1 | 580 | 320 | 12 | 17 | 142,1 | 7 |
| 60Ш2 | 587 | 320 | 16 | 20,5 | 176,9 | 5,7 |
| 60Ш3 | 595 | 320 | 18 | 24,5 | 205,5 | 4,9 |
| 60Ш4 | 603 | 320 | 20 | 28,5 | 234,2 | 4,3 |
| 70Ш1 | 683 | 320 | 13,5 | 19 | 169,9 | 5,9 |
| 70Ш2 | 691 | 320 | 15 | 23 | 197,6 | 5,1 |
| 70Ш3 | 700 | 320 | 18 | 27,5 | 235,4 | 4,2 |
| 70Ш4 | 708 | 320 | 20,5 | 31,5 | 268,1 | 3,7 |
| 70Ш5 | 718 | 320 | 23 | 36,5 | 305,9 | 3,3 |
Балка двутавровая колонная
| Номер двутавра | Размеры, мм | Вес метра, кг | Метров в тонне | |||
| h | b | s | t | |||
| 20К1 | 195 | 200 | 6,5 | 10 | 41,5 | 24,1 |
| 20К2 | 198 | 200 | 7 | 11,5 | 46,9 | 21,3 |
| 23К1 | 227 | 240 | 7 | 10,5 | 52,2 | 19,2 |
| 23К2 | 230 | 240 | 8 | 12 | 59,5 | 16,8 |
| 26К1 | 255 | 260 | 8 | 12 | 65,2 | 15,3 |
| 26К2 | 258 | 260 | 9 | 13,5 | 73,2 | 13,7 |
| 26К3 | 262 | 260 | 10 | 15,5 | 83,1 | 12 |
| 30К1 | 296 | 300 | 9 | 13,5 | 84,8 | 11,8 |
| 30К2 | 300 | 300 | 10 | 15,5 | 96,3 | 10,4 |
| 30К3 | 304 | 300 | 11,5 | 17,5 | 108,9 | 9,2 |
| 35К1 | 343 | 350 | 10 | 15 | 109,7 | 9,1 |
| 35К2 | 348 | 350 | 11 | 17,5 | 125,9 | 7,9 |
| 35К3 | 353 | 350 | 13 | 20 | 144,5 | 6,9 |
| 40К1 | 393 | 400 | 11 | 16,5 | 138 | 7,2 |
| 40К2 | 400 | 400 | 13 | 20 | 165,6 | 6 |
| 40К3 | 409 | 400 | 16 | 24,5 | 202,3 | 4,9 |
| 40К4 | 419 | 400 | 19 | 29,5 | 242,2 | 4,1 |
| 40К5 | 431 | 400 | 23 | 35,5 | 291,2 | 3,4 |
Балки двутавровая дополнительной серии
| Номер двутавра | Размеры, мм | Вес метра, кг | Метров в тонне | |||
| h | b | s | t | |||
| 24ДБ1 | 239,0 | 115,0 | 5,5 | 9,3 | 27,8 | 36,0 |
| 27ДБ1 | 269,0 | 125,0 | 6,0 | 9,5 | 31,9 | 31,3 |
| 35ДБ1 | 349,0 | 127,0 | 5,8 | 8,5 | 33,6 | 29,8 |
| 36ДБ1 | 360,0 | 145,0 | 12,3 | 18,0 | 49,1 | 20,4 |
| 40ДБ1 | 399,0 | 139,0 | 6,2 | 9,0 | 39,7 | 25,2 |
| 45ДБ1 | 450,0 | 152,0 | 11,0 | 15,0 | 52,6 | 19,0 |
| 45ДБ2 | 450,0 | 180,0 | 7,6 | 13,3 | 65,0 | 15,4 |
| 30ДШ1 | 300,6 | 201,9 | 9,4 | 16,0 | 72,7 | 13,8 |
| 40ДШ1 | 397,6 | 302,0 | 11,5 | 18,7 | 124,0 | 8,1 |
| 50ДШ1 | 496,2 | 303,8 | 14,2 | 21,0 | 155,0 | 6,5 |
Балка двутавровая нормальная
| Номер двутавра | Размеры, мм | Вес метра, кг | |||
| h | b | s | t | ||
| 10Б1 | 100 | 55 | 4,1 | 5,7 | 8,1 |
| 12Б1 | 117,6 | 64 | 3,8 | 5,1 | 8,7 |
| 12Б2 | 120 | 64 | 4,4 | 6,3 | 10,4 |
| 14Б1 | 137,4 | 73 | 3,8 | 5,6 | 10,5 |
| 14Б2 | 140 | 73 | 4,7 | 6,9 | 12,9 |
| 16Б1 | 157 | 82 | 4 | 5,9 | 12,7 |
| 16Б2 | 160 | 82 | 5 | 7,4 | 15,8 |
| 18Б1 | 177 | 91 | 4,3 | 6,5 | 15,4 |
| 18Б2 | 180 | 91 | 5,3 | 8 | 18,8 |
| 20Б1 | 200 | 100 | 5,6 | 8,5 | 22,4 |
| 23Б1 | 230 | 110 | 5,6 | 9 | 25,8 |
| 25Б1 | 248 | 124 | 5 | 8 | 25,7 |
| 26Б1 | 258 | 120 | 5,8 | 8,5 | 28 |
| 26Б2 | 261 | 120 | 6 | 10 | 31,2 |
| 30Б1 | 295 | 140 | 5,8 | 8,5 | 32,9 |
| 30Б2 | 299 | 140 | 6 | 10 | 36,6 |
| 35Б1 | 346 | 155 | 6,2 | 8,5 | 38,9 |
| 35Б2 | 349 | 155 | 6,5 | 10 | 43,3 |
| 40Б1 | 392 | 165 | 7 | 9,5 | 48,1 |
| 40Б2 | 396 | 165 | 7,5 | 11,5 | 54,7 |
| 45Б1 | 443 | 180 | 7,8 | 11 | 59,8 |
| 45Б2 | 447 | 180 | 8,4 | 13 | 67,5 |
| 50Б1 | 492 | 200 | 8,8 | 12 | 73 |
| 50Б2 | 496 | 200 | 9,2 | 14 | 80,7 |
| 55Б1 | 543 | 220 | 9,5 | 13,5 | 89 |
| 55Б2 | 547 | 220 | 10 | 15,5 | 97,9 |
| 60Б1 | 593 | 230 | 10,5 | 15,5 | 106,2 |
| 60Б2 | 597 | 230 | 11 | 17,5 | 115,6 |
| 70Б1 | 691 | 260 | 12 | 15,5 | 129,3 |
| 70Б2 | 697 | 260 | 12,5 | 18,5 | 144,2 |
| 80Б1 | 791 | 280 | 13,5 | 17 | 159,5 |
| 80Б2 | 798 | 230 | 14 | 20,5 | 177,9 |
| 90Б1 | 893 | 300 | 15 | 18,5 | 194 |
| 90Б2 | 900 | 300 | 15,5 | 22 | 213,8 |
| 100Б1 | 990 | 320 | 16 | 21 | 230,6 |
| 100Б2 | 998 | 320 | 17 | 25 | 258,2 |
| 100Б3 | 1006 | 320 | 18 | 29 | 285,7 |
| 100Б4 | 1013 | 320 | 19,5 | 32,5 | 314,5 |
производство, расчет, как сделать своими руками
Если вы слышали об инновационном методе легкого, и, в то же время, прочного и надежного строительства из балок необычного вида и заинтересовались им, значит, эта статья как раз для вас! Давно используемые за рубежом деревянные двутавровые балки перекрытия пока еще в новинку на отечественном рынке, хотя у них куда больше преимуществ, чем у любого другого материала.
А, самое приятное во всем этом то, что их совершенно реально изготовить прямо в домашних условиях при помощи стандартных подручных инструментов. Строите дом своими силами? Тогда познакомьтесь еще с одной технологией, которая облегчит вам жизнь!
Для начала предлагаем вам посмотреть интересное видео про основные характеристики двутавровых балок:
Двутавровые балки особенно популярны за рубежом: в Канаде и европейских странах, а в России они только набирают свою популярность. Причем в некоторых регионах их даже не найти в продаже! Почему? Если мировой опыт показывает, что такой строительный материал действительно качественный и надежный, как так получилось, что двутавровые балки не заняли лидирующие позиции на отечественном рынке?
Дело в том, что истинная русская душа мастера привыкла работать с крепкими и надежными материалами: массивными, которые тяжело поднять и которые внушают уважение одним своим только видом.
И перекрытие издавна привыкли строить из прочных больших и тяжелых деревянных балок или даже цельных бревен, но уж точно не из «хитрых» инновационных конструкций с тонкой перегородкой. А то, что здесь надежность обеспечивают все те же законы физики, без которых не обойтись ни в строительстве, ни в архитектуре – это уже другой вопрос.
И до сих пор большинство российских застройщиков готовы сделать балки перекрытия даже из металла, чем из двух планок и OSB. Хотя на самом деле такие балки обладают целым рядом преимуществ!
Давайте рассмотрим все преимущества двутавровых балок как материала для строительства перекрытия:
Преимущество №1. Удивительная прочность
Благодаря такой гениально продуманной конструкции довольно хрупкие на вид балки оказываются во много раз прочнее и надежнее обычных. Верхняя часть балки работает на изгиб, а нижняя – на растяжение. Т.е. здесь уже речь идет не об одном монолитном элементе, которому приходится принимать на себя оба вида нагрузки одновременно:
Преимущество №2.
 Точная геометрия
Точная геометрия
Второй очень важный момент: идеальная геометрия самих балок. Даже со временем они не прогибаются, не выкручиваются, не рассыхаются и не изменяют свои своих параметров. Как утверждают производители, даже через 100 лет такие балки будут вести себя все также, как через год после постройки.
Что это дает? Для начала – безупречно ровное перекрытие, на которое легко монтировать любое половое покрытие, особенно паркет и ламинат. Дело в том, что когда вы имеете дело с брусьями и обычными деревянными балками, то должны знать, что согласно стандартам нормам их прогиб может достигать 3 см! И, поверьте даже это уже ощутимо: пол будет просто «ходить» под вашими ногами. И подобное точно хорошо не скажется ни на одном половом покрытии (кроме дешевого линолеума, пожалуй).
И это нормально: натуральная древесина – материал живой, и для нее свойственно сжиматься, усыхать или, наоборот, набирать в себя влагу. А вот двутавровые балки уже изготавливается из клееной древесины, с применением особо прочного соединяющего состава, и своих размеров они не изменяют.
Преимущество №3. Комфортный вес
Следующий важный аспект: двутавровые балки достаточно легкие, чтобы поднять одну из них самостоятельно, а потому с подобной работой без проблем справляются два обычных рабочих. Что это дает?
Во-первых, вам не понадобится тяжелая техника, которая должна будет поднимать обычные деревянные балки или металлические.
Во-вторых, работы на высоте станут более безопасными, ведь никому на голову не свалится слишком тяжелая балка.
В-третьих, применение двутавровых балок позволят немало сэкономить на фундаменте, ведь нагрузка на него уже будет на порядок меньше. И, если брать во внимание, что до 50% бюджета строительства обычно идет на надежный, крепкий фундамент, который выдержит не только стены, но и не менее тяжелые балки, тогда экономия получается существенной.
Преимущество №4. Изготовление в домашних условиях
Двутавровые балки вы можете изготовить самостоятельно, если будете знать, какими должны быть их параметры и узлы соединения. И в итоге у вас будет не только уверенность в качестве перекрытия, но и немало сэкономленный бюджет.
И в итоге у вас будет не только уверенность в качестве перекрытия, но и немало сэкономленный бюджет.
Преимущество №5. Практичность в утеплении
И, наконец, последний приятный момент: двутавровые балки особенно удобны для утепления междуэтажного перекрытия и последующей отделки потолка:
Единственный неприятный момент заключается в том, что в России качественные двутавровые балки поставляют единицы компаний, и если уж их приобретать, то важно уметь правильно рассмотреть все технологические недочеты. Речь ведь идет о будущем перекрытии!
Вам наверняка интересно узнать, почему двутавровая балка называется именно так? Дело в том, что она состоит из двух основных элементов, которые напоминают соединенные буквы Т. А балка Т-образной формы, в свою очередь, называется тавром. Вот откуда произошло это необычное название.
Что представляет собой такая балка в разрезе? Прежде всего, это заготовка из OSB или фанеры, которые выступают в роли ребер жесткости. А для этого в балках предварительно фрезеруют паз нужной формы. Высота балки получается от 140 до 470 миллиметров, и на практике та оказывается достаточно жесткой на прогиб. Если говорить о выборе проекта балок для стандартного коттеджного строительства с самыми популярными пролетами до 6 м, наиболее выгодной будет балка высотой 302 мм.
Высота балки получается от 140 до 470 миллиметров, и на практике та оказывается достаточно жесткой на прогиб. Если говорить о выборе проекта балок для стандартного коттеджного строительства с самыми популярными пролетами до 6 м, наиболее выгодной будет балка высотой 302 мм.
Самыми первыми в России стали выпускаться наскоровские балки, и их обозначениями современные производители пользуются до сих пор. Их делят на серии в зависимости от толщины полок: на тонкие балки и широкополочные:
- Тонкие окантовочные балки серии NJ. Это балки с толщиной полок 38 мм. Такие заготавливают для обустройства периметра внешнего контура перекрытия, там, где необходим проем под лестницу или для других нагруженных мест. Они бывают однослойным и многослойными.
- Широкополочные балки серии NJH и NJU. Это балки с толщиной полок 64 мм или 89 мм, конкретно для несущих пролетов. Как вы понимаете, в таких местах нагрузка на балки наиболее сильна.
Вот как отличаются обе серии:
Отметим такой важный момент. В интернете часто можно встретить опасное заблуждение, согласно которому изготавливают деревянные двутавровые балки перекрытия: расчет производится по старой таблице наскоровских балок. Хотя на самом деле на то время еще не существовало СНиПов для двутавров, и эта таблица предполагала снеговую нагрузку около 90 кг/м, которые соответствуют как раз Ростовской области.
В интернете часто можно встретить опасное заблуждение, согласно которому изготавливают деревянные двутавровые балки перекрытия: расчет производится по старой таблице наскоровских балок. Хотя на самом деле на то время еще не существовало СНиПов для двутавров, и эта таблица предполагала снеговую нагрузку около 90 кг/м, которые соответствуют как раз Ростовской области.
Но сегодня использовать такие данные неправильно, так как вы понимаете, что снеговая нагрузка может быть намного выше в более северных районах РФ. А поэтому руководствуйтесь только такой таблицей, которую составили уже современные производители:
Помните также, что не все виды двутавровых балок, которые сегодня применяются при строительстве, пригодны для устройства перекрытия. Например, двутавровые балки опалубки.
В заводских условиях двутавры изготавливают из ценной древесины хвойных пород: лиственницы или сосны. Если вы решили приобрести готовые двутавровые деревянные балки, дадим вам пару ценных советов:
- Пункт 1.
 Обратите внимание на шов: должен быть заметен небольшой выход клея. Это нормально.
Обратите внимание на шов: должен быть заметен небольшой выход клея. Это нормально. - Пункт 2. По всей полке вырез должен быть конической формы, а сама OSB должна быть фрезерирована и вставлена правильно.
- Пункт 3. OSB должна быть через каждые полметра пристрелена скобами прямо в полку. Это помогает сохранять давление до того, как полностью застынет клей.
- Пункт 4. Вы имеете право попросить сертификат качества продукта и посмотреть, применяется ли нужный тип клея – тот, который допущен для клееных несущих конструкций.
- Пункт 5. Проверьте, есть ли в сопутствующей документации протокол испытания образцов балок, их номер технических условий и выпуска.
Выглядеть качественные двутавровые балки должны так:
Здесь секрет кроется в том, такие балки предварительно хорошо высушены, тогда как обычная древесина все еще содержит определенный процент влажности. Да и сама конструкция балки позволяет легко прорезать отверстия в перекрытии для проведения канализации, вентиляции газа и воды, а в условиях строительства частного дома или коттеджа это – важный момент.
Что касается клеевого соединения заметим, что некоторые российские застройщики уже давно отказались от заказа сырья от более мелких фирм и приобретают заграничные двутавровые балки, т.к. отечественное производство двутавровых деревянных балок и его итоговое качество не всегда радует. Да и опыта мало, канадская технология пока еще слишком непривычна и не находит в нашей стране большого количества последователей. Вот поэтому порой проще изготовить двутавровую деревянную балку своими руками – здесь нет ничего сложного. А мы расскажем, что и как.
Когда вы приступите к самостоятельному изготовлению заморской балки для строительства своего дома, то у вас уйдет около суток для первого образца, зато на второй день работа пойдет намного быстрее. Все делайте согласно такой пошаговой инструкции:
- Шаг 1. Приобретите листы OSB толщиной 12 мм и нарежьте их на равные части.
- Шаг 2. Далее вам понадобятся доски, в которых нужно сделать фрезу «ласточкин хвост» посередине доски, глубиной около 12-14 мм.

- Шаг 3. Залейте специальный клей в отверстие и вставьте лист OSB.
- Шаг 4. Чтобы быстро просушить участок, достаточно использовать обогреватель.
Главное при этом ни в коем случае не приобретать свежеспиленные или непросушенные доски, так как они могут непрогнозируемо повести себя в долгосрочной перспективе.
Высоту балки рассчитывайте по такому принципу:
- Для листа с размерами 2440 мм оптимальным шагом балок будет 305, 406, 488 и 610 мм.
- Для листа в 2500 мм рациональный шагом будет 312, 417 и 500 мм. А вот двутавровыебалки с шагом более 6 метров уже не применяют.
В заводских условиях двутавровые балки всегда фрезируются так, что прорезь у них получается как бы зауженой книзу, и лист OSB вклеивается в полку внатяг. Так лист и дерево прилегают наиболее плотно.
Для этого используется полиуретановый или меламиновый клей, а сам лист зажимают струбцинами и забивают еще дополнительно под углом 45 градусов по длине через каждые 20 см. На каждую такую балку уходит не более 2 часов, и уже через 6 часов ее можно устанавливать:
На каждую такую балку уходит не более 2 часов, и уже через 6 часов ее можно устанавливать:
Соединяйте балки между собой при помощи специальных блок-вставок:
Вот небольшой видео-урок, как вставлять лист в древесину:
И наконец, самый ответственный этап! Изготавливая деревянные двутавровые балки для строительства своего дома, еще задолго до их монтажа вам нужно точно просчитать пустоты в перекрытиях – для будущей прокладки инженерных коммуникаций. Конечно вы будете проводить сантехнические трубы, электрические кабеля и инженерные системы. И здесь важно определеть все изначально правильно, чтобы потом не допустить ослабление перекрытия.
Сверление отверстий для коммуникаций
А теперь также подойдем вплотную к такому важному вопросу, как правильно сверлить двутавровые деревянные балки. Дело в том, что это необходимо делать еще на земле – до монтажа. И здесь важно соблюсти все правила, иначе даже небольшие отверстия способны ослабить балку по всей длине. Где именно могут располагаться сквозные отверстия в балках перекрытия зависит от того, по какой технологии они были произведены.
Где именно могут располагаться сквозные отверстия в балках перекрытия зависит от того, по какой технологии они были произведены.
Так, у двутавровых балок отверстия должны быть не более 40 мм. Располагать их разрешено практически в любом месте между таврами, но только не ближе 150 мм к торцу балки или опоры на несущий элемент. Идеально, если такие отверстия будут располагаться прямо по центру относительно полок, а не выше или ниже. А максимально допустимый диаметр отверстия 10 см.
Кроме того следите за тем чтобы расстояние между соседними отверстиями было в 2 раза больше диаметра самого большого из них.
Узлы крепления балок со стеной
Если вы подготовили балки правильно, можете смело приступать их монтажу:
Вот основные узлы крепление двутавровых деревянных балок к стене:
В готовое перекрытие из деревянных двутавров вставьте утеплитель:
А теперь давайте разберем главные ошибки при изготовлении таких балок.
Ошибка №1. Покупка неподготовленной древесины
Если вы беретесь самостоятельно изготовить изготавить такое основание для перекрытия, помните, что в заводских условиях балки готовят по специальной технологии, используя только калиброванный сухой материал. Это позволяет полностью исключить возникновение перекручивания балок так называемым «вертолетом», которое нередко происходит при применении обычных деревянных балок и досок.
Это позволяет полностью исключить возникновение перекручивания балок так называемым «вертолетом», которое нередко происходит при применении обычных деревянных балок и досок.
Вам наверняка будет интересно посмотреть на сам процесс заводского изготовления таких балок:
Ошибка №2. Использование неподходящего клеевого состава
Нельзя для склейки элементов двутавровой балки использовать эпоксидную смолу. У нее достаточно слабая адгезия конкретно в древесине, и придется выжидать немало времени, пока она затвердеет. А вот полиуретановый клей как раз подходит хорошо. Главное преимущество его в том, что он не горит и при этом сам термоактивен. Говоря простым языком, чем выше температура, тем крепче становится само изделие.
И уж точно нельзя использовать в качестве клея ПВА, ведь он совершенно не предусмотрен для применения в таких конструкциях.
Ошибка №3.
 Неправильное сопряжение балок
Неправильное сопряжение балок
Речь идет о перерасходе балок. Дело в том, что в отличие от обычных деревянных балок, двутавры не крепятся внахлест. Для их крепления необходимо приложить балки встык и закрепить при помощи перфорированных пластин. Но не перфорированной лентой, применение которой потом приведет к опрокидыванию балки! Причем место установки перфорированных пластин определяется точными инженерными расчетами.
Ошибка №4. Применение не тех крепежных элементов
Еще одна популярная ошибка – это крепление двутавровых балок к стене и заделка их места монтажной пеной. А на самом деле использовать можно исключительно специальные закладные элементы.
Нельзя также применять слабые кронштейны, ведь после этого уже нельзя будет гарантировать несущую способность такого перекрытия и существует риск обрушения всей конструкции.
Не крепят двутавровые балки также обычными саморезами. Ведь сам по себе саморез – это не конструкционный элемент, и он не рассчитан выдерживать повышенную нагрузку, и используется только для крепления легких и не несущих конструкций.
Обратите внимание и на размер кронштейна, достаточность его высоты. Соотношение высоты кронштейна и балки должно стремиться к единице, то есть быть почти одинаковым. Чем меньше кронштейн – тем хуже.
Ошибка №5. Задействование посторонних элементов
Неправильно также использовать дополнительные элементы, которые не были предусмотрены конструкцией. На самом деле стандартное крепление двутавра достаточно жесткое, и еще как-то закреплять его нет необходимости.
Мы подготовили для вас иллюстрацию, которая поможет разобраться с самыми типичными ошибками монтажа таких балок:
Следуйте нашим советам – и у вас все получится!
Будьте в курсе!
Подпишитесь на новостную рассылку
Вес двутавра – калькулятор, таблицы
Калькулятор веса двутавра использует для расчета табличные значения в соответствии со следующми ГОСТ:
- «ГОСТ 8239-89 Двутавры стальные горячекатаные». Используется для классификации балок с уклоном внутренних полок.
- «ГОСТ 26020-83 Двутавры стальные горячекатаные с параллельными гранями полок»
Двутавры с параллельными гранями полок имеют следующие разновидности и соответствующие обозначения:
- Б – нормальные;
- Ш – широкополочные;
- К – колонные;
- Д – дополнительной серии;
Формула для расчета веса двутавровой балки
Помимо определения веса балки по значениям таблиц ГОСТа, можно воспользоваться следующей формулой:
W = ρ × (2 × b × t + (h — 2 × t) × s) × L
h – высота балки, мм
t – толщина полки, мм
b – ширина полки, мм
s – толщина стенки, мм
ρ – плотность металла
Таблицы размеров и веса двутавровых балок
Двутавр с уклоном полок
| Номер двутавра | h | b | s | t | Вес метра, кг | Метров в тонне |
|---|---|---|---|---|---|---|
| 10 | 100 | 55 | 4.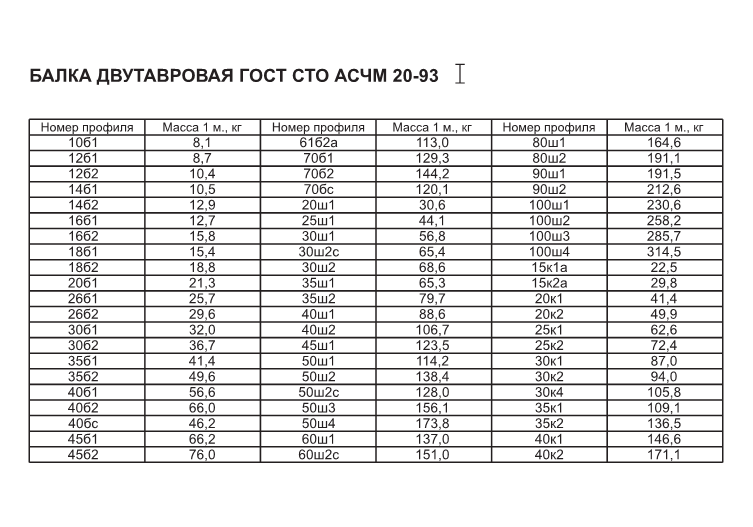 5 5 | 7.3 | 9.46 | 105.71 |
| 12 | 120 | 64 | 4.8 | 7.3 | 11.5 | 86.96 |
| 14 | 140 | 73 | 4.9 | 7.5 | 13.7 | 72.99 |
| 16 | 160 | 81 | 5 | 7.8 | 15.9 | 62.89 |
| 18 | 180 | 90 | 5.1 | 8.1 | 18. 4 4 | 54.35 |
| 20 | 200 | 100 | 5.2 | 8.4 | 21 | 47.62 |
| 22 | 220 | 110 | 5.4 | 8.7 | 24 | 41.67 |
| 24 | 240 | 115 | 5.6 | 9.5 | 27.3 | 36.63 |
| 27 | 270 | 125 | 6 | 9.8 | 31.5 | 31.75 |
| 30 | 300 | 135 | 6. 5 5 | 10.2 | 36.5 | 27.4 |
| 33 | 330 | 140 | 7 | 11.2 | 42.2 | 23.7 |
| 36 | 360 | 145 | 7.5 | 12.3 | 48.6 | 20.58 |
| 40 | 400 | 155 | 8.3 | 13 | 57 | 17.54 |
| 45 | 450 | 160 | 9 | 14.2 | 66. 5 5 | 15.04 |
| 50 | 500 | 170 | 10 | 15.2 | 78.5 | 12.74 |
| 55 | 550 | 180 | 11 | 16.5 | 92.6 | 10.8 |
| 60 | 600 | 190 | 12 | 17.8 | 108 | 9.26 |
Нормальный двутавр (Б)
| Номер двутавра | h | b | s | t | Вес метра, кг | Метров в тонне |
|---|---|---|---|---|---|---|
| 10Б1 | 100 | 55 | 4. 1 1 | 5.7 | 8.1 | 123.46 |
| 12Б1 | 117.6 | 64 | 3.8 | 5.1 | 8.7 | 114.94 |
| 12Б2 | 120 | 64 | 4.4 | 6.3 | 10.4 | 96.15 |
| 14Б1 | 137.4 | 73 | 3.8 | 5.6 | 10.5 | 95.24 |
| 14Б2 | 140 | 73 | 4.7 | 6.9 | 12. 9 9 | 77.52 |
| 16Б1 | 157 | 82 | 4 | 5.9 | 12.7 | 78.74 |
| 16Б2 | 160 | 82 | 5 | 7.4 | 15.8 | 63.29 |
| 18Б1 | 177 | 91 | 4.3 | 6.5 | 15.4 | 64.94 |
| 18Б2 | 180 | 91 | 5.3 | 8 | 18.8 | 53.19 |
| 20Б1 | 200 | 100 | 5. 6 6 | 8.5 | 22.4 | 44.64 |
| 23Б1 | 230 | 110 | 5.6 | 9 | 25.8 | 38.76 |
| 26Б1 | 258 | 120 | 5.8 | 8.5 | 28 | 35.71 |
| 26Б2 | 261 | 120 | 6 | 10 | 31.2 | 32.05 |
| 30Б1 | 296 | 140 | 5.8 | 8.5 | 32. 9 9 | 30.4 |
| 30Б2 | 299 | 140 | 6 | 10 | 36.6 | 27.32 |
| 35Б1 | 346 | 155 | 6.2 | 8.5 | 38.9 | 25.71 |
| 35Б2 | 349 | 155 | 6.5 | 10 | 43.3 | 23.09 |
| 40Б1 | 392 | 165 | 7 | 9.5 | 48.1 | 20.79 |
| 40Б2 | 396 | 165 | 7. 5 5 | 11.5 | 54.7 | 18.28 |
| 45Б1 | 443 | 180 | 7.8 | 11 | 59.8 | 16.72 |
| 45Б2 | 447 | 180 | 8.4 | 13 | 67.5 | 14.81 |
| 50Б1 | 492 | 200 | 8.8 | 12 | 73 | 13.7 |
| 50Б2 | 496 | 200 | 9.2 | 14 | 80. 7 7 | 12.39 |
| 55Б1 | 543 | 220 | 9.5 | 13.5 | 89 | 11.24 |
| 55Б2 | 547 | 220 | 10 | 15.5 | 97.9 | 10.21 |
| 60Б1 | 593 | 230 | 10.5 | 15.5 | 106.2 | 9.42 |
| 60Б2 | 597 | 230 | 11 | 17.5 | 115.6 | 8.65 |
| 70Б1 | 691 | 260 | 12 | 15. 5 5 | 129.3 | 7.73 |
| 70Б2 | 697 | 260 | 12.5 | 18.5 | 144.2 | 6.93 |
| 80Б1 | 791 | 280 | 13.5 | 17 | 159.5 | 6.27 |
| 80Б2 | 798 | 280 | 14 | 20.5 | 177.9 | 5.62 |
| 90Б1 | 893 | 300 | 15 | 18.5 | 194 | 5. 15 15 |
| 90Б2 | 900 | 300 | 15.5 | 22 | 213.8 | 4.68 |
| 100Б1 | 990 | 320 | 16 | 21 | 230.6 | 4.34 |
| 100Б2 | 998 | 320 | 17 | 25 | 258.2 | 3.87 |
| 100Б3 | 1006 | 320 | 18 | 29 | 285.7 | 3.5 |
| 100Б4 | 1013 | 320 | 19. 5 5 | 32.5 | 314.5 | 3.18 |
Широкополочный двутавр (Ш)
| Номер двутавра | h | b | s | t | Вес метра, кг | Метров в тонне |
|---|---|---|---|---|---|---|
| 20Ш1 | 193 | 150 | 6 | 9 | 30.6 | 32.68 |
| 23Ш1 | 226 | 155 | 6.5 | 10 | 36.2 | 27.62 |
| 26Ш1 | 251 | 180 | 7 | 10 | 42.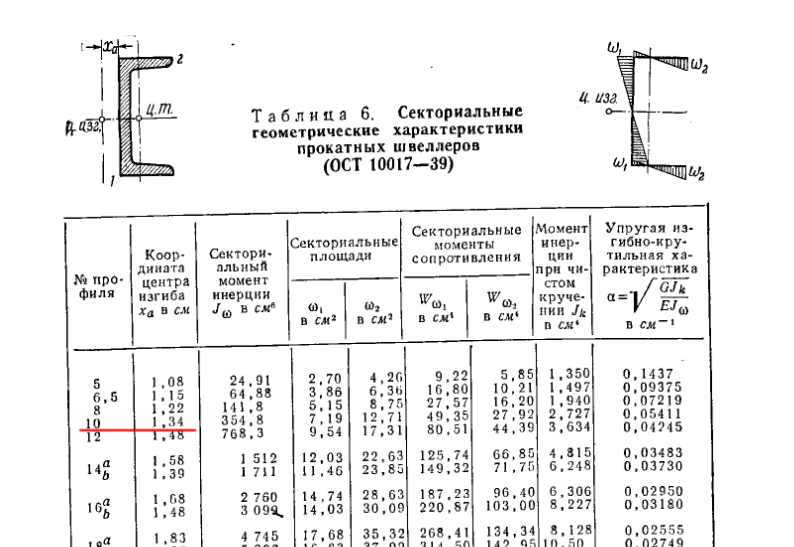 7 7 | 23.42 |
| 26Ш2 | 255 | 180 | 7.5 | 12 | 49.2 | 20.33 |
| 30Ш1 | 291 | 200 | 8 | 11 | 53.6 | 18.66 |
| 30Ш2 | 295 | 200 | 8.5 | 13 | 61 | 16.39 |
| 30Ш3 | 299 | 200 | 9 | 15 | 68.3 | 14.64 |
| 35Ш1 | 338 | 250 | 9. 5 5 | 12.5 | 75.1 | 13.32 |
| 35Ш2 | 341 | 250 | 10 | 14 | 82.2 | 12.17 |
| 35Ш3 | 345 | 250 | 10.5 | 16 | 91.3 | 10.95 |
| 40Ш1 | 388 | 300 | 9.5 | 14 | 96.1 | 10.41 |
| 40Ш2 | 392 | 300 | 11.5 | 16 | 111.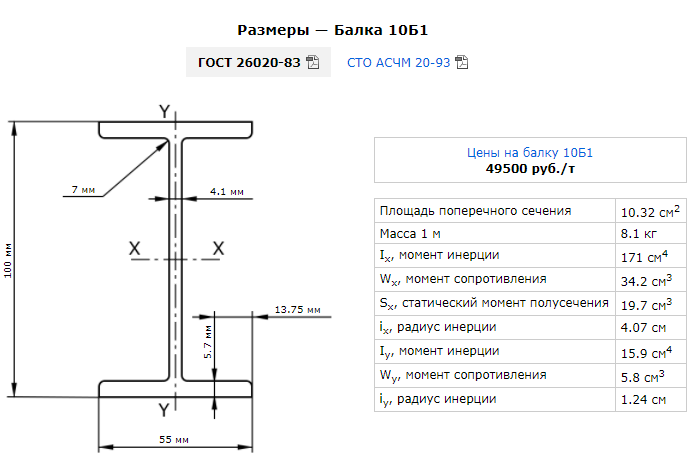 1 1 | 9 |
| 40Ш3 | 396 | 300 | 12.5 | 18 | 123.4 | 8.1 |
| 50Ш1 | 484 | 300 | 11 | 15 | 114.4 | 8.74 |
| 50Ш2 | 489 | 300 | 14.5 | 17.5 | 138.7 | 7.21 |
| 50Ш3 | 495 | 300 | 15.5 | 20.5 | 156.4 | 6.39 |
| 50Ш4 | 501 | 300 | 16.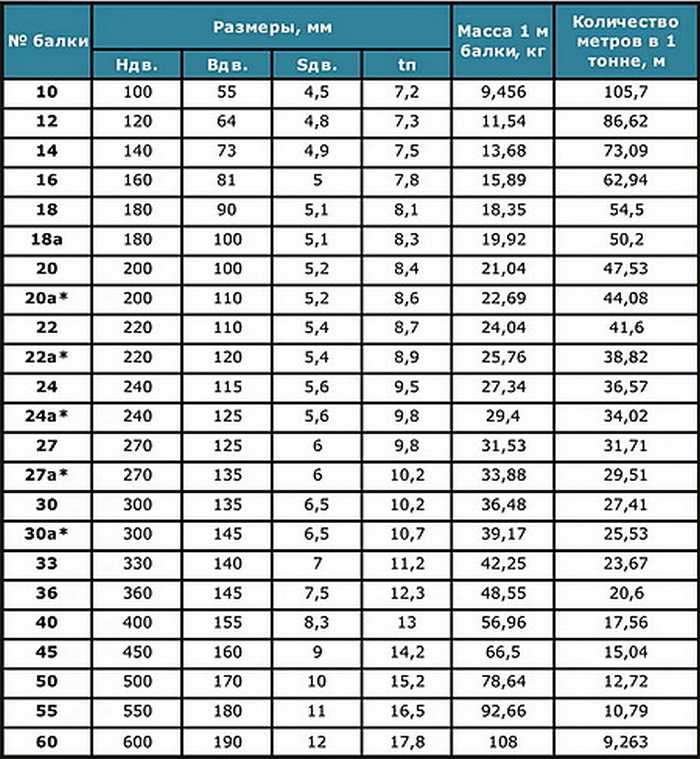 5 5 | 23.5 | 174.1 | 5.74 |
| 60Ш1 | 580 | 320 | 12 | 17 | 142.1 | 7.04 |
| 60Ш2 | 587 | 320 | 16 | 20.5 | 176.9 | 5.65 |
| 60Ш3 | 595 | 320 | 18 | 24.5 | 205.5 | 4.87 |
| 60Ш4 | 603 | 320 | 20 | 28.5 | 234.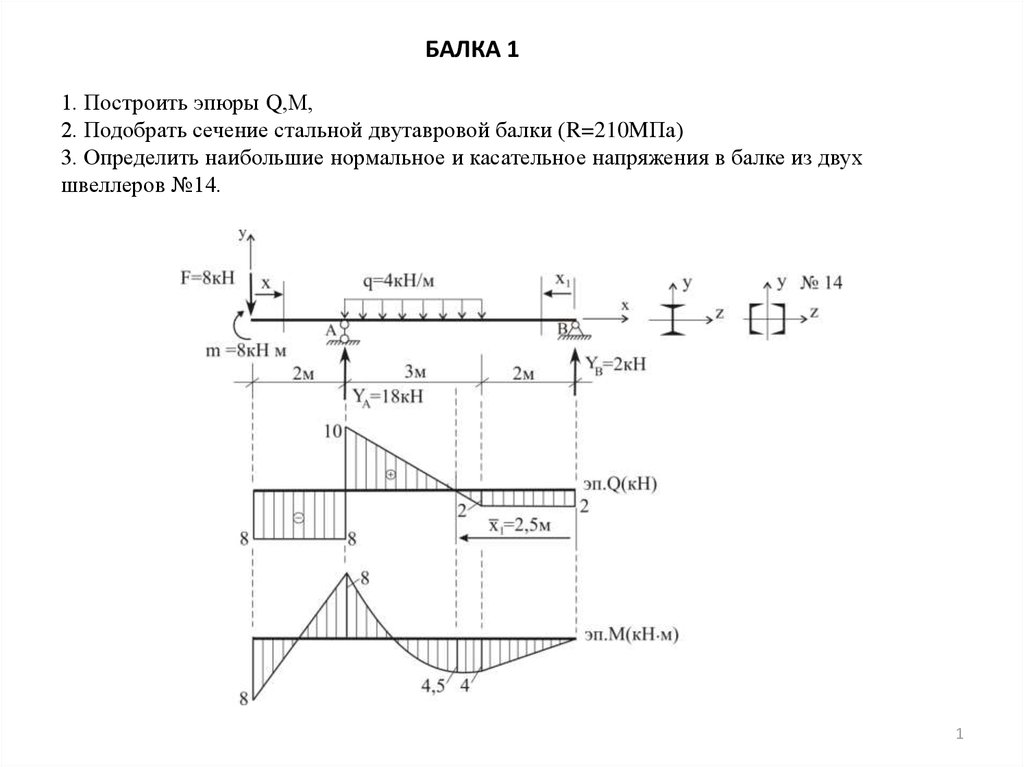 2 2 | 4.27 |
| 70Ш1 | 683 | 320 | 13.5 | 19 | 169.9 | 5.89 |
| 70Ш2 | 691 | 320 | 15 | 23 | 197.6 | 5.06 |
| 70Ш3 | 700 | 320 | 18 | 27.5 | 235.4 | 4.25 |
| 70Ш4 | 708 | 320 | 20.5 | 31.5 | 268.1 | 3.73 |
| 70Ш5 | 718 | 320 | 23 | 36. 5 5 | 305.9 | 3.27 |
Колонный двутавр (К)
| Номер двутавра | h | b | s | t | Вес метра, кг | Метров в тонне |
|---|---|---|---|---|---|---|
| 20К1 | 195 | 200 | 6.5 | 10 | 41.5 | 24.1 |
| 20К2 | 198 | 200 | 7 | 11.5 | 46.9 | 21.32 |
| 23К1 | 227 | 240 | 7 | 10. 5 5 | 52.2 | 19.16 |
| 23К2 | 230 | 240 | 8 | 12 | 59.5 | 16.81 |
| 26К1 | 255 | 260 | 8 | 12 | 65.2 | 15.34 |
| 26К2 | 258 | 260 | 9 | 13.5 | 73.2 | 13.66 |
| 26К3 | 262 | 260 | 10 | 15.5 | 83.1 | 12. 03 03 |
| 30К1 | 296 | 300 | 9 | 13.5 | 84.8 | 11.79 |
| 30К2 | 300 | 300 | 10 | 15.5 | 96.3 | 10.38 |
| 30К3 | 304 | 300 | 11.5 | 17.5 | 108.9 | 9.18 |
| 35К1 | 343 | 350 | 10 | 15 | 109.7 | 9.12 |
| 35К2 | 348 | 350 | 11 | 17.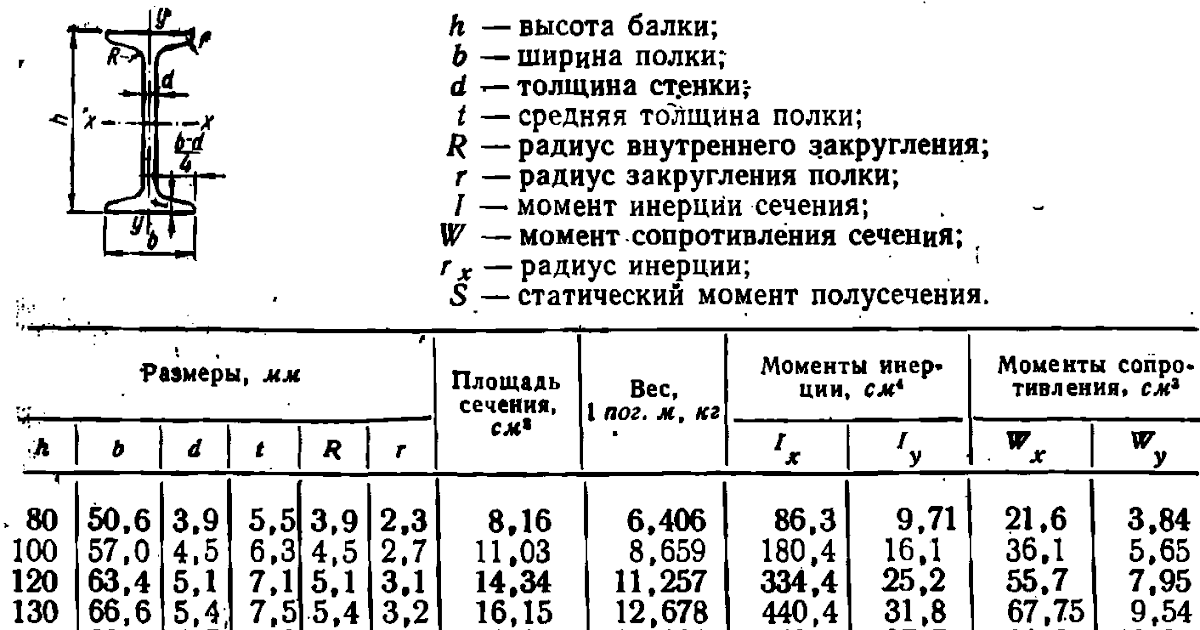 5 5 | 125.9 | 7.94 |
| 35К3 | 353 | 350 | 13 | 20 | 144.5 | 6.92 |
| 40К1 | 393 | 400 | 11 | 16.5 | 138 | 7.25 |
| 40К2 | 400 | 400 | 13 | 20 | 165.6 | 6.04 |
| 40К3 | 409 | 400 | 16 | 24.5 | 202.3 | 4. 94 94 |
| 40К4 | 419 | 400 | 19 | 29.5 | 242.2 | 4.13 |
| 40К5 | 431 | 400 | 23 | 35.5 | 291.2 | 3.43 |
Двутавр дополнительной серии (Д)
| Номер двутавра | h | b | s | t | Вес метра, кг | Метров в тонне |
|---|---|---|---|---|---|---|
| 24ДБ1 | 239 | 115 | 5.5 | 9.3 | 27.8 | 35. 97 97 |
| 27ДБ1 | 269 | 125 | 6 | 9.5 | 31.9 | 31.35 |
| 36ДБ1 | 360 | 145 | 12.3 | 18 | 49.1 | 20.37 |
| 35ДБ1 | 349 | 127 | 5.8 | 8.5 | 33.6 | 29.76 |
| 40ДБ1 | 399 | 139 | 6.2 | 9 | 39.7 | 25.19 |
| 45ДБ1 | 450 | 152 | 11 | 15 | 52. 6 6 | 19.01 |
| 45ДБ2 | 450 | 180 | 7.6 | 13.3 | 65 | 15.38 |
| 30ДШ1 | 300.6 | 201.9 | 9.4 | 16 | 72.7 | 13.76 |
| 40ДШ1 | 397.6 | 302 | 11.5 | 18.7 | 124 | 8.06 |
| 50ДШ1 | 496.2 | 303.8 | 14.2 | 21 | 155 | 6. 45 45 |
Сварной двутавр (С)
| Номер двутавра | h | b | s | t | Вес метра, кг | Метров в тонне |
|---|---|---|---|---|---|---|
| 45БС1 | 444 | 200 | 8 | 12 | 64.1 | 15.6 |
| 45БС2 | 460 | 300 | 12 | 20 | 133.8 | 7.47 |
| 45БСЗ | 448 | 180 | 8 | 14 | 65.9 | 15. 17 17 |
| 50БС1 | 482 | 200 | 10 | 16 | 85.6 | 11.68 |
| 50БС2 | 482 | 300 | 12 | 16 | 117.8 | 8.49 |
| 50БСЗ | 500 | 300 | 12 | 25 | 160.1 | 6.25 |
| 50БС4 | 510 | 300 | 14 | 30 | 190.8 | 5.24 |
| 55БС1 | 551 | 220 | 10 | 18 | 102. 6 6 | 9.75 |
| 55БС2 | 547 | 200 | 10 | 16 | 90.7 | 11.03 |
| 60БС1 | 577 | 240 | 12 | 16 | 111.6 | 8.96 |
| 60БС2 | 585 | 240 | 12 | 20 | 126.7 | 7.89 |
| 60БСЗ | 585 | 320 | 12 | 20 | 151.8 | 6.59 |
| 60ВС4 | 595 | 320 | 14 | 25 | 185. 5 5 | 5.39 |
| 60БС5 | 605 | 320 | 16 | 30 | 219.2 | 4.56 |
| 60БС6 | 597 | 190 | 12 | 16 | 101 | 9.9 |
| 70БС1 | 685 | 260 | 12 | 20 | 142.4 | 7.02 |
| 70БС2 | 685 | 320 | 14 | 20 | 171.4 | 5.83 |
| 70БСЗ | 695 | 320 | 14 | 25 | 196. 5 5 | 5.09 |
| 70БС4 | 705 | 320 | 16 | 30 | 231.7 | 4.32 |
| 70БС5 | 725 | 320 | 20 | 40 | 302.2 | 3.31 |
| 70БС6 | 692 | 230 | 12 | 16 | 119.9 | 8.34 |
| 80БС1 | 791 | 280 | 14 | 18 | 162.1 | 6.17 |
| 80БС2 | 815 | 300 | 18 | 30 | 248 | 4. 03 03 |
| 90БС1 | 895 | 300 | 16 | 20 | 201.6 | 4.96 |
| 90БС2 | 927 | 300 | 16 | 36 | 276.9 | 3.61 |
| 100БС1 | 995 | 320 | 16 | 25 | 244.3 | 4.09 |
| 100БС2 | 1005 | 320 | 16 | 30 | 269.4 | 3.71 |
| 100БСЗ | 1017 | 320 | 20 | 36 | 329. 2 2 | 3.04 |
| 120БС1 | 1280 | 400 | 12 | 20 | 242.4 | 4.13 |
| 120БС2 | 1280 | 450 | 14 | 20 | 277.6 | 3.6 |
| 140БС1 | 1440 | 400 | 12 | 20 | 257.5 | 3.88 |
| 140БС2 | 1440 | 450 | 12 | 20 | 273.2 | 3.66 |
| 140БСЗ | 1450 | 500 | 14 | 25 | 350. 1 1 | 2.86 |
| 160БС1 | 1640 | 450 | 12 | 20 | 392 | 2.55 |
| 160БС2 | 1640 | 500 | 12 | 20 | 307.7 | 3.25 |
| 160БСЗ | 1650 | 500 | 14 | 25 | 372.1 | 2.69 |
| 160БС4 | 1650 | 560 | 14 | 25 | 395.6 | 2.53 |
| 180БС1 | 1800 | 560 | 12 | 25 | 384. 6 6 | 2.6 |
| 180БС2 | 1800 | 500 | 14 | 25 | 388.6 | 2.57 |
| 180БСЗ | 1810 | 500 | 14 | 30 | 427.8 | 2.34 |
| 180БС4 | 1810 | 600 | 16 | 30 | 502.4 | 1.99 |
| 200БС1 | 2000 | 560 | 12 | 25 | 403.5 | 2.48 |
| 200БС2 | 2010 | 500 | 16 | 30 | 480.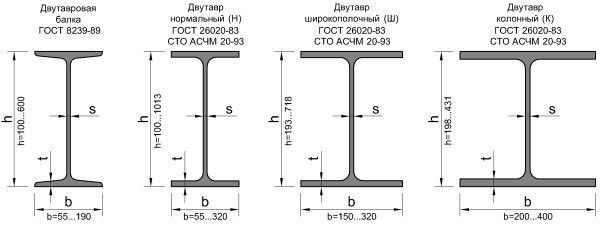 4 4 | 2.08 |
| 200БСЗ | 2010 | 600 | 16 | 30 | 527.5 | 1.9 |
Двутавр является стандартным профилем конструктивных элементов. Изготавливается из черного металлопроката или древесины. Сечение напоминает букву «Н». Отличительная особенность балки двутаврового профиля заключается в том, что она имеет в 30 раз более жесткую конструкцию и в 7 раз прочнее балки с квадратным профилем, имеющим аналогичное сечение.
Сфера применения двутавров огромна. Их используют, чаще всего, при строительстве, судостроении, мотостроении и т.д. Двутавры позволяют сделать потолочное перекрытие более жестким.
Изготовление металлических двутавров выполняется согласно установленным нормативам и требованиям ГОСТов и ТУ. Поэтому у них регламентированная форма и состав, позволяющие без проблем рассчитать нужные размеры и параметры, включая вес двутавра. Для этого используйте представленные ниже таблицы ГОСТ и калькулятор для автоматического расчета.
Для этого используйте представленные ниже таблицы ГОСТ и калькулятор для автоматического расчета.
1 Порядок расчета сварной двутавровой балки
Определить
высоту балки:
– построить эпюры сил и моментов;
– найти опасное сечение;
– определить высоту балки из условий
жесткости;
– определить высоту балки из условий
прочности и экономичности;
– откорректировать высоту балки при
недогрузе и округлить до значения,
кратного 50 мм.
Спроектировать
сечение балки.
Проверить сечение балки:
– по распределению металла;
– по прочности.
Обеспечить
общую и местную устойчивость балки:
рассчитать, спроектировать, расставить
вертикальные и горизонтальные ребра
жесткости.
Рассчитать или назначить параметры
сварных соединений балки.
Спроектировать
необходимые стыки балки: конструктивные,
технологические и монтажные.
Спроектировать и рассчитать опорные
части балки.
Рассчитать вес основного и наплавленного
металла.
Вычертить
балку в масштабе 1:100 с необходимыми
разрезами, сечениями, размерами и
условными обозначениями, необходимыми
для изготовления и монтажа балки.
2 Расчета сварной двутавровой балки
2.1 Задание на проектирование сварной двутавровой балки
Спроектировать
сварную двутавровую балку при следующих
параметрах:
L = 4,5 м;q1
= 15 КН/м;P =50
КН; [σр] = 225 МПа; [τср]
= 135 МПа;
fmax/l= 1/500; Материал –
14Г2; Нагрузка статическая.
Рис.1 Расчетная схема балки
2.2 Определение высоты балки
Для определения опорных реакций составим
уравнения моментов относительно точек
А иВ:
= 92,5 кН;
кН.
Для определения внутренних силовых
факторов и моментов применяем метод
сечений.
Определим поперечные усилия Qв данной балке:
Определим изгибающие моменты Мв
данной балке:
Анализ эпюр Qyи Mxпоказывает, что опасным сечением является
сечениеС, где
.
Определяем высоту балки из условий
жесткости:
.
Определяем высоту балки из условия
прочности и экономичности:
.
В данном случае
,
поэтому в соответствии с рекомендациями
принимаем высоту балки из условия
жесткости.
Округляем и принимаем
.
2.3 Расчет и проектирование сечения балки
Толщина стенки двутавровой балки:
.
Принимаем δв = 10 мм.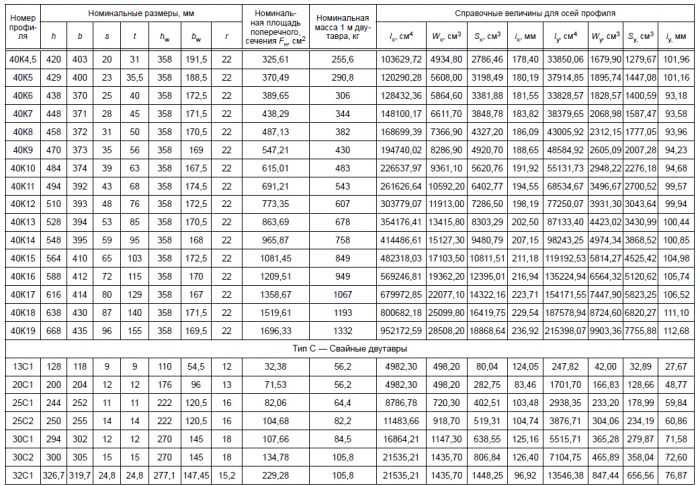
Толщина пояса :
.
Предварительно принимаем δп
= 25 мм.
Ширина
пояса :
Для
обеспечения местной устойчивости полок
сжатого пояса рекомендуется:
,
поэтому еще одно значение bn:.
Кроме
того, в поясах балки должно быть не
меньше 30 % металла. Из этих соображений:
м = 196 мм .
Учитывая то, что по ГОСТ 6009–74 стальная
горячекатаная лента (полоса) при ширине
свыше 140 мм выпускается с минимальной
толщиной 25 мм, откорректируем размеры
пояса, приняв полосу толщиной 25 мм и
шириной 180 мм.
Принимаем размеры сечения балки:
Уточнив
все размеры сечения, определим истинный
момент инерции сечения балки:
2.
 4 Проверка сечения балки
4 Проверка сечения балки
Выполним четыре проверки сечения
1
По использованию материала (в поясах
должно быть не менее 30 % материала):
.
2 По максимальным изгибающим
напряжениям:
;
3 По максимальным
касательным напряжениям:
4. По эквивалентным напряжениям в
верхней кромке стенки балки:
230,319 МПа < 225 МПа.
Балка
перегружена. Перегруз оправдан выбором
высоты балки из условия жесткости.
Окончательные размеры балки:
Расчет балок на прогиб. Максимальный прогиб балки: формула
Балка – элемент в инженерии, представляющий собой стержень, который нагружают силы, действующие в направлении, перпендикулярном стержню. Деятельность инженеров зачастую включает в себя необходимость расчета прогиба балки под нагрузкой. Этой действие выполняется для того, чтобы ограничить максимальный прогиб балки.
Деятельность инженеров зачастую включает в себя необходимость расчета прогиба балки под нагрузкой. Этой действие выполняется для того, чтобы ограничить максимальный прогиб балки.
Типы
На сегодняшний день в строительстве могут использоваться балки, изготовленные из разных материалов. Это может быть металл или дерево. Каждый конкретный случай подразумевает под собой разные балки. При этом расчет балок на прогиб может иметь некоторые отличия, которые возникают по принципу разницы в строении и используемых материалов.
Деревянные балки
Сегодняшнее индивидуальное строительство подразумевает под собой широкое применение балок, изготовленных из дерева. Практически каждое строение содержит в себе деревянные перекрытия. Балки из дерева могут использоваться как несущие элементы, их применяют при изготовлении полов, а также в качестве опор для перекрытий между этажами.
Ни для кого не секрет, что деревянная, так же как и стальная балка, имеет свойство прогибаться под воздействием нагрузочных сил.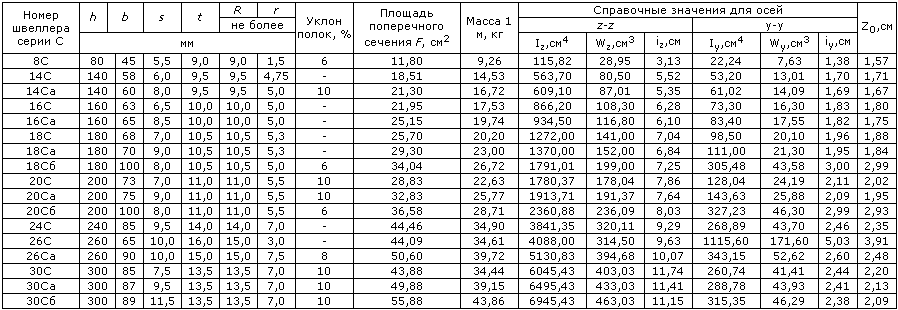 Стрелка прогиба зависит от того, какой материал используется, геометрических характеристик конструкции, в которой используется балка, и характера нагрузок.
Стрелка прогиба зависит от того, какой материал используется, геометрических характеристик конструкции, в которой используется балка, и характера нагрузок.
Допустимый прогиб балки формируется из двух факторов:
- Соответствие прогиба и допустимых значений.
- Возможность эксплуатации здания с учетом прогиба.
Проводимые при строительстве расчеты на прочность и жесткость позволяют максимально эффективно оценить то, какие нагрузки сможет выдерживать здание в ходе эксплуатации. Также эти расчеты позволяют узнать, какой именно будет деформация элементов конструкции в каждом конкретном случае. Пожалуй, никто не будет спорить с тем, что подробные и максимально точные расчеты – это часть обязанностей инженеров-строителей, однако с использованием нескольких формул и навыка математических вычислений можно рассчитать все необходимые величины самостоятельно.
Для того чтобы произвести правильный расчет прогиба балки, нужно также брать во внимание тот факт, что в строительстве понятия жесткости и прочности являются неразрывными. Опираясь на данные расчета прочности, можно приступать к дальнейшим расчетам относительно жесткости. Стоит отметить, что расчет прогиба балки – один из незаменимых элементов расчета жесткости.
Опираясь на данные расчета прочности, можно приступать к дальнейшим расчетам относительно жесткости. Стоит отметить, что расчет прогиба балки – один из незаменимых элементов расчета жесткости.
Обратите ваше внимание на то, что для проведения таких вычислений самостоятельно лучше всего использовать укрупненные расчеты, прибегая при этом к достаточно простым схемам. При этом также рекомендуется делать небольшой запас в большую сторону. Особенно если расчет касается несущих элементов.
Расчет балок на прогиб. Алгоритм работы
На самом деле алгоритм, по которому делается подобный расчет, достаточно прост. В качестве примера рассмотрим несколько упрощенную схему проведения расчета, при этом опустив некоторые специфические термины и формулы. Для того чтобы произвести расчет балок на прогиб, необходимо выполнить ряд действий в определенном порядке. Алгоритм проведения расчетов следующий:
- Составляется расчетная схема.
- Определяются геометрические характеристики балки.

- Вычисляется максимальную нагрузку на данный элемент.
- В случае возникновения необходимости проверяется прочность бруса по изгибающему моменту.
- Производится вычисление максимального прогиба.
Как видите, все действия достаточно просты и вполне выполнимы.
Составление расчетной схемы балки
Для того чтобы составить расчетную схему, не требуется больших знаний. Для этого достаточно знать размер и форму поперечного сечения элемента, пролет между опорами и способ опирания. Пролетом является расстояние между двумя опорами. К примеру, вы используете балки как опорные брусья перекрытия для несущих стен дома, между которыми 4 м, то величина пролета будет равна 4 м.
Вычисляя прогиб деревянной балки, их считают свободно опертыми элементами конструкции. В случае балки перекрытия для расчета принимается схема с нагрузкой, которая распределена равномерно. Обозначается она символом q. Если же нагрузка несет сосредоточенный характер, то берется схема с сосредоточенной нагрузкой, обозначаемой F. 3/12, где:
3/12, где:
b – ширина сечения;
h – высота сечения балки.
Вычисления максимального уровня нагрузки
Определение максимальной нагрузки на элемент конструкции производится с учетом целого ряда факторов и показателей. Обычно при вычислении уровня нагрузки берут во внимание вес 1 погонного метра балки, вес 1 квадратного метра перекрытия, нагрузку на перекрытие временного характера и нагрузку от перегородок на 1 квадратный метр перекрытия. Также учитывается расстояние между балками, измеренное в метрах. Для примера вычисления максимальной нагрузки на деревянную балку примем усредненные значения, согласно которым вес перекрытия составляет 60 кг/м², временная нагрузка на перекрытие равна 250 кг/м², перегородки будут весить 75 кг/м². Вес самой балки очень просто вычислить, зная ее объем и плотность. Предположим, что используется деревянная балка сечением 0,15х0,2 м. В этом случае ее вес будет составлять 18 кг/пог.м. Также для примера примем расстояние между брусьями перекрытия равным 600 мм. 3/48*E*J, где:
3/48*E*J, где:
F – сила давления на брус.
Также обращаем внимание на то, что значение модуля упругости, используемое в расчетах, может различаться для разных видов древесины. Влияние оказывают не только порода дерева, но и вид бруса. Поэтому цельная балка из дерева, клееный брус или оцилиндрованное бревно будут иметь разные модули упругости, а значит, и разные значения максимального прогиба.
Вы можете преследовать разные цели, совершая расчет балок на прогиб. Если вы хотите узнать пределы деформации элементов конструкции, то по завершении расчета стрелки прогиба вы можете остановиться. Если же ваша цель – установить уровень соответствия найденных показателей строительным нормам, то их нужно сравнить с данными, которые размещены в специальных документах нормативного характера.
Двутавровая балка
Обратите внимание на то, что балки из двутавра применяются несколько реже в силу их формы. Однако также не стоит забывать, что такой элемент конструкции выдерживает гораздо большие нагрузки, чем уголок или швеллер, альтернативой которых может стать двутавровая балка.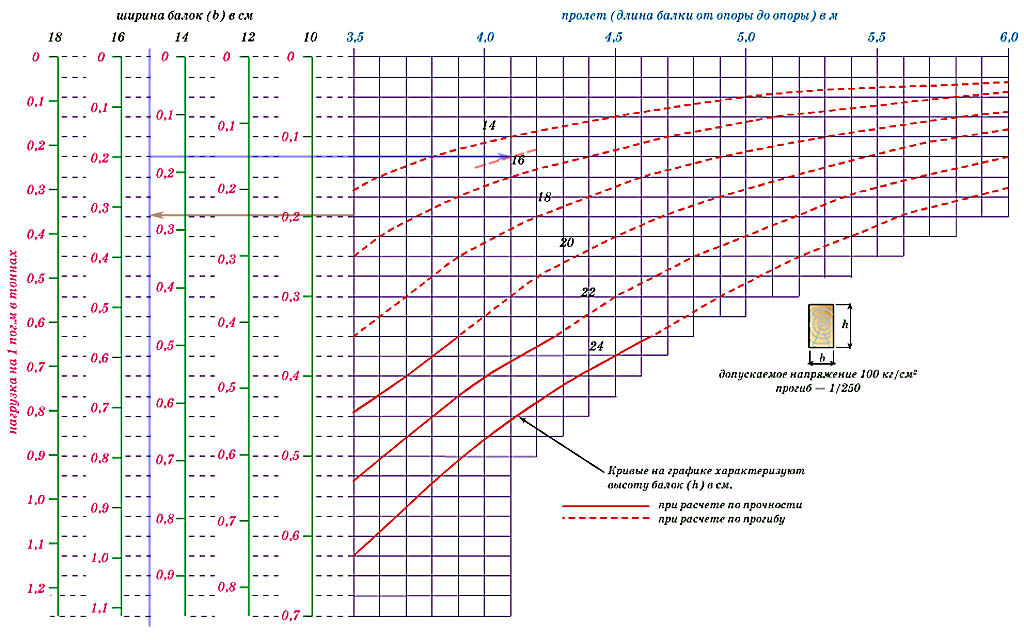
Расчет прогиба двутавровой балки стоит производить в том случае, если вы собираетесь использовать ее в качестве мощного элемента конструкции.
Также обращаем ваше внимание на то, что не для всех типов балок из двутавра можно производить расчет прогиба. В каких же случаях разрешено рассчитать прогиб двутавровой балки? Всего таких случаев 6, которые соответствуют шести типам двутавровых балок. Эти типы следующие:
- Балка однопролетного типа с равномерно распределенной нагрузкой.
- Консоль с жесткой заделкой на одном конце и равномерно распределенной нагрузкой.
- Балка из одного пролета с консолью с одной стороны, к которой прикладывается равномерно распределенная нагрузка.
- Однопролетная балка с шарнирным типом опирания с сосредоточенной силой.
- Однопролетная шарнирно опертая балка с двумя сосредоточенными силами.
- Консоль с жесткой заделкой и сосредоточенной силой.
Металлические балки
Расчет максимального прогиба одинаковый, будь это стальная балка или же элемент из другого материала.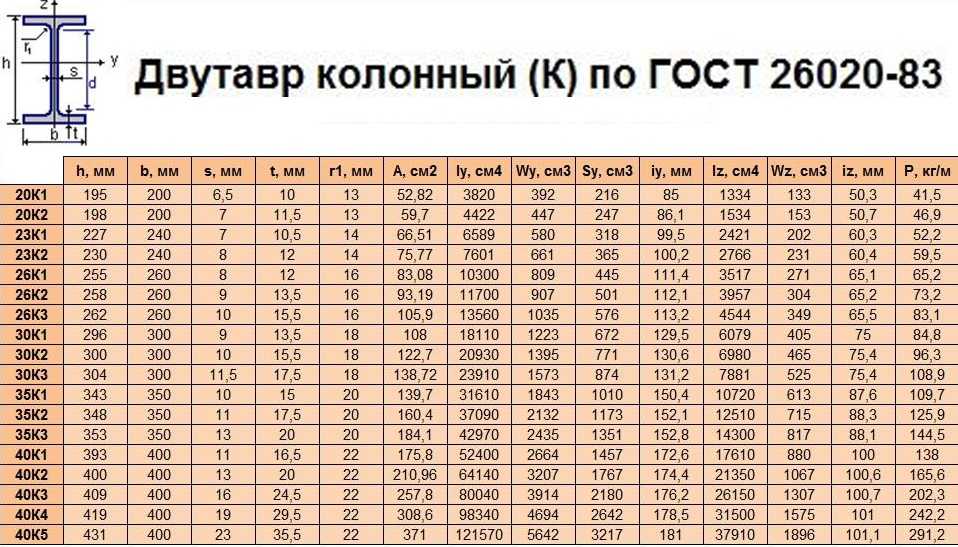 Главное — помнить о тех величинах, которые специфические и постоянные, как к примеру модуль упругости материала. При работе с металлическими балками, важно помнить, что они могут быть изготовлены из стали или же из двутавра.
Главное — помнить о тех величинах, которые специфические и постоянные, как к примеру модуль упругости материала. При работе с металлическими балками, важно помнить, что они могут быть изготовлены из стали или же из двутавра.
Прогиб металлической балки, изготовленной из стали, вычисляется с учетом, что константа Е в данном случае составляет 2·105Мпа. Все остальные элементы, вроде момента инерции, вычисляются по алгоритмам, описанным выше.
Расчет максимального прогиба для балки с двумя опорами
В качестве примера рассмотрим схему, в которой балка находится на двух опорах, а к ней прикладывается сосредоточенная сила в произвольной точке. До момента прикладывания силы балка представляла собой прямую линию, однако под воздействием силы изменила свой вид и вследствие деформации стала кривой.
Предположим, что плоскость ХУ является плоскостью симметрии балки на двух опорах. Все нагрузки действуют на балку в этой плоскости. В этом случае фактом будет то, что кривая, полученная в результате действия силы, также будет находиться в этой плоскости. Данная кривая получила название упругой линии балки или же линии прогибов балки. Алгебраически решить упругую линию балки и рассчитать прогиб балки, формула которого будет постоянной для балок с двумя опорами, можно следующим образом.
Данная кривая получила название упругой линии балки или же линии прогибов балки. Алгебраически решить упругую линию балки и рассчитать прогиб балки, формула которого будет постоянной для балок с двумя опорами, можно следующим образом.
Прогиб на расстоянии z от левой опоры балки при 0 ≤ z ≤ a
F(z)=(P*a2*b2)/(6E*J*l)*(2*z/a+z/b-z3/a2*b)
Прогиб балки на двух опорах на расстоянии z от левой опоры при а ≤ z ≤l
f(z)=(-P*a2*b2)/(6E*J*l)*(2*(l-z)/b+(l-z)/a-(l-z)3/a+b2), где Р – прикладываемая сила, Е – модуль упругости материала, J – осевой момент инерции.
В случае балки с двумя опорами момент инерции вычисляется следующим образом:
J=b1h13/12, где b1 и h1 – значения ширины и высоты сечения используемой балки соответственно.
Заключение
В заключение можно сделать вывод о том, что самстоятельно вычислить величину максимального прогиба балки разных типов достаточно просто. Как было показано в этой статье, главное — знать некоторые характеристики, которые зависят от материала и его геометрических характеристик, а также провести вычисления по нескольким формулам, в которых каждый параметр имеет свое объяснение и не берется из ниоткуда.
Как было показано в этой статье, главное — знать некоторые характеристики, которые зависят от материала и его геометрических характеристик, а также провести вычисления по нескольким формулам, в которых каждый параметр имеет свое объяснение и не берется из ниоткуда.
Расчет металлической балки
Двутавp колонный (К) по ГОСТ 26020-83
20К1
20К2
23К1
23К2
26К1
26К2
26К3
30К1
30К2
30К3
35К1
35К2
35К3
40К1
40К2
40К3
40К4
40К5
Двутавp с уклоном полок по ГОСТ 8239-89
10
12
14
16
18
20
22
24
27
30
33
36
40
45
50
55
60
Двутавp дополнительной серии (Д) по ГОСТ 26020-83
24ДБ1
27ДБ1
36ДБ1
35ДБ1
40ДБ1
45ДБ1
45ДБ2
30ДШ1
40ДШ1
50ДШ1
Двутавp нормальный (Б) по ГОСТ 26020-83
10Б1
12Б1
12Б2
14Б1
14Б2
16Б1
16Б2
18Б1
18Б2
20Б1
23Б1
26Б1
26Б2
30Б1
30Б2
35Б1
35Б2
40Б1
40Б2
45Б1
45Б2
50Б1
50Б2
55Б1
55Б2
60Б1
60Б2
70Б1
70Б2
80Б1
80Б2
90Б1
90Б2
100Б1
100Б2
100Б3
100Б4
Двутавp широкополочный по ГОСТ 26020-83
20Ш1
23Ш1
26Ш1
26Ш2
30Ш1
30Ш2
30Ш3
35Ш1
35Ш2
35Ш3
40Ш1
40Ш2
40Ш3
50Ш1
50Ш2
50Ш3
50Ш4
60Ш1
60Ш2
60Ш3
60Ш4
70Ш1
70Ш2
70Ш3
70Ш4
70Ш5
Двутавp нормальный (Б) по СТО АСЧМ 20-93
10Б1
12Б1
12Б2
14Б1
14Б2
16Б1
16Б2
18Б1
18Б2
20Б1
25Б1
25Б2
30Б1
30Б2
35Б1
35Б2
40Б1
40Б2
45Б1
45Б2
50Б1
50Б2
50Б3
55Б1
55Б2
60Б1
60Б2
70Б0
70Б1
70Б2
Двутавp широкополочный (Ш) по СТО АСЧМ 20-93
20Ш1
25Ш1
30Ш1
30Ш2
35Ш1
35Ш2
40Ш1
40Ш2
45Ш1
50Ш1
50Ш2
50Ш3
50Ш4
60Ш1
60Ш2
60Ш3
60Ш4
70Ш1
70Ш2
70Ш3
70Ш4
80Ш1
80Ш2
90Ш1
90Ш2
100Ш1
100Ш2
100Ш3
100Ш4
Двутавp колонный (К) по СТО АСЧМ 20-93
20К1
20К2
25К1
25К2
25К3
30К1
30К2
30К3
30К4
35К1
35К2
40К1
40К2
40К3
40К4
40К5
Как рассчитать вес i балки и конструкции
Как рассчитать вес i балки / Как найти вес i балки, в этой теме мы узнаем, как рассчитать вес i балки. Сегодня инженеры широко используют балку в строительстве, формируя колонны и балки, а также множество типов различных конструкций, имеющих разную длину, размер и размер.
Сегодня инженеры широко используют балку в строительстве, формируя колонны и балки, а также множество типов различных конструкций, имеющих разную длину, размер и размер.
I-образная балка в основном выглядит как Н-образная балка , также называемая широкой балкой и универсальный луч .
Как рассчитать вес двутавровой балки
Различные полные формы ISMB, ISMC, ISJB, ISLB и ISWB, относящиеся к i-балке
В проектировании металлоконструкций и строительных конструкций технические термины используются для i-балки инженерами, т.е. ISMB , ISMC, ISJB, ISLB и ISWB
◆Разные полные формы
1) ISMB – Индийский стандарт балки среднего веса
2) ISMC – Индийский стандарт среднего веса канала
3) ISJB – Индийский стандарт, юношеская балка
4) ISLB – Индийский стандарт, легкая балка
5) ISWB – Индийский стандарт, широкополочная балка
◆Вы можете подписаться на меня в Facebook и подписаться на наш канал Youtube
—
1) что такое бетон, его виды и свойства
Что такое балка?
В основном двутавровая балка, имеющая Н-образную форму, состоит из двух горизонтальных плоских частей, называемых полками, которые соединены одним вертикальным элементом, известным как стенка.
И форма фланца, и стенка образуют двутавровое поперечное сечение из стали и балки. Он имеет множество применений в строительстве каркасов, мостов и инженерных сооружений. Это форма выбора для зданий из конструкционной стали, дизайн и структура i-образной балки делают ее уникальной и способной выдерживать различные нагрузки, действующие на нее. Теперь мы обсудим, как рассчитать вес i балки.
Как рассчитать вес двутавровой балки
Как рассчитать массу двутавровой балки
ISMB (Индийский стандарт балки среднего веса) формула расчета веса
ismb 75×40×4,8: – размеры ismb 75 мм × 40 мм × 4,8 мм имеют вес 2,176 кг/фут или 7,14 кг/метр.
ismb 100×50×5 :- размеры ismb 100 мм × 50 мм × 5 мм имеют вес 2,914 кг/фут или 9,56 кг/метр.
ismb 125×65×5,3 :- размеры ismb 125 мм × 65 мм × 5,3 мм имеют вес 3,993 кг/фут или 13,10 кг/метр.
ismb 150×75×5,7 :- размеры ismb 150 мм × 75 мм × 5,7 мм имеют вес 5,121 кг/фут или 16,80 кг/метр.
ismb 175×75×6 :- размеры ismb 175 мм × 75 мм × 6 мм имеют вес 5,975 кг/фут или 19,60 кг/метр.
ismb 200×75×6,2: – размеры ismb 200 мм × 75 мм × 6,2 мм имеют вес 6,798 кг/фут или 22,30 кг/метр.
ismb 250×82×9 :- размеры ismb 250 мм × 82 мм × 9 мм имеют вес 10,426 кг/фут или 34,20 кг/метр.
ismb 300×90×7,8: – размеры ismb 300 мм × 90 мм × 7,8 мм имеют вес 11,067 кг/фут или 36,3 кг/метр.
исмб 400×100×8,8 : размер 400 мм × 100 мм × 8,8 мм имеет вес 15,274 кг/фут или 50,1 кг/метр.
Полная форма ISMB : полная форма ISMB — это балка среднего веса индийского стандарта.
Вес ISMB 200:- Индийский стандарт, средний вес Вес балки 200 на метр составляет 25,40 кг/м, их площадь поперечного сечения составляет 32,33 см2, глубина сечения 200 мм, ширина полки 100 мм, толщина полки 10,80 мм и толщина Сеть 5,70 мм.
Мы дали:-
◆ фланец (A) компонент
длина полки = 100 мм
толщина полки = 15 мм
высота полки = 1000 мм
◆ стенка (B) компонента
9000 Толщина стенки = 15 мм
Высота стенки = 1000 мм
Плотность стали = 7850 кг/м3
Теперь нам нужно рассчитать объем полки и стенки
Теперь объем полки = l×b×h
Объем фланца = 100×15×1000 мм
Переведем в метры, получим
Объем фланца = 0,1×0,015×1 м3
Объем фланца = 0,0015 м3
На данном рисунке у нас есть два фланца одинакового объема, поэтому мы должны умножить на 2 объем одна полка
Объем полки = 2×0,0015 м3
Общий объем полки = 0,0030 м3
Теперь нужно рассчитать объем стенки
Объем стенки = l × b× h
Длина стенки = 200 мм – толщина двух фланцев
Длина полотна = 200 – (2×15) мм
Длина полотна = 170 мм
Объем полотна = 170×15×1000 мм
Теперь перевести в метры
Объем полотна = 0,17×0,015×1 м3
Объем стенки = 0,00255 м3
Теперь мы должны рассчитать общий объем i-й балки, который представляет собой сумму объема полки и объема стенки
Общий объем i-балки = 0,0030+0,00255 м3
Объем i-балки = 0,00555 м3
Теперь надо вычислить массу двутавровой балки, которая равна произведению плотности стали на объем i-й балки
Вес = объем × плотность
Вес = 0,00555 м3×7850 кг/м3
Вес = 43,57 кг Beams
ToolCrowd поддерживает считыватель. Когда вы покупаете по ссылкам на нашем сайте, мы можем получать партнерскую комиссию. Узнать большеОбъявления
Когда вы покупаете по ссылкам на нашем сайте, мы можем получать партнерскую комиссию. Узнать большеОбъявления
Главная » Строительные материалы » Калькулятор веса двутавровой балки – рассчитать вес двутавровой балки
Наш удобный калькулятор веса двутавровой балки позволяет быстро и легко рассчитать вес на фут, метр или общий вес двутавровой балки как с наклонными, так и с параллельными полками.
Инструкции по использованию калькулятора см. в руководстве пользователя под калькулятором. Мы также включили пошаговое руководство, если вы предпочитаете рассчитывать вес двутавровой балки вручную, а также удобные таблицы веса для балок типа IPE и IPN.
Калькулятор веса двутавровой балки:
Выберите тип угла:
Материал двутавровой балки:
Плотность:
кг/м 3
Количество:
Ширина двутавровой балки (Д):
I Be
Высота балки (H):
Толщина стенки (WT):
Толщина фланца (FT):
Внутренний радиус (IR):
Внешний радиус (OR):
Общий вес = 0,00 фунта / 0,00 кг
Отказ от ответственности: веса, показанные в приведенном выше калькуляторе, предназначены только для справки и не должны служить основой для каких-либо расчетов, где требуется точная или точная информация. Теоретический вес и плотность металла нередко значительно отличаются от фактического веса и плотности, например, из-за различий в производственных процессах и составе материалов. Поэтому, если требуются точные расчеты веса, вы должны получить актуальную и точную информацию от производителей.
Теоретический вес и плотность металла нередко значительно отличаются от фактического веса и плотности, например, из-за различий в производственных процессах и составе материалов. Поэтому, если требуются точные расчеты веса, вы должны получить актуальную и точную информацию от производителей.
Advertisements
Как пользоваться калькулятором веса двутавровой балки
Первым шагом является выбор типа двутавровой балки, вес которой вы хотите рассчитать, с «наклонной полкой» или «параллельной полкой». доступные варианты.
- Далее вам нужно выбрать материал, используемый для двутавровой балки в вашем расчете, и вы можете выбрать его в раскрывающемся списке «Материал двутавровой балки» в поле (2).
Вы можете изменить количество двутавровых балок, которые вы включаете в свой расчет, обновив ввод «Количество» в поле (2).
Поле «Плотность» будет автоматически заполнено в зависимости от выбранного вами типа материала.

При необходимости вы можете обновить показатель «Плотность» до другого значения, хотя мы основывали значение, используемое для каждого материала, на отраслевых рекомендациях.
Вам потребуется ввести различные размеры для расчета, включая «Длину», «Ширину», «Высоту», «Толщину стенки», «Толщину фланца» и одно или два значения «Радиуса» в зависимости от вашего выбора. двутаврового профиля.
Вы можете выбрать соответствующие единицы для каждого измерения, используя раскрывающиеся списки «Единицы», включая миллиметры, сантиметры, метры, дюймы и футы.
!
Примечание: Если вы выберете в качестве единицы «дюйм», вам нужно будет использовать целые или десятичные числа вместо дробей. Например, 0,25 вместо 1 / 4 .
- Используйте кнопку «Рассчитать», чтобы завершить расчет, или кнопку «Сброс», чтобы сбросить калькулятор веса двутавровой балки, если вы хотите начать сначала.
Advertisements
Как рассчитать вес двутавровой балки
Вот как вручную рассчитать вес двутавровой балки, если вы предпочитаете обход калькулятора выше:
Как рассчитать вес параллели- Полковая двутавровая балка
Сначала вам необходимо рассчитать объем двутавровой балки с параллельными полками, и вы можете сделать это с помощью следующего уравнения:
V1 = (Ш x ФУ x Д) x 2
V2 = (H – (2 x FT)) x WT x L
V3 = ((R x 2) 2 – (π x R 2 )) x L
Общий объем = V1 + V2 + V3
Приведенная выше формула веса двутавровой балки состоит из следующих элементов :
V1 = Часть расчета объема полки
V2 = Часть расчета объема стенки
V3 = Часть расчета объема радиуса
W = Ширина Двутавровая балка
H = Высота двутавровой балки
L = Длина двутавровой балки
FT = Толщина полки двутавровой балки
WT = Толщина стенки двутавровой балки 7 R 9
7 = Радиус двутавровой балки
Чтобы продемонстрировать приведенные выше уравнения в действии, мы рассмотрим пример двутавровой балки из мягкой стали (т. е. углеродистой стали) со следующими размерами:
е. углеродистой стали) со следующими размерами:
- Длина – 3000 мм
- Высота – 300 мм
- Ширина – 150 мм
- Толщина стенки – 7,1 мм
- Толщина полки – 10,7 мм
- Внутренний радиус – 15,0 мм
Так как мы будем использовать плотность 7850 кг/м для низкоуглеродистой стали 9 39019 расчет, нам нужно будет преобразовать вышеуказанные размеры в метры. Длина становится 3,0 м, высота 0,3 м, ширина 0,15 м, толщина стенки 0,0071 м, толщина полки 0,0107 м, а внутренний радиус 0,015 м для расчета.
Here’s an overview of how the I-beam volume calculation works using the dimensions in this example:
V1 = (0.15 x 0.0107 x 3.0) x 2
V1 = 0.00963m 3
V2 = (0.3 – (2 x 0.0107)) x 0.0071 x 3.0
V2 = 0.005
m 3
V3 = ((0.015 x 2) 2 – (3.142 x 0.015 2 )) x 3,0
V3 = 0,00057915m 3
Overall Volume = 0. 00963m 3 + 0.005
00963m 3 + 0.005
m 3 + 0.00057915m 3
Overall Volume = 0.01614333m 3
Mild Steel Density = 7850 кг/м 3
Если мы умножим значение объема 0,0076 м 3 на значение плотности 7850 кг/м 3 , мы получим вес 7 127,73 кг 9024.0248 .
Рекламные объявления
Балки IPE и IPN — в чем разница?
Существует два распространенных типа двутавровых балок европейского стандарта, включая IPE и IPN.
IPE — это обозначение, данное двутавровым балкам с параллельными внутренними полками, и они доступны в размерах, установленных в EN 10365, с допусками на продукцию в соответствии с EN 10034:1993.
IPN (или INP, как часто используется) — это обозначение, данное двутавровым балкам с наклонными внутренними полками. Как и балки IPE, балки IPN доступны с размерами, указанными в EN 10365. Однако допуски для балок IPN указаны в EN 10024:19.95.
Однако допуски для балок IPN указаны в EN 10024:19.95.
Балки IPE и IPN обычно изготавливаются из стали марок S235JR, S275JR/J0 и S355JR/J2, но могут использоваться и другие марки.
Стандартные длины балок включают 6000 мм, 6100 мм, 12000 мм и 12100 мм. Однако многие производители могут предложить эти балки нестандартных размеров.
Вот обзор информации о весе и размерах для каждого типа поперечного сечения:
Балки из IPE
Характеризуются параллельными внутренними полками, вот сводка данных о массе и размерах балок из IPE:
IPE Beam Size and Weight Chart
| |||||||
| IPE Beam Classification | Height | Width | Web Thickness (WT) | Flange Thickness ( FT) | Радиус | I Вес балки на фут | I Вес балки на метр |
| IPE 570 | 80mm | 46mm | 3. 8mm 8mm | 5.2mm | 5.0mm | 1.83 kg / 4.03 lbs | 6.00 kg / 13.23 lbs |
| IPE 100 | 100mm | 55mm | 4.1mm | 5.7 mm | 7.0mm | 2.47 kg / 5.44 lbs | 8.10 kg / 17.87 lbs |
| IPE 120 | 120mm | 64mm | 4.4mm | 6.3mm | 7.0mm | 3.16 kg / 6.96 lbs | 10.37 kg / 22.86 lbs |
| IPE 140 | 140mm | 73mm | 4.7mm | 6.9mm | 7.0mm | 3.92 kg / 8.65 lbs | 12.89 kg / 28.43 lbs |
| IPE 160 | 160mm | 82mm | 5.0mm | 7.4mm | 9.0mm | 4.80 kg / 10.58 lbs | 15.77 kg / 34.77 lbs |
| IPE 180 | 180mm | 91mm | 5.3mm | 8.0mm | 9.0mm | 5.72 kg / 12.61 lbs | 18. 80 kg / 41.44 lbs 80 kg / 41.44 lbs |
| IPE 200 | 200mm | 100mm | 5.6mm | 8.5mm | 12.0mm | 6.80 kg / 15.00 lbs | 22.36 kg / 49.29 lbs |
| IPE 220 | 220mm | 110mm | 5.9mm | 9.2mm | 12.0mm | 7.97 kg / 17.57 lbs | 26.20 kg / 57.75 9 фунтов0457 |
| IPE 240 | 240mm | 120mm | 6.2mm | 9.8mm | 15.0mm | 9.34 kg / 20.60 lbs | 30.71 kg / 67.69 lbs |
| IPE 270 | 270mm | 135mm | 6.6mm | 10.2mm | 15.0mm | 10.97 kg / 24.20 lbs | 36.07 kg / 79.51 lbs |
| IPE 300 | 300mm | 150mm | 7.1mm | 10.7mm | 15.0mm | 12.85 kg / 28.34 lbs | 42.24 kg / 93.13 lbs |
| IPE 330 | 330mm | 160mm | 7. 5mm 5mm | 11.5mm | 18.0mm | 14.95 kg / 32.97 lbs | 49.14 kg / 108.35 lbs |
| IPE 360 | 360mm | 170mm | 8.0mm | 12.7mm | 18.0mm | 17.37 kg / 38.30 lbs | 57.09 kg / 125.86 lbs |
| IPE 400 | 400mm | 180mm | 8.6mm | 13.5mm | 21.0mm | 20.18 kg / 44.48 lbs | 66.30 kg / 146.17 lbs |
| IPE 450 | 450mm | 190mm | 9.4mm | 14.6mm | 21.0mm | 23.61 kg / 52.04 lbs | 77.57 kg / 171.02 lbs |
| IPE 500 | 500mm | 200mm | 10.2mm | 16.0mm | 21.0mm | 27.59 kg / 60.84 lbs | 90.68 kg / 199.92 lbs |
| IPE 550 | 550mm | 210mm | 11.1mm | 17.2mm | 24.0mm | 32. 11 kg / 70.79 lbs 11 kg / 70.79 lbs | 105.51 kg / 232.62 lbs |
| IPE 600 | 600mm | 220mm | 12.0mm | 19.0mm | 24.0mm | 37.26 kg / 82.14 lbs | 122.45 kg / 269.95 lbs |
IPN Beams
Characterized by sloped internal flanges, here’s a summary of the weight and dimension data of IPN beams:
IPN Beam Size and Weight Chart
| ||||||||
| IPN Beam Классификация | Высота | Ширина | Толщина стенки (WT) Радиус | Толщина полки (FT)
0004 | Radius 2 | I Beam Weight per Foot | I Beam Weight per Meter | |
| IPN 80 | 80mm | 42mm | 3. 9mm 9mm | 5.9mm | 3.9mm | 2.3mm | 1.81 kg / 3.99 lbs | 5.94 kg / 13.10 lbs |
| IPN 100 | 100mm | 50mm | 4.5mm | 6.8mm | 4.5mm | 2.7mm | 2.54 kg / 5.60 lbs | 8.34 kg / 18.39 lbs |
| IPN 120 | 120mm | 58mm | 5.1mm | 7.7mm | 5.1mm | 3.1mm | 3.38 kg / 7.46 lbs | 11.10 kg / 24.47 lbs |
| IPN 140 | 140mm | 66mm | 5.7mm | 8.6mm | 5.7mm | 3.4mm | 4.36 kg / 9.61 lbs | 14.30 kg / 31.53 lbs |
| IPN 160 | 160mm | 74mm | 6.3mm | 9.5mm | 6.3mm | 3.8mm | 5.46 kg / 12.03 lbs | 17.90 kg / 39.46 lbs |
| IPN 180 | 180mm | 82mm | 6. 9mm 9mm | 10.4mm | 6.9mm | 4.1mm | 6.68 kg / 14.72 lbs | 21.90 kg / 48.28 lbs |
| IPN 200 | 200mm | 90mm | 7.5mm | 11.3mm | 7.5mm | 4.5mm | 7.99 kg / 17.61 lbs | 26.20 kg / 57.76 lbs |
| IPN 220 | 220mm | 98mm | 8.1mm | 12.2mm | 8.1mm | 4.9mm | 9.48 kg / 20.90 lbs | 31.10 kg / 68.56 lbs |
| IPN 240 | 240mm | 106mm | 8.7mm | 13.1mm | 8.7mm | 5.2mm | 11.03 kg / 24,33 фунта | 36.20 kg / 79.81 lbs |
| IPN 260 | 260mm | 113mm | 9.4mm | 14.1mm | 9.4mm | 5.6mm | 12.77 kg / 28.16 lbs | 41.90 kg / 92.37 lbs |
| IPN 280 | 280mm | 119mm | 10. 1mm 1mm | 15.2mm | 10.1mm | 6.1mm | 14.60 kg / 32.19 lbs | 47.90 kg / 105.60 lbs |
| IPN 300 | 300mm | 125mm | 10.8mm | 16.2mm | 10.8mm | 6.5mm | 16.52 kg / 36.42 lbs | 54.20 kg / 119.49 lbs |
| IPN 320 | 320mm | 131mm | 11.5mm | 17.3mm | 11.5mm | 6.9mm | 18.59 kg / 40.99 lbs | 61.00 kg / 134.48 lbs |
| IPN 340 | 340mm | 137mm | 12.2mm | 18.3mm | 12.2mm | 7.3mm | 20.73 kg / 45.69 lbs | 68.00 kg / 149.91 lbs |
| IPN 360 | 360mm | 143mm | 13.0mm | 19.5mm | 13.0mm | 7.8mm | 23.20 kg / 51.14 lbs | 76.10 kg / 167.77 lbs |
| IPN 380 | 380mm | 149mm | 13. 7mm 7mm | 20.5mm | 13.7mm | 8.2mm | 25.60 kg / 56.45 lbs | 84.00 kg / 185.19 lbs |
| IPN 400 | 400mm | 155mm | 14.4mm | 21.6mm | 14.4mm | 8.6mm | 28.16 kg / 62.09 lbs | 92.40 kg / 203.71 lbs |
| IPN 450 | 450mm | 170mm | 16.2mm | 24.3mm | 16.2mm | 9.7mm | 35.05 kg / 77.28 lbs | 115.00 kg / 253.53 lbs |
| IPN 500 | 500mm | 185mm | 18.0mm | 27.0mm | 18.0mm | 10.8mm | 42.98 kg / 94.75 lbs | 141.00 kg / 310.85 lbs |
| IPN 550 | 550mm | 200mm | 19.0mm | 30.0mm | 19.0mm | 11.9mm | 50.60 kg / 111.55 lbs | 166.00 kg / 365.97 lbs |
| IPN 600 | 600mm | 215mm | 21. 6mm 6mm | 32.4mm | 21.6mm | 13.0mm | 60.78 kg / 133.99 lbs | 199.40 kg / 439.60 lbs |
Advertisements
Other Helpful Weight Calculators
Calculators by Тип сечения:
Хотите ли вы рассчитать вес металлической трубы, круглого стержня, квадратной или прямоугольной трубы, катаного швеллера, листового материала или другого типа формы, у нас есть выбор удобных онлайн-калькуляторов, которые помогут вам :
- C-Channel
- Equal / Unequal Angle
- H-Beam
- Hex Bar
- Metal Plate
- Metal Tube
- Round Bar
Calculators by Material:
- Steel
- Drywall
- MDF
- OSB
Автор: Джон Максвелл
Старший писатель, ToolCrowd
Джон Максвелл пишет на различные темы для ToolCrowd, включая обзоры инструментов, советы по материалам, распространенные бытовые проблемы, а также общие советы по самостоятельной работе и статьи с инструкциями. Его работы публиковались в национальных изданиях для широкой аудитории, включая потребителей, домовладельцев и отраслевых экспертов. Джон имеет степень бакалавра в области геодезии зданий и степень магистра в области гражданского строительства, специализирующейся на долговечности бетона и стали. Когда он не пишет для ToolCrowd, Джон любит заниматься своими руками дома, а также заниматься деревообработкой в своей домашней мастерской, кататься на сноуборде и разрабатывать веб-сайты. Связаться с Jonarrow_right_alt
Его работы публиковались в национальных изданиях для широкой аудитории, включая потребителей, домовладельцев и отраслевых экспертов. Джон имеет степень бакалавра в области геодезии зданий и степень магистра в области гражданского строительства, специализирующейся на долговечности бетона и стали. Когда он не пишет для ToolCrowd, Джон любит заниматься своими руками дома, а также заниматься деревообработкой в своей домашней мастерской, кататься на сноуборде и разрабатывать веб-сайты. Связаться с Jonarrow_right_alt
Калькулятор нагрузки на балку
Создано Kenneth Alambra
Отзыв от Dominik Czernia, кандидата наук и Джека Боуотера
Последнее обновление: 06 апреля 2022 г.
Содержание:
- Что такое реакция поддержки?
- Как рассчитать опорные реакции в балке?
- Пример расчета опорной реакции
- Использование нашего калькулятора нагрузки на балку
- Хотите узнать больше?
Калькулятор нагрузки на балку поможет вам определить реакции на опоры свободно опертой балки, вызванные вертикальными точечными нагрузками или силами. В этом калькуляторе вы узнаете, что такое поддержите реакцию и изучите основы расчета несущей способности балки.
В этом калькуляторе вы узнаете, что такое поддержите реакцию и изучите основы расчета несущей способности балки.
Знание того, как найти опорные реакции, является отличным началом при анализе балок, например, при определении прогиба балки. Продолжайте читать, чтобы узнать больше.
Что такое реакция поддержки?
Согласно третьему закону движения Ньютона , каждая сила, действующая на объект, имеет равную и противоположную реакцию. Если вы пытаетесь на что-то надавить, скажем, на стену, вам кажется, что стена тоже отталкивает вас. Именно это явление описывает третий закон движения Ньютона.
В инженерии элементы конструкции, такие как балки и колонны, взаимодействуют друг с другом в точках, где они встречаются. Представьте себе балку, которая поддерживается двумя колоннами. Вес балки давит на колонны, и из-за третьего закона движения Ньютона мы можем также сказать, что колонны воздействуют на балку эквивалентной противоположной реактивной силой.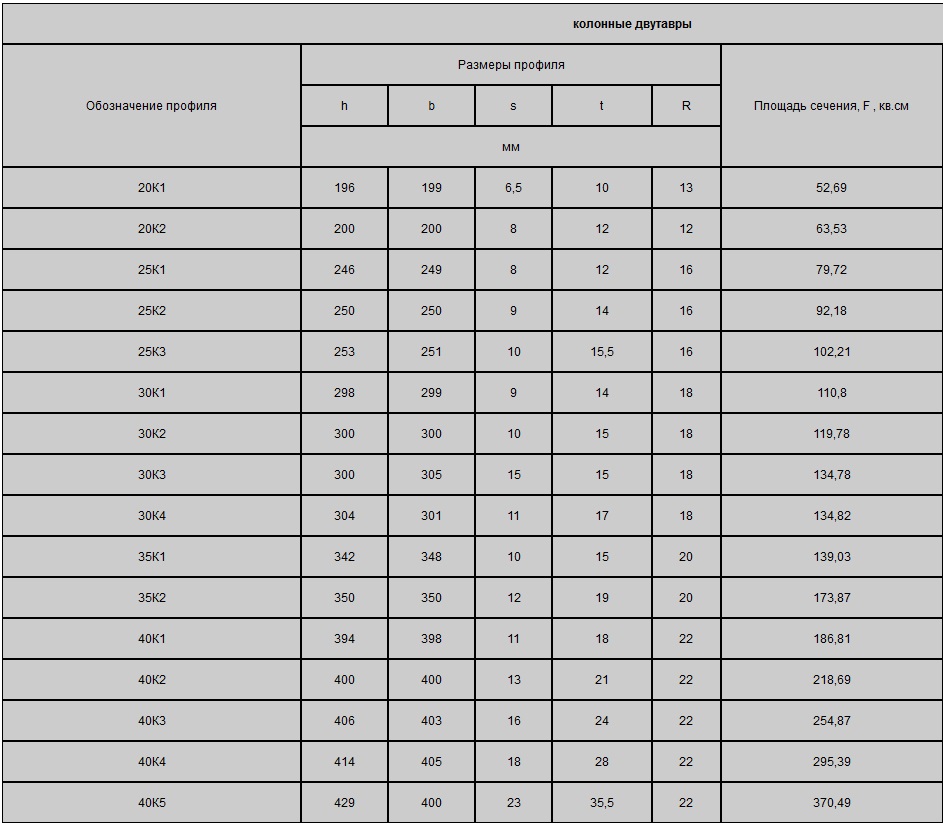 Мы называем эти противодействующие силы опорными реакциями .
Мы называем эти противодействующие силы опорными реакциями .
На свободно опертой балке опорные реакции на каждом конце балки могут быть либо равны друг другу, либо иметь разные значения. Их значения зависят от приложенных к балке нагрузок. Если на более близком расстоянии от одной опоры находится больше нагрузок, эта опора испытывает большее усилие и, следовательно, большую реакцию.
Как рассчитать опорные реакции в балке?
Поскольку опорные реакции действуют в направлении, противоположном силе, можно сказать, что вся система находится в равновесии. Это означает, что балка не движется, а сумма сил и моментов равна нулю. Приравняв момента от нагрузки к моментам от опорных реакций , мы можем определить реакции на опорах.
Как и при расчете крутящего момента, мы также можем выполнить суммирование моментов на каждой опоре для определения реакций. Ниже мы выражаем суммирование Σ , моментов на опоре A для нахождения реакции на опоре B, обозначенной как R B , как показано ниже:
Σ(F * x) - (R B * размах) = 0
(F 1 * x 1 ) + (F 2 * x 2 ) + (F 3 * x 3 ) + . .. + (F n * x n ) - (R B * размах) = 0
.. + (F n * x n ) - (R B * размах) = 0
где:
-
F,F 1,F 2,F 3andF n— The point loads on the beam at distancesx,x 1,x 2х 3их nот опоры А соответственно; -
R B— Реакция на опоре B; и -
пролет— Длина балки между опорой A и опорой B.
Преобразовав уравнение, мы можем выделить R B следующим образом:
R B * размах = (F 1 * x 1 ) + (F 25 2 2 * 2 ) + (F 3 * x 3 ) + ... + (F n * x n )
R B = ((F 1 * x 1 ) + (Ф 2 * х 2 ) + (Ф 3 * х 3 ) + . ✔ .. + (Ф n * x n )) / span
.. + (Ф n * x n )) / span
Теперь, когда у нас есть выражение для нахождения R B , и поскольку мы знаем, что суммарные приложенные силы равны сумме реакций, мы можем теперь также Найдите реакцию при поддержке A R A , используя следующие уравнения:
σ (F) = Rᴀ + Rʙ
R A = σ (F) -Rʙ 4477777777777777777777777777777777777777777777777777799777977979797979797977797777977777777779777777777777797777777977799967979797977979797979797979797979797779967
= σ. Пример расчета опорной реакции
Допустим, у нас есть Свободно опертая балка длиной 4,0 м с приложенной точечной нагрузкой 10,0 килоньютонов (кН) в 2,0 м от опоры A и другой приложенной точечной нагрузкой 3,5 кН в 1,5 м от опоры B , как показано ниже:
Для расчета R B сформулируем уравнение равновесия моментов следующим образом:
R B = (F 1 * x 1 + F 2 * x 2 )34 пролет
R B = (10 кН * 2,0 м + 3,5 кН * (4,0 м - 1,5 м)) / 4,0 м M
R B = (20 кН-M + 8,75 кН-M) / 4,0 M
R B = 7,1875 кН
.
Σ(F n ) = 0
F 1 + F 2 + (-Rᴀ) + (-Rʙ) = 0
10 kN + 3.5 kN + (-Rᴀ) + (-7.1875 kN) = 0
R A = 10 kN + 3.5 kN - 7.1875 kN
R A = 6.3125 kN
Обратите внимание, что для этого суммирования , мы рассмотрели все направленные вниз силы как положительные и все направленные вверх силы как отрицательные . Основываясь на наших расчетах, приведенных выше, мы получили, что реакции на опорах A и B составляют 6,3125 кН и 7,1875 кН соответственно.
Также обратите внимание, что в этом примере и в калькуляторе нагрузки на балку мы исходили из того, что балка невесома. Однако, если указан вес балки, вы можете рассматривать вес балки как еще одну направленную вниз нагрузку в центре или центроиде балки.
Использование нашего калькулятора нагрузки на балку
Наш калькулятор прост и удобен в использовании. Все, что вам нужно сделать, это ввести пролет балки , величину точечных нагрузок , а их расстояния от опоры A . Сначала вы увидите только поля для двух загрузок (загрузка 1 и загрузка 2), но как только вы введете значение для x 2 , отобразятся поля для загрузки 3 и так далее.
Если вы хотите ввести восходящую нагрузку, просто введите отрицательное значение для величины нагрузки. Всего в наш калькулятор нагрузки на балку можно ввести до 11 точечных нагрузок.
Хотите узнать больше?
Теперь, когда вы узнали, как рассчитать грузоподъемность балки, определяя реакции на опорах, возможно, вы также захотите узнать больше о том, что такое прогиб и изгиб балки.
Kenneth Alambra
Деталь луча
SPAN, L
Нагрузка 1
Расстояние от поддержки A, X₁
Нагрузка 2
Расстояние от поддержки A, X₂
Выходные значения
Покажите значения в.
При полной загрузке балки:
▪ Реакция опоры в точке A составляет Rᴀ = 3,3333 фунт-сила
▪ Реакция опоры в точке B составляет Rʙ = 1,6667 фунт-сила
аналоги0007
Алюминиевый груз БалясиныБолтовые круги… Еще 40
Неравнополочное двутавровое сечение (двутавр) | calcresource
Перейти к
- Калькулятор
- Теоретическая основа
РЕКЛАМА
Неравный калькулятор I/H Section
- Д-р Минас Э. Лемонис, PhD > Неравнополочный двутавровый профиль
Этот инструмент вычисляет свойства двутаврового сечения с неравнополочными полками (также называемого неравнополочным двутавром или неравнополочным двутавром). Введите размеры формы ниже. Вычисленные результаты будут иметь те же единицы измерения, что и введенные вами. Пожалуйста, используйте согласованные единицы для любых входных данных.
h = | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
t w = | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
b u = | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
t u = | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
b d = | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
t d = | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Geometric properties: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Area = | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Perimeter = | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
h w = | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
y c = | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Свойства, относящиеся к оси х-х: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
I x | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
S x = | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Z x = | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
y pna = | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
R GX = | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Реклама | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
S y = | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Z y = | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
R gy = | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Other properties: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
I z = | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Поделиться этим
СОДЕРЖАНИЕ
-Калькулятор
-Теоретический фон
-Геометрия
-Момент инициации
-Основной Аксиз
-Минор.
- Модуль упругости сечения
- Напряжение упругого изгиба
- Модуль упругости сечения
- Вокруг сильной оси
- Вокруг слабой оси
-Пластическое изгиб
-Радиус круга
-Неравный I/H Section Formulas
-Связанные страницы
См. Также
Также
Реклама
Реклама
Теоретический фон
Таблица
-Geomtry
-
-GAOMETRY
-
-GAOMETRY
. Момент инерции
- Большая ось
- Малая ось
- Полярная
- Приложения
- Модуль упругого сечения
- Напряжение упругого изгиба
-Модуль пластиковой секции
-вокруг сильной оси
-вокруг слабой оси
-Пластическое изгиб
-Радиус круга
-Неравный I/H Секция
-Связанные страницы
Геометрия
-Область. А и периметр Р двутавра с неравными полками можно найти по следующим двум формулам: чистая высота стенки, h_w, которая появляется в приведенных выше формулах, является чистым расстоянием между двумя полками:
h_{w}=h-t_u-t _d
Из-за симметрии вокруг оси y центроид поперечного сечения также должен лежать на оси y. Следовательно, х_с=0. Однако этого нельзя сказать о другой оси (xx), поскольку вокруг нее не существует симметрии из-за неравных фланцев. Следовательно, необходимо рассчитать точное местоположение центроида. Чтобы найти его расстояние, y_c, от удобной оси отсчета, скажем, нижней кромки поперечного сечения, используются первые моменты площади стенки и двух полок относительно одной и той же кромки (примечание: первый момент площади определяется как площадь, умноженная на расстояние центра тяжести площади от оси отсчета). То есть:
Следовательно, необходимо рассчитать точное местоположение центроида. Чтобы найти его расстояние, y_c, от удобной оси отсчета, скажем, нижней кромки поперечного сечения, используются первые моменты площади стенки и двух полок относительно одной и той же кромки (примечание: первый момент площади определяется как площадь, умноженная на расстояние центра тяжести площади от оси отсчета). То есть:
A \ y_{c} = A_{d} \ y_{d} + A_{u} \ y_{u} +A_w \ y_{w}
, где
- A_{d}=b_{d} t_{d} , площадь нижней полки
- A_{u}=b_{u} t_{u} , площадь верхней полки,
- A_{w}=h_{w} t_{w } , — площадь стенки,
- y_{d}=\frac{ t_{d}}{2}, — расстояние от центра тяжести нижней полки до нижнего края,
- y_{u}=h- \frac{ t_{u}}{2} , расстояние от центра тяжести верхней полки до нижнего края,
- y_{w}=t_{d}+\frac{ h_{w}}{2} — расстояние от центра тяжести полотна до нижнего края.
Из последнего выражения положение центра масс можно рассчитать напрямую, как:
\ y_{c} = { A_{d} \ y_{d} + A_{u} \ y_{u} +A_w \ y_{w} \over A}
Момент инерции
Большая ось
Аналогично, чтобы найти момент инерции неравнополочного двутавра, полное сечение разбивается на три, меньшие, одно для нижнего фланца, один для верхнего и один для стенки. Следовательно, момент инерции I_x относительно центральной оси x-x определяется следующим образом: 92, момент инерции полотна относительно центроидальной оси х-х.
Следовательно, момент инерции I_x относительно центральной оси x-x определяется следующим образом: 92, момент инерции полотна относительно центроидальной оси х-х.
Для каждого из приведенных выше выражений была использована так называемая «теорема о параллельных осях» для оценки соответствующих моментов инерции трех частей. Для получения дополнительной информации об этой технике, проверьте здесь.
Второстепенная ось
Опять же, общая площадь поперечного сечения разделена на три части: одна для нижней полки, одна для верхней и одна для стенки. Однако на этот раз ось изгиба (y-y) также является осью симметрии (для всех трех частей), и поэтому вычисления немного проще (поскольку использование теоремы о параллельных осях не требуется). Суммарный момент инерции I_y находится как: 93}{12}, момент инерции стенки относительно центральной оси y,
РЕКЛАМА
Полярный
Полярный момент инерции описывает жесткость поперечного сечения по отношению к крутящим моментам, тогда как плоский моменты инерции, описанные выше, связаны с изгибом. Расчет полярного момента инерции I_z вокруг оси z (перпендикулярной сечению) можно выполнить с помощью теоремы о перпендикулярных осях:
Расчет полярного момента инерции I_z вокруг оси z (перпендикулярной сечению) можно выполнить с помощью теоремы о перпендикулярных осях:
I_z = I_x + I_y
, где I_x и I_y — моменты инерции вокруг осей x и y, которые взаимно перпендикулярны оси z и пересекаются в общем начале координат.
Применение
Момент инерции (второй момент или площадь) используется в теории балок для описания жесткости балки при изгибе. Изгибающий момент M, приложенный к поперечному сечению, связан с его моментом инерции следующим уравнением:
M = E\times I \times \kappa
, где E - модуль Юнга, свойство материала, и \kappa, кривизна балки из-за приложенной нагрузки. Таким образом, из предыдущего уравнения видно, что при приложении определенного изгибающего момента M к поперечному сечению балки развиваемая кривизна обратно пропорциональна моменту инерции I.94 .
Модуль упругости сечения
Модуль упругости сечения S_x любого поперечного сечения вокруг оси x (в центре) описывает реакцию сечения на упругий изгиб при изгибе.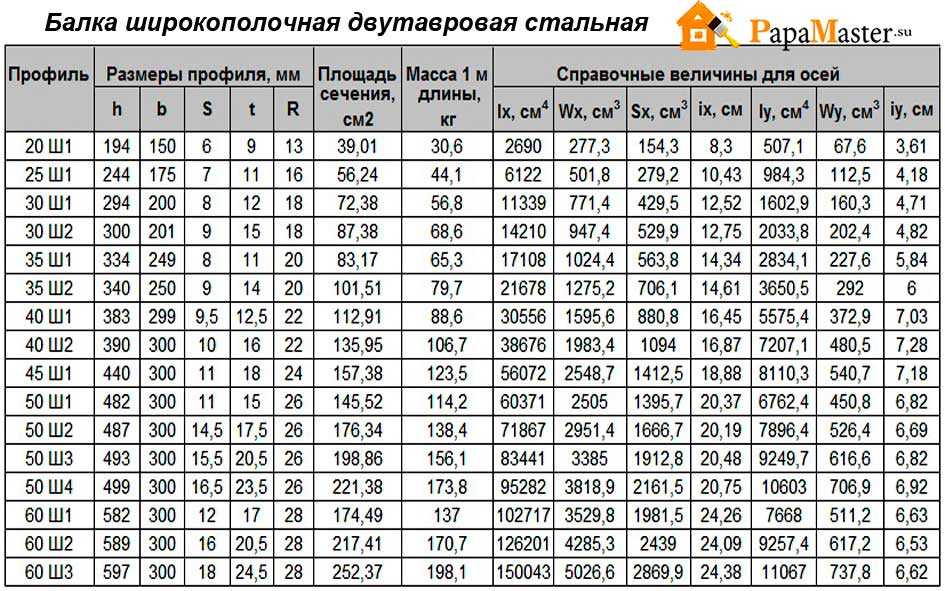 Он определяется как:
Он определяется как:
S_x = \frac{I_x}{Y}
, где I_x - момент инерции секции вокруг оси x, а Y - расстояние от волокна секции (как правило, самой удаленной) от той же ось х. Поскольку неравнополочная двутавровая балка несимметрична относительно оси x, расстояние Y должно быть разным для верхнего и нижнего волокна секции. В результате можно рассчитать два разных модуля сечения. Как правило, представляет интерес меньший из них (соответствующий большему Y), потому что он связан с более напряженным волокном, как объясняется далее в этом разделе.
Аналогично, модуль сечения S_y вокруг оси y, которая для неравнополочного двутавра также является осью симметрии, записывается как:
S_y = \frac{I_y}{X}
, где I_y - момент инерции сечения вокруг оси y и X, расстояние бокового краевого волокна от той же оси y. Однако на этот раз расстояние X одинаково для левого и правого волокон поперечного сечения и равно \max(0,5b_{u}; 0,5b_{d}).
Упругое изгибающее напряжение
Если к оси x приложен изгибающий момент M_x, сечение будет реагировать нормальными напряжениями, линейно изменяющимися в зависимости от расстояния от нейтральной оси (которая в упругом режиме совпадает с центроидальной осью x). Вдоль нейтральной оси напряжения равны нулю. Абсолютный максимум \сигма будет иметь место на самом удаленном волокне, величина которого определяется формулой: 93 .
Вдоль нейтральной оси напряжения равны нулю. Абсолютный максимум \сигма будет иметь место на самом удаленном волокне, величина которого определяется формулой: 93 .
Модуль пластического сечения
Модуль пластического сечения аналогичен упругому, но определяется с допущением полной пластической текучести поперечного сечения за счет изгибного изгиба. В этом случае все сечение разделено на две части, одну на растяжение и одну на сжатие, каждая из которых находится в однородном поле напряжений. Для материалов с равными напряжениями текучести при растяжении и сжатии это приводит к разделению сечения на две равные области, A_t при растяжении и A_c при сжатии, разделенные нейтральной осью. Это результат уравновешивания внутренних сил в поперечном сечении при пластическом изгибе. В самом деле, сжимающая сила будет равна A_cf_y, если предположить, что предел текучести равен f_y при сжатии, и что материал по всей сжимаемой площади поддался (таким образом, напряжения везде равны f_y). Точно так же растягивающая сила будет равна A_t f_y, если использовать те же предположения. Обеспечение равновесия:
Точно так же растягивающая сила будет равна A_t f_y, если использовать те же предположения. Обеспечение равновесия:
A_cf_y = A_t f_y\Rightarrow
A_c= A_t
Ось называется пластической нейтральной осью , и для несимметричных сечений она не идентична упругой нейтральной оси (которая снова является центроидальной). Неравное сечение I/H действительно не симметрично относительно сильной оси (оси x). В результате пластическая нейтральная ось неравнополочного двутавра при сильном изгибе оси не проходит через центр тяжести.
Вокруг сильной оси
Для неравнополочной двутавровой балки ось x, параллельная полкам, обычно является сильной осью поперечного сечения. Поскольку пластическая нейтральная ось делит поперечное сечение на равные площади, она должна быть:
A_c=A_t = \frac{A}{2}
Приведенное выше выражение можно использовать для расчета положения нейтральной оси. Во-первых, давайте предположим, что пластическая нейтральная ось имеет расстояние, равное y_{pna} от нижнего края. Также предположим, что он расположен где-то между двумя фланцами. В математических терминах:
Также предположим, что он расположен где-то между двумя фланцами. В математических терминах:
t_d \lt y_{pna} \lt h-t_u
Это всего лишь предположение. Несмотря на то, что кажется интуитивно понятным, что пластиковая нейтральная ось расположена между двумя фланцами, это не всегда так. Это действительно зависит от относительных размеров двух фланцев. Тем не менее, будем считать, что приведенное выше предположение на данный момент верно. Площадь половины сечения ниже нейтральной пластиковой оси должна быть:
A_t=b_{d} t_{d}+ t_w \left(y_{pna}-t_{d}\right) =\frac{A}{2}
Единственным неизвестным является y_{pna}. Преобразовывая уравнение, мы получаем:
y_{pna}=t_{d}+\frac{ A-2b_{d} t_{d} }{2t_w}
Последнее выражение позволяет рассчитать расстояние пластической нейтральной оси от нижний край, если наше исходное предположение справедливо. Для этого легко найти подходящие условия. Подставляя вычисленное y_{pna} в предполагаемое неравенство, получаем:
t_d \lt t_{d}+\frac{ A-2b_{d} t_{d} }{2t_w} \lt h-t_u\Rightarrow
0\lt \frac{ A-2b_{d} t_{d } }{2t_w} \lt h_w\Rightarrow
0 \lt A-2b_{d} t_{d} \lt 2t_wh_w\Rightarrow
0 \lt A-2A_{d} \lt 2(A-A_d-A_u )
, где A_{d} — площадь нижней полки, а A_{u} — площадь верхней полки. Приведенное выше неравенство эквивалентно выполнению следующих двух неравенств:
Приведенное выше неравенство эквивалентно выполнению следующих двух неравенств:
A_d \lt {A\over2}
A_u \lt {A\over2}
двутавра неравнополочного сечения, если ни одна из двух полок не занимает более половины общей площади сечения. 92\over 2} + \\&+A_w(y_w-y_\textit{pna})+A_u(y_u-y_\textit{pna})\end{split}
где:
- y_{u}= h-\frac{ t_{u}}{2} ,
- y_{w}=t_{d}+\frac{ h_{w}}{2} ,
- A_{u}=b_{u} t_ {u} ,
- A_{w}=h_w t_w .
Наконец, если нейтральная ось пластика проходит через верхний фланец (должно происходить, когда этот фланец имеет более половины общей площади сечения, т. е. A_u\ge{A\over2}), выводится следующая формула для пластического модуль:
92\over 2} + \\+&A_w(y_\textit{pna}-y_w)+A_d(y_\textit{pna}-y_d)\end{split}
где:
- y_{d}=\ frac{ t_{d}}{2} ,
- y_{w}=t_{d}+\frac{ h_{w}}{2} ,
- A_{d}=b_{d} t_{d} ,
- A_{w}=h_w t_w .
Вокруг слабой оси
Для неравнополочной двутавровой балки ось Y, перпендикулярная полкам, обычно является слабой осью. Это также ось симметрии поперечного сечения. В результате пластическая нейтральная ось на этот раз не нуждается в расчетах. Она идентична центроидальной оси Y. Кроме того, модуль пластичности гораздо легче оценить. Этому способствуют три прямоугольные области, все симметрично расположенные вокруг оси Y: две области для фланцев и одна для стенки. Выводится следующая формула: 92}{4}
Это также ось симметрии поперечного сечения. В результате пластическая нейтральная ось на этот раз не нуждается в расчетах. Она идентична центроидальной оси Y. Кроме того, модуль пластичности гораздо легче оценить. Этому способствуют три прямоугольные области, все симметрично расположенные вокруг оси Y: две области для фланцев и одна для стенки. Выводится следующая формула: 92}{4}
Пластический изгиб
Модуль пластичности связан с напряжениями поперечного сечения при изгибе в пластическом режиме, аналогичным образом модуль упругости относится к упругому режиму. Если вокруг оси x приложен изгибающий момент M_x, и все сечение становится полностью пластифицированным, так что каждое волокно достигает предела текучести материала, \sigma_y, то следующая формула верна:
\sigma_y = \frac{M_x }{Z_x}
Из последнего уравнения можно определить изгибающий момент, вызывающий полную деформацию поперечного сечения, обычно называемый пластическим моментом. 93 .
Радиус вращения
Радиус вращения R_g поперечного сечения относительно оси определяется по формуле:
R_g = \sqrt{\frac{I}{A}}
где I момент инерции поперечного сечения вокруг той же оси и A его площади. Размеры радиуса вращения [Длина]. Он описывает, насколько далеко от центра тяжести распределена область. Малый радиус указывает на более компактное сечение. Круг — это форма с минимальным радиусом вращения по сравнению с любым другим сечением той же площади A.
Размеры радиуса вращения [Длина]. Он описывает, насколько далеко от центра тяжести распределена область. Малый радиус указывает на более компактное сечение. Круг — это форма с минимальным радиусом вращения по сравнению с любым другим сечением той же площади A.
Формулы неравнополочного двутаврового сечения
В следующей таблице перечислены основные формулы, относящиеся к механическим свойствам неравнополочного двутаврового сечения (также называемого двутавровым сечением).
Неравные свойства I/H Секции | |
|---|---|
| Количество | Формула |
| Область: | ARTEMPER \ TEXTRIT {d}\ t_\textit{d} +h_w t_w |
| Периметр: 93}{12} | |
| Модуль упругости: | S_x = \frac{I_x}{y_\textit{max}} \quad ,\mathrm{где}: y_\textit{max}=\mathrm{ max}\left\{y_c;\ h-y_c\right\} S_y = \frac{2I_y}{b_\textit{max}} \quad ,\mathrm{где}: b_\textit{max}=\ mathrm{max}\left\{b_u;\ b_d\right\} |
| Модуль пластичности: | Сильная ось If A_d \lt {A\over2}\textrm{ and }A_u \lt {A\over2}: \begin{split}Z_x =& {b_d y_\textit{pna}^2\over 2}-{(b_d-t_w)(y_\textit{pna}-t_d)^2\ over2}+\\& +{b_u (h-y_\textit{pna})^2\over 2}-{(b_u-t_w)(h-t_u-y_\textit{pna})^2\over2}\ конец {разделить} 92}{4} |
Пластиковая нейтральная ось: (расстояние от нижнего края) | y_{pna}= \left\{\begin{array}{ll} &t_{d}+\frac { A-2A_d }{2t_w} &\quad,\ \textrm{if }A_d \lt {A\over2}\textrm{ и }A_u \lt {A\over2} \\ &{A\over 2b_d} & \ quad,\ \textrm{if }A_d \ge {A\over2} \\ &h-{A\over 2b_u} & \quad,\ \textrm{if }A_u \ge {A\over2}\end{массив}\ Правильно. |
где: h_w=h-t_d-t_u A_d=t_db_d A_u=t_ub_u A_w=t_wh_w y_d={t_d\over2} y_u=h-{t_u\over2} y_w=t_d+{h_w\over2} | |
Related pages
Понравилась эта страница? Поделись с друзьями!
РЕКЛАМА
См. также
Балка кручения | Инженерная библиотека
На этой странице представлены разделы о кручении балки из «Руководства по анализу напряжений», Лаборатория динамики полета ВВС, октябрь 1986 г.
Другие связанные главы из «Руководства по анализу стресса» ВВС можно увидеть справа.
Номенклатура
| А | = | площадь поперечного сечения |
| и | = | 1/2 большего диаметра эллипса |
| и | = | линейный размер |
| б | = | 1/2 меньшего диаметра эллипса |
| б | = | ширина секции |
| б | = | развернутая длина шлифа |
| б | = | линейный размер |
| с | = | линейный размер |
| Д | = | диаметр |
| д | = | линейный размер |
| F ст | = | модуль упругости при кручении |
| Ф Су | = | предельное напряжение при чистом сдвиге |
| Ф си | = | Предел текучести при чистом сдвиге |
| Ф ту | = | предельное напряжение растяжения |
| ж с | = | расчетное напряжение сдвига |
| Г | = | модуль упругости при сдвиге |
| ч | = | высота или глубина - высота поперечной балки между центрами тяжести полок |
| I р | = | полярный момент инерции |
| Л | = | длина |
| р | = | давление |
| q | = | сдвиговое течение |
| р | = | радиус |
| р и | = | внутренний радиус |
| р или | = | внешний радиус |
| С | = | усилие натяжения на краю мембраны (фунт/дюйм) |
| с | = | расстояние, измеренное по криволинейной траектории |
| Т | = | крутящий момент |
Т макс. | = | максимально допустимый крутящий момент |
| т | = | толщина |
| т е | = | эффективная толщина |
| т с | = | толщина кожи |
| т ст | = | толщина закрытого элемента жесткости |
| θ | = | угол закручивания балки |
| х, у, з | = | прямоугольные координаты |
1.5 Введение в торсионные балки
В целях обсуждения торсионные балки разбиты на две категории: круглые балки, которые рассматриваются в разделе 1.5.1, и некруглые балки, которые рассматриваются в разделе 1.5.2. Круглые балки подразделяются на балки с постоянным поперечным сечением (раздел 1.5.1.1) и балки с неравномерным поперечным сечением (раздел 1.5.1.2). Некруглые балки делятся на открытые некруглые балки (раздел 1. 5.2.1) и закрытые или полые балки (раздел 1.5.2.2), а влияние торцевого ограничения на некруглые балки рассматривается в разделе 1.5.2.3.
5.2.1) и закрытые или полые балки (раздел 1.5.2.2), а влияние торцевого ограничения на некруглые балки рассматривается в разделе 1.5.2.3.
В разделе 1.5.3 рассматриваются аналогии мембраны и кучи песка для балок при кручении. Поскольку нагрузка на проволоку винтовых пружин в основном крутильная, они перечислены под балками при кручении и рассматриваются в разделе 1.5.4.
1.5.1 Круговые балки на кручение
В этом разделе рассматривается кручение сплошных или концентрически полых круглых балок.
1.5.1.1 Однородные круглые балки в кручении
На рис. 1-42 показана однородная круглая балка в чистом кручении. Если напряжения в такой балке находятся в области упругости, распределение напряжений в поперечном сечении будет таким, как показано на рис. 1-43.
94) Г } $$
(1-48)
Для обработки сплошных круглых валов r и могут быть установлены равными нулю в уравнениях (1-47) и (1-48).
Следует отметить, что уравнения (1-47) и (1-48) применимы только к балкам с круглым поперечным сечением.
Максимальное касательное напряжение возникает на внешних поверхностях балки и может быть рассчитано путем установки r равным r o в уравнении (1-47). Максимальные напряжения растяжения и сжатия также возникают на внешней поверхности, и оба по величине равны максимальному напряжению сдвига.
Если круглую балку скрутить за пределами предела текучести до тех пор, пока внешние части не достигнут предела прочности при кручении, получается распределение напряжения, подобное показанному на рис. 1-44. Максимальный крутящий момент, который такая балка может выдержать при статической нагрузке, определяется выражением
$$ T_{max} = { F_{st} I_p \over r_o } $$
(1-49)
где F st обозначен как модуль прочности при кручении. Этот модуль упругости при кручении показан графически для стальных балок на рис. 1-45.
Во многих случаях модуль упругости при кручении материала может быть недоступен. Их можно устранить, приняв равномерное распределение напряжения сдвига, показанное на рис. 1-46.
Их можно устранить, приняв равномерное распределение напряжения сдвига, показанное на рис. 1-46.
Величину равномерного напряжения сдвига можно принять равной пределу текучести при сдвиге (F sy ) для консервативных результатов или предельному напряжению сдвига (F su ) для неконсервативных результатов. В первом случае максимальный крутящий момент в балке может быть выражен как
$$ T_{max} = { 4 \over 3 } { F_{sy} ~I_p \over r_o } $$
(1-50)
а во втором случае максимальный крутящий момент в балке может быть выражен как
$$ T_{max} = { 4 \over 3 } { F_{su} ~I_p \over r_o } $$
(1-51)
Следует отметить, что возможность деформации тонкостенных труб в предыдущем обсуждении не рассматривалась. Деформация круглых труб рассматривается в Главе 8. Эти трубы должны быть проверены на деформацию.
Нужен калькулятор луча?
Попробуйте этот калькулятор луча.
- Расчет напряжений и прогибов в прямых балках
- Построение диаграмм сдвига и моментов
- Можно указать любую конфигурацию ограничений, сосредоточенных сил и распределенных сил
1.5.1.2 Неоднородные круглые балки в кручении
При скручивании круглой балки неравномерного поперечного сечения радиусы поперечного сечения искривляются. Поскольку предполагалось, что радиусы поперечного сечения остаются прямыми при выводе уравнений для напряжения в однородных круглых балках, эти уравнения больше не выполняются, если балка неоднородна. Однако напряжение в любом сечении неоднородной круглой балки с достаточной точностью определяется по формулам для однородных стержней при плавном изменении диаметра. Если изменение сечения резкое, как в случае уступа с небольшим закруглением, необходимо применить концентрацию напряжения, как описано в главе 10.
94) } = 3260 ~\text{psi} $$
Нужен калькулятор луча?
Попробуйте этот калькулятор луча.
- Расчет напряжений и прогибов в прямых балках
- Построение диаграмм сдвига и моментов
- Можно указать любую конфигурацию ограничений, сосредоточенных сил и распределенных сил
1.5.2 Некруглые балки на кручение
При выводе формул для круглых балок при кручении предполагалось, что плоские сечения остаются плоскими, а радиусы остаются прямыми в деформированной конфигурации. Поскольку эти предположения больше не выполняются для некруглых сечений, уравнения для круглых сечений не выполняются. Деформация плоских сечений квадратного стержня при кручении показана на рис. 1-49..
В этом разделе сначала обрабатываются открытые балки, а затем закрытые балки. Закрытые балки имеют полые сечения, а другие балки называются открытыми балками. Поскольку плоские сечения остаются плоскими для круглых балок при кручении, торцевое ограничение такой балки не влияет на ее поведение. Однако торцевое ограничение может быть важным фактором при обработке некруглых балок при кручении и рассматривается в разделе 1. 5.3.3. Однако на достаточном расстоянии от приложения нагрузки напряжения зависят только от величины приложенного крутящего момента в соответствии с принципом Сен-Венана.
5.3.3. Однако на достаточном расстоянии от приложения нагрузки напряжения зависят только от величины приложенного крутящего момента в соответствии с принципом Сен-Венана.
1.5.2.1 Некруглые открытые балки на кручение
В этом разделе рассматриваются некруглые балки, поперечное сечение которых не является полым. В разделе 1.5.2.1.1 дается распределение напряжения в эллиптических балках при кручении, а в разделе 1.5.2.1.2 рассматриваются балки с прямоугольным поперечным сечением. Раздел 1.5.2.1.3 рассматривает открытые некруглые балки с тонкими сечениями с формулами для тонких прямоугольных сечений. В таблице 1-15 в разделе 1.5.2.1.5 приведены формулы для напряжений и деформаций в некруглых балках различного сечения.
93 ~G } $$
(1-58)
где β указано в таблице 1-14.
| б/т | 1,00 | 1,50 | 1,75 | 2,00 | 2,50 | 3,00 | 4 | 6 | 8 | 10 | ∞ |
| α | 0,208 | 0,231 | 0,239 | 0,246 | 0,258 | 0,267 | 0,282 | 0,299 | 0,307 | 0,313 | 0,333 |
| β | 0,141 | 0,196 | 0,214 | 0,229 | 0,249 | 0,263 | 0,281 | 0,299 | 0,307 | 0,313 | 0,333 |
Максимальное напряжение и угол закручивания прямоугольной балки при кручении также могут быть вычислены с удовлетворительной точностью (ошибка менее 4%) из следующих уравнений:
93 Г } $$
(1-62)
Из Таблицы 1-14 видно, что эти выражения верны с точностью до 10 процентов, если b/t = 8.
Хотя уравнения (1-61) и (1-62) были разработаны для прямоугольных балок, их можно применять для приблизительного анализа форм, состоящих из тонких прямоугольных элементов, таких как на рис. 1-52. Однако при наличии острых углов может возникнуть большая концентрация напряжений, так что уравнение (1-61) недействительно. Эффект острых углов объясняется аналогией с мембраной в разделе 1.5.3.1. Уравнения (1-61) и (1-62) могут быть применены непосредственно к сечениям, таким как те, что показаны вверху на рис. 1-52, если b принять за развернутую длину поперечного сечения, как показано.
93 + ~... } $$
(1-66)
В приведенных выше уравнениях f max.n — максимальное напряжение в прямоугольной части сечения n th , L — длина балки, а T — приложенный крутящий момент.
Если секция состоит из толстых прямоугольных секций, следует использовать уравнения из раздела 1.5.2.1.5. Преимущество уравнений в этом разделе состоит в том, что они могут быть применены к конкретным формам, для которых может быть недоступна более точная формула.
1.5.2.1.4 Пример задачи. Некруглые балки с тонкими незамкнутыми сечениями при кручении
Дано : Балка длиной 50 дюймов с поперечным сечением, показанным на рис. 1-53, под скручивающей нагрузкой 500 дюйм-фунтов.
Найдите : максимальное напряжение сдвига и угол закручивания балки.
Решение : Развернутая длина секции составляет
$$ b = 3 + 3 + 2 + \pi = 11,14 ~\text{in} $$
Теперь можно применить уравнения (1-61) и (1-62) для получения
9{\circ} $$
1.5.2.1.5 Некруглые открытые балки различного поперечного сечения при кручении
В таблице 1-15 приведены формулы для деформации и напряжения открытых некруглых балок с различными поперечными сечениями при кручении. Формулы для случая 1 основаны на строгом математическом анализе, а остальные формулы получены либо с помощью приближенного математического анализа, либо с помощью аналогии с мембраной и обычно имеют точность в пределах 10 процентов.
Для случаев с (3) по (9) включительно \(f_{smax}\) возникает в одной из точек или очень близко к ней, где наибольшая вписанная окружность касается границы, если только в какой-либо другой точке на границе нет острого входящего угла. граница, вызывающая высокое местное напряжение. Из точек, где наибольшая вписанная окружность касается границы, \(f_{smax}\) происходит в той, где кривизна границы алгебраически наименьшая. (Выпуклость представляет собой положительную, а вогнутость отрицательную кривизну границы. В точке, где кривизна положительна (граница сечения прямая или выпуклая), максимальное напряжение приблизительно определяется выражением где \(D =\) диаметр наибольшей вписанной окружности \(r =\) радиус кривизны границы в точке (положительный для данного случая) \(A=\) площадь сечения В точках, где граница сечения вогнута или вогнута, максимальное напряжение приблизительно определяется выражением $$ f_{smax} = {G \theta c \over L} $$ где 94 } } ~ \Bigg[ 1 + \bigg\{ 0,118 ~\ln{\left( 1 - {D \over 2r } \right)} \nonumber \\ где \(D\), \(A\) и \(r\) имеют тот же смысл, что и раньше, и \(\phi\) = угол, на который поворачивается касательная к границе при повороте или обходе входящей части, измеряется в радианах. |
Любой удлиненный отрезок или тонкая трубка. где суммирование производится по составляющим L сечениям, рассчитанным как для случая (8) |
Нужен калькулятор луча?
Попробуйте этот калькулятор луча.
- Расчет напряжений и прогибов в прямых балках
- Построение диаграмм сдвига и моментов
- Можно указать любую конфигурацию ограничений, сосредоточенных сил и распределенных сил
1.5.2.2 Некруглые замкнутые балки на кручение
Закрытые балки имеют в поперечном сечении одну или несколько полых частей. Этот тип балки гораздо более эффективен при кручении, чем открытая балка.
В разделе 1.5.2.2.1 рассматриваются закрытые или коробчатые балки с одной ячейкой при кручении, а в разделе 1.5.2.2.7 — закрытые балки с несколькими ячейками при кручении.
1.5.2.2.1 Одноэлементные некруглые замкнутые балки на кручение
В этом разделе рассматриваются балки коробчатого сечения с единственной полой частью в поперечном сечении. В разделе 1.5.2.2.2 рассматриваются такие балки, имеющие одинаковое поперечное сечение, а в разделе 1.5.2.2.3 рассматриваются конические коробчатые балки. Влияние ребер жесткости и вырезов в балках коробчатого сечения рассматривается в разделах 1.5.2.2.4 и 1.5.2.2.6 соответственно.
В разделе 1.5.2.2.2 рассматриваются такие балки, имеющие одинаковое поперечное сечение, а в разделе 1.5.2.2.3 рассматриваются конические коробчатые балки. Влияние ребер жесткости и вырезов в балках коробчатого сечения рассматривается в разделах 1.5.2.2.4 и 1.5.2.2.6 соответственно.
92 ~G } \int { dU \over t } $$
(1-67)
В этом уравнении A — это площадь, ограниченная срединной линией, t — толщина в любой точке, а U — длина вдоль срединной линии. Сдвиговое течение в такой трубе однородно во всех точках и определяется выражением
$$ q = { T \над 2A } $$
(1-68)
Если предполагается, что касательное напряжение одинаково по всей толщине, оно определяется выражением
$$ f_s = { q \over t } = { T \over 2 A t } $$
92 G т } $$
(1-70)
и Уравнения (1-68) и (1-69) остаются прежними.
1.5.2.2.3 Одноэлементные некруглые конические закрытые балки в кручении
На рис. 1-55 показана коническая балка коробчатого сечения под действием скручивающей нагрузки T. Поскольку все четыре стороны сужаются таким образом, что углы коробчатого сечения пересекаются при расширении, уравнения из раздела 1.5.2.2.2 могут быть применены к этой балки, если за А взять площадь в рассматриваемом поперечном сечении.
1-55 показана коническая балка коробчатого сечения под действием скручивающей нагрузки T. Поскольку все четыре стороны сужаются таким образом, что углы коробчатого сечения пересекаются при расширении, уравнения из раздела 1.5.2.2.2 могут быть применены к этой балки, если за А взять площадь в рассматриваемом поперечном сечении.
Однако эти уравнения больше не применяются для балок коробчатого сечения, для которых коэффициент конусности горизонтальных стенок не совпадает с коэффициентом конусности вертикальных стенок, поскольку сдвиговые потоки не будут иметь одинакового распределения для всех стенок. Такой пучок показан на рис. 1-56. Хотя уравнения в разделе 1.5.2.2.2 неприменимы для коробчатой балки, такой как показанная на рис. 1-56, они достаточно точны для обычной конструкции крыла самолета с близко расположенными нервюрами. Ребра делят стенку на несколько меньших перемычек и служат для распределения сдвиговых потоков таким образом, что они примерно равны в горизонтальной и вертикальной стенках.
1.5.2.2.4 Влияние ребер жесткости на некруглые замкнутые балки при кручении
Тонкостенные конструкции самолетов обычно содержат продольные ребра жесткости, расположенные вокруг внешних стенок, как показано на рис. 1-57. Если используется элемент жесткости открытого типа, как показано слева на рис. 1-57, жесткость на кручение отдельных элементов жесткости настолько мала по сравнению с жесткостью на кручение тонкостенной ячейки, что ею можно пренебречь. Однако элемент жесткости закрытого типа представляет собой небольшую трубку, поэтому его жесткость намного больше, чем жесткость открытой секции того же размера. Таким образом, ячейку с прикрепленными к ее наружным стенкам ребрами жесткости замкнутого типа можно рассматривать как многоячеистую замкнутую балку, где каждое ребро жесткости образует дополнительную ячейку. Поскольку расчет балки с большим количеством ячеек затруднен и, как правило, жесткость на кручение, обеспечиваемая ребрами жесткости, мала по сравнению с общей ячейкой, с достаточной точностью можно использовать приближенную упрощенную процедуру.
В приближенном методе тонкостенная труба и закрытые элементы жесткости преобразуются в эквивалентную одиночную тонкостенную трубу путем модификации закрытых элементов жесткости с помощью одной из двух процедур. Эта эквивалентная трубка затем анализируется в соответствии с материалом, изложенным в разделе 1.5.2.2.2. Две процедуры изменения закрытых ребер жесткости:
- Замените каждый закрытый элемент жесткости удвоенной пластиной, эффективная толщина которой определяется выражением
$$ t_e = t_{st} ~s / d $$
(1-71)
Эта процедура и необходимая номенклатура показаны на рис. 1-58.
- Замените обшивку над каждым элементом жесткости «лайнером» толщиной, определяемой формулой
$$ t_e = t_s ~d/s $$
(1-72)
Этот метод и необходимая номенклатура показаны на рис. 1-59. Первая из этих процедур несколько переоценивает эффект жесткости ребер жесткости, тогда как вторая процедура немного занижает этот эффект.

902:30
Поскольку угловые элементы усиленной ячейки обычно представляют собой открытые или сплошные секции, такие как те, что показаны на рис. 1-57, их сопротивление скручиванию можно просто добавить к жесткости кручению всей тонкостенной ячейки.
1.5.2.2.5 Пример задачи. Некруглая замкнутая усиленная балка однородного сечения при кручении
Дано : 120-дюймовый. - длинная балка с крутящим моментом 10 000 дюймов на фунт с поперечным сечением, как показано на рис. 1-60.
Найдите : угол закручивания и максимальное напряжение сдвига в балке.
Решение . Из раздела 1.5.2.2.4 можно нарисовать удвоенную пластину, эквивалентную элементу жесткости, как показано на рис. 1-61. Таким образом, площадь, ограниченная срединной линией преобразованного сечения, равна
$$ A = (24 \times 16) - 8 \left({t_e \over 2}\right) (d) - 4 \left({ 1 \over 16 }\right) (2) $$
где последний член учитывает влияние углов угла. Таким образом,
Таким образом,
94 \over 2 (381,5) t } = { 13,1 \over t } $$
Таким образом, максимальное касательное напряжение возникает в точке минимальной толщины и
$$ f_s = { 13,1 \более 0,0625 } = 210 ~\text{psi} $$
1.5.2.2.6 Влияние вырезов на закрытые одноэлементные балки при кручении
Типовые конструкции самолетов состоят из закрытых коробов с продольными ребрами жесткости и поперечными переборками. В идеальной непрерывной конструкции необходимо предусмотреть множество отверстий для колесных арок, установок вооружения, дверей, окон и т. д. Эти вырезы нежелательны с конструктивной точки зрения, но всегда необходимы. Закрытая коробка крутящего момента необходима для большей части размаха крыла самолета, но ее можно не использовать на короткой длине, например, на длине проема колесной арки. Когда часть обшивки отсутствует в такой области, сопротивление кручению достигается за счет дифференциального изгиба лонжеронов, как показано на рис. 1-62, поскольку открытое сечение имеет низкую жесткость на кручение. Если предполагается, что скручиванию сопротивляются две боковые стенки, действующие независимо как консольные балки, как показано на рис. 1-62(b), один конец должен быть встроен, как показано на рис. 1-62(a).
1-62, поскольку открытое сечение имеет низкую жесткость на кручение. Если предполагается, что скручиванию сопротивляются две боковые стенки, действующие независимо как консольные балки, как показано на рис. 1-62(b), один конец должен быть встроен, как показано на рис. 1-62(a).
Наличие выреза и результирующие осевые нагрузки во фланцах также увеличивают сдвиг в закрытых частях коробки, прилегающих к вырезам.
1.5.2.2.7 Многоячеистые замкнутые балки на кручение
На рис. 1-63 показана картина течения с внутренним сдвигом в многоячеистой трубе, состоящей из n ячеек, при чисто скручивающей нагрузке T. Крутящий момент, приложенный к этой трубке, определяется выражением
$$ T = 2 q_1 A_1 + 2 q_2 A_2 + ... + 2 q_n A_n $$
(1-73)
где от A 1 до A n — площади, ограниченные средними линиями ячеек с 1 по n. Линейный интеграл ∫ds/t, где s — длина медианы стены, а t — толщина стенки, может быть представлен как a. Тогда a KL представляет собой значение этого интеграла вдоль стенки между ячейками K и L, где площадь вне трубки обозначена как ячейка (0). Используя это обозначение, следующие уравнения могут быть записаны для ячеек (1) через (n):
Тогда a KL представляет собой значение этого интеграла вдоль стенки между ячейками K и L, где площадь вне трубки обозначена как ячейка (0). Используя это обозначение, следующие уравнения могут быть записаны для ячеек (1) через (n):
$$ \text{cell (1):} ~ {1 \over A_1} [ q_1 a_{10} + (q_1 - q_2) a_{12} ] = 2 G \theta $$
(1-74)
$$ \text{cell (2):} ~ {1 \over A_2} [ (q_2 - q_1) a_{12} + q_2 a_{20} + (q_2 - q_3) a_ {23} ] = 2 G \theta $$
(1-75)
$$ \text{cell (3):} ~ {1 \over A_3} [ (q_3 - q_2) a_{23} + q_3 a_{30} + (q_3 - q_4) a_{34} ] = 2 G \theta $$
(1-76)
$$ \text{cell (n-1):} ~ {1 \over A_ {n-1}} [ (q_{n-1} - q_{n-2}) a_{n-2, n-1} + q_{n-1} a_{n-1,0} + (q_ {n-1} - q_{n}) a_{n-1,n} ] = 2 G \theta $$
(1-77)
$$ \text{cell (n):} ~ {1 \over A_n} [ (q_n - q_{n-1}) a_{n-1, n} + q_n a_{n,0} ] = 2 G \theta $$
(1-78)
Сдвиговые потоки от q 1 до q n могут быть найдены путем одновременного решения уравнений (1-73) – (1-78). По этим сдвиговым потокам можно найти распределение напряжения сдвига, поскольку f s = q/t.
По этим сдвиговым потокам можно найти распределение напряжения сдвига, поскольку f s = q/t.
1.5.2.2.8 Пример задачи — многоячеистые замкнутые балки в кручении
Дано : Многоячеистая балка с поперечным сечением, показанным на рис. 1-64, под скручивающей нагрузкой 5000 фунтов на дюйм.
Найти 92 $$
$$ a_{10} = [2(6,5) + 2,5] / 0,1875 = 77,3 $$
$$ a_{12} = 2,5/0,250 = 10 $$
$$ a_{20} = [2(4) + 2,5] / 0,125 = 84 $$
Применение уравнений (1-73), (1-74) и (1-75) к данному лучу дает
$$ T = 2 q_1 A_1 + 2 q_2 A_2 $$
$$ {1 \over A_1} [ q_1 a_{10} + (q_1 - q_2) a_{12} ] = 2 G \theta $$
и
$$ {1 \over A_2} [ (q_2 - q_1) a_{12} + q_2 a_{20} ] = 2 G \theta $$
Вставка числовых значений в эти уравнения дает
9{\circ} $$
Касательное напряжение в стене (1) равно
$$ f_s = {q_1 \over t_1} = {78 \over 0,1875} = 415 ~\text{psi} $$
Напряжение сдвига в стене (2) равно
$$ f_s = {q_2 \over t_2} = {123 \over 0,125} = 984 ~\text{psi} $$
Касательное напряжение в стене (1,2) равно
$$ f_s = { q_1 - q_2 \over t_{1,2} } = { 123 - 78 \over 0,250 } = 180 ~\text{psi} $$
1.
 5.2.3 Влияние торцевого крепления на некруглые балки при кручении
5.2.3 Влияние торцевого крепления на некруглые балки при кручении
Уравнения для некруглых балок при кручении в предыдущих разделах предполагали, что поперечные сечения по всей длине элементов кручения могут свободно деформироваться из их плоскости, и, таким образом, не может быть нормальных к поперечным сечениям напряжений. В реальных конструкциях часто присутствует ограничитель от свободного коробления сечений в месте крепления балки. Например, крыло самолета свободно отклоняется от места крепления к довольно жесткой конструкции фюзеляжа и удерживается от коробления в месте крепления. Эффект концевого ограничения больше в точках, близких к ограничителю, чем в точках, удаленных дальше. Такие секции, как двутавровые балки, более подвержены торцевым ограничениям, чем компактные секции, такие как круги и квадраты.
На рис. 1-65 показана двутавровая балка с одним концом, защемленным под скручивающей нагрузкой T. Максимальный изгибающий момент полки равен
$$ M_{max} = {T \over h} ~a ~\tanh{ L \over a } $$
(1-79)
где
$$ a = {h \over 2} \sqrt{ 2 ~I y ~E \theta \over T L } $$
(1-80)
θ — угол закручивания двутавровой балки с незакрепленными концами, указанный в Таблице 1-15. Угол закручивания такого двутавра с защемленными концами равен
Угол закручивания такого двутавра с защемленными концами равен
$$ \theta_r = \theta \left( 1 - {a \over L} ~\tanh{L \over a} \right) $$
(1-81)
Из этого уравнения видно, что концевое крепление оказывает на балку эффект жесткости.
Нужен калькулятор луча?
Попробуйте этот калькулятор луча.
- Расчет напряжений и прогибов в прямых балках
- Построение диаграмм сдвига и моментов
- Можно указать любую конфигурацию ограничений, сосредоточенных сил и распределенных сил 902:30
1.5.3 Аналогии балок на кручение
Две аналогии для балок при кручении полезны как для визуализации распределения и величины напряжений, так и для экспериментальной работы. Аналогия с мембраной, описанная в разделе 1.5.3.1, действительна для открытых балок, для которых напряжение сдвига находится в области упругости. Аналогия с песчаной кучей (раздел 1.5.3.2) может использоваться для обработки открытых балок при скручивающих нагрузках, для которых напряжение пластического сдвига одинаково во всех точках поперечного сечения.
1.5.3.1 Мембранная аналогия для балок в упругом кручении
Уравнение кручения балки в области упругости аналогично уравнению для малых прогибов мембраны при всестороннем давлении. На рис. 1-66 показана такая мембрана. Давление на мембрану обозначим как p, а S — равномерное на единицу натяжение на ее границе. Аналогия с мембраной дает следующие соотношения между отклоненной мембраной и балкой того же поперечного сечения при кручении:
- Линии одинакового прогиба на мембране (контурные линии) соответствуют линиям касательных напряжений скрученного стержня.
- Касательная к контурной линии в любой точке поверхности мембраны дает направление результирующего напряжения сдвига в соответствующей точке поперечного сечения скручиваемого стержня.
- Максимальный наклон прогибаемой мембраны в любой точке по отношению к плоскости опоры кромки пропорционален касательному напряжению в соответствующей точке поперечного сечения скрученного стержня. Таким образом, напряжение сдвига больше всего там, где контурные линии находятся ближе всего.

902:30 - Приложенное к скрученному стержню кручение пропорционально удвоенному объему, заключенному между отклоняемой мембраной и плоскостью, проходящей через опорные ребра. Если p/S = 2Gθ, этот крутящий момент равен удвоенному объему.
Аналогию с мембраной можно использовать для экспериментального измерения величин для балок при кручении. Однако, возможно, главное преимущество мембранной теории заключается в том, что она обеспечивает метод визуализации со значительной степенью точности того, как изменяются условия напряжения в сложном поперечном сечении балки при кручении. Например, рассмотрим стержень с прямоугольным поперечным сечением, показанный на рис. 1-67 (а). Мембрана может быть натянута на отверстие такой же формы и прогнута равномерным давлением. Линии одинакового прогиба для прогибаемой мембраны примут форму, показанную на рис. 1-67(b). Эти контурные линии имеют тенденцию принимать форму границы стержня по мере приближения к ней, как и направление касательного напряжения. Касательное напряжение максимально там, где контурные линии находятся ближе всего (в центре длинной стороны). Поскольку приложенное кручение пропорционально объему мембраны, более вытянутый из двух прямоугольных стержней равной площади имеет меньшую жесткость на кручение. Также очевидно, что сгибание длинного тонкого прямоугольного отрезка не приведет к заметному изменению объема мембраны и, следовательно, жесткости на кручение стержня такой формы.
Касательное напряжение максимально там, где контурные линии находятся ближе всего (в центре длинной стороны). Поскольку приложенное кручение пропорционально объему мембраны, более вытянутый из двух прямоугольных стержней равной площади имеет меньшую жесткость на кручение. Также очевидно, что сгибание длинного тонкого прямоугольного отрезка не приведет к заметному изменению объема мембраны и, следовательно, жесткости на кручение стержня такой формы.
Аналогия с мембраной также делает очевидным, что напряжения очень малы на концах выступающих фланцев или выступающих углов и очень высоки там, где граница резко вогнута. Например, в Таблице 1-16 приведен коэффициент концентрации напряжений для вогнутой стороны профиля, показанного на Рисунке 1-68. Умножение максимального напряжения, полученного из формулы для тонких прямоугольных профилей при кручении, на этот коэффициент дает максимальное напряжение на вогнутой стороне тонкого изогнутого профиля.
| р/т | 1/8 | 1/4 | 1/2 | 1 |
| Фактор | 2-1/2 | 2-1/4 | 2 | 1-3/4 |
1.
 5.3.2 Аналогия с песчаной кучей для балок в пластическом кручении
5.3.2 Аналогия с песчаной кучей для балок в пластическом кручении
Максимальный предельный крутящий момент, который открытая балка может выдержать при кручении, определяется выражением
$$ T = 2 ~V ~F_{st} $$
93 \более 24 } $$
Треугольник
A = площадь треугольника
r = радиус вписанной окружности
Рабочий пример конструкции стальной балки [Универсальная балка]
В рабочем примере конструкции стальной балки разрабатывается конструкция свободно опертой балки с равномерно распределенной нагрузкой. Балка считается свободно опертой, расчетные данные для расчета изгибающего момента и поперечных сил приведены ниже.
Кроме того, свойства раздела, которые необходимо учитывать, также указываются на каждом этапе проверки раздела.
Теоретические аспекты и процедуры проектирования кодов обсуждаются в статье о конструкции стальной балки в соответствии с BS 5950 .
Конструктивные данные
- Нагрузка UDL 20 кН/м
- Пролет балки 6м
- Балка свободно опертая
- Расчетная прочность стали, Py =
- D = 500 mm
- T = 16 mm
- t = 10 mm
- B = 200 мм
- b = 100 мм
- r 1 = 20 мм
- D = 500 - 16 x 2 - 2 x 20 = 428 мм
- S x = 2175 × 10 3 мм 3
- Z x 3
- Z x 3
- .
 3
3 - r y = 43,3 мм
- Классификация секций
- Конструкция на сдвиг
- Конструкция на изгиб
- Проверка на наличие бокового торсионального загиба
- Проверка отклонения
- Проверка веб -подшипника
- Проверка веб -штук
20002 Максимальный момент изгиба
= WL 2 /8 = 20 x 6 2 /8 = 90 кН
Максимальный силу сдвига
= WL / 2 = 20 x 6/ 60 KN
= WL / 2 = 20 x 6 /2 = 60 кН
= WL / 2 = 20 x 6 / 60 кН
= WL / 2 = 20 x 6 / 6.
Consider universal beam 500x200x89.7 kg/m (P y = 275 N/mm 2 )
Section Data
Приступим к расчету конструкции стальной балки. При расчете конструкции стальной балки выполняются следующие проверки.
Классификация Секции
СТАРИЦИЯ СТАРИТА СТАВИЙ СТАЛЬ СТАЛЬНАЯ СТАЛЬНА. сечение, чтобы узнать, пластичное оно, полупластичное, компактное, тонкое.
T = 16 мм, P y = 275 Н/мм 2
ε = (275/P y ) 0,5 = 1
Контрфланец
b/T = 100 / 16 = 6,25 < 9ε = 9 – Фланец пластиковый
Контрфланец
<2 8 =
d/t = 1,8 /t = 1,8 80 – Стенка пластиковая
Кроме того, d/t < 70ε = 70 – Следовательно, нет необходимости проверять коробление при сдвиге
Следовательно, сечение пластиковое
Расчет на сдвиг
Расчетное усилие сдвига, F v = 60 кН
P v = 0,6 P y A v = 0. 6 P y tD = 0.6 x 275 x 10 x 500 x 10 -3 = 825 kN
6 P y tD = 0.6 x 275 x 10 x 500 x 10 -3 = 825 kN
F v < P v Shear capacity is OK
Depending on сила сдвига, решается, подвергается ли сечение низкому или высокому сдвигу в конструкции стальной балки.
Расчет на изгиб
Проверить, подвергается ли секция малому или высокому сдвигу
60% x P v = 0,6 x 825 = 495 кН
F v < 0,6 P v Секция, подвергающаяся малому сдвигу
M c должна быть меньше 1,2P y Z x или P y S x по кл. 4.2.5.1 и кл. 4.2.5.2
M C ≤ 1,2P Y Z x = 1,2 x 275 x 1914 x10 3 x 10 -6 = 613,62 КН
M -6 = 613,62 КН
M C C C C C C C C C C C C C C C. х = 275 х 2175 х 10 3 х 10 -6 = 598,125 кНм
Следовательно,
M c = 598. 125 kNm > 90 kNm
125 kNm > 90 kNm
Bending ok
Check Lateral Torsional Buckling
M x < M b / m LT
In this example, no intermediate restrains were considered
м LT = 0,925, Таблица 18, БС 5950
М б = П б S х Кл. 4.3.6.4
Существует два метода проверки продольного изгиба при кручении, как описано в статье 9.Конструкция стальной балки 3673 согласно BS 5950 . Это строгий метод и упрощенный метод.
В этом примере конструкции стальной балки мы обсудили оба метода для уточнения процедур, которым необходимо следовать при использовании любого метода.
Кроме того, основное различие между этими двумя методами заключается в оценке прочности на изгиб .
Строгий метод
M b = P b S x
P B в зависимости от λ LT и P Y
λ LT = UVλ√ (β W )
λ = L E W )
λ = L E W )
λ = L E W )
λ = L E W )
λ = L E W )
λ = L E W ) Е – брать из таблицы 13 по кл. 4.3.5.1 и учтите L LT = L – пролет
4.3.5.1 и учтите L LT = L – пролет
L E = 1,0 L LT = 1 x 6 = 6 м
λ = L E / r 1 y 4 138.568
Для двутаврового и двутаврового проката кл. 4.3.6.8
x = D / T используется с u = 0,9
x = D / T = 500 / 10 = 50
β w следует получить из Cl 4.3.6.9
β w = 1 для класса пластик или Класс 2 Компактные секции
v – коэффициент гибкости, полученный из таблицы 19 на основе λ / x и η
λ / x = 138,568 / 50 = 2,771
η = 0,5 для равнополочных фланцев
v = 0,919 из таблицы 19
λ LT = uvλ√(β w ) = 0,9x 0,919 x 138,568 x √(1) = 114,6
λ LO можно получить из таблицы 16 (см. конец таблицы)
Если λ LO ≥ 1 λ 2 LT 9025; P b = P y или в противном случае P b следует принимать по таблице 16 для сортового проката.
Если λ LO ≥ λ LT , не нужно делать допуск на потерю устойчивости при поперечном кручении, в противном случае необходимо проверить коробление при поперечном кручении.
P y = 275 Н/мм 2 ; λ LO = 37,3
λ LO < λ LT Поэтому проверьте боковую потерю устойчивости при кручении
Из таблицы 16 для λ LT = 114,6 ; P b = 102 N/mm 2
M b = P b S x = 102 x 2175 x 10 3 x 10 -6 = 221.85 kNm
M b / м LT = 221,85 / 0,925 = 239,838 кНм
Таким образом, M x = 90 кНм < M b / м LT = 239,838 кНм
Сечение соответствует .
Упрощенный метод
Примечание. При проектировании балки не обязательно использовать оба метода. Следование либо упрощенному методу, либо строгому методу является адекватным.
Следование либо упрощенному методу, либо строгому методу является адекватным.
M b = P b S x : кл. 4.3.7
В этом методе определение P b отличается по сравнению с предыдущим методом. Этот метод дает консервативные ответы. P b можно получить из таблицы 20 BS 5950 на основе √(β w ) (L E / r y ) и D/T
β w = 1; предыдущий расчет
L E / r y = 138,568 ; предыдущий расчет
√(β w ) (L E / r y ) = 1 0,5 x 135,568 = 138,568
D / T = 500 / 16 = 31.25
P b = 116.646 N/mm 2 From Table 20
M b = P b S x = 116.646 x 2175 x 10 3 x 10 -6 = 253,705 КНМ
M B / M LT = 253,705 / 0,925 = 274,3
С. LT = 274,3 кНм
LT = 274,3 кНм
Сечение соответствует
Прогиб
Максимальный прогиб ( δ ) для свободно опертой балки, имеющей равномерное распределение, можно оценить по следующему уравнению.
δ = 5W e L 4 / (384EI)
Это уравнение можно упростить следующим образом.
δ = 0,104M max L 2 / (EI)
Поскольку мы оцениваем отклонение из-за приложенных нагрузок, в этом расчете примем приложенную нагрузку как 10 кН/м.
δ = 0,104 х 90 x 10 6 6000 2 / (205 x 10 3 x 478 x 10 6 ) = 1.7 mm
Assuming brittle finishes to be used
Span / 360 = 6000 / 360 = 16.7 mm
δ < Span / 360, Следовательно, прогиб в порядке.
Несущая способность стенки
Необходимо проверить несущую способность стенки стальной балки. В этой категории выполняются подшипник и изгиб паутины.
P BW = (B 1 + NK) TP YW
Рисунок 01: Расположение веб -подшипника - извлечено из кода
T = 10 мм
T = 10 мм
R = 10 MM
G0007 T = 10 мм
R = 100007
G0007 T = 10 MM
R = 100007
G0007 T = 100007
R = 100007
G0007 T = 100007
R = 100007
G0007 T = 100007
R = 100007
G0007 T = 100007
R = 100007
T = 100007
R = 100002
= 5 мм
b e = 5 мм
b 1 = t + T + 0,8r – g = 10 + 10 + 0,8 x 10 – 5 = 23 мм
k = T + r = 16 + 20 = 36 мм (для катаного профиля)
на конце,
n = (2 + 0,6b e /k), но ≤ 5
n = (2 + 0,6 x 5/36) = 2,083 < 5 P yw = 275 Н/мм 2 из таблицы 9
P bw = (b 1 + nk) tP yw = (23 +2,083 x 01 х 01 3 х 36) = 269,5 кН
Опорная нагрузка 60 кН.
Опора перемычки в порядке, ребра жесткости не требуются.
Когда F x > P bw , нам необходимо предусмотреть ребра жесткости, чтобы компенсировать усилие (F x – P bw ). Несущая способность ребер жесткости должна быть получена из P s = A s.net P y . Где А с.нет - площадь поперечного сечения жесткости. Если стенка и жесткость имеют разную прочность, для расчета P s и P bw следует использовать меньшее значение.
Web Backling
Когда E ≥ 0,7D
P x = 25εt P BW /√ [(B 1 + NK) D]
, когда A E + NK) D]
, когда A 1 + NK) D]
, когда A 1 + NK) D]
.
P x = [ (a e +0,7d)/1,4d] {25εt P bw /√[ ( b 1 + nk ) d ] }
Где
a e = 1,7 d = 1,7 d
< 0,7 x 428 = 300 мм
P x = [ (a e +0,7d)/1,4d] {25εt P bw /√[ ( b 1 9 0 7 0 0 0 0 0 0 ] nk } ) ) P x = [ (11,5 +0,7×428)/1,4×428] {25x1x10x275 /√[ ( 23 + 2,083×36 ) 428 ] } = 174,3 кН
F x < P требуются ребра жесткости.

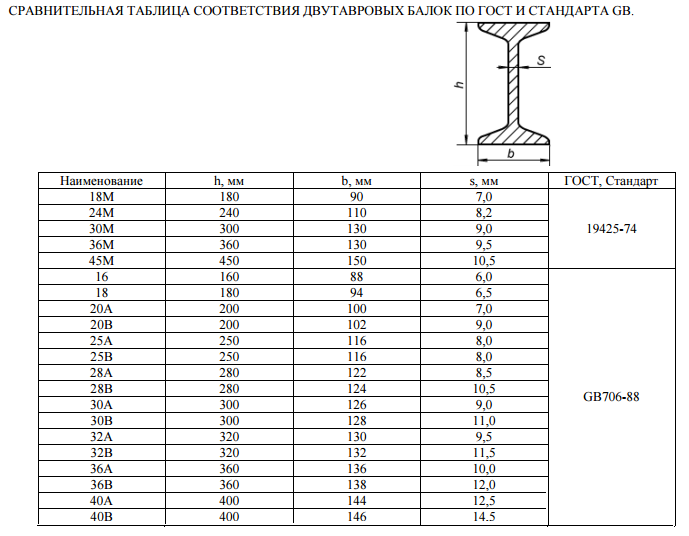 0251 y =
0251 y =