Центр тяжести швеллера и двутавра: 1.3. Определение положения центра тяжести сечения
Содержание
Центр тяжести — методы нахождения.
Наиболее часто для нахождения центра тяжести тела или фигуры применяют следующие методы:
- метод симметрии;
- метод разбиения;
- метод отрицательных масс.
Рассмотрим приемы, применяемые в каждом из перечисленных методов.
***
Метод симметрии
Представим себе однородное тело, которое имеет плоскость симметрии. Выберем такую систему координат, чтобы оси x и z лежали в плоскости симметрии (см. рисунок 1).
В этом случае каждой элементарной частице силой тяжести Gi с абсциссой yi = +a соответствует такая же элементарная частица с абсциссой yi = -a, тогда:
yC = Σ(Gixi)/ΣGi = 0.
Отсюда вывод: если однородное тело имеет плоскость симметрии, то центр тяжести тела лежит в этой плоскости.
Аналогично можно доказать и следующие положения:
- Если однородное тело имеет ось симметрии, то центр тяжести тела лежит на этой оси;
- Если однородное тело имеет две оси симметрии, то центр тяжести тела находится в точке их пересечения;
- Центр тяжести однородного тела вращения лежит на оси вращения.

***
Метод разбиения
Этот метод заключается в том, что тело разбивают на наименьшее число частей, силы тяжести и положение центров тяжести которых известны, после чего применяют приведенные ранее формулы для определения общего центра тяжести тела.
Допустим, что мы разбили тело силой тяжести G на три части G’, G», G»’, абсциссы центров тяжести этих частей x’C, x»C, x»’C известны.
Формула для определения абсциссы центра тяжести всего тела:
xC = Σ(Gixi)/ΣGi.
Перепишем ее в следующем виде:
xCΣGi = Σ(Gixi) или GxC = Σ(Gixi).
Последнее равенство запишем для каждой из трех частей тела отдельно:
G’x’C = Σ(G’x’i), G»x»C = Σ(G»ix»i), G»’x»’C = Σ(G»’ix»’i).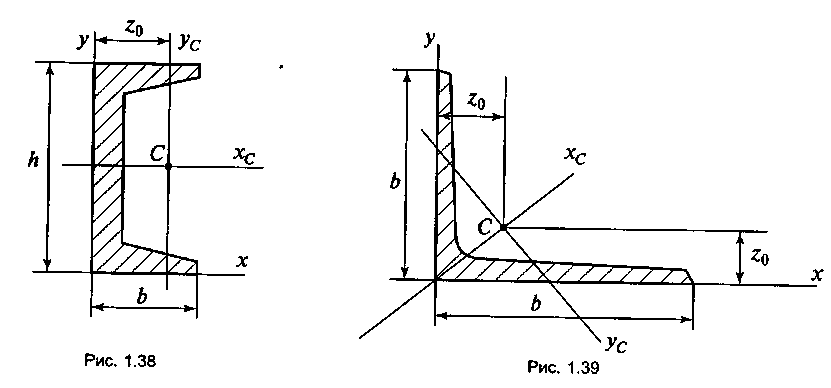
Сложив левые и правые части этих трех равенств, получим:
G’x’C + G»x»C + G»’x»’C = Σ(G’ix’i) + Σ(G»x»i) + Σ(G»’ix»’i) = Σ(Gixi).
Но правая часть последнего равенства представляет собой произведение GxC, так как
GxC = Σ(Gixi),
Следовательно, xC = (G’x’C + G»x»C + G»’x»’C)/G, что и требовалось доказать.
Аналогично определяются координаты центра тяжести на координатных осях y и z:
yC = (G’y’C + G»y»C + G»’y»’C)/G,
zC = (G’z’C + G»z»C + G»’z»’C)/G.
Полученные формулы аналогичны формулам для определения координат цента тяжести, выведенные выше. Поэтому в исходные формулы можно подставлять не силы тяжести элементарных частиц Gi, а силы тяжести конечных частей; под координатами xi, yi, zi понимают координаты центров тяжести частей, на которые разбито тело.
***
Метод отрицательных масс
Этот метод заключается в том, что тело, имеющее свободные полости, считают сплошным, а массу свободных полостей – отрицательной. Вид формул для определения координат центра тяжести тела при этом не меняется.
Таким образом, при определении центра тяжести тела, имеющего свободные полости, следует применять метод разбиения, но считать массу полостей отрицательной.
***
Практические методы определения центра тяжести тел
На практике для определения центра тяжести плоских тел сложной формы часто применяют метод подвешивания, который заключается в том, что плоское тело подвешивают на нити за какую-нибудь точку. Прочерчивают вдоль нити линию, и тело подвешивают за другую точку, не находящуюся на полученной линии.
Затем вновь проводят линию вдоль нити.
Точка пересечения двух линий и будет являться центром тяжести плоского тела.
Еще один способ определения центра тяжести, применяемый на практике, называется метод взвешивания. Этот метод часто применяется для определения центра тяжести крупных машин и изделий – автомобилей, самолетов, колесных тракторов и т. п., которые имеют сложную объемную форму и точечную опору на грунт.
Этот метод часто применяется для определения центра тяжести крупных машин и изделий – автомобилей, самолетов, колесных тракторов и т. п., которые имеют сложную объемную форму и точечную опору на грунт.
Метод заключается в применении условий равновесия, исходя из того, что сумма моментов всех сил, действующих на неподвижное тело равна нулю.
Практически это осуществляется взвешиванием одной из опор машины (задние или передние колеса устанавливаются на весы), при этом показания весов, по сути, являются реакцией опоры, которая учитывается при составлении уравнения равновесия относительно второй точки опоры (находящейся вне весов).
По известной массе (соответственно – весу) тела, показанию весов в одной из точек опоры, и расстоянию между точками опоры можно определить расстояние от одной из точек опоры до плоскости, в которой расположен центр тяжести.
Чтобы найти подобным образом линию (ось), на которой расположен центр тяжести машины, необходимо произвести два взвешивания по принципу, изложенному выше для метода подвешивания (см. рис. 1а).
рис. 1а).
***
Положение центра тяжести некоторых фигур
Прямоугольник. Так как прямоугольник имеет две оси симметрии, то центр тяжести его площади находится в точке пересечения этих осей, иначе говоря, в точке пересечения диагоналей прямоугольника.
Треугольник. Пусть дан треугольник АBD (см. рисунок 2).
Разобьем его на элементарные (бесконечно узкие) полоски, параллельные стороне AD. Центр тяжести каждой полоски будет лежать на медиане Bd (т. е. в середине каждой полоски), следовательно, на этой медиане будет лежать и центр тяжести всей площади треугольника. Разбив треугольник на элементарные полоски, параллельные стороне AB, увидим, что искомый центр тяжести лежит и на медиане aD.
Проделав аналогичное действие с треугольником относительно стороны ВD, получим тот же результат – центр тяжести находится на соответствующей медиане.
Следовательно, центр тяжести всей площади треугольника лежит на точке пересечения его медиан, поскольку эта точка является единственной общей точкой для всех трех медиан данной геометрической фигуры.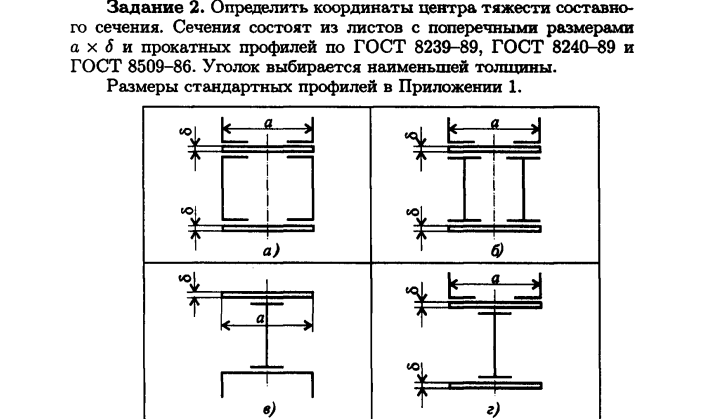
Из геометрии известно, что медианы треугольника пересекаются в одной точке и делятся в соотношении 1:2 от основания. Следовательно, центр тяжести треугольника расположен на расстоянии одной трети высоты от каждого основания.
Дуга окружности. Возьмем дугу окружности АВ радиусом R с центральным углом 2α (см. рисунок 3). Систему координат выберем так, чтобы начало координат было в центре окружности, а ось x делила дугу пополам, тогда yC= 0 вследствие симметрии дуги относительно оси x. Определим координату центра тяжести xC.
Разобьем дугу АВ на элементарные части li, одна из которых изображена на рисунке. Тогда, согласно сделанным выше выводам,
xC =Σ(lixCi)/Σli.
Дугу li вследствие малости примем за отрезок прямой. Из подобия треугольника ODiCi и элементарного треугольника S (на рисунке заштрихован) получим:
Li/Δyi = R/xCi или lixi = RΔyi.
Тогда:
xC =Σ(lixCi)/Σli = Σ(RΔyi)/l = RΣΔyi/l = R×AB/l,
поскольку RΣΔyi = AB, а Σli = l – длина дуги АВ. Но АВ = 2R sinα, а l = 2Rα, следовательно,
xC = (R sinα)/α.
При α = π/2 рад (полуокружность), xC = 2R/π.
Круговой сектор. Возьмем сектор радиусом R с центральным углом 2α (см. рисунок 3а). Проведем оси координат, как показано на рисунке (ось x направлена вдоль оси симметрии сектора), тогда yC = 0.
Определим xC, для чего разобьем сектор на ряд элементарных секторов, каждый из которых из-за малости дуги li можно принять за равнобедренный треугольник с высотой R. Тогда центр тяжести каждого элементарного сектора будет находиться на дуге радиуса 2R/3 и задача определения центра тяжести сектора сводится к определению центра тяжести этой дуги.
Очевидно, что
xC = 2 R sinα/(3α).
При α = π/2 рад (полукруг): xC = 4R/(3π).
***
Пример решения задачи на определение центра тяжести
Задача:
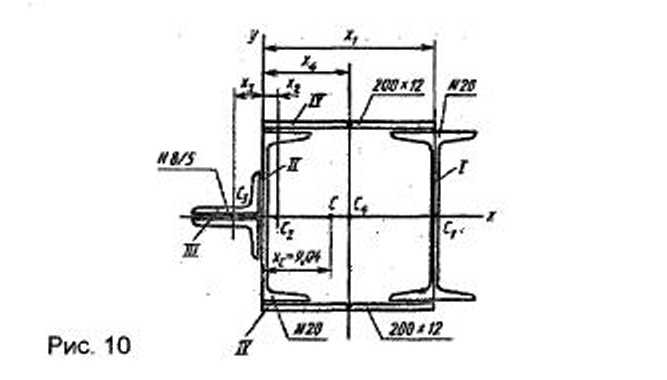
Определить положение центра тяжести сечения, составленного из двутавра № 22 и швеллера № 20, как показано на рисунке 4.
Решение.
Из курса инженерной графики известно, что номер проката соответствует наибольшему габаритному размеру его сечения, выраженного в сантиметрах.
Так как сечение, составленное из двутавра и швеллера, представляет собой фигуру, симметричную относительно оси y, то центр тяжести такого сечения лежит на этой оси, т. е. xC = 0.
По справочнику определим площади и координаты центров тяжести двутавра 1 и швеллера 2.
Для двутаврового сечения: А1 = 15,2 см2; y1 = 22/2 = 11 см.
Для швеллерного сечения: А2 = 12 см2; y2 = 22 + d – z0 = 22 + 0,32 – 1,25 = 21,07 см,
где d – толщина стенки швеллера; z0 – размер, определяющий положение центра тяжести швеллера.
Применим формулу для определения координаты центра тяжести всего сечения:
yC = Σ(Aiyi)/ΣAi,
тогда:
yC = (A1y1 +A2y2)/(A1 +A2) = (15,2×11 + 12×21,07)/(15,2 + 12) = 15,4 см.
Задача решена.
***
Кинематика точки
Главная страница
- Страничка абитуриента
Дистанционное образование
- Группа ТО-81
- Группа М-81
- Группа ТО-71
Специальности
- Ветеринария
- Механизация сельского хозяйства
- Коммерция
- Техническое обслуживание и ремонт автотранспорта
Учебные дисциплины
- Инженерная графика
- МДК.
 01.01. «Устройство автомобилей»
01.01. «Устройство автомобилей» - Карта раздела
- Общее устройство автомобиля
- Автомобильный двигатель
- Трансмиссия автомобиля
- Рулевое управление
- Тормозная система
- Подвеска
- Колеса
- Кузов
- Электрооборудование автомобиля
- Основы теории автомобиля
- Основы технической диагностики
- Основы гидравлики и теплотехники
- Метрология и стандартизация
- Сельскохозяйственные машины
- Основы агрономии
- Перевозка опасных грузов
- Материаловедение
- Менеджмент
- Техническая механика
- Советы дипломнику
Олимпиады и тесты
- «Инженерная графика»
- «Техническая механика»
- «Двигатель и его системы»
- «Шасси автомобиля»
- «Электрооборудование автомобиля»
Центр тяжести — презентация онлайн
Похожие презентации:
Влияния состава и размера зерна аустенита на температуру фазового превращения и физико-механические свойства сплавов
Газовая хроматография
Геофизические исследования скважин
Искусственные алмазы
Трансформаторы тока и напряжения
Транзисторы
Воздушные и кабельные линии электропередач
Создание транспортно-энергетического модуля на основе ядерной энергодвигательной установки мегаваттного класса
Магнитные аномалии
Нанотехнологии
Тема : Центр
тяжести
1. Сила тяжести как
Сила тяжести как
равнодействующая вертикальных
сил.
2.Центр тяжести. Методы
нахождения.
3. Центр тяжести простых
геометрических фигур
1.Сила тяжести как
равнодействующая
вертикальных сил.
Сила тяжести – это сила, с
которой тела притягиваются к
земле
Сила тяжести тела – это
равнодействующая сил тяжести
отдельных частиц тела; модуль
этой силы – вес тела.
G – сила тяжести.
8. Сила тяжести
2.Центр тяжести.
Методы
нахождения
Центр тяжести тела – это такая
неизменно связанная с этим телом
точка, через которую проходит линия
действия силы тяжести данного тела
при любом положении тела в
пространстве.
12. Методы определения центра тяжести тела
— Способ подвешивания;
— Способ взвешивания;
— Аналитический способ.
Способ взвешивания
Способ взвешивания
15. Аналитический способ
1 Метод симметрии
2 Метод разделения
(разбиения)
3 Метод отрицательных
масс
1 Метод симметрии
1. 1 Если однородное тело имеет плоскость
1 Если однородное тело имеет плоскость
симметрии, то центр тяжести лежит в этой
плоскости
1.2 Если однородное тело имеет ось
симметрии, то центр тяжести лежит на
этой оси. Центр тяжести однородного тела
вращения лежит на оси вращения.
1.3 Если однородное тело имеет две оси
симметрии, то центр тяжести находится в
точке их пересечения.
18. 2 Метод разделения (разбиения)
Тело разбивается на наименьшее
число частей, силы тяжести и
положение центров тяжести
которых известны
19. 3 Метод отрицательных масс
При определении центра
тяжести тела, имеющего
свободные полости, следует
применять метод разбиения,
но массу свободных полостей
считать отрицательной.
20. Координаты центра тяжести тела
n
Xń
GiXi
i 1
n
Gi
i 1
n
n
Zń
GiZi
i 1
n
Gi
Yń
i 1
GiYi
i 1
n
Gi
i 1
Xc, Yc, Zc – координаты центра тяжести тела;
Xi ,Yi , Zi – координаты i- ой частицы;
Gi — сила тяжести i- ой частицы тела
3. Центр тяжести
Центр тяжести
простых
геометрических
фигур
22. Координаты центра тяжести плоской фигуры
n
Őń
AiXi
i 1
n
Ai
n
i 1
Yс
AiYi
i 1
n
Ai
i 1
Медиана делится точкой
пересечения в отношении 2:1,
начиная с вершины
Xc = 1/3 OB
Yc = 1/3 OA
Медиана делится точкой пересечения в
отношении 2:1, считая с вершины
2R
ŔŃ
3
R – радиус полукруга
30. Центр тяжести кругового сектора
R – радиус
сектора;
α – угол
сектора.
2R
ОС
sin
3
32. Центр тяжести двутавра
34. Центр тяжести швеллера
36. Центр тяжести уголка
37. Определение центра тяжести фигуры неправильной формы.
1)
Метод подвешивания на
острие;
2) Теоретический метод
38. 1.Способ подвешивания
39. 2. Теоретический метод
В этом случае сложная фигура
разбивается на определенное
количество элементарных фигур,
имеющих правильную геометрическую
форму. Затем определяется
Затем определяется
положение центра тяжести и
площади каждой элементарной
фигуры.
40. Задача: Найти положение центра тяжести плоской пластины
1)Прямоугольник
А1 = 10*4 = 40 см2
С1(6;12)
2) Прямоугольник
А2 = 12*24 = 288 см2
С2(-5;2)
n
Хс
AiXi
i 1
n
Ai
i 1
n
3)Треугольник
А3 = 0,5*6*9= 27 см2
С3(3;22)
Yс
AiYi
i 1
n
Ai
i 1
1)Прямоугольник
А1 = 10*4 = 40 см2
С1(6;12)
2) Прямоугольник
А2 = 12*24 = 288 см2
С2(-5;2)
3)Треугольник
А3 = 0,5*6*9= 27 см2
С3(3;22)
40 6 288 ( 5) 27 3
4,2ńě
40 288 27
n
Őń
AiXi
i 1
n
Ai
i 1
n
Yń
AiYi
i 1
n
Ai
i 1
40 12 288 2 27 22
1,5ńě
40 288 27
1. Сегодняшний урок мне
(понравился или не
понравился)
2. Мне понравилось
…(назвать, что именно)
3. Пригодятся ли эти
знания в вашей
профессиональной
деятельности?
Задание на дом
СРС : Определить координаты
центра тяжести плоской фигуры
Аркуша А. И., Фролов М.И.
И., Фролов М.И.
Техническая механика с.67-77
English
Русский
Правила
Момент инерции площади — типичные поперечные сечения I
Момент инерции площади или Момент инерции площади — , также известный как Второй момент площади — I , является свойством формы, которое используется прогнозировать прогиб, изгиб и напряжение в балках.
МОМЕНТ Инерции — ИМПИМАЛЬНЫЕ ЕДИНИЦЫ
- дюймов 4
Площадь Момент инерции — Метрические единицы
- мм 4
- см 4
- м 4
Преобразование единиц измерения
- 1 см 4 = 10 -8 м 4 = 10 4 мм 4
- 1 дюйм 4 = 4,16×10 5 мм 4 = 41,6 см 90 019 4
Пример — преобразование между единицами площади момента инерции
9240 см 4 можно преобразовать в мм 4 путем умножения на 10 4
90 002 (9240 см 4 ) 10 4 = 9,24 10 7 мм 4
Площадь Момент инерции (момент инерции для площади или второй момент площади)
для изгиба вокруг оси x может быть выражен как
I х = ∫ у 2 дА (1)
где
I x = момент инерции площади относительно оси x ( м 4 , мм 4 , дюймы 4 )
y = расстояние по перпендикуляру от оси x до элемента dA (м, мм, дюймов )
дА = площадь элемента ( м 2 , мм 2 , дюймов 2 )
Момент инерции при изгибе вокруг оси Y можно выразить как
I y = ∫ x 2 dA (2)
где
I y = момент инерции площади относительно оси y ( м 9001 9 4 , мм 4 , дюймы 4 )
x = перпендикулярное расстояние от оси y до элемента dA (м, мм, дюймов ) 9 0010
Площадь Момент инерции для типовых сечений I
- Момент инерции площади для типичных сечений II
Сплошное квадратное сечение
Момент инерции площади для сплошного квадратного сечения можно рассчитать как
I x = a 4 / 12 (2)
где
a = сторона (мм, м, дюймы) . .)
.)
I у = а 4 / 12 (2b)
Сплошное прямоугольное сечение
Момент инерции площади для прямоугольного сечения можно рассчитать как
90 002 I x = b h 3 / 12 (3)
где
b = ширина
h = высота
I y = b 3 h / 12 (3b)
Сплошное круглое сечение
Момент инерции площади для твердого цилиндрического сечения можно рассчитать как 4 / 64 (4)
где
r = радиус
d = диаметр 9 0010
I y = π r 4 / 4
= π d 4 / 64 (4b)
Полое цилиндрическое поперечное сечение
Момент инерции площади для полого цилиндрического сечения можно рассчитать как
I x = π (d o 4 — d i 4 ) / 64 (5)
где
d o = наружный диаметр цилиндра
d i = внутренний диаметр цилиндра 9 4 — d i 4 ) / 64 (5b)
Квадратное сечение — диагональные моменты
Моменты инерции площади диагонали квадратного сечения можно рассчитать как
I x = I y = a 4 / 12 (6)
Прямоугольное сечение – Моменты площади на любой линии, проходящей через центр тяжести
Прямоугольное сечение и площадь момента на линии, проходящей через центр тяжести, можно рассчитать как
I x = (b h / 12) (h 2 cos 2 a + b 2 sin 2 a) (7)
Симметричная форма
Площадь Момент инерции для симметричного сечения может вычисляется как
I x = (a h 3 / 12) + (b / 12) (H 3 — h 3 ) (8)
I у = (а 3 h / 12) + (b 3 / 12) (H — h) (8b)
Несимметричная форма
Площадь Момент инерции для сечения несимметричной формы можно рассчитать как
I x = (1 / 3) (B y b 3 — В 1 h b 3 + b y t 3 — b1 h t 3 ) (9) 90 086
- Момент инерции площади для типичных сечений II
Момент инерции площади в зависимости от Полярный момент инерции против момента инерции
- «Площадь момента инерции» — это свойство формы, которое используется для прогнозирования прогиба, изгиба и напряжения в балках.
 скручивание балки под действием крутящего момента
скручивание балки под действием крутящего момента - «Момент инерции» является мерой сопротивления объекта изменению направления вращения.
Модуль упругости сечения
- «Модуль сечения» определяется как W = I / y , где I — момент инерции площади, а y — расстояние от нейтральной оси до любого заданного волокна.
Профиль балки ISMB 400 | ISSP 6.1
Площадь сечения
Поперечное сечение объекта — это форма, которую вы получаете, когда разрезаете объект прямо. Для цилиндра это может быть прямоугольник, круг и даже овал, в зависимости от того, как он был вырезан.
Глубина сечения
Эффективная глубина сечения d определяется как расстояние от крайней сжатой нити бетона до центра тяжести продольной растянутой арматуры.
Ширина фланца
Фактическая ширина полки – это шаг балки, равный расстоянию между средними точками соседних пролетов плиты.
Толщина фланца
Duis autem vel eum iriure dolor in hendrerit in vulputate. Ut wisi enim ad minim veniam, quis nostrud exercitation ullamcorper suscipit lobortis nisl ut.
Anim pariatur cliche reprehenderit, enim eiusmod high life accusamus Terry Richardson ad Squid. 3 wolf moon officia aute, non cupidatat скейтборд dolor brunch. Продовольственный грузовик лебеда nesciunt Laborum
эйусмод. Бранч 3 Волчий лунный темп.
Бранч 3 Волчий лунный темп.
Duis autem vel eum iriure dolor in hendrerit in vulputate. Ut wisi enim ad minim veniam, quis nostrud exercitation ullamcorper suscipit lobortis nisl ut.
Активировать этот раздел через URL
Толщина паутины
Duis autem vel eum iriure dolor in hendrerit in vulputate. Ut wisi enim ad minim veniam, quis nostrud exercitation ullamcorper suscipit lobortis nisl ut.
Anim pariatur cliche reprehenderit, enim eiusmod high life accusamus Terry Richardson ad Squid. 3 wolf moon officia aute, non cupidatat скейтборд dolor brunch. Продовольственный грузовик лебеда nesciunt Laborum
Продовольственный грузовик лебеда nesciunt Laborum
эйусмод.
Момент инерции
111111Duis autem vel eum iriure dolor in hendrerit in vulputate. Ut wisi enim ad minim veniam, quis nostrud exercitation ullamcorper suscipit lobortis nisl ut.
Anim pariatur cliche reprehenderit, enim eiusmod high life accusamus Terry Richardson ad Squid. 3 wolf moon officia aute, non cupidatat скейтборд dolor brunch. Продовольственный грузовик лебеда nesciunt Laborum
эйусмод.
Duis autem vel eum iriure dolor in hendrerit in vulputate. Ut wisi enim ad minim veniam, quis nostrud exercitation ullamcorper suscipit lobortis nisl ut.
Ut wisi enim ad minim veniam, quis nostrud exercitation ullamcorper suscipit lobortis nisl ut.
Радиус вращения
Anim pariatur cliche reprehenderit, enim eiusmod high life accusamus Terry Richardson ad Squid. 3 wolf moon officia aute, non cupidatat скейтборд dolor brunch. Продовольственный грузовик лебеда nesciunt Laborum
эйусмод. Бранч 3 Волчий лунный темп.
Duis autem vel eum iriure dolor in hendrerit in vulputate. Ut wisi enim ad minim veniam, quis nostrud exercitation ullamcorper suscipit lobortis nisl ut.
Модуль сечения
Duis autem vel eum iriure dolor in hendrerit in vulputate.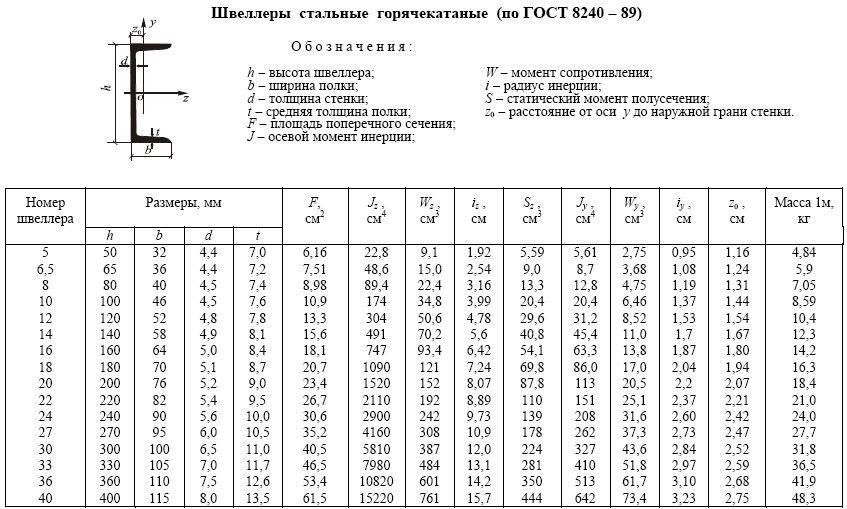 Ut wisi enim ad minim veniam, quis nostrud exercitation ullamcorper suscipit lobortis nisl ut.
Ut wisi enim ad minim veniam, quis nostrud exercitation ullamcorper suscipit lobortis nisl ut.
Anim pariatur cliche reprehenderit, enim eiusmod high life accusamus Terry Richardson ad Squid. 3 wolf moon officia aute, non cupidatat скейтборд dolor brunch. Продовольственный грузовик лебеда nesciunt Laborum
эйусмод. Бранч 3 Волчий лунный темп.
Duis autem vel eum iriure dolor in hendrerit in vulputate. Ut wisi enim ad minim veniam, quis nostrud exercitation ullamcorper suscipit lobortis nisl ut.
Радиус корня
Duis autem vel eum iriure dolor in hendrerit in vulputate. Ut wisi enim ad minim veniam, quis nostrud exercitation ullamcorper suscipit lobortis nisl ut.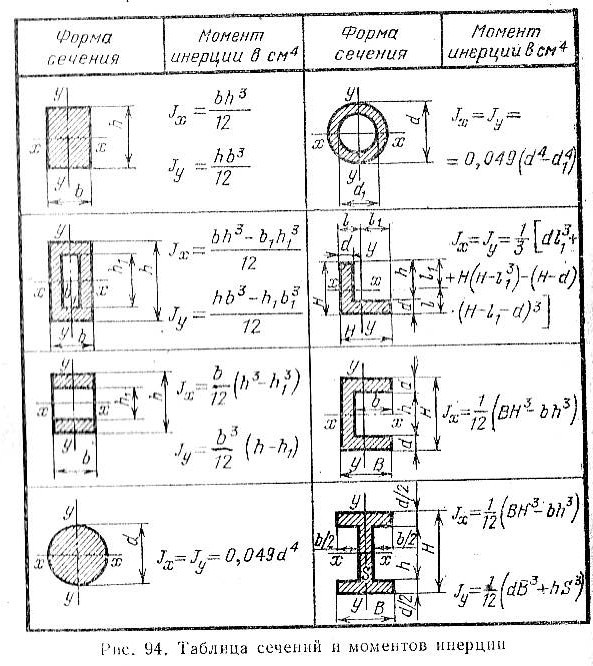
Anim pariatur cliche reprehenderit, enim eiusmod high life accusamus Terry Richardson ad Squid. 3 wolf moon officia aute, non cupidatat скейтборд dolor brunch. Продовольственный грузовик лебеда nesciunt Laborum
эйусмод.
Радиус пальца ноги
111111Duis autem vel eum iriure dolor in hendrerit in vulputate. Ut wisi enim ad minim veniam, quis nostrud exercitation ullamcorper suscipit lobortis nisl ut.
Anim pariatur cliche reprehenderit, enim eiusmod high life accusamus Terry Richardson ad Squid. 3 wolf moon officia aute, non cupidatat скейтборд dolor brunch. Продовольственный грузовик лебеда nesciunt Laborum
Продовольственный грузовик лебеда nesciunt Laborum
эйусмод.
Duis autem vel eum iriure dolor in hendrerit in vulputate. Ut wisi enim ad minim veniam, quis nostrud exercitation ullamcorper suscipit lobortis nisl ut.
Наклон фланца
Anim pariatur cliche reprehenderit, enim eiusmod high life accusamus Terry Richardson ad Squid. 3 wolf moon officia aute, non cupidatat скейтборд dolor brunch. Продовольственный грузовик лебеда nesciunt Laborum
эйусмод. Бранч 3 Волчий лунный темп.
Duis autem vel eum iriure dolor in hendrerit in vulputate. Ut wisi enim ad minim veniam, quis nostrud exercitation ullamcorper suscipit lobortis nisl ut.
Ut wisi enim ad minim veniam, quis nostrud exercitation ullamcorper suscipit lobortis nisl ut.
Максимальный размер фланцевой заклепки
Duis autem vel eum iriure dolor in hendrerit in vulputate. Ut wisi enim ad minim veniam, quis nostrud exercitation ullamcorper suscipit lobortis nisl ut.
Anim pariatur cliche reprehenderit, enim eiusmod high life accusamus Terry Richardson ad Squid. 3 wolf moon officia aute, non cupidatat скейтборд dolor brunch. Продовольственный грузовик лебеда nesciunt Laborum
эйусмод. Бранч 3 Волчий лунный темп.
Duis autem vel eum iriure dolor in hendrerit in vulputate.

