- R – радиус вычисляемой окружности. Он равен половине её диаметра;
- Π – постоянная равная 3,14;
- S – вычисляемая площадь поперечного сечения трубы.
- S = π • (D/2 – N)2;
- В этой записи D – внешний диаметр окружности;
- N – толщина стенки трубы.
- A — площадь поперечного сечения (м²)
- P — смоченный периметр (м)
- Ю. И. Дытнерский. Процессы и аппараты химической технологии. Часть 1. Теоретические основы процессов химической технологии. — М.: Химия, 1995. — 400 с. — 6500 экз. — ISBN 5-7245-1006-5.
Формула длины окружности через радиус или диаметр. Периметр трубы
Формула длины окружности через радиус или диаметр
Окружность это замкнутая кривая линия, все точки которой, равноудалены от другой, определенной точки (центр окружности) на заданном расстоянии (радиус).Радиус окружности - отрезок, соединяющий её центр и любую другую точку расположенную на линии окружности.Диаметр окружности - отрезок, соединяющий две любые точки расположенные на линии окружности и проходящий через её центр. Диаметр, в два раза больше радиуса
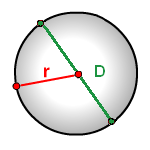
r - радиус окружности
D - диаметр окружности
π ≈ 3.14
Формула длины окружности через радиус или диаметр, (L):

Калькулятор для расчета длины окружности через радиус
Калькулятор для расчета длины окружности через диаметр
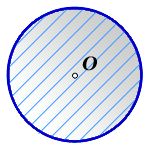
S - площадь круга
O - центр круга
π ≈ 3.14
Формула длины окружности через площадь, (L):

Калькулятор для расчета длины окружности через площадь
Формулы для окружности и круга:
Подробности Автор: Сергей Кондратов Опубликовано: 07 сентября 2011 Обновлено: 09 октября 2017
Опубликовано: 07 сентября 2011 Обновлено: 09 октября 2017 www-formula.ru
Формула расчета длины окружности
Окружностью называется ряд равноудалённых точек от одной точки, которая, в свою очередь, является центром этой окружности. Окружность имеет также свой радиус, равный расстоянию этих точек от центра.
Отношение длины, какой либо окружности к её диаметру, для всех окружностей одинаково. Это отношение есть число, являющееся математической константой, которое обозначается греческой буквой π.
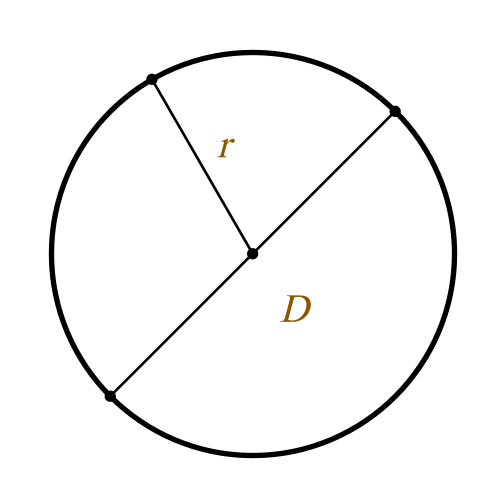
Определение длины окружности
Произвести расчёт окружности можно по следующей формуле:
L = πD = 2πr
r – радиус окружности
D – диаметр окружности
L – длина окружности
π – 3.14
Задача:Вычислить длину окружности, имеющей радиус 10 сантиметров.
Решение:Формула для вычисления дины окружности имеет вид:
L = πD = 2πr
где L – длина окружности, π – 3,14, r – радиус окружности, D – диаметр окружности.
Таким образом, длина окружности, имеющей радиус 10 сантиметров равна:
L = 2 × 3,14 × 10 = 62,8 сантиметра
Окружность представляет собой геометрическую фигуру, являющуюся совокупностью всех точек на плоскости, удаленных от заданной точки, которая называется ее центром, на некоторое расстояние, не равное нулю и именуемое радиусом. Определять ее длину с различной степенью точности ученые умели уже в глубокой древности: историки науки считают, что первая формула для вычисления длины окружности была составлена примерно в 1900 году до нашей эры в древнем Вавилоне.
С такими геометрическими фигурами, как окружности, мы сталкиваемся ежедневно и повсеместно. Именно ее форму имеет внешняя поверхность колес, которыми оснащаются различные транспортные средства. Эта деталь, несмотря на свою внешнюю простоту и незатейливость, считаются одним из величайших изобретений человечества, причем интересно, что аборигены Австралии и американские индейцы вплоть до прихода европейцев совершенно не имели понятия о том, что это такое.
По всей вероятности, самые первые колеса представляли собой отрезки бревен, которые насаживались на ось. Постепенно конструкция колеса совершенствовалась, их конструкция становилась все более и более сложной, а для их изготовления требовалось использовать массу различных инструментов. Сначала появились колеса, состоящие из деревянного обода и спиц, а затем, для того, чтобы уменьшить износ их внешней поверхности, ее стали обивать металлическими полосами. Для того чтобы определить длины этих элементов, и требуется использовать формулу расчета длины окружности (хотя на практике, вероятнее всего, мастера это делали «на глаз» или просто опоясывая колесо полосой и отрезая требуемый ее участок).
Следует заметить, что колесо используется отнюдь не только в транспортных средствах. Например, его форму имеет гончарный круг, а также элементы шестеренок зубчатых передач, широко применяемых в технике. Издавна колеса использовались в конструкциях водяных мельниц (самые древние из известных ученым сооружений такого рода строились в Месопотамии), а также прялок, применявшихся для изготовления нитей из шерсти животных и растительных волокон.
Окружности нередко можно встретить и в строительстве. Их форму имеют достаточно широко распространенные круглые окна, очень характерные для романского архитектурного стиля. Изготовление этих конструкций – дело весьма непростое и требует высокого мастерства, а также наличия специального инструмента. Одной из разновидностей круглых окон являются иллюминаторы, устанавливаемые в морских и воздушных судах.
Таким образом, решать задачу определения длины окружности часто приходится инженерам-конструкторам, разрабатывающим различные машины, механизмы и агрегаты, а также архитекторам и проектировщикам. Поскольку число π, необходимое для этого, является бесконечным, то с абсолютной точностью определить этот параметр не представляется возможным, и поэтому при вычислениях учитывается та ее степень, которая в том или ином конкретном случае является необходимой и достаточной.
simple-math.ru
Как рассчитать длину окружности и периметр круга? :: SYL.ru
Окружность встречается в повседневной жизни не реже, чем прямоугольник. А у многих людей задача о том, как рассчитать длину окружности, вызывает затруднение. И все потому, что у нее нет углов. При их наличии все стало бы намного проще.
Что такое окружность и где она встречается?
Эта плоская фигура представляет собой некоторое количество точек, которые расположены на одинаковом удалении от еще одной, которая является центром. Это расстояние называется радиусом.
В повседневной жизни нечасто приходится вычислять длину окружности, кроме людей, которые являются инженерами и конструкторами. Они создают проекты механизмов, в которых используются, например, шестеренки, иллюминаторы и колеса. Архитекторы создают дома, имеющие круглые или арочные окна.
В каждом из этих и других случаях требуется своя точность. Причем высчитать длину окружности совершенно точно оказывается невозможно. Связано это с бесконечностью основного числа, имеющегося в формуле. «Пи» до сих пор уточняется. И используется чаще всего округленное значение. Степень точности выбирается такой, чтобы дать максимально верный ответ.
Обозначения величин и формулы
До того как рассчитать длину окружности, потребуется договориться о том, какая буква что обозначает. Это удобно записать в таблице.
| Величина | Обозначение |
| радиус | r |
| диаметр | d |
| длина окружности | l |
Теперь легко ответить на вопрос о том, как рассчитать длину окружности по радиусу, для этого потребуется такая формула:
l =2π * r.
Здесь и далее π берется округленным. Чаще всего в задачах используют значение 3,14. Но иногда нужна большая точность и тогда применяют такое число: 3,14159.
Поскольку радиус и диаметр связаны друг с другом, то есть и другая формула для расчетов. Так как радиус в два раза меньше, то выражение немного видоизменится. И формула того, как рассчитать длину окружности, зная диаметр, будет следующей:
l = π * d.
Как быть, если нужно вычислить периметр круга?
Просто вспомнить, что круг включает в себя все точки внутри окружности. А значит, его периметр совпадает с ее длиной. И после того, как рассчитать длину окружности, поставить знак равенства с периметром круга.
Кстати, и обозначения у них такие же. Это касается радиуса и диаметра, а периметром является латинская буква P.
Примеры заданий
Задача первая
Условие. Узнать длину окружности, радиус которой равен 5 см.
Решение. Здесь несложно понять, как рассчитать длину окружности. Нужно только воспользоваться первой формулой. Поскольку радиус известен, то потребуется только подставить значения и сосчитать. 2 умноженное на радиус, равный 5 см, даст 10. Осталось еще умножить его на значение π. 3,14 * 10 = 31,4 (см).
Ответ: l = 31,4 см.
Задача вторая
Условие. Имеется колесо, длина окружности которого известна и равна 1256 мм. Необходимо вычислить его радиус.
Решение. В этом задании потребуется воспользоваться той же формулой. Но только известную длину нужно будет разделить на произведение 2 и π. Получается, что произведение даст результат: 6,28. После деления остается число: 200. Это искомая величина.
Ответ: r = 200 мм.
Задача третья
Условие. Вычислить диаметр, если известна длина окружности, которая равна 56,52 см.
Решение. Аналогично предыдущей задаче потребуется разделить известную длину на значение π, округленное до сотых. В результате такого действия получается число 18. Результат получен.
Ответ: d = 18 см.
Задача четвертая
Условие. Стрелки часов имеют длину 3 и 5 см. Нужно вычислить длины окружностей, которые описывают их концы.
Решение. Поскольку стрелки совпадают с радиусами окружностей, то потребуется первая формула. Ею нужно воспользоваться два раза.
Для первой длины произведение будет состоять из множителей: 2; 3,14 и 3. Итогом будет число 18,84 см.
Для второго ответа нужно перемножить 2, π и 5. Произведение даст число: 31,4 см.
Ответ: l1 = 18,84 см, l2= 31,4 см.
Задача пятая
Условие. Белка бегает в колесе диаметром 2 м. Какое расстояние она пробегает за один полный оборот колеса?
Решение. Это расстояние равно длине окружности. Поэтому нужно воспользоваться подходящей формулой. А именно перемножить значение π и 2 м. Подсчеты дают результат: 6,28 м.
Ответ: Белка пробегает 6,28 м.
www.syl.ru
3.5. Живое сечение. Смоченный периметр. Гидравлический радиус
В гидравлических расчётах для характеристики размеров и формы поперечного сечения потока вводят понятие о живом сечении и его элементах: смоченном периметре и гидравлическом радиусе.
Живым сечением называется поверхность в пределах потока, проведённая нормально к линиям тока.
Для круглого трубопровода, когда всё поперечное сечение заполнено жидкостью, живым сечение является площадь круга: (рис.3.6).
Рис. 3.6. Элементы потока
Смоченным периметром называют ту часть периметра живого сечения, по которой жидкость соприкасается со стенками трубопровода (рис.3.6). Смоченный периметр обычно обозначают греческой (хи). Для круглой трубы полностью заполненной жидкостью смоченный периметр равен длине окружности:
.
Гидравлическим радиусом называют отношение живого сечения к смоченному периметру, т.е. величину
.
Эта величина характеризует удельную, т.е. приходящуюся на единицу длины смоченного периметра, площадь живого сечения. Легко сделать вывод, что поток с наибольшим гидравлическим радиусом при прочих равных условиях имеет минимальную силу трения, приложенную к смоченной поверхности.
Для круглых труб, полностью заполненных жидкостью, гидравлический радиус равен четверти диаметра:
.
Введение гидравлического радиуса как характерного размера позволяет сравнивать по критерию подобия (Re) потоки с разными формами живого сечения.
Рассмотренные основные понятия позволяют решать самые различные практические задачи гидравлики.
Пример 3.1. Определить скорость потока в трубопроводе. Диаметр , расход воды (несжимаемой жидкости) -.
Решение. Искомая скорость .
Определим площадь живого сечения:
.
Скорость потока:
.
3.6. Уравнение количества движения для потока жидкости
Гидравлика – это техническая механика жидкости, в которой часто используются упрощённые методы для решения инженерных задач. Во многих случаях при решении практических задач гидравлики удобно применять такие центральные понятия механики, как количество движения (уравнение импульсов) и кинетическая энергия.
В связи с этим необходимо рассмотреть возможность вычисления количества движения и кинетическую энергию потока жидкости по средней скорости, а не по действительным местным скоростям. Это позволит существенно упростить гидравлические расчёты.
Для материального тела массой , движущегося со скоростью, изменение количества движения за времявследствие действия силывыразится векторным уравнением
, (3.7)
где - приращение количества движения, обусловленное импульсом.
Жидкость представляет собой материальную систему, поэтому основной закон механики может быть приложен к любой выделенной из неё массе.
Применим эту теорему механики к участку потока жидкости с расходом между сечениями 1-1 и 2-2 (выделенный участок заштрихован). Ограничимся рассмотрением только установившегося движения жидкости (рис. 3.7).
За время этот участок переместится в положение, определяемое сечениямии. Объёмы этих элементов, а, следовательно, и их массыодинаковы, поэтому приращение количества движения будет равно
. (3.8)
Это приращение количества движения обусловлено импульсом всех внешних сил, действующих на объём жидкости между сечениями 1-1 и 2-2. Внешними силами, приложенными к выделенному объёму, являются сила тяжести всего объёма , силы давления в первом и втором сеченияхи(нормальные к этим сечениям и направленные внутрь объёма), а также реакции стенок трубы, которая складывается из сил давления и трения, распределённых по боковой поверхности объёма.
Рис. 3.7. Применение уравнения количества движения
к потоку жидкости
Уравнение импульсов (3.7) для рассматриваемого случая можно записать в виде
.
После сокращения на
. (3.9)
Составив проекции этого векторного уравнения на три координатные оси, получим три алгебраических уравнения с тремя неизвестными - .
Л. Эйлер предложил удобный графический способ нахождения силы . Перенося в формуле (3.?) все слагаемые в одну сторону, можно представить его в виде суммы векторов:
= 0, (3.10)
где вектор взят с обратным знаком (т.е. по направлению обратный действительному). В соответствии с этим выражением (3.10) силуможно найти, построив замкнутый многоугольник сил, как это показано на рис. 3.7,а.
Анализ показывает, что при вычислении количества движения и кинетической энергии по средней скорости допускается ошибка, которую можно учесть с помощью двух коэффициентов:
- коэффициента Буссинеска при вычислении количества движения;
- коэффициента Кориолиса в уравнении Бернулли при вычислении кинетической энергии.
Величина обоих коэффициентов зависит от характера распределения скоростей в поперечном сечении потока жидкости. На практике при турбулентном режиме движения коэффициент Кориолиса , а коэффициент Буссинеска. Поэтому обычно полагают. Однако встречаются отдельные случаи, когдадостигает больших значений, и тогда пренебрежение им может привести к значительным погрешностям.
Пример 3.2. Определить силу воздействия потока жидкости на преграду. Пусть жидкость вытекает в атмосферу и наталкивается на безграничную стенку, установленную нормально к потоку. В результате жидкость растекается по стенке, изменяя направление своего течения на 900 (рис. 3.8). Известны площадь сечения потока , скорость истеченияи плотность жидкости.
Рис. 3.8. Воздействие струи на преграду
Для решения данной задачи берём фиксированный объём, показанный штриховой линией, и применяем теорему Эйлера. Так как давление внутри струи и по поверхности жидкости равно атмосферному, т.е. избыточное давление равно нулю, уравнение, выражающее теорему Эйлера, для направления, совпадающего с вектором скорости истечения , будет иметь вид
,
или . (3.11)
Это и есть сила воздействия потока жидкости на преграду. При другом угле установке стенки или других её форме и размерах в правую формулы (3.11) вводится безразмерный коэффициент, отличный от единицы, но пропорциональность силы произведениюсохранится.
studfiles.net
Методы расчета площади сечения трубы
Параметры труб определяются согласно расчётам, сделанным при помощи специальных формул. Сегодня большинство вычислений производится посредством онлайн сервисов, однако в большинстве случаев требуется индивидуальный подход к вопросу, поэтому важно понимать, каким образом производится расчёт площади сечения трубы.

Как делаются вычисления?
Как известно, труба – это цилиндр. Следовательно, площадь её сечения рассчитывается по простым формулам, известным нам из курса геометрии. Основная задача – вычислить площадь круга, диаметр которого равен наружному диаметру изделия. При этом толщина стенок вычитается для получения истинного значения.
Как мы знаем из курса общеобразовательной школы, площадь круга равна произведению числа π на квадрат радиуса:
S = π • R2.
Здесь:

Приступаем к расчёту
Так как задача – найти истинную площадь, то из полученного значения необходимо вычесть величину толщины стенки. Следовательно, формула приобретает вид:
Чтобы вычисления были максимально точными, следует вписать больше знаков после запятой в числе π (пи).
К примеру, требуется рассчитать сечение трубы, внешний диаметр которой 1 метр. Толщина её стенок 10 мм. (или 0,01 м.). Следовательно, нам известно:
D = 1 м.; N = 0,01 м.
Для упрощения возьмём π = 3,14. Подставляем значения в формулу:
S = π • (D/2 – N)2 = 3,14 • (1/2 – 0,01)2 = 0,754 м2.
Некоторые физические особенности
От площади сечения трубы зависит скорость движения жидкостей и газов, которые по ней транспортируются. Надо выбрать оптимальный диаметр. Не менее важным является и внутреннее давление. Именно от его величины зависит целесообразность выбора сечения.

При расчёте учитывается не только давление, но и температура среды, её характер и свойства. Знание формул не освобождает от необходимости изучения теории. Расчёт труб канализации, водоснабжения, газоснабжения и отопления опирается на информацию справочников. Важно, чтобы выполнялись все необходимые условия при выборе сечения. Его величина также зависит и от характеристик используемого материала.
О чём стоит помнить?
Площадь сечения трубы – один из важных параметров, который следует учитывать при расчёте системы. Но наравне с тем высчитываются параметры прочности, определяется, какой материал выбрать, изучаются свойства системы в целом и пр.
trubygid.ru
Гидравлический диаметр — WiKi
Гидравлический (эквивалентный) диаметр — мера эффективности русла в пропускании потока жидкости. Чем меньше гидравлический диаметр, тем бо́льшее сопротивление потоку оказывает русло (при одинаковой площади поперечного сечения потока).
Нахождение
Определяется по формуле:
DΓ=4AP{\displaystyle D_{\Gamma }={\frac {4A}{P}}}где A — площадь поперечного сечения потока жидкости и P — смоченный периметр (см. ниже) поперечного сечения потока.
Для трубы круглого поперечного сечения, полностью (без пустот) заполненной жидкостью, эта формула принимает вид:
DΓ=4πD24πD=D{\displaystyle D_{\Gamma }={\frac {4{\frac {\pi D^{2}}{4}}}{\pi D}}=D}То есть, для круглого сечения гидравлический диаметр равен геометрическому диаметру.
Для кольца гидравлический диаметр равен:
DΓ=4⋅0,25π(D2−d2)π(D+d)=D−d{\displaystyle D_{\Gamma }={\frac {4\cdot 0{,}25\pi (D^{2}-d^{2})}{\pi (D+d)}}=D-d}где D{\displaystyle D} — наружный диаметр кольца, d{\displaystyle d} — внутренний диаметр кольца.
Для каналов прямоугольного сечения гидравлический диаметр определяют по формуле:
DΓ=4ab2a+b{\displaystyle D_{\Gamma }={\frac {4ab}{2a+b}}}где a — уровень заполнения канала и b — ширина канала.
Смоченный периметр
Пояснение понятия «смоченный периметр». Изменение смоченного периметра (синий) канала в форме равнобедренной трапеции в зависимости от угла откоса ѱ.Смоченный периметр — длина части границы канала, касающейся жидкости.
Понятие смоченного периметра имеет большое значение при проектировании каналов. Расход воды равен произведению площади поперечного сечения канала на скорость течения. Скорость же течения, по формуле Шези, при постоянной площади сечения канала и гидравлическом уклоне, прямо пропорциональна квадратному корню из гидравлического радиуса, то есть обратно пропорциональна квадратному корню из смоченного периметра. Поэтому при заданной площади поперечного сечения стараются минимизировать смоченный периметр, чтобы увеличить скорость течения, а, следовательно, и расход воды. Поперечное сечение канала обычно представляет собой равнобедренную трапецию, нижнее основание которой больше верхнего. Смоченный периметр такого канала равен сумме нижнего основания и боковых сторон этой трапеции. Считая площадь такой трапеции заданной, находят минимум смоченного периметра в зависимости либо от угла откоса (угол, смежный углу при нижнем основании) при постоянной глубине (то есть высоте трапеции), либо от глубины при постоянном угле откоса. В первом случае наименьший смоченный периметр будет при угле откоса, равном 60°[1].
Гидравлический радиус
Существует также понятие «гидравлический радиус». Несмотря на своё название, гидравлический диаметр не равен двум гидравлическим радиусам.
Гидравлический радиус вычисляется по формуле:
Rh=AP{\displaystyle R_{h}={\frac {A}{P}}} ,где:
См. также
Примечания
Литература
ru-wiki.org
Распределение теплового потока по периметру трубы
Распределение теплового потока по периметру трубы [c.72]В. Теплоприемник. Наиболее часто в таких топках в качестве теплоприемника используются один или два ряда труб, расположенных напротив отражающей стенки. Такое расположение увеличивает эффективность труб как поглотителей теплоты, поскольку на большую часть периметра труб излучение не попадает — оно поступает на отражатель, от которого снова попадает на трубы. В общем, распределение теплового потока по периметру труб не является однородным. В случае одного ряда труб максималь-НЫЙ тепловой поток будет со стороны прямого излучения от продуктов сгорания и меньшие значения теплового ното-ка будут с обратной стороны поверхности труб от отраженного излучения и излучения горячен поверхности отражателя. Отношение максимального теплового потока к среднему может быть установлено изменением шага размещения труб (рис. 3). Для обычного шага размещения труб, равного двум наружным диаметрам, это отношение равно [c.114]
В случае некруглых труб описанные выше условия изменяются, что можно видеть из рис. 2. Для случая постоянной температуры стенки (случай а) условия по существу те же, что и для круглой трубы. Для случая постоянного тепловыделения в стенках отсутствие симметрии в некруглых трубах приводит к существованию градиента температуры по периметру, что в свою очередь обусловливает наличие теплового потока в стенке. Этот тепловой поток влияет на распределение температуры в стенке и, следовательно, термические свойства стенки могут оказаться существенными при решении уравнения (3). [c.262]Учет свойств стенки при вычислении распределения температуры в жидкости встречает затруднения, которые можно обойти определенным выбором одного из двух видов граничных условий для труб некруглого сечения. Граничные условия первого вида (случай Ь на рис. 2) состоят в задании постоянной плотности теплового потока в направлении течения и постоянной температуры стенки по периметру в каждом сечении. Такие условия имеют место в стенке с большой теплопроводностью. Второй вид граничных условий (случай с на рис. 2) состоит в задании постоянной плотности теплового потока в обоих направлениях как по течению, так и по периметру. Это имеет место при низкой тепло-262 [c.262]
Условия, при которых происходит переход от пузырькового потока к пленочному, зависят от весовой скорости, паросодержания, теплофизических свойств жидкой и паровой фаз (т. е. от рабочего давления среды), величины теплового потока и характера его распределения по длине и периметру трубы, от геометрических размеров трубы, наличия и величины пульсации расхода рабочей среды [15, 16]. Заметим, что в котлах-утилизаторах аммиачного производства локальные тепловые потоки достигают 0,6 МВт/м . [c.468]
Плотность теплового потока оказывает решающее действие на распределение локальных коэффициентов теплоотдачи а по периметру трубы. В режиме испарения максимальные значения л приходятся на верхнюю часть трубы, на которую падает струя с выше-расположенной части пучка. В режиме кипения значения а , распределяются по периметру практически равномерно. [c.128]
ПО радиусам, даны в зависимости от положения точки на периметре одиночного обогреваемого паром цилиндра. Кривая дает действительное распределение тепловой нагрузки, причем можно отметить, что максимальный локальный поток наблюдается в лобовой и тыльной частях трубы, а минимальный, равный примерно 40% от максимального, был установлен на боковых частях цилиндра. [c.352]
Как вытекает пз предыдущего примера (табл. VIII), отдельные точки пернметра трубы для теплоотдачи излучением эффективны неодинаково, и тепловой поток распределяется по периметру трубы неравномерно. На рис. 23 показано распределение теплового потока для различного распо.ложения труб при шаге, faBHOM двум диаметрам. [c.72]
Так, анализ и визуальный осмотр возникающих дефектов в змеевиках трубчатых печей установок термокрекинга АО НУНПЗ показал, что наиболее распространенным является деформирование (прогиб) печных труб на величину более 2 О. Отложение кокса на внутренней поверхности деформированных участках змеевиков происходит неравномерно по периметру трубы. Причиной тому является односторонний нагрев печных труб. Неравномерное распределение теплового потока способствует наиболее интенсивному отложению кокса на более нагретой поверхности. Кроме этого, образовавшийся кокс вследствие значительного термического сопротивления приводит к перефеву печной трубы, а неравномерность его отложения вызывает деформацию. Величина деформации трубы определяется разницей толщины кокса (следовательно, и температур) в диаметрально противоположных точках [I]. [c.265]
Кроме казанных факторов, на 9нр1 могут оказывать влиянне пульсации двухфазного потока на предвключенном участке, неравномерность распределения теплового потока по длине и периметру трубы, способ обогрева поверхностн теплообмена. [c.326]
Другой распространенной конструкцией теплонрнем-ника являются горизонтальные трубы, ра шещенные в вертикальной плоскости между стенками-отра,жателями.Такое расположение труб используется в критических условиях, когда требуется равномерное распределение труб по периметру. Как правило, шаг разме цения труб равен двум диаметрам и отношение максимального теплового потока к среднему равно 1,2. Строгое описание такой конфигурации представляет собой серьезную проблему. В 19 предложено заменить каждую трубу вертикальной плоско11 поверхностью, которая поглощала бы такое же количество излучения, как и труба (см. рис. 4). Высота каждой плоской поверхности равна расстоянию между трубами, умноженному на параметр Р, определяемый по (5). Эффективный коэффициент излучения плоской поверхности, заменяющей трубы, больше, чем коэффициент излучения труб, и равен [c.114]
Появлению намагниченности могут способствовать многие факторы, например тепловые возмущения, существенная неравномерность тепловых потоков по высоте и периметру труб, изменение температуры стенки, действие мазутного факела как низкотемпературной плазмы, акустоэлектрический эффект вследствие работы отрыва паровых пузырей и их захлопывания. Рассмотрение этих процессов в динамике показывает, что важнейшим фактором следует считать именно термоволновой эффект. Очевидно, эффект проявляется в наибольшей мере в мазутных котлах давлением 110-155 кгс/см на участках с высокой тепловой нагрузкой, особенно при нарушении стабильного пузырькового кипения, в результате чего максимум магнитной индукции наблюдается вдоль образующей экранной трубы, наиболее выступающей в топку. Действие такой магнитной ловушки оказывается достаточным для образования отложений на узком участке внутренней поверхности парогенерирующей трубы вдоль указанной образующей даже в условиях весьма незначительного содержания взвешенных ферромагнитных примесей в котловой воде. Наблюдаемое в практике эксплуатации явно выраженное неравномерное (чередующееся) распределение отложений по длине экранной трубы с обогреваемой ее стороны, по-видймому, соответствует узлам пучности волн магнитной индукции. [c.54]
Неравномерность распределения скоростей может повлиять на теплообменные процессы в большей степени, чем на гидравлическо сопротивление неравномерное распределение локальных скоростей газа по периметру горизонтального трубопровода является причиной неравномерности локальных тепловых потоков в верхней и нижней частях трубы [42]. [c.159]
chem21.info