Расчет балки на изгиб, прогиб и прочность, включая калькулятор. Расчет балки стальной

Расчет балки на прочность: онлайн-калькуляторы, пример, последовательность действий

Одной из важнейших задач для строителя считается расчет балки. Сегодня придумано немало средств, позволяющих решать данную задачу максимально быстро и точно. Наиболее удобными считаются онлайн-калькуляторы, которые за несколько секунд предоставляют необходимое решение. В данной статье мы разберем расчет балки на изгиб, прогиб, прочность с применением калькулятора.

Как рассчитывать балки на прочность

Расчет балки на прогиб, калькулятор для которого можно найти в интернете, можно произвести следующими методами:

• Рассчитать максимальную нагрузку, которую способна выдержать заданная схема;
• Подобрать сечение;
• Проверочный перерасчет по максимальным значениям напряжения.

Для наглядности следует рассмотреть общий принцип подбора сечения двутавра, расположенной на двух опорах. Загрузка происходит равномерно распределенной нагрузкой или сосредоточенной силой.

Последовательность действий

Для начала расчета балки на прогиб калькулятором необходимо определить точку, в которой будет максимальное значение момента. Все будет зависеть от того, какая схема представлена в задаче. Наиболее популярны следующие схемы:

1. Заделка — шарнир;
2. Заделка — заделка;
3. Шарнир — шарнир;
4. Заделка — свободный конец.

Остальные варианты являются в той или иной степени разновидностями вышеуказанных схем.

Как только вы нашли изгибающий момент, по таблице ищется момент сопротивления Wx указанного сечения по формулам, которые указываются в соответствующих таблицах. При делении максимального момента изгиба на момент сечения можно отыскать максимальное значение напряжения, которое необходимо сравнить с напряжением, которое максимально выдерживает определяемая конструкция.

Сравнение полученных напряжений с напряжением материалов

Онлайн-расчет балки на прочность сопровождается сравнением полученного значения напряжения в сечении с максимально возможным. Здесь необходимо смотреть на таблицу материалов, из которых производятся такие конструкции.

Если материал пластичен, то максимальное напряжение схемы будет равно пределу текучести материала. К таковым относят алюминий, сталь, иные металлы. Хрупкие же материалы по типу чугуна имеют максимальное значение напряжения, равное пределу прочности. Для каждого конкретного материала имеется свое максимальное значение, которое можно найти в таблицах в специальной литературе.

Пример расчета

Предположим, что нам надо проверить на прочность двутавр номер 10. Его длина 2 метра, он жестко заделан в стену, человек массой 90 килограммов решил повиснуть на двутавре. Порядок решения здесь следующий:

• Выбираем расчетную схему, в этом случае заделка — свободный конец;
• Максимальное значение находится в заделке, двутавр имеет на всей длине одинаковое сечение. Тогда P = m*g = 90*10=0,9 кН, M = P*I= 1,8 кН*м;
• Находим по таблице сортаментов для данного двутавра момент сопротивления;
• Затем находим максимальные напряжения в балке б = M/W = 1,8 / 0. 0000397 = 45,34 Мпа;
• Сравниваем с максимально допустимым напряжением, равным пределу текучести стали, из которой сделан двутавр. Так как 45,34 Мпа меньше 245 Мпа, то такой двутавр выдержит человека массой 90 килограммов.

Можно также решить и вторую задачу, связанной с нахождением максимальной массы человека, которую может выдержать данная балка. Здесь приравнивают значения предела текучести и напряжения в сечении балки, найти максимальный момент и затем наибольшую массу. Для более точного результата следует учитывать различные коэффициенты и брать двойной запас прочности.

Онлайн-калькуляторы

Расчет прогиба балки онлайн-калькулятором достаточно быстрый и точный. Здесь выбирается одна из схем, затем набираются соответствующие числовые значения и происходит расчет по всем необходимым параметрам.

Необходимо указать значения моментов, изгибающих сил, длин участков. Итогом станут эпюры моментов и сил. Решение данными программами достаточно точное и позволяет оперативно посчитать силы и моменты для балок на прочность, изгибы и прогибы.

Преимуществом подобных средств является большой набор схем для расчета, быстрота, точность, простота применения. Однако для уточнения полученного результата надо произвести самостоятельное письменное решение.

В заключение можно сказать следующее: расчет балки на прочность можно произвести как вручную, так и с применением онлайн-калькуляторов. Их можно комбинировать, использовав один из них для проверки другого метода. Рассчитать балку может понадобиться в разных случаях, особенно актуально это становится при строительстве. Только правильно рассчитанная балка позволит построить или реконструировать сооружение с тем условием, что оно прослужит длительное время.

Также данный расчет полезен для всех тех, кто учится или имеет дело с техническими науками, ибо прикладная механика является неотъемлемой частью программы любого технического вуза. Удачных расчетов на прочность!

tokar.guru

Основные формулы для расчета прогиба балки

Балка является основным элементом несущей конструкции сооружения. При строительстве важно провести расчет прогиба балки. В реальном строительстве на данный элемент действует сила ветра, нагружение и вибрации. Однако при выполнении расчетов принято принимать во внимание только поперечную нагрузку или проведенную нагрузку, которая эквивалентна поперечной.

Балки в доме

При расчете балка воспринимается как жесткозакрепленный стержень, который устанавливается на двух опорах. Если она устанавливается на трех и более опорах, расчет ее прогиба является более сложным, и провести его самостоятельно практически невозможно. Основное нагружение рассчитывается как сумма сил, которые действуют в направлении перпендикулярного сечения конструкции. Расчетная схема требуется для определения максимальной деформации, которая не должна быть выше предельных значений. Это позволит определить оптимальный материал необходимого размера, сечения, гибкости и других показателей.

Виды балок

Для строительства различных сооружений применяются балки из прочных и долговечных материалов. Такие конструкции могут отличаться по длине, форме и сечению. Чаще всего используются деревянные и металлические конструкции. Для расчетной схемы прогиба большое значение имеет материал элемента. Особенность расчета прогиба балки в данном случае будет зависеть от однородности и структуры ее материала.

Деревянные

Для постройки частных домов, дач и другого индивидуального строительства чаще всего используются деревянные балки. Деревянные конструкции, работающие на изгиб, могут использоваться для потолочных и напольных перекрытий.

Деревянные перекрытия

Для расчета максимального прогиба следует учитывать:

1. Материал. Различные породы дерева обладают разным показателем прочности, твердости и гибкости.
2. Форма поперечного сечения и другие геометрические характеристики.
3. Различные виды нагрузки на материал.

Допустимый прогиб балки учитывает максимальный реальный прогиб, а также возможные дополнительные эксплуатационные нагрузки.

Конструкции из древесины хвойных пород

Стальные

Металлические балки отличаются сложным или даже составным сечением и чаще всего изготавливаются из нескольких видов металла. При расчете таких конструкций требуется учитывать не только их жесткость, но и прочность соединений.

Стальные перекрытия

Металлические конструкции изготавливаются путем соединения нескольких видов металлопроката, используя при этом такие виды соединений:

• электросварка;
• заклепки;
• болты, винты и другие виды резьбовых соединений.

Стальные балки чаще всего применяются для многоэтажных домов и других видов строительства, где требуется высокая прочность конструкции. В данном случае при использовании качественных соединений гарантируется равномерно распределенная нагрузка на балку.

Для проведения расчета балки на прогиб может помочь видео: 

Прочность и жесткость балки

Чтобы обеспечить прочность, долговечность и безопасность конструкции, необходимо выполнять вычисление величины прогиба балок еще на этапе проектирования сооружения. Поэтому крайне важно знать максимальный прогиб балки, формула которого поможет составить заключение о вероятности применения определенной строительной конструкции.

Использование расчетной схемы жесткости позволяет определить максимальные изменения геометрия детали. Расчет конструкции по опытным формулам не всегда эффективен. Рекомендуется использовать дополнительные коэффициенты, позволяющие добавить необходимый запас прочности. Не оставлять дополнительный запас прочности – одна из основных ошибок строительства, которая приводит к невозможности эксплуатации здания или даже тяжелым последствиям.

Существует два основных метода расчета прочности и жесткости:

1. Простой. При использовании данного метода применяется увеличительный коэффициент.
2. Точный. Данный метод включает в себя использование не только коэффициентов для запаса прочности, но и дополнительные вычисления пограничного состояния.

Последний метод является наиболее точным и достоверным, ведь именно он помогает определить, какую именно нагрузку сможет выдержать балка.

Расчет балок на прогиб

Расчет на жесткость

Для расчета прочности балки на изгиб применяется формула:

Где:

M – максимальный момент, который возникает в балке;

Wn,min – момент сопротивления сечения, который является табличной величиной или определяется отдельно для каждого вида профиля.

Ry является расчетным сопротивлением стали при изгибе. Зависит от вида стали.

γc представляет собой коэффициент условий работы, который является табличной величиной.

Расчет жесткости или величины прогиба балки является достаточно простым, поэтому расчеты может выполнить даже неопытный строитель. Однако для точного определения максимального прогиба необходимо выполнить следующие действия:

1. Составление расчетной схемы объекта.
2. Расчет размеров балки и ее сечения.
3. Вычисление максимальной нагрузки, которая воздействует на балку.
4. Определение точки приложения максимальной нагрузки.
5. Дополнительно балка может быть проверена на прочность по максимальному изгибающему моменту.
6. Вычисление значения жесткости или максимально прогиба балки.

Чтобы составить расчетную схему, потребуются такие данные:

• размеры балки, длину консолей и пролет между ними;
• размер и форму поперечного сечения;
• особенности нагрузки на конструкцию и точно ее приложения;
• материал и его свойства.

Если производится расчет двухопорной балки, то одна опора считается жесткой, а вторая – шарнирной.

Расчет моментов инерции и сопротивления сечения

Для выполнения расчетов жесткости потребуется значение момент инерции сечения (J) и момента сопротивления (W). Для расчета момента сопротивления сечения лучше всего воспользоваться формулой:

Важной характеристикой при определении момента инерции и сопротивления сечения является ориентация сечения в плоскости разреза. При увеличении момента инерции увеличивается и показатель жесткости.

Определение максимальной нагрузки и прогиба

Для точного определения прогиба балки, лучше всего применять данную формулу:

Где:

q является равномерно-распределенной нагрузкой;

E – модуль упругости, который является табличной величиной;

l – длина;

I – момент инерции сечения.

Чтобы рассчитать максимальную нагрузку, следует учитывать статические и периодические нагрузки. К примеру, если речь идет о двухэтажном сооружении, то на деревянную балку будет постоянно действовать нагрузка от ее веса, техники, людей.

Особенности расчета на прогиб

Расчет на прогиб проводится обязательно для любых перекрытий. Крайне важен точный расчет данного показателя при значительных внешних нагрузках. Сложные формулы в данном случае использовать необязательно. Если использовать соответствующие коэффициенты, то вычисления можно свести к простым схемам:

1. Стержень, который опирается на одну жесткую и одну шарнирную опору, и воспринимает сосредоточенную нагрузку.
2. Стержень, который опирается на жесткую и шарнирную опору, и при этом на него действует распределенное нагружение.
3. Варианты нагружения консольного стержня, который закреплен жестко.
4. Действие на конструкцию сложной нагрузки.

Применение этого метода вычисления прогиба позволяет не учитывать материал. Поэтому на расчеты не влияют значения его основных характеристик.

Пример подсчета прогиба

Чтобы понять процесс расчета жесткости балки и ее максимального прогиба, можно использовать простой пример проведения расчетов. Данный расчет проводится для балки с такими характеристиками:

• материал изготовления – древесина;
• плотность составляет 600 кг/м3;
• длина составляет 4 м;
• сечение материала составляет 150*200 мм;
• масса перекрывающих элементов составляет 60 кг/м²;
• максимальная нагрузка конструкции составляет 249 кг/м;
• упругость материала составляет 100 000 кгс/ м²;
• J равно 10 кг*м².

Для вычисления максимальной допустимой нагрузки учитывается вес балки, перекрытий и опор. Рекомендуется также учесть вес мебели, приборов, отделки, людей и других тяжелых вещей, который также будут оказывать воздействие на конструкцию. Для расчета потребуются такие данные:

• вес одного метра балки;
• вес м2 перекрытия;
• расстояние, которое оставляется между балками;
• временная нагрузка;
• нагрузка от перегородок на перекрытие.

Чтобы упросить расчет данного примера, можно принять массу перекрытия за 60 кг/м², нагрузку на каждое перекрытие за 250 кг/м², нагрузки на перегородки 75 кг/м², а вес метра балки равным 18 кг. При расстоянии между балками в 60 см, коэффициент k будет равен 0,6.

Если подставить все эти значения в формулу, то получится:

q = ( 60 + 250 + 75 ) * 0,6 + 18 = 249 кг/м.

Для расчета изгибающего момента следует воспользоваться формулой f = (5 / 384) * [(qn * L4) / (E * J)] £ [¦].

Подставив в нее данные, получается f = (5 / 384) * [(qn * L4) / (E * J)] = (5 / 384) * [(249 * 44) / (100 000 * 10)] = 0,13020833 * [(249 * 256) / (100 000 * 10)] = 0,13020833 * (6 3744 / 10 000 000) = 0,13020833 * 0,0000063744 = 0,00083 м = 0,83 см.

Именно это и является показателем прогиба при воздействии на балку максимальной нагрузки. Данные расчеты показывают, что при действии на нее максимальной нагрузки, она прогнется на 0,83 см. Если данный показатель меньше 1, то ее использование при указанных нагрузках допускается.

Использование таких вычислений является универсальным способом вычисления жесткости конструкции и величины их прогибания. Самостоятельно вычислить данные величины достаточно легко. Достаточно знать необходимые формулы, а также высчитать величины. Некоторые данные необходимо взять в таблице. При проведении вычислений крайне важно уделять внимание единицам измерения. Если в формуле величина стоит в метрах, то ее нужно перевести в такой вид. Такие простые ошибки могут сделать расчеты бесполезными. Для вычисления жесткости и максимального прогиба балки достаточно знать основные характеристики и размеры материала. Эти данные следует подставить в несколько простых формул.

viascio.ru

Расчет прогиба балки на двух опорах

Процесс проектирования современных строений и построек регулируется огромным количеством различных строительных норм и правил. В большинстве случаев нормы требуют обеспечения определенных характеристик, например, деформации или прогиба балок плит перекрытия под статической или динамической нагрузкой. Например, СНиП № 2.09.03-85 определяет для опор и эстакад прогиб балки не более чем в 1/150 длины пролета. Для чердачных перекрытий этот показатель составляет уже 1/200, а для межэтажных балок и того меньше – 1/250. Поэтому одним из обязательных этапов проектирования является выполнение расчета балки на прогиб.

Способы выполнить расчет и проверку на прогиб

Причина, по которой СНиПы устанавливают столь драконовские ограничения, проста и очевидна. Чем меньше деформация, тем больше запас прочности и гибкости конструкции. Для прогиба менее 0,5% несущий элемент, балка или плита все еще сохраняет упругие свойства, что гарантирует нормальное перераспределение усилий и сохранение целостности всей конструкции. С увеличением прогиба каркас здания прогибается, сопротивляется, но стоит, с выходом за пределы допустимой величины происходит разрыв связей, и конструкция лавинообразно теряет жесткость и несущую способность.

Просчитать прогиб конструкции можно несколькими способами:

• Воспользоваться программным онлайн-калькулятором, в котором «зашиты» стандартные условия, и не более того;
• Использовать готовые справочные данные для различных типов и видов балок, для различных опор схем нагрузок. Нужно только правильно идентифицировать тип и размер балки и определить искомый прогиб;
• Посчитать допустимый прогиб руками и своей головой, большинство проектировщиков так и делают, в то время как контролирующие архитектурные и строительные инспекции предпочитают второй способ расчета.

Измерив, насколько просела балка потолочного перекрытия, можно с 99% уверенностью определить, находится ли конструкция в аварийном состоянии или нет.

Методика выполнения расчета на прогиб

Прежде чем приступать к расчету, нужно будет вспомнить некоторые зависимости из теории сопротивления материалов и составить расчетную схему. В зависимости от того, насколько правильно выполнена схема и учтены условия нагружения, будет зависеть точность и правильность расчета.

Используем простейшую модель нагруженной балки, изображенной на схеме. Простейшей аналогией балки может быть деревянная линейка, фото.

В нашем случае балка:

1. Имеет прямоугольное сечение S=b*h, длина опирающейся части составляет L;
2. Линейка нагружена силой Q, проходящей через центр тяжести изгибаемой плоскости, в результате чего концы поворачиваются на небольшой угол θ, с прогибом относительно начального горизонтального положения, равным f;
3. Концы балки опираются шарнирно и свободно на неподвижных опорах, соответственно, не возникает горизонтальной составляющей реакции, и концы линейки могут перемещаться в произвольном направлении.

Для определения деформации тела под нагрузкой используют формулу модуля упругости, который определяется по соотношению Е=R/Δ, где Е – справочная величина, R— усилие, Δ— величина деформации тела.

Вычисляем моменты инерции и сил

Для нашего случая зависимость будет выглядеть так: Δ = Q/(S·Е). Для распределенной вдоль балки нагрузки q формула будет выглядеть так: Δ = q·h/(S·Е).

Далее следует наиболее принципиальный момент. Приведенная схема Юнга показывает прогиб балки или деформацию линейки так, если бы ее раздавливали под мощным прессом. В нашем случае балку изгибают, а значит, на концах линейки, относительно центра тяжести, приложены два изгибающих момента с разным знаком. Эпюра нагружения такой балки приведена ниже.

Чтобы преобразовать зависимость Юнга для изгибающего момента, необходимо обе части равенства умножить на плечо L. Получаем Δ*L = Q·L/(b·h·Е).

Если представить, что одна из опор жестко закреплена, а на второй будет приложен эквивалентный уравновешивающий момент сил Mmax = q*L*2/8, соответственно, величина деформации балки будет выражаться зависимостью Δх = M·х/((h/3)·b·(h/2)·Е). Величину b·h3/6 называют моментом инерции и обозначают W. В итоге получается Δх = M·х/(W·Е) основополагающая формула расчета балки на изгиб W=M/E через момент инерции и изгибающий момент.

Чтобы точно выполнить расчет прогиба, потребуется знать изгибающий момент и момент инерции. Величину первого можно посчитать, но конкретная формула для расчета балки на прогиб будет зависеть от условий контакта с опорами, на которых находится балка, и способа нагружения, соответственно для распределенной или концентрированной нагрузки. Изгибающий момент от распределенной нагрузки считается по формуле Mmax = q*L2/8. Приведенные формулы справедливы только для распределенной нагрузки. Для случая, когда давление на балку сконцентрировано в определенной точке и зачастую не совпадает с осью симметрии, формулу для расчета прогиба приходится выводить с помощью интегрального исчисления.

Момент инерции можно представить, как эквивалент сопротивления балки изгибающей нагрузке. Величину момента инерции для простой прямоугольной балки можно посчитать по несложной формуле W=b*h4/12, где b и h – размеры сечения балки.

Реальные сечения строительных конструкций могут иметь самые разные профили, от квадрата, круга до сложных двутавровых или швеллерных форм. При этом определение момента инерции и величины прогиба вручную, «на бумажке», для таких случаев становится нетривиальной задачей для непрофессионального строителя.

Формулы для практического использования

На практике чаще всего стоит обратная задача – определить запас прочности перекрытий или стен для конкретного случая по известной величине прогиба. В строительном деле очень сложно дать оценку запасу прочности иными, неразрушающими методами. Нередко по величине прогиба требуется выполнить расчет, оценить запас прочности здания и общее состояние несущих конструкций. Мало того, по выполненным измерениям определяют, является деформация допустимой, согласно расчету, или здание находится в аварийном состоянии.

Совет! В вопросе расчета предельного состояния балки по величине прогиба неоценимую услугу оказывают требования СНиПа. Устанавливая предел прогиба в относительной величине, например, 1/250, строительные нормы существенно облегчают определение аварийного состояния балки или плиты.

Например, если вы намерены покупать готовое здание, простоявшее достаточно долго на проблемном грунте, нелишним будет проверить состояние перекрытия по имеющемуся прогибу. Зная предельно допустимую норму прогиба и длину балки, можно безо всякого расчета оценить, насколько критическим является состояние строения.

Строительная инспекция при оценке прогиба и оценке несущей способности перекрытия идет более сложным путем:

• Первоначально измеряется геометрия плиты или балки, фиксируется величина прогиба;
• По измеренным параметрам определяется сортамент балки, далее по справочнику выбирается формула момента инерции;
• По прогибу и моменту инерции определяют момент силы, после чего, зная материал, можно выполнить расчет реальных напряжений в металлической, бетонной или деревянной балке.

Вопрос – почему так сложно, если прогиб можно получить, используя для расчета формулу для простой балки на шарнирных опорах f=5/24*R*L2/(E*h) под распределенным усилием. Достаточно знать длину пролета L, высоту профиля, расчетное сопротивление R и модуль упругости Е для конкретного материала перекрытия.

Ответ  прост — необходимо непросто рассчитать, но и сохранить на бумаге ход выполнения проверочного расчета, чтобы сделанные выводы о состоянии перекрытия можно было проверить и перепроверить по всем этапам проверки.

Совет! Используйте в своих расчетах существующие ведомственные сборники различных проектных организаций, в которых в сжатом виде сведены все необходимые формулы для определения и расчета предельного нагруженного состояния.

Заключение

Аналогичным образом поступает большинство разработчиков и проектантов серьезных построек. Программа – это хорошо, она помогает очень быстро выполнить расчет прогиба и основных параметров нагружения перекрытия, но важно также предоставить заказчику документальное подтверждение полученных результатов в виде конкретных последовательных расчетов на бумаге.

Что еще почитать по теме?

Сергей Новожилов - эксперт по кровельным материалам с 9-летним опытом практической работы в области инженерных решений в строительстве.

Facebook

Twitter

Вконтакте

Одноклассники

Google+

proroofer.ru

1.5. Пример расчета прокатной балки

1.5.1. Материалы для прокатной балки

Согласно табл. 50 [4] ригель многоэтажного промышленного здания относится ко второй группе конструкций. По табл. 53 [4] для конструкций второй группы может быть использована сталь марки С235.

Расчетное сопротивление для первой группы предельных состояний для фасонного проката при толщине полок от 11 до 20 мм Ry = 230 МПа. Модуль упругости для всех строительных сталей одинаковый Е = 2,1 ∙ 105 МПа.

1.5.2 Предварительный подбор сечения прокатной балки

Расчетная схема конструкции – разрезная балка (рис. ), загруженная равномерно распределенной нагрузкой от плит перекрытия.

Расчетный пролет балки при опирании ее на консоли колонн

lo = l – hcol – с/2 = 7,2 – 0,4 – 0,475/2 = 6,56 м

где l – шаг колонн в поперечном направлении;

hcol – размер поперечного сечения колонн;

0,04 – зазор на свободную укладку ригеля на консоли колонн.

Вычисляем расчетную нагрузку на 1м длины ригеля. Подсчет нагрузок на 1м2 перекрытия приведен в табл.1.

Ширина грузовой полосы, с которой нагрузка передается от плит на ригель, равна шагу колонн в продольном направлении здания 5,6 м.

Расчетные нагрузки на ригель для расчета по первой группе предельных состояний (табл.1):

– постоянная нагрузка

q = 4,5 ∙ 5,6 = 25,2 кН/м

– временная нагрузка

ν = 9,0 ∙ 5,6 = 50,4 кН/м

Итого, с учетом коэффициента надежности по назначению здания γn = 1,0:

– расчетная нагрузка для расчета по второй группе предельных состояний

q = (25,2 + 50,4) ∙ 1,0 = 75,6 кН/м

Расчетные усилия:

– изгибающий момент для расчетов по первой группе:

кН ∙ м

14

1.5.2.1. Расчет прочности ригеля.

Требуемый момент сопротивления

где γc = 1 – коэффициент условий работы металлических конструкций в промышленных зданиях [4, табл.6].

По сортаменту [1, приложение 10] подбираем требуемый номер двутавра (№55), Wх = 2035 см3 > Wmp = 1768 см3 , момент инерции Iх = 55962 см4, масса единицы длины прокатного двутавра – 926 Н/м.

1.5.2.2. Расчет ригеля по второй группе предельных состояний.

Расчётные нарузки на ригель для расчёта по второй группе предельных состояий:

Нагрузка от веса панели и пола 4,0 ∙ 5,6 =22,4 кН/м.

Нагрузка от собственного веса ригеля 0,926 кН/м.

- постоянная нагрузка gn =22,4 + 0,926 = 23,326 кН/м;

- временная нагрузка νn=7,5 · 5,6 = 42,0 кН/м.

q = (23,326 + 42,0)∙1 = 65,326кН/м.

Расчетный изгибающий момент для расчетов по второй группе:

Проверяем достаточность высоты подобранной балки по формуле 7.1 [6].

Для балок междуэтажных перекрытий отношение допустимого прогиба fu к пролету балки lо не должно превышать fu =

Следовательно, fu = 16,4 мм.

Расчетный прогиб балки в середине пролета будет равен

13,4 мм < 16,4мм

Следовательно, высота подобранной балки достаточна.

15

studfiles.net

Расчет балки онлайн

Для расчета балок первым делом необходимо определить усилия, возникающие в конструкциях. В данном разделе показано, как находить усилия, опорные реакции, прогибы и углы поворота в различных изгибаемых конструкциях. Для самых распространенных из них вы можете воспользоваться онлайн расчетом. Для редких - приведены все формулы определения необходимых значений.

Онлайн расчет балки на двух опорах (калькулятор).

Приведен расчет на момент, прогиб и опорные реакции от сосредоточенной и распределнной силы.

Синие ячейки - ввод данных. (Белые ячейки - ввод координаты для определения промежуточного итога).

Зеленые ячейки - расчетные, промежуточный итог.

Оранжевые ячейки -  максимальные значения.

>>> Перейти к расчету балки на двух опорах <<<

Онлайн расчет консольной балки (калькулятор).

Приведен расчет на момент, прогиб и опорные реакции от сосредоточенной и распределнной силы.

Синие ячейки - ввод данных. (Белые ячейки - ввод координаты для определения промежуточного итога).

Зеленые ячейки - расчетные, промежуточный итог.

Оранжевые ячейки -  максимальные значения.

>>> Перейти к расчету консольной балки <<<

Расчет однопролетной балки на двух шарнирных опорах.

Рис.1 Расчет балки на двух шарнирных опорах при одной сосредоточенной нагрузке

Рис.2 Расчет балки на двух шарнирных опорах при двух сосредоточенных нагрузках

Рис.3 Расчет балки на двух шарнирных опорах при одной равномерно-распределенной нагрузке

Рис4. Расчет балки на двух шарнирных опорах при одной неравномерно-распределенной нагрузке

Рис5. Расчет балки на двух шарнирных опорах при действии изгибающего момента

Расчет балок с жестким защемлением на двух опорах

Рис6. Расчет балки с жестким защемлением на опорах при одной сосредоточенной нагрузке

Рис7. Расчет балки с жестким защемлением на опорах при двух сосредоточенных нагрузках

Рис8. Расчет балки с жестким защемлением на опорах при одной равномерно-распределенной нагрузке

Рис9. Расчет балки с жестким защемлением на опорах при одной неравномерно-распределенной нагрузке

Рис10.Расчет балки с жестким защемлением на опорах при действии изгибающего момента

Расчет консольных балок

Рис11. Расчет однопролетной балки с жестким защемлением на одной опоре при одной сосредоточенной нагрузке

Рис12. Расчет однопролетной балки с жестким защемлением на одной опоре при одной равномерно-распределенной нагрузке

Рис13. Расчет однопролетной балки с жестким защемлением на одной опоре при одной неравномерно-распределенной нагрузке

Рис14. Расчет однопролетной балки с жестким защемлением на одной опоре при действии изгибающего момента

Расчет двухпролетных балок

Рис15. Расчет двухпролетной балки с шарнирными опорами при одной сосредоточенной нагрузке

Рис16. Расчет двухпролетной балки с шарнирными опорами при одной равномерно-распределенной нагрузке

Рис17. Расчет двухпролетной  балки с шарнирными опорами при одной неравномерно-распределенной нагрузке

stroit-prosto.ru

Расчет металлической балки на прогиб: учимся составлять формулы

В качестве примера, возьмем металлическую балку на двух опорах. Запишем для нее формулу для вычисления прогиба, посчитаем его численное значение. И также в конце этой статьи дам ссылки на другие полезные статьи с примерами определения прогибов для различных расчетных схем.

Что такое прогиб балки?

Под действием внешней нагрузки, поперечные сечения балки перемещаются вертикально (вверх или вниз), эти перемещения называются прогибами. Сопромат позволяет нам определить прогиб балки, зная ее геометрические параметры: длину, размеры поперечного сечения. И также нужно знать материал, из которого изготовлена балка (модуль упругости).

Кстати! Помимо вертикальных перемещений, поперечные сечения балки, поворачиваются на определенный угол. И эти величины также можно определить методом начальных параметров.

ν-прогиб сечения C; θ-угол поворота сечения C.

Прогибы балки необходимо рассчитывать, при расчете на жесткость. Расчётные значения прогибов не должны превышать допустимых значений. Если расчетное значение меньше, чем допустимое, то считают, что условие жесткости элемента конструкции соблюдается. Если же нет, то принимаются меры по повышению жесткости. Например, задаются другим материалом, у которого модуль упругости БОЛЬШЕ. Либо же меняют геометрические параметры балки, чаще всего, поперечное сечение. Например, если балка двутаврового профиля №12, не подходит по жесткости, принимают двутавр №14 и делают перерасчет. Если потребуется, повторяют подбор, до того момента пока не найдут тот самый – двутавр.

Метод начальных параметров

Метод начальных параметров, является довольно универсальным и простым методом. Используя этот метод можно записывать формулу для вычисления прогиба и угла поворота любого сечения балки постоянной жесткости (с одинаковым поперечным сечением по длине.)

Под начальными параметрами понимаются уже известные перемещения:

• в опорах прогибы равны нулю;
• в жесткой заделке прогиб и угол поворота сечения равен нулю.

Расчет прогибов балки

Посмотрим, как пользоваться методом начальных параметров на примере простой балки, которая загружена всевозможными типами нагрузок, чтобы максимально охватить все тонкости этого метода:

Реакции опор

Для расчета нужно знать все внешние нагрузки, действующие на балку, в том числе и реакции, возникающие в опорах.

Система координат

Далее вводим систему координат, с началом в левой части балки (точка А):

Распределенная нагрузка

Метод начальных параметров, который будем использовать чуть позднее, работает только в том случае, когда распределенная нагрузка доходит до крайнего правого сечения, наиболее удаленного от начала системы координат. Конкретно, в нашем случае, нагрузка обрывается и такая расчетная схема неприемлема для дальнейшего расчета.

Если бы нагрузка была приложена вот таким способом:

То можно было бы сразу приступать к расчету перемещений. Нам же потребуется использовать один хитрый прием – ввести дополнительные нагрузки, одна из которых будет продолжать действующую нагрузку q, другая будет компенсировать это искусственное продолжение. Таким образом, получим эквивалентную расчетную схему, которую уже можно использовать в расчете методом начальных параметров:

Вот, собственно, и все подготовительные этапы, которые нужно сделать перед расчетом.

Приступим непосредственно к самому расчету прогиба балки. Рассмотрим наиболее интересное сечение в середине пролета, очевидно, что это сечение прогнется больше всех и при расчете на жесткость такой балки, рассчитывалось бы именно это сечение. Обзовем его буквой – C:

Относительно системы координат записываем граничные условия. Учитывая способ закрепления балки, фиксируем, что прогибы в точках А и В равны нулю, причем важны расстояния от начала координат до опор:

\[ { V }_{ A }=0\quad при\quad x=0 \]

\[ { V }_{ B }=0\quad при\quad x=8м \]

Записываем уравнение метода начальных параметров для сечения C:

\[ E{ I }_{ z }{ V }_{ C }=… \]

Произведение жесткости балки EI и прогиба сечения C будет складываться из произведения EI и прогиба сечения в начале системы координат, то есть сечения A:

\[ E{ I }_{ z }{ V }_{ C }=E{ I }_{ z }{ V }_{ A }+ … \]

Напомню, E – это модуль упругости первого рода, зависящий от материала из которого изготовлена балка, I – это момент инерции, который зависит от формы и размеров поперечного сечения балки. Также учитывается угол поворота поперечного сечения в начале системы координат, причем угол поворота дополнительно умножается на расстояние от рассматриваемого сечения до начала координат:

\[ E{ I }_{ z }{ V }_{C }=E{ I }_{ z }{ V }_{ A }+E{ I }_{ z }{ \theta }_{ A }\cdot 4+… \]

Учет внешней нагрузки

И, наконец, нужно учесть внешнюю нагрузку, но только ту, которая находится левее рассматриваемого сечения C. Здесь есть несколько особенностей:

• Сосредоточенные силы и распределенные нагрузки, которые направленны вверх, то есть совпадают с направлением оси y, в уравнении записываются со знаком «плюс». Если они направленны наоборот, соответственно, со знаком «минус»:

• Моменты, направленные по часовой стрелке – положительные, против часовой стрелки – отрицательные:

• Все сосредоточенные моменты нужно умножать дробь:

\[ M\cdot \frac { { x }^{ 2 } }{ 2 } \]

• Все сосредоточенные силы нужно умножать дробь:

\[ F\cdot \frac { { x }^{ 3 } }{ 6 } \]

• Начало и конец распределенных нагрузок нужно умножать на дробь:

\[ q\cdot \frac { { x }^{ 4 } }{ 24 } \]

Откуда такие цифры и степени взялись? Все эти вещи вытекают при интегрировании дифференциального уравнения упругой линии балки, в методе начальных параметров все эти выводы опускаются, то есть он является как бы упрощенным и универсальным методом.

Формулы прогибов

С учетом всех вышеописанных правил запишем окончательное уравнение для сечения C:

\[ E{ I }_{ z }{ V }_{ C }=E{ I }_{ z }{ V }_{ A }+E{ I }_{ z }{ \theta }_{ A }\cdot 4+\frac { { R }_{ A }\cdot { 4 }^{ 3 } }{ 6 } -\frac { F\cdot { 4 }^{ 3 } }{ 6 } -\frac { q\cdot { 2 }^{ 4 } }{ 24 } \]

В этом уравнении содержится 2 неизвестные величины – искомый прогиб сечения C и угол поворота сечения A.

Поэтому, чтобы найти прогиб, составим второе уравнение для сечения B, из которого можно определить угол поворота сечения A. Заодно закрепим пройденный материал:

\[ E{ I }_{ z }{ V }_{ B }=E{ I }_{ z }{ V }_{ A }+E{ I }_{ z }{ \theta }_{ A }\cdot 8+\frac { { R }_{ A }\cdot { 8 }^{ 3 } }{ 6 } -\frac { F\cdot { 8 }^{ 3 } }{ 6 } -\frac { q\cdot 6^{ 4 } }{ 24 } +\frac { q\cdot 2^{ 4 } }{ 24 } =0 \]

Упрощаем уравнение:

\[ E{ I }_{ z }{ \theta }_{ A }\cdot 8+874.67=0 \]

Выражаем угол поворота:

\[ { \theta }_{ A }=-\frac { 874.67 }{ 8E{ I }_{ z } } =-\frac { 109.33кН{ м }^{ 2 } }{ E{ I }_{ z } } \]

Подставляем это значение в наше первое уравнение и находим искомое перемещение:

\[ E{ I }_{ z }{ V }_{ C }=\frac { -109.33\cdot 4E{ I }_{ z } }{ E{ I }_{ z } } +\frac { { R }_{ A }\cdot { 4 }^{ 3 } }{ 6 } -\frac { F\cdot { 4 }^{ 3 } }{ 6 } -\frac { q\cdot { 2 }^{ 4 } }{ 24 } =-\frac { 280кН{ м }^{ 3 } }{ E{ I }_{ z } } \]

Вычисление прогиба

Значение получили в общем виде, так как изначально не задавались тем, какое поперечное сечение имеет рассчитываемая балка. Представим, что металлическая балка имеет двутавровое поперечное сечение №30. Тогда:

\[ { V }_{ C }=-\frac { 280кН{ м }^{ 3 } }{ E{ I }_{ z } } =-\frac { 280\cdot { 10 }^{ 9 }Н\cdot { см }^{ 3 } }{ 2\cdot { 10 }^{ 7 }\frac { Н }{ { см }^{ 2 } } \cdot 7080{ см }^{ 4 } } =-2см \]

Таким образом, такая балка прогнется максимально на 2 см. Знак «минус» указывает на то, что сечение переместится вниз.

sopromats.ru

Расчет балок перекрытий | ЗАО «Техстройпроект»

Деревянные балки перекрытий

Деревянные балки перекрытий часто являются наиболее экономичным вариантом. Деревянные балки легки в изготовлении и монтаже, имеют низкую теплопроводность по сравнению со стальными или железобетонными балками. Недостатки деревянных балок — более низкая механическая прочность, требующая больших сечений, низкая пожаростойкость и устойчивость к поражению микроорганизмами и термитами (если они водятся в вашей местности). Поэтому, деревянные балки перекрытий требуется тщательно обрабатывать антисептиками и антипиренами, например ХМ-11 или ХМББ производства фирмы Антисептик (С-Петербург).

Как расчитать необходимое сечение деревянной балки перекрытий?

Оптимальный пролет для деревянных балок — 2,5- 4 метра. Лучшее сечение для деревянной балки — прямоугольное с соотношением высоты к ширине 1,4:1. В стену балки заводят не менее чем на 12 см и гидроизолируют по кругу, кроме торца. Желательно закрепить балку анкером, заделанным в стену.

При выборе сечения балки перекрытия учитывают нагрузку собственного веса, которая для балок междуэтажных перекрытий, как правило стоставляет 190-220 кг/м2, и нагрузку временную (эксплуатационную), её значение принимают равной 200 кг/м2. Балки перекрытия укладывают по короткому сечению пролёта. Шаг монтажа деревянных балок рекомендуется выбирать равным шагу установки стоек каркаса.

Для расчета минимального и оптимального сечения деревянной балки перекрытия можно воспользоваться он-лайн калькулятором Романова для деревянных балок перекрытий

Ниже приведены несколько таблиц, со значениями минимальных сечений деревянных балок для различных нагрузок и длинн пролетов:

Таблица сечений деревянных балок перекрытия в зависимости от пролёта и шага установки, при нагрузке 400кг/м2. — рекомендуется расчитывать именно на эту нагрузку

Если вы не используете утеплитель или не планируете нагружать перекрытия (например, перекрытие необитаемого чердака), то можно использовать таблицу для меньших значений нагрузок деревянных балок перекрытий:

Таблица минимальных сечений деревянных балок перекрытия в зависимости от пролёта и нагрузки, при нагрузках от 150 до 350 кг/м2.

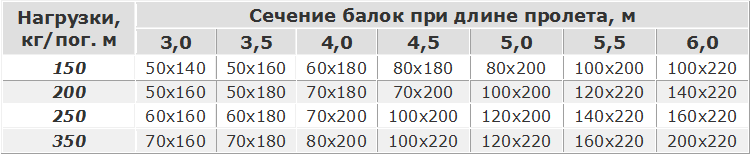
Если вы используете вместо балок прямоугольного сечения круглы бревна, можно пользоваться следующей таблицей:

Минимальный допустимый диаметр круглых бревен, используемых в качестве балок междуэтажных перекрытий в зависимости от пролета при нагрузке 400 кг на 1 м2

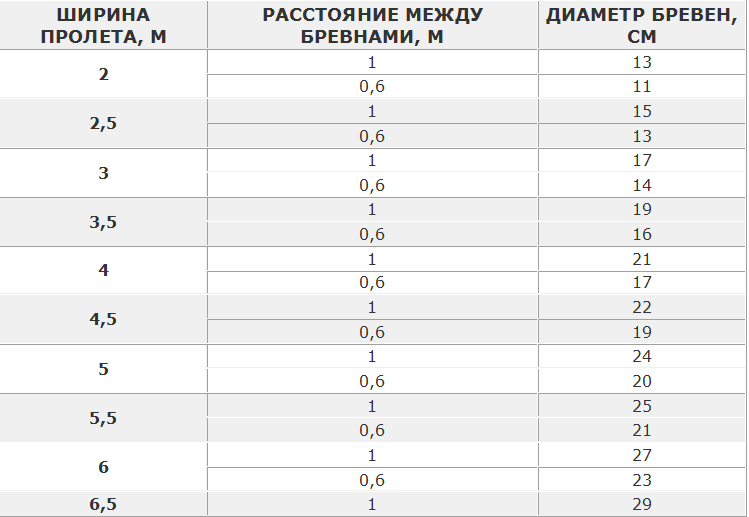
Если вы хотите перекрыть большие прогоны, то рекомендуем воспользоваться опытом с сайта Околоток.

Стальные (металлические) двутавровые балки перекрытий

Двутавровая металлическая балка перекрытий обладает рядом неоспоримых преимуществ, только при одном недостатке — высокой стоимости. Металлической двутавровой балкой можно перекрыть большие пролеты со значительной нагрузкой, металлическая стальная балка негорюча и устойчива к биологическим воздействиям. Однако, металлическая балка может корродировать при отсутствии защитного покрытия и наличия в помещении агрессивных сред.

Для расчета параметров двутавровой металлической балки можно воспользоваться хорошей программой расчета Beam

Вес одного метра двутавровой балки можно посмотреть в таблице веса двутавровых балок

В большинстве случаев в самодеятельном строительстве при расчетах в вышеуказанной программе или других ей подобных, следует считать, что металлическая балка имеет шарнирные опоры (то есть концы не фиксированы жестко — например, так как в каркасной стальной конструкции). Нагрузку на перекрытие со стальными двутавровыми металлическими балками с учетом собственного веса следует рассчитывать, как 350 (без стяжки) -500 (со стяжкой) кг/м2Шаг между двутавровыми металлическими балками рекомендуется делать равным 1 метру. В случае экономии возможно увеличение шага между металлическими балками до 1200 мм.

Таблица для выбора номера двутавровой металлической балки при различном шаге и длине прогонов

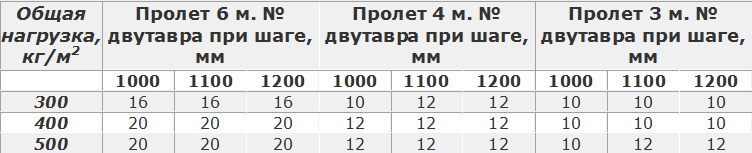
Железобетонные балки перекрытий

При устройстве железобетонных балок нужно использовать следующие правила (по Владимиру Романову):

1. Высота железобетонной балки должна быть не менее 1/20 длины проема. Делим длину проема на 20 и получаем минимальную высоту балки. Например при проеме в 4 м высота балки должна быть не менее 0,2 м.
2. Ширину балки рассчитывают исходя из соотношения 5 к 7 (5 — ширина, 7 — высота).
3. Армировать балку следует минимум 4 прутками арматуры d12-14 (снизу можно толще) — по два сверху и снизу. Таблицы соотношения длины и массы арматуры различного сечения.
4. Бетонировать за один раз, без перерывов, чтобы ранее уложенная порция раствора не успела схватиться до укладки новой порции. С бетономешалкой бетонировать балки сподручнее, чем заказывать миксер. Миксер хорош для быстрой заливки больших объемов.

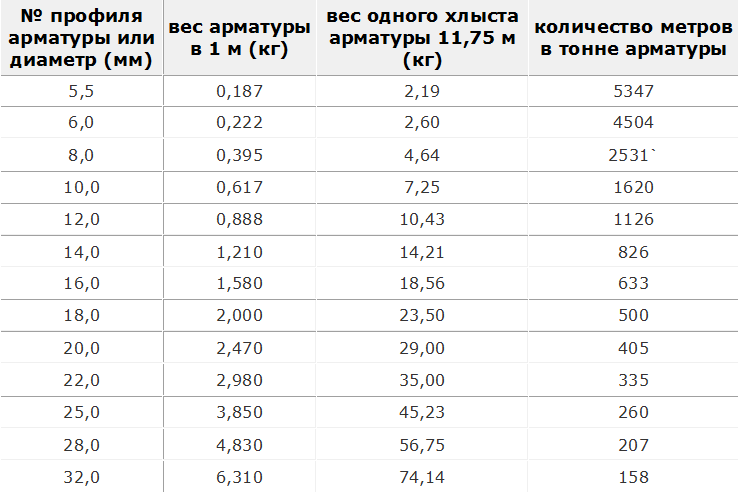
Вес строительной арматуры или сколько метров арматуры в тонне. Вес арматуры длиной 11,75 м. Вес арматуры диаметром от 5,5 до 32 мм. 

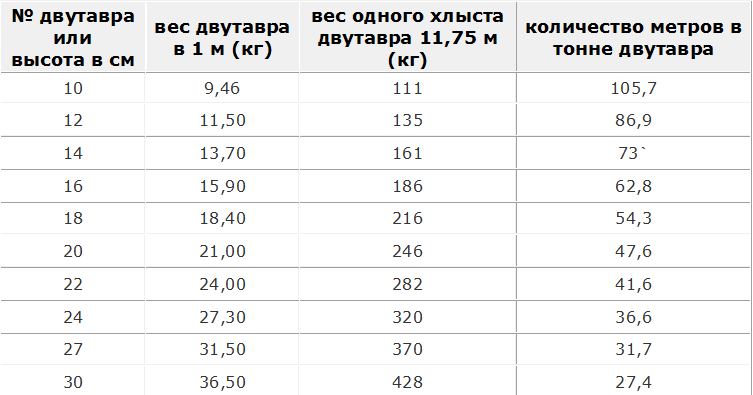
Вес двутавра и количество метров в тонне двутавра

Популярность: 19%

tsp76.ru

• 
  Угольник стальной
• 
  Швеллер из нержавеющей стали
• 
  Анодированная сталь
• 
  Класс прочности стали
• 
  Резка стали
• 
  Класс стали
• 
  Канат стальной гост 2688 80 характеристики
• 
  Стальные канаты
• 
  Труба гофрированная нержавеющая сталь
• 
  Вес стали и алюминия
• 
  Температура закалки и отпуска сталей таблица